Extreme sea levels in the Baltic Sea under climate change scenarios – Part 1: Model validation and sensitivity

We analyze extreme sea levels (ESLs) and related uncertainty in an ensemble of regional climate change scenarios for the Baltic Sea. The ERA-40 reanalysis and five Coupled Model Intercomparison Project phase 5 (CMIP5) global general circulation models (GCMs) have been dynamically downscaled with the coupled atmosphere–ice–ocean model RCA4-NEMO (Rossby Centre regional atmospheric model version 4 – Nucleus for European Modelling of the Ocean). The 100-year return levels along the Swedish coast in the ERA-40 hindcast are within the 95 % confidence limits of the observational estimates, except those on the west coast. The ensemble mean of the 100-year return levels averaged over the five GCMs shows biases of less than 10 cm. A series of sensitivity studies explores how the choice of different parameterizations, open boundary conditions and atmospheric forcing affects the estimates of 100-year return levels. A small ensemble of different regional climate models (RCMs) forced with ERA-40 shows the highest uncertainty in ESLs in the southwestern Baltic Sea and in the northeastern part of the Bothnian Bay. Some regions like the Skagerrak, Gulf of Finland and Gulf of Riga are sensitive to the choice of the RCM. A second ensemble of one RCM forced with different GCMs uncovers a lower sensitivity of ESLs against the variance introduced by different GCMs. The uncertainty in the estimates of 100-year return levels introduced by GCMs ranges from 20 to 40 cm at different stations and includes the estimates based on observations. It is of similar size to the 95 % confidence limits of 100-year return levels from tide gauge records.

1 Introduction

The coastal area of the Baltic Sea is home to around 15 million people. Sea level rise (SLR) and sea level extremes in the densely populated areas are an immediate concern to the public, to authorities and to other stakeholders. In Sweden, several thousand people live in areas that are at risk to be flooded during extreme storm surges (Perbeck, 2018). Fredriksson et al. (2017) have shown that the exposure to storm surges has increased, and if an event like the storm surge in November 1872 that flooded a number of cities in the southwestern Baltic Sea happened today, the impact would be greater than back in 1872.

Since the beginning of industrialization, the global warming trend has caused an accelerating global mean sea level (GMSL) rise (Church et al., 2013). These authors give an average of 3.2 mm a⁻¹ GMSL rise for the period of 1993 to 2009. The main contribution to GMSL rise has been from the expansion of the warming water in the global oceans. Meltwater from glaciers and ice sheets that increase the amount of water in the global ocean has contributed another one-third to the GMSL rise. To assess possible trajectories of climate change and related GMSL rise, the Coupled Model Intercomparison Project phase 5 (CMIP5) (Taylor et al., 2012) has coordinated an ensemble of model runs with GCMs. These models take into account, apart from natural forcing, Representative Concentration Pathways (RCPs) of how much extra warming is projected at the end of the 21st century (van Vuuren et al., 2011). This ensemble of global climate scenarios is extensively discussed in the Fifth Assessment Report (AR5) of the IPCC (Stocker et al., 2013). The GMSL rise in the year 2100 relative to the period of 1986 to 2005 ranges from 44 cm (RCP2.6) to 74 cm (RCP8.5), according to Church et al. (2013). The uncertainty for those estimates across the RCPs ranges from 28 cm (RCP2.6) to 98 cm (RCP8.5).

Today's estimates for the land uplift relative to the geoid range between −0.2 mm a⁻¹ for the German and Polish coasts up to 9 mm a⁻¹ at Höga Kusten (Jivall et al., 2016; Ågren and Svensson, 2011) in the Bothnian Bay. The land is still rising since the last ice age due to the glacial isostatic adjustment (GIA). At the end of the century, relative to the period of 1986 to 2005, the combined effects of GIA and GMSL rise are of the same order of magnitude. The median estimate of GMSL rise in the RCP8.5 scenario is canceled out on a line that divides the Bothnian Sea from the Baltic Proper. North of it, the GIA is dominating and mean sea level (MSL) relative to land is falling. In the Gulf of Finland, Gulf of Riga, Baltic Proper, Arkona Basin, Danish straits, Kattegat and Skagerrak, MSL is projected to rise relative to land. For other RCPs with less anthropogenic warming, the zero line of the combined effect would shift southeastwards. With the most recent estimates, including high-end and extreme scenarios (e.g., Sweet et al., 2017), GMSL rise could also reach 250 cm in the year 2100 in which case there will be sea level rise relative to land all around the Baltic Sea.

Another factor that determines the MSL of the Baltic Sea is related to the large-scale atmospheric circulation over the North Atlantic. Kauker and Meier (2003) have found a good correlation of the zonal wind component with the sea level at station Landsort. The sea level at Landsort is a good measure for the volume of water (or the averaged mean sea level) in the Baltic Sea (Matthäus and Franck, 1992). For the interannual variations, Andersson (2002) has shown that sea level variations in Stockholm correlate significantly with the North Atlantic Oscillation (NAO) index. For positive phases of the NAO, which are characterized by a more zonal and a stronger atmospheric circulation, the MSL of the Baltic Sea is expected to rise. According to AR5 (Stocker et al., 2013), the NAO is likely to become slightly more positive under projected climate change. That would translate to a possible rise of the MSL of the Baltic Sea. Recently, Karabil et al. (2018) found good correlation of interannual and decadal sea level variability in the Baltic Sea with the Baltic Sea and North Sea Oscillation (BANOS) index that reflects more closely the variability in geostrophic wind in the entrance region of the Baltic Sea.

It has long been known (Ekman, 2009) that the sea level in the Baltic Sea is highest during winter. Samuelsson and Stigebrandt (1996) have shown that, on the seasonal and shorter timescales, sea level variations in the Baltic Sea are caused by large-scale atmospheric circulation patterns. Together with a potential increase in positive NAO phases and a concurrent increase in the strength of low pressure systems (Schneidereit et al., 2007; Pinto et al., 2009), higher extreme sea levels (ESLs) in the Baltic Sea during winter must be anticipated. However, Meier (2006) has found that ESL may rise faster than MSL even without significant changes in the wind field in downscaled projections of the Baltic Sea.

Analyses of ESLs by Weisse et al. (2014) at specific locations along the European coast, including the Baltic Sea, have shown an increase in the past 100 years. Their projections show a continuing increase of ESLs, with MSL rise being the main contributor. They expect decadal variability to contribute to ESL changes in the near future. In their study, Vousdoukas et al. (2016) have projected ESLs for the entire coastline of Europe using the bias-corrected output of a shallow water model driven with an ensemble of eight CMIP5 models and two RCP scenarios. Both Vousdoukas et al. (2016) and Wahl et al. (2017) discuss the uncertainty of ESLs introduced by the method used to estimate the sea level with long return periods. Wahl et al. (2017) also set into relation the uncertainty of the methodology to the uncertainty introduced by SLR scenarios and conclude that, especially for the near future, the uncertainty from the choice of the method is dominating. While Wahl et al. (2017) present a global analysis, Eelsalu et al. (2014) has shown for the Estonian coast that no method for extreme value estimation was able to accommodate all observed and hindcast extremes, and that the spread among different methods can be substantial.

A number of modeling studies have focused on ESLs in the Baltic Sea. Meier et al. (2004) downscaled two SRESs (Special Report on Emission Scenarios) with two different GCMs. They found large uncertainties in ESLs both from the use of different GCMs and the use of different SLR scenarios. Kowalewski and Kowalewska-Kalkowska (2017) showed that, in general, modeled sea level variability in the Baltic Sea can be improved by an increase in resolution. Gräwe and Burchard (2012) used a high-resolution model for the western Baltic Sea and could show that the increased resolution (∼1 km) allowed the realistic simulation of extremes in the Danish straits. They also could show that MSL rise causes a non-linear response in sea level extremes by up to an order of 10 cm (O(10 cm)) in shallow and narrow locations in the western and southern Baltic Sea. Hieronymus et al. (2017) investigated the contribution of various forcing mechanisms on the sea level in the North Sea and Baltic Sea and showed that contributions from local wind forcing, atmospheric pressure, as well as remote sea level forcing are important for the Baltic sea levels, and that they interact in a non-linear way to increase the variability. They also showed that the influence of external sea level forcing on periods less than 50 d is damped inside the Baltic Sea.

The present study contributes with an ensemble of regional sea level projections that consistently combines global climate scenarios with their effects on regional SLR, climate and weather in the Baltic Sea region. We aim to identify and quantify different sources of uncertainty in ESLs in the Baltic Sea. This is important for how reliable information on ESLs can be distilled from observations and models under a changing climate. Our analysis is based on model simulations for the past and future climates. The model used in this study is a regional atmosphere–ice–ocean model that was used to downscale model solutions of the CMIP5 ensemble. In this study, we validate the modeled ESLs against estimates from tide gauge observations, address the model sensitivity and map the uncertainty introduced by GCMs. Projections of ESLs for the 21st century and their sources of uncertainty are discussed in a companion paper (Dieterich et al., 2019b).

One advantage of regional models versus global models is the higher resolution that can be used to resolve orography and bathymetry. The atmospheric and oceanic dynamics that interact with the regional features give rise to the specific characteristics of the region (e.g., Stein and Alpert, 1993; Feser et al., 2011; Jeworrek et al., 2017). To faithfully model sea level dynamics in the Baltic Sea, Kattegat and Skagerrak, a reasonable representation of the driving agents wind and pressure is a minimum requirement. The Rossby Centre regional atmospheric model version 4 (RCA4) has been shown to yield a good climate compared to observational data sets (Kjellström et al., 2016; Strandberg et al., 2014). Wind from a A1B scenario downscaled with RCA4-NEMO has been analyzed and compared to other RCM results by Ganske et al. (2016). They found low wind speeds in RCA4-NEMO for the highest (99th) percentile for the North Sea compared to other RCMs. Dieterich et al. (2013) have shown that the mean wind speed in RCA4-NEMO compares well with observations. Gröger et al. (2015) compared wind speed from RCA4-NEMO with corresponding values from an uncoupled run with RCA4. The largest improvements in wind speed in the coupled model were found in the winter season in regions where the Baltic Sea was covered with sea ice. In uncoupled RCA4 runs, the sea surface temperature (SST) is determined by the ocean component of global hindcast simulations that only coarsely resolves the Baltic Sea. This points to an added value of using a coupled model for modeling sea level in the Baltic Sea. That is especially true for ESLs that are caused by storms, predominantly in wintertime (Samuelsson and Stigebrandt, 1996) when air–sea interaction is underrepresented (Gröger et al., 2015).

The model is briefly described in Sect. 2. A validation with emphasis on ESLs is presented in Sect. 3. Section 4 discusses the sensitivity of the ESLs against changes in subgrid-scale parameterizations, open boundary conditions and atmospheric forcing. An attempt is made in Sect. 5 to map the uncertainty due to RCMs and the one introduced by GCMs. Finally, Sect. 6 discusses the results and identifies topics that need to be addressed for future progress in modeling ESLs in the Baltic Sea. Conclusions can be found at the end.

2 Model description

A coupled RCM was used to investigate mean and extreme sea levels and how they might change under scenario assumptions. The RCM is set up for the North Sea and Baltic Sea region and consists of an atmosphere component and an ocean component. The atmosphere model covers all of Europe as defined by the Coordinated Regional Climate Downscaling Experiment (CORDEX) and is used at the Swedish Meteorological and Hydrological Institute (SMHI) in different resolutions. The one used in the coupled version has a resolution of 0.22^∘ and 40 levels. The ocean component includes an ice model and resolves the North Sea and the Baltic Sea with 2 nautical miles and with 56 vertical levels. This coupled system is called RCA4-NEMO and has been introduced by Wang et al. (2015). The version used here for the scenario simulations is the one evaluated by Dieterich et al. (2013, 2019a) and Gröger et al. (2019) without the river routing model.

Other aspects of this model ensemble have been discussed previously: major Baltic inflow (Schimanke et al., 2014), air–sea coupling (Gröger et al., 2015), changes in wind speed and direction (Ganske et al., 2016), snow bands (Jeworrek et al., 2017), model intercomparison (Pätsch et al., 2017), changes in heat fluxes (Dieterich et al., 2019a) and changes in stratification (Gröger et al., 2019).

A regional model comes at the expense of having to formulate boundary conditions that allow information from the global atmosphere and the global ocean to enter the model domain. The treatment of the open boundaries follows the strategies laid out in Wang et al. (2015) and Dieterich et al. (2019a). The sea surface height (SSH) along the open boundaries of the ocean component determines the averaged SSH in the regional model domain. Together with the atmospheric forcing, the SSH information on the open boundaries also contributes to the sea surface variability on timescales from hours (Büchmann et al., 2011) to decades (Karabil et al., 2018).

To represent the tides in the regional model, 11 harmonic constituents from the global tidal model at Oregon State University (Egbert et al., 2010) are applied as open boundary conditions.

For sensitivity runs discussed in Sect. 4, the hourly SSH from a storm surge model covering the northeast Atlantic is added to the other components of the SSH on the open boundary. This vertically integrated model has a resolution of 0.44^∘ and is driven with wind stress and atmospheric pressure. It has been used at the SMHI for many years in combination with sea level forecasts.

The monthly SSH prescribed along the open boundaries is derived from the global solutions of ocean general circulation models (OGCMs) and transfers the information of seasonal, interannual and decadal SSH variability from the global to the regional scale. Details of the procedure are described in Dieterich et al. (2019a). The varying SSH of the OGCMs in the northern North Sea represents characteristics of the regional circulation. A high SSH along the European shelf might indicate a weakening North Atlantic Current in the global model (e.g., Saenko et al., 2017). This leads to different averaged SSHs in the regional model, which in turn might interact with sea level dynamics on a more local scale (e.g., Gräwe and Burchard, 2012; Pelling et al., 2013). The water level in the Kattegat and the Danish straits also has consequences for the ventilation and the ecosystem of the Baltic Sea (e.g., Hordoir et al., 2015; Arneborg, 2016; Meier et al., 2017).

In order to obtain an ensemble of sea level solutions for the present climate, we have downscaled the historical periods of a number of CMIP5 GCMs from 1961 to 2005 in addition to the ERA-40 reanalysis. The scenario part (2006 and onward) of these CMIP5 runs represents different RCPs. They have been downscaled too, and the ESLs in the Baltic Sea in these projections are discussed in a companion paper (Dieterich et al., 2019b).

Table 1 Ensemble of regional climate experiments for the North Sea and Baltic Sea region. The table lists the ERA-40 reanalysis and the historical periods of five CMIP5 GCMs that have been downscaled with RCA4-NEMO.

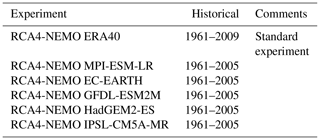
The RCA4-NEMO runs discussed in the next sections are summarized in Table 1. This small ensemble offers a first insight into the uncertainty that is generated due to different large-scale conditions represented by the GCMs.

(Hordoir et al., 2019)(Höglund et al., 2017)

Table 2 Sensitivity experiments with different RCMs forced with ERA-40. RCA4-NEMO-1hr ERA40 is the same setup as RCA4-NEMO ERA40 but the atmosphere and ice–ocean components are coupled every hour. RCA4-NEMO-alt is another coupled setup, where the ocean component is replaced by an alternative NEMO-Nordic setup. RCA4-NEMO-50km is a setup where the RCA4 is run at a resolution of 0.44^∘. NEMO-Nordic indicates the ocean component used in the regular RCA4-NEMO setup. Here, it is used as an ocean-only setup that has been forced with the output of RCA4 ERA40. NEMO-Nordic 3.6 ERA40 is the ocean-only setup validated by Hordoir et al. (2019). STORMWINDS ERA40 is an ocean-only setup for the Baltic Sea that has been used in the STORMWINDS project (Höglund et al., 2017).

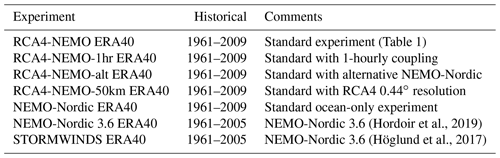
To set into relation the uncertainty that is inherent in the RCA4-NEMO ensemble forced with different GCMs, a second group of experiments is analyzed that uses one GCM but different RCMs. These experiments are listed in Table 2. The RCMs are not independent of each other but originate from different model setups that are used at the SMHI. The first five setups, except RCA4-NEMO-alt, use the same ocean component NEMO-Nordic. RCA4-NEMO-alt differs from the standard experiment (RCA4-NEMO ERA40) by using a different ocean component. Some of the relevant differences are lateral mixing along geopotential surfaces, instead of isopycnic ones. Also, the alternative NEMO-Nordic uses mixing coefficients according to Smagorinsky (1963). The bottom friction is larger and lateral walls impose a free-slip condition. The model setups RCA4-NEMO-1hr and RCA4-NEMO-50km differ from RCA4-NEMO by 1-hourly coupling and a 0.44^∘ resolution in RCA4, respectively. For more details on NEMO-Nordic 3.6, see Hordoir et al. (2019) and Höglund et al. (2017) for the model setup used in the STORMWINDS project.

A number of sensitivity experiments that go into more detail about the effect of different analysis periods, atmospheric forcing, open boundary conditions and miscellaneous model parameters are discussed in Sect. 4.

3 Model validation

3.1 Mean sea levels

The five different GCMs used for the regional downscaling exhibit different MSLs, where the regional model domain has its open boundaries. For this reason, the MSL averaged over the regional model domain varies between −20 and 160 cm among different ensemble members. To match observed MSLs in the Baltic Sea, the model results need to be adjusted using observed time series and estimates of their MSL. Here, we have used the estimated MSL at station Landsort for the year 1986 as a reference. It has been determined with a linear regression using long-term observations (Hammarklint, 2009). The model results for sea level are each corrected with a constant, so that the modeled MSL at Landsort in the period of 1970 to 1999 matches the estimated MSL from observations.

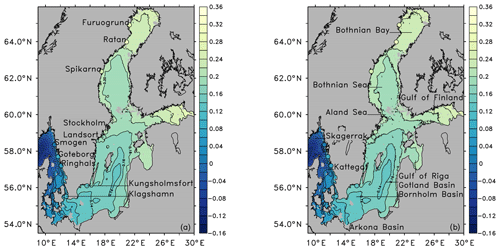
The modeled mean sea surface for the period of 1970 to 1999 is shown in Fig. 1. For comparison, the observed MSL for a number of stations is included. The increase of the mean sea surface from the Skagerrak to the Kattegat through the Baltic Proper into the Gulf of Finland and to the Bothnian Bay is clearly reproduced. The differences from observational estimates are within 5 cm (Table 3) for both the hindcast simulation and the ensemble mean of the historical period, except for station Ratan. There, the model underestimates the MSL by 7 cm. Meier et al. (2004) have shown a good correspondence of their model results with MSL estimates by Ekman and Mäkinen (1996). Compared to our model ensemble, Meier et al. (2004) apply observed SSH in the Kattegat as a boundary condition to their model. We speculate that this is the main reason for the somewhat larger discrepancy between our model results and observational estimates.

Figure 1 Mean sea level (m) for the period of 1970 to 1999 for the hindcast RCA4-NEMO ERA40 (a) and the ensemble mean of the GCMs listed in Table 1 (b). The colored dots indicate MSL estimated from long-term tide gauge observations (WISKI, 2017).

Table 3 Mean sea levels (cm) in the period of 1970 to 1999 for selected stations along the Swedish coast (see Fig. 1). The values in brackets indicate model biases relative to the observational estimates. Estimates from the observational network WISKI (2017) are based on a long-term regression at that station. Model results are the MSL at that station referenced to station Landsort.

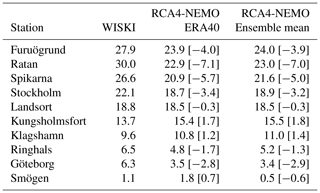
ESLs are measured against the mean sea surface and it is therefore important to get the mean sea surface right. A confirmation of a representative ensemble for sea level estimates is the fact that the mean sea surface of the ensemble mean differs only slightly from the one found in the hindcast simulation. The maximum differences between hindcast and ensemble mean are seen at station Spikarna with less than 1 cm.

Since the five different GCMs plus the ERA-40 reanalysis provide a range of distinct atmospheric conditions, it is unlikely that the atmospheric forcing is responsible for the biases seen in the modeled mean sea surface of the Baltic Sea. On the other hand, Meier et al. (2004) have shown in a sensitivity study that an increase of 30 % in wind speed does increase the MSL gradient along the Swedish coast from Smögen to Furuögrund by around 4 cm. That would bring the three northernmost stations in Table 3 closer to the estimated mean sea surface based on the tide gauge network. This could indicate that the model system used here generally produces low wind speeds at least when inferred from the mean sea surface of the Baltic Sea.

In a second sensitivity study, Meier et al. (2004) increased the river discharge to the Baltic Sea by 34 %. The pattern is different from the one caused by an increased wind speed and would fit with the data presented in Fig. 1 and Table 3 because the Baltic Proper would show a mean sea surface around 1 cm higher than the Kattegat and the Bothnian Bay. Our modeled mean sea surface with positive biases in the Baltic Proper suggests that the model system has a fresh bias, which has been found by Dieterich et al. (2013, 2019a) as well.

3.2 Extreme sea levels

To calculate return levels, we have selected the most extreme sea levels for each season, starting in July and ending in June. These values represent the tail of the distribution for a certain time period and are fitted against theoretical distributions with known parameters. Those distributions are then used to estimate return levels with corresponding return periods. An investigation on ESLs along the Swedish coast by Södling and Nerheim (2017) has shown that return levels in the region are best estimated using a generalized extreme value (GEV) distribution with the blockmaxima method. Using the same technique, the different model runs have been analyzed to produce return sea levels for different return periods at the sea level stations operated by the SMHI. These are listed in Table 4, together with the values estimated from observations by Södling and Nerheim (2017), including the tides.

ESLs with associated return periods are a way to characterize the most extreme events. A return level with a return period of 100 years occurs on average once in 100 years. Its probability is 1/100 in any one year. There are different protection standards that depend on the acceptable risk of being flooded and the corresponding consequences and range from return periods of 100 to 10 000 years (Van der Meer et al., 2018).

Table 4 Extreme sea levels (cm) using a GEV distribution with the blockmaxima method. The first line is reproduced from Södling and Nerheim (2017, Table 5.3); the second line is from RCA4-NEMO ERA40 (1961 to 2005); the third line is from NEMO-Nordic 3.6 ERA40 (1961 to 2005). The values in brackets indicate the 95 % confidence interval.

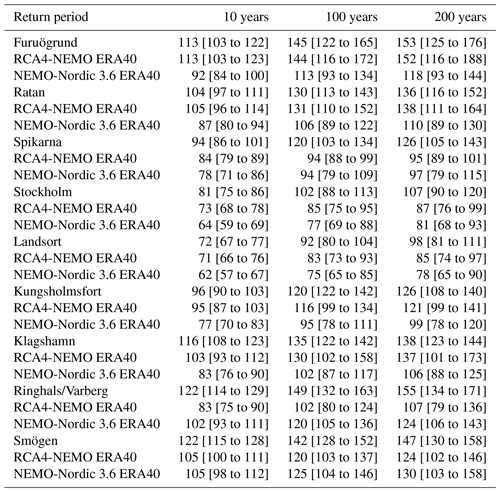
The table contains the estimates from the ERA-40 hindcast with the coupled model RCA4-NEMO in the second lines. In the northern Baltic Sea, the agreement between RCA4-NEMO ERA40 results and the observational estimates is good. In the central Baltic Sea, the model underestimates return levels. In the southern Baltic Sea, the agreement is good. On the west coast of Sweden, the largest differences are found between model and observational estimates.

The third lines in Table 4 show return levels estimated from an ocean-only model that has been driven with a downscaled ERA-40 reanalysis. Except for the west coast, the model setup NEMO-Nordic 3.6 ERA40 produces lower return levels than the coupled model RCA4-NEMO ERA40.

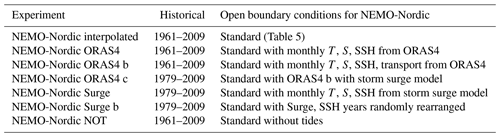
Figure 2 shows a comparison of ESLs from seven different model configurations (Table 2) with corresponding estimates from the tide gauge network. Generally, the model estimates of the 100-year return levels are lower than those from the observations. The same is true for the 20-year return levels (not shown). In the Bothnian Bay (Furuögrund and Ratan) and in the southern Baltic Sea (Kungsholmsfort and Klagshamn), the model estimates from the coupled model (RCA4-NEMO ERA40) are within the confidence limits of the observational estimates. In the central Baltic Sea (Stockholm and Landsort), all models estimate somewhat lower return levels than the observations would suggest. On the west coast (Göteborg and Smögen), none of the model setups reproduce the 100-year return levels. Since some model configurations include a storm surge model in the formulation of the open boundary conditions, the cause for the underestimation of ESLs lies probably either in the atmospheric forcing or the unresolved effects in the ocean, due to an insufficient (2 nautical miles) resolution. At those stations where the coupled model matches the estimates derived from observations, the ESLs are to a large degree determined by atmospheric forcing. The different treatment of the air–sea interaction between a coupled atmosphere–ocean model and an ocean-only model would explain most of the discrepancy. Among the coupled model runs, the one with a reduced atmospheric resolution is clearly an outlier. It shows that all along the Swedish coast good atmospheric information is essential to estimate ESLs. The exception is station Smögen, where the storm surges are generated further west under open ocean conditions, and an atmospheric resolution of 50 km produces a surge of roughly the same height as a resolution of 25 km. The next section discusses the sensitivity of the ESLs and addresses some of the issues identified here.

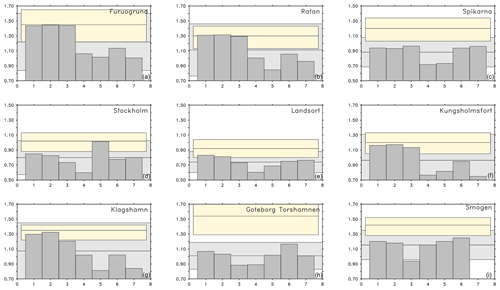
Figure 2 Sensitivity of ESLs using different RCMs. Extreme sea levels (m) with 100-year return period for nine stations along the Swedish coast: Furuögrund (a), Ratan (b), Spikarna (c), Stockholm (d), Landsort (e), Kungsholmsfort (f), Klagshamn (g), Göteborg (h), Smögen (i). The different realizations have been estimated using different model setups: RCA4-NEMO ERA40 (1), RCA4-NEMO-1h (2), RCA4-NEMO-alt (3), RCA4-NEMO-50km (4), NEMO-Nordic (5), NEMO-Nordic 3.6 (6), STORMWINDS (7). The different experiments are summarized in Table 2. The horizontal lines represent the mean of the different estimates. The lightly shaded area around it shows 1.96 times the ensemble dispersion. The estimates from the tide gauge network by Södling and Nerheim (2017) with the 95 % confidence intervals are drawn as colored areas.

4 Model sensitivity

The light gray shading in Fig. 2 is the spread among the solutions of different RCMs. All RCMs have been driven with the same atmospheric reanalysis. The spread in the model solutions can be explained by how air–sea interaction is implemented in different model setups and from the use of different formulations of subgrid-scale processes. Comparing it with the colored shading shows that, overall, the RCMs disagree more than the confidence limit of the GEV estimation. This is true, however, only for the mixed ensemble of coupled and uncoupled RCMs. Clearly, the two groups are clustered and the ensemble is not normally distributed. The uncertainty within the first three coupled RCMs and the three uncoupled RCMs in Table 2 and Fig. 2 is much smaller.

ESLs in the Baltic Sea are sensitive to details of how physics and dynamics are implemented in the numerical model. It is well known that bottom friction has a major impact on the amplitude and phase of sea level variations (Gräwe and Burchard, 2012). In this section, a series of sensitivity runs is presented that is set up to explore how ESLs depend on different aspects of model implementation and forcing.

4.1 Decadal variability

From the relatively small spread of O(20 cm) among the estimates in Figs. 3 and S1 in the Supplement, it can be concluded that the ESLs are not very sensitive against the choice of different long-term (30 years or longer) analysis intervals, with the exception of station Klagshamn. This might be true, however, only for return periods shorter than 100 years. The estimates differ most between the two mutually exclusive 25-year periods for the first and second halves of the 50-year model run (Fig. S1). In the Bothnian Bay and in the Kattegat, the extremes are higher in the first half. In the Baltic Proper, the extremes are higher in the second half. The same tendency, although smaller, is seen between other periods that cover the first and second halves of the historical period. The case of the two 25-year periods can be interpreted as the point where the length of the analysis period became too short to yield a robust estimate of a 100-year return level. At the most sensitive station (Klagshamn), at least 40 years are necessary for a robust estimate. ESLs in the northern Baltic Sea seem to be more affected by different choices of analysis periods compared to the Baltic Proper. That might have to do with the ice cover, which is known to be sensitive to decadal variability (Jevrejeva et al., 2003). During positive phases of NAO, the Baltic Sea tends to experience mild winters with less ice cover (Omstedt and Chen, 2001), together with stronger westerlies. This situation promotes the momentum transfer from the atmosphere to the ocean and the generation of storm surges.

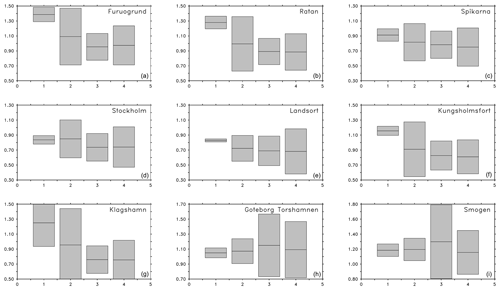
Figure 3 Sensitivity of ESLs using different sets of experiments. Extreme sea levels (m) with 100-year return period for the same stations as in Fig. 2. The different sets of experiments are decadal variability (1), atmospheric forcing (2), open boundary conditions (3) and model parameters (4). The horizontal line represents the mean of the different estimates and the lightly shaded area around it is the 95 % confidence interval.

4.2 Atmospheric forcing

Different RCMs have been forced with different reanalysis data sets and Table 5 gives an overview of these sensitivity experiments. Differences between the different RCMs may be larger than differences between different atmospheric forcing data sets. That should be kept in mind when interpreting the results. NEMO-Nordic ERA-Interim uses the ERA-Interim reanalysis instead of the ERA-40 reanalysis. Usually, the atmospheric forcing like wind, pressure and so on is available every 3 h. Either these fields are kept constant or they are linearly interpolated. In a sensitivity run, NEMO-Nordic forcing fields are linearly interpolated in time, and the ocean model experiences a smooth change in the forcing variables. The model setup NEMO-Nordic 3.6 has been driven with two different atmospheric reanalyses. The EURO4M reanalysis uses an atmosphere model with a higher resolution and has been shown to improve on results of the ERA-40 reanalysis (Dahlgren et al., 2016). The reference setup (RCA4-NEMO ERA40) may be compared with a setup like RCA4-NEMO-1hr ERA40, where the atmosphere and ice–ocean components exchange fluxes and surface temperatures every hour. This sensitivity study may answer the question of whether a more frequent coupling than 3-hourly is necessary.

Table 5 Sensitivity experiments with different atmospheric forcing for different RCMs. RCA4-NEMO-1hr ERA40 is the same setup as RCA4-NEMO ERA40 but the atmosphere and ice–ocean components are coupled every hour. NEMO-Nordic ERA40 and NEMO-Nordic ERA-Interim are two ocean-only setups forced with the output of RCA4 ERA40 and RCA4 ERA-Interim, respectively. NEMO-Nordic interpolated is the same setup as NEMO-Nordic ERA40 but with linearly interpolated forcing (see text for more details). NEMO-Nordic 3.6 ERA40 and NEMO-Nordic 3.6 EURO4M (Hordoir et al., 2019) are two of the ocean-only setups forced with ERA-40 and EURO4M, respectively.

The influence of atmospheric forcing on ESLs is shown in Fig. S2, and the overall effect on the spread in the solutions is seen in Fig. 3. What can be deduced from Fig. S2 is that the sensitivity of ESLs at station Smögen depends on whether the ERA-40 or the ERA-Interim reanalysis has been used to force the ocean model. Other differences, even between different model setups, have a minor (O(10 cm)) impact. At the stations in the Bothnian Bay and Bothnian Sea, ESLs turn out differently depending on whether the ERA-40 or the EURO4M reanalysis has been used as forcing. Together with the EURO4M experiment, the two coupled runs show similar 100-year return levels in the Bothnian Bay, which are all much more realistic than those from the other experiments. In the Bothnian Bay, at least a part of this difference needs to be attributed to the higher wind speeds found in the EURO4M data set (Dahlgren et al., 2016) and the coupled experiments (Gröger et al., 2015). The experiment NEMO-Nordic interpolated confirms that with lower return levels compared to the regular experiment (NEMO-Nordic ERA40), where the forcing was not interpolated between time steps. In the latter case, the stepwise forcing includes higher harmonics that generate high-frequency gravity waves that add to the sea level extremes. As can be seen from Fig. S2, ESLs at Stockholm are O(40 cm) higher if high-frequency noise is present in the forcing. On the other hand, the 1-hourly coupling in RCA4-NEMO-1hr ERA40 compared to its reference run (RCA4-NEMO ERA40) does not generate different return levels. The hypothesis here could have been that a more frequent update of the atmospheric forcing would improve the sea level simulation. Apparently, it is sufficient for this model setup to update the path of the storms that generate sea level extremes every 3 h. The stations Kungsholmsfort and Klagshamn are very sensitive to the choice of the atmospheric forcing. Overall, Fig. 3 shows that stations in the northern and southern Baltic Sea are most sensitive to atmospheric forcing. Compared to other sensitivity studies, the atmospheric forcing plays a less important role in the central Baltic and on the Swedish west coast.

4.3 Open boundary conditions

The need to formulate open boundary conditions at the boundary of the computational domain of the model introduces an additional model sensitivity. To look into the effects of what type of information is available at the open boundary of the model domain, a number of sensitivity runs (see Table 6) were performed. The regular open boundary that is used in the ensemble of scenarios discussed in Sect. 2 provides monthly mean temperature, salinity and sea surface height.

Table 6 Sensitivity runs forced with RCA4 ERA40. The runs differ from each other by the open boundary conditions that have been applied at the open boundaries of NEMO-Nordic. All runs in this table are ocean-only experiments. These sensitivity runs have been described in more detail in Dieterich et al. (2019a). ORAS4 stands for Operational Ocean Reanalysis System 4 and has been evaluated by Balmaseda et al. (2013).

The experiments ORAS4, ORAS4 b and ORAS4 c resolve the conditions in the northern North Sea with a monthly resolution. Monthly mean temperature, salinity and sea surface height from the Ocean Reanalysis System 4 (ORAS4) (Balmaseda et al., 2013) are applied at the open boundaries. That introduces low-frequency variability in the open boundaries of the ocean model, like the NAO. The experiments ORAS4 c, Surge and Surge b add hourly SSH from a storm surge model to the ocean model. This technique adds high-frequency SSH variability that has been generated in the northeast Atlantic and traveled to the open boundary of the ocean model. The experiment NEMO-Nordic NOT is set up to check the influence of tidal forcing on ESLs in the Baltic Sea.

At all stations (Fig. S3), the effect of an additional storm surge model (experiments ORAS4 c, Surge, Surge b) is visible in the ESL estimates. Generally, ESLs are higher by O(20 cm) with the additional information on the barotropic answer of the northeast Atlantic to atmospheric disturbances. The largest effect is seen at stations Göteborg and Smögen, with 100-year return levels O(40 cm) higher than without storm surges generated and imported from the northeast Atlantic. The difference between ESLs from the experiments ORAS4 c, Surge, Surge b is small. The presence of hourly sea level variability, even in the case it is out of phase with the atmospheric forcing (Surge b), provides nearly the same increase in ESLs as the deterministically driven model (Surge). On the contrary, tidal forcing on the open boundaries does not affect the 100-year return levels in the Baltic Sea. Only on the west coast is there a significant contribution of O(30 cm) to the extremes compared to the model setup NOT. The use of temporally resolved temperature, salinity and SSH on the open boundaries in experiments ORAS4 and ORAS4 b leads to somewhat higher 100-year return levels. In the Baltic Sea, the effect is probably related to the NAO that is resolved in the open boundary conditions. At station Smögen, an interaction of sea level dynamics with a higher recirculation in the Skagerrak in ORAS4 and specially in ORAS4 b might add to the difference of O(10 cm). What is interesting to note comparing experiments ORAS4, ORAS4 c and Surge is the vanishing influence of the long timescales in the open boundary conditions (ORAS4 c and Surge) as soon as there is high-frequency information provided on the open boundaries. Figure 3 summarizes the influence of the open boundary conditions on the 100-year return levels. In the Baltic Sea, other aspects of model formulations give a higher spread of model solutions than open boundary conditions. On the west coast, the open boundary conditions have the highest impact on the solutions.

4.4 Model parameters

Table 7 Sensitivity runs that use different model parameters, parameterizations, mean sea level and river discharge. All runs in this table are ocean-only experiments. The sensitivity run NEMO-Nordic viscous uses constant lateral viscosity, while NEMO-Nordic no-slip uses coefficients according to Smagorinsky (1963). NEMO-Nordic free-slip differs by the slip conditions along lateral walls compared to NEMO-Nordic no-slip. In NEMO-Nordic MSL, the MSL is 58 cm higher compared to NEMO-Nordic interpolated (see Table 5). NEMO-Nordic E-HYPE and NEMO-Nordic discharge differ by the river discharge, which is O(1500 m³ a⁻¹) higher in NEMO-Nordic E-HYPE and which is used in all other experiments.

Table 7 lists sensitivity studies where miscellaneous model parameters and different parameterizations have been varied to estimate their influence on ESLs in the Baltic Sea. Figure 3 shows that the choice of model parameterization and parameters causes the model solutions to vary by O(50 cm).

NEMO-Nordic viscous employs constant lateral viscosity with a harmonic operator, while NEMO-Nordic no-slip uses viscosity coefficients that are large where the velocity field shows a large shear (Smagorinsky, 1963). In the case of NEMO-Nordic no-slip, the selective viscosity prevents the degradation of gradients near the coast, where the ESLs are measured, and leads to much higher ESLs (Fig. S4). Different stations show different sensitivity between O(10 cm) and O(40 cm).

The experiment NEMO-Nordic free-slip can be compared to NEMO-Nordic no-slip. Constant lateral viscosity and no-slip conditions are the standard for all experiments. The impact on ESLs can be quite large O(25 cm). Presumably, the nearshore ESLs interact with the near-surface velocity field, which is more distorted in the no-slip case, and lead to higher ESLs. However, there is also the opposite effect in a different model setup (not shown). There, the no-slip conditions lead to O(20 cm) lower ESLs in the Baltic Sea compared to the same model with free-slip conditions.

This situation shows the difficulty and limitation of these sensitivity studies. The ESLs do not depend on different model parameters in a simple way. Depending on where in the parameter space resulting ESLs are compared, this can lead to opposite conclusions.

The experiment NEMO-Nordic MSL has a higher MSL (58 cm) than NEMO-Nordic interpolated. At none of the stations shown in Fig. S4 is there a marked effect on ESLs due to differing MSLs. This is in agreement with a study by Hieronymus et al. (2018), where the parameters of the GEV used to estimate ESLs do not change with MSL. A small effect can be seen at station Smögen, where ESLs are higher with a lower MSL. This is in accordance with the theory where shallower regions exhibit higher sea level signals (Pelling et al., 2013).

The last two experiments (NEMO-Nordic E-HYPE and NEMO-Nordic discharge) in Fig. S4 show the sensitivity of ESLs against the river discharge. The former model run uses the standard discharge as any other experiment, while experiment NEMO-Nordic discharge uses the river discharge that was used by Meier et al. (2004). NEMO-Nordic E-HYPE with a higher O(1500 m³ a⁻¹) freshwater input than NEMO-Nordic discharge shows a minor increase of ESLs in the Bothnian Bay. The freshwater signal is also visible in the MSL, which is 2 mm lower in the Bothnian Bay and 0.2 mm lower in the Baltic Proper. Since the spatial and temporal changes of the river discharge are different in the two experiments, the effect of the higher freshwater input in NEMO-Nordic E-HYPE is masked by other processes. The integrated effect of the higher freshwater input in NEMO-Nordic E-HYPE can be observed on the west coast of Sweden. The ESLs are higher in this sensitivity run, where the zonal and vertical gradients in salinity and meridional velocity in the Baltic Sea outflow are larger. The changes in the freshwater distribution on the eastern side of the Kattegat also lead to changes in sea ice cover and wind stress. The interactions of storm surges with the background fields give rise to an increase in ESLs at stations Göteborg and Smögen.

As an overview, Fig. 2 shows ESLs from seven different model configurations. Not all stations show the same sensitivity. At stations Furuögrund and Ratan, the coupled models with an atmospheric resolution of 0.22^∘ show much higher extremes than the uncoupled models. In this case, all models were driven with the ERA-40 hindcast. The coupled models translate the atmospheric momentum more efficiently into ESLs, compared to ocean-only models that employ a bulk formula to calculate wind stress. Additionally, a different sea ice cover in the coupled and uncoupled models might explain differences in the Bothnian Bay. Also, at stations Kungsholmsfort and Klagshamn, the first three models show more realistic ESLs. Uncoupled models generally produce too-low ESLs, and all models fail to reproduce ESLs as high as those estimated from observations on the Swedish west coast. At station Smögen, ESLs are much less sensitive to the choice of the model system, according to the sensitivity study presented in Fig. 2.

5 Model uncertainty

In this section, the GCM uncertainty is compared to uncertainty that comes with the RCM. With RCM uncertainty, we mean the range of solutions for ESLs that arise from the use of different model formulations or choice of parameters, as shown in Fig. 2.

5.1 100-year return levels

In Fig. 4, the 100-year return levels for the five historical periods at nine sea level stations along the Swedish coast are compared to the results from the downscaled hindcast (RCA4-NEMO ERA40) and to observational estimates. One argument to use an ensemble of model runs is to gain insight into the spread of possible solutions. Additionally, for a meaningful ensemble, the ensemble mean should be better than individual model members. In this figure, it becomes apparent that the ensemble mean is closer to the estimates from the tide gauge network at all stations compared to individual model runs. Even though none of the historical model runs could have been compared to observations directly, Fig. 4 shows that the statistics of ESLs are realistic. As in Fig. 2, there are stations where the modeled 100-year return levels are underestimated. Except for stations Göteborg and Smögen, the ensemble means of 100-year return levels are within the 95 % confidence limits of the observational estimates. It is therefore not wrong to assume that the ensemble-averaged ESLs are from the same distribution as the ones estimated from observations.

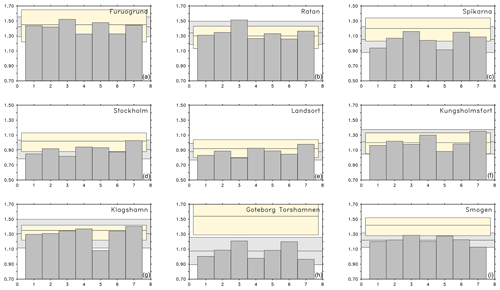
Figure 4 Extreme sea levels (m) with 100-year return period for nine stations along the Swedish coast: Furuögrund (a), Ratan (b), Spikarna (c), Stockholm (d), Landsort (e), Kungsholmsfort (f), Klagshamn (g), Göteborg (h), Smögen (i). The different realizations have been estimated from RCA4-NEMO ERA40 (1), RCA4-NEMO ensemble mean HISTORICAL (2), RCA4-NEMO MPI-ESM-LR HISTORICAL (3), RCA4-NEMO EC-EARTH HISTORICAL (4), RCA4-NEMO GFDL-ESM2M HISTORICAL (5), RCA4-NEMO HadGEM2-ES HISTORICAL (6), RCA4-NEMO IPSL-CM5A-MR HISTORICAL (7) (see Table 1). The horizontal lines and shaded areas are as in Fig. 2. All model estimates are based on the common historical period of 1961 to 2005.

The confidence limits for the 100-year return levels in Fig. 4 are based on how well the theoretical distributions can be approximated by the sampled ones. In the end, it is a matter of how long the available time series are to estimate return levels. Long time series are rare and are usually available from a few stations only. So, natural variability tends to be underrepresented in observed time series. Another way to produce a measure of uncertainty is the use of a model ensemble. It allows to estimate the spread or the dispersion of the ensemble for the whole model domain. There is still the need for reasonably long time series but the uncertainty in the ensemble can be reduced by increasing the number of ensemble members. The question is then how the spread in the ensemble is related to the confidence limits of the return levels estimated by the blockmaxima method with the GEV distribution.

Figure 4 shows that 1.96 times the ensemble dispersion is larger than the 95 % confidence limits for the GEV estimates for four stations. In the Baltic Proper and on the west coast, the two measures are comparable. These are also the stations that are least sensitive to model formulation (Fig. 2) and atmospheric forcing (Fig. S2). At other stations, the uncertainty in the ensemble could be reduced by increasing the number of ensemble members.

5.2 The 99.9th percentile sea levels

To be able to map the ESLs and their uncertainty for the whole Baltic Sea, we turn to somewhat less extreme sea levels than the 100-year return levels. Figure 5 compares the warning levels used by the SMHI (Table 8) to the mean of the uppermost 99.9 % of sea levels within the time period of 1970 to 1999.

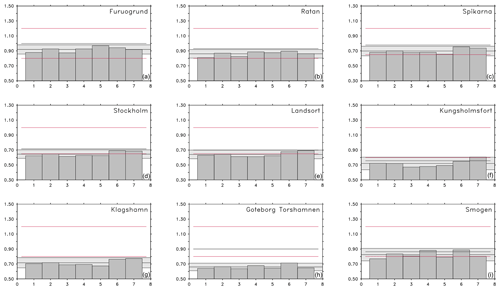
Figure 5 Mean 99.9th percentile of ESLs (m) for the same stations and the same realizations as in Fig. 4. The red lines represent SMHI's warning level 1 and warning level 2, respectively. The black line is the 99.9th percentile of the observations. All estimates are based on the common historical period of 1970 to 1999.

The individual estimates for the mean 99.9th percentile of ESLs (Fig. 5) agree very well with each other. Overall, 95 % of all values are within no more than O(15 cm). This is the estimate of GCM uncertainty based on the 99.9th percentile. It is much lower than the 20 to 40 cm disagreement among the 100-year return levels in different GCMs (Fig. 4). The uncertainty estimates based on the 99.9th percentile are therefore minimum estimates for the uncertainty attributed to GCMs. Figure 5 indicates that the 99.9th percentiles are close to warning level 1 used at the SMHI.

Table 8 Warning level for the Baltic Sea, Kattegat and Skagerrak used at the SMHI (Schöld et al., 2017). If sea level is predicted to be higher than or equal to a specific warning level, a public warning is issued. Warning levels are given relative to the mean sea level.

The 99.9th percentiles of ESLs are shown in Fig. 6. They are between 70 and 120 cm higher than the mean sea surface. The most extreme sea levels occur at the eastern end of the Gulf of Finland and the northern end of the Bothnian Bay. In the western part of the Kattegat, the southwestern Baltic Sea and the Gulf of Riga, the 99.9th percentiles are up to 100 cm higher than the mean sea surface.

Since the mean sea surface is increasing towards the east and the north, the 99.9th percentile relative to bedrock shows a more pronounced gradient towards the east and the north. Non-linear effects in the Bothnian Bay and the Gulf of Finland can be identified by the crowding of contour lines.

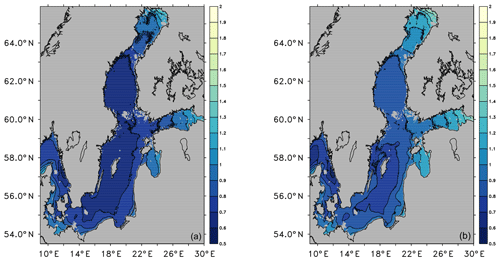
Figure 6 Ensemble median of the 99.9th percentile of ESLs (m) for the period of 1970 to 1999 relative to the mean sea surface (a) and relative to bedrock (b).

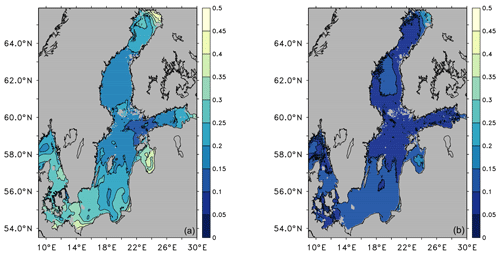
Figure 7 Uncertainty of ESL (m) for the period of 1970 to 1999 for the RCM ensemble (a) and the GCM ensemble (b). The uncertainty is defined here as the likely range (5 % to 95 % range of ensemble solutions).

While Fig. 6 shows the median of the GCM ensemble, Fig. 7 shows the likely range (5 % to 95 %) of the GCM and the RCM ensemble. Both sources of uncertainty depicted in Fig. 7 yield the largest disagreement in ESLs in the northeastern part of the Bothnian Bay. Ensemble members driven with different GCMs show different sea ice covers that introduce an uncertainty in the transfer the horizontal momentum of the wind to the momentum of the barotropic motion in the ocean. The RCMs among themselves also show a variety of patterns in ice cover. Additionally, the momentum transfer is implemented differently between coupled and uncoupled RCMs, which adds to the uncertainty in ESLs in the northeastern Bothnian Bay. For the RCMs, that uncertainty amounts to 50 cm. It can be reduced to 25 cm for the coupled-only RCM ensemble (not shown).

The shallower (<100 m) parts of the Baltic Proper also are more uncertain in the model solutions than deeper parts. In shallow areas, a small uncertainty in barotropic transport makes a relatively larger signal in the sea surface elevation than in deeper water. Interestingly, the Gulf of Riga and the bays along the German and Polish coasts show high disagreement among different RCM solutions but not among GCMs. That points to the importance of the details in how atmospheric variability is translated into ESLs by the RCMs. The disagreement disappears for the coupled-only RCM ensemble. In both regions, the disagreement, together with the extremes themselves, is higher closer to the coast. Since topography, resolution and forcing are the same in these regions, the disagreement comes from a higher setup in shallower coastal regions, which is more sensitive to wind stress and bottom stress. Since the spatial scales are relatively small here, non-linear amplification of small differences becomes increasingly important.

Generally, for the Baltic Sea, Kattegat and Skagerrak, the RCMs contribute about double the uncertainty compared to what the GCM uncertainty shows. There may be different explanations. From Fig. 2, it is obvious that the RCM ensemble shows a clustering between lower and higher extremes. For example, those solutions with the uncoupled RCMs (not shown) do not show any disagreement in the northeastern Bothnian Bay or in the eastern part of the Gulf of Finland. On the other hand, it shows a higher degree of uncertainty on the Swedish side of the Kattegat. The ensemble of RCM solutions is too small to provide a robust basis to estimate uncertainty. It should be understood as an upper bound for RCM uncertainty. Future model development should aim to reduce the disagreement.

6 Discussion

The validation of the modeled ESLs has shown that the ensemble mean of the historical period compares well to observational estimates, except for the Swedish west coast (see Table 9). The modeled ESLs are lower than the ones inferred from observations. The results are, however, compatible with the assumption that the model generates the same distribution of ESLs as the observed ones. The biases in ESLs for the ensemble mean are smaller than O(10 cm), except for stations Göteborg and Smögen.

Table 9 Extreme sea levels (cm) with 100-year return period (1961 to 2005) for selected stations along the Swedish coast (cf. Fig. 4). The values in brackets indicate model biases relative to the observational estimates. Note that the results in this table are from model runs that do not use a storm surge model.

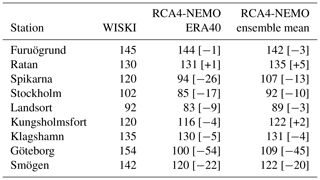
Table 9 also shows that the ensemble mean estimates are closer to the estimates based on observations than those calculated from the single ERA-40 hindcast. By means of sensitivity studies, model deficiencies could be identified. At station Smögen, the model is sensitive to sea level variability that is generated in the northeast Atlantic. In the standard model configuration, this information is not provided. The model results do improve, however, when extra variability from the North Sea is present. At station Stockholm, the model shows ESLs that are affected by processes and geography the model does not resolve properly. This can serve to formulate hypotheses for the development of improved model versions.

On the list of model improvements in the RCM is the reduction of the fresh bias in the Baltic Sea that would bring the mean sea surface closer to the observed one and thus reduce the underestimation of ESLs in the Kattegat and the northern Baltic Sea. Another model deficiency that needs to be addressed is the too-low wind speed in the highest (99th) percentile that is responsible for the generation of ESLs in the Baltic Sea.

A regional model can only to some extent represent effects that are caused by local characteristics of the bathymetry and orography. Impact models are necessary to prolong the chain of climate downscaling and close the gap of spatial scales in the realm of ESLs in specific locations and climate change adaption on site. Johansson et al. (2017) have shown that the estimates of ESLs in Göteborg are very sensitive to how far away the measurements are taken from the open sea. The resolution of the RCM is too coarse to resolve the river mouth of the Göta älv in Göteborg, where sea level measurements are taken. Some model development, however, can be envisioned for regional models that potentially improve ESL estimation. Drying and wetting of adjacent low-lying land can help to more realistically represent the energy budget of storm surges. A wave model could improve the representation of how momentum is transferred from the atmosphere to the ocean, and vice versa. Today, most coupled regional models treat the sea surface between the atmosphere and the ocean as an interface to exchange fluxes of momentum, energy and matter. A wave model can be integrated as an individual component in a coupled system to describe in more detail the air–sea exchange of momentum, energy and matter. A wave model would also help to integrate the Stokes drift into an ocean model that would allow interaction between the near-surface flow field and the storm surges (wave setup). Eelsalu et al. (2014) have shown that wave setups on ESLs are visible by the clustering of return levels along the Estonian coast. For coastal areas in the eastern Baltic Sea, Viitak et al. (2016) have shown that the interaction also affects the wave height. Other processes that have been shown to be important in Baltic Sea ESLs, like the position of storm tracks (Averkiev and Klevanny, 2007), coupling to atmospheric low pressure systems (Wiśniewski and Wolski, 2011) and seiches (Weisse and Weidemann, 2017), are included in the model. A higher resolution in the atmosphere model can, however, improve the representation of these processes and their interaction with sea level.

In this study, we presented a validation and analysis of simulated ESLs for the Baltic Sea, Kattegat and Skagerrak. To calculate regional sea level scenarios, we have downscaled five members of the CMIP5 ensemble for the historical period. The ensemble spread within the regional climate ensemble allows us to assess the uncertainty that is inherent to different GCM solutions. One source of uncertainty which is missing from our ensemble is how different RCMs influence the uncertainty of ESLs. An approximate estimate, based on interdependent RCMs, is approximately double that of the uncertainty generated by the GCMs.

The uncertainty estimate based on the RCMs has several weaknesses. First of all, the ensemble is small, especially since the models are not independent from each other. That would tend to yield a small uncertainty. On the other hand, the bulk of the uncertainty is due to two different clusters of solutions. The coupled models generally behave differently than the uncoupled ones. That increases the RCM uncertainty in a somewhat artificial way. Sea level in the Baltic Sea can be tuned to some extent (Meier et al., 2004; Gräwe and Burchard, 2012) and should eventually lead to a smaller uncertainty. Sea level is probably the one variable in the Baltic Sea or North Sea and Baltic Sea models that can be used to forecast, even without assimilation of data, at least direct assimilation into the ocean model. The atmospheric forcing is the other crucial ingredient and that is usually derived from the weather forecast. That is the regular procedure in the agencies concerned with sea level forecast around the North Sea and Baltic Sea.

If the RCM uncertainty was determined from the coupled models only, without the coarse resolution version, the uncertainty was an order of magnitude smaller. An uncertainty estimate from the ocean-only models would be reduced by a factor of 2, except for stations Stockholm and Göteborg. Overall, the present, crude estimate of RCM uncertainty gives an upper bound of what can be expected from an analysis of a true multi-model ensemble. This effort should be tackled in the near future to better understand the uncertainty in ESLs inherent in the choice of the RCM. It would be important to assess the RCM uncertainty based on an ensemble of RCMs that have been driven with different GCMs. That would sample the full matrix and would potentially uncover GCM/RCM combinations that yield ESLs outside of our basic estimate that uses one RCM only.

Another task concerns the reduction of the uncertainty that stems from the GCMs. In our ensemble, we have used five different CMIP5 GCMs that span the parameter space. The addition of well-behaved but independent GCMs into the ensemble of regional projections would be valuable to generate more robust estimates and presumably a smaller uncertainty. In our ensemble, the GCM uncertainty of 20 to 50 cm is larger at half of the stations than the confidence limits related to the estimation of the 100-year return levels. Observation-based estimates of return levels are known to produce outliers on the Swedish west coast (Fredriksson et al., 2016). It is not clear whether these are among the 5 % that are bound to be outside the 95 % confidence limits or whether the length of the time series or details of the algorithm must be improved. Arns et al. (2013); Vousdoukas et al. (2016); Wahl et al. (2017) have shown that the choice of the algorithm with which return levels are estimated can have a substantial impact on the result. On the other hand, Lang and Mikolajewicz (2019) have shown for the German Bight that 100-year return levels based on observations significantly underestimate the range of possible outcomes since they do not properly sample natural variability.

For planning and management purposes, it is important to consider the spread of possible solutions along with the mean or median estimates. For ESLs along the Swedish coast, we see potential for the reduction in uncertainty from both improvements on the RCMs and the representation of the climate by the GCMs. We have considered only one estimator for the 100-year return levels, but Södling and Nerheim (2017) has shown that different approaches yield a range of results, also along the Swedish coast. These uncertainties should be taken into account as well in future investigations.

Recently, Meier et al. (2019) assessed different sources of uncertainty in projections of biogeochemical cycles in the Baltic Sea. Some of the uncertainties may be reduced by developing better modeling strategies, boundary and forcing data. Other uncertainties are related to unknown future nutrient input and greenhouse gas emissions. They stress the importance of regular information on current knowledge which includes the uncertainty in model results that stem from different sources. In the context of high-end climate change scenarios, Capela Lourenço et al. (2018) did not find climate change uncertainty as being perceived as a barrier in the implementation of climate adaption. Uncertainty estimates are also planned to be included in management tools such as Symphony within the ClimeMarine project.

7 Conclusions

In this study, we have analyzed ESLs in a regional sea level ensemble for the Baltic Sea. The ensemble uses one RCM forced with different GCMs. This allows to assess the uncertainty of 100-year return levels introduced by large-scale circulation patterns represented by the GCMs. This uncertainty is 1 to 2 times the confidence limits of the observational GEV estimates. The observational confidence limits express the uncertainty in 100-year return levels from the use of short time series. Another source of uncertainty lies in the use of a specific RCM. We have estimated an upper bound for this uncertainty to be double the size of the GCM uncertainty. With the analysis of sensitivity studies, processes and shortcomings have been identified that will allow model development to reduce this uncertainty below the GCM uncertainty.

The main findings of this study may be summarized as follows:

• The ensemble mean 100-year return levels range from 90 cm in the central Baltic Sea to 140 cm in the Bothnian Bay and southwestern Baltic Sea. These estimates are within O(10 cm) and within the 95 % confidence limits of the observational estimates, except for the stations Göteborg and Smögen. The uncertainty for 100-year return levels amounts to 20 to 50 cm.

• The GCM uncertainty for the 99.9th percentile is largest where the ESLs are largest: in the Bothnian Bay, Gulf of Finland, Gulf of Riga and in the southwestern Baltic Sea. Along the Swedish coast, the largest uncertainty is on the south and west coasts of Sweden.

• The GCM uncertainty of the ensemble mean 100-year return levels is the same order of magnitude as the 95 % confidence limits from the GEV estimates with the blockmaxima method.

• The bias in ESLs at stations Göteborg and Smögen needs to be reduced. Sensitivity studies have shown that high-frequency variability should be included at the open boundaries of the regional ocean model. Model development should also aim to reduce the RCM uncertainty.