The Ekman spiral for piecewise-uniform viscosity

We re-visit Ekman's (1905) classic problem of wind-stress-induced ocean currents to help interpret observed deviations from Ekman's theory, in particular from the predicted surface current deflection of 45^∘. While previous studies have shown that such deviations can be explained by a vertical eddy viscosity varying with depth, as opposed to the constant profile taken by Ekman, analytical progress has been impeded by the difficulty in solving Ekman's equation. Herein, we present a solution for piecewise-constant eddy viscosity which enables a comprehensive understanding of how the surface deflection angle depends on the vertical profile of eddy viscosity. For two layers, the dimensionless problem depends only on the depth of the upper layer and the ratio of layer viscosities. A single diagram then allows one to understand the dependence of the deflection angle on these two parameters.

1 Introduction

The motion of the near-surface ocean layer is a superposition of waves, wind-driven currents and geostrophic flows. The basic theory of wind-driven surface currents in the ocean, away from the Equator, is due to Ekman (1905) and constitutes a cornerstone of oceanography (see Vallis, 2017). Ekman dynamics is due to the balance between Coriolis and the frictional forces generated by the wind stress. Its main features, consistent with observations of steady wind-driven ocean currents, are the following:

• i.

  The surface current is deflected to the right and left of the prevailing wind direction in the Northern Hemisphere and Southern Hemisphere, respectively.

• ii.

  With increasing depth in the boundary layer, the current speed is reduced, and the direction rotates farther away from the wind direction following a spiral.

• iii.

  The net transport is at right angles to the wind direction, to the right and left of the wind direction in the Northern Hemisphere and Southern Hemisphere, respectively.

While near the Equator wind-drift currents move in the same direction as the wind (see the discussion in Boyd, 2018), away from the Equator a deflection of steady wind-driven currents with respect to the prevailing wind direction occurs in a surface boundary layer, whose typical depth is tens of metres. Ekman's pioneering solution (see Ekman, 1905), derived for a constant vertical eddy viscosity, captures the general qualitative behaviour, but differences of detail between observations and Ekman theory were recorded in the last decades. While the characteristics (ii)–(iii) hold for any depth-dependent vertical eddy viscosity (see Constantin, 2020), there is a need to explain the occurrence of surface currents at an angle in the range 10–75^∘ to the wind (rather than the 45^∘ predicted by Ekman), with large variations depending on the regional and seasonal climate (see the data in Röhrs and Christensen, 2015; Yoshikawa and Masuda, 2009).

This discrepancy is typically ascribed to the effect of a vertical eddy viscosity that varies with depth. The explicit solution found by Madsen (1977), for a vertical eddy viscosity that varies linearly with depth, leads to a plausible, although somewhat low, surface current deflection angle of about 10^∘. The avenue of seeking explicit solutions is not very promising, since only a few are available and the intricacy of the details makes it difficult to extract broad conclusions (we refer to Constantin and Johnson, 2019; Grisogno, 1995, for a survey of known Ekman-type solutions). The challenging nature of the task is highlighted by the recent analysis pursued in Bressan and Constantin (2019) and Constantin (2020) where asymptotic approaches, applicable for eddy viscosities that are small perturbations of a constant, revealed the convoluted way in which the eddy viscosity influences the deflection angle: while a slow and gradual variation of the eddy viscosity with depth results in a deflection angle larger than 45^∘, the typical outcome of an eddy viscosity concentrated in the middle of the boundary layer is a deflection angle below 45^∘. A better understanding of the deflection angle is important theoretically but also for operational oceanography, e.g. in the context of search-and-rescue operations or in remedial action for oil spills.

The important issue of a quantitative relation between the vertical eddy viscosity and the magnitude of the deflection angle remains open. The aim of this paper is to discuss this issue in cases when the eddy viscosity is piecewise uniform. The in-depth analysis that can be pursued in this relatively simple setting permits us to gain insight into the way the turbulent parametrization (e.g. of general circulation models) controls the deflection angle. This paper is organized as follows: in Sect. 2 we present the Ekman equations for wind-driven oceans having depth-dependent eddy viscosities, and we perform a suitable scaling that reduces the number of parameters. In Sect. 3, an explicit solution is constructed and illustrated for an infinitely deep ocean with two constant values of eddy viscosity. This solution covers the full range of possibilities and exhibits deflection angles covering the full range between 0 and 90^∘. Various special or limiting cases are highlighted. Finally, Sect. 4 offers our conclusions.

2 Equations of motion and scaling

For a deep, vertically homogeneous ocean, of infinite lateral extent, the horizontal momentum equation for steady flow takes the following (complex) form under the f-plane approximation:

$$\begin{array}{}\text{(1)}& if\mathit{U}={\displaystyle \frac{\mathrm{1}}{\mathit{\rho }}}{\displaystyle \frac{\partial \mathit{\tau }}{\partial Z}}-{\displaystyle \frac{\mathrm{1}}{\mathit{\rho }}}\mathrm{\nabla }P+\text{higher-order terms},\end{array}$$

where $\mathit{U}\left(Z\right)=U+iV$ is the complex horizontal velocity in the (X,Y) plane, Z is the depth below the mean surface Z=0, f is the Coriolis parameter, ρ is the (constant) density, $\mathrm{\nabla }P=\partial P/\partial X+\mathrm{i}\partial P/\partial Y$ is the horizontal pressure gradient, $\mathit{\tau }\left(Z\right)={\mathit{\tau }}_x+i{\mathit{\tau }}_y$ is the shear stress due to molecular and turbulent processes, and the higher-order terms, representing interactions between the variables, are presumed to be small. Decomposing the horizontal velocity into pressure-driven (geostrophic) and wind-driven (Ekman) components $\mathit{U}={\mathit{U}}_{\mathrm{g}}+{\mathit{U}}_{\mathrm{e}}$, we see from Eq. (1) that the leading-order geostrophic and wind-driven flows separate, with the linear equation

$$\begin{array}{}\text{(2)}& if{\mathit{U}}_{\mathrm{e}}={\displaystyle \frac{\mathrm{1}}{\mathit{\rho }}}{\displaystyle \frac{\partial \mathit{\tau }}{\partial Z}}\end{array}$$

governing the dynamics of the wind-driven flow. By relating the stress vector within the fluid, τ, to the shear profile through a turbulent eddy viscosity coefficient ν(Z),

$$\begin{array}{}\text{(3)}& \mathit{\tau }=\mathit{\rho }\mathit{\nu }{\displaystyle \frac{\partial {\mathit{U}}_{\mathrm{e}}}{\partial Z}},\end{array}$$

from Eq. (2) we obtain Ekman's equations for wind-driven ocean currents

$$\begin{array}{}\text{(4)}& if{\mathit{U}}_{\mathrm{e}}={\displaystyle \frac{\partial }{\partial Z}}\left(\mathit{\nu }{\displaystyle \frac{\partial {\mathit{U}}_{\mathrm{e}}}{\partial Z}}\right).\end{array}$$

Let us now discuss the appropriate boundary conditions. At the surface, the shear stress balances the wind stress, τ₀:

$$\begin{array}{}\text{(5)}& {\mathit{\tau }}_{\mathrm{0}}=\mathit{\rho }\mathit{\nu }{\displaystyle \frac{\partial {\mathit{U}}_{\mathrm{e}}}{\partial Z}}\text{on}Z=\mathrm{0}.\end{array}$$

The “bottom” boundary condition expresses the vanishing of the wind-driven current with depth (necessary to keep the total kinetic energy finite), where the flow is essentially geostrophic:

$$\begin{array}{}\text{(6)}& {\mathit{U}}_{\mathrm{e}}\to \mathrm{0}\text{as}Z\to -\mathrm{\infty }.\end{array}$$

Letting τ₀ denote the magnitude of the surface wind stress, we non-dimensionalize the problem by scaling U_e by $\sqrt{\mathrm{2}{\mathit{\tau }}_{\mathrm{0}}/\mathit{\rho }}$ and Z by $\sqrt{\mathrm{2}{\mathit{\tau }}_{\mathrm{0}}/\mathit{\rho }}/f$, since τ₀∕ρ has units of L²∕T². The factor of 2 is introduced for convenience below. Upon defining a dimensionless eddy viscosity $K=f\mathit{\rho }\mathit{\nu }/{\mathit{\tau }}_{\mathrm{0}}$, velocity $\mathit{u}={\mathit{U}}_{\mathrm{e}}/\sqrt{\mathrm{2}{\mathit{\tau }}_{\mathrm{0}}/\mathit{\rho }}$ and depth $z=Zf/\sqrt{\mathrm{2}{\mathit{\tau }}_{\mathrm{0}}/\mathit{\rho }}$, the equations transform to

$$\begin{array}{}\text{(7)}& {\displaystyle }& {\displaystyle }(K{\mathit{\psi }}^{\prime }{)}^{\prime }-\mathrm{2}i\mathit{\psi }=\mathrm{0}\text{for}z<\mathrm{0},\text{(8)}& {\displaystyle }& {\displaystyle }{\mathit{\psi }}^{\prime }\left(\mathrm{0}\right)=\mathrm{1}\text{on}z=\mathrm{0},\text{(9)}& {\displaystyle }& {\displaystyle }\mathit{\psi }\to \mathrm{0}\text{as}z\to -\mathrm{\infty },\end{array}$$

where ψ=uK(0) and a prime means a derivative with respect to z (cf. Eqs. 14–16 in Gill, 1982). The scaling performed does not change the surface deflection angle θ₀, equal to the argument of the complex vector ψ(0), even if the scaling results in an orientation of the horizontal axes such that the surface wind stress points in the positive x direction. Finally, we note that this formulation is appropriate for the Northern Hemisphere where f>0. The formulation for the Southern Hemisphere is obtained by taking the complex conjugate in Eq. (7), noticing that K is real-valued.

3 Exact solution for piecewise-constant eddy viscosity

For piecewise-constant K, without loss of generality we can further scale z so that K=1 in $z\in [-h,\mathrm{0}]$ while K=ℓ² in $z\in (-\mathrm{\infty },-h)$, where h is the dimensionless depth of the upper layer. Note that ℓ is the ratio of the lower-layer to upper-layer viscous lengths. The analysis below can be readily extended to any number of regions of constant K, but the simplest to understand is two regions, since then the solution depends on only two dimensionless parameters, ℓ and h.

3.1 Constructing the solution

In each region, the complex velocity ψ satisfies a simple constant-coefficient equation:

$$\begin{array}{}\text{(10)}& {\displaystyle }{\mathit{\psi }}^{\prime \prime }-\mathrm{2}i\mathit{\psi }=\mathrm{0}\text{for}-h<z<\mathrm{0},\text{(11)}& {\displaystyle }{\mathrm{\ell }}^{\mathrm{2}}{\mathit{\psi }}^{\prime \prime }-\mathrm{2}i\mathit{\psi }=\mathrm{0}\text{for}-\mathrm{\infty }<z<-h,\end{array}$$

having exponential solutions

$$\begin{array}{}\text{(12)}& {\displaystyle }\mathit{\psi }\left(z\right)& {\displaystyle }=A{e}^{(\mathrm{1}+\mathrm{i})z}+B{e}^{-(\mathrm{1}+\mathrm{i})z}\text{for}-h<z<\mathrm{0},\text{(13)}& {\displaystyle }\mathit{\psi }\left(z\right)& {\displaystyle }=C{e}^{(\mathrm{1}+\mathrm{i})z/\mathrm{\ell }}\text{for}-\mathrm{\infty }<z<-h,\end{array}$$

where A, B and C are (generally complex) constants. The boundary condition ψ→0 as $z\to -\mathrm{\infty }$ has been used to eliminate the growing solution in Eq. (13).

At the discontinuity in K, at $z=-h$, we require continuity of ψ, i.e. $\mathit{\psi }(-h^{+})=\mathit{\psi }(-h^{-})$. Moreover, by integrating the equation above across an infinitesimal region centred on $z=-h$, we obtain

$$\begin{array}{}\text{(14)}& {\mathit{\psi }}^{\prime }(-h^{+})={\mathrm{\ell }}^{\mathrm{2}}{\mathit{\psi }}^{\prime }(-h^{-}).\end{array}$$

The upper surface boundary condition ${\mathit{\psi }}^{\prime }\left(\mathrm{0}\right)=\mathrm{1}$ implies

$$\begin{array}{}\text{(15)}& (\mathrm{1}+\mathrm{i})(A-B)=\mathrm{1}\end{array}$$

while continuity of ψ at $z=-h$ implies

$$\begin{array}{}\text{(16)}& A{e}^{-(\mathrm{1}+i)h}+B{e}^{(\mathrm{1}+i)h}=C{e}^{-(\mathrm{1}+i)h/\mathrm{\ell }}\end{array}$$

and finally the jump condition (Eq. 14) on ψ^′ at $z=-h$ implies

$$\begin{array}{}\text{(17)}& A{e}^{-(\mathrm{1}+i)h}-B{e}^{(\mathrm{1}+i)h}=C\mathrm{\ell }{e}^{-(\mathrm{1}+i)h/\mathrm{\ell }}.\end{array}$$

It follows that

$$\begin{array}{}\text{(18)}& \begin{array}{rl}& A={\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}C{e}^{-(\mathrm{1}+i)h/\mathrm{\ell }}(\mathrm{1}+\mathrm{\ell })e^{(\mathrm{1}+i)h}\text{and}\\ & B=\frac{\mathrm{1}}{\mathrm{2}}C{e}^{-(\mathrm{1}+i)h/\mathrm{\ell }}(\mathrm{1}-\mathrm{\ell })e^{-(\mathrm{1}+i)h}.\end{array}\end{array}$$

Applying the surface boundary condition (Eq. 15) determines C as

$$\begin{array}{}\text{(19)}& C={\displaystyle \frac{(\mathrm{1}-i)e^{(\mathrm{1}+i)h/\mathrm{\ell }}}{(\mathrm{1}+\mathrm{\ell })e^{(\mathrm{1}+i)h}-(\mathrm{1}-\mathrm{\ell })e^{-(\mathrm{1}+i)h}}}.\end{array}$$

The surface current deflection angle, θ₀, measured clockwise, is determined from

$$\begin{array}{}\text{(20)}& \tan {\mathit{\theta }}_{\mathrm{0}}=-{\displaystyle \frac{\mathfrak{I}\left(\mathit{\psi }\right(\mathrm{0}\left)\right)}{\mathfrak{R}\left(\mathit{\psi }\right(\mathrm{0}\left)\right)}}=-{\displaystyle \frac{\mathfrak{I}(A+B)}{\mathfrak{R}(A+B)}}.\end{array}$$

But given C above in Eq. (19), we have

$$A+B={\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}(\mathrm{1}-i){\displaystyle \frac{(\mathrm{1}+\mathrm{\ell })e^{(\mathrm{1}+i)h}+(\mathrm{1}-\mathrm{\ell })e^{-(\mathrm{1}+i)h}}{(\mathrm{1}+\mathrm{\ell })e^{(\mathrm{1}+i)h}-(\mathrm{1}-\mathrm{\ell })e^{-(\mathrm{1}+i)h}}}.$$

Introducing the real values $\mathit{\alpha }=(\mathrm{1}+\mathrm{\ell })e^h$ and $\mathit{\beta }=(\mathrm{1}-\mathrm{\ell })e^{-h}$ enables us to write

$$A+B={\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}(\mathrm{1}-i){\displaystyle \frac{\mathit{\alpha }{e}^{ih}+\mathit{\beta }{e}^{-ih}}{\mathit{\alpha }{e}^{ih}-\mathit{\beta }{e}^{-ih}}},$$

which, after multiplying top and bottom by the complex conjugate of the denominator, simplifies to

$$A+B={\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}(\mathrm{1}-i){\displaystyle \frac{{\mathit{\alpha }}^{\mathrm{2}}-{\mathit{\beta }}^{\mathrm{2}}-\mathrm{2}i\mathit{\alpha }\mathit{\beta }\sin \left(\mathrm{2}h\right)}{{\mathit{\alpha }}^{\mathrm{2}}+{\mathit{\beta }}^{\mathrm{2}}-\mathrm{2}\mathit{\alpha }\mathit{\beta }\cos \left(\mathrm{2}h\right)}}.$$

Hence, taking the (negative of the) ratio of the imaginary to real parts of this, we obtain

$$\begin{array}{}\text{(21)}& \tan {\mathit{\theta }}_{\mathrm{0}}={\displaystyle \frac{{\mathit{\alpha }}^{\mathrm{2}}-{\mathit{\beta }}^{\mathrm{2}}+\mathrm{2}\mathit{\alpha }\mathit{\beta }\sin \left(\mathrm{2}h\right)}{{\mathit{\alpha }}^{\mathrm{2}}-{\mathit{\beta }}^{\mathrm{2}}-\mathrm{2}\mathit{\alpha }\mathit{\beta }\sin \left(\mathrm{2}h\right)}}.\end{array}$$

3.2 Results

First, we examine certain special cases.

When ℓ=1, there is no discontinuity in eddy viscosity. Since in this case β=0, we have tan θ₀=1, i.e. ${\mathit{\theta }}_{\mathrm{0}}={\mathrm{45}}^{\circ }$ in agreement with the classical Ekman spiral solution.

As ℓ→0, the eddy viscosity vanishes in the lower layer, and the flow field ψ must also vanish. In this case, tan θ₀ reduces to

$$\begin{array}{}\text{(22)}& \tan {\mathit{\theta }}_{\mathrm{0}}={\displaystyle \frac{\sinh \left(\mathrm{2}h\right)+\sin \left(\mathrm{2}h\right)}{\sinh \left(\mathrm{2}h\right)-\sin \left(\mathrm{2}h\right)}},\end{array}$$

which has a non-trivial dependence on h. The maximum value is attained as h→0; then tan θ₀→∞ or θ₀→90^∘.

As ℓ→∞, corresponding to an extremely viscous lower layer, tan θ₀ reduces to the inverse of the previous expression, i.e.

$$\begin{array}{}\text{(23)}& \tan {\mathit{\theta }}_{\mathrm{0}}={\displaystyle \frac{\sinh \left(\mathrm{2}h\right)-\sin \left(\mathrm{2}h\right)}{\sinh \left(\mathrm{2}h\right)+\sin \left(\mathrm{2}h\right)}}.\end{array}$$

The minimum occurs for h→0 and there tan θ₀→0 or θ₀→0.

For general ℓ, there are also values of h for which tan θ₀=1. These occur when the numerator and the denominator of the general expression above for tan θ₀ are equal. But this means αβsin (2h)=0 or $(\mathrm{1}-{\mathrm{\ell }}^{\mathrm{2}})\sin \left(\mathrm{2}h\right)=\mathrm{0}$. One solution is the classical Ekman spiral with ℓ=1 noted above. But we also have $h=n\mathit{\pi }/\mathrm{2}$ for non-negative integers n. When n=0, the upper layer vanishes and the eddy viscosity is uniform throughout the entire depth. The classical Ekman spiral is expected in this case. The other special depths imply θ₀ exhibits a non-monotonic dependence on h for fixed ℓ. In fact, tan θ₀ exhibits a decaying oscillation about a value of unity.

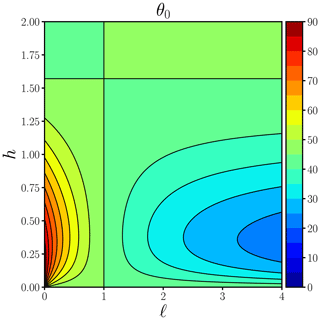
Figure 1 Surface deflection angle θ₀ (in degrees) as a function of the lower-layer non-dimensional viscous length ℓ and the non-dimensional depth of the upper layer h.

A summary of the results in the ℓ–h plane is provided in Fig. 1. Along any line ℓ = constant (excluding ℓ=1), θ₀ reaches a minimum or maximum in h when the following relation holds:

$$\begin{array}{}\text{(24)}& {\displaystyle \frac{\mathrm{1}-\mathrm{\ell }}{\mathrm{1}+\mathrm{\ell }}}=\pm e^{\mathrm{2}h}\sqrt{{\displaystyle \frac{\cos \left(\mathrm{2}h\right)-\sin \left(\mathrm{2}h\right)}{\cos \left(\mathrm{2}h\right)+\sin \left(\mathrm{2}h\right)}}}\end{array}$$

obtained by setting the partial derivative of tan θ₀ with respect to h equal to zero. The first extremum with increasing h occurs for $h<\mathit{\pi }/\mathrm{8}$ (when $h=\mathit{\pi }/\mathrm{8}$ the above equation yields ℓ=1). Note that as h→0, $(\mathrm{1}-\mathrm{\ell })/(\mathrm{1}+\mathrm{\ell })\to \pm \mathrm{1}$, implying either ℓ→0 or ℓ→∞ as noted previously. Extrema also occur for larger h since the function in the square root above is periodic, but these involve much weaker variations in θ₀ about 45^∘, diminishing like e^−nπ for positive integers n. When n=1, the maximum excursion in tan θ₀ is approximately 0.05735.

4 Conclusions

We have re-visited the famous problem originally posed by Nansen (see the discussion in Huntford, 2002) and solved by Ekman (1905) to understand wind-driven currents in the ocean. By balancing viscous and Coriolis forces, and assuming a constant vertical eddy viscosity, Ekman (1905) predicted that the surface current is deflected by 45^∘ to the right and left of the prevailing wind direction in the Northern Hemisphere and Southern Hemisphere, respectively. Moreover, Ekman (1905) found that the net fluid transport is 90^∘ to the right and left of the wind direction.

Since then, a number of studies have sought to explain observed discrepancies with Ekman's theory (Röhrs and Christensen, 2015; Yoshikawa and Masuda, 2009), in particular deflection angles significantly different from the 45^∘ prediction (Madsen, 1977; Grisogno, 1995; Bressan and Constantin, 2019; Constantin and Johnson, 2019; Constantin, 2020). The main conclusion is that these discrepancies can be explained by vertically varying eddy viscosities. However, due to the mathematical difficulty in constructing exact or asymptotic solutions, no general scenario has yet emerged relating the deflection angle to the profile of eddy viscosity.

This study makes a first step in this direction by considering the case of piecewise-constant eddy viscosities for which analytical solutions may be readily constructed and analysed. We have presented results for the simplest situation of two regions having different uniform viscosities in an infinitely deep ocean. (In fact the results also apply when the two regions have different densities, such as a mixed layer of density ρ₁ overlying a denser deep layer of density ρ₂. In that case the lower-layer dimensionless viscosity ℓ² includes the density ratio ρ₁∕ρ₂.) By an appropriate scaling of the governing equations, the solutions can be shown to depend on only two parameters: the ratio of the lower-to-upper viscous lengths ℓ and the dimensionless depth of the upper layer h. This permits one to see at a glance how both ℓ and h determine the surface deflection angle θ₀.

In appropriate limits, we recover Ekman's classical solution, but additionally the 45^∘ deflection angle may also occur for arbitrary ℓ, when h assumes special values. In general, for h sufficiently small and ℓ<1 (a less viscous lower layer), the deflection angle exceeds 45^∘ (and can reach nearly 90^∘ for ℓ≪1). When ℓ>1 (a more viscous lower layer), the deflection angle is less than 45^∘ and tends to zero as ℓ→∞ for h≪1. For ℓ∼1 our conclusions are in agreement with the results obtained recently in Bressan and Constantin (2019) and Constantin (2020). Indeed, writing $K\left(z\right)={\mathrm{\ell }}^{\mathrm{2}}+\mathit{\epsilon }{K}_{\mathrm{1}}\left(z\right)$ for z≤0, with $\mathit{\epsilon }=|\mathrm{1}-{\mathrm{\ell }}^{\mathrm{2}}|$ and

$$K_{\mathrm{1}}\left(z\right)=\left\{\begin{array}{ccc}& (\mathrm{1}-{\mathrm{\ell }}^{\mathrm{2}})/\mathit{\epsilon },& z\in [-h,\mathrm{0}],\\ & \mathrm{0},& z<-h,\end{array}\right.$$

the perturbative approach developed in Bressan and Constantin (2019) and Constantin (2020) shows that a positive and negative value of the integral

$${\displaystyle \frac{\mathrm{1}-{\mathrm{\ell }}^{\mathrm{2}}}{\mathit{\epsilon }}}\underset{-h}{\overset{\mathrm{0}}{\int }}{\mathrm{e}}^{\mathrm{2}s}\sin (\mathrm{2}s+{\displaystyle \frac{\mathit{\pi }}{\mathrm{4}}})\mathrm{d}s,$$

corresponds to a deflection angle larger and smaller than 45^∘. respectively. The relation

$$\underset{-h}{\overset{\mathrm{0}}{\int }}{e}^{\mathrm{2}s}\sin (\mathrm{2}s+{\displaystyle \frac{\mathit{\pi }}{\mathrm{4}}})\mathrm{d}s={\displaystyle \frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}}{e}^{-\mathrm{2}h}\sin \left(\mathrm{2}h\right)$$

shows that this is consistent with our conclusions.

The results obtained may help better formulate appropriate parameterizations of eddy viscosities in global circulation models of the ocean. For example, it is typical for the upper 100 m of the ocean that solar heating quenches turbulence during the day (see the discussion in Woods, 2002). Our model captures these changes: during the day we set ℓ>1, with ℓ<1 during the night, thus explaining the observation that often the deflection angle exceeds 45^∘ during the day, and is below 45^∘ during the night (see Krauss, 1993). The same reasoning applies to the large seasonal variations of the deflection angle observed at some locations (see the data in Yoshikawa and Masuda, 2009) and explains why one observes angles below 45^∘ in arctic regions, where the ice cover quells the turbulence near the ocean surface. On the other hand, the regularity of strong winds in the Drake Passage makes the assumption of a uniform eddy viscosity reasonable (i.e. ℓ=1) so that in this region the deflection angle is typically close to 45^∘ (see the data in Polton et al., 2013; Roach et al., 2015). We are not aware of detailed observational studies relating the deflection angle to the vertical profile of eddy viscosity, but we hope that our work will serve as a guide.