Study of the tidal dynamics of the Korea Strait using the extended Taylor method

The Korea Strait (KS) is a major navigation passage linking the Japan Sea (JS) to the East China Sea and Yellow Sea. Almost all existing studies of the tides in the KS employed either data analysis or numerical modelling methods; thus, theoretical research is lacking. In this paper, we idealize the KS–JS basin as four connected uniform-depth rectangular areas and establish a theoretical model for the tides in the KS and JS using the extended Taylor method. The model-produced K₁ and M₂ tides are consistent with the satellite altimeter and tidal gauge observations, especially for the locations of the amphidromic points in the KS. The model solution provides the following insights into the tidal dynamics. The tidal system in each area can be decomposed into two oppositely travelling Kelvin waves and two families of Poincaré modes, with Kelvin waves dominating the tidal system. The incident Kelvin wave can be reflected at the connecting cross section, where abrupt increases in water depth and basin width occur from the KS to JS. At the connecting cross section, the reflected wave has a phase-lag increase relative to the incident wave of less than 180^∘, causing the formation of amphidromic points in the KS. The above phase-lag increase depends on the angular velocity of the wave and becomes smaller as the angular velocity decreases. This dependence explains why the K₁ amphidromic point is located farther away from the connecting cross section in comparison to the M₂ amphidromic point.

1 Introduction

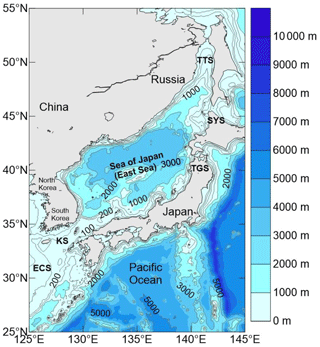
The Korea Strait (KS, also called the Tsushima Strait) connects the East China Sea (ECS) to the southwest and the Japan Sea (the JS, also called the East Sea, or the Sea of Japan) to the northeast. It is the main route linking the JS to the ECS and the Yellow Sea and is thus an important passage for navigation. The strait is located on the continental shelf, and it has a length of approximately 350 km, a width of 250 km and an average water depth of approximately 100 m. The JS, which is adjacent to the KS, is a deep basin that has an average depth of approximately 2000 m and a depth of more than 3000 m at its deepest part. A steep continental slope separates the KS and the JS, and it presents abrupt depth and width changes (Fig. 1). Such topographic characteristics create the unique tidal waves that occur in the KS.

Ogura (1933) first conducted a comprehensive study of the tides in the seas adjacent to Japan using data from the tidal stations along the coast and gained a preliminary understanding of the characteristics of the tides, including amphidromic systems in the KS. Since then, many researchers have investigated the tides in the strait via observations (Odamaki, 1989a; Matsumoto et al., 2000; Morimoto et al., 2000; Teague et al., 2001; Takikawa et al., 2003) and numerical simulations (Fang and Yang, 1988; Kang et al., 1991; Choi et al., 1999; Book et al., 2004). The results of these studies show consistent structures of the tidal waves in the KS. Figure 2 displays the distributions of the K₁ and M₂ tidal constituents based on the global tidal model DTU10, which is based on satellite altimeter observations (Cheng and Andersen, 2011). The figures show that the amplitudes of the diurnal tides are smaller than the semidiurnal tides. The peak amplitude of the semidiurnal tide appears on the south coast of South Korea, and lower amplitudes occur along the southern shore of the strait from the ECS to the JS. Distinguishing features include (1) K₁ and M₂ amphidromic points in the strait that appear in the northeast part of the KS close to the southern coast of the Korean Peninsula and (2) the M₂ amphidromic point appears further northeast and closer to the shelf break relative to the K₁ tide.

However, almost all previous studies have employed either data analysis or numerical modelling methods; thus, theoretical research is lacking. In particular, the existence of amphidromic points in the northeast KS for both diurnal and semidiurnal tides has not been explained based on geophysical dynamics. In this paper, we intend to establish a theoretical model for the K₁ and M₂ tides in the KS–JS basin using the extended Taylor method. The model idealizes the KS–JS basin into three connected uniform-depth rectangular areas, with the effects of bottom friction and Coriolis force included in the governing equations and with the observed tides specified as open-boundary conditions. The extended Taylor method enables us to obtain semi-analytical solutions consisting of a series of Kelvin waves and Poincaré modes.

Figure 1 Map of the Korea Strait and its neighbouring areas. (TTS: Tartar Strait; SYS: Soya Strait; TGS: Tsugaru Strait; KS: Korea Strait; ECS: East China Sea). Isobaths are in metres (based on ETOPO1 from US National Geophysical Center).

Figure 2 Tidal charts of the KS and its neighbouring areas based on DTU10 (Cheng and Andersen, 2011) for the (a) K₁ tide and (b) M₂ tide. Solid lines represent the Greenwich phase lag (in degrees), and dashed lines represent amplitude (in metres).

2 The extended Taylor method and its application to multiple rectangular areas

The Taylor problem is a classic tidal dynamic problem (Hendershott and Speranza, 1971). Taylor (1922) first presented a theoretical solution for tides in a semi-infinite rotating rectangular channel of uniform depth to explain the formation of amphidromic systems in gulfs and applied the theory to the North Sea. The classic Taylor problem was subsequently improved by introducing frictional effects (Fang and Wang, 1966; Webb, 1976; Rienecker and Teubner, 1980) and open-boundary conditions (Fang et al., 1991) to study tides in multiple rectangular basins (Jung et al., 2005; Roos and Schuttelaars, 2011; Roos et al., 2011) as well as to solve tidal dynamics in a strait (Wu et al., 2018).

The method initiated by Taylor and developed afterwards is called the extended Taylor method (Wu et al., 2018). This method is especially useful in understanding the tidal dynamics in marginal seas and straits because the tidal waves in these sea areas can generally be represented by combinations of the Kelvin waves and Poincaré waves/modes (e.g. Taylor, 1922; Fang and Wang, 1966; Hendershott and Speranza, 1971; Webb, 1976; Fang et al., 1991; Carbajal, 1997; Jung et al., 2005; Roos and Schuttelaars, 2011; Roos et al., 2011; Wu et al., 2018).

2.1 Governing equations and boundary conditions for multiple rectangular areas

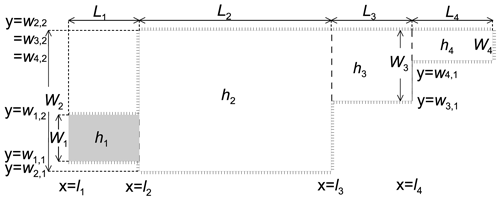
A sketch of the model geometry is shown in Fig. 3, and it consists of a sequence of J rectangular areas with length L_j, width W_j and uniform depth h_j for the jth rectangular area (denoted as Areaj, j=1, …, J). For convenience, the shape of the study region shown in Fig. 3 is the same as that for the idealized KS–JS basin, which will be described in the next section. In particular, Area1 represents the KS, which is our focus area in this study.

Figure 3 Model geometry.

Consider a tidal wave of angular velocity σ and typical elevation amplitude H. We assume $H/h\ll \mathrm{1}$, and the conservation of momentum and mass leads to the following depth-averaged linear shallow water equations on the f plane:

$$\begin{array}{}\text{(1)}& \left\{\begin{array}{l}\frac{\partial {\stackrel{\mathrm{̃}}{u}}_j}{\partial t}-f_j{\stackrel{\mathrm{̃}}{\mathit{\upsilon }}}_j=-g\frac{\partial {\stackrel{\mathrm{̃}}{\mathit{\zeta }}}_j}{\partial x}-{\mathit{\gamma }}_j{\stackrel{\mathrm{̃}}{u}}_j\\ \frac{\partial {\stackrel{\mathrm{̃}}{\mathit{\upsilon }}}_j}{\partial t}+f_j{\stackrel{\mathrm{̃}}{u}}_j=-g\frac{\partial {\stackrel{\mathrm{̃}}{\mathit{\zeta }}}_j}{\partial y}-{\mathit{\gamma }}_j{\stackrel{\mathrm{̃}}{\mathit{\upsilon }}}_j\\ \frac{\partial {\stackrel{\mathrm{̃}}{\mathit{\zeta }}}_j}{\partial t}=-h_j\left[\frac{\partial {\stackrel{\mathrm{̃}}{u}}_j}{\partial x}+\frac{\partial {\stackrel{\mathrm{̃}}{\mathit{\upsilon }}}_j}{\partial y}\right]\end{array}\right.,\end{array}$$

where x and y are coordinates in the longitudinal (along-channel) and transverse (cross-channel) directions; t represents time; ${\stackrel{\mathrm{̃}}{u}}_j$ and ${\stackrel{\mathrm{̃}}{\mathit{\upsilon }}}_j$ represent the depth-averaged flow velocity components in the x and y directions, respectively, with the subscript j indicating the area number; ${\stackrel{\mathrm{̃}}{\mathit{\zeta }}}_j$ represents the free surface elevation above the mean level; γ_j represents the frictional coefficient, which is taken as a constant for each tidal constituent in each area; g=9.8 ms⁻² represents the acceleration due to gravity; and f_j represents the Coriolis parameter, which is also taken as a constant based on the average of the concerned area. The equations in Eq. (1) for each j are two-dimensional linearized shallow water equations on an f plane with momentum advection neglected. For any j, the equations are the same as those used in the work of Taylor (1922) except that bottom friction is now incorporated, such as in Fang and Wang (1966), Webb (1976) and Rienecker and Teubner (1980). When a monochromatic wave is considered, $\left({\stackrel{\mathrm{̃}}{\mathit{\zeta }}}_j,{\stackrel{\mathrm{̃}}{u}}_j,{\stackrel{\mathrm{̃}}{\mathit{\upsilon }}}_j\right)$ can be expressed as follows:

$$\begin{array}{}\text{(2)}& \left({\stackrel{\mathrm{̃}}{\mathit{\zeta }}}_j,{\stackrel{\mathrm{̃}}{u}}_j,{\stackrel{\mathrm{̃}}{\mathit{\upsilon }}}_j\right)=\mathrm{Re}\left({\mathit{\zeta }}_j,u_j,{\mathit{\upsilon }}_j\right)e^{i\mathit{\sigma }t},\end{array}$$

where Re stands for the real part of the complex quantity that follows; $\left({\mathit{\zeta }}_j,u_j,{\mathit{\upsilon }}_j\right)$ are referred to as complex amplitudes of $\left({\stackrel{\mathrm{̃}}{\mathit{\zeta }}}_j,{\stackrel{\mathrm{̃}}{u}}_j,{\stackrel{\mathrm{̃}}{\mathit{\upsilon }}}_j\right)$, respectively; $i\equiv \sqrt{-\mathrm{1}}$ is the imaginary unit; and σ is the angular velocity of the wave. For this wave, Eq. (1) can be reduced as follows:

$$\begin{array}{}\text{(3)}& \left\{\begin{array}{l}\left({\mathit{\mu }}_j+i\right)u_j-{\mathit{\nu }}_j{\mathit{\upsilon }}_j=-\frac{g}{\mathit{\sigma }}\frac{\partial {\mathit{\zeta }}_j}{\partial x}\\ \left({\mathit{\mu }}_j+i\right){\mathit{\upsilon }}_j+{\mathit{\nu }}_j{u}_j=-\frac{g}{\mathit{\sigma }}\frac{\partial {\mathit{\zeta }}_j}{\partial y}\\ {\mathit{\zeta }}_j=\frac{i{h}_j}{\mathit{\sigma }}\left[\frac{\partial u_j}{\partial x}+\frac{\partial {\mathit{\upsilon }}_j}{\partial y}\right]\end{array}\right.,\end{array}$$

in which

$$\begin{array}{}\text{(4)}& {\mathit{\mu }}_j={\displaystyle \frac{{\mathit{\gamma }}_j}{\mathit{\sigma }}}\text{and}{\mathit{\nu }}_j={\displaystyle \frac{f_j}{\mathit{\sigma }}}.\end{array}$$

Provided that the jth rectangular area, denoted as Areaj, has a width of W_j, has a length of L_j and ranges from x=l_j to $x=l_{j+\mathrm{1}}$ ($l_{j+\mathrm{1}}=l_j+L_j$) in the x direction and from $y=w_{j,\mathrm{1}}$ to $y=w_{j,\mathrm{2}}$ ($w_{j,\mathrm{2}}=w_{j,\mathrm{1}}+W_j$) in the y direction, the boundary conditions along the sidewalls within $x\in [l_j,l_{j+\mathrm{1}}]$ are taken as follows:

$$\begin{array}{}\text{(5)}& {\mathit{\upsilon }}_j=\mathrm{0}\text{at}y=w_{j,\mathrm{1}}\text{and}y=w_{j,\mathrm{2}}.\end{array}$$

Along the cross sections, such as x=l_j, various choices of boundary conditions are applicable depending on the problem:

$$\begin{array}{}\text{(6)}& u_j=\mathrm{0},\end{array}$$

if the cross section is a closed boundary;

$$\begin{array}{}\text{(7)}& u_j=\pm \sqrt{{\displaystyle \frac{g}{\left(\mathrm{1}-i{\mathit{\mu }}_j\right)h_j}}}{\mathit{\zeta }}_j,\end{array}$$

if the free radiation in the positive/negative x direction occurs on the cross section;

$$\begin{array}{}\text{(8)}& {\mathit{\zeta }}_j={\widehat{\mathit{\zeta }}}_j,\end{array}$$

if the tidal elevation is specified as ${\widehat{\mathit{\zeta }}}_j$ along the cross section; and

$$\begin{array}{}\text{(9)}& \left\{\begin{array}{l}{\mathit{\zeta }}_j={\mathit{\zeta }}_{j+\mathrm{1}},\\ u_j{h}_j=u_{j+\mathrm{1}}{h}_{j+\mathrm{1}},\end{array}\right.\end{array}$$

if the cross section is a connecting boundary of the areas j and j+1, with each having a different uniform depth of h_j and h_j+1.

Equation (9) is matching conditions accounting for sea level continuity and volume transport continuity. The individual Eqs. (6) to (9), or their combination, may be used as boundary conditions for the cross sections. The relationship between u_j and ζ_j shown in Eq. (7) is based on the solution for progressive Kelvin waves in the presence of friction, which will be given in Eqs. (10) and (11) below.

2.2 General solution

For the jth rectangular area, that is, for $x\mathit{ϵ}[l_j,l_{j+\mathrm{1}}]$ and $y\mathit{ϵ}[w_{j,\mathrm{1}},w_{j,\mathrm{2}}]$, the governing equations in Eq. (3) only have the following four forms satisfying the sidewall boundary condition of Eq. (5) (see for example Fang et al., 1991):

$$\begin{array}{}\text{(10)}& {\displaystyle }\left\{\begin{array}{l}{\mathit{\upsilon }}_{j,\mathrm{1}}=\mathrm{0},\\ u_{j,\mathrm{1}}=-a_j\exp \left[{\mathit{\alpha }}_{j}y+i{\mathit{\beta }}_j\left(x-l_j\right)\right],\\ {\mathit{\zeta }}_{j,\mathrm{1}}=\frac{{\mathit{\beta }}_j}{\mathit{\sigma }}{h}_j{a}_j\exp \left[{\mathit{\alpha }}_{j}y+i{\mathit{\beta }}_j\left(x-l_j\right)\right];\end{array}\right.\text{(11)}& {\displaystyle }\left\{\begin{array}{l}\begin{array}{l}{\mathit{\upsilon }}_{j,\mathrm{2}}=\mathrm{0},\\ u_{j,\mathrm{2}}=b_j\exp \left[-{\mathit{\alpha }}_{j}y-i{\mathit{\beta }}_j\left(x-l_j\right)\right],\end{array}\\ {\mathit{\zeta }}_{j,\mathrm{2}}=\frac{{\mathit{\beta }}_j}{\mathit{\sigma }}h{b}_j\exp \left[-{\mathit{\alpha }}_{j}y-i{\mathit{\beta }}_j\left(x-l_j\right)\right];\end{array}\right.\text{(12)}& {\displaystyle }\left\{\begin{array}{l}{\mathit{\upsilon }}_{j,\mathrm{3}}={\sum }_{n=\mathrm{1}}^{\mathrm{\infty }}{\mathit{\kappa }}_{j,n}\sin r_{j,n}y\exp \left[-s_{j,n}\left(x-l_j\right)\right],\\ u_{j,\mathrm{3}}={\sum }_{n=\mathrm{1}}^{\mathrm{\infty }}{\mathit{\kappa }}_{j,n}\left(A_{j,n}\cos r_{j,n}y+B_{j,n}\sin r_{j,n}y\right)\\ \exp \left[-s_{j,n}\left(x-l_j\right)\right],\\ {\mathit{\zeta }}_{j,\mathrm{3}}=\frac{i{h}_j}{\mathit{\sigma }}{\sum }_{n=\mathrm{1}}^{\mathrm{\infty }}{\mathit{\kappa }}_{j,n}\left(C_{j,n}\cos r_{j,n}y+D_{\mathrm{1},n}\sin r_{j,n}y\right)\\ \exp \left[-s_{j,n}\left(x-l_j\right)\right];\end{array}\right.\end{array}$$

and

$$\begin{array}{}\text{(13)}& \left\{\begin{array}{l}{\mathit{\upsilon }}_{j,\mathrm{4}}={\sum }_{n=\mathrm{1}}^{\mathrm{\infty }}{\mathit{\lambda }}_{j,n}\sin r_{j,n}y\exp \left[-s_{j,n}\left(l_{j+\mathrm{1}}-x\right)\right],\\ u_{j,\mathrm{4}}={\sum }_{n=\mathrm{1}}^{\mathrm{\infty }}{\mathit{\lambda }}_{j,n}\left(A_{j,n}^{\prime }\cos r_{j,n}y+B_{j,n}^{\prime }\sin r_{j,n}y\right)\\ \exp \left[-s_{j,n}\left(l_{j+\mathrm{1}}-x\right)\right],\\ {\mathit{\zeta }}_{j,\mathrm{4}}=\frac{i{h}_j}{\mathit{\sigma }}{\sum }_{n=\mathrm{1}}^{\mathrm{\infty }}{\mathit{\lambda }}_{j,n}\left(C_{j,n}^{\prime }\cos r_{j,n}y+D_{j,n}^{\prime }\sin r_{j,n}y\right)\\ \exp \left[-s_{j,n}\left(l_{j+\mathrm{1}}-x\right)\right],\end{array}\right.\end{array}$$

where α_j, β_j, r_j,n and s_j,n are equal to the following:

$$\begin{array}{}\text{(14)}& {\displaystyle }{\mathit{\alpha }}_j={\displaystyle \frac{{\mathit{\nu }}_j}{{\left(\mathrm{1}-i{\mathit{\mu }}_j\right)}^{\mathrm{1}/\mathrm{2}}}}{k}_j,\text{(15)}& {\displaystyle }{\mathit{\beta }}_j={\left(\mathrm{1}-i{\mathit{\mu }}_j\right)}^{\mathrm{1}/\mathrm{2}}{k}_j,\text{(16)}& {\displaystyle }{r}_{j,n}={\displaystyle \frac{n\mathit{\pi }}{W_j}},\end{array}$$

and

$$\begin{array}{}\text{(17)}& s_{j,n}={\left(r_{j,n}^{\mathrm{2}}+{\mathit{\alpha }}_j^{\mathrm{2}}-{\mathit{\beta }}_j^{\mathrm{2}}\right)}^{\frac{\mathrm{1}}{\mathrm{2}}},\end{array}$$

in which $k_j=\mathit{\sigma }/c_j$ is the wave number, with $c_j=\sqrt{g{h}_j}$ being the wave speed of the Kelvin wave in the absence of friction. The parameters s_j,n in Eq. (17) are of fundamental importance in determining the characteristic of the Poincaré modes. If $\mathrm{Re}({\mathit{\beta }}_j^{\mathrm{2}}-{\mathit{\alpha }}_j^{\mathrm{2}}{)}^{\mathrm{1}/\mathrm{2}}<\mathit{\pi }/W_j$, all Poincaré modes are bound in the vicinity of the open, connecting or closed cross sections (see Fang and Wang, 1966; Hendershott and Speranza, 1971, for an absence of friction), while if $\mathrm{Re}({\mathit{\beta }}_j^{\mathrm{2}}-{\mathit{\alpha }}_j^{\mathrm{2}}{)}^{\mathrm{1}/\mathrm{2}}>n\mathit{\pi }/W_j$, the nth and lower-order Poincaré modes are propagating waves. In the present study, the inequality $\mathrm{Re}({\mathit{\beta }}_j^{\mathrm{2}}-{\mathit{\alpha }}_j^{\mathrm{2}}{)}^{\mathrm{1}/\mathrm{2}}<\mathit{\pi }/W_j$ holds for all rectangular areas shown in Fig. 3, so that all Poincaré modes in the present study appear in a bound form. The parameter s_j,n has two complex values for each n, and here we choose the one that has a positive real part. To satisfy the equations in Eq. (3), ($A_{j,n},B_{j,n},C_{j,n},D_{j,n}$) and ($A_{j,n}^{\prime },B_{j,n}^{\prime },C_{j,n}^{\prime },D_{j,n}^{\prime }$) should be as follows:

$$\begin{array}{}\text{(18)}& {\displaystyle }{A}_{j,n}={\displaystyle \frac{\left[{\left({\mathit{\mu }}_j+i\right)}^{\mathrm{2}}+{\mathit{\nu }}_j^{\mathrm{2}}\right]r_{j,n}{s}_{j,n}}{{\left({\mathit{\mu }}_j+i\right)}^{\mathrm{2}}{r}_{j,n}^{\mathrm{2}}+{\mathit{\nu }}_j^{\mathrm{2}}{s}_{j,n}^{\mathrm{2}}}}{s}_{j,n},\text{(19)}& {\displaystyle }{B}_{j,n}={\displaystyle \frac{{\mathit{\nu }}_j\left({\mathit{\mu }}_j+i\right)\left({\mathit{\alpha }}_j^{\mathrm{2}}-{\mathit{\beta }}_j^{\mathrm{2}}\right)}{{\left({\mathit{\mu }}_j+i\right)}^{\mathrm{2}}{r}_{j,n}^{\mathrm{2}}+{\mathit{\nu }}_j^{\mathrm{2}}{s}_{j,n}^{\mathrm{2}}}},\text{(20)}& {\displaystyle }{C}_{j,n}=r_{j,n}-s_{j,n}{A}_{j,n},\text{(21)}& {\displaystyle }{D}_{j,n}=-s_{j,n}{B}_{j,n},\text{(22)}& {\displaystyle }{A}_{j,n}^{\prime }=-A_{j,n},\text{(23)}& {\displaystyle }{B}_{j,n}^{\prime }=B_{j,n},\text{(24)}& {\displaystyle }{C}_{j,n}^{\prime }=C_{j,n},\end{array}$$

and

$$\begin{array}{}\text{(25)}& D_{j,n}^{\prime }=-D_{j,n}.\end{array}$$

Equations (10) and (11) represent Kelvin waves propagating in the −x and x directions, respectively; and Eqs. (12) and (13) represent two families of Poincaré modes bound along the cross sections x=l_j and l_j+1 in the jth rectangular area, respectively. The coefficients ($a_j,b_j,{\mathit{\kappa }}_{j,n},{\mathit{\lambda }}_{j,n}$) determine amplitudes and phase lags of Kelvin waves and Poincaré modes. These coefficients must be chosen to satisfy the boundary conditions, preferably using the collocation approach.

2.3 Defant's collocation approach

The collocation approach was first proposed by Defant in 1925 (see Defant, 1961) and is convenient in determining the coefficients ($a_j,b_j,{\mathit{\kappa }}_{j,n},{\mathit{\lambda }}_{j,n}$). In the simplest case, that is, if the model domain contains only a single rectangular area, then J=1 and the index j has only one value: j=1, the calculation procedure can be as follows. First, we truncate each of the two families of Poincaré modes in Eqs. (12) and (13) at the N₁th order so that the number of undetermined coefficients for two families of Poincaré modes is 2N₁ and the total number of undetermined coefficients (plus those for a pair of Kelvin waves) is thus 2N₁+2. To determine these unknowns, we take equally spaced N₁+1 dots, which are called collocation points, located at $y=w_{\mathrm{1},\mathrm{1}}+\frac{W_{\mathrm{1}}}{\mathrm{2}(N_{\mathrm{1}}+\mathrm{1})}$, $w_{\mathrm{1},\mathrm{1}}+\frac{\mathrm{3}{W}_{\mathrm{1}}}{\mathrm{2}(N_{\mathrm{1}}+\mathrm{1})}$, …, $w_{\mathrm{1},\mathrm{1}}+\frac{\left(\mathrm{2}{N}_{\mathrm{1}}+\mathrm{1}\right)W_{\mathrm{1}}}{\mathrm{2}(N_{\mathrm{1}}+\mathrm{1})}$ on both cross sections x=l₁ and l₂. At these points, one of the boundary conditions given by Eqs. (6) to (8) should be satisfied, which yields 2N₁+2 equations. By solving this system of equations, we can obtain 2N₁+2 coefficients ($a_{\mathrm{1}},b_{\mathrm{1}},{\mathit{\kappa }}_{\mathrm{1},n},{\mathit{\lambda }}_{\mathrm{1},n}$). Because the high-order Poincaré modes, which have great values of n and s_1,n in Eqs. (12) and (13), decay from the boundary very quickly, it is generally necessary to retain only a few lower-order terms. In the above single-rectangle case, the spacing of collocation points is equal to $\mathrm{\Delta }y=W_{\mathrm{1}}/(N_{\mathrm{1}}+\mathrm{1})$.

For J>1, that is, when the model contains multiple rectangular areas connected one by one, we can treat the approach in the following way. First, we may choose a common divisor of W₁, W₂, …, W_J as a common spacing, which is denoted by Δy, for all areas. For the jth rectangle (Fig. 3), we may select the collocation points at $y=w_{j,\mathrm{1}}+\frac{\mathrm{\Delta }y}{\mathrm{2}}$, $w_{j,\mathrm{1}}+\frac{\mathrm{3}\mathrm{\Delta }y}{\mathrm{2}}$, …, $w_{j,\mathrm{2}}-\frac{\mathrm{\Delta }y}{\mathrm{2}}$ on the cross sections x=l_j and $x=l_{j+\mathrm{1}}$, where $w_{j,\mathrm{2}}=w_{j,\mathrm{1}}+W_j$. The number of collocation points on each cross section in this area is equal to $W_j/\mathrm{\Delta }y$. Thus the number of undetermined coefficients for the Poincaré modes is selected to be $N_j=(W_j/\mathrm{\Delta }y)-\mathrm{1}$. Accordingly, there will be in total ${\sum }_{j=\mathrm{1}}^J(\mathrm{2}{N}_j+\mathrm{2})$ collocation points in J areas. Note that on the cross section connecting Areaj and Area(j+1), the collocation points that belong to Areaj and those that belong to Area(j+1) are located at the same positions. For the points located on the open or closed boundaries, Eqs. (6) to (8) are applicable, while for the points located on the cross sections connecting two areas, Eq. (9) should be applied. From these ${\sum }_{j=\mathrm{1}}^J(\mathrm{2}{N}_j+\mathrm{2})$ equations, we can obtain ${\sum }_{j=\mathrm{1}}^J(\mathrm{2}{N}_j+\mathrm{2})$ coefficients ($a_j,b_j,{\mathit{\kappa }}_{j,n},{\mathit{\lambda }}_{j,n}$), in which j=1, 2, …, J and n=1, 2, …, N_j.

3 Tidal dynamics of the Korea Strait

As noted by Odamaki (1989b), the co-oscillating tides are dominant in the JS, which is mainly induced by inputs at the opening of the KS rather than those through the Tsugaru Strait (TGS) and Soya Strait (SYS). Furthermore, our study focuses on the KS, in which influences of the tide-generating force and the inputs from the TGS and SYS are negligible. Therefore, we idealize the KS–JS basin as a semi-enclosed basin with a sole opening connected to the ECS and study the co-oscillating tides generated by the tidal waves from the ECS through the opening.

3.1 Model configuration and parameters for the Korea Strait and Japan Sea

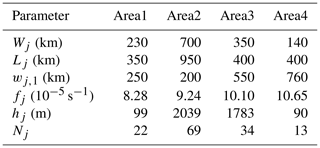
To establish an idealized analytical model for the KS–JS basin, we use four rectangular areas as shown in Fig. 4 to represent the study region. The first rectangle, designated as Area1, represents the KS, which is our focus area. According to the shape of its coastline, we use three rectangles designated as Area2 and Area3 to represent the JS. We place the x axis parallel to but 200 km away from the southeast sidewall of the KS (that is w_1,1 in Fig. 3 is equal to 200 km), and the y axis is in the direction perpendicular to the x axis through the opening of the KS (Fig. 4). The selected depths are the mean depths calculated based on the topographic dataset ETOPO1. The K₁ and M₂ angular velocities are equal to $\mathrm{7.2867}\times {\mathrm{10}}^{-\mathrm{5}}$ and $\mathrm{1.4052}\times {\mathrm{10}}^{-\mathrm{4}}$ s⁻¹, respectively. The details of the model parameters can be found in Table 1.

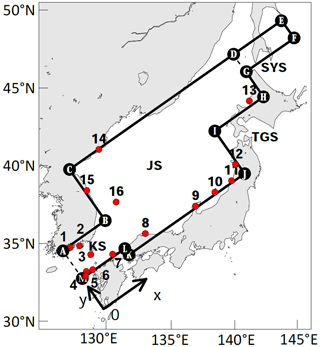
Figure 4 Idealized model domain fitting the Korea Strait and Japan Sea. The dashed line represents an open boundary, and the solid lines represent closed boundaries. A, B, …, M indicate the localities of the points used in Fig. 6 for model–observation comparison. Numbered red dots are tidal gauge stations where the observed harmonic constants are used for model validation in Table 2.

Based on the depths listed in Table 1, the wavelengths of the K₁ Kelvin waves in these four areas are 2686, 12 189, 11 398 and 2561 km, respectively, and those of the M₂ Kelvin waves are 1393, 6321, 5911 and 1328 km, respectively. Because the widths of the areas are all smaller than half the corresponding Kelvin wavelengths, the inequality $\mathrm{Re}({\mathit{\beta }}_j^{\mathrm{2}}-{\mathit{\alpha }}_j^{\mathrm{2}})<\mathit{\pi }/W_j$ as stated in the Sect. 2.2 is satisfied (see also Godin, 1965; Fang and Wang, 1966; Wu et al., 2018), Thus the Poincaré modes can only exist in a bound form.

Table 1 Parameters used in the model.

In addition to the parameters listed in Table 1, we need to estimate the parameters ${\mathit{\mu }}_{M_{\mathrm{2}}}$ and ${\mathit{\mu }}_{K_{\mathrm{1}}}$ as defined by Eq. (4). Since M₂ has the largest tidal current in the KS (Teague et al., 2001), and we assume that the tidal currents are rectilinear, the linearized frictional coefficient for M₂ is approximately equal to the following, after Pingree and Griffiths (1981), Fang (1987) and Inoue and Garrett (2007),

$$\begin{array}{}\text{(26)}& {\mathit{\gamma }}_{M_{\mathrm{2}}}\approx {\displaystyle \frac{C_{\mathrm{D}}}{h}}{\displaystyle \frac{\mathrm{8}}{\mathrm{3}\mathit{\pi }}}{U}_{M_{\mathrm{2}}}\left(\mathrm{1}+{\displaystyle \frac{\mathrm{3}}{\mathrm{4}}}{\sum }_{i=\mathrm{2},\mathrm{3},\mathrm{\dots }}{\mathit{ϵ}}_i^{\mathrm{2}}\right),\end{array}$$

where C_D is the drag coefficient and $U_{M_{\mathrm{2}}}$ is the tidal current amplitude of M₂, ${\mathit{ϵ}}_i=U_i/U_{M_{\mathrm{2}}}$, with U_i representing the tidal current amplitude of the constituent i (here, we designate i=1 for M₂ and i=2, 3, …for any constituents other than M₂). According to Fang (1987) and Inoue and Garrett (2007), the linearized frictional coefficient for the non-dominant constituent i is approximately equal to the following:

$$\begin{array}{}\text{(27)}& {\mathit{\gamma }}_i\approx {\displaystyle \frac{C_D}{h}}{\displaystyle \frac{\mathrm{4}}{\mathit{\pi }}}{U}_{M_{\mathrm{2}}}\left(\mathrm{1}+{\displaystyle \frac{{\mathit{ϵ}}_i^{\mathrm{2}}}{\mathrm{8}}}+{\displaystyle \frac{\mathrm{1}}{\mathrm{4}}}{\sum }_{\begin{array}{l}k=\mathrm{2},\mathrm{3},\mathrm{\dots }\\ k\ne i\end{array}}{\mathit{ϵ}}_k^{\mathrm{2}}\right).\end{array}$$

Inserting Eqs. (26) and (27) into Eq. (4), we can obtain the parameter μ. Teague et al. (2001) provided tidal current harmonic constants at 10 mooring stations along two cross sections in the KS. The averaged values of the major semi-axes of the tidal current ellipses at these stations are 0.154, 0.119, 0.101 and 0.062 m s⁻¹ for M₂, K₁, O₁ and S₂, respectively. Here, we use these values and C_D≈0.0026 to estimate the parameters in Eqs. (26) and (27). Then, after inserting these values into Eq. (4), we obtain rough estimates of ${\mathit{\mu }}_{M_{\mathrm{2}}}$ and ${\mathit{\mu }}_{K_{\mathrm{1}}}$ for the KS (Area1), which are approximately 0.05 and 0.09, respectively. Since the JS is much deeper and has much weaker tidal currents than the KS, we simply let ${\mathit{\mu }}_{K_{\mathrm{1}}}={\mathit{\mu }}_{M_{\mathrm{2}}}=\mathrm{0}$ for both Area2 and Area3.

For the collocation approach, we take 10 km as the spacing between collocation points. Thus in this model, a total of 198 collocation points are used to establish 256 equations, and the parameters of 3 pairs of Kelvin waves and 125 pairs of Poincaré modes can be obtained. Along the open boundary of the KS, the open-boundary condition Eq. (8) is employed, with the value of $\widehat{\mathit{\zeta }}$ equal to the observed harmonic constants from the global tide model DTU10 (Cheng and Anderson, 2011). Along the cross sections connecting Area1 with Area2 and Area2 with Area3, the matching conditions Eq. (9) are applied. Along the solid cross sections, condition Eq. (6) is used.

3.2 Model results and validation

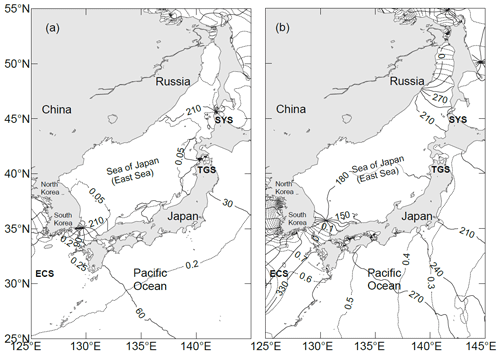
The obtained analytical solutions of the K₁ and M₂ tides using the extended Taylor method are shown in Fig. 5a and b, respectively. The maximum amplitude of the K₁ tide is 0.34 m, which appears at the southwest corner of the KS. The amplitude decreases from southwest to northeast, and a counter-clockwise tidal wave system occurs in the northeast part of the KS, with amplitudes less than 0.05 m near the amphidromic point. A co-tidal line with a phase lag of 210^∘ runs from the amphidromic point in the KS into the southwest JS.

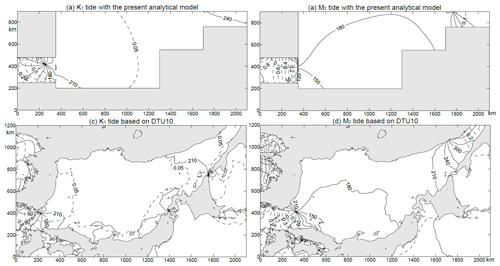
Figure 5 Comparison of tidal system charts. (a) K₁ and (b) M₂ tides from the present theoretical model and (c) K₁ and (d) M₂ tides from DTU10 (Cheng and Andersen, 2011).

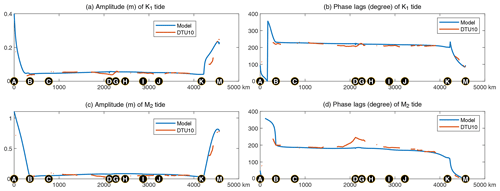
Figure 6 Comparison of model results (blue) and observations based on DTU10 (orange) along the coasts. (a) K₁ amplitudes, (b) K₁ phase lags, (c) M₂ amplitudes, and (d) M₂ phase lags. The locations of the points A, B, C, D, G, H, I, J K, L and M are shown in Fig. 4.

The maximum amplitude of the M₂ tide is 1.02 m, which appears at the westernmost corner of the KS. The amplitude decreases gradually from southwest to northeast along the direction of the strait, and the amphidromic point occurs at the junction of the KS and JS. The amplitudes near the amphidromic point are lower than 0.1 m, and the phase lags in most parts of the JS vary from 150 to 210^∘. A degenerated amphidromic point appears near the entrance of the Tartar Strait. The comparison with the tidal charts based on data from DTU10 (Fig. 5c, d) shows that the model-produced tidal systems agree fairly well with the observations.

To quantitatively validate the model results, we first extract the data along the solid boundary of the model for comparison as shown in Fig. 6. For the K₁ tide, the model-produced amplitudes and phase lags along the boundary in the JS both agree well with the observed data, although small differences occur at the northern corner of the JS. For the M₂ tide, the greatest phase-lag errors are approximately 64^∘ near the entrance of the Tartar Strait due to the existence of a degenerated amphidromic point near this area (Fig. 2b).

For further validation, we select 16 tide gauge stations where harmonic constants are available from the International Hydrographic Bureau (1930). The station locations are shown in Fig. 4. The result of the comparison is given in Table 2, which also shows that the model results are consistent with the data obtained from gauge observations: the RMS (root mean square) differences of amplitudes of K₁ and M₂ are 0.014 and 0.032 m, respectively; and those of the phase lags are 7.0 and 5.2^∘, respectively.

Table 2 Comparison between harmonic constants from the observations and models at coastal tide gauge stations.

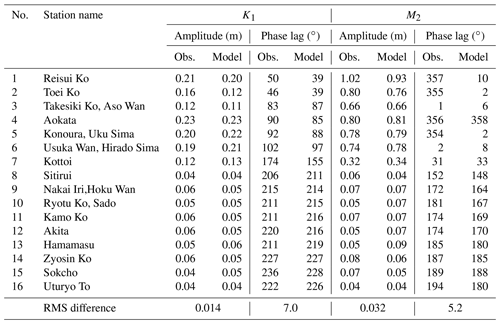
Although the theoretical model greatly simplifies the topography and boundary, the amplitude and phase-lag differences of these two tidal constituents are very small in the KS and its surroundings, and the basic characteristics of the tidal patterns are well retained (Fig. 5). These findings show that the simplification of the model is reasonable and the extended Taylor method is appropriate for modelling the tides in the KS–JS basin. Therefore, it is meaningful to use the model results for theoretical analysis.

3.3 Tidal waves in the Korea Strait

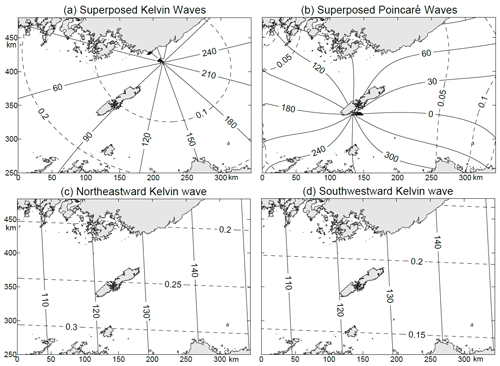
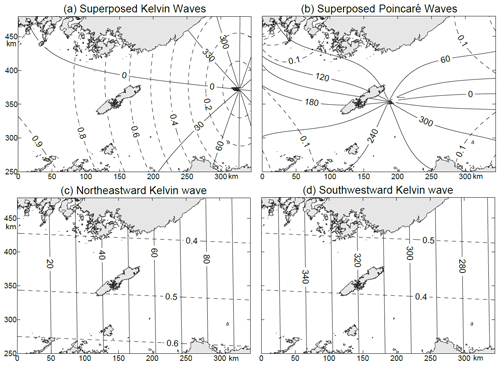
To reveal the relative importance of the Kelvin waves versus Poincaré modes in the modelled Korea Strait, the superposition of Kelvin waves and that of the Poincaré modes are given in Fig. 7a–b for K₁ and in Fig. 8a–b for M₂.

For the K₁ tide in the KS, the superposition of the incident (northeastward) and the reflected (southwestward) Kelvin waves appears as a counter-clockwise amphidromic system, with the amphidromic point located near the middle of the strait, but closer to the southeast coast of Korea (Fig. 7a). The highest amplitude of the superposed Kelvin waves is 0.3 m, and the mean difference from the observations is less than 0.03 m. The superposition of all Poincaré modes has amplitudes of approximately 0.1 m near the cross sections on both left and right sides, and a counter-clockwise amphidromic point exists nearly at the centre of the strait (Fig. 7b). Since the amplitudes of the superposed Poincaré modes are significantly smaller than those of the superposed Kelvin waves, the latter can basically represent the total tidal pattern, including the counter-clockwise amphidromic system.

For the M₂ tide, the highest amplitude of the superposition of two Kelvin waves is approximately 0.95 m, which appears at the southwest corner of the strait (Fig. 8a). The amplitude decreases from southwest to northeast along the strait, and the amphidromic point appears near the cross section connecting to the JS, where a topographic step exists. The maximum deviation of the amplitudes of the superposed Kelvin waves from the observations is 0.06 m, and the structure of the superposed Kelvin waves is consistent with the observation. The amplitudes of the superposed Poincaré modes are generally less than 0.2 m on both left and right sides of the KS, and they decay rapidly towards the middle of the strait, thus forming a counter-clockwise amphidromic system structure (Fig. 8b). Therefore, the M₂ tide in the KS is also mainly controlled by Kelvin waves.

The above results show that the Poincaré modes only exist along the open boundary and the connecting cross section and their amplitudes quickly approach zero away from these cross sections. In fact, these properties of the Poincaré wave are inherent in any narrow strait. Therefore, in the following, we will focus on Kelvin waves and analyse the characteristics of the incident (northeastward) and reflected (southwestward) Kelvin waves.

The incident and reflected K₁ Kelvin waves are shown in Fig. 7c and d, respectively. The area-mean amplitude of the incident Kelvin wave in the KS is 0.248 m, and that of the reflected Kelvin wave is 0.190 m, which is 77 % of the incident Kelvin wave. On the connecting cross section, the section-mean amplitude of the incident Kelvin wave is 0.243 m, and the section-mean phase lag is 151.6^∘. The section-mean amplitude of the reflected Kelvin wave is 0.194 m, which is 80 % of the incident Kelvin wave. The section-mean phase lag is 295.8^∘, indicating that the phase lag increases by 144.2^∘ when the wave is reflected. The amphidromic point of the superposed Kelvin wave is 137 km away from the step and close to the northwest shore of the KS.

The incident and reflected M₂ Kelvin waves are shown in Fig. 8c and d, respectively. The area-mean amplitude of the incident Kelvin wave in the KS is 0.471 m, and that of the reflected Kelvin wave is 0.439 m, which is 93 % of the incident Kelvin wave. This ratio is larger than the K₁ tide because the bottom friction of M₂ is smaller and less energy is lost in the propagation process. On the connecting cross section, the mean amplitude of the incident Kelvin wave is 0.462 m, and the phase lag is 97.9^∘. The mean amplitude of the reflected Kelvin wave is 0.447 m, which is 97 % of the incident Kelvin wave, and the phase lag is approximately 266.4^∘, with a phase-lag increase of 168.5^∘, which is closer to 180^∘ as compared to the corresponding value of the K₁ tide. Accordingly, the M₂ amphidromic point of the superposed Kelvin wave shifts to approximately 21 km away from the step. A comparison between Figs. 7a and 8a shows that the amphidromic point of K₁ is located west of that of M₂. This result reproduces well the observed phenomenon as seen from Fig. 2.

The above results indicate that the relation of the amplitudes and phase lags of the reflected Kelvin wave with the incident wave plays a decisive role in the tidal system in the KS, especially in the formation of amphidromic points, for both the K₁ and M₂ tides.

Figure 7 Decomposed charts for the model-produced K₁ tide in the Korea Strait: (a) contribution of Kelvin waves, (b) contribution of Poincaré modes, (c) northeastward (incident) Kelvin wave and (d) southwestward (reflected) Kelvin wave.

Figure 8 Same as in Fig. 7 but for M₂.

4 Discussion on the formation mechanism of amphidromic points

To explore the tidal dynamics of the KS–JS basin, especially the formation mechanism of amphidromic points, we consider the simplest case: a one-dimensional tidal model in channels. In the one-dimensional case, the amphidromic point is equivalent to the wave node. As previously mentioned, an important feature of the topography of the KS–JS basin is that there is a steep continental slope between the KS and JS, and to the northeast of this slope, the JS is much deeper and wider than the KS. Thus, the channel is idealized to contain two areas, with the first one (Area1) having uniform depth h₁ and uniform width W₁ and the second one (Area2) having uniform depth h₂ and uniform width W₂. Therefore, the idealized channel contains abrupt changes in depth and width at the connection of these two areas. An incident wave enters the first area and propagates toward the second area passing over the topographic step. For simplicity, we neglect friction.

If the second area is semi-infinitely long, allowing for the wave radiating out from the second area freely, then a part of the wave is reflected at the connecting point and another part is transmitted into the second area. The amplitude of the transmitted wave is (see for example Dean and Dalrymple, 1984)

$$\begin{array}{}\text{(28)}& H_{\mathrm{T}}={\mathit{\kappa }}_{\mathrm{T}}{H}_I,\end{array}$$

where H_I is the amplitude of the incident wave and κ_T is called the transmission coefficient, which is equal to

$$\begin{array}{}\text{(29)}& {\mathit{\kappa }}_{\mathrm{T}}={\displaystyle \frac{\mathrm{2}}{\mathrm{1}+\mathit{\rho }}},\end{array}$$

where

$$\begin{array}{}\text{(30)}& \mathit{\rho }={\displaystyle \frac{c_{\mathrm{2}}{W}_{\mathrm{2}}}{c_{\mathrm{1}}{W}_{\mathrm{1}}}}={\displaystyle \frac{\sqrt{h_{\mathrm{2}}}}{\sqrt{h_{\mathrm{1}}}}}{\displaystyle \frac{W_{\mathrm{2}}}{W_{\mathrm{1}}}},\end{array}$$

with $c_j=\sqrt{g{h}_j}$ representing the wave speed in the jth area; j=1, 2. c_j is in fact proportional to $\sqrt{h_j}$. The amplitude of the reflected wave H_R is

$$\begin{array}{}\text{(31)}& H_{\mathrm{R}}={\mathit{\kappa }}_{\mathrm{R}}{H}_I,\end{array}$$

where κ_R is called the reflection coefficient and is equal to the following:

$$\begin{array}{}\text{(32)}& {\mathit{\kappa }}_{\mathrm{R}}={\displaystyle \frac{\mathrm{1}-\mathit{\rho }}{\mathrm{1}+\mathit{\rho }}}.\end{array}$$

If ρ>1, namely, if $\sqrt{h_{\mathrm{2}}}{W}_{\mathrm{2}}>\sqrt{h_{\mathrm{1}}}{W}_{\mathrm{1}}$, then κ_R<0, Eq. (32) can be rewritten in the form

$$\begin{array}{}\text{(33)}& {\mathit{\kappa }}_{\mathrm{R}}={\displaystyle \frac{\mathit{\rho }-\mathrm{1}}{\mathit{\rho }+\mathrm{1}}}\exp (-i\mathit{\pi }).\end{array}$$

The above equation indicates that at the connecting point, the reflected wave changes its phase lag by 180^∘. Therefore, the superposition of incident and reflected waves in Area1 has the minimum amplitude at the connecting point. This theory explains how the reflected wave can be generated by abrupt increases in water depth and basin width, and why the reflected wave there has a phase lag opposite to the incident wave.

The complete solution for this case is as follows (see also Dean and Dalrymple, 1984):

$$\begin{array}{}\text{(34)}& \left\{\begin{array}{l}\mathit{\zeta }\left(x\right)=H_I\left(\exp \mathit{\right\{}-i\left[k_{\mathrm{1}}\left(x-l_{\mathrm{1}}\right)+{\mathit{\theta }}_{\mathrm{1}}\right]\mathit{\}}+\frac{\mathit{\rho }-\mathrm{1}}{\mathit{\rho }+\mathrm{1}}\\ \exp \mathit{\{}-i\left[-k_{\mathrm{1}}\left(x-l_{\mathrm{1}}\right)+\mathrm{2}{\mathit{\chi }}_{\mathrm{1}}+{\mathit{\theta }}_{\mathrm{1}}+\mathit{\pi }\right]\mathit{\}}),\\ l_{\mathrm{1}}\ll x\ll l_{\mathrm{2}}\\ \mathit{\zeta }\left(x\right)=\frac{\mathrm{2}}{\mathrm{1}+\mathit{\rho }}{H}_I\exp \mathit{\{}-i\left[k_{\mathrm{2}}\left(x-l_{\mathrm{2}}\right)+{\mathit{\chi }}_{\mathrm{1}}+{\mathit{\theta }}_{\mathrm{1}}\right]\mathit{\}},\\ l_{\mathrm{2}}\ll x\end{array}\right.\end{array}$$

where θ₁ represents the phase lag of the incident wave at the opening of Area1; $k_j=\mathit{\sigma }/c_j$ is the wave number, with $c_j=\sqrt{g{h}_j}$ representing the wave speed in Areaj, j=1, 2; and χ₁=k₁L₁. This solution for the K₁ and M₂ constituents for h₁=99 m, L₁=350 km, W₁=230 km, h₂=2039 m and W₂=700 km is plotted with the blue curves in Fig. 9.

However, Sect. 3.3 shows that the phase-lag changes of the reflected waves relative to the incident waves are not exactly equal to 180^∘ but rather are smaller than 180^∘, and the discrepancy increases with the decreasing angular frequency. To explain this discrepancy, we improve the above theory by introducing the reflected wave in the second area. In fact, the JS is represented with a semi-closed area in the two-dimensional model (Sect. 3.1), namely, all boundaries except those connected to KS are solid ones (Fig. 4). Therefore, in the following one-dimensional model, the second area is closed at its right end so that the reflection will occur at this end. In this case, the solution becomes more complicated and is dependent on the length of the second area L₂. The reflection coefficient κ_R now has the following form (see Supplement for derivation):

$$\begin{array}{}\text{(35)}& {\mathit{\kappa }}_{\mathrm{R}}=\exp (-i\mathrm{2}\mathit{\delta }),\end{array}$$

in which δ is determined by the following equations:

$$\begin{array}{}\text{(36)}& \left\{\begin{array}{l}\cos \mathit{\delta }=\frac{\mathrm{1}+\cos \mathrm{2}{\mathit{\chi }}_{\mathrm{2}}}{{\left[{\left(\mathrm{1}+\cos \mathrm{2}{\mathit{\chi }}_{\mathrm{2}}\right)}^{\mathrm{2}}+{\left(\mathit{\rho }\sin \mathrm{2}{\mathit{\chi }}_{\mathrm{2}}\right)}^{\mathrm{2}}\right]}^{\mathrm{1}/\mathrm{2}}},\\ \sin \mathit{\delta }=\frac{\mathit{\rho }\sin \mathrm{2}{\mathit{\chi }}_{\mathrm{2}}}{{\left[{\left(\mathrm{1}+\cos \mathrm{2}{\mathit{\chi }}_{\mathrm{2}}\right)}^{\mathrm{2}}+{\left(\mathit{\rho }\sin \mathrm{2}{\mathit{\chi }}_{\mathrm{2}}\right)}^{\mathrm{2}}\right]}^{\mathrm{1}/\mathrm{2}}},\end{array}\right.\end{array}$$

where χ₂=k₂L₂. Equation (36) indicates that the length, width and depth of Area2 are also important in determining the phase-lag increase of the reflected wave relative to the incident wave in Area1. Comparison of Eq. (35) with Eq. (33) indicates that the phase-lag increase is now 2δ instead of π. The difference $\mathrm{\Delta }=\mathit{\pi }-\mathrm{2}\mathit{\delta }$ characterizes the influence of Area2 upon the phase-lag increase at the connection of two areas. To show the influence of the length, width and depth of Area2 on the value of Δ, we first retain the width and depth unchanged and increase the length by 10 %; it is shown that the value of Δ for K₁ is reduced by 15 % (reduced to 10.44^∘ from 12.27^∘) and that the value of Δ for M₂ is reduced by 37 % (reduced to 2.37^∘ from 3.78^∘). Next we retain the length and depth unchanged and increase the width by 10 %; it is shown that the value of Δ for K₁ is reduced by 9 % (reduced to 11.16^∘ from 12.27^∘) and that the value of Δ for M₂ is reduced by 9 % (reduced to 3.44^∘ from 3.78^∘). Then we retain the length and width unchanged and increase the depth by 10 %; it is shown that the value of Δ for K₁ increases by 1 % (increases to 12.42^∘ from 12.27^∘) and that the value of Δ for M₂ increases by 9 % (increases to 4.12^∘ from 3.78^∘).

The complete solution for this case is as follows:

$$\begin{array}{}\text{(37)}& \left\{\begin{array}{l}\mathit{\zeta }\left(x\right)=H_I\left(\exp \mathit{\right\{}-i\left[k_{\mathrm{1}}\left(x-l_{\mathrm{1}}\right)+{\mathit{\theta }}_{\mathrm{1}}\right]\mathit{\}}\\ +\exp \mathit{\{}-i\left[-k_{\mathrm{1}}\left(x-l_{\mathrm{1}}\right)+\mathrm{2}{\mathit{\chi }}_{\mathrm{1}}+{\mathit{\theta }}_{\mathrm{1}}+\mathrm{2}\mathit{\delta }\right]\mathit{\}}),\\ l_{\mathrm{1}}\ll x\ll l_{\mathrm{2}}\\ \mathit{\zeta }\left(x\right)=\mathit{ϵ}{H}_I\left(\exp \mathit{\right\{}-i\left[k_{\mathrm{2}}\left(x-l_{\mathrm{2}}\right)+\left({\mathit{\chi }}_{\mathrm{1}}+\mathit{\varphi }+{\mathit{\theta }}_{\mathrm{1}}\right)\right]\mathit{\}}\\ +\exp \mathit{\{}-i\left[-k_{\mathrm{2}}\left(x-l_{\mathrm{2}}\right)+\left(\mathrm{2}{\mathit{\chi }}_{\mathrm{2}}+{\mathit{\chi }}_{\mathrm{1}}+\mathit{\varphi }+{\mathit{\theta }}_{\mathrm{1}}\right)\right]\mathit{\}}),\\ l_{\mathrm{2}}\ll x\ll l_{\mathrm{3}}\end{array}\right.\end{array}$$

where $\mathit{\epsilon }=\mathrm{2}{E}^{-\mathrm{1}}$. E and ϕ are determined by the following relations:

$$\begin{array}{}\text{(38)}& \left\{\begin{array}{l}E\cos \mathit{\varphi }=\left(\mathit{\rho }+\mathrm{1}\right)-\left(\mathit{\rho }-\mathrm{1}\right)\cos \mathrm{2}{\mathit{\chi }}_{\mathrm{2}},\\ E\cos \mathit{\varphi }=(\mathit{\rho }-\mathrm{1})\sin \mathrm{2}{\mathit{\chi }}_{\mathrm{2}}.\end{array}\right.\end{array}$$

The first terms on the right-hand side of the two equations in Eq. (37) represent the waves propagating in the positive x direction, and the second terms are those propagating in the negative x direction. This solution for the K₁ and M₂ constituents for the case h₁=99 m, L₁=350 km, W₁=230 km, h₂=2039 m, L₂=1150 km and W₂=700 km is plotted with the red curves in Fig. 9.

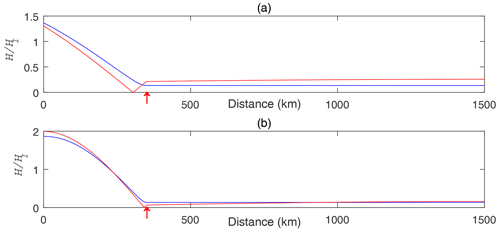
Figure 9 Amplitude distribution along the channel. (a) K₁ and (b) M₂. Blue/red curves are solutions for semi-infinite/finite Area2. The red arrow indicates the position of the connecting point between the Korea Strait and the Japan Sea. Amplitudes are given as ratios to the incident wave in Area1.

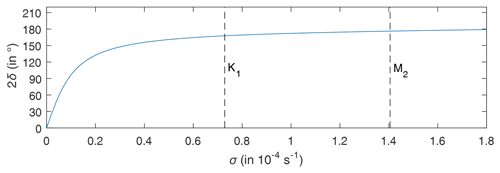
Figure 10 Phase-lag increase of the reflected wave relative to the incident wave as a function of the angular velocity at the connecting point. See the text for details.

Equation (35) indicates that the amplitude of the reflected wave in the first area is equal to that of the incident wave. This result is natural because friction is not considered and no dissipation is present during wave propagation. Equation (35) also indicates that the phase lag of the reflected wave at the connecting point is greater than that of the incident wave at the same point by 2δ. Since the node of the superposition of the incident and reflected waves appears at the place where the phase lags of these two waves are opposite, the first node should appear at Δx away from the connecting point with

$$\begin{array}{}\text{(39)}& \mathrm{\Delta }x=(\mathit{\pi }-\mathrm{2}\mathit{\delta })/\left(\mathrm{2}{k}_{\mathrm{1}}\right).\end{array}$$

The above relationship can also be obtained from the first equation of Eq. (37). The dependence of 2δ on σ for the case h₁=99 m, L₁=350 km, W₁=230 km, h₂=2039 m, L₂=1150 km and W₂=700 km is plotted in Fig. 10. This figure shows that 2δ=0 when σ=0 and 2δ increases with increasing σ, although it is always less than 180^∘. In particular, $\mathrm{2}\mathit{\delta }=\mathrm{167.7}{}^{\circ }$ when $\mathit{\sigma }={\mathit{\sigma }}_{K_{\mathrm{1}}}$ and $\mathrm{2}\mathit{\delta }=\mathrm{176.2}{}^{\circ }$ when $\mathit{\sigma }={\mathit{\sigma }}_{M_{\mathrm{2}}}$. Based on this theory, the M₂ and K₁ amphidromic points should be located at 7.4 and 45.9 km away from the connecting point, respectively. Compared with the two-dimensional model results given in Sect. 3.3, this theory roughly explains one-third of the changes. The remaining two-thirds of the changes may be due to the effect of the Coriolis force. The solution of phase-lag changes at the cross section in the two-dimensional rotating basin involves interactions among three Kelvin waves (an incident and a reflected Kelvin wave in Area1 and a transmitted Kelvin wave in Area2) and two families of Poincaré modes at the connecting cross section (one family in each area). Taylor (1922), Fang and Wang (1966) and Thiebaux (1988) have studied the Kelvin-wave reflection at the closed cross section of semi-infinite rotating two-dimensional channels. In their studies, only two Kelvin waves and one family of Poincaré modes were involved. In comparison to their studies, the present problem is much more complicated. Because of the complexity of the problem, we will presently leave it for a future study.

5 Summary

In this paper, we establish a theoretical model for the KS–JS basin using the extended Taylor method. The model idealizes the study region as three connected flat rectangular areas, incorporates the effects of the Coriolis force and bottom friction in the governing equations, and is forced by observed tides at the opening of the KS. The analytical solutions of the K₁ and M₂ tidal waves are obtained using Defant's collocation approach.

The theoretical model results are consistent with the satellite altimeter and tidal gauge observations, which indicates that the model is suitable and correct. The model reproduces well the K₁ and M₂ tidal systems in the KS. In particular, the model-produced locations of the K₁ and M₂ amphidromic points are consistent with the observed ones.

The model solution provides the following insights into the tidal dynamics in the KS. (1) The tidal system in each rectangular area can be decomposed into two oppositely travelling Kelvin waves and two families of Poincaré modes, with Kelvin waves dominating the tidal system due to the narrowness of the area. (2) The incident Kelvin wave from the ECS through the opening of the KS travels toward the JS and is reflected at the connecting cross section between the KS and JS, where abrupt increases from the KS to JS in water depth and basin width occur. (3) The phase lag of the reflected wave at the connecting cross section increases by less than 180^∘ relative to that of the incident wave, thus enabling the formation of the amphidromic points in the KS. (4) The phase-lag increase of the reflected wave relative to the incident wave is dependent on the angular frequency of the wave and becomes smaller as the angular frequency decreases. This feature explains why the K₁ amphidromic point is located farther away from the connecting cross section in comparison to the M₂ amphidromic point. (5) The length, width and depth of the JS is also important in determining the phase-lag increase of the reflected Kelvin wave in the KS.