the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Can wave coupling improve operational regional ocean forecasts for the north-west European Shelf?
Huw W. Lewis
Juan Manuel Castillo Sanchez
John Siddorn
Robert R. King
Marina Tonani
Andrew Saulter
Peter Sykes
Anne-Christine Pequignet
Graham P. Weedon
Tamzin Palmer
Joanna Staneva
Lucy Bricheno
Operational ocean forecasts are typically produced by modelling systems run using a forced mode approach. The evolution of the ocean state is not directly influenced by surface waves, and the ocean dynamics are driven by an external source of meteorological data which are independent of the ocean state. Model coupling provides one approach to increase the extent to which ocean forecast systems can represent the interactions and feedbacks between ocean, waves, and the atmosphere seen in nature. This paper demonstrates the impact of improving how the effect of waves on the momentum exchange across the ocean–atmosphere interface is represented through ocean–wave coupling on the performance of an operational regional ocean prediction system. This study focuses on the eddy-resolving (1.5 km resolution) Atlantic Margin Model (AMM15) ocean model configuration for the north-west European Shelf (NWS) region.
A series of 2-year duration forecast trials of the Copernicus Marine Environment Monitoring Service (CMEMS) north-west European Shelf regional ocean prediction system are analysed. The impact of including ocean–wave feedbacks via dynamic coupling on the simulated ocean is discussed. The main interactions included are the modification of surface stress by wave growth and dissipation, Stokes–Coriolis forcing, and wave-height-dependent ocean surface roughness. Given the relevance to operational forecasting, trials with and without ocean data assimilation are considered.
Summary forecast metrics demonstrate that the ocean–wave coupled system is a viable evolution for future operational implementation. When results are considered in more depth, wave coupling was found to result in an annual cycle of relatively warmer winter and cooler summer sea surface temperatures for seasonally stratified regions of the NWS. This is driven by enhanced mixing due to waves, and a deepening of the ocean mixed layer during summer. The impact of wave coupling is shown to be reduced within the mixed layer with assimilation of ocean observations. Evaluation of salinity and ocean currents against profile measurements in the German Bight demonstrates improved simulation with wave coupling relative to control simulations. Further, evidence is provided of improvement to simulation of extremes of sea surface height anomalies relative to coastal tide gauges.
- Article
(12202 KB) - Full-text XML
- BibTeX
- EndNote
There is a growing understanding of the role that ocean surface waves play in the Earth system, modulating the exchange of momentum, energy, and other fluxes between the atmosphere and oceans (Cavaleri et al., 2012). A key effect is in absorbing momentum and energy from the atmosphere as waves grow, and releasing it to the ocean when they break.
Prediction systems of the ocean, waves, or atmosphere have typically been developed in relative isolation and with little or no interaction between each component. However, the development of coupled prediction approaches is increasingly enabling research on the sensitivity of the Earth system to wave impacts (e.g. Pullen et al., 2017). Through exchange of information between different model components, coupled systems can begin to explicitly represent the feedbacks and interactions that occur across the air–sea interface in nature. The next evolution in the development of coupled models is in their application to provide improved forecast information to a range of users through operational ocean prediction systems.
This paper discusses the implementation of surface wave effects in an eddy-resolving regional ocean forecasting system of the north-west European Shelf (NWS) through dynamic ocean–wave coupling. The ocean model configuration is the Atlantic Margin Model at 1.5 km resolution (AMM15; Graham et al., 2018a). This is currently used operationally as part of the Copernicus Marine Environment Monitoring Service (CMEMS) in ocean-only mode for which external forcing is provided from a global-scale resolution meteorological forecast system and the effect of waves is mostly omitted other than where implicitly captured within the standard ocean model parameterisations (Tonani et al., 2019, this issue).
AMM15 uses the NEMO ocean model (Nucleus for European Modelling of the Ocean; Madec et al., 2016). Breivik et al. (2015) presented the first discussion of including surface wave effects in NEMO based on global-scale ocean simulations at 1∘ resolution. They included parameterisations for the modification of surface stress from wave growth and dissipation (Janssen et al., 2004), the Stokes–Coriolis force (Hasselmann, 1970), and the turbulent kinetic energy flux from breaking waves (Craig and Banner, 1994). Breivik et al. (2015) demonstrated reduced sea surface and subsurface temperature biases relative to observations, and improved predictions of the total ocean heat content at global scales. This led to the operational implementation of wave-related processes in a coupled ensemble forecast system at the European Centre for Medium-Range Weather Forecasts (ECMWF; e.g. Janssen and Bidlot, 2018). Most recently, these feedbacks have been applied within its coupled reanalysis (Laloyaux et al., 2018).
Law Chune and Aouf (2018) recently discussed the impact of these wave effects in a global NEMO ocean model configuration at higher resolution in the context of aiming to improve the performance of the CMEMS global ocean model forecast system and showed a significant reduction in sea surface temperature (SST) bias focused in tropical regions, driven by the modified momentum flux. In their ocean-only control simulation, SST was generally too warm in semi-enclosed seas, including along western European seas. It was expected that mid-latitude SST would conversely cool due to enhanced stress and mixing, although results showed relatively smaller and more variable impacts than in the tropics. Law Chune and Aouf (2018) also demonstrated enhanced surface current speeds generally, with improved validation relative to observations of the order of 5 %. In agreement with previous work, wave breaking was considered to be the most important wave process for mid-latitude regions while Stokes–Coriolis forcing was found to have relatively little impact on the large-scale validation. A clear future development for this system would be to move from wave forcing to dynamic coupling in order to allow the ocean and wave states to feed back on each other during the simulation.
Cavaleri et al. (2018) argue that the interaction of waves with the ocean is particularly critical in coastal and inner seas, as typically simulated using limited-area or regional ocean model domains. This results from the prevalence of younger, steeper, and shorter-wavelength waves that are more sensitive to variability in the near-surface wind and ocean currents, often with non-linear interactions. A number of studies have assessed the influence of surface waves on regional ocean dynamics, although to date this has often been through a case study approach rather than with an operational focus (Cavaleri et al., 2018).
For example, Clementi et al. (2017) introduced a relatively reduced-complexity coupling of the mean momentum transfer of waves and wind speed stability parameter between the WAVEWATCH III wave model (Tolman et al., 2004) and NEMO ocean model codes. They demonstrated that for the Mediterranean Sea while the coupling was found to improve wave performance, there was limited impact on mean SST results over the 5-year study period. However, focusing on a short-range case study period for a strong storm event showed a marked improvement in the evolution of surface currents relative to observations.
Some of the earliest studies of wave–ocean interactions for regional seas focused on coastal regions of the UK (e.g. Wolf, 2008; Brown and Wolf, 2009; Brown et al., 2011; Bricheno et al., 2013; Bolaños et al., 2014) using the POLCOMS ocean (Holt and James, 2001) and WAM (WAMDI, 1988) wave models. Brown et al. (2011) presented the sensitivity of results to model resolution during an extreme storm and found that representing wave–current interactions in a system with 1.8 km horizontal resolution, most analogous to AMM15 used in this study, gave results as good if not better than using a yet higher resolution (180 m grid).
Several studies have applied the Coupled–Ocean–Atmosphere–Wave–Sediment Transport modelling system (COAWST; Warner et al., 2010) to assess the impact of wave and atmosphere coupling on regional ocean dynamics. For example, Bruneau and Toumi (2016) used a regional model configuration of the Caspian Sea and found that surface wave processes led to enhanced mixing and a relative deepening of the mixed layer depth, particularly in summer. Carniel et al. (2016) applied COAWST for a cold air outbreak episode over the northern Adriatic Sea and found the interaction with waves provided further improved forecast skill beyond that obtained by introducing ocean–atmosphere feedbacks to improve the simulated heat fluxes. The impacts of wave–ocean coupling in the absence of atmosphere feedbacks were considered by Benetazzo et al. (2014).
COAWST has also been implemented for a domain covering the north-west European shelf seas by Reza Hashemi et al. (2015), similar to that used in this study, using a horizontal grid spacing of the order of 4 km (1∕24∘). Their analysis focused on the impact of coupling on the wave simulations for wave energy resource applications (Hashemi and Lewis, 2017). Lewis et al. (2019) used the same COAWST system for the role of tidal dynamics on the wave climate of the Irish Sea.
Staneva et al. (2017) considered the effect of wave forcing from the WAM wave model on NEMO simulations (3.7 km grid resolution) of water level and currents for two extreme storm cases over the North Sea. They found a significant change in simulated storm surge along southern North Sea coasts for each storm, especially in near-coastal areas, and improved representation of observed vertical current profiles. These changes were also predominantly driven by the wave-modified surface stress, with a secondary contribution from Stokes–Coriolis forcing. Staneva et al. (2016a, b) and Schloen et al. (2017) considered the impact of ocean–wave coupling in the near-coastal German Bight region of the southern North Sea. Alari et al. (2016) assessed the implementation of a similar coupled NEMO–WAM system in the Baltic Sea. In this region, use of a wave-modified surface stress led to a relative warming of SST, both due to changes in advection and turbulent fluxes, which reduced the model bias compared with observations. The impact of Stokes–Coriolis feedbacks was constrained to coastal areas.
The role of wave effects on storm surge in the NWS region was also studied by Bertin et al. (2015) for two case studies on the west coast of France in the Bay of Biscay using unstructured model grid approaches. For one case, the predicted storm surge was increased by up to 25 % and much improved relative to observations when using a wave-dependent surface stress in the presence of young and steep waves. For a contrasting case, with larger but more developed waves, coupling did not improve or degrade the forecast quality substantially.
The work presented in this paper aims to inform the future evolution of the operational AMM15 prediction system implemented as part of CMEMS. Lewis et al. (2018b) presented some initial results on the impact of wave coupling on ocean results for a similar configuration based on a series of month-long duration simulations. This study differs in several respects, notably that
- i.
results are presented from 2-year duration simulation trials, enabling more robust statistics to be established across seasonal timescales;
- ii.
simulation experiments make use of the CMEMS operational forecast system for the NWS, using the same sources and treatment of atmospheric forcing and boundary conditions as used in operations;
- iii.
comparisons are made between free-running simulations and those including assimilation of in situ, satellite, and profile ocean observations, enabling new insights into the impact of coupling in assimilative systems.
Note that the studies discussed above were all conducted in the framework of “free running” ocean simulations, with no assimilation of observations active. By explicitly considering the role of ocean assimilation in this study, the likely impact of coupling on operational forecasts can be assessed.
The rest of this paper is organised as follows. The AMM15 coupled model and assimilation configurations are introduced in Sect. 2, along with a discussion of the wave coupling experiments. Results from a first-order evaluation of ocean surface variables against observations are shown in Sect. 3, and comparison against selected research-mode observations is discussed in Sect. 4. Conclusions and proposed next steps for the operational system development are highlighted in Sect. 5.
The sensitivity of ocean predictions to the representation of ocean–wave feedbacks is assessed by running a number of simulation experiments, as summarised in Table 1, covering the 2-year period 2016–2017. Experiments are conducted with and without ocean data assimilation active and with and without wave coupling in order to examine the influence of wave coupling in both free-running and assimilative systems. This leads to a comparison between four configurations, which for brevity will be referred to in this paper as FR (no coupling, no assimilation), DA (no coupling, assimilation), CPL_FR (coupling, no assimilation), and CPL_DA (coupling and assimilation active).
2.1 Regional NEMO ocean model configurations
All simulations have been conducted using the AMM15 configuration of the NEMO ocean model (Madec et al., 2016). Full details on the operational implementation of the AMM15 configuration for CMEMS are provided by Tonani et al. (2019, this issue). The science settings and further background on model performance are detailed by Graham et al. (2018a, b). Through use of a 1.5 km grid spacing, sufficient to resolve the internal Rossby radius on the NWS, it has been demonstrated that AMM15 can represent local-scale processes such as eddies, fronts, internal tides, and exchanges across the shelf break.
Meteorological forcing is provided by interpolation from the operational European Centre for Medium-Range Weather Forecasts (ECMWF) global forecast data at around 14 km horizontal resolution and applied at 3-hourly temporal frequency. Surface forcing is implemented using the CORE bulk parameterisations (Large and Yeager, 2004). All simulations are initialised from the same initial condition, based on a 30-year non-assimilative AMM15 run detailed by Graham et al. (2018a). Lateral boundary conditions for the Atlantic are provided every 3 h from the uncoupled Met Office operational 1∕12∘ North Atlantic ocean system (Blockley et al., 2014) and for the Baltic Sea every hour using the operational Baltic Sea products from CMEMS (Berg and Weismann Poulsen, 2012). All simulations are run with a 60 s integration time step. Details of the meteorological forcing, ocean initial condition, and boundary conditions are identical to those described by Tonani et al. (2019, this issue) and are therefore consistent with the current operational implementation of AMM15.
Ocean data assimilation in the DA and CPL_DA runs use the NEMOVAR 3D-variational assimilation scheme (Waters et al., 2015) which employs a multi-variate balance to account for correlations between ocean variables as defined in Weaver et al. (2005). Increments are applied to the 3-D temperature, salinity, u and v velocities, and the sea surface height (SSH). As detailed by King et al. (2018), assimilated observations include in situ and satellite observations of SST and subsurface profile observations of temperature and salinity from Argo floats, XBTs (expendable bathythermographs), CTDs (conductivity, temperature, and depth), gliders, and marine mammals. Sea level anomaly (SLA) observations from satellite altimeters are assimilated in the deep parts of the domain (where the ocean is deeper than 700 m).
2.2 Regional WAVEWATCH III wave model configuration
Wave simulations are produced for the NWS using a configuration of the WAVEWATCH III (Tolman et al., 2014) spectral wave model (Saulter et al., 2017). The wave model is defined to cover the same domain extent as AMM15, but using a spherical multiple cell grid refinement approach (Li, 2012), which has variable horizontal resolution nesting from 3 km across much of the domain down to 1.5 km spacing for all cells adjacent to the coast and/or where the depth of a 3 km grid cell would be shallower than 40 m. A wave model global time step of 600 s is used. The wave model is forced by winds from the same ECMWF global atmospheric model as used for ocean forcing at 3-hourly temporal frequency. The influence of the ocean state on wave evolution is already captured in the current operational NWS wave forecasting system through use of previously forecast ocean currents as an additional external forcing (Palmer and Saulter, 2016).
For brevity, the following discussion therefore focuses on the impact of wave effects on the ocean model results only. The case study results presented by Lewis et al. (2018a), for example, suggest that the impact of two-way ocean–wave feedbacks on wave results is limited compared with including ocean processes through external forcing without feedbacks, as currently applied in the Met Office operational wave forecast system.
2.3 Wave–ocean coupling
The implementation of wave–ocean coupling in the AMM15 system follows that described by Lewis et al. (2018b). Coupling between the ocean and wave model components is achieved by exchanging information between NEMO and WAVEWATCH III using the OASIS3-MCT libraries (vn3.0; Valcke et al., 2015). All variables are averaged and exchanged at hourly frequency. Limited-period case study experiments using more frequent exchanges have previously suggested that hourly coupling is sufficient to assess the first-order impact of wave coupling on the ocean state.
The scientific basis for representing wave–ocean interactions in AMM15 is described in Sect. 3 of Lewis et al. (2018b), with technical details of the NEMO ocean model wave coupling code used in this study provided in Appendix B of Lewis et al. (2018b). This implementation closely follows the work of Breivik et al. (2015) and Staneva et al. (2017), and for brevity these details are not repeated here. The associated code is now supported for wider use by the ocean modelling community from NEMO version 4. In brief, the main interactions introduced in the CPL and CPL_DA experiments are
- a.
modification of water-side surface stress on the ocean by wave growth and dissipation (Eq. 3; Lewis et al., 2018b);
- b.
Stokes–Coriolis force in momentum (Eq. 4; Lewis et al., 2018b) and tracer advection equations, using the parameterisation of Breivik et al. (2015);
- c.
wave-height-dependent ocean surface roughness (Eq. 11; Lewis et al., 2018b), following Rascle et al. (2008).
Note that the wave coupling by Lewis et al. (2018b) was applied using the direct flux surface forcing scheme of NEMO, rather than the CORE bulk forcing used here, and using meteorological forcing from the Met Office Unified Model simulations.
As a further improvement from Lewis et al. (2018b), the zonal and meridional components of the wave-modified surface stress (i.e. τocn components) are exchanged directly from WAVEWATCH III to NEMO, rather than defining a fraction of the total atmospheric stress acting on the ocean as in Breivik et al. (2015). This avoids the need for NEMO to recalculate the surface stress using a wave-modified drag coefficient, thereby removing a source of potential inconsistency between the wave and ocean models. However, note that the WAVEWATCH III surface scheme assumes a neutral atmospheric boundary layer, and use of the wave-modified momentum flux may no longer be in equilibrium with heat and humidity fluxes. While initial testing (not shown) indicated a relatively small effect from the change in representation of the surface stress, further work is required to more fully review the representation of the surface momentum across atmosphere, ocean, and wave model codes.
Only wave effects acting on the ocean momentum budget are considered in this study. Wave impacts on the calculation of turbulent heat and moisture fluxes and accounting for the wave energy flux transferred to the ocean are omitted. Instead, the treatment of wave breaking on the surface boundary for TKE (turbulent kinetic energy) is parameterised using the Craig and Banner (1994) scheme, with the default value of the Craig and Banner coefficient of 100 used in all simulations. There is also no explicit treatment of Langmuir turbulence, such as through use of a vortex-force formulation (e.g. Uchiyama et al., 2010), or of ocean bed stress (e.g. Soulsby et al., 1995), both of which may be important in the regional ocean context. These simplifications are appropriate for an initial implementation of wave coupling within the NWS forecast system, given known sensitivities of the vertical mixing and radiation schemes to parameter choices. Future work will need to reassess model tuning when including these additional coupled processes. For example, while several studies have introduced a wave dependence in the TKE parameterisation, the values of this coefficient can be highly variable, and further testing will be required to assess a suitable choice for the range of this parameter in the ocean–wave coupled system.
2.4 Wave effects in the NWS
As highlighted by a number of studies discussed in the introduction, a key driver of ocean dynamics by waves has been found to be the modification of surface stress. In equilibrium, for a fully developed wind-sea state, the input of momentum to surface waves from the wind is matched by its dissipation into the ocean, and the water-side stress acting at the top of the ocean, τocn, is equal to the total atmospheric stress, τatm. For younger, growing waves, there is a net input of momentum from the atmosphere to waves (τocn<τatm). Where waves break, the input of momentum from waves to the ocean exceeds the local input atmospheric stress (τocn>τatm). The distribution of τocn∕τatm simulated by WAVEWATCH III is shown in Fig. 1b and e for summer and winter, respectively. The magnitude of changes due to waves is shown to be larger in winter than summer, although common features can be identified in both seasons. Regions of wave breaking are identifiable by darker red shading immediately along western coastlines of the UK, France, and Denmark. Waves tend to enhance the momentum transferred to the ocean in regions of prevailing wave activity – to the north-west of the NWS in winter and more directly west of the NWS in summer. Momentum transfer is also enhanced on average across the Celtic Sea (south-western approaches to the UK) and through the central North Sea, particularly in summer. In contrast, regions to the lee of land such as through the Irish Sea and to the east of the UK are characterised as regions of growing waves where momentum is stored in waves rather than transferred from the atmosphere to the ocean (blue areas in Fig. 1b and e).
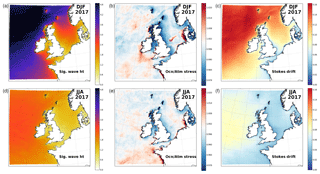
Figure 1Seasonal mean of wave model simulated (a, d) significant wave height, (b, e) fraction of ocean to atmosphere surface stress, and (c, f) Stokes drift speed during (a–c) winter 2016/2017 and (d–f) summer 2017.
Also shown are seasonal mean distributions of simulated significant wave height (Fig. 1a, d) and Stokes drift speed (Fig. 1c, f). The Stokes drift speed generally increases with wave height (and forcing wind speed), with highest seasonal mean values of up to 16 cm s−1 in regions of greatest wave activity across north-western approaches to the UK. There is also a dependency on water depth, leading to lower values (approximately 5 cm s−1) in near-coastal regions.
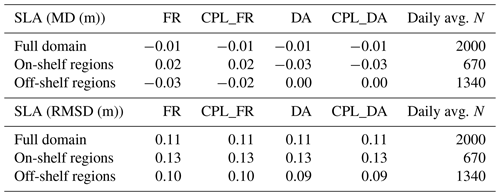
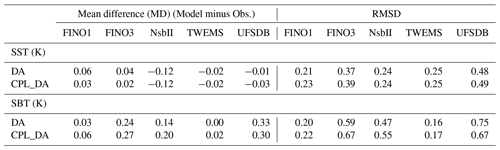
Differences between observed and model values for assimilated variables (SST, SLA, and profiles of temperature and salinity) are calculated in each experiment, from which summary metrics for each 2-year trial can be compared. While not fully independent, when assimilation is active, differences to observations are computed using the model background before assimilation (King et al., 2018). Resulting mean difference (MD, expressed here as (Model Background minus Observation) and root-mean-square difference (RMSD) statistics, averaged across the AMM15 domain and covering the full 2016–2017 period, are given for SST against in situ data in Table 2 and for SLA in Table 3.
Table 2SST mean difference (MD = Model minus Observation), and root-mean-square difference (RMSD) statistics computed over 2-year period (2016–2017) comparing each simulation experiment with available in situ observations. The daily average number of observations (N) used for each comparison is also listed.
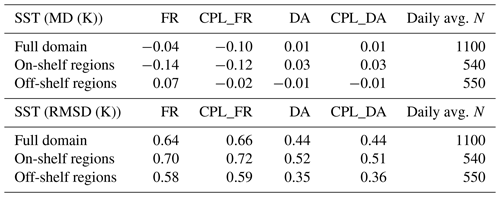
Table 3SLA mean difference (MD = Model minus Observation) and root-mean-square difference (RMSD) statistics computed over the 2-year period (2016–2017) comparing each simulation experiment with satellite altimeter observations. Results are listed separately for the full model domain and discriminating between areas on-shelf and off-shelf.
In general, the statistics in Tables 2 and 3 show relatively small differences between simulations with and without wave coupling. The biggest impact is seen in MD scores for SST, with a cold model bias (MD < 0) in the FR results made worse with coupling (i.e. in the CPL_FR simulation), for example, from −0.04 to −0.1 K relative to in situ observations across the full domain. This signal is dominated by compensating biases on and off the shelf in FR (i.e. in shallower and deeper water). When comparing with on-shelf observations only, the FR and CPL_FR results are more similar (MD = −0.14 and −0.12 K, respectively). The corresponding difference in RMSD is relatively small (of the order of 2 %). When SST observations are assimilated as in the operational CMEMS system, statistics are improved and the difference between DA and CPL_DA is negligible, with neither system demonstrating clearly better performance in terms of summary metrics.
Results for SLA comparisons against observations are summarised in Table 3 and are similarly consistent between simulations with and without wave coupling over the 2-year trial period, regardless of whether runs were with or without assimilation.
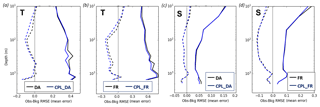
Figure 2Vertical profiles of (dashed lines) Observation minus Model differences and (solid lines) RMSD statistics for ocean-only and coupled simulations, computed over 2-year simulation period (2016–2017) for (a, b) temperature and (c, d) salinity, comparing runs (a, c) with and (b, d) without assimilation.
A comparison of the variation in mean statistics with depth for simulated temperature and salinity against observed profiles during 2016 and 2017 is shown in Fig. 2. The average temperature error profiles show that, in contrast to SST results (Table 2), over much of the ocean depth wave feedbacks result in warming (model increasingly larger than observations). Over all depths, the RMSD is marginally lower for CPL_FR than FR (Fig. 2b), and this impact is preserved across most depths in the comparison of CPL_DA with DA in Fig. 2a. Salinity error profiles (Fig. 2c, d) are unaffected by coupling away from the surface layers, where the RMSD for CPL_FR is on average slightly reduced relative to FR. However, this impact is greatly reduced when comparing the assimilative results.
Given that wave coupling has been applied in a system that has been optimised to run operationally in an uncoupled mode (most analogous to the DA configuration here) with no subsequent tuning of the ocean model physics or assimilation, it is encouraging that these summary results are generally neutral. This indicates that the addition of coupled wave processes is a viable evolution for the NWS forecast system and an initial operational implementation would not be anticipated to degrade forecast quality in terms of summary verification metrics. However, as discussed by Tonani et al. (2019, this issue) for example, ocean model assessment in terms of such metrics does not provide a sufficient evaluation of the system, particularly when considering regional configurations at eddy-resolving scales. Section 4 therefore presents a more detailed analysis of the impact of wave coupling across the NWS in the AMM15 system.
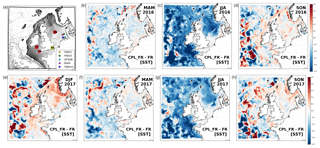
Figure 3(a) Illustration of AMM15 model bathymetry (see Tonani et al., 2019, for more details) and location of NWS observing sites referenced in the paper. The filled-shading region indicates where model bathymetry in less than 200 m depth and highlights the region on the shelf. Elsewhere contour lines are drawn every 500 m depth. Filled circles are at “Celtic Sea”, “Perranporth” and “North Sea” sites (see Sect. 4.1, 4.3). Starred locations in the German Bight are listed in the legend (see Sect. 4.2, 4.4). The yellow square is the “Sheerness” tide gauge (see Sect. 4.5). (b–h) Difference in seasonal mean SST (CPL_FR minus FR) due to wave coupling calculated as 3-month means from spring 2016 to autumn 2017.
4.1 Sea surface temperature (SST)
The impact of wave coupling on simulated SST, in the absence of data assimilation, is shown in Fig. 3 as seasonal mean differences between FR and CPL_FR through the 2016–2017 trial period. Figure 3 shows substantial spatial and temporal variability in mean differences due to wave effects in the eddy-dominated deeper ocean off the NWS to the west of the model domain. In contrast, results on the shallow NWS show relatively little inter-annual variation in the impact of coupling, with a consistent spatial distribution of differences for a given season in both 2016 and 2017. Figure 3b also highlights that the impact of wave coupling takes relatively little time to spin up from common initial conditions in January 2016. For brevity, the subsequent analysis therefore focuses on results from winter 2016/2017 and spring, summer, and autumn 2017 only as being representative, and results on the NWS as being of primary interest to users of operational forecast data in this region.
Away from the immediate vicinity of coastlines, an annual cycle in the influence of wave coupling on simulated SST can be seen on the NWS, with a mean reduction of up to 0.5 K during summer (Fig. 3c, g). In winter, the impact is a lot more mixed, with much of the NWS having slightly increased SST in the CPL_FR simulation by approximately 0.2 K (Fig. 3e) around frontal systems (Ushant front, Celtic Sea front) and the Norwegian trench, but some areas still show slight warming. On average, the regions most impacted have increased momentum transfer into the ocean in coupled relative to uncoupled simulations (Fig. 1), in both winter and summer, which drives enhanced mixing. These results are consistent with shorter-duration case study experiments presented by Lewis et al. (2018b) and will be discussed in further detail in Sect. 4.3.
The influence of wave coupling is relatively smaller through the Irish Sea, English Channel, and southern North Sea. This is likely to be due to a combination of these areas being well mixed throughout the year (e.g. Huthnance et al., 2009; van Leeuwen et al., 2015), and also coincident with areas of net storage of momentum within growing waves (Fig. 1). The influence of waves in the English Channel and southern North Sea appears to be increased during spring, where the mean SST is slightly increased in CPL_FR relative to FR (Fig. 3b, f).
While the main sensitivity of SST to wave coupling on the NWS can be characterised as a net warming in the winter and cooling in the summer, closer examination shows this pattern can be reversed in the immediate vicinity of some coasts. Most notable differences occur along the south-eastern coast of England.
In contrast to Fig. 3, the mean impact of wave coupling on SST in the simulations with ocean data assimilation is relatively small across all seasons (e.g. Fig. 4 shows summer 2017 results for reference). This was reflected in the consistency of the summary statistics for DA and CPL_DA discussed in Sect. 3. Also shown in Fig. 4 are maps of the largest instantaneous differences in simulated SST between CPL_DA and DA at each model grid cell during the season. This highlights that while the seasonal mean SST differences are small, the instantaneous impact of wave coupling can be non-negligible even for the assimilative systems and of the order of 1 to 2 K. Highest variability in SST due to wave feedbacks is found in off-shelf regions and in the near-coastal regions, particularly where wave breaking is prevalent such as along the eastern Bay of Biscay. There is also notable sensitivity around coasts and seasonal mixing fronts, presumably due to their highly dynamic nature. However, regions with increased sensitivity to wave processes are not necessarily reflected in the distribution of mean SST changes (Fig. 3).
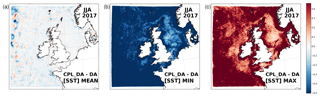
Figure 4Difference in (a) mean SST (CPL_DA minus DA) due to wave coupling between experiments with data assimilation, calculated as a 3-month seasonal mean for summer 2017; and (b) minimum instantaneous difference; (c) maximum instantaneous difference between simulations at each grid point during the 3-month period.
The relative cooling due to waves in summer is reflected in an increase in a mean cool bias of AMM15 between FR and CPL_FR simulations in the summary metrics discussed in Sect. 3. This is also highlighted in Fig. 5, which compares the spatial distribution of RMSD computed between the model and all observations for CPL_DA during 2017, binned in latitude and longitude areas of 0.25∘ spacing across the region where data were assimilated. Differences are negligible with data assimilation active (Fig. 5b), but comparing RMSD for CPL_FR and FR suggests that the regions of greatest cooling coincide with a relative degradation in RMSD, by of approximately 10 %–20 % in the central North Sea and by up to a maximum of 50 % in the Celtic Sea (south-west approaches to the UK, Fig. 5c).
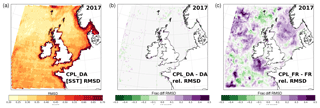
Figure 5(a) Distribution of RMSD for CPL_DA during 2017 comparing simulated SST with all in situ and satellite observations prior to assimilation. (b) Fractional change in RMSD ((CPL_DA – DA)/DA) due to wave coupling in assimilative runs. Panel (c) as (b) comparing RMSD ((CPL – FR)/FR) due to wave coupling for non-assimilating runs. Positive differences (purple shading) indicate a relative degradation of performance with wave coupling.
The comparison against in situ observations on the NWS for each season (not shown) is more variable than Fig. 5, noting that most available sites are located near the coast (e.g. Lewis et al., 2018b). Results are improved for CPL_FR relative to FR at several locations, most notably around southern and eastern UK coasts, although the general pattern is of wave coupling leading to poorer verification scores at many locations.
Example comparisons between model and observations from two locations are highlighted in Fig. 6. Given the high resolution of the ocean model data, and to compensate for potential co-location errors, mean model values in a 5×5 grid cell region around each location point are compared with observations, unless otherwise stated. This may lead to some smoothing of features but is considered to be more representative.
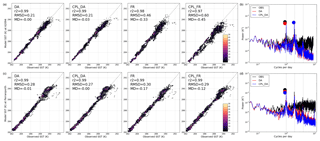
Figure 6(a) Scatter plots comparing hourly simulated SST during 2017 from DA, CPL_DA, FR, and CPL_FR simulations with observed values in the Celtic Sea (buoy 62094; marked CS in Fig. 3a). Summary r2 correlation coefficient, RMSD, and MD (Model minus Observation) statistics are listed for each model run. Shading reflects the number of points within data bins. (b) Computed power spectra (K2) for observed, DA and CPL_DA simulated SST at the Celtic Sea location. Filled circles highlight the amplitude of the peak power for each time series. Vertical dotted lines mark diurnal, semi-diurnal, and quarter-diurnal frequencies. (c) Scatter plots comparing model and observed SST and (d) power spectra computed for time series at the Perranporth coastal buoy (marked PP in Fig. 3a).
The Celtic Sea observation (buoy 62094; marked as “CS” in Fig. 3a) is located to the south of Ireland where the influence of waves on SST was shown to be seasonally varying. The summer cooling results in greater scatter of CPL_FR results relative to observations for warmest temperatures (Fig. 6a). Results from a nearby coastal site on the south-west English peninsula at Perranporth (marked “PP” in Fig. 3a) show relatively warmer simulated SST in summer (warmest temperatures) with wave coupling in improved agreement with observations.
RMSD and MD are relatively crude summary indicators of model performance, in particular for assessing systems which are highly variable in space and time, and when making comparisons to a control system with relatively high skill, as in this study. To gain further insight into model variability, time series of coincident observed and simulated SST were compared spectrally. To support spectral comparison across a wide range of frequencies, the time series were initially “pre-whitened” (i.e. converted to rates of change) by computing the differences of successive values. A linear trend was also removed and a split cosine taper was added to the ends of the detrended series in order to minimise “periodogram leakage” (Weedon et al., 2015). The irregular spacing of the data in time required use of the Lomb–Scargle discrete Fourier transform (Press et al., 1992) and the output periodogram (with 2 degrees of freedom) was smoothed using three applications of a discrete Hanning spectral window thereby increasing the degrees of freedom to 8.
Figure 6 shows that the power spectra of the rates of change of SST at the CS and PP locations are in good agreement with observed spectra for both the DA and CPL_DA simulations (Fig. 6b, d). In particular spectral peaks at the diurnal and semi-diurnal (M2 tide) frequencies are well represented. To formally compare the time series, cross-spectral analysis was used (Weedon et al., 2015). For example, for the SST variability at the diurnal scale, the amplitude ratio of the rate of change of the DA simulation compared to the rate of change of the observations at the CS site is 0.87±0.04 K (±95 % confidence interval). The phase difference at this frequency is 9.3±5.0∘, indicating that at the diurnal scale the DA simulation is approximately in phase with (i.e. not leading or lagging) the observations. Similarly, at the diurnal scale the CPL_DA simulation has an amplitude ratio of 0.77±0.05 K and a phase difference of 8.0±4.9∘.
At periods shorter than the semi-diurnal scale (i.e. at higher frequencies), the average power for both DA and CPL_DA drop relative to observed at the CS and PP buoys. Additionally, a simulated quarter-daily (M4 tide) spectral peak is not detected in the observations. This initial assessment demonstrates the utility of cross-spectral analysis as a tool for assessing model performance and for highlighting areas for required improved representation of high-frequency variability.
4.2 Seabed temperature (SBT)
A collection of observing sites in the German Bight provide a rare source of in situ subsurface temperature observations (Fig. 3a). Figure 7 compares observed seabed temperature (SBT) at the UFSDB (UFS Deutsche Bucht) buoy location with simulations during 2017. Summary statistics for all sites in the region are listed in Table 4 for comparison. In general, results for CPL_DA and DA are very similar, with wave coupling leading to a small degradation in RMSD and MD metrics at all sites other than UFSDB. Given that the German Bight is a well-mixed region of the NWS, the consistency between SST and SBT impacts should be expected. For much of the year, SBT simulations at UFSDB for DA and CPL_DA are in good agreement with observations (correlation coefficient 0.98 for 2017). However, both clearly warm too quickly relative to observed from mid-May, perhaps due to stronger mixing than observed in NEMO, and remain biased warm until early August (noting observations are unavailable from this time until mid-September). In contrast, SST results at this location (not shown) are much more consistent with observations throughout the year (MD of −0.03 K; Table 4). It is notable that the rate of springtime seabed warming is slightly reduced in CPL_DA compared to CPL, and an observed sharp increase in SBT in mid-June is also much better captured with wave coupling.
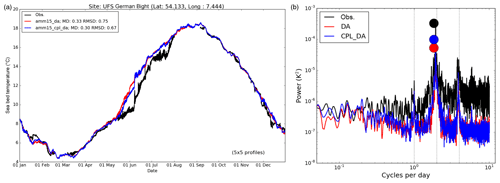
Figure 7(a) Time series of simulated seabed temperature (SBT) during 2017 from DA and CPL_DA simulations and observed values in the German Bight (buoy UFSDB). Summary MD and RMSD statistics are listed for each run. (b) Computed power spectra for observed, DA and CPL_DA simulated SBT. Filled circles highlight the amplitude of the peak power for each time series. Vertical dotted lines mark diurnal, semi-diurnal, and quarter-diurnal frequencies.
Table 4Summary statistics comparing DA and CPL_DA results for sea surface temperature (SST) and seabed temperature (SBT) with co-located observations during 2017 at sites in the German Bight (starred symbols in Fig. 3a).
Power spectra of SBT at UFSDB (Fig. 7b) highlight the overall consistency between CPL_DA and DA, although the spectral peak at semi-diurnal frequency is slightly more pronounced for CPL_DA. Both simulations generally underestimate the amplitude of variability relative to observations at most frequencies.
4.3 Mixed layer depth (MLD) and temperature profiles
To better characterise and understand the impact of wave coupling in the NWS, the evolution of model temperature profiles during 2017 is considered. Figure 8 shows an example of temperature differences due to wave coupling through the shallow NWS depth at a location in the central North Sea (labelled “NS” in Fig. 3a). Results are compared both with and without ocean assimilation, and temperature profiles are averaged daily and across a 5×5 collection of nearby grid cells. Also plotted in Fig. 8 are time series of the ocean-model-diagnosed mixed layer depth (MLD), using the density-based definition of Kara et al. (2000). The annual variation in MLD illustrates that the selected location is seasonally stratified – well mixed during winter and transitioning to being stratified below a shallow mixed layer during summer (e.g. Huthnance et al., 2009).
In summer there is a clear dipole in the structure of temperature differences with relative cooling due to waves through the shallow mixed layer and warming at depth (Fig. 8b, c). The intervening layer within 10 m below the MLD shows large temperature differences (> 1 K). This structure is consistent with a mechanism of enhanced mixing due to a net input of momentum from surface waves (Fig. 1b, e), deepening the MLD, thickening the pycnocline, and encouraging mixing of warmer near-surface water further from the surface. A deepening MLD in summer also implies that surface heating is warming a larger volume of water with wave coupling, thereby leading to a relatively cooler mixed layer and SST (Fig. 3). The model-diagnosed MLD is typically deepened by a few metres between simulations with and without wave coupling in summer. However, differences of up to 10 m (for a MLD which is typically of the order of 20–30 m deep in summer) can be seen for isolated periods of time and specifically during the autumn transition back to a well-mixed state.
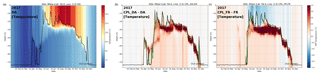
Figure 8Evolution of daily mean temperature profiles through 2017 at a central North Sea location (see Fig. 3a). Temperature differences due to wave coupling are shown in (b) between CPL_DA and DA and in (c) for CPL_FR and FR. The lines plotted show MLD for simulations without wave coupling in black and with wave coupling in green.
Although the AMM15 ocean assimilation scheme has introduced assimilation of temperature profiles, very few are located in the seasonally stratified regions of the NWS (e.g. Fig. 3 of King et al., 2018) and none were available during the 2016–2017 experiment period. It is therefore not surprising that assimilation of SST limits the region of temperature differences due to wave coupling to the mixed layers in Fig. 8b. The impact of wave coupling on the temperature structure at and below the MLD is therefore consistent between the experiments with and without assimilation.
The spatial patterns of seasonal MLD differences due to wave coupling across the NWS (Fig. 9) are most consistent with the pattern of SST differences between CPL_FR and FR (Fig. 3e–h). This result also highlights that the MLD variability on the NWS is mostly temperature driven. The relative deepening by approximately 10 m due to wave coupling through the autumn transition in Fig. 8 is particularly pronounced and widespread throughout the Celtic Sea and along the full extent of the shelf break between Bay of Biscay to the south to Shetland Islands in the north.

Figure 9Seasonal mean differences in simulated mixed layer depth (MLD) in CPL_DA relative to DA during 2017.
The MASSMO4 glider campaign (e.g. Palmer et al., 2018) during spring and summer 2017 provides an independent source of high vertical resolution data against which to assess the simulated MLD results. A glider followed a westward trajectory in the North Atlantic as plotted in Fig. 10a between 21 May and 6 June 2017, crossing the shelf break on 31 May 2017. This time of year coincides with a shallowing mixed layer in seasonally stratified areas of the NWS (e.g. Fig. 8). Figure 10a shows the simulated MLD in the region on 1 June 2016 of about 40 m on the shelf. Figure 10b compares the MLD recalculated from model and observation temperature and salinity data, based on Kara et al. (2000) from vertical profiles measured by the glider. There is considerable variability in MLD during the observed period, which is captured relatively well by all simulations (RMSD of about 9 m). On average, the uncoupled FR and DA results are biased too shallow (by 2.9 m for FR and 2.2 m for DA) while the deepening due to wave coupling results in a smaller MLD difference, although now biased deep (by 0.9 m for CPL_FR and 1.7 m for CPL_DA). Periods when coupled MLD values were deeper than observations occur during late May, when the glider was located on the NWS. In June, when the glider was off-shelf and simulation errors are increased, the impact of wave coupling leads to clearer improvement relative to uncoupled simulations.
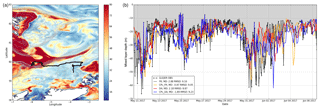
Figure 10(a) Daily mean MLD on 1 June 2017 simulated by FR for a section of the model domain to the north of Scotland. Contours mark the model bathymetry in 50 m intervals and the thick black line marks the glider trajectory. (b) MLD calculated from observed and model profiles following the glider trajectory over the observation period. Grey shading indicates the mixed layer according to glider observations.
This analysis has demonstrated an annually varying cycle in the impact of wave coupling on ocean temperatures on the NWS, associated with a deepening of the mixed layer through enhanced mixing. It is encouraging that the quantitative agreement between model results and observations is not degraded considerably, and improves in some respects. In practice, the ocean model physics (e.g. turbulence and radiation schemes) and assimilation options are developed to provide forecast systems which best match the available observations. To date, these have been developed in a forced-mode ocean-only context. Having established an effective baseline wave-coupled configuration for the NWS, it is clear that further improvements can be realised through revisiting parameter choices within these schemes.
4.4 Salinity
The impact of wave coupling on the NWS sea surface salinity (SSS) during 2017 is summarised by the mean differences between CPL_DA and DA in Fig. 11a. To first-order approximation these results are independent of whether ocean data assimilation was active, so CPL_FR and FR results are omitted. There is also no clear variation in the impact of waves across the different seasons.
As expected, the greatest sensitivity of salinity to wave coupling is focused on areas where river freshwater mixes into the ocean. The net tendency is for increased SSS across NWS in all seasons of up to 1 psu along the Bay of Biscay and German Bight coasts, but more typically less than 0.3 psu across the North Sea, English Channel, and some western UK coastal areas. This suggests that the effect of river freshening is diminished, perhaps through a combination of enhanced vertical mixing or lateral advection. By contrast, wave coupling leads to reduced SSS at the outflow from the Bristol Channel and northward through the Irish Sea.
Schloen et al. (2017) studied the impact of wave coupling on salinity in the southern North Sea in detail using ocean and wave models with unstructured grids based on a month-long simulation, and described how wave-induced transport of salt led to changes in the horizontal salinity distribution in the vicinity of the German Wadden Sea islands. There is remarkably strong agreement between Fig. 11b and the results of Schloen et al. (2017; Fig. 10a) in the distribution of fresher and saltier surface water due to wave coupling over a broader area along the Dutch and German coasts. Both this study and their results show saltier water north and southward of the Wadden Sea islands (fed from the river Ems), and larger increases in salinity along the Danish coast focused near the outflow of the Elbe. Immediately to the west, a dipole of salinity differences occurs at the outflow from the Weser, which leads to relatively fresher water propagating further off-shore into the North Sea. Finally, the impact of wave coupling in a relatively constrained area near the Rhine outflow towards the south in Fig. 11b is characterised by a relative freshening, again in good agreement with Schloen et al. (2017). Apart from some near-coastal differences along eastern England, the distribution of mean seabed salinity (SBS) differences (Fig. 11c) in the region is highly consistent with the SSS results. This implies that wave-induced changes to horizontal rather than vertical mixing processes are dominant. Summary statistics comparing model simulations during 2017 with observed SSS and SBS are listed in Table 5.
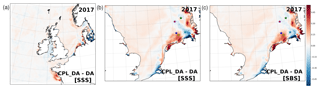
Figure 11(a) Annual mean differences in simulated sea surface salinity (SSS) in CPL_DA relative to DA during 2017. (b) Zoom of annual mean SSS differences across the southern North Sea; and (c) differences in annual mean seabed salinity (SBS) in this region. The location of observing sites in the German Bight referenced in the text are shown (see also Fig. 3a).
Table 5Summary statistics comparing DA and CPL_DA results for sea surface salinity (SSS) and seabed salinity (SBS) with co-located observations during 2017 at sites in the German Bight (starred symbols in Figs. 3a and 11b, c).
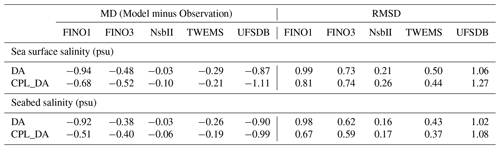
Results in Table 5 reflect the larger sensitivity to wave effects for the three locations closer to the coast, for which summary metrics for both SSS and SBS are markedly improved with wave coupling at FINO1 (yellow star) and TWEMS (dark blue), both located in the area of increased SSS, while results are degraded at UFSDB in the region of freshening salinity (light blue; Fig. 11).
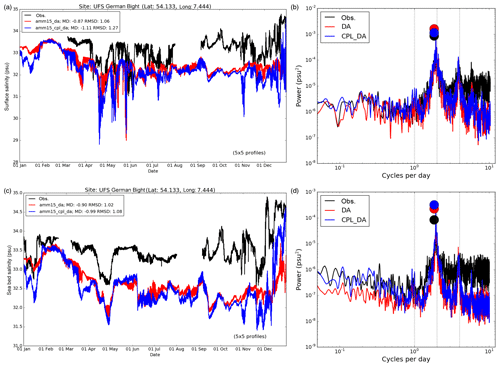
Figure 12(a, c) Time series of observed and simulated salinity at (a) sea surface (SSS) and (c) seabed (SBS) during 2017 from DA and CPL_DA simulations with observed values in the German Bight (buoy UFSDB). (b, d) Computed power spectra for observed, DA, and CPL_DA simulated SSS and SBS, respectively. Filled circles highlight the amplitude of the peak power for each time series. Vertical dotted lines mark diurnal, semi-diurnal, and quarter-diurnal frequencies.
Figure 12 shows a comparison between CPL_DA and DA simulations with observed SSS and SBS through 2017 at UFSDB. Both CPL_DA and DA are clearly too fresh with substantial biases in SSS and SBS. This can be partly attributed to the use of a climatological freshwater boundary condition in the operational AMM15 configuration considered in this study. However, there is also a clear impact of wave coupling on the salinity variability throughout 2017. CPL_DA results show greater variability across the year at both levels, with good correspondence to the observed variability which is not reflected in the summary MD and RMSD metrics. This is demonstrated further by the agreement between power spectra for the observed and simulated time series in Fig. 12b and d. Both simulations reproduce the observed peak at the semi-diurnal M2 tidal frequency (12.42 h) well, with limited impact of wave coupling evident. The results are also consistent at this site for higher frequencies, with further spectral peaks in surface salinity corresponding to the M4 and M6 tidal components. While these spectral peaks are maintained in the salinity simulations at the seabed, they are not observed. This might suggest that accounting for the effects of seabed–wave coupling in shallow seas could lead to further improvement (e.g. Soulsby et al., 1995). Alternatively, this difference in observations could be related to how freshwater flux boundary conditions are distributed vertically in NEMO. There is also a clear difference in the variance in CPL_DA and DA at periods longer than daily, especially for SBS (Fig. 12d). CPL_DA shows improved results compared to DA relative to the observed spectrum. This is consistent with the more qualitative assessment of longer-term variability in Fig. 12c.
Results from the nearby TWEMS buoy, located on the edge of the region of increased salinity in Fig. 11b (dark blue marker in Figs. 3a and 11), are shown in Fig. 13. The increased salinity at TWEMS reduces the negative bias against observations. Power spectra from the 2017 results in Fig. 13b and d highlight a much greater amplitude of the salinity semi-diurnal cycle at both the surface and seabed in the DA simulation than in observations, which is improved for CPL_DA results. Focusing on the time series of SSS and SBS during January 2017 only (Fig. 13a and c) demonstrates a remarkable improvement of the agreement between observed and simulated salinity at both the surface and seabed with the inclusion of wave processes. This change of amplitude suggests the influence of wave coupling in modulating wave–tide interactions in the region (e.g. Lewis et al., 2019), but a more systematic study is beyond the scope of the current work.
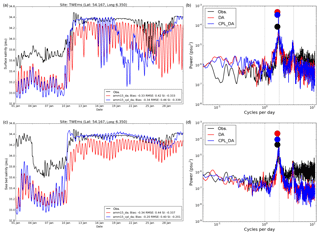
Figure 13(a, c) Time series of observed and simulated salinity at (a) sea surface (SSS) and (c) seabed (SBS) during January 2017 from DA and CPL_DA simulations with observed values in the German Bight (buoy UFSDB). (b, d) Computed power spectra for observed, DA, and CPL_DA simulated SSS, and SBS during all of 2017. Filled circles highlight the amplitude of the peak power for each time series. Vertical dotted lines mark diurnal, semi-diurnal, and quarter-diurnal frequencies.
4.5 Sea surface height (SSH)
The summary statistics presented in Sect. 3 indicate that the net impact of wave processes on sea surface height (SSH) is negligible in terms of long-term statistics for the simulated sea level anomaly (SLA) in comparison with satellite altimeter observations. The spatial distribution of RMSD for each experiment (not shown) indicates generally neutral changes across much of the NWS but improvements of approximately 10 % across the North Sea with wave coupling.
Of more relevance for natural hazard prediction are the extremes of simulated SSH, given the requirement of accurate SSH simulation for warnings of coastal storm surge and inundation. Figure 14 therefore shows the distribution of the largest positive and negative SSH differences between CPL_DA and DA during winter 2016/2017, noting these differences are independent of whether ocean data assimilation was active or not. Greatest variability occurs during winter and autumn seasons, focused around coastlines as might be expected. Instantaneous SSH reductions of up to 10 cm can be found due to wave coupling on the NWS. However, on the western and eastern UK and southern North Sea coastlines, known to be susceptible to storm surges and coastal flooding (e.g. Wolf, 2008), more substantial increases in SSH of over 25 cm are simulated with wave coupling. This result is consistent with the conclusions of Staneva et al. (2017). Impacts along the Bay of Biscay coastline are constrained to areas very close to the coast, in agreement with Bertin et al. (2015).
SSH is a combination of the long-term mean sea level, diurnally varying tide, and additional residuals, mostly driven by meteorological variability as illustrated through storm surges. In order to provide a more quantitative assessment of forecast skill against in situ tide gauge observations around the UK coast, a Doodson X0 low-pass filter is applied to co-located observed and simulated SSH (e.g. Pugh, 1987; Consoli et al., 2004) within each 3-month season. The mean sea level for each simulation or observation site is first removed by computing a long-term mean for each time series. This is beneficial in that any offset errors or drifts between observed and model chart datums and variations across different gauge locations are implicitly removed from the analysis. The low-pass filter then attempts to remove the main tidal variations. The filtered value at each output time, XF(t), is computed separately for each observation and simulated time series from hourly values, X(t), based on Eq. (1) with M=19 samples as
The filter, Fm, provides a weighted average with 30 weights as listed by Consoli et al. (2004).
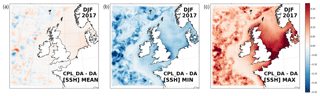
Figure 14Difference in (a) mean SSH (CPL_DA − DA) due to wave coupling between experiments with data assimilation, calculated as a 3-month seasonal mean for winter 2017, and (b) minimum instantaneous difference, (c) maximum instantaneous difference in SSH between simulations at each grid point during the 3-month period.
Figure 15a shows a typical example of filtered SSH observed and simulated at Sheerness on the south-east coast of England (marked “Sh” in Fig. 3a) during winter 2016/2017. Similar results are found for other coastal tide gauge comparisons and times of year. Unlike when considering the total SSH, for which the variability is dominated by tidal energy, there is a clear difference between CPL_DA and DA results for the subtidal (or low-pass filtered) part of the signals (Fig. 15a). In particular, the CPL_DA (and CPL, not shown) simulations give improved agreement with the filtered tide gauge observations when they exceeded 0.4 m on several occasions between late December and mid-January 2018. The peak observed and CPL_DA simulated values above 0.6 m occurred during a period when storm surge warnings were issued for south-eastern England due to coincidence with high tides. In addition to better capturing periods of maximum positive filtered SSH, Fig. 15a shows improved agreement with largest negative SSH during early February 2017. All observed and simulated filtered SSH at Sheerness during 2017 are compared in Fig. 15b, applying separate Doodson filter calculations for each 3-month season. Due to the filtering methodology, the summary RMSD statistics are small (and bias zero by definition), but the CPL_DA results indicate a reduced RMSD and increased correlation coefficients relative to DA results. Most critical, it is clear that the positive and negative tails of the filtered SSH distributions are better captured with wave coupling.
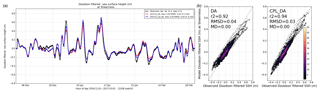
Figure 15(a) Time series of Doodson-filtered SSH for observations and simulation at Sheerness tidal buoy during winter 2016/2017. (b) Scatter plots comparing hourly simulated filtered SSH during all of 2017 from DA and CPL_DA simulations with observed values at Sheerness (marked “Sh” in Fig. 3a). Summary r2 correlation coefficient, RMSD and MD (Model minus Observation) statistics are listed for each model run. Shading reflects the number of points within data bins.
Figure 16 summarises the relative improvement in RMSD between CPL_DA and DA for each season at all UK coastal tide gauge sites. This shows substantially improved statistics at all locations, particularly during periods of highest SSH residual in winter 2016/2017 and autumn 2017 and focused in regions most susceptible to storm surges around north-western and eastern UK coastlines.
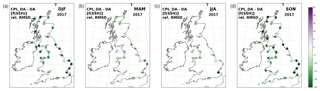
Figure 16Percentage change in RMSD for Doodson-filtered SSH results from CPL_DA and DA, comparing all simulated data during 2017 with filtered in situ tide gauge observations around UK coasts. Positive differences (purple shading) indicate a relative degradation of performance with wave coupling, negative differences (green shading) indicate relative improvement.
In summary, these results briefly highlight that inclusion of wave–ocean feedbacks in the operational NWS forecast system is expected to improve coastal SSH simulations, in particular by enhancing the simulated extreme values driven by positive and negative storm surges. This initial assessment also enhances the prospect for longer-term evolution towards the use of regional coupled systems for both operational ocean and storm surge prediction, converging with existing ensemble-forced barotropic ocean modelling approaches, as part of more integrated natural hazard prediction capabilities (e.g. O'Neill and Saulter, 2017).
4.6 Ocean currents
The mean change in surface currents on the NWS due to wave coupling is small (Fig. 17). The impact of waves is found to be consistent across different seasons and independent of whether ocean assimilation was active. Figure 17 focuses on the impact of wave coupling during October 2019, a period coincident with acoustic Doppler current profiler (ADCP) observations at the FINO1 and FINO3 locations in the German Bight (Fig. 3a). This highlights a tendency for increased current speeds in the central and northern North Sea, and reduced to the west of the NWS in the southern North Sea and English Channel. This distribution is more consistent with Stokes drift speed computed from the wave model (Fig. 1c and f) than the net momentum storage and release by waves. Figure 17b shows a complex response to wave coupling but with large areas of enhanced wave-induced currents at coastlines, although the net impact is small when averaged over longer periods.
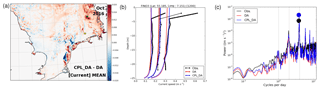
Figure 17(a) Zoom of monthly mean differences in simulated surface current speed in CPL_DA relative to DA during October 2016 across the southern North Sea. (b) Monthly mean profiles of observed (black) and simulated (red, blue) current speed at the FINO3 location (green star) valid at 12:00 UTC each day during October 2016. Mean profiles are plotted with symbols, and thick lines indicate 1 standard deviation range from mean profiles. (c) Computed power spectra for observed, DA and CPL_DA simulated current speed at 4 m depth during October 2016. Filled circles highlight the amplitude of the peak power for each time series (note DA and CPL_DA maxima are identical). Vertical dotted lines mark diurnal, semi-diurnal, and quarter-diurnal frequencies.
A comparison of current profiles with ADCP observations at the FINO3 location (green star in Fig. 17b and Fig. 3a) during October 2016 is shown in Fig. 17c. Comparisons between observations and simulations are made using the nearest grid cell value only (rather than a 5×5 region mean) in order to better capture extremes in a highly variable field. The FINO3 site is located in a region of enhanced currents with wave coupling, which is shown to have better agreement with observations of both the mean and standard deviation through much of the profile. This enhancement is consistent with previous results in the region described by Staneva et al. (2016), who found increased currents during storm conditions. Simulated current profile results at FINO1 (yellow star in Fig. 17b) show very little impact of wave coupling during this period, consistent with the distribution of surface changes in Fig. 17b.
Wave coupling has the potential to improve operational regional ocean forecasts of the NWS, based on the initial implementation of representing the impact of wave–ocean feedbacks focused on the momentum budget at the ocean surface discussed in this paper.
The main impact of wave coupling, as applied in these experiments, is on the temperature evolution of the NWS. Enhanced vertical mixing due to waves leads to a relatively warmer surface and well-mixed layers during winter. In summer, wave-enhanced mixing deepens the summer MLD resulting in a relative cooling of surface and upper ocean temperatures during periods of stratification. This changes the shape of the summer temperature profile in stratified regions of the NWS. The impacts of wave coupling are weaker for areas that are well mixed throughout the year. It has proved instructive to compare the relative impact of coupling for simulations with and without ocean assimilation active. The impact of wave coupling on ocean temperatures was consistent between CPL_FR and CPL_DA simulations below the mixed layer, with both demonstrating deepening of the MLD. Ocean assimilation tends to diminish the impact of coupling on temperatures within the MLD. This situation suggests the potential for wave coupling to provide performance improvements in future, but also presents a new challenge for system development. It summary, it can be concluded that the initial condition surface temperature is well constrained within the DA simulations, and this is not markedly degraded with the addition of wave coupling in the first implementation of the CPL_DA system.
It could be argued that the degradation of summary metrics for CPL_FR relative to FR is indicative that the AMM15 ocean model configuration and assimilation have been well optimised for running in an uncoupled mode given the implicit assumptions introduced in its science parameters and model parameterisations. By changing the characteristics of mixing in the system through wave coupling, these optimisations will require revisiting. For example, the mean warming on the NWS during winter may be compensated by the tuning of the radiation scheme in the current operational system. King et al. (2018) identified the need to increase the number of temperature profile observations available for assimilation, which is supported by this analysis and by the difference in wave coupling impact within and below the mixed layer. Even given current observation volumes, further tuning of the assimilation system will be required in the presence of wave coupling. For example, work is in progress to compute adjusted model background error covariances from the wave–ocean coupled system.
Further, a number of wave processes have been omitted for this initial implementation – most notably the effect of wave breaking on the surface turbulent kinetic energy budget (e.g. Breivik et al., 2015) and the impact of Langmuir turbulence (e.g. Cavaleri et al., 2012). For example, inclusion of bottom friction effects (e.g. Soulsby et al., 1995) due to waves is another potential future evolution that might enhance near-surface variability and improve simulation of SBT and SBS. The effect of wave breaking is implicit in the parameterisation of Craig and Banner (1994), used in the current operational configuration. Adapting this approach would likely require retuning of model parameters to continue to provide robust results. The initial wave-coupled implementation described here now provides a suitable benchmark against which to undertake this next development. Future development and evaluation of ocean mixing parameterisations should also make use of wave-coupled configurations.
The results presented in this study are therefore considered to represent a worst-case rather than best-case implementation. The fact that the summary metrics suggest a relatively neutral impact on SST with wave coupling is encouraging.
Beyond SST impacts, it has been shown that wave coupling has a beneficial impact on the simulation of surface and seabed salinity, SSH, and currents when compared with observations. Given that these variables are less impacted by the ocean assimilation also provides encouragement that the representation of wave coupling is physically robust, and that further optimisations will therefore be possible prior to implementation in operations. The impact of wave coupling on salinity in the German Bight highlights the way that wave coupling improves representation of near-coastal mixing and advection. By applying a Doodson low-pass filter to simulated and observed SSH data, the beneficial impact of representing wave coupled processes on capturing high and low extremes of the water level anomaly around the UK coast has been demonstrated. This result has particularly significant implications for the future use of wave–ocean coupled systems for underpinning natural hazard warning predictions related to storm surges and coastal inundation. Further work to assess the impact of wave coupling over shorter timescales, for example through a case study approach, would be of value to focus on evaluation of finer-scale processes including the role of wave–tide interactions. Finally, an initial assessment of (limited) available current profiles suggests that improvements in current predictive skill are possible with wave coupling, but is worthy of further investigation, for example through comparison to high-frequency (HF) radar observations (e.g. Tonani et al., 2019, this issue). In particular, the impact of Stokes drift effects for the applications of ocean model data, such as tracer transports or renewable energy resources, is of interest.
Although the results presented in this paper are encouraging, it is clear that model coupling only is not a sufficient strategy for improving all aspects of model performance. Rather, ongoing investment in research and development balancing aspects of coupling, model physics, and assimilation are all required in order to deliver improved information for operational users of the system in the future.
The nature of the 4-D data generated in running the various ocean and wave model experiments at 1.5 km resolution requires a large tape storage facility. These data are of the order of tens of terabytes. However, the data can be made available upon contacting the authors. Each simulation namelist and input data are also archived under configuration management, and can be made available to researchers to promote collaboration upon contacting the authors.
All authors contributed scientific evaluation and analysis of the results. Additional specific contributions are listed below. JMC developed the technical configurations used, including the NEMO wave coupling codes, and supported running the simulations. RK developed the NEMO regional ocean assimilation system. AS developed the regional ocean wave configuration. ACP undertook the evaluation against glider observations. GW developed the spectral analysis tools and interpretation. JSt supported the development of the wave coupling algorithms assessed.
The authors declare that they have no conflict of interest.
This article is part of the special issue “The Copernicus Marine Environment Monitoring Service (CMEMS): scientific advances”. It is not associated with a conference.
This work originated from initial studies and technical developments conducted under the Copernicus Marine Environment Monitoring Service (CMEMS) evolution project on Ocean-Wave-Atmosphere Interactions in Regional Seas (OWAIRS). CMEMS is implemented by Mercator Ocean in the framework of a delegation agreement with the European Union.
This paper was edited by Angelique Melet and reviewed by Stéphane Law-Chune and one anonymous referee.
Alari, V., Staneva, J., Breivik, Ø., Bidlot, J.-R., Mogensen, K., and Janssen, P.: Surface wave effects on water temperature in the Baltic Sea: simulations with the coupled NEMO-WAM model, Ocean Dynam., 66, 917–930, https://doi.org/10.1007/s10236-016-0963-x, 2016.
Benetazzo, A., Bergamasco, A., Bonaldo, D., Falcieri, F. M., Sclavo, M., Langone, L., and Carniel, S.: Response of the Adriatic Sea to an intense cold air outbreak: Dense water dynamics and wave-induced transport, Prog. Oceanogr., 128, 115–138, https://doi.org/10.1016/j.pocean.2014.08.015, 2014.
Berg, P. and Weismann Poulsen, J.: Implementation details for HBM, DMI Technical Report No. 12-11, available at: http://beta.dmi.dk/fileadmin/Rapporter/TR/tr12-11.pdf (last access: 3 June 2019), 2012.
Bertin, X., Kai Li, K., Aron Roland, A., and Jean-Raymond Bidlot, J.-R.: The contribution of short-waves in storm surges: Two case studies in the Bay of Biscay, Cont. Shelf Res., 96, 1–15, https://doi.org/10.1016/j.csr.2015.01.005, 2015.
Blockley, E. J., Martin, M. J., McLaren, A. J., Ryan, A. G., Waters, J., Lea, D. J., Mirouze, I., Peterson, K. A., Sellar, A., and Storkey, D.: Recent development of the met-office operational ocean forecasting system: an overview and assessment of the new global FOAM forecasts, Geosci. Model Dev., 7, 2613–2638, https://doi.org/10.5194/gmd-7-2613-2014, 2014.
Bolaños, R., Brown, J. M., and Souza, A. J.: Wave–current interactions in a tide dominated estuary, Cont. Shelf Res., 87, 109–123, https://doi.org/10.1016/j.csr.2014.05.009, 2014.
Breivik, Ø., Mogensen, K., Bidlot, J.-R., Balmaseda, M. A., and Janssen, P. A. E. M.: Surface wave effects in the NEMO ocean model: Forced and coupled experiments, J. Geophys. Res.-Ocean, 120, 2973–2992, https://doi.org/10.1002/2014JC010565, 2015.
Bricheno, L. M., Soret, A., Wolf, J., Jorba, O., and Baldasano, J. M.: Effect of High-Resolution Meteorological Forcing on Nearshore Wave and Current Model Performance, J. Atmos. Ocean. Tech., 30, 1021–1037, https://doi.org/10.1175/JTECH-D-12-00087.1, 2013.
Brown, J. M. and Wolf, J.: Coupled wave and surge modelling for the eastern Irish Sea and implications for model wind-stress, Cont. Shelf Res., 29, 1329–1342, https://doi.org/10.1016/j.csr.2009.03.004, 2009.
Brown, J. M., Bolaños, R., and Wolf, J.: Impact assessment of advanced coupling features in a tide–surge–wave model, POLCOMS-WAM, in a shallow water application, J. Mar. Syst., 87, 13–24, https://doi.org/10.1016/j.jmarsys.2011.02.006, 2011.
Bruneau, N. and Toumi, R.: A fully-coupled atmosphere-ocean-wave model of the Caspian Sea, Ocean Model., 107, 97–111, https://doi.org/10.1016/j.ocemod.2016.10.006, 2016.
Carniel, S., Benetazzo, A., Bonaldo, D., Falcieri, F. M., Miglietta, M. M., Ricchi, A., and Sclavo, M.: Scratching beneath the surface while coupling atmosphere, ocean and waves: Analysis of a dense water formation event, Ocean Model., 101, 101–112, https://doi.org/10.1016/j.ocemod.2016.03.007, 2016.
Cavaleri, L., Fox-Kemper, B., and Hemer, M.: Wind Waves in the Coupled Climate System, B. Am. Meteorol. Soc., 93, 1651–1661, https://doi.org/10.1175/BAMS-D-11-00170.1, 2012.
Cavaleri, L., Abdalla, S., Benetazzo, A., Bertotti, L., Bidlot, J.-R., Breivik, Ø., Carniel, S., Jensen, R. E., Portilla-Yandun, J., Rogers, W. E., Roland, A., Sanchez-Arcilla, A., Smith, J. M., Staneva, J., Toledo, Y., van Vledder, G. Ph., and van der Westhuysen, A. J.: Wave modelling in coastal and inner seas, Prog. Oceanogr., 167, 164–233, https://doi.org/10.1016/j.pocean.2018.03.010, 2018.
Clementi, E., Oddo, P., Drudi, M., Pinardi, N., Korres, G., and Grandi, A.: Coupling hydrodynamic and wave models: first step and sensitivity experiments in the Mediterranean Sea, Ocean Dynam., 67, 1293, https://doi.org/10.1007/s10236-017-1087-7, 2017.
Consoli, S., Recupero, D. R., and Zavarella, V.: A survey on tidal analysis and forecasting methods for tsunami detection, Science of Tsunami Hazards, 33, 1–54, 2014.
Craig, P. D. and Banner, M. L.: Modeling wave-enhanced turbulence in the ocean surface layer, J. Phys. Oceanogr., 24, 2546–2559, 1994.
Graham, J. A., O'Dea, E., Holt, J., Polton, J., Hewitt, H. T., Furner, R., Guihou, K., Brereton, A., Arnold, A., Wakelin, S., Castillo Sanchez, J. M., and Mayorga Adame, C. G.: AMM15: a new high-resolution NEMO configuration for operational simulation of the European north-west shelf, Geosci. Model Dev., 11, 681–696, https://doi.org/10.5194/gmd-11-681-2018, 2018a.
Graham, J. A., Rosser, J. P., O'Dea, E., and Hewitt, H. T.: Resolving shelf break exchange around the European northwest shelf, Geophys. Res. Lett., 45, 12386–12395, https://doi.org/10.1029/2018GL079399, 2018b.
Hashemi, M. R. and Lewis, M.: Wave-Tide Interactions in Ocean Renewable Energy, in: Marine Renewable Energy, edited by: Yang, Z. and Copping, A., Springer, Cham, https://doi.org/10.1007/978-3-319-53536-4_6, 2017.
Hashemi, M. R., Neill, S. P., and Davies, A. G.: A coupled tide-wave model for the NW European shelf seas, Geophys. Astro. Fluid, 109, 234–253, https://doi.org/10.1080/03091929.2014.944909, 2015.
Hasselmann, K.: Wave-driven inertial oscillations, Geophys. Fluid Dynam., 1, 463–502, https://doi.org/10.1080/03091927009365783, 1970.
Holt, J. T. and James, I. D.: An s coordinate density evolving model of the northwest European continental shelf: 1. Model description and density structure, J. Geophys. Res., 106, 14015–14034, https://doi.org/10.1029/2000JC000304, 2001.
Huthnance, J. M., Holt, J. T., and Wakelin, S. L.: Deep ocean exchange with west-European shelf seas, Ocean Sci., 5, 621–634, https://doi.org/10.5194/os-5-621-2009, 2009.
Janssen, P.: The Interaction of Ocean Waves and Wind, Cambridge Univ. Press, Reading, UK, 300 pp., 2004.
Janssen, P. A. E. M. and Bidlot, J.-R.: Progress in Operational Wave Forecasting, Procedia IUTAM, 26, 14–29, https://doi.org/10.1016/j.piutam.2018.03.003, 2018.
Kara, A. B., Rochford, P. A., and Hurlburt, H. E.: An optimal definition for ocean mixed layer depth, J. Geophys. Res., 105, 16803–16821, 2000.
King, R. R., While, J., Martin, M. J., Lea, D.J., Lemieux-Dudon, B., Waters, J., and O'Dea, E.: Improving the initialisation of the Met Office operational shelf-seas model, Ocean Model., 130, 1–14, https://doi.org/10.1016/j.ocemod.2018.07.004, 2018.
Laloyaux, P., de Boisseson, E., Balmaseda, M., Bidlot, J.-R., Broennimann, S., Buizza, R., Dalhgren, P., Dee, D., Haimberger, L., Hersbach, H., Kosaka, Y., Martin, M., Poli, P., Rayner, N., Rustemeier, E., and Schepers, D.: CERA-20C: A coupled reanalysis of the twentieth century, J. Adv. Model. Earth Syst., 10, 1172–1195, https://doi.org/10.1029/2018MS001273, 2018.
Large, W. and Yeager, S.: Diurnal to decadal global forcing for ocean and seaice models: the data sets and climatologies, Technical Report TN-460+STR, NCAR, 105 pp., 2004.
Law Chune, S. and Aouf, L.: Wave effects in global ocean modeling: parametrizations vs. forcing from a wave model, Ocean Dynam., 68, 1739–1758, https://doi.org/10.1007/s10236-018-1220-2, 2018.
Lewis, H. W., Castillo Sanchez, J. M., Graham, J., Saulter, A., Bornemann, J., Arnold, A., Fallmann, J., Harris, C., Pearson, D., Ramsdale, S., Martínez-de la Torre, A., Bricheno, L., Blyth, E., Bell, V., Davies, H., Marthews, T., O'Neill, C., Rumbold, H., O'Dea, E., Brereton, A., Guihou, K., Hines, A., Butenschon, M., Dadson, S. J., Palmer, T., Holt, J., Reynard, N., Best, M., Edwards, J., and Siddorn, J.: The UKC2 regional coupled environmental prediction system, Geosci. Model Dev., 11, 1–42, https://doi.org/10.5194/gmd-11-1-2018, 2018a.
Lewis, H. W., Castillo Sanchez, J. M., Arnold, A., Fallmann, J., Saulter, A., Graham, J., Bush, M., Siddorn, J., Palmer, T., Lock, A., Edwards, J., Bricheno, L., Martínez de la Torre, A., and Clark, J.: The UKC3 regional coupled environmental prediction system, Geosci. Model Dev. Discuss., https://doi.org/10.5194/gmd-2018-245, in review, 2018b.
Lewis, M. J., Palmer, T., Hashemi, R., Robins, P., Saulter, A., Brown, J., Lewis, H., and Neill, S.: Wave-tide interaction modulates nearshore wave height, Ocean Dynam., 69, 367–384, https://doi.org/10.1007/s10236-018-01245-z, 2019.
Li, J.-G.: Propagation of ocean surface waves on a spherical multiple-cell grid, J. Comput. Phys., 231, 8262–8277, https://doi.org/10.1016/j.jcp.2012.08.007, 2012.
Madec, G. and the NEMO team: NEMO reference manual 3_6_STABLE : NEMO ocean engine, Note du Pôle de modélisation, Institut Pierre-Simon Laplace (IPSL), France, No. 27 ISSN, No. 1288-1619, 2016.
O'Neill, C. and Saulter, A.: NEMO-Surge forecast performance during 2016–17 winter trial, Met Office Forecasting Research Technical Report No. 622, available at: https://www.metoffice.gov.uk/binaries/content/assets/mohippo/pdf/library/weather-science-technical-reports/frtr_622_2017p.pdf (last access: 3 June 2019), 2017.
Palmer, T. and Saulter, A.: Evaluating the effects of ocean current fields on a UK regional wave model, Met Office Forecasting Research Technical Report No. 612, available at: https://www.metoffice.gov.uk/binaries/content/assets/mohippo/pdf/j/i/frtr_612_2016p.pdf (last access: 3 June 2019), 2016.
Palmer, M., Williams, C., and Horsburgh, K.: Synoptic multi-variable multi-glider study, AtlantOS Deliverable, D4.3, AtlantOS, 25 pp., https://doi.org/10.3289/atlantos_d4.3, 2018.
Press, W. H., Teukolsky, S. A., Vetterling, W. T., and Flannery, B. P. L: Numerical Recipes in Fortran, The Art of Scientific Computing, Cambridge University Press, Cambridge, 963 pp., 1992.
Pugh D. T.: Tides, Surges and Mean Sea-Level, John Wiley & Sons, New York, 472 pp., 1987.
Pullen, J., Allard, R., Seo, H., Miller, A. J., Chen, S., Pezzi, L. P., Smith, T., Chu, P., Alves, J., and Caldeira, R.: Coupled ocean-atmosphere forecasting at short and medium time scales, J. Mar. Res., 75, 877–921, https://doi.org/10.1357/002224017823523991, 2017.
Rascle, N., Ardhuin, F., Queffeulou, P., and Croizé-Fillon, D.: A global wave parameter database for geophysical applications. Part 1: Wave-current–turbulence interaction parameters for the open ocean based on traditional parameterizations, Ocean Model., 25, 154–171, https://doi.org/10.1016/j.ocemod.2008.07.006, 2008.
Reza Hashemi, M., Neill, S. P., and Davies, A. G.: A coupled tide-wave model for the NW European shelf seas, Geophys. Astro. Fluid, 109, 234–253, https://doi.org/10.1080/03091929.2014.944909, 2015.
Saulter, A., Bunney, C., Li, J.-G., and Palmer, T.: Process and resolution impacts on UK coastal wave predictions from operational global-regional wave models, Proc. 15th International Workshop on Wave Hindcasting and Forecasting & 6th Coastal Hazard Symposium, available at: http://www.waveworkshop.org/15thWaves/Papers/K1_WHF_SaulterEtAl_UKCoastalWave_20170913.pdf (last access: 3 June 2019), 2017.
Schloen, J., Stanev, E. V., and Grashorn, S.: Wave-current interactions in the southern North Sea: The impact on salinity, Ocean Model., 111, 19–37, https://doi.org/10.1016/j.ocemod.2017.01.003, 2017.
Soulsby, R. L.: Bed shear-stresses due to combined waves and currents, in: Advances in Coastal Morphodynamics, edited by: Stive, M. J. F., de Vriend, H. J., Fredsøe, J., Hamm, L., Soulsby, R. L., Teisson, C., and Winterwerp, J. C., Delft Hydraulics, the Netherlands, 4-20–4-23, 1995.
Staneva, J., Wahle, K., Koch, W., Behrens, A., Fenoglio-Marc, L., and Stanev, E. V.: Coastal flooding: impact of waves on storm surge during extremes – a case study for the German Bight, Nat. Hazards Earth Syst. Sci., 16, 2373–2389, https://doi.org/10.5194/nhess-16-2373-2016, 2016a.
Staneva, J., Wahle, K., Günther, H., and Stanev, E.: Coupling of wave and circulation models in coastal–ocean predicting systems: a case study for the German Bight, Ocean Sci., 12, 797–806, https://doi.org/10.5194/os-12-797-2016, 2016b.
Staneva, J., Alari, V., Breivik, Ø., Bidlot, J-.R., and Mogensen, K.: Effects of wave-induced forcing on a circulation model of the North Sea, Ocean Dynam., 67, 81–101, https://doi.org/10.1007/s10236-016-1009-0, 2017.
Tolman, H. L.: User manual and system documentation of WAVEWATCH III® version 4.18, NOAA/NWS/NCEP/MMAB Technical Note 316, 282 pp. + Appendices, 2014.
Tonani, M., Sykes, P., King, R. R., McConnell, N., Pequignet, A.-C., O'Dea, E., Graham, J. A., Polton, J., and Siddorn, J.: The impact of a new high-resolution ocean model on the Met Office North-West European Shelf forecasting system, Ocean Sci. Discuss., https://doi.org/10.5194/os-2019-4, in review, 2019.
Uchiyama, Y., McWilliams, J. C., and Shchepetkin, A. F.: Wave-current interaction in an oceanic circulation model with a vortex-force formalism: Application to the surf zone, Ocean Model., 34, 16–35, https://doi.org/10.1016/j.ocemod.2010.04.002
Valcke, S., Craig, T., and Coquart, L.: OASIS3-MCT User Guide, Technical Report TR/CMGC/15/38, CERFACS, 2015.
van Leeuwen, S., Tett, P., Mills, D., and van der Molen, J.: Stratified and nonstratified areas in the North Sea: Long-term variability and biological and policy implications, J. Geophys. Res.-Ocean., 120, 4670–4686, https://doi.org/10.1002/2014JC010485, 2015.
WAMDI Group: The WAM Model—A Third Generation Ocean Wave Prediction Model, J. Phys. Oceanogr., 18, 1775–-1810, https://doi.org/10.1175/1520-0485(1988)018<1775:TWMTGO>2.0.CO;2, 1988.
Warner, J. C., Armstrong, B., He, R., and Zambon, J. B.: Development of a Coupled Ocean-Atmosphere-Wave-Sediment Transport (COAWST) modeling system, Ocean Model., 35, 230–244, https://doi.org/10.1016/j.ocemod.2010.07.010, 2010.
Waters, J., Lea, D. J., Martin, M. J., Mirouze, I., Weaver, A., and While, J.: Implementing a variational data assimilation system in an operational 1∕4∘ global ocean model, Q. J. R. Meteorol. Soc., 141, 333–349, https://doi.org/10.1002/qj.2388, 2015.
Weaver, A. T., Deltel, C., Machu, E., Ricci, S., and Daget, N.: A multivariate balance operator for variational ocean data assimilation, Q. J. R. Meteorol. Soc., 131, 3605–3625, https://doi.org/10.1256/qj.05.119, 2005.
Weedon, G. P., Prudhomme, C., Crooks, S., Ellis, R. J., Folwell, S. S., and Best, M. J.: Evaluating the Performance of Hydrological Models via Cross-Spectral Analysis: Case Study of the Thames Basin, UK, J. Hydrometeorol., 16, 214–231, https://doi.org/10.1175/JHM-D-14-0021.1, 2015.
Wolf, J.: Coupled wave and surge modelling and implications for coastal flooding, Adv. Geosci., 17, 19–22, https://doi.org/10.5194/adgeo-17-19-2008, 2008.






