Using canonical correlation analysis to produce dynamically based and highly efficient statistical observation operators

Observation operators (OOs) are a central component of any data assimilation system. As they project the state variables of a numerical model into the space of the observations, they also provide an ideal opportunity to correct for effects that are not described or are insufficiently described by the model. In such cases a dynamical OO, an OO that interfaces to a secondary and more specialised model, often provides the best results. However, given the large number of observations to be assimilated in a typical atmospheric or oceanographic model, the computational resources needed for using a fully dynamical OO mean that this option is usually not feasible. This paper presents a method, based on canonical correlation analysis (CCA), that can be used to generate highly efficient statistical OOs that are based on a dynamical model. These OOs can provide an approximation to the dynamical model at a fraction of the computational cost.

One possible application of such an OO is the modelling of the diurnal cycle of sea surface temperature (SST) in ocean general circulation models (OGCMs). Satellites that measure SST measure the temperature of the thin uppermost layer of the ocean. This layer is strongly affected by atmospheric conditions, and its temperature can differ significantly from the water below. This causes a discrepancy between the SST measurements and the upper layer of the OGCM, which typically has a thickness of around 1 m. The CCA OO method is used to parameterise the diurnal cycle of SST. The CCA OO is based on an input dataset from the General Ocean Turbulence Model (GOTM), a high-resolution water column model that has been specifically tuned for this purpose. The parameterisations of the CCA OO are found to be in good agreement with the results from the GOTM and improve upon existing parameterisations, showing the potential of this method for use in data assimilation systems.

1 Introduction

Data assimilation (DA) strives to improve the forecast skill of a numerical model by combining the model with observations. Observations are incorporated into the model by applying a series of corrections to the internal state of the model. As the state variables of a numerical model are usually not observed directly, this procedure requires an observation operator (OO) to project the model state variables onto the variable that is observed. The difference between the observation and the model prediction, the so-called innovation, forms the basis for calculating the correction to the model state. The accuracy of the OO is paramount in this process: any bias in the projection will lead to a bias in the innovation and therefore result in a biased correction to the model state. For this reason, bias correction procedures have been built considering not only systematic errors in observations but also in observation operators (see e.g. Harris and Kelly, 2001, for satellite radiance data).

Many different types of OO exist. In its simplest form, an OO could just select one of the state variables in a point near the observation or, perhaps, perform an interpolation. More complex OOs may include corrections for processes that influence the observation but are not modelled or are insufficiently modelled. Ultimately, one could even consider a dynamical OO that wraps a second numerical model to locally refine the results of the parent model. The latter solution may very well provide the most accurate results, but the vast number of observations that need to be assimilated in a typical atmospheric or oceanographic model means that this approach would require a prohibitive amount of computing resources. This limits OOs in most practical applications to relatively simple parameterisations in terms of the model state variables. Moreover, variational data assimilation requires observation operators to be linearised around the background within the inner loops (tangent-linear approximation). This translates into a need to construct OOs that can be formally and practically differentiated.

This paper presents a method of parameterising the results of a specialised model in such a way that it can be efficiently used within an OO. The parameterisation is based on canonical correlation analysis (CCA), a well-established mathematical method for finding cross-correlations between datasets. A new pseudo-dynamical OO is generated using the canonical correlation between the inputs and outputs of the specialised model on a large and representative dataset. Once this correlation has been calculated, the application of the pseudo-dynamical OO involves only a matrix multiplication that can be performed at a fraction of the computational cost of the dynamical OO. A similar method has been used previously to build reduced-order OOs in atmospheric data assimilation (Haddad et al., 2015).

This work is part of the SOSSTA (Statistical-dynamical observation Operator for SST data Assimilation) project, funded by the EU Copernicus Marine Environment Monitoring Service (CMEMS) through the Service Evolution grants. The aim of SOSSTA is to formulate an efficient OO for sea surface temperature (SST) DA that accounts for the diurnal variability of the ocean skin temperature. The results of the project are presented in multiple publications. The modelling of the diurnal cycle of SST is described in Pimentel et al. (2019), while the current paper focuses on the method for constructing the OO. The project includes pilot studies in the Mediterranean Sea and the Aegean Sea that will be described in forthcoming publications.

The paper is organised as follows: Sect. 2 provides a quick review of CCA; Sect. 3 discusses how CCA can be used to construct the OO matrix; Sect. 4 applies the CCA OO to the modelling of satellite sea surface temperature (SST) measurements in oceanographic models; and Sect. 5 discusses the performance of the method and other possible applications. Conclusions are presented in Sect. 6.

2 The CCA method

CCA (Hotelling, 1936) is a method to find cross-correlations between two datasets X and Y. The datasets are considered to be matrices structured such that the columns represent different variables and the rows represent the measurements of these variables. CCA then aims to find transformation matrices A and B that transform the anomaly of the variables of X and Y, denoted X^′ and Y^′, into the set of canonical variables F and G:

$$\begin{array}{}\text{(1)}& {\displaystyle }\mathbf{F}={\mathbf{X}}^{\prime }\mathbf{A}\mathbf{G}={\mathbf{Y}}^{\prime }\mathbf{B}.\end{array}$$

The structure of F and G matches that of X and Y. The canonical variables are constructed such that the variable F_i is maximally correlated with the variable G_i. At the same time, both F_i and G_i are uncorrelated with F_j and G_j for i≠j; therefore, each additional canonical variable describes the maximal remaining correlation between the two datasets. The number of canonical variables that can be obtained with this procedure is limited to the smallest number of variables in X or Y.

The calculation of the matrices A and B is relatively straightforward using the algorithm of Björck and Golub (1973). Writing the requirements outlined above in equation form yields

$$\begin{array}{}\text{(2a)}& {\displaystyle }{\mathbf{F}}^T\mathbf{F}={\mathbf{G}}^T\mathbf{G}& {\displaystyle }=\mathbf{I},\text{(2b)}& {\displaystyle }{\mathbf{F}}^T\mathbf{G}& {\displaystyle }=\mathbf{D},\end{array}$$

with I the unit matrix and D a diagonal matrix. The algorithm uses a QR decomposition to decompose both X^′ and Y^′ into an orthogonal matrix Q and an upper-triangular matrix R:

$$\begin{array}{}\text{(3)}& {\displaystyle }{\mathbf{X}}^{\prime }={\mathbf{Q}}_x{\mathbf{R}}_x{\mathbf{Y}}^{\prime }={\mathbf{Q}}_y{\mathbf{R}}_y.\end{array}$$

The algorithm proceeds by applying a singular value decomposition (SVD) on the product ${\mathbf{Q}}_x^T{\mathbf{Q}}_y$:

$$\begin{array}{}\text{(4)}& {\displaystyle }{\mathbf{Q}}_x^T{\mathbf{Q}}_y={\mathbf{USV}}^T.\end{array}$$

By trying the ansatz,

$$\begin{array}{}\text{(5)}& {\displaystyle }\mathbf{A}\equiv {\mathbf{R}}_x^{-\mathrm{1}}\mathbf{U}\mathbf{B}\equiv {\mathbf{R}}_y^{-\mathrm{1}}\mathbf{V},\end{array}$$

the orthonormality requirement of Eq. (2a) becomes

$$\begin{array}{}\text{(6)}& \begin{array}{rl}{\displaystyle }{\mathbf{F}}^T\mathbf{F}& {\displaystyle }={\mathbf{A}}^T{\mathbf{X}}^{\prime }{}^T{\mathbf{X}}^{\prime }\mathbf{A}\\ {\displaystyle }& {\displaystyle }=\left({\mathbf{U}}^T{\left({\mathbf{R}}_x^{-\mathrm{1}}\right)}^T\right)\left({\mathbf{R}}_x^T{\mathbf{Q}}_x^T\right)\left({\mathbf{Q}}_x{\mathbf{R}}_x\right)\left({\mathbf{R}}_x^{-\mathrm{1}}\mathbf{U}\right)\\ {\displaystyle }& {\displaystyle }=\mathbf{I},\end{array}\end{array}$$

and an analogous result follows for G^TG.

The orthogonality requirement of Eq. (2b) becomes

$$\begin{array}{}\text{(7)}& \begin{array}{rl}{\displaystyle }\mathbf{D}& {\displaystyle }={\mathbf{F}}^T\mathbf{G}={\mathbf{A}}^T{{\mathbf{X}}^{\prime }}^T{\mathbf{Y}}^{\prime }\mathbf{B}\\ {\displaystyle }& {\displaystyle }=\left({\mathbf{U}}^T{\left({\mathbf{R}}_x^{-\mathrm{1}}\right)}^T\right)\left({\mathbf{R}}_x^T{\mathbf{Q}}_x^T\right)\left({\mathbf{Q}}_y{\mathbf{R}}_y\right)\left({\mathbf{R}}_y^{-\mathrm{1}}\mathbf{V}\right)\\ {\displaystyle }& {\displaystyle }={\mathbf{U}}^T\left({\mathbf{USV}}^T\right)\mathbf{V}=\mathbf{S}.\end{array}\end{array}$$

Therefore, the ansatz of Eq. (5) is a valid solution for the matrices A and B. Moreover, by counting the number of degrees of freedom in these matrices and the number of constraints provided by Eq. (2), it can be shown that all solutions are permutations of Eq. (5) (Press, 2011). The canonical basis is therefore uniquely defined. In the case that X and Y contain different numbers of variables N_x and N_y, the SVD of Eq. (4) selects the N largest correlations, with $N=min(N_x,N_y)$.

As QR decomposition and SVD are common matrix operations that are efficiently implemented in most numerical libraries, this algorithm is straightforward to implement in most programming languages.

3 Using CCA to construct an OO

The CCA method can be used to construct an OO. Let X be a set of (possibly) relevant model state variables and Y the corresponding observation values. Here Y could be obtained from a specialised model but also from a historical dataset of real observations. Applying the algorithm of Sect. 2 yields the matrices A, B, and D. The first two convert the mean subtracted model states X^′ and observation values Y^′ into their canonical counterparts F and G. The diagonal matrix D holds for each pair of canonical variables i the best fit to the slope of the correlation: ${\mathbf{D}}_{ii}=\mathrm{d}{\mathbf{G}}_i/\mathrm{d}{\mathbf{F}}_i$.

Assuming that N_x≥N_y  – i.e. the number of model state variables is at least equal to the number of observed variables – it is possible to calculate Y^′ from X^′ by passing through canonical space and applying the fitted slope D,

$$\begin{array}{}\text{(8)}& {\displaystyle }{\mathbf{Y}}^{\prime }={\mathbf{X}}^{\prime }{\mathbf{ADB}}^{-\mathrm{1}}\equiv {\mathbf{X}}^{\prime }\mathbf{M},\end{array}$$

defining the CCA OO matrix,

$$\begin{array}{}\text{(9)}& {\displaystyle }\mathbf{M}\equiv {\mathbf{ADB}}^{-\mathrm{1}},\end{array}$$

of size N_x×N_y. As the CCA considers only the anomaly of X and Y, an additional offset term needs to be considered to accommodate the mean values of X and Y in the input dataset. However, the mean values of X and Y can be combined by applying the matrix M:

$$\begin{array}{}\text{(10)}& \begin{array}{rl}{\displaystyle }\mathbf{Y}-\stackrel{\mathrm{‾}}{\mathbf{Y}}& {\displaystyle }=\left(\mathbf{X}-\stackrel{\mathrm{‾}}{\mathbf{X}}\right)\mathbf{M}\\ {\displaystyle }\mathbf{Y}& {\displaystyle }=\mathbf{XM}+\mathit{K},\end{array}\end{array}$$

with

$$\begin{array}{}\text{(11)}& {\displaystyle }\mathit{K}\equiv \stackrel{\mathrm{‾}}{\mathbf{Y}}-\stackrel{\mathrm{‾}}{\mathbf{X}}\mathbf{M},\end{array}$$

a combined offset vector of length N_y.

During the training phase of the CCA OO, the datasets X and Y are used to calculate the matrix M and the offset K. Once computed, they can be used to form an observation operator H that transforms a state x as

$$\begin{array}{}\text{(12)}& {\displaystyle }\mathrm{H}\left(\mathit{x}\right){\displaystyle }=\mathit{x}\mathbf{M}+\mathit{K}.\end{array}$$

Furthermore, the tangent-linear approximation used in variational DA schemes requires that

$$\begin{array}{}\text{(13)}& {\displaystyle }\mathrm{H}\left(\mathit{x}\right)\sim \mathrm{H}\left({\mathit{x}}^{\mathrm{b}}\right)+{\mathbf{H}}^{\prime }\mathrm{d}\mathit{x},\end{array}$$

where H^′ is the tangent-linear version of the OO, x^b the background state, and dx the deviation from the background. The CCA OO is straightforward to implement in this scheme, since for H^′ and its adjoint H^′T it follows that

$$\begin{array}{}\text{(14)}& {\displaystyle }{\mathbf{H}}^{\prime }={\mathbf{M}}^T{\mathbf{H}}^{\prime }{}^T=\mathbf{M}.\end{array}$$

4 Use case: satellite SST

One possible application of the new CCA OO is the assimilation of SST in ocean general circulation models (OGCMs). In recent years OGCMs have seen significant improvements in vertical resolution, particularly near the surface, where the first layer has been reduced to a thickness of the order of 1 m or less. At this resolution, the diurnal cycle of SST should be taken into account. Although diurnal variability is included to some extent (Marullo et al., 2014), the vertical resolution of OGCMs is still insufficient to fully resolve the variability of the skin and subskin ocean temperature.

This issue becomes particularly evident when assimilating satellite SST observations. The different types of sensors used on satellites probe the ocean temperature at different depths. Infrared (IR) sensors measure the temperature at about 10 µm, a layer that is referred to as the ocean skin. Microwave (MW) sensors, on the other hand, measure the temperature of the layer below that, the subskin, with a depth of about 1 mm. This is much shallower than the vertical resolution of a typical OGCM, while these layers are strongly affected by the atmospheric conditions. The ocean skin cools due to thermodynamic processes at the air–sea interface, while the absorption of solar heat causes a warming of the subskin. At the same time, wind can mix the skin and subskin with the water below, smoothing the temperature variations. During days of low wind and/or high insolation conditions the amplitude of the SST diurnal cycle can be larger than the combined accuracy of the model and observations, causing a straightforward assimilation of SST to degrade the performance of the model (Marullo et al., 2016). Under favourable conditions this amplitude is typically of the order of a few degrees (see e.g. Flament et al., 1994), but values as high as 6 ^∘C have been observed (Merchant et al., 2008).

Representation errors have been extensively discussed within ocean applications (Oke and Sakov, 2008; Janjić et al., 2018) and generally include errors due to e.g. limited spatial resolution or unrepresented processes. However, the diurnal variability of skin SST represents a potentially systematic error that requires a proper treatment rather than just increasing the representation component of the observational error.

An important source of SST observational data is the Spinning Enhanced Visible and Infrared Imager (SEVIRI) instrument onboard the Meteosat satellites of the second generation. As these are geostationary satellites, SEVIRI can provide continuous measurements of the same area with a 15 min temporal resolution. Although the IR imager is sensitive to skin temperature, the calibration algorithm of SEVIRI corrects for the cool-skin bias, and the resulting SST products should be considered the subskin temperature (Saux Picart and Legendre, 2018). For wind speeds greater than 6 m s⁻¹ the skin temperature may be calculated as $T_{\mathrm{skin}}=T_{\mathrm{subskin}}-\mathrm{0.17}$ ^∘C (Donlon et al., 2002), but this is only an approximation.

This section will discuss how to use the output of a water column model specifically tuned for modelling the diurnal cycle of SST together with the CCA OO to build an observation operator for SST that accounts for the diurnal variability.

4.1 General Ocean Turbulence Model

The SST diurnal cycle is modelled using the General Ocean Turbulence Model (GOTM). The GOTM is a one-dimensional water column model that includes multiple turbulence closure schemes (Burchard et al., 1999; Umlauf et al., 2005). It has been successfully adapted to model the near-surface variability of ocean temperature, including both the diurnal cycle and the cool-skin effect (Pimentel et al., 2008a, b). Recently it has been used to systematically simulate the atmospheric and oceanographic conditions in the Mediterranean Sea (Pimentel et al., 2019). The latter study has resulted in a multi-year dataset modelling the diurnal cycle in the Mediterranean Sea on a grid of $\mathrm{0.75}{}^{\circ }\times \mathrm{0.75}{}^{\circ }$ resolution with hourly time resolution. For this dataset the GOTM is configured with the k-ε turbulent kinetic energy parameterisation with internal waves. The top 75 m of the water column is resolved using 122 vertical layers with fine resolution near the surface and gradually becoming coarser with depth. The uppermost 1 m contains a total of 21 layers, with the highest level at 1.5 cm of depth. This dataset is used in the present paper to build the CCA OO for SST.

The subskin SST represents the temperature at the base of the conductive laminar sub-layer of the ocean surface; for practical purposes it is represented by the temperature of the top model layer of the GOTM (1.5 cm). The conductive sub-layer of the air–sea interface, associated with the cool-skin effect, is parameterised and dynamically computed within the GOTM to produce a modelled skin SST. Further details are provided in Pimentel et al. (2019).

4.2 Operator setup

The aim for the CCA OO is to parameterise the IR and MW satellite SST observations as a function of temperature in the water column below. While the dataset of Pimentel et al. (2019) uses a fine vertical resolution to calculate the SST observations, the CCA OO will consider only the levels of a typical OGCM. Within the SOSSTA project this OGCM is the CMEMS Mediterranean Forecasting System (MFS) (Simoncelli et al., 2014), but the parameterisation can be performed for any vertical distribution of levels.

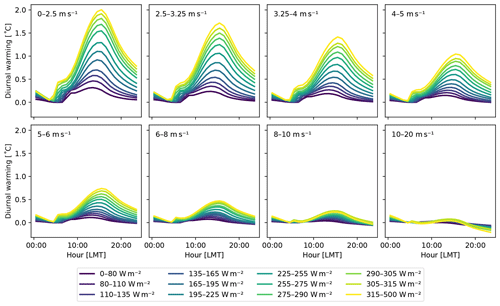
Figure 1 The magnitude of the diurnal warming at the subskin level as a function of the time of the day for different wind and insolation categories. The diurnal warming is measured with respect to the SST at local sunrise. The wind categories are represented by the different panels, while the insolation categories are shown as different curves within each panel.

The magnitude of the diurnal signal depends strongly on the atmospheric conditions, most importantly the insolation and wind speed. Insolation causes the ocean skin to heat up during the course of the day, while wind mixes the upper layers of the ocean, leading to the dissipation of the heat. Due to latent heat loss, the ocean skin may even cool down below the bulk temperature. To accommodate a non-linear dependence on the different insolation and wind scenarios in the CCA OO, the GOTM dataset is divided into 12 insolation and 8 wind categories. Insolation and wind are defined in each location as the daily mean value in local mean time (LMT). The category boundaries were chosen to equally divide the dataset. The magnitude of the diurnal warming for the different categories is shown in Fig. 1.

The GOTM dataset has been compared to SEVIRI data at the skin level in Pimentel et al. (2019) and was found to be in good agreement over the whole period of 2013 and 2014. However, after dividing the dataset into atmospheric categories, it is found that categories with high diurnal warming may have a warm bias of up to 0.5 ^∘C and categories with low diurnal warming a cold bias of typically 0.1–0.2 ^∘C. This category bias is corrected for by subtracting the mean difference between SEVIRI and GOTM at subskin level for each category.

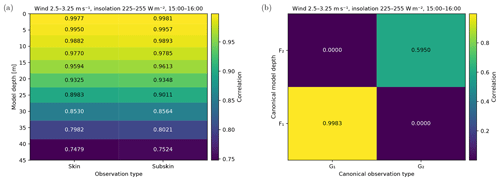
Figure 2 The correlation coefficients between the model variables and observations (a), with the canonical equivalent of these variables (b).

For each category of wind and insolation, and at hourly time resolution, the CCA OO is calculated to project the 10 uppermost levels of the MFS model onto the skin and subskin SST temperatures. The 10 levels extend down to a depth of approximately 40 m, which was chosen to be well below the depth influenced by the diurnal cycle of temperature. Figure 2a shows the correlation between the model temperature at various depths and the two SST observation types. As expected, the SST is strongly correlated with the highest levels and the correlation decreases with depth. It is important to note that in this case the various levels are also strongly correlated with each other. Figure 2b shows the correlation after transforming to canonical coordinates. It can be seen that the strongest correlation has not significantly changed, as the first canonical variable is very similar to the highest model level. The second pair of canonical variables (F₂,G₂), however, describes an additional correlation of around 60 % between model water temperature and SST.

4.3 Validation

The CCA OO is validated by comparing its performance to that of the full GOTM. To use the operator effectively in a DA system, it should be able to provide an accurate approximation of the GOTM results. The validation is performed against GOTM profiles that are withheld from the CCA OO calculation. The GOTM dataset is split in two, withholding every other profile in the zonal direction from the calculation. The validation then uses the withheld profiles and extracts the depths corresponding to the MFS levels, mimicking the use of the operator inside a DA system. The CCA OO, based on the atmospheric category and closest time, is subsequently applied to project the model temperature onto the skin and subskin SST. The projected SST values are then compared to the values in the original GOTM profile.

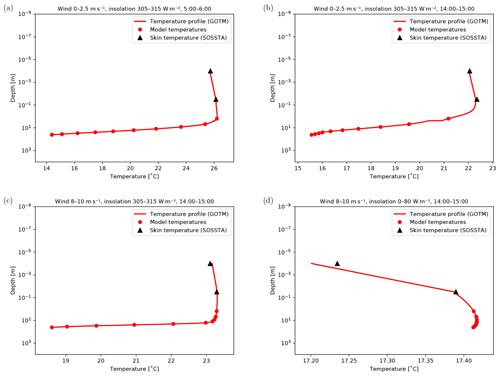
Figure 3 Examples of temperature profiles in various conditions and at different times. The GOTM profiles are shown by the red curve, while the filled circles indicate the values used as input to the CCA OO. The output of the CCA OO is shown by the black triangles. (a) Low wind, high insolation, early morning; (b) low wind, high insolation, afternoon; (c) high wind, high insolation, afternoon; (d) high wind, low insolation, afternoon.

Some examples of the validation are shown in Fig. 3. Each panel shows a profile from the GOTM dataset, together with the model levels that were used as input to the CCA OO. The output of the CCA OO is superimposed onto the GOTM profile so that a comparison can be made. Figure 3a shows a temperature profile in the early morning, during a day of low wind and high insolation. At this time, diurnal warming is limited, and due to the clear-sky conditions the skin and subskin temperatures have cooled down slightly below the temperature of the first model level. Figure 3b shows an afternoon profile on a similar day. At this time, diurnal warming is around its maximum, and the skin temperature has increased about 1 ^∘C above the first level of the model. In the case of high wind speed, the increased mixing of the upper layer of the ocean can completely cancel the effect of the high insolation, as shown in Fig. 3c. In this situation the temperature in the upper 10 m of the ocean is almost constant. When high wind conditions coincide with low insolation, the surface can also cool quite significantly, as shown in Fig. 3d. The CCA OO is able to correctly reproduce the GOTM skin and subskin temperature under different atmospheric conditions. The atmospheric categories with strong diurnal warming have a root mean square error (RMSE) of up to 0.4 ^∘C; for all other categories the RMSE is around 0.1 ^∘C. The bias of the CCA OO compared to the GOTM was found to be negligible.

Figure 4 Skill score of the CCA OO compared to the OGCM upper layer for all wind and insolation categories at midnight (a) and in the afternoon (b).

5 Performance and discussion

The performance of the GOTM-based CCA OO for SST is compared to other commonly used methods. For this comparison the GOTM dataset is again split along the zonal direction using every other profile to calculate the CCA OO. The remaining profiles are matched to SEVIRI subskin retrievals using only profiles matched to a measurement with an acceptable (4) or good (5) quality control level. The performance can be conveniently expressed in terms of the skill score (SS), defined by Murphy (1988) as

$$\begin{array}{}\text{(15)}& {\displaystyle }\mathrm{SS}=\mathrm{1}-{\displaystyle \frac{{\mathrm{MSE}}_{\mathrm{model}}}{{\mathrm{MSE}}_{\mathrm{reference}}}}.\end{array}$$

The skill score is based on the mean square error (MSE) of the model under testing and of a reference model. Specifically, it expresses the difference in MSE as a fraction of the reference MSE. The skill score is straightforward to interpret: a perfect model (MSE=0) results in a skill score of 1, while a model that shows no improvement over the reference model receives a skill score of 0. Negative skill scores indicate that the model performs worse and its MSE has increased with respect to the reference. In this case the CCA OO will be used as the model and the reference will be another commonly used OO. The MSE is calculated with respect to the SEVIRI subskin temperature.

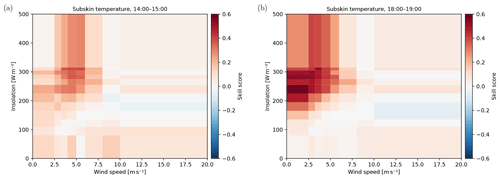
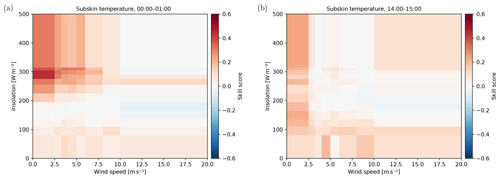
Figure 5 Skill score of the CCA OO compared to the parameterisation of Bernie et al. (2007) in the afternoon (a) and early evening (b).

The simplest method of assimilating satellite SST observations in a model that insufficiently describes the diurnal cycle of SST is to assimilate only at night or during high wind; see, for example, Waters et al. (2015). During the night the cycle of SST is close to its minimum value and the temperature of the upper layer of an OGCM forms a reasonable approximation for the skin temperature. In this situation the assimilation is performed without additional corrections. Figure 4a shows the skill score of the CCA OO at midnight local time using the temperature of the OGCM upper layer as a reference method. Figure 4b shows the same situation, but in the afternoon. For high wind and low insolation the CCA OO performs, as expected, similarly to using the upper OGCM layer. However, for low wind speeds and high insolation the CCA OO shows a clear improvement, even at midnight. This can be explained by the fact that at midnight some diurnal signal still remains and, even using the wind and insolation values of the next day, this is correctly modelled by the CCA OO.

A more advanced solution is the parameterisation of Bernie et al. (2007), which estimates the diurnal signal as a function of wind, insolation, and time. This is a commonly used parameterisation; for example, it is included with the NEMO ocean model (Madec et al., 1998). Figure 5 shows the skill score for the CCA OO compared to the parameterisation of Bernie et al. (2007) at the peak of the diurnal cycle (a) and in the early evening (b). It can be seen that for high insolation and low wind, conditions for which the diurnal warming is largest, both methods perform similarly. However, the CCA OO is better at accommodating different atmospheric conditions and shows significant improvements for the intermediate insolation and wind categories. Moreover, Fig. 5b shows that the CCA OO is able to better parameterise the cooling of the subskin in the late afternoon–evening after the peak of the diurnal warming has passed.

Using the CCA OO to improve the description of SST has many potential applications. For example, the CCA OO could be used as a parameterisation of diurnally varying skin SST within an OGCM as part of the air–sea flux calculations. The skin SST is the true interface temperature for air–sea fluxes, so this approach should result in improved air–sea heat transfer in OGCMs and coupled ocean–atmosphere models. See, for example, Marullo et al. (2016). Another possibility would be the use of the CCA OO as a parameterisation of diurnally varying SST within a climate model. The diurnal cycle is a fundamental signal of the climate system, yet for climate models the lack of vertical structure (and temporal resolution) is even more critical. See, for example, Large and Caron (2015).

Due to the way in which it is constructed, the CCA OO is an inherently linear operator. This makes it straightforward to implement in DA schemes that require linearised and differentiable OOs. However, non-linear effects can be accommodated to some extent by constructing a series of CCA OOs conditioned on such a non-linear dependency. For example, in the case of SST, this method has been used to condition the CCA OO on insolation, wind, and time. The only requirement in this case is that the datasets X and Y of Sect. 3 are sufficiently large to divide them by such a dependent variable.

The minimum size of the input dataset required ultimately depends on the number of model variables used (N_x) and the number of observation variables to predict (N_y). The number of free parameters in the CCA OO matrix M and the offset K equals (N_x+1)N_y. As each entry in the input dataset also provides N_y observation values, Eq. (4) requires a minimum of N_x+1 entries to be mathematically solvable. However, at this point the CCA OO will be overfitted. It will simply be able to memorise the input datasets rather than being based on general characteristics of the data. Care has to be taken to avoid this situation, making sure the input dataset contains a number of entries n with n>>N_x. Whether a given size n is sufficient should be tested using independent data. One possible method for this test is to withhold part of the input dataset from the CCA OO calculation and then use this subset to calculate the CCA OO performance.

6 Conclusions

Observation operators (OOs) form a central component in any data assimilation (DA) system, as they transform the state variables of a numerical model into real-world observable variables. Often, an OO also needs to correct for processes that are not fully described by the parent model. Such processes may be best modelled by interfacing the OO to a specialised model, but this is generally not feasible due to computational constraints.

The assimilation of satellite sea surface temperature (SST) in ocean general circulation models (OGCMs) is a prime example of a situation in which insufficiently modelled processes play an important role. The diurnal cycle of SST causes a discrepancy in the temperature of the very thin upper layer measured by a satellite and the rather coarse upper layer in a typical OGCM. On a clear summer day with low wind, this discrepancy can amount to as much as 2 ^∘C or more (Pimentel et al., 2019).

The current paper presented a method, based on canonical correlation analysis (CCA), to build parameterisations based on an output dataset of a specialised model. These parameterisations, referred to as the CCA OO, can provide an efficient approximation to the results of the specialised model and are therefore well-suited for use in DA systems.

The case of SST assimilation has been used to demonstrate the new CCA OO. Using an output dataset of the General Ocean Turbulence Model (GOTM), a high-resolution water column model specifically tuned for modelling the diurnal cycle of SST, a new CCA OO has been derived. Subsequently, the operator has been applied to reduced-resolution temperature profiles from the GOTM to simulate its use in a DA system. The approximations provided by the CCA OO are found to be in good agreement with the GOTM at various times of the day and across all atmospheric conditions. The results indicate that the CCA OO could be used to enable the assimilation of SST in conditions under which this was previously not possible. Moreover, the atmospheric categories that were introduced in the construction of the CCA OO for SST show that the linear assumption implicit in CCA can be partially relaxed. This makes the CCA OO versatile for any condition. Compared to commonly used methods for SST assimilation, the CCA OO can provide substantial improvements. This is especially true for measurements of the skin SST, since the CCA OO profits from the modelling of the cool-skin effect that is included in the GOTM.

The ability of the CCA OO to handle complicated physical models in a relatively simple way is attractive for a large number of problems in DA, for which reduced-order OOs are desirable due to computational constraints. Remotely sensed data are the obvious target given the complexity of their relationships with state variables. Observations in coupled assimilations (e.g. ocean–atmosphere, ocean–sea ice, or ocean–biogeochemistry) are examples of challenging problems that could be investigated in the future with the CCA OO.