Enhanced bed shear stress and mixing in the tidal wake of an offshore wind turbine monopile

Tidal flow past offshore wind farm (OWF) infrastructure generates a turbulent vortex wake. The wake is hypothesised to enhance seabed stress and water column turbulence mixing, thereby affecting seabed mobility, water column stratification and the transport of nutrients and oxygen and resulting in ecological impacts. We collect novel hydrodynamic data 40 m from an OWF monopile over a spring–neap cycle and use high-frequency velocity measurements to quantify turbulence. Outside of the wake, we observe a classical depth-limited boundary layer, with strong turbulence production and dissipation forced by tidal shear at the seabed. Inside the wake, turbulence production, dissipation and stress are enhanced throughout the full water column and are maximised in the upper half of the water column, where they correspond to a strong mean velocity deficit. Our results show that the seabed drag coefficient is doubled from $C_{\mathrm{d}}=\mathrm{3.5}\times {\mathrm{10}}^{-\mathrm{3}}$ to $\mathrm{7.8}\times {\mathrm{10}}^{-\mathrm{3}}$, suggesting greater seabed mobility, and the eddy viscosity is increased by 1 order of magnitude, indicating enhanced water column mixing. This research provides some valuable insight as OWFs expand into deeper seasonally stratified waters using both bottom-fixed and floating structures, where the addition of enhanced wake turbulence may have broad impacts as the additional mixing energy is added to regions with low rates of background mixing.

1 Introduction

There is growing interest in tidal flow past offshore wind turbine foundations and in the impact of the associated wake on the environment through seabed sediment scour, water column mixing and the resultant ecological impacts (e.g. Chambel et al., 2024; Schultze et al., 2020; Dannheim et al., 2020). This is being driven by the planned massive expansion in offshore wind generation over the coming decade in the drive for net-zero energy production. In northwestern European waters (the EU and UK) there was 36 GW of operational offshore wind in 2023, which is planned to be increased to 110 GW by 2030 as large arrays of turbines are being installed in increasingly deep waters (TCE, 2022; European Commission, Directorate-General for Energy, 2023).

In a natural tidal flow, small-scale turbulent eddies generate strong velocity gradients (shear) close to the seabed that impart a high stress onto the bed. Moving away from the seabed, the scale of the turbulent eddies mediating the transfer of momentum increases, which reduces the velocity gradients and results in correspondingly smaller stresses; this leads to the law-of-the-wall benthic boundary layer. Turbine foundations add barotropic drag to the tidal flow, creating a deficit in the mean velocity and forming a vortex wake that generates additional turbulence at the scale of the monopile. In shallow waters, the wake turbulence can directly impact the seabed and enhance the stresses, which may, in turn, modify seabed morphology (Couldrey et al., 2020) and sediment composition (McCarron et al., 2019) and impact benthic ecological communities (Damveld et al., 2018). The spatial and temporal persistence of the wake depends on the level of background turbulence, with wakes being efficiently eroded in highly turbulent (i.e. shallow and tidally energetic) regions (e.g. Eames et al., 2011).

In lower-energy deeper waters where stratification may occur – and particularly with the transition to deep-draft floating foundations (e.g. Hywind Scotland 78 m draft spar buoy foundations; Equinor, 2023) – the combination of barotropic and baroclinic drag may significantly affect the water column by directly adding turbulent energy to the pycnocline. The addition of wake turbulence to these lower-energy deeper environments will likely lead to more persistent regions of enhanced turbulent mixing (Dorrell et al., 2022); at the array scale, this may affect seasonal stratification (Schultze et al., 2020) and cause cumulative ecological impacts (Isaksson et al., 2023).

The aim of this paper is to investigate how the signature of the turbulent wake from an offshore wind turbine monopile differs from that of the background flow. Specific objectives are to quantify the changes in relation to (1) the rate of turbulence dissipation and production measured inside and outside the wake and (2) their vertical distribution through the water column, following which we (3) assess the potential impact of the wake on seabed stress and water column mixing. We use field observations in a tidally energetic well-mixed environment and, through the precise deployment of instruments 40 m from a fixed seabed monopile, measure natural background flows during the flood tide but sample directly within the wake during the ebb.

2 Location and methods

2.1 Field site

New observations were made in the western region of Liverpool Bay, UK, in the eastern Irish Sea during September 2022 (Fig. 1a, b). This shallow region experiences very large tides in the form of a semi-diurnal standing wave, with spring ranges at Liverpool approaching 10 m and strong currents that frequently exceed 1 m s⁻¹ and which, away from the region of freshwater influence, maintain a well-mixed water column (e.g. Rippeth et al., 2001).

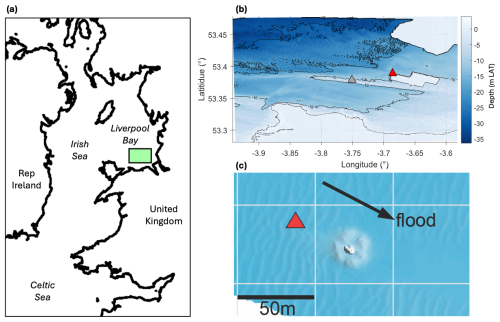
Figure 1 Field setting of the observations. (a) Outline map showing the location of the study site (green box) within Liverpool Bay in the eastern Irish Sea. (b) Bathymetry plotted with depths as metres below the lowest astronomical tide (mLAT), showing the location of the Rhyl Flats OWF (UKHO, 2024), with the ADCP (red triangle) positioned at its northwestern corner and the Constable Bank ADCP 3 km further to the southwest, away from the influence of the OWF (Unsworth et al., 2023). (c) Zoomed bathymetry showing the monopile and its surrounding rock scour protection and the ADCP location (red triangle), as well as indicating the flood tide direction.

2.2 Monopile wake measurements

High-resolution measurements were made x= 41 m northwest of a D= 4.7 m diameter monopile of the Rhyl Flats offshore wind farm (OWF) in Liverpool Bay (53.38922° N, 3.6866° W); this equates to a non-dimensional distance $x/D$ of 8.7 (Fig. 1b, c). The location was selected so that, during the flood tide, it was upstream of the monopile and experienced natural background flows, whereas, during the ebb, it was downstream of the monopile within the wake. During the observations, the water depth varied between 12.5 and 21 m during peak spring tides. The depth-averaged flow velocities confirm the rectilinear nature of the tidal flows (Fig. 2a). The dominant easterly component of the flood peaked at 0.8 m s⁻¹; the ebb tides were weaker, reaching −0.6 m s⁻¹, and showed greater scatter, as also observed at a nearby location by Unsworth et al. (2023). The cylinder Reynolds number Re_d,

$$\begin{array}{}\text{(1)}& {\mathit{Re}}_d={\displaystyle \frac{u_{\mathrm{\infty }}d}{\mathit{\nu }}},\end{array}$$

where u_∞ is the freestream flow velocity and ν is the kinematic viscosity (1.36 × 10⁻⁶ m² s⁻¹), was 𝒪(10⁴−10⁶) for the range of observed depth-averaged flood tide velocities (Fig. 2b). The transition to the turbulent critical flow regime around a cylinder and the formation of an asymmetric Karman vortex (KV) lee wake begins at ${\mathit{Re}}_d\gtrsim \mathrm{2}\times {\mathrm{10}}^{\mathrm{5}}$, which equates to a minimum velocity of 0.06 m s⁻¹, and at ${\mathit{Re}}_d\gtrsim \mathrm{5}\times {\mathrm{10}}^{\mathrm{5}}$, a further transition to the super-critical flow regime and a symmetrical KV wake occurs (e.g. Williamson, 1996). We therefore expect to observe a turbulent symmetric KV wake in the lee of the monopile for the majority of the survey. The seabed was composed of rippled sand with a median grain size of d₅₀=0.25 mm, determined by standard sieve analysis of multiple seabed grab samples. Following the method of van Rijn (1987), the seabed roughness height was found to be k_b= 0.122 m, including both grain and bedform roughness elements. Rock scour protection is deployed up to a diameter of ∼ 20 m in the immediate area surrounding the base of the monopile.

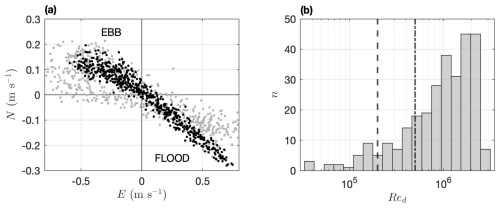
Figure 2 (a) Depth-averaged eastern and northern tidal current velocities (black); also plotted (grey) are velocities from 3 km to the southwest (grey triangle in Fig. 1b), away from the influence of the OWF (Unsworth et al., 2023). (b) Histogram of cylinder Reynolds number Re_d, showing the transition to a turbulent boundary layer around the monopile and asymmetric KV wake at ${\mathit{Re}}_d\gtrsim \mathrm{2}\times {\mathrm{10}}^{\mathrm{5}}$ (dashed) and the super-critical transition to a symmetric wake at ${\mathit{Re}}_d\gtrsim \mathrm{5}\times {\mathrm{10}}^{\mathrm{5}}$ (dot-dash) (Williamson, 1996; Rodríguez et al., 2015).

Direct measurements of the wave field were obtained from the nearby Rhyl Flats wave buoy (53.38241° N, 3.6062° W; Channel Coastal Observatory, 2022). The wave height and period were typically less than H_s= 1 m and T_z= 4 s, respectively, but peaked at H_s= 1.5 m and T_z= 4.5 s during 15–16 September (Fig. 3d). In this shallow, tidally energetic region, the water column generally remains well-mixed (see Rippeth et al., 2001; Simpson et al., 2002). No profiles of water temperatures were recorded, but time series of surface and bottom temperatures recorded nearby during 2018 indicate that thermal stratification typically only occurs during peak neap tide conditions during the months of June–July.

2.3 Observational setup

A Nortek Signature 1000 five-beam acoustic Doppler current profiler (ADCP) was installed on a bed-mounted frame and profiled the water column within 44 bins of 0.5 m thickness; the centre of the lowest bin was at z= 0.8 m above the seabed. The instrument heading was 220°, with the plane of beams 2 and 4 aligned with the streamwise current; the pitch and roll of the instrument on the seabed were −0.5 and 5.3°, respectively. The ADCP recorded along-beam velocities with a ping rate of 8 Hz and operated in burst mode, collecting 2048 samples at the start of each hour. The Doppler noise level was reported by the instrument as σ_N= 0.016 m s⁻¹, as configured for this deployment.

2.4 Turbulence metrics

The dissipation rate (ε₅) of turbulent kinetic energy (TKE) was estimated from the along-beam velocities of the vertical fifth beam of the ADCP using the structure function method (Wiles et al., 2006). In the presence of surface gravity waves, the vertical gradient in wave orbital velocity will bias the along-beam velocities, and we use the modified approach of Scannell et al. (2017) to remove this bias (Eq. A3 in the Appendix).

The Reynolds stresses were estimated using the variance method (Lu and Lueck, 1999; Rippeth et al., 2003), extended by Dewey and Stringer (2007) for a five-beam ADCP and including non-zero pitch and roll. The fifth beam provides an independent measure of the vertical velocity w and allows the stress components to be estimated with a reduced bias because the approximation due to the orthogonal beam is removed. The coordinate system was rotated to provide the streamwise ($\stackrel{\mathrm{‾}}{u^{\prime }{w}^{\prime }}$), cross-stream ($\stackrel{\mathrm{‾}}{v^{\prime }{w}^{\prime }}$) and vertical stresses ($\stackrel{\mathrm{‾}}{w^{\prime }{w}^{\prime }}$).

In a well-mixed tidally dominated environment, TKE production P is primarily achieved through energy transfer from the mean flow to turbulence via shear at the seabed; the buoyancy term can be neglected. P was estimated from the Reynolds stresses and the mean velocity vertical shear (e.g. Rippeth et al., 2003).

3 Results

3.1 Variation in rates of turbulence dissipation and production

The principal environmental parameters measured adjacently to the monopile are shown in Fig. 3. The profile of the mean streamwise velocity $\stackrel{\mathrm{‾}}{U_x}$ (Fig. 3a) indicates that the semi-diurnal tidal wave is standing and exhibits strong semi-diurnal and spring–neap variations. The largest velocities are observed during the peak spring tides (+0.8, −0.6 m s⁻¹) and are reduced to ± 0.35 m s⁻¹ during neaps.

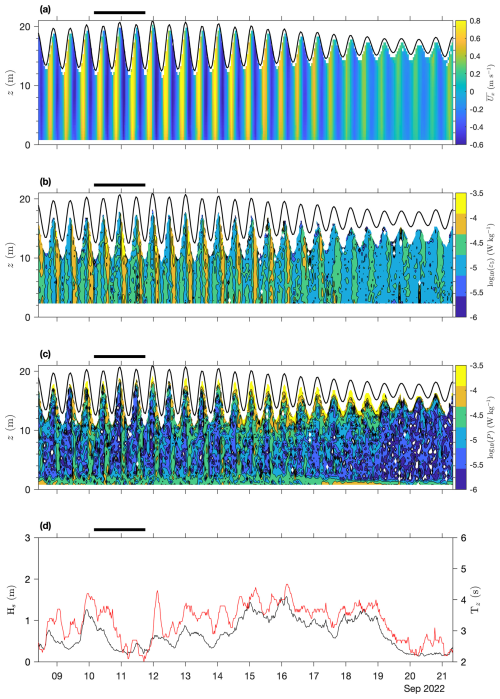
Figure 3 Overview of observations during the survey: (a) streamwise mean velocity $\stackrel{\mathrm{‾}}{U_x}$, (b) turbulence dissipation rate ε, (c) turbulence production P, and (d) significant wave height H_s (black) and period T_z (red). The water surface elevation is shown by the black line in (a)–(c). The white band at z < 2 m in (b) is due to the minimum of four bins for the regression of D(z,r) against $r^{\mathrm{2}/\mathrm{3}}$ in Eq. (A3). The horizontal black bar above each panel highlights the period shown in Fig. 4.

The TKE dissipation rate ε₅ (Fig. 3b) has both a spring–neap variation and a pronounced quarter-diurnal variation. During the flood, maximum values of ε₅ are −4.5 log₁₀(W kg⁻¹) during springs and -5 log₁₀(W kg⁻¹) during neaps. In contrast, maximum ε₅ during the ebb increases by almost 1 order of magnitude during springs (−3.7 log₁₀(W kg⁻¹)) and by half an order of magnitude during neaps. During spring tides, significant levels of ε₅ are observed to occur through the full depth of the water column.

The TKE production rate P (Fig. 3c) follows a similar temporal pattern to ε₅. During both phases of the tide, strong production (−4.5 log₁₀(W kg⁻¹)) consistent with shear at the seabed extends up to z ≈ 3 m above the bed, but during the ebb, an additional vertical band of strong P is present through the full water column. At several points throughout the survey (e.g. 15–19 September), intense regions ($>-$4 log₁₀(W kg⁻¹)) of near-surface P occur, which propagate downwards into the water column to z= 10 m. Comparing these periods to the surface waves recorded at the nearby wave buoy (Fig. 3d), steep waves (H_s= 1.5 m, T_z= 4 s) are likely to be injecting TKE directly into the surface layers, contributing to P. This wave contamination is not observed in ε₅ due to our use of the modified structure function (Eq. A3).

3.2 Wake-modified vertical distribution of turbulence

To provide further insight into the distribution of turbulence in the water column and to identify the balance between seabed and water column processes, we explore three spring tidal cycles in greater detail and compare with theoretical scaling. Figure 4a highlights the significant flood–ebb asymmetry in the strength and spatial distribution of ε₅. During the upstream (flood) phase, ε₅ appears to be forced at the seabed and propagates vertically toward the surface as the flow accelerates before weakening prior to high water slack. In contrast, during the downstream (ebb) phase, high ε₅ persists through the full water depth, with maximum values observed in the upper water column. This flood ebb asymmetry is unlikely to be attributable to tidal straining or convection because of the well-mixed nature of the environment. In Fig. 4b, we integrate ε₅ across 2 m thick bands of the water column close to the seabed and near the sea surface and through the full water column. All three display a quarter-diurnal variation in ε₅, but contrasting behaviour is seen at the seabed and near the surface during upstream and downstream phases. During the upstream phase, ε₅ at the seabed exceeds that near the surface, but during the downstream phase, this pattern is reversed, and the difference between them is approximately twice as large. Integrating through the full depth of the water column, ε₅ approaches being 1 order of magnitude greater during the downstream phase. We do note that ε₅ is possibly underestimated at the seabed since, due to the requirement of a minimum of four bins for the regression in Eq. A3, the lower 2 m is excluded.

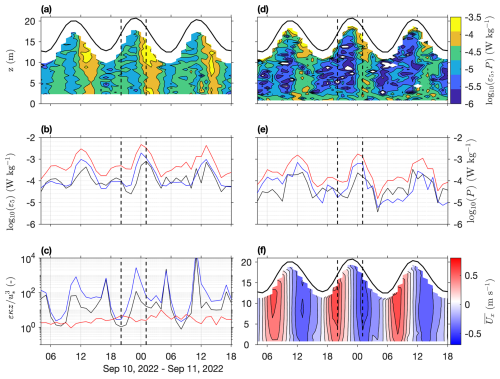
Figure 4 Vertical water column distribution of turbulence dissipation and production rate. (a) Dissipation rate ε₅; (b) seabed (black), near-surface (blue) and total (red) dissipation rate ε₅; (c) similarity scaling of dissipation rate ε₅ at the seabed (black) and near the surface (blue), as well as the total observed ratio ${\mathit{\epsilon }}_{\mathrm{5}}/P$ (red); (d) turbulence production P; (e) seabed (black), near-surface (blue) and total (red) turbulence production P; and (f) mean streamwise velocity $\stackrel{\mathrm{‾}}{U_x}$. Vertical dashed lines highlight equivalent mid-tide upstream (flood) and downstream (ebb) periods.

Following similarity theory, a local balance should exist between ε and P based on a constant-stress relationship, with the local production of turbulence by tidal shear at the seabed. This leads to a scaling factor ${\mathit{\epsilon }}_{\mathrm{s}}=-u_{*}^{\mathrm{3}}/\mathit{\kappa }z$, where u_* is the friction velocity, calculated as $u_{*}=({\mathit{\tau }}_{\mathrm{b}}/\mathit{\rho }{)}^{\mathrm{1}/\mathrm{2}}$ for bottom shear stress τ_b and seawater density ρ=1027 kg m⁻³, and κ is the von Karman constant (= 0.41). Here, we use the method of Soulsby and Clarke (2005) to compute the current-only τ_b,c with the measured bottom roughness length-scale k_b= 0.122 m, accounting for both bedform and skin friction roughness. During the upstream phase (Fig. 4c), ε₅ close to the seabed is in almost perfect balance with similarity theory, but, at the surface, it is approximately 20 % higher. During downstream conditions, ε₅ is 1 and 1.5 orders of magnitude greater than predicted at the seabed and near the surface, respectively, and peaks prior to the occurrence of the strongest flows (mid-ebb); this likely reflects the addition of wake turbulence to the water column. The similarity scaling breaks down at slack water as ε₅ is maintained despite the cessation of local production from the mean flow.

A flood-ebb asymmetry of P is clearly shown in Fig. 4d, which shows a consistent near-bed TKE production during both upstream and downstream flow phases and a strong production throughout the full water column during the downstream phase. Figure 4c integrates P into vertical zones and also shows the asymmetric flood–ebb behaviour, with greater downstream TKE production ($P=-\mathrm{3.5}$ log₁₀(W kg⁻¹)) compared to during upstream conditions ($P=-\mathrm{4.5}$ log₁₀(W kg⁻¹)). The difference between seabed and near-surface P is more variable, but, overall, we observe a trend of greater seabed production during upstream flows and greater near-surface production during downstream flows. When integrated through the full water column, P and ε₅ are in close agreement in terms of magnitude and trend, and the observed budget ${\mathit{\epsilon }}_{\mathrm{5}}/P$ remains within 1 order of magnitude (Fig. 4c, red line).

The mean streamwise velocity $\stackrel{\mathrm{‾}}{U_x}$ highlights the clear differences between the background upstream flood–tide flows and the downstream wake-affected ebb (Fig. 4f). During the upstream phase, the characteristic tidal benthic boundary layer structure is evident, with the strongest flows at the surface, which are reduced towards the bed developing shear. During the downstream phase, the velocity magnitude is reduced by approximately 35 %, with the strongest flows occurring at mid-depth and shear developing close to the bed. In the upper water column, a significant velocity deficit indicates the presence of the monopile wake and is in-phase with the peaks in ε₅ and P.

3.3 Enhanced Reynolds stress, seabed drag and mixing

To provide insight into the effect of the monopile wake through the water column, we compute ensemble-averaged vertical profiles of mean velocity, stress and TKE dissipation rate (Fig. 5). Vertical profiles at mid-flood and mid-ebb, when flow accelerations are expected to be minimal, were extracted from the seven spring tides between 9 and 13 September and were geometrically averaged in $z/h$ space to account for tidal changes in water depth. During the upstream phase (flood), the mean velocity profile displays a logarithmic form and extends the full thickness of the water column, as expected in a system dominated by tidal shear at the seabed (Fig. 5a). The maximum values of the stress occur at or just above the seabed (Fig. 5b) and tend towards zero, moving away from the seabed (Rippeth et al., 2002); an increase in stress is observed for $z/h>\mathrm{0.65}$, which may be due to surface waves. Following Rippeth et al. (2003), for our observed wave amplitude and period of ∼ 0.5 m and ∼ 4 s, respectively, we may expect a bias in the stress term close to the surface of ∼𝒪(0.5) N m⁻², decreasing with depth to ∼𝒪(0.05) N m⁻² at the bed, which is in close agreement with our observations.

During the downstream wake-affected ebb tide, a strong velocity deficit is present above $z/h>\mathrm{0.5}$ (Fig. 5a), indicative of the core of the wake. The stress increases from minimum values near the seabed to extreme values at the surface, but there is also a region of highly variable stress at $\mathrm{0.1}\le z/h\le \mathrm{0.3}$ (Fig. 5b). It is noteworthy that, for equivalent stages of the tide, whilst the downstream velocities are significantly weaker than during the upstream phase, the stresses are up to 6 times larger; this far exceeds the potential bias in the stress terms due to surface waves.

The profiles of ε₅ display a similar upstream–downstream asymmetry compared to that of the stresses (Fig. 5c). Peak ε₅ values occur during the downstream phase, with extreme values (−3.5 log₁₀(W kg⁻¹)) at $z/h=$ 0.25 and above mid-depth $z/h>\mathrm{0.50}$. Again, despite the stronger upstream velocities, ε₅ is almost 1 order of magnitude weaker during the upstream phase, displaying maximum values close to the seabed and decreasing linearly up to the surface.

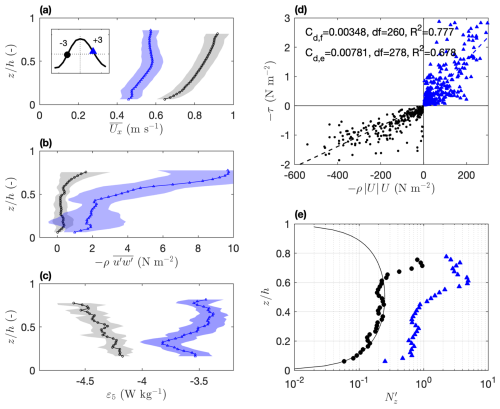
Figure 5 Summary of stress and drag. Peak upstream (black) and downstream (blue) ensemble-averaged (a) mean streamwise velocity profiles ${\stackrel{\mathrm{‾}}{U}}_x$, where the inset shows the peak flood and ebb times in the tidal cycle; (b) Reynolds stress $-\mathit{\rho }\stackrel{\mathrm{‾}}{u^{\prime }{w}^{\prime }}$; and (c) dissipation rate ε₅. Shaded regions plot ± standard deviation. (d) Comparison of the Reynolds stress estimates with the quadratic drag law during upstream (black) and downstream (blue) periods. The Reynolds stress averaged over the four bins closest to the bed (z= 0.8–2.3 m) is plotted against −ρ|U|U, where U is the mean current speed at z= 1 m, and the drag coefficient C_d is evaluated by linear fitting with the respective R² and degrees of freedom (df). (e) Non-dimensional eddy viscosity $N_z^{\prime }$ (where $N_z^{\prime }=N_z/\mathit{\kappa }{u}_{*}h$) for ensemble-averaged upstream and downstream phases compared to the steady-flow model (solid line).

Stress at the seabed is often parameterised using the drag coefficient C_d and the quadratic stress law ${\mathit{\tau }}_{\mathrm{b}}=\mathit{\rho }{C}_{\mathrm{d}}{\stackrel{\mathrm{‾}}{U}}^{\mathrm{2}}$ to relate the mean flow speed $\stackrel{\mathrm{‾}}{U}$ defined at some elevation above the seabed (frequently z=1 m, e.g. Soulsby, 1998) directly to the turbulent stress. We compare the total shear stress $\mathit{\tau }=-\mathit{\rho }\sqrt{{\stackrel{\mathrm{‾}}{u^{\prime }{w}^{\prime }}}^{\mathrm{2}}+{\stackrel{\mathrm{‾}}{v^{\prime }{w}^{\prime }}}^{\mathrm{2}}}$, averaged over the lowest 2 m of the water column, with the quadratic stress law evaluated at z= 1 m above the bed (Fig. 5d). Upstream (flood) and downstream (ebb) data are independently fitted to a straight line (both with R²∼ 0.7 and ∼ 270° of freedom) with significantly different slopes. This yields a downstream ebb drag coefficient of $C_{\mathrm{d},\mathrm{e}}=\mathrm{7.8}\times {\mathrm{10}}^{-\mathrm{3}}$, which is twice that observed during the upstream flood phase ($C_{\mathrm{d},\mathrm{f}}=\mathrm{3.5}\times {\mathrm{10}}^{-\mathrm{3}}$).

The eddy viscosity N_z relates the vertical velocity gradients to the horizontal stress and reflects the role of turbulent eddies in mediating the transfer of momentum. If we assume a steady-flow model where the velocity shear is described by $\partial u/\partial z=u_{*}/\mathit{\kappa }z$ and where the stress decreases linearly from its maximum value at the bed ${\mathit{\tau }}_{\mathrm{b}}=-\mathit{\rho }{u}_{*}^{\mathrm{2}}$ to zero at the surface, N_z takes a parabolic form (Rippeth et al., 2002):

$$\begin{array}{}\text{(2)}& N_z=\mathit{\kappa }{u}_{*}z(\mathrm{1}-{\displaystyle \frac{z}{h}}).\end{array}$$

We compare N_z computed for the ensemble-averaged peak upstream and downstream tidal phases in Fig. 5e. During the upstream phase, although there is some significant deviation from the steady-flow model approaching the sea surface for $z/h>\mathrm{0.6}$, the observations are consistent with the model in terms of both trend and magnitude. However, during the wake-affected ebb tide, N_z is almost 1 order of magnitude larger than the steady-flow model, and, although approximating a parabolic form at $z/h<\mathrm{0.35}$, it rapidly increases in the upper water column between $z/h=\mathrm{0.35}$ and $z/h=\mathrm{0.6}$; this corresponds to the region where shear, stress and ε₅ are observed to increase for the wake-affected flow in Fig. 5a–c and suggests that the monopile drives enhanced vertical mixing through the water column.

4 Discussion

4.1 Wake-enhanced turbulence

The present study utilises high-frequency five-beam ADCP data to provide turbulence metrics over multiple tidal cycles within the tidal wake 40 m downstream of an offshore wind turbine monopile. Observations of the TKE dissipation rate and Reynolds stresses have been combined with the mean velocity shear to provide new insight into the changes to the vertical structure of the water column inside and outside of the wake. Upstream of the monopile, these parameters generally accord to a classical depth-limited law-of-the-wall boundary layer, with peak values of mean velocity shear and stress close to the bed and correspondingly high rates of TKE production and dissipation that are balanced at the seabed (Fig. 4). The reduction in ε₅ moving away from the seabed indicates that the Kolmogorov length scale $({\mathit{\nu }}^{\mathrm{3}}/\mathit{\epsilon }{)}^{\mathrm{1}/\mathrm{4}}$ and, thus, the size of the energy-containing eddies are increasing as a function of κz. Downstream of the monopile within the wake, a strong velocity deficit forms in the upper half of the water column, and the production and dissipation rates of TKE deviate from theoretical similarity scaling and increase throughout the water column above the region of tidal shear in the bottom boundary layer (Fig. 4). We have further tested the impact of these wake-generated variations on the seabed and on the vertical water column mixing and show that the seabed drag coefficient and the eddy viscosity, respectively, are enhanced.

The monopile spans the full depth of the water column and extracts momentum from the mean flow, which is transferred to TKE at a (large) scale similar to that of the monopile itself (4.7 m); this leads to the observed velocity deficit in the wake that advects downstream in a self-similar manner. In the present ebb-tide data, we observe that the velocity deficit is largely eliminated in the lower half of the water column ($z/h\le \mathrm{0.5}$). This indicates that the high levels of shear and stress measured close to the bed, which result from the combination of natural small-scale eddy interactions and the additional TKE introduced by the monopile itself (Fig. 5), provide an important restorative mechanism for the mean flow by eroding the wake as it is advected downstream (Eames et al., 2011). Further support for this argument is provided by the high rate of TKE dissipation ε₅ also observed close to the bed.

Higher in the water column, the velocity deficit is maintained due to a reduction in the efficiency of the ambient flow in eroding the wake. First, the difference between the ambient flow and the velocity deficit is much greater due to the reduction in frictional drag from the seabed, and so the work required to restore the mean flow near the surface is therefore much greater. Second, we expect a decrease in the ambient shear and stress as the eddy length scale increases in proportion to κz to also reduce the rate at which the wake is eroded. The combination of these factors, as well as the continued addition of TKE from the deficit (Scott et al., 2023), leads to the maintenance of a region of elevated shear above $z/h=$ 0.5 that is associated with very high stress and ε₅, which is maximised at 0.5 $\le z/h\le \mathrm{0.7}$. Overall, this combination of seabed and water column factors suggests that wakes should persist for longer in environments with lower rates of background turbulence mixing, for example, deeper, less tidally energetic regions.

4.2 Implications of enhanced seabed drag

We show that the high levels of stress observed in the wake directly increase the drag coefficient at the seabed. Outside of the wake, $C_{\mathrm{d},\mathrm{f}}=\mathrm{3.5}\times {\mathrm{10}}^{-\mathrm{3}}$, which is comparable to standard values reported for sandy and sand–gravel seabed mixtures (e.g. Soulsby, 1998), but this is more than doubled to $C_{\mathrm{d},\mathrm{e}}=\mathrm{7.8}\times {\mathrm{10}}^{-\mathrm{3}}$ within the wake. Unless this wake-enhanced transfer of momentum from the mean flow to turbulence is accounted for, shelf-scale models (e.g. Telemac, FVCOM) that generally use the quadratic stress law as the default method of estimating bed shear stress will under-predict seabed stress even if they include monopiles as point drag sources (e.g. Rennau et al., 2012; Christiansen et al., 2023). The elevated C_d within the wake can be directly linked to enhanced sediment transport and observations of morphological change in the lee of monopiles. Wakes can modify the seabed, flattening bedforms by forcing a change towards an upper-stage plane bed regime, as observed at the Rhyl Flats OWF downstream of the monopile (Fig. 1c), and, in extreme cases, causing seabed scour, or they can force a live-bed regime to transition towards one that supports bedform development (Couldrey et al., 2020). At the array scale, wake formation will increase the spatial variability of the seabed morphology, change grain size mixtures and likely promote greater seabed heterogeneity; this can impact the make-up and functionality of the benthic ecosystem (van der Kooij et al., 2008; Gates et al., 2019) and feed up to higher trophic levels.

4.3 Implications of enhanced eddy viscosity

The wake enhances water column mixing by modifying the local momentum flux, and the eddy viscosity provides a useful concept for estimating wake-mixing efficiency and persistence by directly relating the mean flow gradients to the turbulent stresses. The magnitude of the eddy viscosity N_z is controlled by the interplay between the mean flow shear, the rate of recovery of the velocity deficit and the dissipation rate ε₅. In the present data, the ADCP is located at $x/D=$ 8.7, which is sufficiently far downstream of the monopile that the velocity deficit starts to recover, and, close to the seabed, where strong frictional drag and high ε₅ occur, N_z is reduced. However, higher in the water column where the velocity deficit remains significant, the rate of transfer of momentum to TKE remains high relative to ε₅, and strong Reynolds stresses are still generated, maximising N_z (Fig. 5). As the velocity deficit continues to weaken moving downstream, we would expect N_z to decrease as ε₅ drives the decay of the Reynolds stresses (Scott et al., 2023). The complex distribution of N_z through the wake-affected water column has significant implications for the inclusion of OWF turbulent wakes in large-scale shelf–sea models. The turbulence is sub-grid scale in these models, and the mixing processes are passed to some form of a generic turbulence closure model, which attempts to balance the production and dissipation of TKE and return this as an N_z value. In light of the many length scales introduced by the structures, robust datasets and fully resolved model simulations are first required to provide further insight into the physics of past flow structures, particularly in stratified regions.

4.4 Broader consequences of enhanced mixing

The observed order of magnitude increase in mixing caused by the monopile is likely to have significant implications for the transition towards floating OWF structures in deeper seasonally stratified waters (Dorrell et al., 2022). In these regions, background mixing rates are low because the pycnocline isolates the surface from the bottom waters, which limits the flux of nutrients and oxygen that drives primary productivity (Sharples et al., 2001). The addition of the high level of anthropogenic mixing caused by tidal flow past OWF structures to the stratified regions will result in a large relative increase in mixing compared to the background levels, potentially affecting the timing of the onset and breakdown of seasonal stratification (Rippeth, 2005), the strength of the stratification (Schultze et al., 2020), and the mixed-layer depth (Pearson et al., 2015); combined, this could result in significant ecological impacts spanning multiple trophic levels from plankton to fish to top predators (Trifonova and Scott, 2023). However, wake-mixing dynamics in stratified fluid flows are presently poorly understood, and high-fidelity large eddy simulation modelling is necessary to capture the baroclinic and advective processes that are required in order to produce a generic wake parameterisation for broad implementation.

5 Conclusions

High-frequency velocity measurements are used to quantify the turbulent vortex wake 40 m downstream of an OWF monopile in a tidally energetic environment. We take advantage of the rectilinear tidal flow to compare the natural background upstream flow during the flood tides with the wake-affected downstream flow during the ebb. The rates of turbulence production and dissipation are driven by tidal shear at the seabed during background flow conditions and reach −4.5 log₁₀(W kg⁻¹). Within the wake, a strong mean flow velocity deficit develops, which drives enhanced dissipation and production of −3.5 log₁₀(W kg⁻¹) through the full depth of the water column. Reynolds stresses are also enhanced within the wake. This doubles the seabed drag coefficient from $C_{\mathrm{d}}=\mathrm{3.5}\times {\mathrm{10}}^{-\mathrm{3}}$ to $C_{\mathrm{d}}=\mathrm{7.8}\times {\mathrm{10}}^{-\mathrm{3}}$ and implies that seabed mobility will increase, resulting in greater seabed heterogeneity. Enhanced stresses also increase the eddy viscosity by 1 order of magnitude, which will drive greater vertical water column mixing. These results provide useful insights as OWF developments progress into deeper, often seasonally stratified waters, where the addition of extra turbulent energy into the water column may alter the present delicate balances and result in widespread ecosystem impacts. Future work should focus on the generic parameterisation of wake turbulence in the shelf-scale numerical models required for planning and impact mitigation purposes.

Appendix A: TKE dissipation rate

The TKE dissipation rate ε was derived from the ADCP velocity measurements using the structure function method (Wiles et al., 2006). Along-beam velocity components b(z) from each beam are used to estimate the second-order structure function:

$$\begin{array}{}\text{(A1)}& D(z,r)=\stackrel{\mathrm{‾}}{\left(b^{\prime }\right(z)-b^{\prime }(z+r){)}^{\mathrm{2}}},\end{array}$$

where the overbar is the burst average, $b^{\prime }=b\left(z\right)-\overline{b}\left(z\right)$ is the fluctuating component of velocity at position z along the beam, and D(z,r) is the mean square of the velocity fluctuation difference between two points separated by distance r based on multiples of the bin size. The maximum separation distance r_max was set as 3 m. For isotropic turbulence, the structure function D(z,r) is related to ε by

$$\begin{array}{}\text{(A2)}& D(z,r)=C_{\mathrm{2}}{\mathit{\epsilon }}^{\mathrm{2}/\mathrm{3}}{r}^{\mathrm{2}/\mathrm{3}},\end{array}$$

where C₂ is a constant (=2.0). In the presence of surface gravity waves, the vertical gradient in wave orbital velocity will bias the along-beam velocities. We use the modified approach of Scannell et al. (2017) to remove this bias, using a least-squares fit to generate a linear model:

$$\begin{array}{}\text{(A3)}& D(z,r)=a_{\mathrm{0}}+a_{\mathrm{1}}{r}^{\mathrm{2}/\mathrm{3}}+a_{\mathrm{3}}{\left(r^{\mathrm{2}/\mathrm{3}}\right)}^{\mathrm{3}},\end{array}$$

where a3 contains the contribution to D(z,r) from the waves, $a_{\mathrm{0}}=\mathrm{2}{\mathit{\sigma }}_{\mathrm{b}}^{\mathrm{2}}$ provides an estimate of the instrument noise, and the gradient a₁ is used to derive ε via

$$\begin{array}{}\text{(A4)}& \mathit{\epsilon }={\left({\displaystyle \frac{a_{\mathrm{1}}}{C_{\mathrm{2}}}}\right)}^{\mathrm{2}/\mathrm{3}}.\end{array}$$

Here, we estimate the dissipation rate from the vertical fifth beam of the ADCP (ε₅).