the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
The characteristics of tides and their effects on the general circulation of the Mediterranean Sea
Bethany McDonagh
Emanuela Clementi
Anna Chiara Goglio
Nadia Pinardi
The effects of tides on the Mediterranean Sea's general circulation, with a particular focus on the horizontal and vertical currents, are investigated using twin simulations with and without tides. Amplitudes of tides in the region are typically low, but an analysis of the potential and kinetic energy demonstrates that tides have effects across many spatial and temporal scales in the basin, including non-linear effects in short periods (less than 1 d) with high kinetic energy peaks at near-inertial basin modes and tidal frequencies. Internal tidal waves are also revealed below 100 m. Tides are found to amplify several basin modes of the Mediterranean Sea, broaden several tidal frequency energy spectra bands, and interact energetically with near-inertial waves. Tides increase the mixed layer depth in the Mediterranean Sea, particularly in the deep and intermediate water formation areas of the western Mediterranean Basin and eastern Mediterranean Basin. The addition of tides in the cases considered does also enhance Western Mediterranean Deep Water formation.
- Article
(10737 KB) - Full-text XML
-
Supplement
(9139 KB) - BibTeX
- EndNote
Tidal forcing is a rather recent addition to large-scale circulation models of the ocean, since horizontal and vertical resolutions have recently become fine enough to allow for an explicit and more accurate representation of tides. This has given rise to novel opportunities to analyse tides and their impacts on the ocean circulation. For an overall review of the topic, see Arbic (2022). Tides are now considered to be essential components of the large-scale circulation (St. Laurent et al., 2002; Müller et al., 2010; Melet et al., 2016): their global average input energy is 3.5 TW (Simmons et al., 2004), the second largest after winds (Ferrari and Wunsch, 2010), and they generate internal tides that then drive internal mixing (de Lavergne et al., 2020). Tides are also an important phenomenon in coupled numerical models, which represents a new opportunity in high-resolution modelling of the ocean and atmosphere (Arbic, 2022) and in long-term simulations.
Internal tides are characterised by relatively high vertical velocities with respect to Ekman suction and pumping, while their horizontal wavelength is similar to general circulation scales (Oddo et al., 2023). Recently, observational and modelling studies began to advance our understanding of internal tides in several regions of the Mediterranean Sea. The presence of internal tides generated in the Strait of Gibraltar is discussed in Morozov et al. (2002), Vlasenko et al. (2009), and Hilt et al. (2020). Diurnal internal tide oscillations are generated around the Adriatic Sea islands in an observational study (Mihanović et al., 2009), leading to baroclinic trapped waves. In a recent paper, Oddo et al. (2023) found observational and modelling evidence of internal tides at the Sicily–Malta escarpment due to diurnal tidal components connected to the bathymetric gradients.
For the Mediterranean Sea, several authors have shown the importance of tidal motion in the Strait of Gibraltar (Armi and Farmer, 1985; Candela et al., 1990; Harzallah et al., 2014; Naranjo et al., 2014; Sannino et al., 2015). Armi and Farmer (1985) and Farmer et al. (1988) first observed the hydraulic control points that are induced by tides, and the importance of tidal dynamics and their variability in the region were discussed more recently by Vázquez et al. (2006), Sánchez-Román et al. (2012), García-Lafuente et al. (2013), and Hilt et al. (2020). Naranjo et al. (2014) and Harzallah et al. (2014) found that tides in the Strait of Gibraltar (1) intensify the high-frequency dynamics in the strait and (2) increase the salinity and, to a lesser extent, decrease the temperature of Atlantic inflowing waters through the enhancement of mixing, affecting the water mass formation processes further downstream from the strait. Tides also change the Mediterranean water outflow, as demonstrated by Izquierdo and Mikolajewicz (2019), where outflowing water is modified by tides, demonstrating the role of tides in the spreading of outflowing water. Moreover, Ambar and Howe (1979) found that tides increase the variability of outflowing salinity.
Other features of the Mediterranean Sea that are important when discussing tides are the free barotropic oscillations induced by atmospheric pressure and wind forcing. The Mediterranean Sea's first barotropic basin mode is at 38.5 h (Schwab and Rao, 1983), beyond that of diurnal tides, but higher modes also exist at 11.4, 8.4, and 7.4 h (Schwab and Rao, 1983) and at 8 h (Lamy et al., 1981; Lozano and Candela, 1995). Many of these free oscillations could be affected or enhanced by tides, especially considering their proximity to tidal frequencies. The Adriatic Sea is characterised by seiches or free barotropic oscillations close to tidal frequencies: at 10.7 and 21.9 h (Medvedev et al., 2020; Leder and Orlić, 2004; Schwab and Rao, 1983) and at 12.0 h (Lozano and Candela, 1995). Medvedev et al. (2020) used tide gauge data to explicitly find that tides resonate with the Adriatic Sea modes, while Lozano and Candela (1995) discussed the interaction of the M2 tide with modes in the Gulf of Gabes, the Adriatic Sea, the Aegean Sea, and the Mediterranean Sea. Palma et al. (2020) found additionally that spectra of kinetic energy in the Strait of Sicily are enhanced at 8 and 6 h due to the non-linear effects of tides. These works demonstrate the potential importance of interactions between tides and higher-frequency features of the Mediterranean Sea, but the interaction between tides and barotropic oscillations in the Mediterranean Sea has not been investigated using a state-of-the-art numerical model.
In the North Atlantic, the addition of tides was found to improve the representation of the mixed layer depth and deep water formation in the Labrador Sea (Müller et al., 2010). Lee et al. (2006) found in the same region that sea surface density was increased by the addition of tides to their model and that this could enhance ventilation and overturning. Internal wave frequencies of around 8 h were also found by van Haren, H., and The ANTARES Collaboration (2014) in the north-western Mediterranean Sea. These relationships have, to our knowledge, not been investigated in detail in the Mediterranean Sea.
In this work, we further characterise the tidal large-scale circulation effects in the entire Mediterranean Sea. Analysis of the effects of tides on circulation was carried out in the western Mediterranean Basin by Naranjo et al. (2014), in the Strait of Gibraltar by Sannino et al. (2014) and Gonzalez (2023), and in the Strait of Sicily by Oddo et al. (2023) and Gasparini et al. (2004). In the whole Mediterranean Basin, the general circulation without tides was analysed by Pinardi et al. (2019). As far as we know, the effects of tides on the circulation of the entire Mediterranean Sea has not been extensively investigated.
To do this, we analyse the differences in a general circulation ocean model with and without tides, focusing on changes in the spectra, in both the horizontal and vertical dynamics across the basin on average, and in several water mass formation regions. Furthermore, we show the impact of tides in the eastern Mediterranean Sea and the amplification of different basin modes by a tidal resonant mechanism.
In the Mediterranean Sea there are four key regions of deep and intermediate water formation (see Fig. 1): the Gulf of Lion (Western Mediterranean Deep Water, WMDW) and southern Adriatic Sea (Eastern Mediterranean Deep Water, EMDW) for deep water formation and the Cretan Sea (Cretan Deep Water, CDW, and Cretan Intermediate Water, CIW) and Rhodes Gyre (Levantine Deep Water, LDW, and Levantine Intermediate Water, LIW) for intermediate water formation (Pinardi et al., 2015). In these regions the vertical velocities are enhanced, and this paper will analyse in detail the differences in water mass formation rates with and without tides.
Section 2 describes the model and observational data used and the analysis methods, while Sects. 3–7 contain the model results and conclusions as follows:
-
Sect. 3: “Sea level energy spectra”;
-
Sect. 4: “Kinetic energy spectra”;
-
Sect. 5: “Mixed layer depth and water mass formation”;
-
Sect. 6: “Temperature and salinity”; and
-
Sect. 7: “Conclusions”.
The general circulation model used is NEMO v3.6, following the implementation of the Mediterranean Sea forecasting system operational in the framework of the Copernicus Marine Service (Coppini et al., 2023; Clementi et al., 2021). The area covered by the model is shown in Fig. 1. The model without tidal forcing is validated in Coppini et al. (2023) and as part of the model information in Clementi et al. (2019), while the experiment with tides is validated in the Quality Information Document in Clementi et al. (2021).
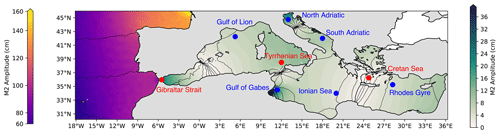
Figure 1Map of the M2 tidal component amplitude in the Atlantic Ocean (contours, colour bar on the left) and Mediterranean Sea (contours, colour bar on the right) as well as the M2 phase in black contour lines, with highlighted points in regions of open-ocean dense water formation (Gulf of Lion, southern Adriatic Sea, Cretan Sea, and Rhodes Gyre) and regions of high tidal amplitude (Strait of Gibraltar, Gulf of Gabes, and northern Adriatic Sea). Additional points that are studied further in Sect. 4 are also shown (Tyrrhenian Sea and Ionian Sea).
The model has a uniform horizontal resolution with 141 uneven vertical levels, using z* vertical coordinates and partial steps. This model is eddy-resolving, since the Rossby radius of deformation is of the order of 10 km in the Mediterranean Sea and the horizontal resolution of the model is approximately 4 km. Atmospheric forcing fields are given by the 6 h European Centre for Medium-Range Weather Forecasts (ECMWF) analyses at horizontal resolutions of (2015–2018) and (2019–2021), and they are used to compute momentum, water, and heat fluxes using specifically designed bulk formulae (Pettenuzzo et al., 2010). Lateral open-boundary conditions are used in the Atlantic Ocean and Dardanelles Strait and are provided by the Copernicus Marine global analysis and forecast system (Galloudec et al., 2022) for the Atlantic Ocean and a mixture of the aforementioned global model and daily climatology derived from a Marmara Sea box model (Maderich et al., 2015) at the Dardanelles Strait boundary. Further details of the boundary conditions are in Clementi et al. (2021).
Additionally, monthly mean climatological freshwater inputs from 39 rivers are added to the surface layer. Several datasets are used for this: the Global Runoff Data Centre dataset (Fakete et al., 1999) for the Po, Ebro, Nile, and Rhône rivers; the dataset from Raicich (1996) for the Vjosë and Seman rivers; the UNEP-MAP dataset (Demiraj et al., 1996) for the Buna and Bojana rivers; and the PERSEUS dataset (Deliverable of Perseus, 2012) for the remaining 32 Mediterranean rivers which have a mean runoff greater than 50 m3 s−1. The bathymetry used is the GEBCO 30 s bathymetry (GEBCO Bathymetric Compilation Group 2014, 2014) interpolated onto the model grid.
In the chosen configuration, vertical diffusivity depends on the Richardson number, calculated according to Pacanowski and Philander (1981). The Richardson number is a ratio of buoyancy to horizontal shear:
where N2 is the Brunt–Väisälä frequency, and is the vertical shear of horizontal flow. Enhanced vertical viscosity and diffusivity are used where layers are unstable ( s−2), imposing a vertical diffusivity coefficient of 10 m2 s−1. Vertical viscosity and diffusivity are then calculated according to
where AvT and Avm are the vertical eddy viscosity and diffusivity respectively, and (maximum viscosity value 100×10−4 m2 s−1), a, and n are adjustable parameters. In the model runs used, a and n are 5 and 2 respectively. The background vertical eddy viscosity and vertical eddy diffusivity values are m2 s−1 and m2 s−1 respectively, which are typical values in the case of constant viscosity and diffusivity representing diapycnal mixing from the breaking of internal waves. The constant values used here follow the NEMO implementation by Tonani et al. (2008).
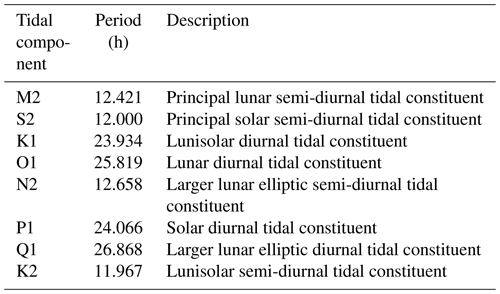
Twin experiments are presented in this work with and without the representation of tides. In the experiment including tides, the eight major tidal components for the Mediterranean Sea (M2, S2, K1, O1, N2, Q1, K2, and P1) are represented, which are detailed further in Table 1. The M2 amplitude is displayed in Fig. 1, showing the well-known high-amplitude areas in the Strait of Gibraltar, the Gulf of Gabes, and the northern Adriatic Sea. Moreover, the Atlantic Ocean lateral open-boundary fields include tidal forcing from TPXO9 (Egbert and Erofeeva, 2002).
Table 1Tidal constituent components used in the model for this work, with their respective periods and astronomical descriptions.
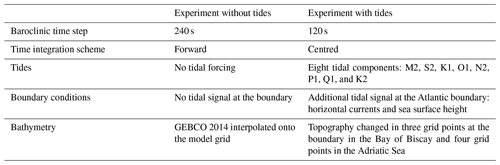
Other than the addition of the tidal forcing itself, there are some further differences between the tidal and non-tidal modelling set-ups (see Table 2), with the primary difference being the time integration method. Both experiments use a split–explicit free surface formulation proposed in Shchepetkin and McWilliams (2005), solving the free surface equation and the associated barotropic velocity equations with a smaller time step than the one used for the three-dimensional prognostic variables. The non-tidal experiment uses forward time integration, in which the external mode (barotropic time step) is integrated between the current and subsequent baroclinic time steps. This was not stable in the experiment including tides, so this instead uses a centred integration scheme, as recommended by the NEMO manual (Madec et al., 2019), where the baroclinic-to-barotropic forcing term given at the actual time step becomes centred in the middle of the integration window. The tidal experiment uses a shorter baroclinic time step, 120 s, rather than 240 s in the experiment without tides, which was changed for stability purposes. The effects of these changes are negligible compared to the effects of adding tidal forcing to the model (see the Supplement). The bathymetry was adjusted at several points in the tidal experiment for stability reasons: in the Bay of Biscay in the northernmost part of the model domain along the French coast, and several points were modified along the Croatian coastline to avoid generation of spurious tidal signals due to islands and complex bathymetry. All of the above changes in the tidal experiment compared to the experiment without tides are implemented as in Agresti (2018).
Table 2Summary of the key differences between the tidal experiment and the experiment without tides.
The model was integrated for 7 years (2015–2021), starting from climatological temperature and salinity initial conditions derived from the winter climatology (2005–2012) of the World Ocean Atlas (Boyer et al., 2013). The first 2 years are removed from the following analysis because they are considered a spin-up period.
Figure 2 shows a spectrum of hourly sea surface height (SSH) in the Mediterranean Sea for 5 years, for both tidal and non-tidal experiments. The diurnal and semi-diurnal tidal components represent the major differences between the two solutions, as expected. Further differences between the two models away from these tidal frequencies are also visible. Tides appear to modulate the spectrum at the mesoscales: energy is reduced in the tidal model at frequencies with a period longer than 2 d.
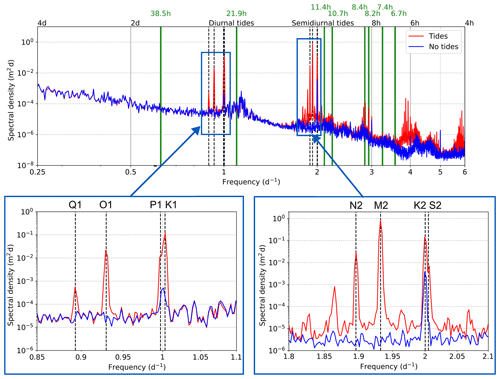
Figure 2Energy density spectrum of hourly mean sea surface height in the Mediterranean Sea for the period 2017–2021, for the experiment without tides (blue) and with tides (red). The basin-mean spectrum is calculated as an area-weighted mean of the periodogram at each grid point in the Mediterranean Sea. Boxes below the figure show the key diurnal and semi-diurnal ranges to highlight the representation of each individual tidal component. Green lines in the figure indicate frequencies of known barotropic oscillations in the Mediterranean Sea and its sub-basins.
Peaks at both 24 and 12 h are apparent, both with and without tides. In the case without tides, the energy peaks can be attributed to basin modes excited by atmospheric pressure forcing, as found by Oddo et al. (2014) using a similar NEMO configuration. In the semi-diurnal range, the tidal model introduces a broad peak around 12 h as well as peaks at the individual tidal component frequencies. This is due to the amplification by tides of the basin modes near and at these frequencies. We argue that the broad 12 h energy peak in Fig. 2 in the tidal run is composed of the amplified 11.4 h Mediterranean Sea basin mode energy (Schwab and Rao, 1983) and the 12 h Adriatic and Aegean Sea modes (Lozano and Candela, 1995). Moreover, interactions between internal tides and other mesoscale phenomena such as eddies could be affecting the internal tidal kinetic energy, as discussed in Guo et al. (2023), but a dedicated analysis would be required to confirm whether this is the case in the Mediterranean Sea. Furthermore, the spatial and temporal averaging of model outputs has likely blurred these peaks slightly. Peaks are also seen at 8 and 6 h, which correspond to the kinetic energy frequencies in the Strait of Sicily as noted by Palma et al. (2020), where these peaks were considered to come from non-linear effects of tides. Further peaks that are enhanced by tides align with the western Mediterranean Basin mode of 8.4 h discussed in Schwab and Rao (1983) and the Gulf of Gabes mode at 8.2 h (Lozano and Candela, 1995). Schwab and Rao (1983) also noted a fourth Mediterranean Sea mode at 7.4 h and the third Adriatic Sea mode at 6.7 h, but these are not visible in the basin-mean spectrum of Fig. 2 and are not affected by tides. Overall, there are many oscillations in the Mediterranean Sea that interact with tides, leading to their enhancement, although not every barotropic oscillation mentioned in the literature is affected by tides.
Considering the amplification of basin modes, Fig. 3 shows sea level spectra in the Adriatic Sea and Gulf of Gabes to understand whether the peaks in Fig. 2 correspond to modes in these regions. In the Adriatic Sea (Fig. 3a), the sea level energy peaks at the frequencies of the barotropic modes of the Adriatic Sea at 10.7 and 12 h (Lozano and Candela, 1995) are enhanced by tides, whereas the mode at 6.7 h (Schwab and Rao, 1983) has a similar energy density in both experiments. This is evidenced by the different amplitudes of the 10.7 and 12 h peaks in the non-tidal case compared to the tidal one, unlike the 6.7 h peak, which remains the same. In the Gulf of Gabes (Fig. 3b), tides also enhance the mode at 8.2 h (Lozano and Candela, 1995).
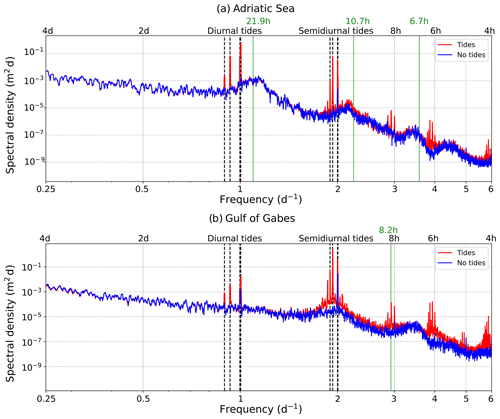
Figure 3Energy density spectra of hourly mean sea surface height in the Mediterranean Sea for the period 2017–2021, for the model without tides (blue) and with tides (red), in (a) the Adriatic Sea (40.5° N–northern boundary) and (b) the Gulf of Gabes (32.5–35.5° N, 9.8–13.0° E). An area-weighted mean of the periodogram at each grid point was taken for each of the sub-basins. Green lines in the figure indicate frequencies of known barotropic oscillations in each region.
Maps of the sea surface height power spectrum at 8.2 and 6 h are shown for both experiments in Fig. 4. These frequencies are presented here as they show the largest differences between the two experiments for the referenced frequencies from the literature (see Sect. 1), other than the tidal frequencies directly. Most of the Mediterranean Sea has enhanced power at 8.2 h in the tidal experiment (Fig. 4a, c), with particularly large changes in the central Mediterranean: the Tyrrhenian Sea, the Gulf of Gabes, and the Adriatic Sea. The barotropic oscillation at 8.2 h is in the Gulf of Gabes, according to Lozano and Candela (1995), but the third mode of the Mediterranean Sea (Schwab and Rao, 1983) and the non-linear effects of tides in the central Mediterranean Sea according to Palma et al. (2020) are at frequencies close to this (8.4 and 8.0 h respectively) and may also have an impact in Fig. 4c. Since many of the calculations of barotropic oscillations in the Mediterranean Sea were made several decades ago, there is a need for an updated confirmation of the frequencies of barotropic oscillations using state-of-the-art methods. In Fig. 4b and d, we see that the Sicily–Malta escarpment region of Palma et al. (2020) again has particularly enhanced power in the experiment with tides, but other regions such as the Alboran Sea and the western Mediterranean Sea see an interaction between tides and potential energy at the 6 h frequency.
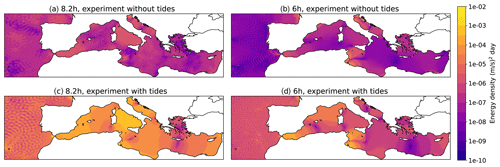
Figure 4Maps of the energy density of sea surface height at (a) 8.2 h without tides, (b) 6 h without tides, (c) 8.2 h with tides, and (d) 6 h with tides for the Mediterranean Sea in 2017–2021.
To summarise the analysis of sea surface height, we find that (1) tides directly affect the sea surface height on spatial and temporal scales away from those of the tides, (2) existing Mediterranean Basin and regional barotropic oscillations at frequencies with time periods shorter than 12 h are excited by tides (particularly at 6 h and at several frequencies close to 8 h), and (3) maps of the energy density at these frequencies reveal the distribution of these interactions in the Mediterranean Sea.
For this analysis, several points are selected across the Mediterranean Sea to understand the effects of tides on local phenomena such as the generation of internal tides and interactions with near-inertial waves. The map in Fig. 1 shows these points. From this, three contrasting points were selected to be shown in this work: the Strait of Gibraltar, the Tyrrhenian Sea, and the Cretan Sea. Results for the other points are available in the Supplement.
We first calculate the rotary spectra for depth-averaged (barotropic) horizontal velocities (Fig. 5) for both clockwise and anti-clockwise components and then combine these to create the rotary kinetic energy density spectra. These rotary spectra visualise the timescales at which there is high kinetic energy at each selected point, over the entire water column. In the Strait of Gibraltar (Fig. 5a), tides enhance kinetic energy at all frequencies, particularly at frequencies close to and higher than 12 h. The basin mode frequency of 8.4 h is enhanced by tides, and a peak at around 6 h is also visible, which is due to non-linear tidal effects (Palma et al., 2020). The Tyrrhenian Sea and Cretan Sea, unlike the Strait of Gibraltar, have broad peaks at the near-inertial frequencies. Peaks at diurnal tidal frequencies are more apparent in the Tyrrhenian Sea than in the Cretan Sea.
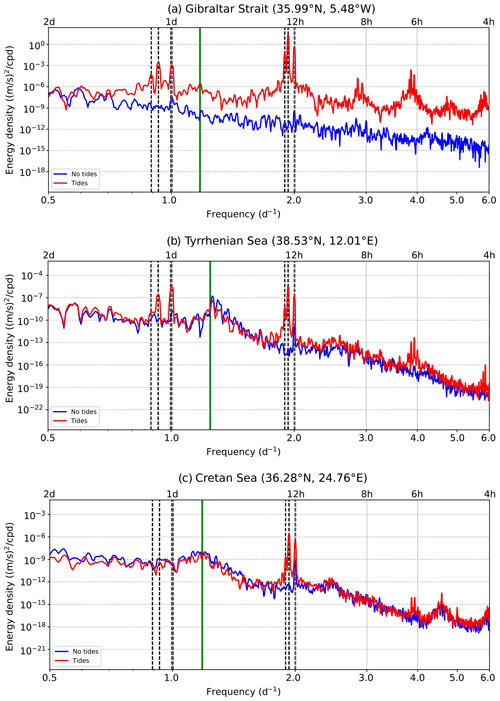
Figure 5Barotropic (depth-mean) rotary kinetic energy density spectra for points in the (a) Strait of Gibraltar (35.99° N, 5.48° W), (b) Tyrrhenian Sea (38.53° N, 12.01° E), and (c) Cretan Sea (36.28° N, 24.76° E), with the tidal experiment in red and the experiment without tides in blue, using hourly outputs over the 6 months January–June 2019. Dashed lines represent the eight tidal components used in the model, and the green line is the inertial frequency. The locations of these points are shown in Fig. 1.
We also analysed the kinetic energy spectra split into vertical levels to consider baroclinic currents and internal wave modes, as shown in Fig. 6. We note that upper-layer currents (0–150 m) are characterised by the entering Atlantic water layer dynamics, while the intermediate layer (150–500 m) currents are on average in the opposite direction to the surface, characterising the intermediate water circulation in the basin. We now analyse the effects of tides on this anti-estuarine zonally oriented conveyor belt described in Pinardi et al. (2019). Figure 6 shows spectra for the three selected points throughout the water column.
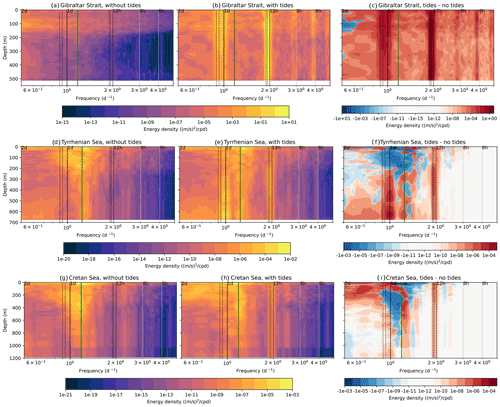
Figure 6Rotary spectra of kinetic energy density over the full water column without tides in the (a) Strait of Gibraltar (35.99° N, 5.48° W), (d) Tyrrhenian Sea (38.53° N, 12.01° E), and (g) Cretan Sea (36.28° N, 24.76° E); with tides in the (b) Strait of Gibraltar, (e) Tyrrhenian Sea, and (h) Cretan Sea; and with the difference between the two spectra in the (c) Strait of Gibraltar, (f) Tyrrhenian Sea, and (i) Cretan Sea. All data are for May 2019. The locations of these points are shown in Fig. 1. The green line represents the inertial frequency at each point, and the dashed lines indicate the frequencies of the eight tidal components included in the tidal experiment.
In the Strait of Gibraltar, it is clear that the entire structure of the kinetic energy is dominated by tides: tides enhance kinetic energy at almost all frequencies and depths (Fig. 6c). There are also internal tides visible in this region: Fig. 6b shows peaks in kinetic energy at around 100 m at the M2 and K1 tidal frequencies, implying the existence of internal tides in the Strait of Gibraltar, as shown by Morozov et al. (2002) and more recently discussed in Gonzalez et al. (2023). Some diurnal internal tidal energy is visible in the Tyrrhenian Sea (Fig. 6e), together with a shift in the near-inertial peak when compared to the experiment without tides (Fig. 6d). The interaction of tides with near-inertial waves is clearer in the Cretan Sea (Fig. 6i), as the peak is shifted to a higher frequency compared to Fig. 6e.
Internal tides are known to have high ageostrophic vertical velocities (Niwa and Hibiya, 2001; Li and von Storch, 2020), and thus an analysis of the vertical motion is mandatory. To visualise the internal tidal motion in the basin, we use Hovmöller diagrams for 1 month (May 2019) of hourly vertical currents for each of the three selected points from Fig. 6. In Fig. 7, the location of the Strait of Gibraltar has a dominant vertical velocity oscillation at 12 h. In contrast, near-inertial waves have greater importance in the Cretan Sea (Fig. 9), and they propagate downwards through the water column, notably around days 10–15 of the month and at 150–500 m (Fig. 9c). The effect of tides on this is shown in Fig. 9d, where interactions between the internal tidal and near-inertial waves create wave–wave patterns during the same period. The Tyrrhenian Sea (Fig. 8) also has both near-inertial waves and internal tides at these depths, but the interaction here is weaker.
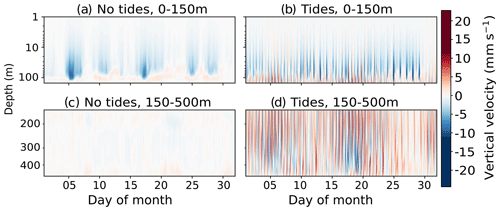
Figure 7Hovmöller diagrams of depth against time of hourly mean vertical velocity at a point in the Strait of Gibraltar (35.99° N, 5.48° W; see Fig. 1) in May 2019, for (a) the model without tides at 0–150 m, (b) the tidal model at 0–150 m, (c) the model without tides at 150–500 m, and (d) the tidal model at 150–500 m. Note that the depth scale is logarithmic.
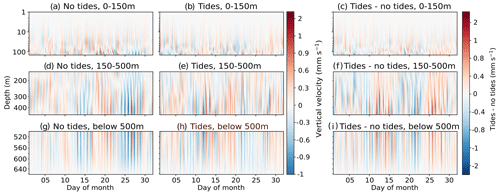
Figure 8Hovmöller diagrams of depth against time of hourly mean vertical velocity at a point in the Tyrrhenian Sea (38.53° N, 12.01° E; see Fig. 1) in May 2019, for (a) the model without tides at 0–150 m, (b) the tidal model at 0–150 m, (c) the tidal model − model without tides at 0–150 m, (d) the model without tides at 150–500 m, (e) the tidal model at 150–500 m, (f) the tidal model − model without tides at 150–500 m, (g) the model without tides below 500 m, (h) the tidal model below 500 m, and (i) the tidal model − model without tides below 500 m. Note that the depth scale is logarithmic.
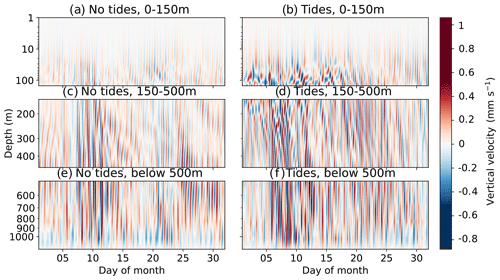
Figure 9Hovmöller diagrams of depth against time of hourly mean vertical velocity at a point in the Cretan Sea (36.28° N, 24.76° E; see Fig. 1) in May 2019, for (a) the model without tides at 0–150 m, (b) the tidal model at 0–150 m, (c) the model without tides at 150–500 m, (d) the tidal model at 150–500 m, (e) the model without tides below 500 m, and (f) the tidal model below 500 m. Note that the depth scale is logarithmic.
An interesting feature of Figs. 7–9 is the baroclinic structure of the vertical velocity in the experiment with and without tides. Two zero crossings appear, one at approximately 150 m, the lower limit of the inflowing branch of the zonal conveyor belt already described above (Pinardi et al., 2019), and the second at 300 m. This is particularly apparent in the Strait of Gibraltar (Fig. 7), where internal tide generation leads to increased tidal velocity in both directions. The continuation of this zero crossing at 150 m in other regions (Figs. 8–9) demonstrates the importance of internal tide generation at the Strait of Gibraltar and how it affects the entire general circulation of the Mediterranean Sea, including in remote regions.
The three contrasting regions of the Mediterranean Basin highlight the varying importance of tides, internal tides, and their interactions with near-inertial internal waves in different regions. While the Strait of Gibraltar (Fig. 7) is dominated by semi-diurnal tides, the other two regions (Figs. 8–9) show propagating near-inertial waves, as in Cozzani (2023), interacting with internal tides, particularly in the Cretan Sea.
Assessing the impact of tides on the mixed layer depth can provide indirect evidence for the impact of internal tides on the vertical mixing and vertical motion. The mixed layer depth is calculated using a density criterion based on a density change of 0.01 kg m−3 (de Boyer Montégut et al., 2004). Figure 10 shows the change in winter (December–March) mixed layer depth in the two experiments and a time series of the Mediterranean Sea mean mixed layer depth for the entire 5-year period. There is an increase in the winter mixed layer depth with tides throughout most of the basin, with notable exceptions in the Strait of Gibraltar–Alboran Sea region and in parts of the Aegean Sea. In the Strait of Gibraltar, this is explained by a thicker interface layer (García-Lafuente et al., 2013), which shrinks the upper layer compared to the experiment without tides, reducing the depth at which the threshold density change for the mixed layer is reached. These effects extend into the upper-layer Alboran Sea water, which originates in the Strait of Gibraltar. In the Aegean Sea, despite having low-amplitude barotropic tides, internal tides are present (Alford et al., 2012) and affect mixing at the bottom (Gregg et al., 2012), which in turn likely affects the water column structure in this shallow region.
However, the biggest change occurs in the Gulf of Lion region, a key area for the formation of deep water (WMDW, Fig. 1). Regarding the seasonality of mixed layer depth (Fig. 10d–e), both the absolute and percentage changes due to tides are positive throughout the year but are greatest in winter. We also note that the largest increase in the mean mixed layer depth in the tidal experiment is evident during winter 2019, which is also the year characterised by the largest WMDW formation (see Fig. 11). The deepening of the mixed layer can be a precursor of increased dense water formation, but a direct analysis of this would be needed to confirm whether the tides are enhancing water mass formation as well as mixed layer depth, and we note that the analysis in this work does not directly establish a connection between the two processes. Other important processes such as weak stratification and localised currents are key precursors of deep water formation in the western Mediterranean.
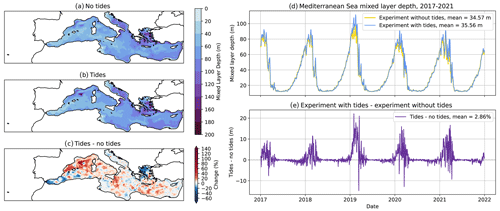
Figure 10Winter (December–March) mean mixed layer depth in the Mediterranean Sea for (a) the experiment without tides, (b) the experiment with tides, and (c) the percentage difference between the tidal and non-tidal experiments. The time series of the daily Mediterranean Sea mean mixed layer depth for 2017–2021 (d) and the difference between the tidal and non-tidal experiment time series (e).
Pinardi et al. (2015) defined intermediate water as having densities of 29.1–29.2 kg m−3 and deep water as having densities greater than 29.2 kg m−3. Figure 11 shows the water mass formation rate in the deep and intermediate formation areas of Fig. 1, which are the same regions indicated by Pinardi et al. (2015) for each winter of the analysed period, with and without tides. The most notable change is in WMDW, particularly during the event of 2019, where the tidal experiment forms several times more deep water at its peak compared to the experiment without tides. This is in agreement with Naranjo et al. (2014), who showed that enhanced WMDW formation occurred with tides in 4 out of the 5 years analysed. Modest increases are also seen in LIW formation. EMDW and LDW have increased water mass formation rates when including tides in some years and decreased rates in other years. We argue that this irregular behaviour is connected to the impact of tides on the strength of the pre-conditioning factors and the air–sea interaction heat fluxes that are affected by tides (Oddo et al., 2023).
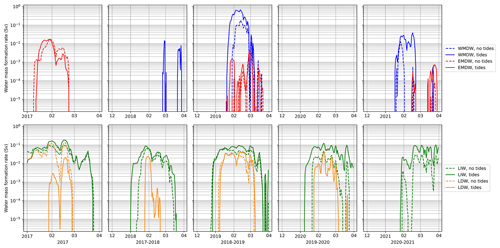
Figure 11Daily water mass formation rate in winter (December–March) 2017–2021, for the tidal experiment (solid lines) and the non-tidal experiment (dashed lines). Four types of water mass are included: Western Mediterranean Deep Water (blue), Eastern Mediterranean Deep Water (red), Levantine Intermediate Water (green), and Levantine Deep Water (orange).
The salinity and temperature of the Mediterranean Sea are affected by tides, primarily in the upper layer above 150 m, as can be seen in Fig. 12. This is the layer affected by the entering low-salinity Atlantic water. As indicated in work by Naranjo et al. (2014), Harzallah et al. (2014), Sanchez-Roman et al. (2018), and Gonzalez et al. (2023), inflowing salinity at Gibraltar increases when tides are introduced and the upper-layer temperature decreases, albeit by a smaller amount. This salinity increase has an upward trend that in time does not stabilise in the few years of our experiment. This was also found by Harzallah et al. (2014), where the salinity difference between the experiments with and without tides increased for several decades before stabilising, since this stabilisation depends on the overturning timescales of the basin that require several decades to spin up in full.
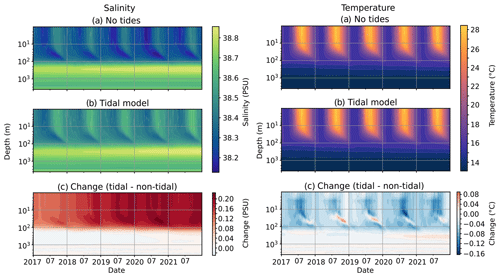
Figure 12Hovmöller plot of depth against time of daily salinity (left) and temperature (right) in the Mediterranean Sea in 2017–2021, for the model without tides (a), with tides (b), and the change without tides (c). Note that the depth scale is logarithmic.
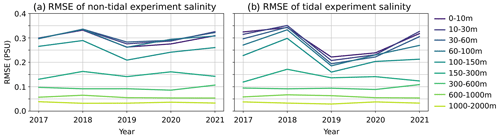
The additional increased salinity in the Mediterranean Sea due to tides and its trend over time can be compared to observations from profiling floats to understand whether the salinity increase follows the observational trend or whether it is overestimated. This was calculated for the Mediterranean Sea and integrated along the vertical layers for each year in the experiment. Figure 13 shows the mean salinity root mean square error (RMSE) of the experiments with respect to observations averaged in the whole basin and provided along nine vertical layers. For the tidal experiment, the RMSE does not present a clear linear trend, instead varying by individual year. The lack of a linear trend is also apparent in the non-tidal experiment, but here the salinity bias is positive throughout the upper layer. Overall, the RMSE of the two experiments is similar in some years, but in 2019 and 2020 the tidal experiment has a much lower RMSE in the upper layers. Figure 13 demonstrates that, in both experiments, the model error is larger at the surface up to 150 m and is reduced to less than 0.15 PSU below this layer, where it also shows a lower temporal variability. The lower layers remain stable with small errors, whereas the surface varies more and produces larger errors when compared to the observations.
The effects of tides on the Mediterranean Sea circulation were studied through a twin numerical experiment approach based on a high-resolution (around 3.8 km) model of the region, with and without the explicit representation of tides. Spectra of sea surface height and kinetic energy in the basin, as well as in key regions characterised by basin modes, revealed that the effects of tides on the energetics of the Mediterranean Sea extend far beyond the spatial and temporal scales of the tides themselves.
Tides enhance the power at 8 and 6 h frequencies due to their non-linear effects across the Mediterranean Basin, amplifying the basin modes, as shown in the Strait of Sicily by Palma et al. (2020). Tides also interact with and amplify the other basin modes at 11.4 and 8.4 h, the Adriatic mode at 10.7 h, and the mode in the Gulf of Gabes at 8.2 h. The Adriatic modes at 12 and 21.9 h are visible in both the tidal and non-tidal experiments, but the 12 h frequency is enhanced by the tides. Results such as these demonstrate the complexity and non-linearity of tidal effects in the Mediterranean Sea.
The study then discussed the rotary spectra of the barotropic and full kinetic energy at several selected points in the Mediterranean Sea. This analysis showed the ubiquitous field of internal waves below around 150 m, both at diurnal and semi-diurnal time frequencies. The Hovmöller diagrams of the vertical velocity components revealed the internal tide field structure in the basin as well as the interaction of internal tides with near-inertial waves in some regions, such as the Cretan Sea. In addition to near-inertial waves, both the semi-diurnal and diurnal internal tides have high energy, potentially at an overall Mediterranean scale not previously highlighted.
Tides affect the mixed layer depth of the basin, with different signs in different regions. The Mediterranean deep and intermediate water formation is enhanced by tides in the WMDW region and in the Levantine Sea, where intermediate water masses are formed. This aligns with increases in the winter mixed layer depth across most of the Mediterranean Sea. It should be noted that, although an increased mixed layer depth is one conditioning element for dense water formation, other concomitant processes are needed for deep water formation events to occur (Marshall and Schott, 1999; Pinardi et al., 2022).
It is important to note that the resolution of this model configuration, although higher than many global ocean models and regional ocean models from past studies, has limitations in its representation of waves with shorter wavelengths, including internal tides. According to Li et al. (2015, 2017), the first two modes of the M2 internal tide and the first three modes of the K1 internal tide all have wavelengths greater than 45 km, but high modes are likely unresolved at the resolution. Furthermore, high vertical resolution is important for simulating internal tides. Our model lacks high vertical resolution at deeper levels, and this could contribute to a lack of internal tides below 500 m.
In this work, the interactions between tides and other high-frequency phenomena have been described, but a longer model integration, such as that of Pinardi et al. (2019) but including tides, would reveal the effects of tides on lower-frequency phenomena. Moreover, a dedicated study of internal tides in the Mediterranean Sea, as has been carried out in the global ocean by Li et al. (2015, 2017), is lacking, and our results provide further motivation for this. The current literature also lacks a calculation of the barotropic modes of the Mediterranean Sea using state-of-the-art techniques which would provide an important dataset for further studies of the barotropic oscillations in the Mediterranean Sea.
The datasets used for the analysis done in this work can be found at https://doi.org/10.5281/zenodo.10911630 (McDonagh et al., 2024).
The supplement related to this article is available online at: https://doi.org/10.5194/os-20-1051-2024-supplement.
BM ran the numerical models, analysed the results, and wrote the manuscript. EC and ACG provided support in the set-up and running of the numerical models and analysis. NP planned the study and supported the analysis of the model results. All the authors reviewed and edited the manuscript.
The contact author has declared that none of the authors has any competing interests.
Publisher’s note: Copernicus Publications remains neutral with regard to jurisdictional claims made in the text, published maps, institutional affiliations, or any other geographical representation in this paper. While Copernicus Publications makes every effort to include appropriate place names, the final responsibility lies with the authors.
We would like to thank two anonymous reviewers and our editor, Joanne Williams, for their feedback that led to the improvement of this work.
This paper is part of a PhD thesis of the Bologna University programme “Future Earth, climate change and societal challenges”. It has also been supported by the EU Copernicus Marine Service's Mediterranean Monitoring and Forecasting Center – contract no. 21002L5-COP-MFC MED-5500.
This paper was edited by Joanne Williams and reviewed by two anonymous referees.
Agresti, V.: Effects of tidal motion on the Mediterranean Sea General Circulation, PhD thesis, Alma Mater Studiorum University of Bologna, https://doi.org/10.6092/unibo/amsdottorato/8516, 2018. a
Alford, M. H., Gregg, M. C., Zervakis, V., and Kontoyiannis, H.: Internal wave measurements on the Cycladic Plateau of the Aegean Sea, J. Geophys. Res., 117, C01015, https://doi.org/10.1029/2011JC007488, 2012. a
Ambar, I. and Howe, M.: Observations of the Mediterranean outflow – I mixing in the Mediterranean outflow, Deep-Sea Res. Pt. I, 26, 535–554, https://doi.org/10.1016/0198-0149(79)90095-5, 1979. a
Arbic, B. K.: Incorporating tides and internal gravity waves within global ocean general circulation models: A review, Progr. Oceanogr., 206, 102824, https://doi.org/10.1016/j.pocean.2022.102824, 2022. a, b
Armi, L. and Farmer, D.: The internal hydraulics of the Strait of Gibraltar and associated sills and narrows, Oceanol. Acta, 8, 37–46, 1985. a, b
Boyer, T., Antonov, J. I., Baranova, O. K., Coleman, C., Garcia, H. E., Grodsky, A., Johnson, D. R., Locarnini, R. A., Mishonov, A. V., O'Brien, T., Paver, C., Reagan, J., Seidov, D., Smolyar, I. V., and Zweng, M. M.: World Ocean Database 2013, NOAA Atlas NESDIS 72 [data set], Silver Spring, MD, https://doi.org/10.7289/V5NZ85MT, 2013. a
Candela, J., Winant, C., and Ruiz, A.: Tides in the Strait of Gibraltar, J. Geophys. Res.-Oceans, 95, 7313–7335, https://doi.org/10.1029/JC095iC05p07313, 1990. a
Clementi, E., Pistoia, J., Escudier, R., Delrosso, D., Drudi, M., Grandi, A., Lecci, R., Cretí, S., Ciliberti, S., Coppini, G., Masina, S., and Pinardi, N.: Mediterranean Sea Analysis and Forecast (CMEMS MED-Currents, EAS5 system) (Version 1), Copernicus Monitoring Environment Marine Service (CMEMS) [data set], https://doi.org/10.25423/CMCC/MEDSEA_ANALYSIS_FORECAST_PHY_006_013_EAS5, 2019. a
Clementi, E., Aydogdu, A., Goglio, A. C., Pistoia, J., Escudier, R., Drudi, M., Grandi, A., Mariani, A., Lyubartsev, V., Lecci, R., Cretí, S., Coppini, G., Masina, S., and Pinardi, N.: Mediterranean Sea Physical Analysis and Forecast (CMEMS MED-Currents, EAS6 system), Copernicus Monitoring Environment Marine Service (CMEMS) [data set], https://doi.org/10.25423/CMCC/MEDSEA_ANALYSISFORECAST_PHY_006_013_EAS6, 2021. a, b, c
Coppini, G., Clementi, E., Cossarini, G., Salon, S., Korres, G., Ravdas, M., Lecci, R., Pistoia, J., Goglio, A. C., Drudi, M., Grandi, A., Aydogdu, A., Escudier, R., Cipollone, A., Lyubartsev, V., Mariani, A., Cretì, S., Palermo, F., Scuro, M., Masina, S., Pinardi, N., Navarra, A., Delrosso, D., Teruzzi, A., Di Biagio, V., Bolzon, G., Feudale, L., Coidessa, G., Amadio, C., Brosich, A., Miró, A., Alvarez, E., Lazzari, P., Solidoro, C., Oikonomou, C., and Zacharioudaki, A.: The Mediterranean Forecasting System – Part 1: Evolution and performance, Ocean Sci., 19, 1483–1516, https://doi.org/10.5194/os-19-1483-2023, 2023. a, b
Cozzani, E.: Oceanic near-inertial internal waves generation, propagation, and interaction with mesoscale eddies, PhD thesis, Alma Mater Studiorum University of Bologna, https://amsdottorato.unibo.it/10961/ (last access: 23 August 2024), 2023. a
de Boyer Montégut, C., Madec, G., Fischer, A. S., Lazar, A., and Iudicone, D.: Mixed layer depth over the global ocean: An examination of profile data and a profile-based climatology, J. Geophys. Res., 109, C12003, https://doi.org/10.1029/2004JC002378, 2004. a
de Lavergne, C., Vic, C., Madec, G., Roquet, F., Waterhouse, A. F., Whalen, C. B., Cuypers, Y., Bouruet-Aubertot, P., Ferron, B., and Hibiya, T.: A Parameterization of Local and Remote Tidal Mixing, J. Adv. Model. Earth Sy., 12, e2020MS002065, https://doi.org/10.1029/2020MS002065, 2020. a
Deliverable of Perseus: Deliverable D4.6, SES land-based runoff and nutrient load data (1980–2000), edited by: Bouwman, L. and van Apeldoorn, D., 2012 PERSEUS H2020 grant agreement n. 287600, European Commission, http://www.perseus-net.eu/assets/media/PDF/deliverables/3321.6_Final.pdf (last access: 19 August 2024), 2012. a
Demiraj, E., Bicja, M., Gjika, E., Gjiknuri, L., Muçaj, L. G., Hoxha, F., Hoxha, P., Karadumi, S., Kongoli, S., Mullaj, A., Mustaqi, V., Palluqi, A., Ruli, E., Selfo, M., Shehi, A., and Sino, Q.: Implications of climate change for the Albanian Coast, Mediterranean Action Plan, MAP Technical Reports Series, 98, UNEP, https://iczmplatform.org/storage/documents/yDhUCslQEwyE5yzECrOBrUOx7wYLLpNDaDivaxaF.pdf (last access: 19 August 2024), 1996. a
Egbert, G. D. and Erofeeva, S. Y.: Efficient inverse modeling of barotropic ocean tides, J. Atmos. Ocean. Tech., 19.2, 183–204, 2002. a
Fakete, B., Vörösmarty, C., and Grabs, W.: Global composite runoff fields based on observed river discharge and simulated water balances, Technical Report 22, Global Runoff Data Centre, Koblenz, Germany, https://www.compositerunoff.sr.unh.edu/ (last access: 19 August 2024), 1999. a
Farmer, D. M., Armi, L., Armi, L., and Farmer, D. M.: The flow of Atlantic water through the Strait of Gibraltar, Progr. Oceanogr., 21, 1–103, https://doi.org/10.1016/0079-6611(88)90055-9, 1988. a
Ferrari, R. and Wunsch, C.: The distribution of eddy kinetic and potential energies in the global ocean, Tellus, 62A, 92–108, https://doi.org/10.1111/j.1600-0870.2009.00432.x, 2010. a
Galloudec, O. L., Chune, S. L., Nouel, L., Fernandez, E., Derval, C., Tressol, M., Dussurget, R., Biardeau, A., and Tonani, M.: Global Ocean Physical Analysis and Forecasting Product, Copernicus Monitoring Environment Marine Service (CMEMS), https://doi.org/10.48670/moi-00016, 2022. a
García-Lafuente, J., Bruque Pozas, E., Sánchez Garrido, J. C., Sannino, G., and Sammartino, S.: The interface mixing layer and the tidal dynamics at the eastern part of the Strait of Gibraltar, J. Mar. Syst., 117–118, 31–42, https://doi.org/10.1016/j.jmarsys.2013.02.014, 2013. a, b
Gasparini, G. P., Smeed, D. A., Alderson, S., Sparnocchia, S., Vetrano, A., and Mazzola, S.: Tidal and subtidal currents in the Strait of Sicily, J. Geophys. Res.-Oceans, 109, C02011, https://doi.org/10.1029/2003JC002011, 2004. a
GEBCO Bathymetric Compilation Group 2014: The GEBCO_2014 Grid, version 20150318, NERC EDS British Oceanographic Data Centre NOC, https://www.gebco.net (last access: 16 August 2024), 2014. a
Gonzalez, N. M.: Modélisation multi-échelle du détroit de Gibraltar et de son rôle de régulateur du climat méditerranéen, PhD thesis, Sciences de l'Univers, de l'Environnement et de l'Espace, University of Toulouse, https://theses.hal.science/tel-04257734 (last access: 16 August 2024), 2023. a
Gonzalez, N. M., Waldman, R., Sannino, G., Giordani, H., and Somot, S.: Understanding tidal mixing at the Strait of Gibraltar: A high-resolution model approach, Progr. Oceanogr., 212, 102980, https://doi.org/10.1016/j.pocean.2023.102980, 2023. a, b
Gregg, M., Alford, M., Kontoyiannis, H., Zervakis, V., and Winkel, D.: Mixing over the steep side of the Cycladic Plateau in the Aegean Sea, J. Mar. Syst., 89, 30–47, https://doi.org/10.1016/j.jmarsys.2011.07.009, 2012. a
Guo, Z., Wang, S., Cao, A., Xie, J., Song, J., and Guo, X.: Refraction of the M2 internal tides by mesoscale eddies in the South China Sea, Deep-Sea Res. Pt. I, 192, 103946, https://doi.org/10.1016/j.dsr.2022.103946, 2023. a
Harzallah, A., Alioua, M., and Li, L.: Mass exchange at the Strait of Gibraltar in response to tidal and lower frequency forcing as simulated by a Mediterranean Sea model, Tellus A, 66, 23871, https://doi.org/10.3402/tellusa.v66.23871, 2014. a, b, c, d
Hilt, M., Auclair, F., Benshila, R., Bordois, L., Capet, X., Debreu, L., Dumas, F., Jullien, S., Lemarié, F., Marchesiello, P., Nguyen, C., and Roblou, L.: Numerical modelling of hydraulic control, solitary waves and primary instabilities in the Strait of Gibraltar, Ocean Modell., 151, 101642, https://doi.org/10.1016/j.ocemod.2020.101642, 2020. a, b
Izquierdo, A. and Mikolajewicz, U.: The role of tides in the spreading of Mediterranean Outflow waters along the southwestern Iberian margin, Ocean Modell., 133, 27–43, https://doi.org/10.1016/j.ocemod.2018.08.003, 2019. a
Lamy, A., Millot, C., and Molines, J. M.: Bottom Pressure and Sea Level Measurements in the Gulf of Lions, J. Phys. Oceanogr., 11, 394–409, https://doi.org/10.1175/1520-0485(1981)011<0394:BPASLM>2.0.CO;2, 1981. a
Leder, N. and Orlic, M.: Fundamental Adriatic seiche recorded by current meters, Ann. Geophys., 22, 1449–1464, https://doi.org/10.5194/angeo-22-1449-2004, 2004. a
Lee, H.-C., Rosatib, A., and Spelman, M. J.: Barotropic tidal mixing effects in a coupled climate model: Oceanic conditions in the Northern Atlantic, Ocean Modell., 11, 464–477, https://doi.org/10.1016/j.ocemod.2005.03.003, 2006. a
Li, Z. and von Storch, J.-S.: M2 internal-tide generation in STORMTIDE2, J. Geophys. Res.-Oceans, 125, e2019JC015453, https://doi.org/10.1029/2019JC015453, 2020. a
Li, Z., von Storch, J.-S., and Müller, M.: The M2 Internal Tide Simulated by a 1/10° OGCM, J. Phys. Oceanogr., 45, 3119–3135, https://doi.org/10.1175/JPO-D-14-0228.1, 2015. a, b
Li, Z., von Storch, J.-S., and Müller, M.: The K1 internal tide simulated by a 1/10° OGCM, Ocean Modell., 113, 145–156, https://doi.org/10.1016/j.ocemod.2017.04.002, 2017. a, b
Lozano, C. J. and Candela, J.: The M2 tide in the Mediterranean Sea: Dynamic analysis and data assimilation, Oceanol. Acta, 18, 419–441, 1995. a, b, c, d, e, f, g, h
Madec, G., Bourdallé-Badie, R., Bell, M., Chanut, J., Clementi, E., Coward, A., Drudi, M., Éthé, C., Iovino, D., Lea, D., Lévy, C., Martin, N., Masson, S., Mathiot, P., Mocavero, S., Müller, S., Nurser, G., Samson, G., and Storkey, D.: NEMO ocean engine, Zenodo, https://doi.org/10.5281/zenodo.1464816, 2019. a
Maderich, V., Ilyin, Y., and Lemeshko, E.: Seasonal and interannual variability of the water exchange in the Turkish Straits System estimated by modelling, Mediterr. Mar. Sci., 16, 444–459, https://doi.org/10.12681/mms.1103, 2015. a
Marshall, J. and Schott, F.: Open-ocean convection: observations, theory, and models, Rev. Geophys., 37, 1–64, https://doi.org/10.1029/98RG02739, 1999. a
McDonagh, B., Clementi, E., Goglio, A. C., and Pinardi, N.: Data from: The characteristics of tides and their effects on the general circulation of the Mediterranean Sea, Zenodo [data set], https://doi.org/10.5281/zenodo.10911630, 2024. a
Medvedev, I. P., Vilibić, I., and Rabinovich, A. B.: Tidal Resonance in the Adriatic Sea: Observational Evidence, J. Geophys. Res.-Oceans, 125, e2020JC016168, https://doi.org/10.1029/2020JC016168, 2020. a, b
Melet, A., Legg, S., and Hallberg, R.: Climatic Impacts of Parameterized Local and Remote Tidal Mixing, J. Climate, 29, 3473–3500, https://doi.org/10.1175/JCLI-D-15-0153.1, 2016. a
Mihanović, H., Orlić, M., and Pasarić, Z.: Diurnal thermocline oscillations driven by tidal flow around an island in the Middle Adriatic, J. Mar. Syst., 78, S157–S168, https://doi.org/10.1016/j.jmarsys.2009.01.021, 2009. a
Morozov, E. G., Trulsen, K., Velarde, M. G., and Vlasenko, V. I.: Internal Tides in the Strait of Gibraltar, J. Phys. Oceanogr., 32, 3193–3206, https://doi.org/10.1175/1520-0485(2002)032<3193:ITITSO>2.0.CO;2, 2002. a, b
Müller, M., Haak, H., Jungclaus, J., Sündermann, J., and Thomas, M.: The effect of ocean tides on a climate model simulation, Ocean Modell., 35, 304–313, https://doi.org/10.1016/j.ocemod.2010.09.001, 2010. a, b
Naranjo, C., Lafuente, J., Sannino, G., and Sanchez-Garrido, J.: How much do tides affect the circulation of the Mediterranean Sea? From local processes in the Strait of Gibraltar to basin-scale effects, Prog. Oceanogr., 127, 108–116, https://doi.org/10.1016/j.pocean.2014.06.005, 2014. a, b, c, d, e
Niwa, Y. and Hibiya, T.: Numerical study of the spatial distribution of the M2 internal tide in the Pacific Ocean, J. Geophys. Res.-Oceans, 106, 22441–22449, https://doi.org/10.1029/2000JC000770, 2001. a
Oddo, P., Bonaduce, A., Pinardi, N., and Guarnieri, A.: Sensitivity of the Mediterranean sea level to atmospheric pressure and free surface elevation numerical formulation in NEMO, Geosci. Model Dev., 7, 3001–3015, https://doi.org/10.5194/gmd-7-3001-2014, 2014. a
Oddo, P., Poulain, P., Falchetti, S., Storto, A., and Zappa, G.: Internal tides in the central Mediterranean Sea: observational evidence and numerical studies, Ocean Dynam., 73, 145–163, https://doi.org/10.1007/s10236-023-01545-z, 2023. a, b, c, d
Pacanowski, R. C. and Philander, S. G. H.: Parameterization of Vertical Mixing in Numerical Models of Tropical Oceans, J. Phys. Oceanogr., 11, 1443–1451, https://doi.org/10.1175/1520-0485(1981)011<1443:POVMIN>2.0.CO;2, 1981. a
Palma, M., Iacono, R., Sannino, G., Bargagli, A., Carillo, A., Fekete, B. M., Lombardi, E., Napolitano, E., Pisacane, G., and Struglia, M. V.: Short-term, linear, and non-linear local effects of the tides on the surface dynamics in a new, high-resolution model of the Mediterranean Sea circulation, Ocean Dynam., 70, 935–963, https://doi.org/10.1007/s10236-020-01364-6, 2020. a, b, c, d, e, f
Pettenuzzo, D., Large, W., and Pinardi, N.: On the corrections of ERA-40 surface flux products consistent with the Mediterranean heat and water budgets and the connection between basin surface total heat flux and NAO, J. Geophys. Res., 115, C06022, https://doi.org/10.1029/2009JC005631, 2010. a
Pinardi, N., Zavatarelli, M., Adani, M., Coppini, G., Fratianni, C., Oddo, P., Simoncelli, S., Tonani, M., Lyubartsev, V., Dobricic, S., and Bonaduce, A.: Mediterranean Sea large-scale low-frequency ocean variability and water mass formation rates from 1987 to 2007: A retrospective analysis, Prog. Oceanogr., 132, 318–332, https://doi.org/10.1016/j.pocean.2013.11.003, 2015. a, b, c
Pinardi, N., Cessi, P., Borile, F., and Wolfe, C. L.: The Mediterranean sea overturning circulation, J. Phys. Oceanogr., 49, 1699–1721, https://doi.org/10.1175/JPO-D-18-0254.1, 2019. a, b, c, d
Pinardi, N., Estournel, C., Cessi, P., Escoudier, R., and Lyubartsev, V.: Dense and deep water formation processes and Mediterranean overturning circulation, chap. 7, 209–262, Elsevier, ISBN 9780128236925, 2022. a
Raicich, F.: On the fresh balance of the Adriatic Sea, J. Mar. Syst., 9, 305–319, https://doi.org/10.1016/S0924-7963(96)00042-5, 1996. a
Sanchez-Roman, A., Jorda, G., Sannino, G., and Gomis, D.: Modelling study of transformations of the exchange flows along the Strait of Gibraltar, Ocean Sci., 14, 1547–1566, https://doi.org/10.5194/os-14-1547-2018, 2018. a
Sannino, G., Sánchez Garrido, J. C., Liberti, L., and Pratt, L.: Exchange Flow through the Strait of Gibraltar as Simulated by a σ-Coordinate Hydrostatic Model and a z-Coordinate Nonhydrostatic Model, chap. 3, 25–50, American Geophysical Union (AGU), ISBN 9781118847572, https://doi.org/10.1002/9781118847572.ch3, 2014. a
Sannino, G., Carillo, A., Pisacane, G., and Naranjo, C.: On the relevance of tidal forcing in modelling the Mediterranean thermohaline circulation, Progr. Oceanogr., 134, 304–329, https://doi.org/10.1016/j.pocean.2015.03.002, 2015. a
Schwab, D. J. and Rao, D. B.: Barotropic oscillations of the Mediterranean and Adriatic Seas, Tellus A, 35A, 417–427, https://doi.org/10.1111/j.1600-0870.1983.tb00216.x, 1983. a, b, c, d, e, f, g, h
Shchepetkin, A. F. and McWilliams, J. C.: The regional oceanic modeling system (ROMS): a split-explicit, free-surface, topography-following-coordinate oceanic model, Ocean Modell., 9, 347–404, https://doi.org/10.1016/j.ocemod.2004.08.002, 2005. a
Simmons, H. L., Jayne, S. R., St. Laurent, L. C., and Weaver, A. J.: Tidally driven mixing in a numerical model of the ocean general circulation, Ocean Modell., 6, 245–263, https://doi.org/10.1016/S1463-5003(03)00011-8, 2004. a
St. Laurent, L. C., Simmons, H. L., and Jayne, S. R.: Estimating tidally driven mixing in the deep ocean, Geophys. Res. Lett., 29, 21-1–21-4, https://doi.org/10.1029/2002GL015633, 2002. a
Sánchez-Román, A., García-Lafuente, J., Delgado, J., Sánchez-Garrido, J., and Naranjo, C.: Spatial and temporal variability of tidal flow in the Strait of Gibraltar, J. Mar. Syst., 98-99, 9–17, https://doi.org/10.1016/j.jmarsys.2012.02.011, 2012. a
Tonani, M., Pinardi, N., Dobricic, S., Pujol, I., and Fratianni, C.: A high-resolution free-surface model of the Mediterranean Sea, Ocean Sci., 4, 1–14, https://doi.org/10.5194/os-4-1-2008, 2008. a
van Haren, H., and The ANTARES Collaboration: High-frequency internal wave motions at the ANTARES site in the deep Western Mediterranean, Ocean Dynam., 64, 507–517, https://doi.org/10.1007/s10236-014-0702-0, 2014. a
Vlasenko, V., Garrido, J. C. S., Stashchuk, N., Garcia-Lafuente, J., and Losada, M.: Three-Dimensional Evolution of Large-Amplitude Internal Waves in the Strait of Gibraltar, J. Phys. Oceanogr., 39, 2230–2246, https://doi.org/10.1175/2009JPO4007.1, 2009. a
Vázquez, A., Stashchuk, N., Vlasenko, V., Bruno, M., Izquierdo, A., and Gallacher, P. C.: Evidence of multimodal structure of the baroclinic tide in the Strait of Gibraltar, Geophys. Res. Lett., 33, L17605, https://doi.org/10.1029/2006GL026806, 2006. a
- Abstract
- Introduction
- Data and methods
- Sea level energy spectra
- Kinetic energy spectra
- Mixed layer depth and water mass formation
- Temperature and salinity
- Conclusions
- Data availability
- Author contributions
- Competing interests
- Disclaimer
- Acknowledgements
- Financial support
- Review statement
- References
- Supplement
- Abstract
- Introduction
- Data and methods
- Sea level energy spectra
- Kinetic energy spectra
- Mixed layer depth and water mass formation
- Temperature and salinity
- Conclusions
- Data availability
- Author contributions
- Competing interests
- Disclaimer
- Acknowledgements
- Financial support
- Review statement
- References
- Supplement