Can seafloor voltage cables be used to study large-scale circulation? An investigation in the Pacific Ocean

Marine electromagnetic (EM) signals largely depend on three factors: flow velocity, Earth's main magnetic field, and seawater's electrical conductivity (which depends on the local temperature and salinity). Because of this, there has been recent interest in using marine EM signals to monitor and study ocean circulation. Our study utilizes voltage data from retired seafloor telecommunication cables in the Pacific Ocean to examine whether such cables could be used to monitor circulation velocity or transport on large oceanic scales. We process the cable data to isolate the seasonal and monthly variations and then evaluate the correlation between the processed data and numerical predictions of the electric field induced by an estimate of ocean circulation. We find that the correlation between cable voltage data and numerical predictions strongly depends on both the strength and coherence of the model velocities flowing across the cable, the local EM environment, as well as the length of the cable. The cable within the Kuroshio Current had good correlation between data and predictions, whereas two of the cables in the Eastern Pacific Gyre – a region with both low flow speeds and interfering velocity directions across the cable – did not have any clear correlation between data and predictions. Meanwhile, a third cable also located in the Eastern Pacific Gyre showed good correlation between data and predictions – although the cable is very long and the speeds were low, it was located in a region of coherent flow velocity across the cable. While much improvement is needed before utilizing seafloor voltage cables to study and monitor oceanic circulation across wide regions, we believe that with additional work, the answer to the question of whether or not seafloor voltage cables can be used to study large-scale circulation may eventually be yes.

1 Introduction

Evaluating and predicting the ocean state is crucially important for reconciling and mitigating the impact of climate change on our planet. Oceanic electromagnetic (EM) signals may be directly related to physical parameters of the ocean state, including flow velocity, temperature, and salinity. This has been known for centuries: in 1832, Michael Faraday was the first to attempt an experiment of measuring the voltage induced by the brackish water of the Thames River (Faraday, 1832). His study was inconclusive, but since then, marine EM signals have been detected by both ground and satellite measurements (Larsen, 1968; Malin, 1970; Sanford, 1971; Cox et al., 1971; Tyler et al., 2003; Sabaka et al., 2016).

Marine electromagnetic fields are produced because saline ocean water is a conducting fluid with a mean electrical conductivity of σ=3–4 S m⁻¹. As this electrically conductive fluid passes through Earth's main magnetic field ($\mathbf{\left|}\mathit{F}\mathbf{\right|}\approx \mathrm{20}$–70 µT), it induces electric fields, electric currents, and secondary magnetic fields. The electric current produced by a specific oceanic flow depends on the flow's velocity, the Earth's main magnetic field, and the seawater electrical conductivity, which in turn depends on salinity and temperature. Thus, ideally, three physical oceanic parameters could be extracted from marine EM studies: velocity, salinity, and temperature. However, extracting multiple parameters would require using multiple oceanic electromagnetic signals (e.g., the signals from multiple tidal modes and perhaps also from circulation) (Irrgang et al., 2017; Schnepf, 2017).

In practice, velocity is the only quantity so far determinable from marine EM data. This was accomplished using a passive seafloor telecommunications cable which recorded the voltage difference between Florida and Grand Bahama Island, a distance of approximately 200 km (Larsen and Sanford, 1985; Spain and Sanford, 1987; Larsen, 1991, 1992; Baringer and Larsen, 2001). As the Florida Current passed over the cable, a voltage was induced, and this voltage was directly related to the depth-integrated velocity across the cable (i.e., they determined the transport volume). Since 1985, the National Oceanic and Atmospheric Administration (NOAA) has been using submarine cables to monitor the transport of the Florida Current through the Straits of Florida (Meinen et al., 2020).

While data from seafloor voltage cables have been used to study a variety of geopotential fields (Lanzerotti et al., 1986, 1992a; Chave et al., 1992; Shimizu et al., 1998; Fujii and Utada, 2000; Lanzerotti et al., 2001), NOAA's work in the Straits of Florida is the only case of a seafloor voltage cable being reliable to determine the overlying oceanic flow. Numerical work suggests that cables spanning larger regions should still strongly correlate with the flow velocities (Flosadóttir et al., 1997; Vanyan et al., 1998; Manoj et al., 2010); however, there are many challenges in using longer cables. These challenges are largely due to the myriad of processes which may also induce marine electromagnetic fields, especially across the length of the cable, such as secular variation (Shimizu et al., 1998), variations in ionospheric tides (Pedatella et al., 2012; Schnepf et al., 2018), geomagnetic storms, or longer period ionospheric and magnetospheric signals (Lanzerotti et al., 1992a, 1995, 2001). Additionally, because the cable voltage is produced from the electric field integrated along the entire cable length, the longer the cable is, the more challenging it is to decompose the total contribution to the cross-cable ocean transport in any particular section of the cable.

This study aims to provide a “first step” answer to the following question: can seafloor voltage cables be used to study large-scale circulation? To investigate whether it may eventually be feasible to use large-scale voltage cables for monitoring ocean flows, we evaluate the correlation between data from large-scale seafloor voltage cables and numerical predictions of the electric field induced by 3-D ocean circulation velocity fields. While this work builds on studies using seafloor voltage cables to monitor flow velocity in ∼ 100 km wide passages, this study aims to examine this application in basin-wide seafloor voltage cables.

Table 1 The seafloor voltage cables used in this study. The HAW1N and HAW1S cables run parallel to each other.

2 Data and data processing

This study used hourly data from four seafloor voltage cables (detailed in Table 1): three retired AT&T cables (the HAW cables) and one cable managed by the University of Tokyo's Earthquake Research Institute (the OKI cable). The HAW1N and HAW1S cables are 3805 km long and run parallel to each other from Point Arena, California, to Hanauma Bay, Hawaii. As shown in Fig. 1, the parallel cables have very similar data, providing a unique and helpful situation for testing the data processing methods and for comparing the observations to numerical predictions. These three cables have been used in previous studies, including those examining geopotential variations (Chave et al., 1992; Lanzerotti et al., 1992b; Fujii and Utada, 2000), ionospheric phenomena (Lanzerotti et al., 1992a), oceanic tides (Fujii and Utada, 2000), and electrical conductivity of the lithosphere and the mantle (Koyama, 2001).

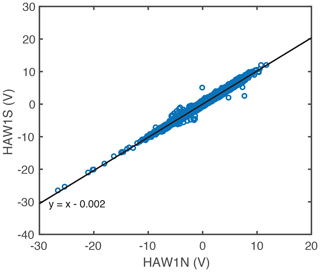
Figure 1 The voltage data of HAW1N versus HAW1S are shown in a correlation scatterplot. As shown by the line of best fit ($y=x-\mathrm{0.002}$), the data from the two cables match very closely.

The first step in processing the hourly data was the removal of geomagnetically noisy days (i.e., days where the geomagnetic Ap index was greater than or equal to 20; see Denig, 2015 for more on the Ap index). In this way, we reduce the contribution from magnetic field variations of magnetospheric origin and their induced counterparts. This shrunk the amount of available data by 16.1 %–21.6 % for each cable. Further reduction of the datasets by using only night-side data is impossible for the HAW cables, which span multiple time zones, and impractical for the OKI cable due to a significant decrease in the dataset size and increase in variance. Next, to remove tidal signals, the 12 dominant daily tidal modes were fit to the data via least squares and then subtracted. The following tidal periods were used: 4 (S₆), 4.8 (S₅), 6 (S₄), 8 (S₃), 11.967236 (K₂), 12 (S₂), 12.421 (M₂), 12.6583 (N₂), 23.934472 (K₁), 24 (S₁), 24.066 (P₁), and 25.891 h (O₁). Because the datasets have many gaps exceeding 24 h in length (for example, see Fig. 2), bandpass filtering was not used. The data were then smoothed using cubic splines. For seasonal variations, we used 90 d knots between splines, and for monthly variations, we used 30.5 d between knots. Although the daily variations should directly relate to barotropic wind-forced processes (Irrgang et al., 2016a, b, 2017), because of both the data's hourly time sampling and frequent data gaps, as well as challenges in producing daily numerical predictions, we chose to focus on monthly and seasonal variations. Each step of the data processing is shown in Fig. 2. As the final step, the mean value is removed from all time series.

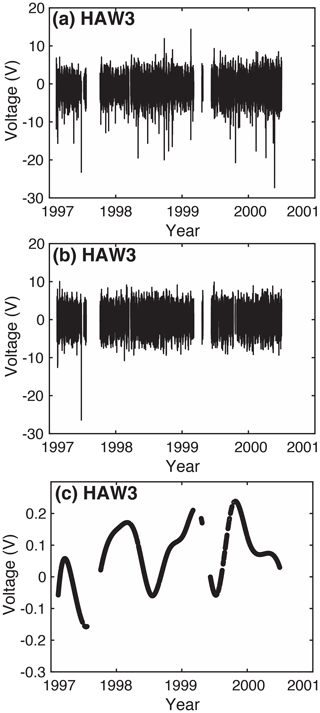
Figure 2 Each step of the data processing is shown here using HAW3 as an example: (a) the raw time series, (b) the time series with days of Ap >20 removed and tidal signals also removed, and (c) the smoothed time series produced by splines with 90 d knots.

A weakness of this data processing is that it does not prevent the inclusion of induced signals due to seasonal changes in ionospheric electromagnetic tidal strength. While we removed tidal signals from a least-squares fit, we applied this fit to the entire dataset and did not attempt to remove seasonal changes in ionospheric tides. Seasonally, ionospheric tides can significantly change amplitude (Pedatella et al., 2012), and the horizontal components of these tides are likely to induce signals at the ground (Schnepf et al., 2018), however, attempting to constrain seasonal changes in tidal strength is challenging. Ideally, the least-squares fit could be conducted on shorter intervals of the data, but this worsens the accuracy of the least-squares inversion. Ionospheric field models could be used, but this would also introduce unknown error quantities. Thus, we did not attempt to remove seasonal changes in tidal amplitude but remind the reader that these signals may influence the monthly and seasonal variations. The contribution of the main field secular variation is not removed from the data, as it is included in the numerical calculations described in the next section.

3 Numerical predictions of the ocean circulation's electric field

We numerically predict the electromagnetic signals produced by ocean circulation using the ElmgTD time-domain numerical solver of the electromagnetic induction equation (Velímský and Martinec, 2005; Velímský, 2013; Šachl et al., 2019; Velímský et al., 2019):

$$\begin{array}{}\text{(1)}& {\mathit{\mu }}_{\mathrm{0}}{\displaystyle \frac{\partial \mathit{B}}{\partial t}}+\mathrm{\nabla }\times \left({\displaystyle \frac{\mathrm{1}}{\mathit{\sigma }}}\mathrm{\nabla }\times \mathit{B}\right)={\mathit{\mu }}_{\mathrm{0}}\mathrm{\nabla }\times \left(\mathit{u}\times \mathit{F}\right).\end{array}$$

Here, B(r;t) is the induced magnetic field, u(r;t) is the velocity, μ₀ is the magnetic permeability of vacuum, σ(r;t) is the electrical conductivity, and F(r;t) is the main geomagnetic field. The observable electric field E(r;t) is obtained from the induced magnetic field by post-processing,

$$\begin{array}{}\text{(2)}& \mathit{E}={\displaystyle \frac{\mathrm{1}}{{\mathit{\mu }}_{\mathrm{0}}\mathit{\sigma }}}(\mathrm{\nabla }\times \mathit{B})-\mathit{u}\times \mathit{F}.\end{array}$$

The ElmgTD time-domain solver is based on spherical harmonic parameterization in lateral coordinates and uses 1-D finite elements for radial discretization. The model is fully 3-D, also incorporating the vertical stratification of the ocean electrical conductivity and of the velocities as well as accounting for the effect of variable bathymetry. Moreover, the seasonal variations in the ocean electrical conductivity and the secular variations in the main field are taken into account. The solution includes both the poloidal and toroidal components of the induced magnetic field (Šachl et al., 2019; Velímský et al., 2019), thereby allowing for the inductive and galvanic coupling between the oceans and the mantle as well as self-induction within the oceans. Numerically, the linear system is solved by the preconditioned iterative BiCGStab(2) scheme (Sleijpen and Fokkema, 1993) with massive parallelization applied across the time levels.

Monthly values of the horizontal and vertical components of ocean velocity from the data-assimilated Estimating the Circulation and Climate of the Ocean (ECCOv4r4) (Forget et al., 2015; Fukumori et al., 2017) model were input into the ElmgTD solver to compute the electromagnetic fields that they induce from January 1997 to November 2001. Along with the monthly velocity values from ECCO, monthly values from the International Geomagnetic Reference Field (IGRF) (Finlay et al., 2010) were used for the main field, and monthly climatological data from NOAA's World Ocean Atlas (WOA) were used to describe the global seawater electrical conductivity σ (Tyler et al., 2017). The conductivity model also includes the coastal and ocean sediments on the seafloor with thickness distribution and conductivity values following Everett et al. (2003).

Figure 3 illustrates these inputs used for the ElmgTD numerical solver. The vertical velocity is not shown here; although it is included in our calculations, as it represents only a minimum additional computational burden, its effect on the induced fields is negligible. Underlying these inputs, the electrical conductivity of the mantle follows the 1-D global profile obtained by the inversion of satellite data (Grayver et al., 2017).

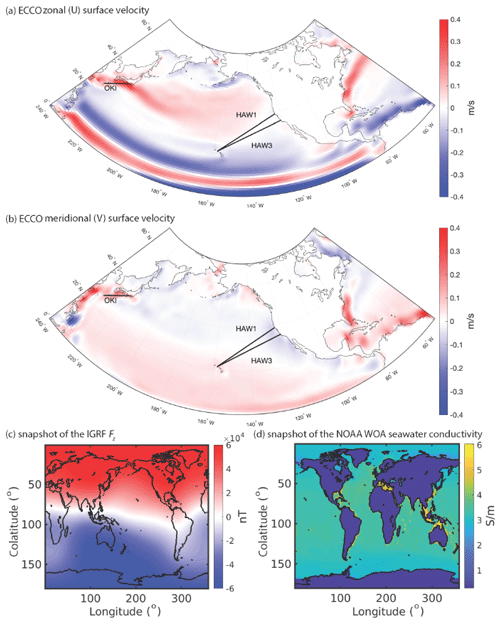
Figure 3 The surface velocities from ECCO are shown (a) for the zonal (U) component and (b) for the meridional (V) component. The labeled, thick black lines denote the seafloor voltage cables used in this study. A snapshot of the IGRF vertical main field, F_z, from 17 January 1997 is illustrated in panel (c), and panel (d) depicts the NOAA World Ocean Atlas seawater electrical conductivity's January climatology in the surface layer.

In the present calculations, we truncate the spherical harmonic expansion at degree 240, corresponding to approximately 0.75^∘ × 0.75^∘ resolution. The radial parameterization within the oceans uses 50 shell layers, following the irregular discretization of the ECCO model. The seawater monthly conductivities from NOAA's WOA were interpolated to the same grid via bilinear formula in angular coordinates and weighted averaging in radial coordinate, which preserves the total conductance.

The model was run from January 1997 through to the end of November 2001. Global results were extracted from the middle of every month (e.g., 17 January, 15 February, 18 March, and 17 April 1997), but daily results were extracted along the transect of the cables' paths.

To compare numerical predictions with the processed seafloor cable observations, the electric field was integrated along the seafloor between the endpoints of each cable. For each cable element, the electric field component along the cable direction was calculated in the lowermost ocean discretization layer. The linear trend was finally removed from each time series of predicted cable voltages.

4 Results and discussion

Figures 4, 5, and 6 summarize the processed voltages and their numerical predictions from the ElmgTD ECCO-based simulation for individual cables. Panel a in each figure shows the time series of cable voltages processed with the 90 d knotted spline fit and the 30.5 d knotted spline fit in red and green, respectively. In the case of the HAW1 cables, the HAW1N and HAW1S branches are distinguished by solid and dashed lines, respectively, and the blue line shows the results of the numerical predictions. A linear trend was removed from all shown time series. Panel b in Figs. 4, 5, and 6 shows the numerical predictions of the voltage gradient (i.e., the electric field) on the seafloor, along the respective cables, before integration. Finally, panel c in Figs. 4, 5, and 6 displays the transport T_⟂ of the ECCO model across each cable. Note that by transport in this context we denote the vertically integrated velocity component perpendicular to the cable for each cable element position and time (hence the unit of m² s⁻¹). Although it is not a direct input to the numerical simulations (contrary to the velocities in individual ECCO layers), it serves as a useful proxy for discussions below.

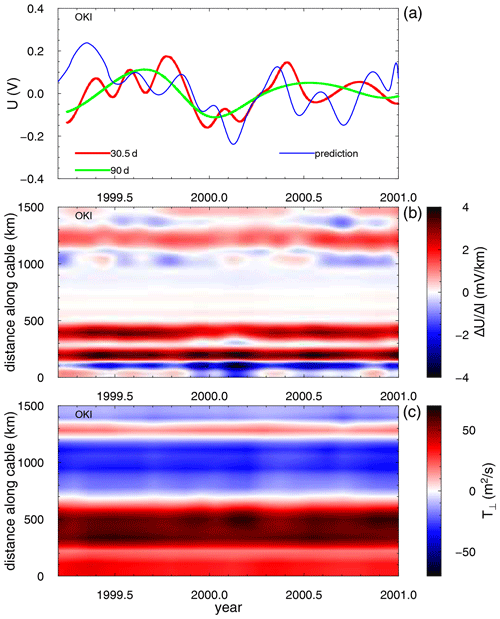
Figure 4 The results for the OKI cable. (a) The smoothed time series of cable voltages using 30.5 and 90 d knot separation are shown in red and green, respectively. The blue line corresponds to the predictions obtained by the numerical model. (b) The time development of the voltage gradient along the cable length from the 3-D model. In panel (c), we plot the ECCOv4r4 vertically integrated transport across the cable in a similar way. The cable orientation follows Table 1, from Honshu to Okinawa.

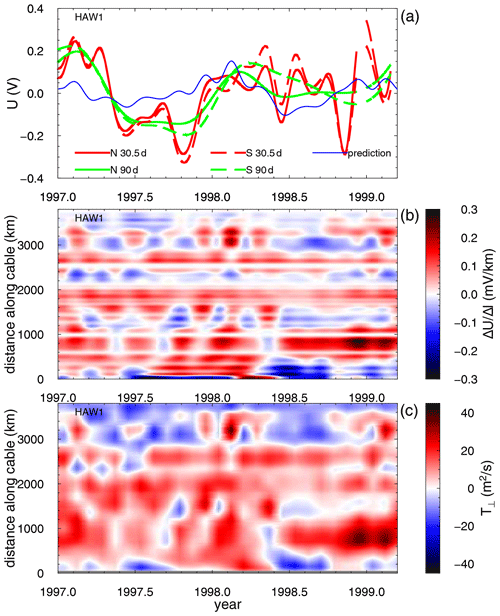
Figure 5 The results for the HAW1 cables. The HAW1N and HAW1S cables are distinguished by the solid and dashed lines in panel (a). The cable orientation is from California to Hawaii. Otherwise, the description corresponds to Fig. 4.

Looking first at the common features of the results for all cables, we note, as expected from basic geometrical considerations, a general similarity between the voltage gradient along the cable and the water transport across the cable T_⟂. We can use these to discuss the effect of individual currents on the numerical predictions. However, while the ocean flows are certainly the dominant term controlling the induced electric fields, the additional contributions of other effects yield a much richer spatiotemporal structure. The main field variations in both space and time can have a linear impact on the large-scale features, as implied by the forcing term of the EM induction Eq. (1). Moreover, the local variations in seawater conductivity, the bathymetry, and the sediment thickness affect the electric field in a non-linear way. In particular, the toroidal magnetic mode, which corresponds to the poloidal electric currents and stems from the galvanic coupling between the ocean and the underlying solid Earth, can play an important role (Chave et al., 1989; Velímský et al., 2019).

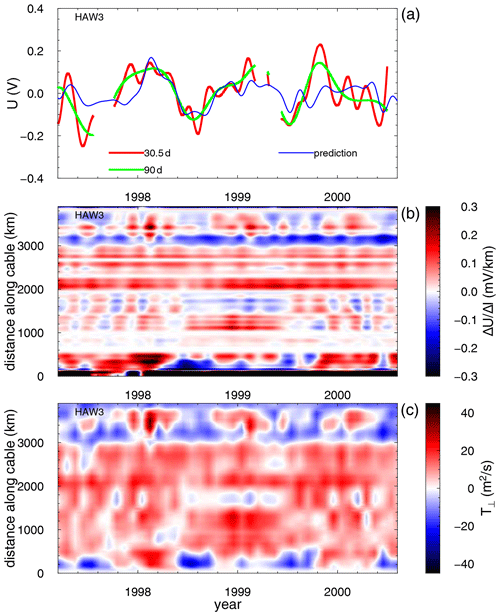
Figure 6 The results for the HAW3 cable. The cable orientation is from California to Hawaii. The description corresponds to Fig. 4.

Upon closer inspection of the OKI cable results, the importance of the Kuroshio Current stands out, at the distance of 300–600 km from Honshu (Fig. 4c). It produces the largest contribution to the predicted voltages by far (Fig. 4a, b). In terms of spatial distribution, the positions along the cable where the largest contributions to the electric field are induced do not match with the peak positions of the cross-cable transport. This discrepancy can be attributed to the electrically strongly heterogeneous environment caused by large bathymetry changes in the vicinity of the Ryukyu arc. The ECCO model suggests an increase in the transport in the last months of 2000, which is consequently responsible for the increased voltage in the numerical model. However, no such increase is present in the observed voltages, and this discrepancy remains an open question. If we trust the OKI voltages, it is possible that the ECCO model is overestimating the Kuroshio strength by the end of 2000.

In the case of HAW1N and HAW1S, the numerical model predicts significantly smaller amplitudes of cable voltage variations when compared with the observations (Fig. 5). The California Current is the main contributor to the total voltages, at distances up to 1000 km from the Californian coast. The spatiotemporal distribution of the cross-cable transport and the induced voltages is in good agreement due to an uncomplicated electrical conductivity distribution in the deep ocean. The ocean transports across the HAW1 cables demonstrate larger seasonal variations than in the case of Kuroshio. However, the lack of significant contributions perpendicular to the cable as well as the changing direction of these flows both along the cable and in time yield poor agreement of the total integrated voltage with the observations.

The HAW3 cable, in contrast, shows good agreement between the predicted and observed voltages (Fig. 6). The numerical model is again dominated by the California Current, which is here closer to the coast. The HAW3 cable lies a bit to the south of the HAW1N and HAW1S cables, and it is also within the low-speed region of the Eastern Pacific Gyre. The transport across the cable in the central Pacific is more coherent, yielding slightly stronger signals than in the case of the HAW1 cables. Again, the pattern of the cross-cable transport is well matched with the spatiotemporal map of the induced voltages.

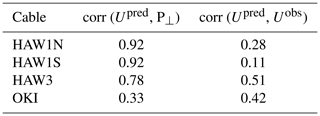
In Table 2, we calculated two sets of correlation coefficients. In the second column of the table, the voltages predicted by the numerical model were correlated with the total ECCO-based water transport (in m³ s⁻¹) across the respective cables:

$$\begin{array}{}\text{(3)}& P_{⟂}=\underset{\mathrm{start}}{\overset{\mathrm{end}}{\int }}{T}_{⟂}\mathrm{d}l.\end{array}$$

These values are independent of the actual cable voltage measurements and can provide an upper limit on what can be achieved by the interpretation of long-cable voltages in terms of ocean flows. Large correlations were obtained for the HAW1 and HAW3 cable locations, whereas the integrated flow across the OKI cable was poorly correlated with the predicted voltage. This stresses the importance of the accurate modeling of the induced electric field in strongly heterogeneous areas.

In the third column of Table 2, we show the correlation coefficients between the predicted and observed voltages using the 30.5 d knot separation datasets. Due to the gaps present in the data, the Gaussian kernel method (Rehfeld et al., 2011) was applied. It is obvious that the discrepancies between the predicted and observed voltages are still large, and significant efforts are required both on the side of data processing and numerical modeling to reconcile the results. The OKI cable in particular presents an interesting case. Although the total cross-cable transport is less correlated with the predicted voltages than in the case of both HAW1 cables, the agreement with the observations is considerably better. This again points to the role of local EM effects.

Table 2 For individual seafloor cables, we show the correlation coefficients between the cable voltages predicted by the numerical model and the total ECCO-derived water transport across the cable P_⟂ in the second column. The third column shows the correlation coefficients between the predicted and observed voltages for 30.5 d spline knot separation.

On the side of numerical modeling, one could devise a comparison study between different ocean models. Indeed, we have used our model to predict the magnetic fields of the LSOMG (Large Scale Ocean Model for Geophysics) model in the past (Velímský et al., 2019), and we have also attempted the calculation of the cable voltages for the eddy-resolving GLORYS (Global Ocean reanalysis and Simulation) ocean model (not shown here). One problem related to this approach is the volume of computational resources necessary to carry out the calculations. As the cable voltages are sensitive to local electric fields, the usual simplifications of the EM induction solver, based on the thin-sheet approximation, or representing the oceans by a single layer with integrated water transports and electrical conductances, are problematic (Šachl et al., 2019; Velímský et al., 2019). The single 5-year calculation of the full physical model presented here, with 50 ocean layers and spherical harmonic truncation degree 240, required about 10⁵ CPU hours to complete. Semi-global or regional modeling tools with local refinement ability are needed for more accurate numerical studies.

The qualitative comparison of the induced voltages and water transports along the cables, as presented in this paper, could be made more exact by applying the principal component analysis methodology. When applied only to the water transports provided by different ocean models, it could reduce the burden of calculating a detailed 3-D EM response to each model and allow a more focused interpretation of the observed voltages. We plan to carry out such analysis in the future.

The studies by Larsen (1992) evaluating transport in the Straits of Florida from seafloor voltage cable data had correlation values corresponding to much higher values than those of this study. As shown in Fig. 20 of Larsen (1992), the correlation squared values ranged from 0.61 to 0.94. However, Larsen's study was fundamentally different: the seafloor voltage cable was an order of magnitude shorter than the cables considered in this study and the Gulf Stream within the Straits of Florida has large speeds as well as coherent velocities flowing perpendicularly to the cables. Therefore, overall, the Larsen (1992) study had a more ideal signal-to-noise ratio.

5 Conclusions

We present an evaluation of using seafloor voltage cables for monitoring circulation across oceanic basins. We compare processed seafloor voltage cable data with the numerical predictions produced using an electromagnetic induction solver, fed by flow velocity estimates from the data-assimilated ECCO model and seawater electrical conductivity climatologies from the NOAA World Ocean Atlas. We find that the correlation between cable voltage data and numerical predictions strongly depends on both the amplitude and direction of the flow velocities across the cable.

Due to the computational constraints, the calculations of the ocean-induced electric field presented here are limited to a single realization of ocean velocity estimates: the ECCO model. Therefore, beside the unmodeled or uncorrected signals in the seafloor cable voltages, a first-order source of discrepancy between the numerical prediction and observation is the inaccuracy of the flow velocity estimates. Therefore, an extended analysis and comparison of the cable voltage calculations driven by other ocean circulation models is desirable in the future as well as the consideration of direct velocity observations (Szuts et al., 2019).

While much improvement is needed before utilizing seafloor voltage cables to study and monitor ocean circulation across large regions, we believe that seafloor voltage cables can eventually be used to study and monitor large-scale ocean flow. The cables used in this study were installed for telecommunication purposes – there was no regard for whether these cables would be best suited to monitor ocean currents. Flow information can most reliably be extracted from seafloor voltage cable data when the flow has mostly unidirectional, perpendicular velocities across the cable. For our study, the OKI cable was in the area with the largest velocities, but because it is oriented mostly parallel to the Kuroshio Current, its correlation would likely greatly improve if it was instead perpendicular to the current's flow.

If voltage cables were strategically placed on the seafloor between Antarctica and Chile (a distance of ∼ 700 km) or between Antarctica and New Zealand (a distance of ∼ 1300 km), the correlation between data and predictions could be quite high, due to both the shorter cable length (compared with the HAW1 and HAW3 cables) and the relatively uniform and large flow velocities. Indeed, seafloor voltage cables may be a very effective method for measuring and continuously monitoring the flow of the Antarctic Circumpolar Current – which is definitely something worth investigating.

Using existing cables, the correlation between data and numerical predictions will likely also improve if the methodology is enhanced to remove induced signals from seasonal variations in ionospheric signals.