Current estimates of K₁* and K₂* appear inconsistent with measured CO₂ system parameters in cold oceanic regions

Seawater absorption of anthropogenic atmospheric carbon dioxide (CO₂) has led to a range of changes in carbonate chemistry, collectively referred to as ocean acidification. Stoichiometric dissociation constants used to convert measured carbonate system variables (pH, pCO₂, dissolved inorganic carbon, total alkalinity) into globally comparable parameters are crucial for accurately quantifying these changes. The temperature and salinity coefficients of these constants have generally been experimentally derived under controlled laboratory conditions. Here, we use field measurements of carbonate system variables taken from the Global Ocean Data Analysis Project version 2 and the Surface Ocean CO₂ Atlas data products to evaluate the temperature dependence of the carbonic acid stoichiometric dissociation constants. By applying a novel iterative procedure to a large dataset of 948 surface-water, quality-controlled samples where four carbonate system variables were independently measured, we show that the set of equations published by Lueker et al. (2000), currently preferred by the ocean acidification community, overestimates the stoichiometric dissociation constants at temperatures below about 8 ^∘C. We apply these newly derived temperature coefficients to high-latitude Argo float and cruise data to quantify the effects on surface-water pCO₂ and calcite saturation states. These findings highlight the critical implications of uncertainty in stoichiometric dissociation constants for future projections of ocean acidification in polar regions and the need to improve knowledge of what causes the CO₂ system inconsistencies in cold waters.

1 Introduction

In the last decades, oceans have absorbed over a quarter of the anthropogenic carbon dioxide (CO₂) emitted to the atmosphere (Le Quéré et al., 2018; Gruber et al., 2019). Upon dissolution in seawater, this CO₂ triggers a suite of reactions that lead to a range of chemical changes jointly termed ocean acidification (Zeebe and Wolf-Gladrow, 2001; Gattuso and Hansson, 2011). To accurately calculate the magnitude of these changes, it is crucial to understand the chemical behaviour of CO₂ in seawater.

Upon dissolution, CO₂ takes the form of solvated CO₂ (${\mathrm{CO}}_{{\mathrm{2}}_{\left(\mathrm{aq}\right)}}$, CO₂•H₂O) or carbonic acid (H₂CO₃), which are here both represented by ${\mathrm{H}}_{\mathrm{2}}{\mathrm{CO}}_{\mathrm{3}}^{*}$, since they can only be readily distinguished by infra-red spectrometry (Zeebe and Wolf-Gladrow, 2001), and the following series of reactions occurs:

$$\begin{array}{}\text{(R1)}& {\displaystyle }& {\displaystyle }{\mathrm{CO}}_{{\mathrm{2}}_{\left(\mathrm{aq}\right)}}+{\mathrm{H}}_{\mathrm{2}}\mathrm{O}\leftrightarrow {\mathrm{H}}_{\mathrm{2}}{\mathrm{CO}}_{\mathrm{3}}^{*},\text{(R2)}& {\displaystyle }& {\displaystyle }{\mathrm{H}}_{\mathrm{2}}{\mathrm{CO}}_{\mathrm{3}}^{*}\leftrightarrow {\mathrm{H}}^{+}+{\mathrm{HCO}}_{\mathrm{3}}^{-},\text{(R3)}& {\displaystyle }& {\displaystyle }{\mathrm{HCO}}_{\mathrm{3}}^{-}\leftrightarrow {\mathrm{H}}^{+}+{\mathrm{CO}}_{\mathrm{3}}^{\mathrm{2}-}.\end{array}$$

Together, these three reactions and their species constitute the marine CO₂−H₂O system, which is responsible for about 95 % of the acid–base buffering capacity of seawater and maintains the pH of the ocean within a narrow range (Bates, 2019; Zeebe and Wolf-Gladrow, 2001).

Each of these reversible reactions is associated with a thermodynamic equilibrium constant, a number that expresses the relationship between the activities of products and reactants present at equilibrium at a given temperature and pressure. Reactions (R2) and (R3) describe the first and second step in the dissociation of carbonic acid. Their equilibrium constants are therefore termed the first and second dissociation constants, K₁ and K₂, respectively. To avoid the use of activity coefficients, which are not straightforward to derive in seawater, marine scientists have developed a set of stoichiometric (or apparent) equilibrium constants to represent the state of the system at a given pressure (P), temperature (T), and salinity (S). To describe the carbonate system, two stoichiometric constants (${\mathrm{K}}_{\mathrm{1}}^{*}$ and ${\mathrm{K}}_{\mathrm{2}}^{*}$, conventionally denoted by a star) are defined in terms of the concentrations of the different species:

$$\begin{array}{}\text{(1)}& {\displaystyle }{\mathrm{K}}_{\mathrm{1}}^{*}& {\displaystyle }={\displaystyle \frac{\left[{\mathrm{HCO}}_{\mathrm{3}}^{-}\right]\left[{\mathrm{H}}^{+}\right]}{\left[{\mathrm{H}}_{\mathrm{2}}{\mathrm{CO}}_{\mathrm{3}}^{*}\right]}},\text{(2)}& {\displaystyle }{\mathrm{K}}_{\mathrm{2}}^{*}& {\displaystyle }={\displaystyle \frac{\left[{\mathrm{H}}^{+}\right]\left[{\mathrm{CO}}_{\mathrm{3}}^{\mathrm{2}-}\right]}{\left[{\mathrm{HCO}}_{\mathrm{3}}^{-}\right]}}.\end{array}$$

Using these stoichiometric equilibrium constants, we can calculate the relative quantities of the dissolved inorganic carbon ($\text{DIC}=\left[{\mathrm{H}}_{\mathrm{2}}{\mathrm{CO}}_{\mathrm{3}}^{*}\right]+\left[{\mathrm{HCO}}_{\mathrm{3}}^{-}\right]+\left[{\mathrm{CO}}_{\mathrm{3}}^{\mathrm{2}-}\right]$) species. With improved analytical techniques, measurement accuracy of carbonate system variables has substantially increased over the past decades. As a result, uncertainty in carbonate system calculations is currently dominated by the uncertainty of ${\mathrm{K}}_{\mathrm{1}}^{*}$ and ${\mathrm{K}}_{\mathrm{2}}^{*}$ values (Orr et al., 2018), justifying the need to investigate whether these uncertainties can be reduced.

Using popular software for carbonate system calculations, e.g. CO2SYS (Lewis and Wallace, 1998; Pierrot et al., 2006; van Heuven et al., 2011) or seacarb (Gattuso et al., 2019), and recently published literature as references, roughly 15 different expressions for ${\mathrm{K}}_{\mathrm{1}}^{*}$ and ${\mathrm{K}}_{\mathrm{2}}^{*}$ are currently in use, some of which are (partly) based on refitting data from earlier experiments (e.g. Dickson and Millero, 1987; Lueker et al., 2000); see Table S1 in the Supplement for an overview. Some expressions are based on measurements in artificial seawater of various compositions, while others were carried out in natural seawater. The vast majority of expressions were obtained in the laboratory under controlled conditions, using electrochemical cells either with (e.g. Millero et al., 2006; Millero, 2010) or without (e.g. Roy et al., 1993; Tishchenko et al., 2013) liquid junction. Within these cells, electromotive force readings of equilibrated seawater are used to compute equilibrium constants. Each expression is valid over its own range of T and S.

The various expressions for ${\mathrm{K}}_{\mathrm{1}}^{*}$ and ${\mathrm{K}}_{\mathrm{2}}^{*}$ obtained this way generally agree well, but discrepancies at low salinities have been highlighted (Cai and Wang, 1998; Millero, 2010; Dinauer and Mucci, 2017; Orr et al., 2018). In addition, the temperature range covered by various ${\mathrm{K}}_{\mathrm{1}}^{*}$ and ${\mathrm{K}}_{\mathrm{2}}^{*}$ expressions, although generally broad, only extends below 0 ^∘C in a few studies (Millero et al., 2002; Goyet and Poisson, 1989; Papadimitriou et al., 2018). In fact, Mehrbach et al. (1973), who provided experimental data used by several authors to derive expressions for ${\mathrm{K}}_{\mathrm{1}}^{*}$ and ${\mathrm{K}}_{\mathrm{2}}^{*}$ (e.g. Dickson and Millero, 1987; Lueker et al., 2000), used data obtained at only four different temperatures (2, 13, 25, and 35 ^∘C), which brings into question the accuracy of the temperature dependency of these constants. Bailey et al. (2018) recently suggested that the same bias exists for the dissolution of CO₂ in seawater and showed that previous expressions of Henry's Law constant for CO₂ underestimate the CO₂ solubility below 0 ^∘C due to a lack of samples in cold waters. As explained by Raimondi et al. (2019), because the only carbonate system variables currently measured by in situ sensor technologies are pH and the partial pressure of CO₂ in seawater (pCO₂), relating laboratory or on-board measurements that are usually performed at temperatures ∼25 ^∘C to these in situ measurements requires an accurate knowledge of the ${\mathrm{K}}_{\mathrm{1}}^{*}$ and ${\mathrm{K}}_{\mathrm{2}}^{*}$ temperature dependency. About 40 % of the ocean volume is at an average temperature lower than 2 ^∘C, outside of the temperature range for which the Mehrbach et al. (1973) and derived constants are valid (from the data of Lauvset et al., 2016). An example of this are high-latitude cold waters, which are a critical component of the current global oceanic carbon cycle, as the Southern Ocean surface waters account for ∼40 % of the annual anthropogenic CO₂ uptake by the ocean (Landschützer et al., 2015). Given past difficulties to obtain direct pCO₂ measurements from ships in the Southern Ocean (Bakker et al., 2016), a number of autonomous floats have been deployed in recent years (see, e.g., Williams et al., 2017; Takeshita et al., 2018). Since these floats estimate pCO₂ from a pH measurement and a calculated total alkalinity (TA), our knowledge of surface pCO₂ in the Southern Ocean strongly relies on the accuracy of dissociation constants in these cold waters.

Best practices for oceanic carbonate system measurements generally recommend the Lueker et al. (2000) constants (Dickson et al., 2007), but the choice for a set of constants may depend on the environment and/or measured carbonate system variables. Only two of the measurable variables are required to characterize the whole carbonate system, except under conditions where substantial impact of dissolved organic carbon on TA is expected (i.e. significant organic alkalinity). Overdetermination of the carbonate system, i.e. the concomitant measurement of at least three of the carbonate system variables (1) pCO₂, (2) DIC, (3) TA, and (4) pH, is often used as a tool to identify the best pair of input variables for carbonate system calculations under specific environmental conditions, e.g. in sea-ice brines (Brown et al., 2014) or in systems with substantial organic alkalinity (Koeve and Oschlies, 2012). We refer the reader to Raimondi et al. (2019) for an overview of internal consistency studies, i.e. the agreement between measured and calculated variables. Disagreement between measured and computed values may arise from uncertainties in measurements and, more importantly, equilibrium constants (Orr et al., 2018) but can also result from the choice of relationship between total boron and salinity, as well as organic alkalinity (Fong and Dickson, 2019).

Field measurements are rarely used to derive stoichiometric equilibrium constants because of their interdependence. For example, ship-based measurements of pH are normally conducted at fixed temperature (commonly 25 ^∘C) and converted to in situ temperature using a second input parameter as well as a set of stoichiometric equilibrium constants (Hunter, 1998). Similarly, using measured TA to calculate the contribution of the carbonate system to total alkalinity (carbonate alkalinity, CA) requires that the proton concentration and thus pH be known (Dickson et al., 2007). To the best of our knowledge, only two studies have so far used overdeterminations of the carbonate system to derive expressions for ${\mathrm{K}}_{\mathrm{1}}^{*}$ and ${\mathrm{K}}_{\mathrm{2}}^{*}$ (Millero et al., 2002; Papadimitriou et al., 2018). Both studies used concurrent measurements of pCO₂, TA, DIC, and pH over a range of temperatures and salinities to calculate ${\mathrm{K}}_{\mathrm{1}}^{*}$ and ${\mathrm{K}}_{\mathrm{2}}^{*}$. Millero et al. (2002) used over 6000 sets of pressure-corrected field measurements. They argued that determinations of stoichiometric dissociation constants measured in natural seawater are preferable over those determined in artificial seawater and concluded that the value of ${\mathrm{K}}_{\mathrm{2}}^{*}$ depends on pCO₂, possibly linked to organic alkalinity, which is not accounted for in carbonate system calculations. Papadimitriou et al. (2018), who focussed especially on highly saline brines down to their freezing points, used the same methods as Millero et al. (2002) for their calculations. However, instead of using field measurements, they overdetermined their system under controlled laboratory temperatures and salinities, thus avoiding temperature corrections of the pH measurements. Their work, like Orr et al. (2018), confirmed the high uncertainties associated with extrapolating expressions for ${\mathrm{K}}_{\mathrm{1}}^{*}$ and ${\mathrm{K}}_{\mathrm{2}}^{*}$ beyond the investigated salinity and temperature ranges.

In the present study, we use the Global Ocean Data Analysis Project version 2 (GLODAPv2; Key et al., 2015; Olsen et al., 2016) and the Surface Ocean CO₂ Atlas (SOCAT; Bakker et al., 2016) global data products to constrain stoichiometric equilibrium constants based on surface-water field measurements. Using an iterative procedure that takes into account the lack of independence of CA and pH, we quantify the temperature dependence of the stoichiometric equilibrium constants. We then use these constants to recommend input pairs for pCO₂ and CaCO₃ saturation state determinations over various temperature ranges and apply them onto a high-latitude dataset.

2 Materials and methods

2.1 Expressions for ${\mathrm{K}}_{\mathrm{1}}^{*}$ and ${\mathrm{K}}_{\mathrm{2}}^{*}$ as a function of carbonate system variables

Aside from recent advances that allow spectrophotometric determinations of ${\mathrm{CO}}_{\mathrm{3}}^{\mathrm{2}-}$ concentrations (Byrne and Yao, 2008; Easley et al., 2013; Sharp and Byrne, 2019), the concentrations of ${\mathrm{H}}_{\mathrm{2}}{\mathrm{CO}}_{\mathrm{3}}^{*}$, ${\mathrm{HCO}}_{\mathrm{3}}^{-}$, and ${\mathrm{CO}}_{\mathrm{3}}^{\mathrm{2}-}$ are normally not directly measured in seawater. Instead, at least two of the four parameters pCO₂, pH, DIC, and TA are measured and the concentrations of the individual species inferred from them. In practical terms, TA is the sum of all bases that are titratable with a strong acid to an equivalence point corresponding to the conversion of ${\mathrm{HCO}}_{\mathrm{3}}^{-}$ to ${\mathrm{H}}_{\mathrm{2}}{\mathrm{CO}}_{\mathrm{3}}^{*}$. Here it is defined as

$$\begin{array}{}\text{(3)}& \text{TA}=\text{CA}+\text{BA}+\text{PA}+\text{SiA}+\left[{\mathrm{OH}}^{-}\right]-\left[{\mathrm{H}}^{+}\right],\end{array}$$

with $\text{CA}=\left[{\mathrm{HCO}}_{\mathrm{3}}^{-}\right]+\mathrm{2}\left[{\mathrm{CO}}_{\mathrm{3}}^{\mathrm{2}-}\right]$ and where BA is the borate alkalinity ($\left[\mathrm{B}\right(\mathrm{OH}{)}_{\mathrm{4}}^{-}]$), PA is the phosphate alkalinity ($\left[{\mathrm{HPO}}_{\mathrm{4}}^{\mathrm{2}-}\right]+\mathrm{2}\left[{\mathrm{PO}}_{\mathrm{4}}^{\mathrm{3}-}\right]-\left[{\mathrm{H}}_{\mathrm{3}}{\mathrm{PO}}_{\mathrm{4}}\right]$), SiA is the silicate alkalinity ($\left[\mathrm{SiO}\right(\mathrm{OH}{)}_{\mathrm{3}}^{-}]$), [OH⁻] is the hydroxide ion concentration, and [H⁺] is the hydrogen ion concentration. Equation (3) approximates the definition of TA provided by Dickson (1981) but does not take into account the hydrogen sulfide and ammonia acid–base systems. The terms BA, PA, and SiA can all be expressed in terms of stoichiometric equilibrium constants, total concentrations, and [H⁺]. Hence, knowing TA, the total concentrations of dissolved silicate ([DSi]), soluble reactive phosphate ([SRP]), and boron, as well as [OH⁻] and [H⁺], CA can be calculated.

To estimate ${\mathrm{K}}_{\mathrm{1}}^{*}$ and ${\mathrm{K}}_{\mathrm{2}}^{*}$ as a function of salinity and temperature based solely on independent measurements, we first need to define expressions that define both constants as functions of CA, DIC, pCO₂, and [H⁺]. Both ${\mathrm{K}}_{\mathrm{1}}^{*}$ and ${\mathrm{K}}_{\mathrm{2}}^{*}$ are normally defined in terms of proton concentration, [H⁺], and the acid–base species they describe; see Eqs. (1) and (2). In this work, we replace $\left[{\mathrm{H}}_{\mathrm{2}}{\mathrm{CO}}_{\mathrm{3}}^{*}\right]$, $\left[{\mathrm{HCO}}_{\mathrm{3}}^{-}\right]$, and $\left[{\mathrm{CO}}_{\mathrm{3}}^{\mathrm{2}-}\right]$ by expressions that only contain the four variables present in the dataset and Henry's constant, K₀, taken from Weiss (1974). This leads to the following set of equations, which are equivalent to those presented in Millero et al. (2002) and Papadimitriou et al. (2018):

$$\begin{array}{}\text{(4)}& {\displaystyle }{\mathrm{K}}_{\mathrm{1}}^{*}& {\displaystyle }={\displaystyle \frac{\left[{\mathrm{H}}^{+}\right]\left(\mathrm{2}\mathrm{DIC}-\mathrm{CA}-\mathrm{2}{\mathrm{K}}_{\mathrm{0}}p{\mathrm{CO}}_{\mathrm{2}}\right)}{{\mathrm{K}}_{\mathrm{0}}p{\mathrm{CO}}_{\mathrm{2}}}},\text{(5)}& {\displaystyle }{\mathrm{K}}_{\mathrm{2}}^{*}& {\displaystyle }={\displaystyle \frac{\left[{\mathrm{H}}^{+}\right]\left(\mathrm{CA}-\mathrm{DIC}+{\mathrm{K}}_{\mathrm{0}}p{\mathrm{CO}}_{\mathrm{2}}\right)}{\mathrm{2}\mathrm{DIC}-\mathrm{CA}-\mathrm{2}{\mathrm{K}}_{\mathrm{0}}p{\mathrm{CO}}_{\mathrm{2}}}}.\end{array}$$

Note that similar expressions can also be derived when only three independently measured variables are available in the dataset. In this case, either ${\mathrm{K}}_{\mathrm{1}}^{*}$ or ${\mathrm{K}}_{\mathrm{2}}^{*}$ remains in the expression, in addition to any three variables of the set CA, DIC, pCO₂, and [H⁺]. Derivations of all these expressions can be found in the Supplement.

2.2 Data

Data for T, P, practical salinity (S_P), DIC, TA, pH, [SRP], and [DSi] were taken from GLODAPv2 (Key et al., 2015; Olsen et al., 2016). Only data associated with a WOCE (World Ocean Circulation Experiment) flag of 2 were retained for this analysis. WOCE flags are associated with each GLODAPv2 variable during quality control. Data associated with a flag of 2 were assessed as “acceptable” by quality controllers of the original dataset. Recalculated or estimated variables and samples with missing T or S_P were always discarded. In total, we obtained 98326 samples for which TA, DIC, and pH are available from independent, high-quality measurements.

pCO₂ values were obtained from SOCAT version 3 (Bakker et al., 2016). Only data associated with a WOCE flag of 2 are used. When available, a pCO₂ value was selected and added to corresponding surface GLODAPv2 samples. To select the most accurate pCO₂ value, we only merged GLODAPv2 and SOCAT samples from the same cruise and taken within the same hour; in most cases within the same 20 min. As a result, we assembled 1024 samples for which TA, DIC, pH, and pCO₂ are all available from independent high-quality measurements. As underway pCO₂ measurements available in the SOCAT database are all from the surface ocean, it was not possible to assign measured pCO₂ values to samples at depth. Note that we discarded data from two cruises (EXPOCODES 33AT20120419 and 49NZ20010828) for reasons explained in the Supplement, ultimately using data from 948 samples for this analysis. Samples within this dataset were taken between 1993 and 2012 over 26 different research cruises. These samples were taken at the ocean surface, always in the top 5 m. They cover a range of practical salinities from 30.73 to 37.57 and temperatures from −1.67 to 31.80 ^∘C at locations shown in Fig. 1.

Figure 1 Spatial coverage of the dataset containing GLODAPv2 and SOCAT samples for which DIC, TA, pH, and pCO₂ are available from independent, high-quality measurements.

2.3 Iterative methods and underlying assumptions

To the 948 samples for which independent, high-quality measurements of pH, DIC, TA, [DSi], [SRP], and pCO₂ are available, we would preferably directly apply Eqs. (4) and (5). This was, however, not possible given the interdependence of pH and CA, both of which are necessary to compute ${\mathrm{K}}_{\mathrm{1}}^{*}$ and ${\mathrm{K}}_{\mathrm{2}}^{*}$ and, in turn, other carbonate system parameters. Rather than estimating the temperature dependence of pH from ΔpH∕ΔT as done by Millero et al. (2002), we used a novel iterative fitting procedure. This procedure is based on an initial estimate of both pH and CA using the Lueker et al. (2000) constants, followed by a recomputation at each iteration using the values of ${\mathrm{K}}_{\mathrm{1}}^{*}$ and ${\mathrm{K}}_{\mathrm{2}}^{*}$ from the previous iteration. The calculations were executed in R (R Core Team, 2019) and detailed below. The code and data files can be downloaded from an online repository (https://doi.org/10.5281/zenodo.3725889, Sulpis et al., 2020).

Since the objective of the present study is to obtain independent measurements of ${\mathrm{K}}_{\mathrm{1}}^{*}$ and ${\mathrm{K}}_{\mathrm{2}}^{*}$, we could not directly use GLODAPv2 in situ pH data because the majority of these data were obtained on board by potentiometric or spectrophotometric methods at an equilibrium temperature often higher than the surface seawater (usually 25 ^∘C, occasionally 20 or 13 ^∘C). In addition, pH data were not always delivered to GLODAPv2 on the total pH scale. Consequently, the in situ pH measurements available in GLODAPv2 are all recalculated using measured TA and the Lueker et al. (2000) stoichiometric dissociation constants and converted to the total pH scale if necessary (Olsen et al., 2016). To obtain the pH values delivered to GLODAPv2, which should be independent of ${\mathrm{K}}_{\mathrm{1}}^{*}$ and ${\mathrm{K}}_{\mathrm{2}}^{*}$, we converted the GLODAPv2 pH values back to their measurement temperatures (labT) and pH scales, as recorded in the cruise reports. For this reconversion, we used the bias-corrected TA value from GLODAPv2 rather than the measured TA values that were used in the GLODAPv2 conversion process. Bias correction of TA was done through crossover and inversion analysis of the data (Olsen et al., 2016); for the 26 research cruises we selected, bias correction resulted in TA adjustments of −1 to 10 µmol kg⁻¹. These adjustments however affected the recalculated pH values by less than 0.0001. We then converted all recalculated pH values to the free pH scale (pH${}_{\mathrm{F}}^{\mathrm{labT}}$) using the default settings of the pHconv function in the seacarb R package (Gattuso et al., 2019). The free pH scale was used during the fitting procedure to avoid further complications with the sulfate and fluoride acid–base systems. Nevertheless, final results are presented on the total pH scale.

Carbonate alkalinity was not directly measured but is instead a pH-dependent quantity computed from TA; see Eq. (3). As a first approximation, we calculated CA from the measured TA by subtracting the contributions of the borate, silicate, and phosphate acid–base systems, as well as the auto-dissociation of water, using [SRP], [DSi], and the in situ pH from GLODAPv2. We estimated the total boron concentration from salinity using the Uppström (1974) relationship and calculated its acid–base speciation using the equilibrium constants of Dickson (1990). For the silicate and phosphate acid–base speciation, the equilibrium constants of Yao and Millero (1995) were used. All of these expressions are only valid for temperatures above 0 ^∘C; thus, extrapolation to lower temperatures yields an additional uncertainty to the method. All equilibrium constants were corrected for pressure following Millero (1995), but given that all samples were taken at depth shallower than 5 m depth, this correction is negligible. Using ${\mathrm{H}}_{\mathrm{F}}^{\mathrm{labT}}$, the proton concentration computed from pH${}_{\mathrm{F}}^{\mathrm{labT}}$, we also calculated carbonate alkalinity at the temperature of pH measurements (CA^labT). This variable was used during the iteration procedure.

Since there are two pH-independent parameters (DIC, pCO₂), we can use these two parameters and one pH-dependent parameter (either pH itself, or CA) to initialize the iterative procedure. This implies that either ${\mathrm{K}}_{\mathrm{1}}^{*}$ or ${\mathrm{K}}_{\mathrm{2}}^{*}$ must be assigned an initial value before starting the iterations. Here, we initially set the in situ ${\mathrm{K}}_{\mathrm{2}}^{*}$ to the value calculated from the Lueker et al. (2000) expressions. The alternative case in which in situ ${\mathrm{K}}_{\mathrm{1}}^{*}$ was initially set to the Lueker et al. (2000) value is described in the Supplement and would have no appreciable impact on the results presented here; i.e. whether the first or the second dissociation constant is assigned an initial value does not affect the results. Each iteration consisted of four different steps:

• 1.

  First, ${\mathrm{K}}_{\mathrm{1}}^{*}$ was computed from in situ DIC, CA, pCO₂, and ${\mathrm{K}}_{\mathrm{2}}^{*}$ from Lueker et al. (2000) using Eq. (4) and a Newton–Raphson technique (function uniroot.all from package rootSolve; Soetaert and Herman, 2009). These calculated ${\mathrm{K}}_{\mathrm{1}}^{*}$ values were subsequently fitted to a general expression as a function of temperature and salinity of the form:

  $$\begin{array}{}\text{(6)}& {\mathrm{pK}}_{\mathrm{1}\mathrm{or}\mathrm{2}}^{*}=a_{\mathrm{1}}+a_{\mathrm{2}}{S}_{\mathrm{P}}+a_{\mathrm{3}}{S}_{\mathrm{P}}^{\mathrm{2}}+{\displaystyle \frac{a_{\mathrm{4}}}{T}}+a_{\mathrm{5}}\ln \left(T\right),\end{array}$$

  where ${\mathrm{pK}}_{\mathrm{i}}^{*}$ corresponds to −log ₁₀(K_i) and a_i are fitting coefficients determined using the Levenberg–Marquardt algorithm for non-linear least-squares estimates (function nlsLM from the minpack.lm package; Elzhov et al., 2016). This expression is of a similar form as Lueker et al. (2000), to facilitate the comparison. Because the salinity range in the sub-dataset where four carbonate system variables are available is narrow (30.73 to 37.57), it was not possible to obtain converging iterations where all the coefficients in Eq. (6) were resolved. Thus, we kept a₂ and a₃ fixed to the Lueker et al. (2000) values, assuming that the salinity dependence of ${\mathrm{K}}_{\mathrm{1}}^{*}$ and ${\mathrm{K}}_{\mathrm{2}}^{*}$ is correct for the salinity range of our dataset, and only solved for a₁, a₄, and a₅.

• 2.

  Second, this new expression for ${\mathrm{K}}_{\mathrm{1}}^{*}$, as well as CA and the expression for ${\mathrm{K}}_{\mathrm{2}}^{*}$ used in step 1, were used to compute pH at in situ temperature. For this, both ${\mathrm{K}}_{\mathrm{1}}^{*}$ and ${\mathrm{K}}_{\mathrm{2}}^{*}$ were calculated at the temperature of pH measurement (${\mathrm{K}}_{\mathrm{1}}^{*,\mathrm{labT}}$ and ${\mathrm{K}}_{\mathrm{2}}^{*,\mathrm{labT}}$). These were used together with the free proton concentration at lab temperature (${\mathrm{H}}_{\mathrm{F}}^{\mathrm{labT}}$) and the calculated carbonate alkalinity (CA^labT), both of which do not change during the iterative procedure, to calculate [H⁺], the free proton concentration at in situ temperature. We expressed DIC as a function of CA, [H⁺], ${\mathrm{K}}_{\mathrm{1}}^{*}$ and ${\mathrm{K}}_{\mathrm{2}}^{*}$, and assumed that the value of DIC is independent of temperature. Thus,

  $$\begin{array}{}\text{(7)}& \begin{array}{rl}\text{CA}& {\displaystyle \frac{{\left[{\mathrm{H}}^{+}\right]}^{\mathrm{2}}+\left[{\mathrm{H}}^{+}\right]{\mathrm{K}}_{\mathrm{1}}^{*}+{\mathrm{K}}_{\mathrm{1}}^{*}{\mathrm{K}}_{\mathrm{2}}^{*}}{\left[{\mathrm{H}}^{+}\right]{\mathrm{K}}_{\mathrm{1}}^{*}+\mathrm{2}{\mathrm{K}}_{\mathrm{1}}^{*}{\mathrm{K}}_{\mathrm{2}}^{*}}}={\text{CA}}^{\mathrm{labT}}\\ & {\displaystyle \frac{{\left({\mathrm{H}}_{\mathrm{F}}^{\mathrm{labT}}\right)}^{\mathrm{2}}+{\mathrm{H}}_{\mathrm{F}}^{\mathrm{labT}}{\mathrm{K}}_{\mathrm{1}}^{*,\mathrm{labT}}+{\mathrm{K}}_{\mathrm{1}}^{*,\mathrm{labT}}{\mathrm{K}}_{\mathrm{2}}^{*,\mathrm{labT}}}{{\mathrm{H}}_{\mathrm{F}}^{\mathrm{labT}}{\mathrm{K}}_{\mathrm{1}}^{*,\mathrm{labT}}+\mathrm{2}{\mathrm{K}}_{\mathrm{1}}^{*,\mathrm{labT}}{\mathrm{K}}_{\mathrm{2}}^{*,\mathrm{labT}}}}.\end{array}\end{array}$$

  This equation was rewritten into a quadratic equation, solved analytically for [H⁺], and converted to pH.

• 3.

  Third, CA – which is dependent on pH – was updated based on the new [H⁺], as per Eq. (3) and the method outlined for the initial calculation of CA.

• 4.

  Fourth, we used Eq. (5) to calculate ${\mathrm{K}}_{\mathrm{2}}^{*}$ as a function of pCO₂, DIC, the new pH, and CA and fit these in situ computed constants to an equation of the form of Eq. (6).

These four steps were repeated, and at each iteration, ${\mathrm{K}}_{\mathrm{2}}^{*}$, CA, and pH from the previous iteration, were used as initial values. Note that this method assumes that the uncertainty in K₀ is minor compared to that in ${\mathrm{K}}_{\mathrm{1}}^{*}$ and ${\mathrm{K}}_{\mathrm{2}}^{*}$. We also assumed that no acid–base systems other than the carbonate, borate, silicate, and phosphate acid–base systems contributed to TA – this point will be elucidated later – and that uncertainties in the calculated contributions of the latter three acid–base systems to TA were also minor compared to the uncertainties in ${\mathrm{K}}_{\mathrm{1}}^{*}$ and ${\mathrm{K}}_{\mathrm{2}}^{*}$.

2.4 Uncertainty propagation

The overall uncertainty on the final ${\mathrm{K}}_{\mathrm{1}}^{*}$ and ${\mathrm{K}}_{\mathrm{2}}^{*}$ values is a combination of the uncertainties associated with measurement errors (hereafter termed “analytical uncertainty”) and the uncertainties resulting from the fitting procedures (hereafter termed “fitting uncertainty”) that are propagated throughout the iterations. The analytical uncertainty (σK^ana.) was computed using the predefined accuracy limits (here, for simplicity, denoted σ) used for the GLODAPv2 secondary quality control procedures. This accuracy limit reflects the minimum bias that can be detected with reasonable certainty (Tanhua et al., 2010) and is based on an objective analysis of systematic biases in ship-based data. Within the GLODAP context the accuracy limit should be interpreted as “the range within which we can realistically expect measurements from the deep ocean to be reproducible”. For each variable the corresponding value is taken from Table 2 in Olsen et al. (2016); i.e. σS_P=0.005, σ[DSi]=2 %, σ[SRP]=2 %, σDIC=4 µmol kg⁻¹, σTA=6 µmol kg⁻¹. σpH is set to 0.01 following Table 3 in Olsen et al. (2019) and σpCO₂ is set to 2 µ atm, corresponding to the minimum accuracy of SOCAT quality control flags A or B. While referred to as accuracy, this number is actually a measure of overall measurement uncertainty and includes uncertainties due to environmental factors (Pierrot et al., 2009). σCA was computed as the square root of the sum of the squares of $\mathit{\sigma }{\mathrm{CO}}_{\mathrm{3}}^{\mathrm{2}-}$ and $\mathit{\sigma }{\mathrm{HCO}}_{\mathrm{3}}^{-}$. In turn, these were computed using TA, pH, [SRP], [DSi], P, T, and S_P as input variables, as well as their respective aforementioned uncertainties, using the error propagation code of Orr et al. (2018). The analytical uncertainty on both ${\mathrm{K}}_{\mathrm{1}}^{*}$ and ${\mathrm{K}}_{\mathrm{2}}^{*}$ was then estimated following the standard rules of error propagation, as per the following equations:

$$\begin{array}{}\text{(8)}& \begin{array}{rl}& \mathit{\sigma }{\mathrm{K}}_{\mathrm{1}}^{\mathrm{ana}.}={\mathrm{K}}_{\mathrm{1}}^{*}\\ & \sqrt{{\left({\displaystyle \frac{\mathit{\sigma }\left[{\mathrm{H}}^{+}\right]}{\left[{\mathrm{H}}^{+}\right]}}\right)}^{\mathrm{2}}+{\left({\displaystyle \frac{\mathit{\sigma }f{\mathrm{CO}}_{\mathrm{2}}}{f{\mathrm{CO}}_{\mathrm{2}}}}\right)}^{\mathrm{2}}+{\left({\displaystyle \frac{\sqrt{{\left(\mathrm{2}\mathit{\sigma }\text{DIC}\right)}^{\mathrm{2}}+{\left(\mathit{\sigma }\text{CA}\right)}^{\mathrm{2}}+{\left(\mathrm{2}{\mathrm{K}}_{\mathrm{0}}\mathit{\sigma }f{\mathrm{CO}}_{\mathrm{2}}\right)}^{\mathrm{2}}}}{\mathrm{2}\mathrm{DIC}-\mathrm{CA}-\mathrm{2}{\mathrm{K}}_{\mathrm{0}}f{\mathrm{CO}}_{\mathrm{2}}}}\right)}^{\mathrm{2}}},\end{array}\end{array}$$

$$\begin{array}{}\text{(9)}& \begin{array}{rl}& \mathit{\sigma }{\mathrm{K}}_{\mathrm{2}}^{\mathrm{ana}.}={\mathrm{K}}_{\mathrm{2}}^{*}\\ & \sqrt{{\left({\displaystyle \frac{\mathit{\sigma }\left[{\mathrm{H}}^{+}\right]}{\left[{\mathrm{H}}^{+}\right]}}\right)}^{\mathrm{2}}+{\left({\displaystyle \frac{\sqrt{{\left(\mathit{\sigma }\text{CA}\right)}^{\mathrm{2}}+{\left(\mathit{\sigma }\text{DIC}\right)}^{\mathrm{2}}+{\left({\mathrm{K}}_{\mathrm{0}}\mathit{\sigma }f{\mathrm{CO}}_{\mathrm{2}}\right)}^{\mathrm{2}}}}{\mathrm{CA}-\mathrm{DIC}+{\mathrm{K}}_{\mathrm{0}}f{\mathrm{CO}}_{\mathrm{2}}}}\right)}^{\mathrm{2}}+{\left({\displaystyle \frac{\sqrt{{\left(\mathrm{2}\mathit{\sigma }\text{DIC}\right)}^{\mathrm{2}}+{\left(\mathit{\sigma }\text{CA}\right)}^{\mathrm{2}}+{\left(\mathrm{2}{\mathrm{K}}_{\mathrm{0}}\mathit{\sigma }f{\mathrm{CO}}_{\mathrm{2}}\right)}^{\mathrm{2}}}}{\mathrm{2}\mathrm{DIC}-\mathrm{CA}-\mathrm{2}{\mathrm{K}}_{\mathrm{0}}f{\mathrm{CO}}_{\mathrm{2}}}}\right)}^{\mathrm{2}}}.\end{array}\end{array}$$

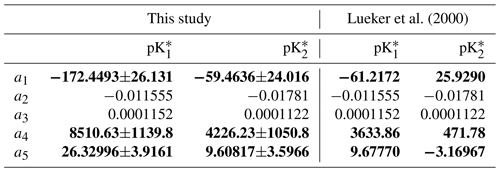
The fitting uncertainty (σK^fit.) was obtained using a Monte Carlo simulation technique that propagates errors in the fitting coefficients to the predicted K values. At the end of the iterations, the non-linear least-square model fits obtained with the nlsLM function were used as an input in the predictNLS function, from the propagate R package (Spiess, 2018), to calculate σK^fit., neglecting any error in the temperature measurements. The overall uncertainty on ${\mathrm{K}}_{\mathrm{1}}^{*}$ and ${\mathrm{K}}_{\mathrm{2}}^{*}$ was then assumed to be the square root of the sum of the squares of the analytical and fitting uncertainties. The 95 % confidence intervals for each of the fitting coefficients, i.e. a_i in Eq. (6), shown in Table 1, were extracted from the result of the non-linear least-squares model fits in R using the summary function. Note that, because we did not solve for the salinity coefficients in Eq. (6) due to the limited salinity range of the four carbonate system variable datasets, a₂ and a₃ are set to the Lueker et al. (2000) values and no confidence interval is computed for these coefficients.

Table 1 Comparison of the coefficients for ${\mathrm{pK}}_{\mathrm{1}}^{*}$ and ${\mathrm{pK}}_{\mathrm{2}}^{*}$ between this study and Lueker et al. (2000), using an equation of the form of Eq. (6). Coefficients are given as value ±95 % confidence interval. In bold are the coefficients (a₁, a₄ and a₅) that were solved for, while the two salinity coefficients (a₂ and a₃) were fixed to the Lueker et al. (2000) values.

3 Results

Using all the data from which T, S_P, DIC, pH, CA, and pCO₂ are available as high-quality, independent measurements, we were able to derive expressions for ${\mathrm{K}}_{\mathrm{1}}^{*}$ and ${\mathrm{K}}_{\mathrm{2}}^{*}$ with a new temperature dependence. The coefficients a_i for ${\mathrm{pK}}_{\mathrm{1}}^{*}$ and ${\mathrm{pK}}_{\mathrm{2}}^{*}$, in an equation of the form of Eq. (6), and after 30 iterations, are reported in Table 1, along with their respective 95 % confidence intervals. In both expressions, all coefficients are significantly different from zero (p values <0.001). As CA and pH are being updated throughout the iterations, CA, pH, ${\mathrm{K}}_{\mathrm{1}}^{*}$, and ${\mathrm{K}}_{\mathrm{2}}^{*}$ all evolved until the 10th iteration, before converging to a final value (Fig. 2). Thus, we stopped the iterative process after 30 iterations. Between the initial GLODAPv2 value and the 30th iteration, [H⁺] values vary by up to 6.6 %. CA values are only weakly affected by these in situ pH updates as they change by a maximum of 0.2 % throughout the first 30 iterations. Largest pH and CA changes occur at the colder end of the temperature range. ${\mathrm{pK}}_{\mathrm{1}}^{*}$ and ${\mathrm{pK}}_{\mathrm{2}}^{*}$ values both shift upward throughout the iterations, the ${\mathrm{pK}}_{\mathrm{1}}^{*}$ increase being higher than that of ${\mathrm{pK}}_{\mathrm{2}}^{*}$, especially in cold waters (Fig. 2).

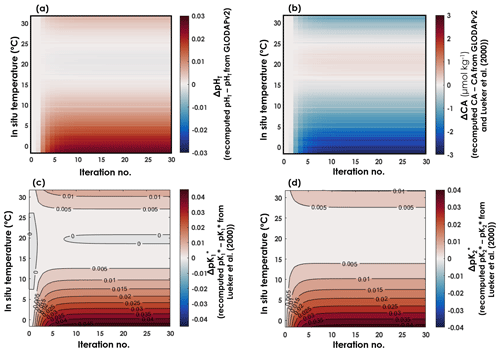
Figure 2 Evolution of pH_T, CA, ${\mathrm{pK}}_{\mathrm{1}}^{*}$, and ${\mathrm{pK}}_{\mathrm{2}}^{*}$ as a function of in situ temperature and iterations. (a) Differences between recomputed pH_T and pH_T from GLODAPv2. (b) Differences between recomputed CA and CA estimated from GLODAPv2 data and the Lueker et al. (2000) constants. Differences between recomputed (c) ${\mathrm{pK}}_{\mathrm{1}}^{*}$ and (d) ${\mathrm{pK}}_{\mathrm{2}}^{*}$ and the Lueker et al. (2000) values at in situ temperature and at a practical salinity of 35.

As shown in Fig. 3, the pK^* values obtained with the iterative procedure are statistically indistinguishable from the pK^* values of Lueker et al. (2000) (i.e. ${\mathrm{pK}}^{\mathrm{this}\mathrm{study}}-\mathit{\sigma }{\mathrm{pK}}^{\mathrm{this}\mathrm{study}}<{\mathrm{pK}}^{\mathrm{Lueker}}<{\mathrm{pK}}^{\mathrm{this}\mathrm{study}}+\mathit{\sigma }{\mathrm{pK}}^{\mathrm{this}\mathrm{study}}$) over most of the temperature range. Nevertheless, in cold waters, below temperatures 8.1 and 9.2 ^∘C respectively, ${\mathrm{pK}}_{\mathrm{1}}^{*}$ and ${\mathrm{pK}}_{\mathrm{2}}^{*}$ are significantly higher than the values reported by Lueker et al. (2000). In Fig. 3, we also provide a comparison of the pK^* values of this study with those of Papadimitriou et al. (2018), as the latter study focuses on low-temperature waters. As shown in Fig. 3c and d, both ${\mathrm{pK}}_{\mathrm{1}}^{*}$ and ${\mathrm{pK}}_{\mathrm{2}}^{*}$ from Papadimitriou et al. (2018) are slightly lower than the fitted values from this study, for a similar salinity, and are also lower than the Lueker et al. (2000) pK^* values except for temperatures below 4.0 and 1.2 ^∘C, respectively. Thus, the fact that the Lueker et al. (2000) study underestimates both ${\mathrm{pK}}_{\mathrm{1}}^{*}$ and ${\mathrm{pK}}_{\mathrm{2}}^{*}$ in waters near freezing point seems to be a consistent feature across studies.

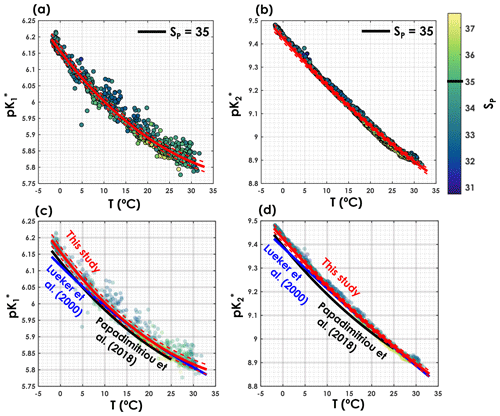
Figure 3 (a) ${\mathrm{pK}}_{\mathrm{1}}^{*}$ and (b) ${\mathrm{pK}}_{\mathrm{2}}^{*}$ as a function of temperature where the colour represents practical salinity (S_P) and the fits are fixed for a S_P of 35. Comparison of (c) ${\mathrm{pK}}_{\mathrm{1}}^{*}$ and (d) ${\mathrm{pK}}_{\mathrm{2}}^{*}$ as a function of temperature from this study (red lines), Lueker et al. (2000, blue line) and Papadimitriou et al. (2018, black line). The solid blue line represents the pK^* fits from Lueker et al. (2000), the solid red line the pK^* from this study computed with the coefficients presented in Table 1. Dashed red lines are overall uncertainties as defined in Sect. 2.4.

4 Discussion

Using underestimated ${\mathrm{pK}}_{\mathrm{1}}^{*}$ and ${\mathrm{pK}}_{\mathrm{2}}^{*}$ values implies that, for a given state, computed $\left[{\mathrm{H}}_{\mathrm{2}}{\mathrm{CO}}_{\mathrm{3}}^{*}\right]$ or pCO₂ would be underestimated and $\left[{\mathrm{CO}}_{\mathrm{3}}^{\mathrm{2}-}\right]$ overestimated. This potentially has strong implications for our representation of seawater carbonate chemistry in low-temperature marine environments, such as polar regions. Hence, we highlight the implications of this work for the estimation of two carbonate system variables in polar regions, i.e. pCO₂ and the saturation state of seawater with respect to calcite (Ω_Ca). But, first, we examine error propagation and the dependence of ${\mathrm{pK}}_{\mathrm{1}}^{*}$ and ${\mathrm{pK}}_{\mathrm{2}}^{*}$ to salinity and discuss the influence of organic alkalinity and the quality of pH measurements on the results presented here.

4.1 Influence of pH and TA measurement quality

The pH of samples that are used to derive the K^* fits presented here was measured using electrodes or spectrophotometrically, between 1993 and 2012. During this period, it was shown that impurities present in commercially available dyes could generate a systematic bias in the measured pH (Yao et al., 2007). Recently, Carter et al. (2018) pointed to systematic discrepancies resulting from differing approaches to pH measurements. Yao et al. (2007) noted that these impurities can contribute to pH offsets as large as 0.01 pH units, which corresponds to the analytical uncertainty in pH (σpH) that we use here, taken from Olsen et al. (2019). We must therefore investigate whether the fact that most pH measurements in the pH dataset are not from spectrophotometric measurements with purified dyes could alter the conclusion of underestimated pK^* values in cold waters. To answer this question, we gathered a sub-dataset of the more recent GLODAPv2.2019 data product (Olsen et al., 2019), composed of samples from nine different cruises (EXPOCODES 320620140320, 06AQ20150817, 33AT20120324, 33AT20120419, 33HQ20150809, 33RO20150410, 33RO20150525, 33RO20161119, and 33RR20160208) for which T, P, S_P, DIC, TA, [SRP], and [DSi] are available and associated with a WOCE flag of 2, for which pH was measured spectrophotometrically using purified dyes only, and for which an associated SOCAT pCO₂ value is available. Although this independent dataset is too small to apply the iterative procedure and obtain acceptable pK^* fits, we can use it to compare the ${\mathrm{K}}_{\mathrm{1}}^{*}{\mathrm{andK}}_{\mathrm{2}}^{*}$ values obtained with Eqs. (4) and (5) and this purified-dye independent dataset to the ${\mathrm{K}}_{\mathrm{1}}^{*}{\mathrm{andK}}_{\mathrm{2}}^{*}$ values obtained with Eqs. (4) and (5) and the regular dataset.

For both the purified-dye independent dataset and the regular dataset, samples were sorted according to in situ temperature and grouped into bins of 0.5  ^∘C. Temperature bins containing a single sample were not used. For each temperature bin, the mean pK^* values, obtained with Eqs. (4) and (5), along with the associated uncertainties, were computed. Plotting the difference between the pK^* values computed using the regular dataset and those computed using the purified-dye independent dataset as a function of seawater in situ temperature (Fig. 4), we do not see any clear systematic bias caused by the use of purified dyes. This means that pK^* values computed from a dataset with purified-dye pH measurements only are not higher or lower than pK^* values computed from a dataset with pH measured using primarily impure dye. More importantly, in colder waters ($T<\sim \mathrm{2}$ ^∘C), the differences between the pK^* values from this study and those from Lueker et al. (2000) (black line in Fig. 4) are larger than what can be explained by the choice of dye for spectrophotometric pH measurements. Thus, the use of impure vs. purified dye in pH measurements should not affect the conclusions presented here.

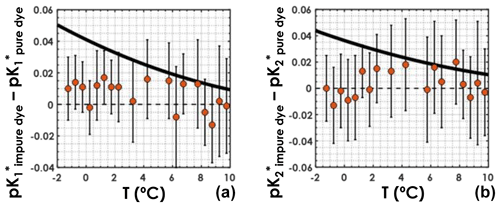
Figure 4 (a) ${\mathrm{pK}}_{\mathrm{1}}^{*}$ and (b) ${\mathrm{pK}}_{\mathrm{2}}^{*}$ differences between those obtained with the regular dataset and those obtained with the purified-dye independent dataset, as a function of in situ seawater temperature. Orange circles represent the mean computed pK^* values within a temperature bin, and the vertical black bars stand for the associated uncertainties deviations. The solid black line is the difference between the pK^* fit from this study and that from Lueker et al. (2000).

Another issue in GLODAPv2 carbonate system measurements may be the fact that some seawater samples contain measurable amounts of organic bases (Fong and Dickson, 2019; Patsavas et al., 2015; Yang et al., 2015). This organic alkalinity is unaccounted for in the definition of total alkalinity of Eq. (3), thus causing biased, overestimated, computed carbonate alkalinity values. This does not only concern coastal waters but also open-ocean waters, where the total concentration of these organic bases could be in the order of a few micromols per kilogram (Fong and Dickson, 2019). This, however, should not substantially alter the results presented here, due to the small amount of these organic bases and consequently small impact on computed pK^* values. If anything, subtracting the contributions of these unaccounted bases to the total alkalinity measurements would have a unidirectional effect on the dissociation constant estimates, shifting the pK^* values upwards – see Eqs. (4) and (5) – further away from the Lueker et al. (2000) values in cold waters.

4.2 Uncertainties in carbonate system calculations

The relative overall uncertainties ($\mathit{\sigma }{\mathrm{K}}^{*}/{\mathrm{K}}^{*}$) were ∼2.5 % for both ${\mathrm{K}}_{\mathrm{1}}^{*}$ and ${\mathrm{K}}_{\mathrm{2}}^{*}$. In both cases, the analytical uncertainty (σK^ana.) was more than twice as high as the fitting uncertainty (σK^fit). The overall pH measurement uncertainty of the GLODAP dataset (σpH =0.01) is relatively high, causing the pH term in Eqs. (8) and (9) to be the dominant factor in σK^ana.. Thus, what dominates the overall uncertainties for K^* estimates from this study is the uncertainty in pH, which explains the fact that the relative uncertainties of ${\mathrm{K}}_{\mathrm{1}}^{*}$ and ${\mathrm{K}}_{\mathrm{2}}^{*}$ are similar. Converting from σK^* to σpK^*, we find $\mathit{\sigma }{\mathrm{pK}}_{\mathrm{1}}^{*}=\mathit{\sigma }{\mathrm{pK}}_{\mathrm{2}}^{*}$ =0.011. The overall uncertainty for ${\mathrm{pK}}_{\mathrm{1}}^{*}$ is higher than that reported by Orr et al. (2018), but the overall uncertainty for ${\mathrm{pK}}_{\mathrm{2}}^{*}$ is smaller. These values are quite high relative to the uncertainties of previous expressions for ${\mathrm{K}}_{\mathrm{1}}^{*}$ and ${\mathrm{K}}_{\mathrm{2}}^{*}$ as reported in Table 2 of Millero (2007), which we attribute to the fact that they reflect both the uncertainty from the fits and from the measurements that we use.

Using the pK^* values from Table 1, setting the analytical uncertainties for each variable to the values reported in Sect. 2.4, and using $\mathit{\sigma }{\mathrm{pK}}_{\mathrm{1}}^{*}=\mathit{\sigma }{\mathrm{pK}}_{\mathrm{2}}^{*}$ =0.011, we use the Excel version of CO2SYS from Orr et al. (2018) and analyse the propagation of uncertainties on two computed variables, pCO₂ and the saturation state of seawater with respect to calcite, Ω_Ca (Mucci, 1983; see discussion in Sect. 4.4). For this purpose, we use all data points from GLODAPv2 that contain T, P, S_P, DIC, TA, pH, [SRP], and [DSi], in the top 10 m of the water column. The quality criterion remains unchanged; i.e. we use only data associated with a WOCE flag of 2. The obtained dataset contains 3392 samples, including the 948 samples of the regular dataset, and covers a salinity range from 3.46 to 37.57 and a temperature range from −1.91 to 31.80 ^∘C. Depending on which carbonate system pair of variables is used, both the magnitude and the uncertainties of computed variables can differ (Orr et al., 2018; Ribas-Ribas et al., 2014). Here, we use three different pairs of variables, i.e. TA–DIC, TA–pH, and DIC–pH, to compute pCO₂ and Ω_Ca and their associated propagated uncertainties, σpCO₂ and σΩ_Ca, respectively.

Relative uncertainties generated with the TA–DIC pair appear to be particularly sensitive to salinity (Fig. 5), increasing from ∼5 % to ∼15 % for both pCO₂ and Ω_Ca as the salinity decreases from 35 to 5. The overall relative uncertainty for both pCO₂ and Ω_Ca is less dependent on salinity when pH is used as an input variable with either DIC or TA. For both the TA–pH and the DIC–pH pairs, the overall relative uncertainty on pCO₂ increases with an increasing temperature, while the overall relative uncertainty on Ω_Ca decreases with an increasing temperature (Fig. 5).

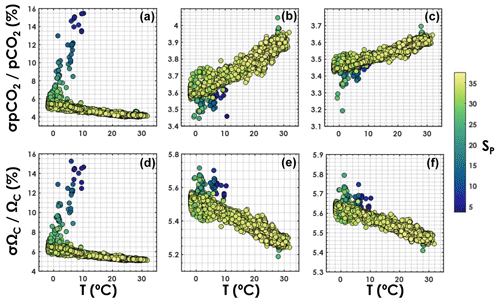
Figure 5 Overall relative uncertainty for (a, b, c) pCO₂ and (d, e, f) Ω_Ca as a function of in situ temperature (horizontal axis) and salinity (colour bar). Panels (a, d) are for the TA–DIC pair, panels (b, e) are for the TA–pH pair, and panels (c, f) are for the DIC–pH pair. This is computed using all data points from GLODAPv2 that contain T, P, S_P, DIC, TA, pH, [SRP], and [DSi], in the top 10 m of the water column (3392 samples).

As depicted in Fig. 6, in agreement with Raimondi et al. (2019), we conclude that the DIC–pH pair offers the lowest overall relative uncertainty for computed pCO₂ over the range of salinities and temperatures investigated. Using the DIC–pH pair also has the important benefit of not having to make any assumption regarding organic alkalinity or the boron-to-salinity ratio (Fong and Dickson, 2019). Conversely, the TA–pH pair is the one generating the highest overall relative uncertainties on computed pCO₂. As for Ω_Ca, the TA–pH pair provides the lowest overall relative uncertainty below a temperature of ∼20 ^∘C, whereas the TA–DIC pair should be preferred in warmer waters (Fig. 6).

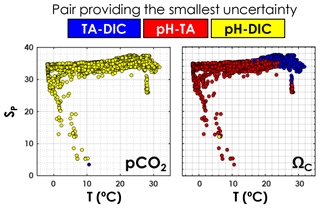
Figure 6 Pair of carbonate system variables (TA–DIC, TA–pH, or DIC–pH) providing the lowest overall relative uncertainty, as a function of in situ temperature and practical salinity, for pCO₂ and Ω_Ca. This is computed using all data points from GLODAPv2 that contain T, P, S_P, DIC, TA, pH, [SRP], and [DSi] in the top 10 m of the water column (3392 samples).

4.3 Implications for surface ocean pCO₂

To evaluate the implications of the revised temperature dependence of the carbonic acid dissociation constants, we compare ocean carbonate chemistry as calculated with the constants from this study, those of Lueker et al. (2000), and those of Millero et al. (2002). Whereas the constants from Lueker et al. (2000) are the most commonly used by the oceanographic community, as recommended by Dickson et al. (2007), the constants from Millero et al. (2002) were derived in an approach similar to that presented here, using a large dataset of in situ measurements. Thus, it appears relevant to include a comparison with Millero et al. (2002) in the present discussion. The major differences between our approach and the approach of Millero et al. (2002) are the calculation of CA from measured TA and pH (iteratively versus direct) and the conversion of pH measurements (iteratively versus estimating ΔpH∕ΔT from the constants of Mehrbach et al., 1973).

For this comparison, we use data from the Southern Ocean Carbon and Climate Observations and Modelling (SOCCOM) project (https://soccom.princeton.edu/, last access: 5 March 2020). The SOCCOM project has deployed more than 100 Argo floats equipped with biogeochemical sensors in the Southern Ocean. These sensors include pH, and SOCCOM routinely calculates the full carbon chemistry (including pCO₂ and Ω_Ca) using a combination of measured T, S_P, pH, O₂, and empirical algorithms for TA (Carter et al., 2018). The SOCCOM data used here, both measured and calculated, were downloaded as a Matlab file from https://library.ucsd.edu/dc/object/bb0515927k (last access: 5 March 2020).

The method used to calculate pCO₂ is detailed in the data file (within the FloatViz structure). Briefly, the SOCCOM project uses the Lueker et al. (2000) ${\mathrm{K}}_{\mathrm{1}}^{*}$ and ${\mathrm{K}}_{\mathrm{2}}^{*}$, Perez and Fraga (1987) for K_F, Dickson (1990) for KSO₄, and Lee et al. (2010) for total boron estimates. Both [DSi] and [SRP] are estimated from the measured nitrate concentration using stoichiometric ratios of 2.5 and 1∕16, respectively. We applied the same method but substituted the Lueker et al. (2000) ${\mathrm{K}}_{\mathrm{1}}^{*}$ and ${\mathrm{K}}_{\mathrm{2}}^{*}$ constants with either the constants from this study or the Millero et al. (2002) constants. We were then able to compare surface ocean (defined as the upper 10 m of the water column) pCO₂ obtained using Lueker et al. (2000) or Millero et al. (2002) with pCO₂ obtained using the constants from this study. The analytical uncertainties were set to σS_P=0.005 and σT=0.005 ^∘C (Olsen et al., 2016), σ[DSi]=0.9 µmol kg⁻¹ and σ[SRP]=0.5 µmol kg⁻¹ (combination of uncertainty in nitrate concentration from Argo data, i.e. 0.5 µmol kg⁻¹ as given in Johnson et al. (2017) and a 30 % uncertainty in stoichiometric ratios), σTA=5.6 µmol kg⁻¹ (Carter et al., 2018), and σpH=0.005 (Johnson et al., 2017). $\mathit{\sigma }{\mathrm{pK}}_{\mathrm{1}}^{*}$ and $\mathit{\sigma }{\mathrm{pK}}_{\mathrm{2}}^{*}$ were set to 0.011, respectively, when the constants from this study were used. For both Lueker et al. (2000) or Millero et al. (2002), they were set to the default values given by Orr et al. (2018), i.e. $\mathit{\sigma }{\mathrm{pK}}_{\mathrm{1}}^{*}=\mathrm{0.0075}$ and $\mathit{\sigma }{\mathrm{pK}}_{\mathrm{2}}^{*}=\mathrm{0.015}$. Uncertainties on the computed pCO₂ were propagated using the Matlab version of the Orr et al. (2018) CO2SYS software with error propagation.

pCO₂ values obtained with the constants derived from this study are clearly higher than the Lueker et al. (2000)-based values in the southernmost regions, where temperatures are lowest (Fig. 7a, b), with a maximum difference ($\mathrm{\Delta }p{\mathrm{CO}}_{\mathrm{2}}=p{\mathrm{CO}}_{\mathrm{2}}^{\mathrm{Lueker}}$–$p{\mathrm{CO}}_{\mathrm{2}}^{\mathrm{this}\mathrm{study}}$) of $-\mathrm{55}\pm \mathrm{17}$ µatm when the surface ocean is near the freezing point. The uncertainty on ΔpCO₂ (σΔpCO₂, grey lines in Fig. 7) is computed as the square root of the sum of the squares of $\mathit{\sigma }p{\mathrm{CO}}_{\mathrm{2}}^{\mathrm{Lueker}}$ and $\mathit{\sigma }\mathit{\text{p}}{\mathrm{CO}}_{\mathrm{2}}^{\mathrm{this}\mathrm{study}}$. Given the large uncertainties, the pCO₂ difference between values based on constants derived from this study and values based on Lueker et al. (2000) is only statistically significant (i.e. $\mathrm{\Delta }p{\mathrm{CO}}_{\mathrm{2}}+\mathit{\sigma }\mathrm{\Delta }p{\mathrm{CO}}_{\mathrm{2}}^{\mathrm{this}\mathrm{study}}<\mathrm{0}$) for temperatures below ∼8 ^∘C (Fig. 7a). pCO₂ values obtained using Millero et al. (2002) constants appear to be midway between pCO₂ values obtained using Lueker et al. (2000) constants and pCO₂ values based on the constants from this study (Fig. 7c, d).

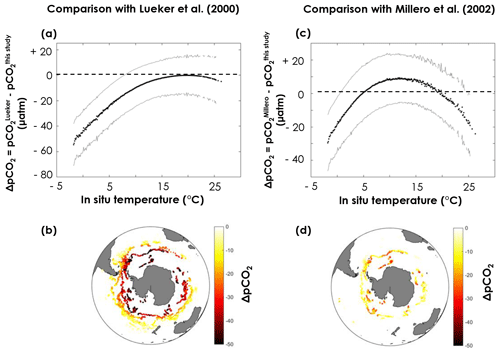
Figure 7 Difference in surface pCO₂ obtained from pH, temperature, practical salinity, and dissolved oxygen measured by the SOCCOM Argo array using (a, b) the Lueker et al. (2000) constants and the constants in Table 1 or (c, d) the Millero et al. (2002) constants and the constants in Table 1. Plots (a, c) represents the pCO₂ difference (ΔpCO₂) as a function of in situ temperature. Solid black lines are the mean ΔpCO₂, while solid grey lines are plus or minus σΔpCO₂ (square root of the sum of the squares of $\mathit{\sigma }p{\mathrm{CO}}_{\mathrm{2}}^{\mathrm{Lueker}}$ and $\mathit{\sigma }p{\mathrm{CO}}_{\mathrm{2}}^{\mathrm{this}\mathrm{study}}$). Maps (b, d) depict the spatial distribution of ΔpCO₂ in the Southern Ocean, where each point corresponds to an Argo float measurement.

Recently the SOCCOM Argo array was used to re-evaluate the Southern Ocean carbon sink (Gray et al., 2018). Traditional ship-based observations indicate a strong CO₂ uptake in the entire Southern Ocean, but these observations are known to have a strong seasonal bias (Bakker et al., 2016), as well as a smaller spatial bias due to many areas being severely undersampled (Takahashi et al., 2012). Using pCO₂ calculated by the above method, Gray et al. (2018) showed that the Southern Ocean CO₂ uptake is considerably smaller than previously estimated. In parallel, Bailey et al. (2018) showed that the CO₂ solubility constant from Weiss (1974) used in the majority of studies, including this one, was underestimated in waters below 0 ^∘C, which implies that surface pCO₂ is underestimated. In this study, using the new constants in Table 1, the computed Southern Ocean pCO₂ is also higher than when computed using the constants of Lueker et al. (2000) or the constants of Millero et al. (2002), as shown in Fig. 7. The Southern Ocean is a net CO₂ sink because the pCO₂ in surface waters is on average lower than the atmospheric pCO₂. If the surface-water pCO₂ is revised upward, the resulting flux of CO₂ from the atmosphere to the surface waters becomes smaller. Thus, results from Gray et al. (2018), Bailey et al. (2018), and the present study all advocate for a weaker CO₂ sink in the Southern Ocean. The ocean CO₂ sink is immensely important and currently estimated to remove ∼25 % of anthropogenic CO₂ emissions (Le Quéré et al., 2018). If the CO₂ uptake by the Southern Ocean is much smaller than previously estimated, there must be missing sinks elsewhere in the Earth system, be it in the oceanic or terrestrial realm. This highlights the need for a better understanding of the dynamics of the ocean carbon sink, including its regional and temporal variability. To validate our results, the high uncertainties associated with stoichiometric constants (Orr et al., 2018), coupled to the low spatial and temporal resolution of measurements in high latitudes, need to be addressed. Whether in the laboratory or in the field, future work should focus on a better understanding of seawater carbonate chemistry in cold waters.

4.4 Implications for calcium carbonate chemistry

In seawater undersaturated with respect to calcite or aragonite, (Ω_Ca or Ω_Ar<1), the CaCO₃ phase of interest should dissolve if present. Ω_Ca depends on the Ca²⁺ concentration in seawater (a function of salinity and therefore nearly invariant at depth), the solubility product of calcite (Mucci, 1983), and the ${\mathrm{CO}}_{\mathrm{3}}^{\mathrm{2}-}$ concentration in seawater. Because of the latter, computed Ω_Ca values are impacted by the choice of carbonic acid dissociation constants. Note that, as reported in Orr et al. (2018), the relative uncertainty on the solubility product of calcite is about 5 %. Below, we test the implications of the ${\mathrm{K}}_{\mathrm{1}}^{*}$ and ${\mathrm{K}}_{\mathrm{2}}^{*}$ values from this study on predictions of calcite saturation state in seawater.

Naviaux et al. (2019) recently observed discrepancies between Ω_Ca computed with the TA–DIC pair and Ω_Ca computed with the TA–pH pair, which they attributed to the internal inconsistency of the carbonate system, i.e. the fact that measured pH does not correspond to calculated pH. Instead, or in addition, the calcite saturation depth calculated by Naviaux et al. (2019) could be erroneously too shallow due to an overestimated ${\mathrm{K}}_{\mathrm{2}}^{*}$ and, consequently, overestimated seawater $\left[{\mathrm{CO}}_{\mathrm{3}}^{\mathrm{2}-}\right]$ and Ω_Ca.

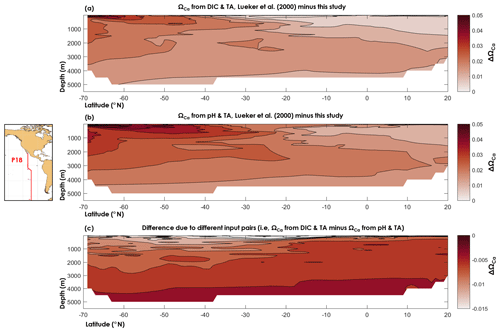
Figure 8 Difference between (a) the calcite saturation state (Ω_Ca) computed from TA and DIC using the dissociation constants of Lueker et al. (2000) and the constants derived from this study, (b) Ω_Ca computed from pH and TA using the dissociation constants of Lueker et al. (2000) and the constants derived from this study, and (c) Ω_Ca computed from the DIC and TA pair and the pH and TA pair and the dissociation constants derived from this study.

Here, we used data from a cruise (33RO20071215, GLODAPv2 cruise no. 345) along the CLIVAR repeat section P18 that took place in 2007, following a latitudinal transect in the south-eastern Pacific Ocean, in which the carbonate chemistry variables DIC, TA, and pH were measured (see Olsen et al., 2016, for details about the data). All calculations were carried out using the discrete data, but for purposes of visualization (Fig. 8) we used a nearest-neighbour interpolation (function griddata in Matlab). In Fig. 8, we compare Ω_Ca as computed using ${\mathrm{K}}_{\mathrm{1}}^{*}$ and ${\mathrm{K}}_{\mathrm{2}}^{*}$ from this study, with Ω_Ca based on Lueker et al. (2000) constants. We also compare Ω_Ca computed from TA–DIC with Ω_Ca computed from TA–pH. From Fig. 8, it can be seen that the Ω_Ca difference between two different carbonate system pairs (TA–DIC, TA–pH) is ∼5 times smaller than the Ω_Ca difference that is due to the set of dissociation constants. Thus, the apparent dissolution observed by Naviaux et al. (2019) may be explained by overestimated dissociation constants atop inconsistencies arising from the choice of carbonate variables used in the calculations. We also note, based on Fig. 8, that Ω_Ca overestimation is largest in the southernmost part of the Pacific surface waters, where the temperature is the lowest. Nevertheless, the maximum calculated Ω_Ca differences, i.e. ΔΩ_Ca=0.06 with TA–DIC and ΔΩ_Ca=0.07 with TA–pH, are 2–3 times lower than the average combined uncertainty, i.e. ($(\mathit{\sigma }{\mathrm{\Omega }}_{\mathrm{Ca}}^{\mathrm{Lueker}}{)}^{\mathrm{2}}+(\mathit{\sigma }{\mathrm{\Omega }}_{\mathrm{Ca}}^{\mathrm{this}\mathrm{study}}{)}^{\mathrm{2}}{)}^{\mathrm{0.5}}=\mathrm{0.20}$ and 0.17, respectively. These high uncertainties are attributed to the high measurement uncertainties that we use (those from Olsen et al., 2016, see Sect. 2.4), the overall uncertainty on the dissociation constants from this study, the uncertainty on Lueker et al. (2000) constants, and especially to the uncertainty in the calcite solubility product. As noted by Orr et al. (2018), the uncertainty on the calcite solubility product (∼5 %) causes the total uncertainty on Ω_Ca to be considerably larger than the uncertainty in seawater $\left[{\mathrm{CO}}_{\mathrm{3}}^{\mathrm{2}-}\right]$. In this study, only the ${\mathrm{K}}_{\mathrm{1}}^{*}$ and ${\mathrm{K}}_{\mathrm{2}}^{*}$ constants have been re-evaluated, but the large overall uncertainties on calculated saturation states clearly indicate that more work is necessary to define the solubility products of calcium carbonate minerals in the ocean. While beyond the scope of the present study, the results presented here show that proper assessments of present and future ocean acidification are highly sensitive to the present knowledge gaps regarding the thermodynamics of ocean carbon chemistry.

5 Conclusion

An iterative procedure allowed us to estimate the temperature dependence of the first and second carbonic acid stoichiometric dissociation constants (${\mathrm{K}}_{\mathrm{1}}^{*}$ and ${\mathrm{K}}_{\mathrm{2}}^{*}$, respectively) from a large dataset of high-quality oceanographic measurements. Both ${\mathrm{K}}_{\mathrm{1}}^{*}$ and ${\mathrm{K}}_{\mathrm{2}}^{*}$ were similar to the constants of Lueker et al. (2000) that are currently used by most of the oceanographic community, as recommended by Dickson (2007), but the ${\mathrm{K}}_{\mathrm{1}}^{*}$ and ${\mathrm{K}}_{\mathrm{2}}^{*}$ values were lower in cold seawater, below a temperature of ∼8–9 ^∘C. Consequently, at these temperatures, pCO₂ computed using the constants of Lueker et al. (2000) may be underestimated and [${\mathrm{CO}}_{\mathrm{3}}^{\mathrm{2}-}$] overestimated, meaning that the cold oceans are more undersaturated with respect to CaCO₃ minerals than expected. We also used a GLODAP sub-dataset to study the internal consistency of the carbonate system and found that the DIC–pH carbonate system pair provides the smallest overall uncertainty when computing seawater pCO₂. When calculating the saturation state of seawater with respect to calcite, the TA–DIC pair should be used to minimize the overall uncertainty when seawater is warmer than ∼20 ^∘C, whereas the TA–pH pair should be preferred below ∼20 ^∘C. These results are of critical importance for scientists contemplating studies of high-latitude marine carbonate chemistry and underline that improved knowledge of what causes the CO₂ system inconsistencies in cold waters is key to improve our understanding of the marine carbon budget.