the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Decorrelation scales for Arctic Ocean hydrography – Part I: Amerasian Basin
Frank Kauker
Michael Karcher
Benjamin Rabe
Mary-Louise Timmermans
Axel Behrendt
Rüdiger Gerdes
Ursula Schauer
Koji Shimada
Kyoung-Ho Cho
Takashi Kikuchi
Any use of observational data for data assimilation requires adequate information of their representativeness in space and time. This is particularly important for sparse, non-synoptic data, which comprise the bulk of oceanic in situ observations in the Arctic. To quantify spatial and temporal scales of temperature and salinity variations, we estimate the autocorrelation function and associated decorrelation scales for the Amerasian Basin of the Arctic Ocean. For this purpose, we compile historical measurements from 1980 to 2015. Assuming spatial and temporal homogeneity of the decorrelation scale in the basin interior (abyssal plain area), we calculate autocorrelations as a function of spatial distance and temporal lag. The examination of the functional form of autocorrelation in each depth range reveals that the autocorrelation is well described by a Gaussian function in space and time. We derive decorrelation scales of 150–200 km in space and 100–300 days in time. These scales are directly applicable to quantify the representation error, which is essential for use of ocean in situ measurements in data assimilation. We also describe how the estimated autocorrelation function and decorrelation scale should be applied for cost function calculation in a data assimilation system.
- Article
(12809 KB) - Full-text XML
-
Supplement
(670 KB) - BibTeX
- EndNote
Any use of observational data requires assumptions, or better knowledge, about the representativeness of each measurement in space and time. This holds even more for in situ observations from data-sparse regions, such as the Arctic Ocean. Interpolation guided by the statistical properties of observed quantities can provide Arctic-wide fields, while data assimilation using comprehensive dynamical models and assimilation methods can, in addition, provide fields that are consistent with the modeled physics. Also, sampling strategies have to take the knowledge of the representativeness of point measurement into account. The temporal and spatial scales, for which a single measurement is representative, depend on local dynamics, external forcing, and the influence of lateral water–mass influxes. Here, we make an attempt to estimate those length scales and timescales in the Arctic Ocean based on observational data from the period 1980–2015. This will be achieved by estimating the autocorrelation function and decorrelation scales of temperature and salinity.
Autocorrelation functions and associated decorrelation scales are useful measures to characterize physical phenomena occurring in the ocean (Stammer, 1997; Eden, 2007). These functions describe spatial and temporal ranges over which ocean properties coherently vary, and the scales provide a measure of the spatial and temporal extent of the variations. The functional form of the autocorrelation depends on the physical properties, the considered scales (e.g., synoptic versus mesoscale) and the area. Many studies have estimated autocorrelation functions through analysis of in situ ocean measurements (e.g., Meyers et al., 1991; Chu et al., 2002; Delcroix et al., 2005) and satellite observations (e.g., Kuragano and Kamachi, 2000; Hosoda and Kawamura, 2004; Tzorti et al., 2016). Generally, the estimated autocorrelation functions have exponential or Gaussian form (Molinari and Festa, 2000). The decorrelation scales are usually given by the e-folding scale of the corresponding autocorrelation functions (see McLean, 2010 for a summary of different definitions).
Estimated decorrelation scales have been applied to a variety of ocean studies. In the context of dynamical studies, the decorrelation scale is used as a measure of the scale of prevailing phenomena and used to relate dynamical processes with the observed signals (e.g., Stammer, 1997; Ito et al., 2004; Kim and Kosro, 2013). In optimal interpolation and objective mapping, the decorrelation scale gives a measure of influential radius of a point measurement; the autocorrelation function, together with the associated decorrelation scale, provides the weight of a point measurement on mean field estimates (Meyers et al., 1991; Chu et al., 1997; Davis, 1998; Wong et al., 2003; Böhme and Send, 2005). For observation network design, decorrelation scales are one guide to estimate optimal sampling intervals in space and time (Sprintall and Meyers, 1991; White, 1995; Delcroix et al., 2005).
One of the prevalent and growing applications of decorrelation scales is data assimilation. Data assimilation synthesizes observed data and modeled physics based on statistical theories. This is an effective approach to fill the gap between observation and modeling studies (Wunsch, 2006; Blayo et al., 2015). Generally, data assimilation minimizes a model–data misfit with an assessment of errors; the autocorrelation function and the decorrelation scale are necessary for these error assessments (Carton et al., 2000; Forget and Wunsch, 2007). For a model–data misfit calculation, the difference of the spatial (and temporal) scales represented by a model and by the observations should be taken into account. Physical properties simulated in general circulation models (GCMs) represent mean values over each grid cell for a certain temporal period, whereas those from in situ measurements represent values at a localized point in space and in time. The error resulting from the difference of the scales represented by these two approaches is referred to as representation error (see van Leeuwen, 2015 for a summary). The autocorrelation function and the decorrelation scales provide a direct measure of the representation error. In ocean data assimilation, an assessment of the representation error is particularly important, since it is generally an order of magnitude larger than the measurement (instrument) error (Ingleby and Huddleston, 2007).
A necessity of decorrelation scale in ocean data assimilation also comes from the sparseness of ocean measurements. An autocorrelation function is necessary to constrain locations distant from a measurement. Li et al. (2003) pointed out that an assimilation of sparsely distributed data into an eddy-permitting model, without taking its influential radius into account, causes serious problems around the locations where the data are assimilated. Artificial eddies appear around the location of the data, since the density at the data location differs from densities at their surrounding grid points in the model. They also pointed out that the assimilated information disappears on the timescale determined by the model's local advection and diffusion. Note that this situation cannot be solved by applying advanced data assimilation techniques (e.g., 4DVar, EnKF), since the artificial eddies are dynamically consistent with the modeled physics. Autocorrelation function and decorrelation scale provide necessary information to solve such problems by imposing a spatial and temporal radius of influence of each measurement (Forget and Wunsch, 2007; Zuo et al., 2011).
Practically, autocorrelation functions are used to define an “observation operator” in data assimilation systems. The observation operator maps modeled variables onto observational points. If the operator is properly defined, a point measurement will constrain the model, not only at the location where measurements exist but also in areas distant from the measurement. An implementation of such an observation operator makes it possible to fully exploit the potential of sparsely distributed measurements, and can solve problems such as those reported by Li et al. (2003). This is of particular importance as the ocean models used for assimilation become eddy-permitting. An additional important feature of the autocorrelation function is to constrain the scale of temporally varying fluctuations. Unlike the static interpolation approaches, data assimilation provides a four-dimensional analysis field. In order to appropriately assimilate observed temporal fluctuations, the temporal scale of fluctuations should be implemented in the observation operator.
In the midlatitude and equatorial regions, there are a number of decorrelation scale estimates (e.g., White and Meyers, 1982; Chu et al., 1997, 2002; Deser et al., 2003; Martins et al., 2015), and these have been applied for a variety of studies including data assimilation (see the papers mentioned above). On the other hand, while a few studies have examined scales of temperature and salinity variability in the Arctic Ocean (e.g., Timmermans and Winsor, 2013; Marcinko et al., 2015), there has been no assessment of basin-wide decorrelation scales of T∕S field to date. One reason is that sea-ice cover greatly inhibits sea surface observation by remote sensing. Another reason is the sparse coverage of in situ ocean measurements due to the inaccessibility and the absence of an Argo float network (that has provided essential data for midlatitude and Southern Ocean studies; e.g., McLean, 2010; Reeve et al., 2016). In the last decade, however, the number of observational activities has been increasing significantly, with the growing concern about the sea-ice retreat and its potential impact on global climate (see, e.g., Ortiz et al., 2011 and references therein). In addition to the increasing number of research cruises, autonomous observation platforms (e.g., ice-tethered profilers – ITPs; Krishfield et al., 2008a; Toole et al., 2011) now provide data throughout a full seasonal cycle in the Arctic. The data acquired from these research activities enable us for the first time to estimate basin-wide decorrelation scales for T and S profiles in the Arctic Ocean.
The objective for the following study is to estimate the autocorrelation functions and decorrelation scales of temperature and salinity in the Arctic Ocean at different depths. Few modelling studies have focused on applications of ocean in situ measurements in the Arctic, due to the absence of comprehensive historical archives and representation error estimates. Only the climatology (PHC3.0; Steele et al., 2001) has been widely applied for model validation (e.g., Ilıcak et al., 2016). In recent years, however, assimilations of in situ measurements in the Arctic Ocean have started (Panteleev et al., 2004, 2007; Nguyen et al., 2011; Zuo et al., 2011; Sakov et al., 2012). To promote and enhance the ongoing ocean data assimilations, archiving historical measurements and estimating decorrelation scales are indispensable. To achieve the objective of the present study, we (1) compile historical observations of temperature and salinity in the Arctic Ocean, (2) construct a background mean field necessary for the decorrelation scale estimate, (3) examine the functional form of autocorrelation in temporal- and spatial-lag space, and finally (4) provide an autocorrelation function, decorrelation scales, and representation error covariance, which are directly applicable to error assessment in ocean data assimilation. Note that the estimation of the autocorrelation quantifies basin-scale variability. Smaller-scale variability (e.g., mesoscale eddies on the deformation scale; Zhao et al., 2014) remains unresolved and is an intrinsic part of the autocorrelation function. The study area is the Amerasian Basin. As will be described in Sect. 3, the second step mentioned above requires a different approach for other regions of the Arctic Ocean. The vertical depth range of the analysis is limited to between 0 to 400 m depth due to data availability.
The rest of the paper is organized as follows: Sect. 2 describes the compilation of historical data and quality-control procedures applied prior to the analysis. Section 3 describes the background temperature and salinity field construction and trend analyses. Section 4 describes examination of two-dimensional autocorrelation functions in spatial- and temporal-lag space, and provides decorrelation scale and error covariance estimates. Section 5 gives conclusions.
2.1 Compilation of historical data
Since there is no comprehensive in situ ocean data archive for the Arctic, we compile historical temperature and salinity measurements with the objective not only to use the data for the present decorrelation scale estimate but also to prepare an archive for future applications in model validation and data assimilation. Since the existing archived data from the Arctic Ocean are widely dispersed in various datasets with different formats, we compile these data into one archive with a standard format focusing on the Arctic and northern North Atlantic Ocean (Table 1). The original data (Table 1) were acquired from various observational platforms (e.g., research vessels, moorings, ITPs, and Argo floats) by conductivity–temperature–depth (CTD) sensors and expendable CTDs (XCTDs). The archiving effort of this study originates from the data compilation described by Rabe et al. (2011, 2014) and Somavilla et al. (2013), and is ongoing thanks to support from many oceanographers. The archived data will be available online (https://www.pangaea.de) after a profile-based thorough quality check (except those data which require additional consent from data providers). This public archive is described in Behrendt et al. (2017).
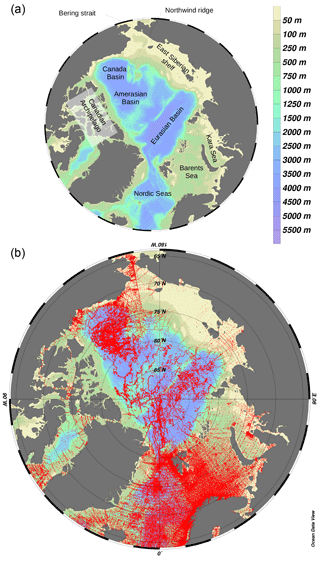
Figure 1The topographic features of the Arctic Ocean (a) and spatial distribution of archived temperature and salinity data for the 1980–2015 period (b); a red dot is shown if there is at least one measurement in the 0–20 m depth range.
The archived information for each measurement profile includes cruise name, station number, data type, time stamp, geographical location, bottom depth (if available), measurement depth (pressure is converted to depth by the method described by Saunders, 1981), temperature, salinity, data quality information provided in the original dataset (if available), and data source information. The spatial coverage of the archived data ranges from 45∘ N to the pole on the Atlantic Ocean side and from 64∘ N (Bering Strait) to the pole on the Pacific Ocean side. The temporal coverage is from 1980 to 2015. Figure 1 shows an example of the spatial distribution of the archived data (0–20 m depth range, north of 64∘ N) for the entire period. The archived data cover the entire Arctic and northern North Atlantic oceans, while the biggest data gaps are on the East Siberian Shelf and north of the Canadian Arctic Archipelago. A basic quality check is applied to the archived data before the duplication checks and statistical screening, described in the following subsections. The basic quality check is composed of (1) a bathymetric test using the merged IBCAO/ETOPO5 (Jakobsson et al., 2012) with a tolerance of 20 m, (2) a valid range test for temperature (−2.2 ∘C ∘C) and salinity (0 psu psu), and (3) a vertical stability test. The bathymetric test is applied to remove data with inconsistent geographic locations (i.e., either on land or indicating profile information at depths deeper than the sea floor at their location). This test excluded a number of erroneous profiles with position errors. The vertical stability test is applied to remove spike data points found in CTD and XCTD profiles. If the stability test program finds vertical density inversions, the data points are removed from the profile. If a data point violates one of the criteria, it is removed from the archive.
2.2 Duplication check
Since data obtained from various sources are prone to duplication issues, it is necessary to identify and remove duplicated data from the archive. A number of past studies, which compiled large oceanographic datasets, have suggested various automated procedures to deal with duplicate profiles (e.g., Ingleby and Huddleston, 2007; Gronell and Wijfefels, 2008; Good et al., 2013). In this study, we apply a simple duplication-check algorithm suitable for the present application. Since we are concerned only with basin-scale variability in this analysis, we count profiles that have small spatial and temporal separations as duplicates. The threshold applied for time difference between profiles is 1 day (date coincidence) and that applied for geographical location difference is 0.05∘ in longitude and 0.01∘ in latitude, respectively; to account for the effect of convergence of meridians toward the pole, a threshold of 2 km separation is also applied. If duplication is found (i.e., both temporal and spatial separation conditions above are met), the profiles are flagged. The profile with the highest reliability according to the data provider's own quality control is retained. For example, if we directly obtain data from PIs who have already applied their own quality-control procedure, we give the data higher priority than those from other data archives (e.g., World Ocean Database, 2013). The final duplication-checked archive is used as input for the statistical screening described below.
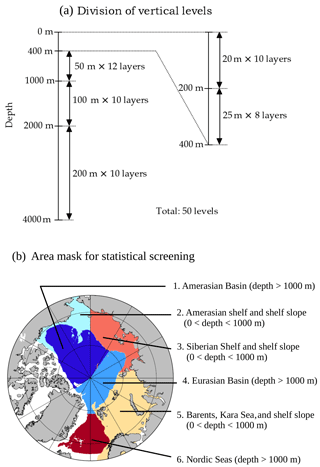
Figure 2(a) Division of vertical levels for the statistical screening and decorrelation scale examination. The archived TS data are classified into 50 levels according to their measurement depth. Data from an identical CTD profile are averaged over each depth range and regarded as one measurement. (b) Area mask for the area-based statistical screening and the decorrelation scale examination.
2.3 Statistical screening
Since the archive contains a number of data that have not been quality controlled, we apply an additional quality-control procedure (QC) before our analyses. Note that although we describe the QC procedure as it is applied to the entire raw dataset in this section, we will use only data from 0 to 400 m depth (after the QC) in the present scale analysis as mentioned in the introduction. The QC is composed of two steps: the first step is a grid-based screening; the second step is an area-based screening. Both steps are based on statistics of the data samples in discretized depth ranges. We divide the vertical profiles of temperature (T) and salinity (S) measurements into 50 depth bins (from a 20 m interval near the sea surface to a 200 m interval in the deep ocean; Fig. 2a). If there are more than two measurements for a certain depth range from one profile, the measurement values (T and S) are averaged. The statistics are calculated and applied in each depth range separately.
First, we apply a grid-based screening. The grid-based screening takes the difference in statistics (mean and standard deviation) in different locations into account. We define 111 km × 111 km (corresponding to 1∘ × 1∘ at the Equator) grid cells over the entire archive domain. The mean (μ) and standard deviation (σ) of T and S on each grid cell and in each depth range are calculated from the data within the surrounding 555 km × 555 km (5∘ × 5∘) area. T and S values outside 5 times the standard deviation (μ±5σ) on each grid cell are removed from the archive (the procedure is repeated twice).
Second, we apply an area-based screening for the data deeper than 750 m depth. In this step, we apply more rigorous statistics calculated from the entire basin and shelf area. This step is necessary to remove problematic data in data-sparse areas and data-sparse depth ranges, since the grid-based screening cannot provide good statistics in these areas due to the small sample size (no ITP data below 750 m). We classify the archived data into six subdomains based on the characteristics of dynamical regimes (Nurser and Bacon, 2014): (1) Amerasian Basin, (2) Amerasian shelf and shelf slope, (3) Siberian Shelf and shelf slope, (4) Eurasian Basin, (5) Barents and Kara seas including their shelf slopes, and (6) Nordic Seas (Fig. 2b). Mean and standard deviation are calculated in individual subdomains. Then, data outside 5 times the standard deviation (μ±5σ) are removed (repeated twice). In this paper, we focus only on the results for the Amerasian Basin; regions 2–5 are considered in a separate analysis.
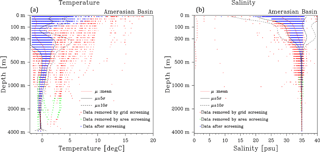
Figure 3Temperature (a) and salinity (b) distributions versus depth (m) in the Amerasian Basin (see Fig. 2b for area definition) after a combined statistical screening. The blue dots denote data distribution after the screening, while the red (green) dots denote data removed by grid-based (area-based) statistical screening. The red line denotes the mean (μ) at each depth level after the screening, and the solid and dotted black lines indicate μ±5σ and μ±10σ, respectively. The mean and standard deviations are calculated by the data from the entire Amerasian Basin. Note that analyses in Sects. 3 and 4 use data from the 0 to 400 m depth range.
The result of the statistical screening in the Amerasian Basin is shown in Fig. 3. The combined statistical screening successfully removes spurious data in deep depth ranges, while retaining the relatively larger variability in shallow depth ranges. After the combined statistical screening, the vertically discretized data are used for the analyses in the following section.
In this section, we describe the construction of a background mean field of T and S, which represents the basin-wide climatology in the Amerasian Basin. The background mean fields will be used to calculate anomaly fields necessary for the decorrelation scale estimates. For the construction of the background mean field, we first examine the functional form and spatial scale of the mean field variation (Sect. 3.1). Second, we apply the derived functional form and scale for the background mean field construction (Sect. 3.2). The temporal linear trends of T and S are also examined to account for the effect of a long-term temporal change of the mean field (Sect. 3.3).
3.1 Spatial scale of variation
To derive the scale for the background field construction, we examine the spatial scale of variation in each depth range (the vertical layers defined in Fig. 2b are used throughout this study to provide decorrelation scales directly applicable to data assimilation systems using z-coordinate systems). In this estimation, we assume isotropy and homogeneity of the spatial scale of variation in a basin. These assumptions are valid if (1) planetary- and (2) topographic-β effects do not dominate in a basin, and (3) no dominant oceanic structure extends toward one specific direction. The first and second conditions are satisfied in the high-latitude Amerasian Basin (small planetary-β effect) away from marginal shelf slopes, where a large topographic-β effect is expected. The third condition is also satisfied in the deep Amerasian Basin, although not necessarily in other sectors of the Arctic Ocean and Nordic Seas. For example, in the Eurasian Basin, there is a prominent extension of the frontal structure along the shelf slope associated with the warm Atlantic-water inflow (Anderson et al., 1994; Rudels et al., 2013). The location of the front is not necessarily trapped over the shelf slope but can be detached from the slope (Jones, 2001). Further, in the Nordic Seas, there are meridionally extending dominant current systems, i.e., the East Greenland Current, Norwegian Current, and West Spitsbergen Current (Hopkins, 1991). These features require a scale examination that takes a spatial anisotropy into account; a different approach for scale estimation will be applied to the Eurasian Basin in a forthcoming paper. For our purposes here, the Amerasian Basin is defined by the area where total water depth is deeper than 1000 m. This definition excludes the area affected by coastal currents and topographically trapped flows (associated with the submarine Northwind Ridge, for example).
To estimate the spatial scale of variation, we introduce a structure function (Davis et al., 2008; Todd et al., 2013) with the assumption of spatial and temporal isotropy of variation,
where x and t are the spatial and temporal separations from location x0 and time t0, Ω is the observed property (in this case, either T or S), and 〈 ⋅ 〉 is the averaging operator over space and time. The structure function, φx, t, gives the mean square difference between two measurements as a function of spatial and temporal separations. It was initially introduced by Kolmogorov (1941) to provide a statistical description of a field without specifying the mean and variance of the field. This is an appropriate approach for the present purpose, since we do not have a priori information regarding the statistics of the background field. We calculate the structure function from all available data in the Amerasian Basin (all depth bins shallower than 400 m):
where N is the number of available data pairs, the spatial and temporal separations of which are x and t, and ΔΩi (x,t) is the difference of observed values of the ith pair. We introduce a function f, which measures the normalized root mean square difference (RMSD) of any two measurements:
where φbg is defined by all the possible combinations of available data in the basin in a certain depth range:
and M is the number of all available data. φbg is a measure of the size of basin-wide and long-term variations; i.e., we introduce it as the “background” mean squared difference used to normalize φx, t.
The function f in Eq. (3) is a unitless measure of RMSD between two measurements as a function of spatial and temporal separations. If φx, t ∼ φbg, i.e., the mean difference between two measurements with (x, t) separation is comparable to those of “large” distance measurement pairs, then f∼ 0. This indicates that no coherent structure exists between data with (x, t) separation. If , i.e., the mean difference between measurements with (x, t) separation is sufficiently small compared to that between sufficiently distant data pairs, then f→1. This indicates a strong coherence exists between the data with (x, t) separation (ultimately, f=1, if the spatial and temporal separations are exactly zero). Note that the function f is not an autocorrelation function, although it has similar properties (e.g., decays from 1 to 0 for spatial and temporal separations from zero to infinity). The function f measures the scale of the coherent structure of the mean field, whereas an autocorrelation function measures the scale of coherent variation of anomalies. A structure function φ can be directly related to an autocorrelation function, if we can define φ by the anomaly from the mean field (e.g., Gandin 1965; Molinari and Festa, 2000). Since we have no a priori statistical information regarding the mean field, we cannot relate the structure function φ with the autocorrelation in our case. The correspondence to the geostatistical approach is given in Appendix A.
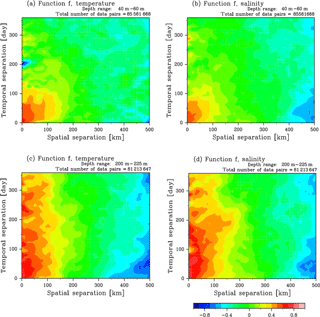
Figure 4Function f (normalized root mean square difference) of temperature (a, c) and salinity (b, d) in 40–60 m (a, b) and in 200–225 m (c, d) depth ranges as a function of spatial (km) and temporal (days) separations of measurement pairs. The color scale is common to the panels.
In order to examine the functional form of f, we construct data pairs from all possible combinations of data in each depth range, classify the pairs into 50 × 36 bins (50 bins for spatial separation with 10 km intervals and 36 bins for temporal separation with a 10-day interval), and calculate f in respective bins. For the binning, we suppose that the spatial and temporal scales of variation are much larger than the scale used for the binning, the validity of which is recursively confirmed by the scales estimated. Examples of the functional form of f for T and S in spatial and temporal separation space are shown in Fig. 4. Small separation gives large f values, while f∼0 when the separation is sufficiently large. Note that f decays with an increase in temporal separation in shallow depth ranges with a timescale of approximately 90–120 days (Fig. 4a, b), while f is relatively insensitive to temporal separations at depths deeper than 80 m (Fig. 4c, d), which is a manifestation of the seasonality. This seasonality is taken into account to estimate the background mean field in Sect. 3.2. Note that we limit our analysis here to consider only the upper water column, from 0 to 400 m depth, as uncertainties in the uncalibrated (“level-2”) ITP salinity data are comparable to the temporal and spatial variability of salinity in the Amerasian Basin below 500 m (see Appendix B).
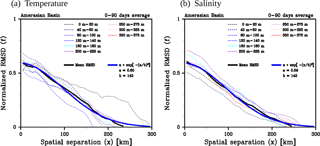
Figure 5The 0- to 90-day temporal average of the function f (normalized RMSD) of (a) temperature and (b) salinity as a function of spatial separation. The thin-dashed lines denote functional form of RMSD in different depth levels, while the thick-solid black line in each panel denotes average of 0–400 m depth range. The thick-solid blue line is the fitted Gaussian function, , the fitting parameters of which are shown in each panel.
To closely examine the functional form of f, we calculate the temporal (0- to 90-day) average of f in respective depth ranges. A survey of the two-dimensional functional form over all depth ranges (shallower than 400 m) revealed that 90 days is a reasonable choice to account for seasonal variation (not shown). Figure 5 shows the 90-day averaged functional form of f in different depth ranges (thin-dotted lines) and the average for all depth ranges (0–400 m; thick-dotted black line). Although the scale of variation varies with depth, the functional form of it be reasonably approximated by a Gaussian function (thick-solid blue line). Note that f does not come close to 1, even if the spatial separation nears 0 km, because the present examination excludes self combination of data (i.e., ), deals with a 0- to 90-day average, and does not resolve mesoscale fluctuations smaller than those at 10 km scale (the spatial separation of the bin).
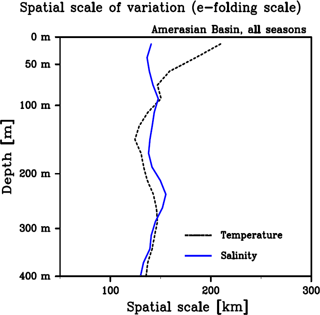
Figure 6Vertical profile of spatial scale of variation (e-folding scale of the normalized RMSD function, f) derived from the fitted Gaussian function for each depth level (see also Fig. 5). The scale in each depth range is calculated from data from all seasons.
The e-folding scales of the fitted Gaussian function for T and S are summarized in Fig. 6. The T profile (dashed black line) exhibits a large spatial scale of variation (∼ 200 km) near the sea surface, indicating the effect of the large-scale thermal forcing at the sea surface. The T profile deeper than 100 m depth is nearly constant (120–150 km). The salinity profile (solid blue line), on the other hand, exhibits nearly constant scale (130–150 km) from the sea surface to 400 m depth, indicating small contributions from large-scale surface salinity fluxes at the sea surface. We apply the e-folding scale of each depth level and the Gaussian function to estimate the background mean field.
3.2 Background mean field
To take the seasonal variation into account, we divide the observed data into four seasons (January–March, April–June, July–September, and October–December), and construct the background mean T and S fields in each season. This is supported by the fact that the temporal e-folding scale is approximately 90 days in shallow layers (Fig. 4a, b) and even longer in the deeper layers. The background field is derived by applying a spatial Gaussian filter with an e-folding scale given by the spatial scale of variation in each depth range (Fig. 6). The background field for Ωi is given by
where N is the number of measurements, whose distance from the ith measurement (Ωi) is less than 3 times the e-folding scale (i.e., ; see below), is the normalized weighting function for the nth data point, and Ωn is the nth measurement surrounding the ith measurement. The normalized weighting function is given by
where Wn is the Gaussian weighting function:
where xi and xn are the geographical location of Ωi and Ωn, respectively, and L(z) is the e-folding scale of the Gaussian filter as a function of depth (Fig. 6). An example of the derived background field for T and S in summer is shown in Fig. 7. The field captures a warm and fresh water mass distribution in the Canada Basin and its smooth transition toward cold and saline water in the northeastern Amerasian Basin. For the anomaly field calculation, we require the background field at the locations where observational data exist. Therefore, we do not apply any spatial and/or temporal interpolations even in data-sparse seasons (winter and spring).
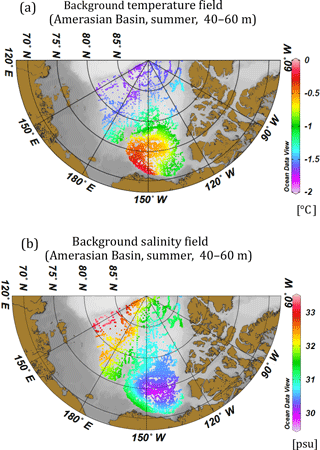
Figure 7Background mean field of (a) temperature and (b) salinity (40–60 m depth range) in summer (July–September) obtained by Gaussian filtering with the e-folding scales shown in Fig. 6. A vertical filter (average of three adjacent layers) is applied to the e-folding scales before the application in order to obtain a smooth transition of the filtering scale in the vertical direction. The background field is calculated only at the locations where data exist in the Amerasian Basin (bottom depth >1000 m).
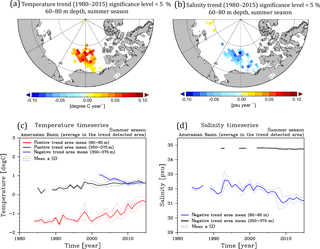
Figure 8A summary of linear temporal trend in the Amerasian Basin: the spatial pattern of (a) temperature and (b) salinity trend in 60–80 m depth range, and the time series of averaged (c) temperature and (d) salinity over the grid cells where a trend is detected in the Amerasian Basin. The trend is calculated in each 111 km × 111 km grid cell for the period covered by data, and the Mann–Kendall rank statistic (Kendal, 1938) is applied to test the significance. In panels (a) and (b), only the grid cells, the trends of which are statistically significant (significance level 5 %), are shown in color. Time series of averaged temperature/salinity over the corresponding area are shown in panels (c) and (d) by the thick-solid lines. Black thick-solid lines in panels (c) and (d) exhibit averages over the grid cells, where positive (negative) trends of T (S) are detected along the southern perimeter of the Canada Basin in the 350–375 m depth range (spatial pattern is not shown). The dashed lines in panels (c, d) depict the range of 1 standard deviation.
3.3 Temporal trend
For the present anomaly derivation, we also take the temporal trend from 1980 to 2015 into account. The trend is estimated in each 111 km × 111 km grid cell (1∘ × 1∘ at Equator scale), in each depth range, and in each season (Mann–Kendall rank statistics; Kendall, 1938) with a significance level of 5 %). The size of the grid cells is chosen to be consistent with the spatial scale of variation (Sect. 3.2). Figure 8 shows representative T and S trends in the 60–80 m depth range in summer and the corresponding average time series for those grid cells for which the trend is statistically significant. A warming (∼ 0.5 ∘ decade−1) and freshening (∼ 0.5 psu decade−1) trend in the Canada Basin is evident in this depth range. The freshening trend extends from the sea surface to 400 m depth without a significant change in spatial pattern, whereas the T trend changes sign and spatial pattern with depth. A positive trend in T is observed in the depth range from 0 to 160 m over the whole analyzed time period (i.e., through the Pacific-water/upper halocline layers, represented by red line in Fig. 8c), while after the year 2002 a decreasing trend in T is observed in the central Canada Basin in the 200–400 m depth range (lower halocline/Atlantic-water layer, represented by blue line in Fig. 8c). A positive trend is observed along the southern perimeter of the Canada Basin in 250–400 m depth range (Atlantic-water layer, represented by black line in Fig. 8c and d).
The warming and freshening trend in the Pacific-water layer has already been reported by many studies (e.g., Proshutinsky et al., 2009; Jackson et al., 2010; Giles et al., 2012; Timmermans et al., 2014). The cooling trend in the central Canada Basin and the warming trend along its southern perimeter are a consequence of deepening of the warm Atlantic water in the central basin and concurrent upwelling of warm Atlantic water at the boundaries, a manifestation of an intensification of the anticyclonic Beaufort Gyre in recent years (e.g., McLaughlin et al., 2009; Karcher et al., 2012; Zhong and Zhao, 2014). Although similar trends can be found in other seasons (from winter to spring), they are not statistically significant.
The temporal trend in each location is used to define a time-varying background field. Since the temporal distribution of the archived data is not spatially uniform, the representative time (i.e., the time that the temporal mean value represents) of the background field varies with space. The representative time is used as a tie point (offset) to connect the mean and trend. Taking the effect of the representative time into account, the time-varying background field for Ωi is defined by
where a(x) is the temporal trend at location x, t is the time, trep(x) is the representative time of the background mean field at location x. We calculate the representative time in each 111 km × 111 km area by the average of measurement times of all the data contained in the corresponding area and apply it to define the time-varying background field (see the Supplement). For the area where no trend can be deduced, we apply a constant background field, .
4.1 Autocorrelation function
Decorrelation scales used in oceanographic studies are generally defined by an e-folding scale of an autocorrelation function, which has a Gaussian or exponential functional form (Molinari and Festa, 2000). Practically, the autocorrelation functions are obtained from a series of autocorrelations estimated by differently lagged points (e.g., White and Meyers, 1982; Meyers et al., 1991). An autocorrelation for Δl lag is given by
where cov(Ωl, Ωl+Δl) is an autocovariance between two data series Ωl and Ωl+Δl, the temporal and/or spatial lag between which is Δl, and var(Ωl) and var(Ωl+Δl) are the variances of Ωl and Ωl+Δl, respectively. We assume isotropy and homogeneity of the autocorrelation in the Amerasian Basin, supported by the weak planetary-β effect in polar regions and the homogeneity of the Rossby radius in the Amerasian Basin (Nurser and Bacon, 2014; Zao et al., 2014). These assumptions enable us to calculate the autocorrelation from data series, which are composed of data pairs having the same temporal and spatial lag Δl but come from different locations in the basin and from different times (e.g., Sprintall and Meyers, 1991; Chu et al., 1997, 2002), i.e.,
where N is the number of data pairs, the spatial and temporal lags between which are Δl, is the anomaly value of the nth data, is the anomaly value of the paired data which locates Δl-lagged point from .
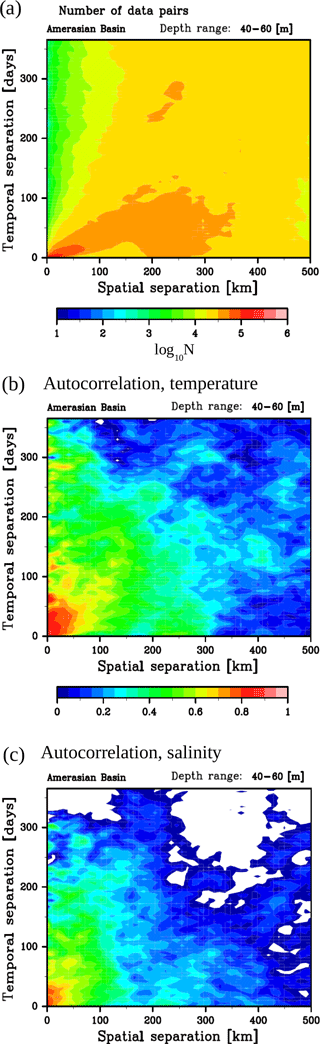
Figure 9(a) Number of data pairs used to calculate autocorrelation in each bin (log-scale) and two-dimensional autocorrelation function for (b) temperature and (c) salinity in 40–60 m depth range. The color bar for panel (b) is common to (c). The white area in panels (b) and (c) indicates negative autocorrelations.
The anomaly dataset Ω′ is defined by subtracting the time-varying background field from the observed data Ω. Each anomaly datum of the set is paired with the other anomalies to construct a set of anomaly data pairs, which consists of all possible combinations of two anomaly data. The data pairs are classified into discretized bins, according to the spatial and temporal lags of the paired data (50 spatial bins with a 10 km interval and 73 temporal bins with a 5-day interval; i.e., the examination window is 500 km lag × 365-day lag). The spatial and temporal sizes of the bin are designed to capture the functional form of the autocorrelation relevant for basin-scale data assimilation (i.e., the functional form of the autocorrelation describing mesoscale fluctuations are not examined in this analysis). Each bin has a sufficient number of data pairs to calculate an autocorrelation (N>O(103); see Fig. 9a). Figure 9b, c show examples of the autocorrelation functions for T and S in the 40–60 m depth range. There is a clear decrease of autocorrelation with increasing spatial and temporal lags, although with some variability about this relationship.
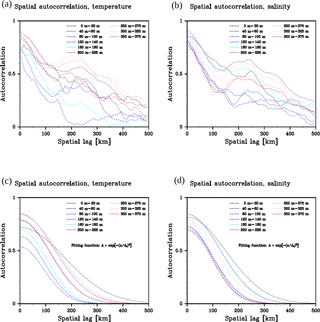
Figure 10Spatial autocorrelation function of temperature (a, c) and salinity (b, d). The upper panels show the temporal averages of the two-dimensional autocorrelation functions (the average of the 0- to 30-day lag for the 0–140 m depth range, 0- to 60-day lag for the 140–400 m depth range) in various depth levels. The lower panels are Gaussian functions, the intercepts and e-folding scales of which are calculated from the function fitting in the 0–150 km spatial-lag range.
Temporal and spatial averages of the autocorrelation are calculated to identify its functional form by fitting a suitable empirical function. Figure 10a and b show the temporal average of the spatial autocorrelation functions of T and S for different depth ranges. To account for the effect of differences of temporal autocorrelation scales in different depth ranges, we define the temporal average by a 0- to 30-day lag in shallow levels (0–140 m depth range) and by a 0- to 60-day lag in deeper levels (below 140 m). The functions generally show their highest values at zero-spatial lag, with decreasing values as the spatial lag increases. Some functions exhibit a second peak around a spatial lag of 200–300 km. We examine the relation between the second peaks and associated background mean field of T and S in different depth ranges, and find that the peaks derive from the circular T and/or S structure of the Beaufort Gyre (see Appendix C). Since the Beaufort Gyre is characterized by bowl-shaped isosurfaces of T and S associated with surface downward Ekman pumping, coherent variation of the isosurfaces gives rise to the second peak. To eliminate the effect of the second peak for our scale estimate, we use the autocorrelation functions just for a spatial lag of 0–150 km to compute a fitting function. We tested exponential and Gaussian functions for the fitting and found that the Gaussian function is generally suitable to represent the observationally derived spatial autocorrelations (Fig. 10c, d).
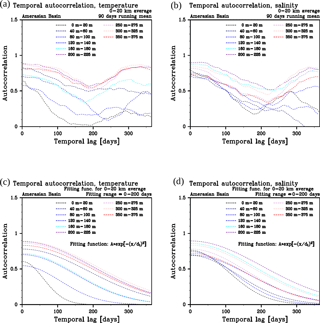
Figure 11Temporal autocorrelation function of temperature (a, c) and salinity (b, d). The upper panels show the spatial averages of the two-dimensional autocorrelation functions (the spatial average of 0–20 km lag) in various depth levels. The lower panels are Gaussian functions, the intercepts and e-folding scales of which are calculated from the function fitting in a 0- to 200-day temporal-lag range. A 90-day temporal filter is applied to the autocorrelation functions in panels (a) and (b) to eliminate noise.
The temporal autocorrelation is also examined by taking spatial-lag averages (0–20 km) of the two-dimensional autocorrelations of T and S. Figure 11a, b show the averaged temporal autocorrelation functions in various depth ranges. The functions show their highest values at zero-temporal lag and a reduction towards large temporal lags, whereas the functions from many depth ranges clearly exhibit an annual cycle. Since the seasonal variability of the background field is already taken into account (Sect. 3.2), the annual cycle found in the temporal autocorrelations indicates the effect of persistent atmospheric forcing, the timescale of which is longer than 1 year (e.g., Arctic Oscillation, Thompson and Wallace, 1998; North Atlantic Oscillation, Hurrell, 1995; Wallace, 2000), and/or spin-up/-down process of gyre-scale circulation, the timescale of which is estimated as 3–4 years (Yoshizawa et al., 2015). To remove the effect of the annual cycle found in Fig. 11a, b, we use the autocorrelation functions from 0 to 200 days of temporal lag to find a fitting function for the temporal autocorrelation. We again tested exponential and Gaussian forms for the fitting, and found that the Gaussian functions are suitable to represent the form of the temporal autocorrelation functions (Fig. 11c, d).
4.2 Decorrelation scale
The spatial and temporal decorrelation scales of T and S are derived from the e-folding scales of the fitted spatial and temporal autocorrelation functions in the respective depth ranges. The spatial autocorrelation function is represented by the Gaussian form,
where As is the autocorrelation at zero-spatial lag, x is a spatial lag, and ds is the spatial decorrelation scale. The temporal autocorrelation function has the same formula but exchanges As for At, x for t, and ds for dt, where At, t, and dt are the autocorrelation at zero-temporal lag, temporal lag, and temporal decorrelation scale, respectively. The autocorrelation at zero-temporal and -spatial lag (As and At) represents the effect of unresolved fluctuations, which have a scale smaller than the resolution of the present analysis at 10 km resolution in space and 5-day resolution in time (1–As represents the magnitude of unresolved fluctuations relative to the basin-scale fluctuations). The effect of mesoscale eddies with the scale of the deformation radius (order of 10 km horizontally) is described by this parameter.
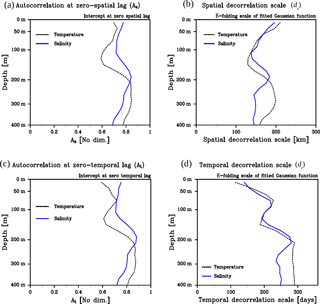
Figure 12Vertical profiles of zero-lag autocorrelation (a, c) and e-folding scale (b, d) of the fitting spatial (a, b) and temporal (c, d) autocorrelation functions. A three-layer vertical filter is applied to eliminate noise.
Figure 12 summarizes the vertical profiles of the spatial and temporal decorrelation scales (ds and dt) of T and S with the associated parameters for zero-lag autocorrelations (As and At). The zero-lag autocorrelations (Fig. 12a, c) show smaller values (0.6–0.7) in the upper 100 m depth range, indicating active mesoscale processes (e.g., eddy activity observed in the Pacific-water layer; e.g., Zhao et al., 2014). The zero-lag autocorrelations for spatial (Fig. 12a) and temporal lags (Fig. 12c) exhibit similar profiles, confirming the appropriateness of the spatial and temporal averages used for the functional form examinations. The vertical profiles of the decorrelation scale (Fig. 12b, d) indicate an influence of the sea surface boundary condition at shallow levels. The spatial decorrelation scale near the sea surface (∼ 200 km) is larger than it is in deeper layers (∼ 150 km), as a consequence of the direct influence of the atmosphere and sea ice, the spatial scale of which is larger than the scale of intrinsic ocean processes. The temporal decorrelation scale near the surface (100–150 days), on the other hand, is shorter than that of the deeper layers (200–300 days), possibly due to the effect of short-timescale variation of the atmospheric field and associated sea-ice motion. It is interesting to note that the scales of the mean field and of the variance are very similar (e.g., compare Figs. 6 and 12b). We currently have no explanation for this feature but assume that it is a peculiarity based on the dynamics of the analyzed basin. In forthcoming papers, we plan to analyze the scales in the Eurasian basin and over the Arctic shelf slope and will revisit this question.
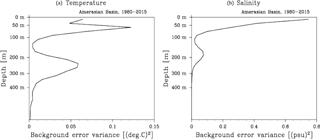
Figure 13Vertical profile of the background mean variance, varbg, for temperature (a) and salinity (b).
Note that the T and S profiles exhibit similar vertical profiles in the depth range shallower than 250 m, while discrepancies stand out in levels deeper than 250 m (Fig. 12b, d). This may be due to small calibration errors associated with our use of ITP level-2 (i.e., not the fully calibrated level-3) data (see Krishfield et al., 2008b; Johnson et al., 2007). In order to incorporate as many data as possible, we have included all available ITP level-2 data, where level-3 data are not yet available. This strategy is beneficial for scale estimation of temperature (ITP level-2 temperature data have the same accuracy as level-3 data, within ±0.001 ∘C) in the entire depth range and salinity shallower than 250 m depth. On the other hand, since salinity variability decreases with depth (Fig. 3b), the uncalibrated ITP level-2 salinity data may yield non-negligible spurious variation at levels deeper than 250 m, which may deteriorate the accuracy of the scale estimates for salinity in this depth range.
4.3 Error covariance
The autocorrelation function derived in Sect. 4.1 can be related to an error covariance by Eq. (9). Since the variance in Eq. (9) used to normalize the covariance does not depend on spatial and/or temporal separation in principle (see the assumption in Sect. 4.1), it can be represented by a variance calculated from all the data in the Amerasian Basin. Therefore, the error covariance associated with the representation error is given by a function of spatial and temporal separations, x and t:
where ρ(x, t) is the autocorrelation function, and varbg is the background mean variance defined by
The vertical profiles of varbg for T and S are shown in Fig. 13. The background mean variance clearly reflects the vertical stratification in the Amerasian Basin (e.g., McLaughlin et al., 2004; Shimada et al., 2005), with highest variance in the depth ranges of vertical extrema in the profile. The temperature profile exhibits two minima (in the mixed layer and around 130 m depth) and two maxima (approximately in 70 and 250 m; Fig. 3a). These shallow extrema are associated with the seasonally, spatially, and interannually varying near-surface temperature maximum (see, e.g., McPhee et al., 1998), and Pacific summer water layers (see, e.g., Timmermans et al., 2014). The deep minimum corresponds to the Pacific winter water layer plus variations in the deeper Atlantic water (see, e.g., Shimada et al., 2005; Fig. 2). The vertical profile of salinity variance also exhibits good correspondence with salinity stratification and its variation (Fig. 3b), with smallest variance (approximately 120 m depth) corresponding to weakest salinity stratification and largest (around 180 m) corresponding to the stratification boundary between the upper and lower halocline. The derived covariance is also necessary to complete the model– observation misfit calculation, as summarized in the following section.
We examined spatial and temporal scales of T and S anomalies from the mean fields in the Amerasian Basin. To provide scales describing the anomalies, we examined the autocorrelation of T and S measurements and calculated spatial and temporal decorrelation scales. Historical T and S measurements in the Arctic and northern North Atlantic oceans were compiled for this study and for future applications to Arctic Ocean data assimilations. The resulting quality-controlled archive was used to construct a background mean field, from which anomaly fields were derived. By assuming spatial and temporal homogeneity of the autocorrelation function in the basin interior, we calculated autocorrelations as a function of spatial and temporal lags. The examination revealed that the autocorrelation function can be well described by a Gaussian function in space and time. The spatial and temporal decorrelation scales were estimated to be 150–200 km in space and 100–300 days in time (e-folding scales of the autocorrelation function). The spatial decorrelation scale is relatively large near the sea surface, while the temporal scale is relatively small near the surface. Mesoscale fluctuations, with scales smaller than 10 km and shorter than 5 days, are represented by the zero-lag autocorrelation. The zero-lag autocorrelation should be re-examined in future work to describe the autocorrelation smaller than the Rossby radius by fully exploiting ITP data.
The estimated function and the scales, together with the associated error covariance, are directly applicable to model–observation misfit calculation in data assimilation systems, which intend to assimilate a spatially and temporally varying field. A cost function measuring the model–observation misfit is given by
where d is the data vector, m is the model vector, H is the observation operator, and R is the observation error covariance matrix. The current study gives the descriptive form of H and R. An observation operator, H, which takes spatial and temporal representativeness of each measurement into account, is given as follows:
where i refers to the ith in situ measurement, j refers to the modeled variable at the jth model grid point, ρ is the autocorrelation between (x, t)-distant locations, xij and tij are the spatial and temporal separations between the ith measurement and the jth model grid point. The operator Hi(m) maps the model field m to the ith measurement location (in space and time), in accordance with the influence of the measurement. We can describe the autocorrelation function ρ by the results shown in Sect. 4.1 and 4.2 in the following formula:
where A is the autocorrelation between zero-lag locations (x<10 km and t<5 days) representing the contributions from unresolved-scale fluctuations (Fig. 12a); ds and dt are the spatial and temporal decorrelation scales (Fig. 12b, d), respectively. This formula provides the representation error of a point measurement at (x, t)-distant locations. Note that the current formula enables us to quantify errors of modeled T and S not only at the location where the measurements exist but also at the locations distant from the measurements. The present study also provides error covariance matrix R associated with the representation error. The representation error covariance between the ith and the i′th measurements is
where , is the autocorrelation between ith and i′th measurements, the spatial and temporal separations between which are given by and , and varbg is the background error variance given as a function of depth (Fig. 13). As summarized here, the current study provides a full descriptive formula to exploit ocean in situ measurements in the Amerasian Basin for a model–observation misfit calculation.
The present scale estimates pose a requirement from a basin-scale data assimilation on a sampling strategy. Static interpolation approaches (e.g., optimal interpolation (Gandin, 1965; Reynolds and Smith, 1994), objective mapping (Wong et al., 2003; Böhme and Send, 2005; Böhme et al., 2008), and data-interpolating variational analyses (Troupin et al., 2010, 2012; Korablev, 2014) exploit statistical information of data to derive a mean analysis field. Data assimilation approaches, in addition, exploit modeled physics and provide temporally and spatially varying four-dimensional analysis fields. The former approaches need a scale representing the mean field, while the latter, in addition, needs spatial and temporal scales representing the anomaly field to fully exploit the information embedded in in situ data. For Arctic Ocean studies, statistical interpolation has been using decorrelation scales of 300–500 km (Steele et al., 2001; Proshutinsky et al., 2009; Rabe et al., 2011, 2014), while the present study suggests the necessity of a smaller measurement interval (150–200 km in space and 100–300 days in time) to describe the anomaly field by a basin-scale data assimilation.
Further studies are necessary to interpret the decorrelation scale of S and T in the context of ocean dynamics and relate it to the hydrographic features in the Amerasian Basin. The scale of ocean variability is governed by external forcings and by various physical processes in the ocean. The local dynamic response to local external forcing (i.e., vertical normal mode in response to basin-scale wind stress curl; Pedlosky, 1987; Olbers et al., 2012) is one very likely mechanism to explain the shape of the vertical profile of the scale. Near the sea surface, the decorrelation scales should be examined in relation to the scale of atmosphere and sea-ice variability (Walsh, 1978; Walsh and Chapman, 1990), and the dynamical processes governing the mixed layer (Peralta-Ferriz and Woodgate, 2015). The effect of remote forcing is another important issue to be examined. Advection of anomalous water masses introduces scales governed by mechanisms outside of the basin and/or shelf–basin interaction, such as the inflow of anomalous Pacific water into the deep basin (Steele et al., 2004; Itoh et al., 2012), its modification processes on the shelf (Pickart et al., 2005, Woodgate et al., 2005), the advection of anomalous Atlantic water (McLaughlin et al., 2009; Karcher et al., 2012), or variations of freshwater supply due to river runoff (Lammers et al., 2001). In this study, we employed level surfaces, as we focus on the applicability of the decorrelation scales for model validation and data assimilation (many models use the so called z-coordinate system). For future studies which aim at a dynamical interpretation of the decorrelation scales, an analysis in isopycnal coordinates would be a logical next step. Autocorrelation and decorrelation scale estimates for other parts of the Arctic Ocean (i.e., the Eurasian Basin and over the shelf slopes) will be presented in forthcoming papers.
The data in the Amerasian Basin were collected and made available by the following research programs: Arctic Switchyard project (http://www.ldeo.columbia.edu/Switchyard), Baufort Gyre Exploration Program based at the Woods Hole Oceanographic Institution (http://www.whoi.edu/beaufortgyre) in collaboration with researchers from Fisheries and Oceans Canada at the Institute of Ocean Sciences, the second and third Chinese National Arctic Research Expeditions (Shi, 2009a, b), Ice-Tethered Profiler Program (Toole at al., 2011; Krishfield et al., 2008) based at the Woods Hole Oceanographic Institution (http://www.whoi/edu/itp), JAMSTEC Compact Arctic Drifter (J-CAD) measurements by the North Pole Environmental Observatory Project led by University of Washington in collaboration with researchers from Japan Agency for Marine-Earth Science and Technology (JAMSTEC) (Kikuchi et al., 2004), the KPDC (http://kpdc.kopri.re.kr) data archived from the project titled “K-AOOS” (Korea Polar Research Institute, PM17040) funded by the Ministry of Oceans and Fisheries, South Korea, LOMROG 2007 Oden cruise (Bjork and Gothenburg University, 2012), Nansen and Amundsen Basins Observational System (NABOS/CAOBS) based at the University of Alaska Fairbanks (http://nabos.iarc.uaf.edu/index.php), North Pole Environmental Observatory (NPEO) (Morison et al., 2011), RV Mirai cruises operated by JAMSTEC (http://www.godac.jamstec.go.jp/darwin/), Submarine Arctic Science Program (SCICEX) (SCICEX Science Advisory Committee, 2009, updated 2014), the UNCLOS 2011 program by Fisheries and Oceans Canada at the Institute of Ocean Science in collaboration with JAMSTEC (Guéguen et al., 2015), and World Ocean Database 2013 (Boyer et al., 2013).
Since data analysis software based on geostatistical approaches (e.g., iSATiS, SURFER) is used in oceanographic studies in recent years, it is useful for providing a summary of the relation between the current approach and geostatistical approaches. The spatial scale of variation estimated in Sect. 3.1 is a different notation of the variogram concept used in geostatistics. In the present formula, we normalize the variance by the sill of the variogram, and a root-squared value is considered. This is because a variogram deals with a variance (i.e., spatial scale of the squared difference between two measurements), while we intend to quantify the spatial scale of difference between two measurements. We also defined the function by the value subtracted from 1, in order to obtain a function decaying to zero at infinity. This is done for mathematical convenience in order to obtain a Gaussian-like function. This is preferable for the framework of the best linear unbiased estimator (BLUE), which is constituting the basis of data assimilation theories. Since the spatial scale of variation originates from the same concept as variograms, it can be related to the terminology used in geostatistical approaches. The function f (i.e., normalized root mean square difference) at zero separation (Fig. 5) is
where Ng is a nugget of the semivariogram plot. The estimated scale (the spatial scale of variation) describes the square root of the scale described by a variogram, although it is not easy to find an exact correspondence, since empirical functions describing the two functions may differ. If we directly translate the function f into a semivariance used to plot a semivariogram, our formulation corresponds to an empirical semivariance with the following form:
where A is the function f value at zero separation, which is related to the nugget in Eq. (A1). Since we modeled the function f by a Gaussian formula, we cannot define the “range” in the corresponding semivariogram (the range goes to infinity in a Gaussian formula). After obtaining a background mean field by using the spatial scale of variation, we do not have to rely on geostatistical approaches any longer, since we can directly calculate the autocorrelation by variance and autocovariance (Eq. 9).
Woods Hole Oceanographic Institution provides ITP temperature and salinity data at different levels of processing; here, we use both level-3 (final processed data) and uncalibrated level-2 data when level-3 data are not available (see Krishfield et al., 2008b). Profile-by-profile conductivity calibration (not applied to the level-2 data) accounts for conductivity sensor drift. The calibration method applied to level-3 data is to adjust the potential conductivity of each profile to the value derived from bottle-calibrated CTD stations on the deep 0.4 ∘C potential temperature surface (Krishfield et al., 2008b).
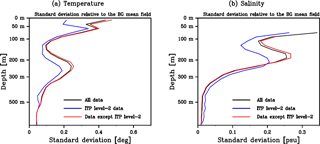
Figure B1Vertical profiles of standard deviation of (a) temperature and (b) salinity in the Amerasian Basin. The black, blue, and red lines indicate the standard deviation calculated from all data, ITP level-2 data, and data except ITP level-2 data, respectively. The standard deviation at each location is calculated by the deviation from the background mean field, and then an averaged standard deviation in the entire basin is calculated.
As a measure of the uncertainty of the uncalibrated ITP level-2 data, we calculate deviations of the ITP level-2 data from the background mean field (Sect. 3.2). We assume that the standard deviations of the background field derived from all data represent the natural variability of T and S in each depth level. If the standard deviation from ITP level-2 data is larger than the natural variability, we can conclude that the ITP level-2 data have an error (bias) expressed by the excess of the standard deviation. Figure B1 depicts vertical profiles of the standard deviations of T and S calculated from all data, from ITP level-2 data only, and from all data except ITP level-2 data. The T profiles exhibit smaller standard deviation of ITP level-2 data than the natural variability throughout the entire water column. On the other hand, the S profile shows that the standard deviation of ITP level-2 data is larger than the natural variability below 250 m depth, and it is almost double as large below 500 m depth. Since the spatial scale estimated in Sect. 3.1 and the decorrelation scale estimated in Sect. 4.2 would be deteriorated by erroneous sensor drifts, we limit our analyses from the sea surface to 400 m depth.
To understand the source of the second peaks found around the 200–300 km lag in the spatial autocorrelation functions, we examine their relation to the background mean fields. The second peaks in the autocorrelation functions are always found where the corresponding T and/or S fields exhibit the classic circular structure associated with the anticyclonic Beaufort Gyre. Figure C2 shows examples of the background mean fields and corresponding autocorrelation functions for various depth ranges. The upper two panels (Fig. C2a and c) exhibit a clear circular spatial pattern in the Canada Basin, while the lower two panels (Fig. C2e and g) do not. The corresponding spatial autocorrelation functions show clear second peaks around 240 km lag corresponding to the presence of the circular pattern (Fig. C2b and d), while they show no such peak where the circular pattern is not present (Fig. C2f and h).
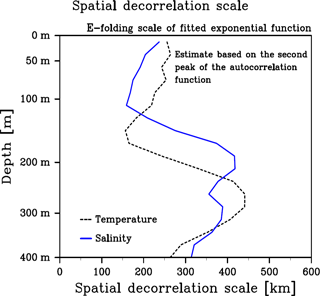
Figure C1Vertical profile of the spatial decorrelation scales estimated from the second peak of the spatial autocorrelation function (see Fig. 10a, b). The scale is obtained from a Gaussian function fitting with two points: zero-lag autocorrelation value from Fig. 12a and the second peak. The second peak is defined by the highest autocorrelation value, the spatial lag of which is larger than 150 km. A three-layer vertical filter is applied to eliminate noise.
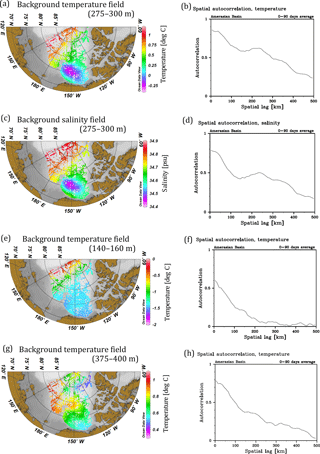
Figure C2(a, c, e, g) Examples of the background mean fields with a circular structure associated with the Beaufort Gyre (a, c) and without the circular structure (e, g). (b, d, f, h) Spatial autocorrelation functions corresponding to their right panels. Panels (a–b) and (e–h) show temperature, while (c–d) shows salinity.
The coincidence between the second peak and the circular structure of the Beaufort Gyre indicates that the peak captures a coherent variation of isothermal (isohaline) depth. We employ level depth surfaces for the present analysis; bowl-shaped isosurfaces of T and S in the Canada Basin exhibit a circular structure on level surfaces. Due to this structure, the same isothermal (isohaline) surface appears on a level surface as it encircles the center of the Beaufort Gyre (Fig. C2a, c). The second peak captures a relatively high autocorrelation between the measurements, both of which belong to nearly the same isothermal (isohaline) surface but are separated by a certain distance in accordance with the circular pattern. A consideration of mechanisms governing the decorrelation scale further supports this interpretation. The basin-scale dynamical response of the ocean to external forcing is manifested as vertical displacements of isopycnal surfaces (with given T and S properties), resulting in coherent variations of these depth surfaces. For follow-on studies to the present one, it is desirable to calculate autocorrelation functions and decorrelation scales in a way that takes such coherent large-scale dynamic features into account. This could be achieved by analyzing anomalies of the isohaline/isothermal depth from their mean state. In the case of the Beaufort Gyre, we expect the autocorrelation functions for the variation of the isohaline/isothermal depth to have larger spatial scales than those for T and S estimated on level surfaces. As an approximate measure of the decorrelation scales for isohaline/isothermal depth anomalies, we fit a Gaussian function using the value at the zero-lag correlation and the second peak obtained from the level surface analysis (Fig. C1), resulting in roughly 200–400 km. The largest scales we find in the 200–350 m depth range for the isothermal depths and in the 150–400 m depth range for the isohaline depths correspond to the depths of strong vertical gradients of T and S. For a sound analysis, a variation of isosurface should be quantified by a variation of isosurface depth. In such an analysis, for example, salinity is no longer a variable to be examined, but depth of constant salinity surface, i.e., , is the variable to be examined.
The supplement related to this article is available online at: https://doi.org/10.5194/os-14-161-2018-supplement.
The authors declare that they have no conflict of interest.
The authors sincerely appreciate three anonymous reviewers for their
thorough reviews and criticism on the first and second manuscripts, and two
anonymous reviewers for the constructive comments on the third manuscript.
Funding by the Helmholtz Climate Initiative REKLIM (Regional Climate Change),
a joint research project of the Helmholtz Association of German research
centers (HGF), is gratefully acknowledged. This work has partly been supported
by European Commission as part of FP7 project Ice, Climate, and Economics –
Arctic Research on Change (ICE-ARC, project no. 603887). We also would like to
express our gratitude towards the German Federal Ministry of Education and
Research (BMBF) for the support of the project “RACE II – Regional Atlantic
Circulation and Global Change” (03F0729E) and various observational efforts
listed in Table 1. The GFD-DENNOU library
(http://dennou.gaia.h.kyoto-u.ac.jp/arch/dcl/) and Ocean Data View
(Schlitzer, 2015) were used to draw the figures.
The article processing
charges for this open-access
publication were covered by a
Research
Centre of the Helmholtz Association.
Edited by: Neil Wells
Reviewed by: two anonymous referees
Anderson, L. G., Björk, G., Holby, O., Jones, E. P., Kattner, G., Koltermann, K. P., Liljeblad, B., Lindgren, R., Rudels, B., and Swift, J.: Water masses and circulation in the Eurasian Basin: Results from the Oden 91 expedition, J. Geophys. Res., 99, 3273–3283, 1994.
Behrendt, A., Sumata, H., Rabe, B., and Schauer, U.: UDASH – Unified Database for Arctic and Subarctic Hydrography, Earth Syst. Sci. Data Discuss., https://doi.org/10.5194/essd-2017-92, in review, 2017.
Bjork, G. and Gothenburg University: Temperature and salinity profile data from CTD casts from the icebreaker ODEN during the Lomonosov Ridge off Greenland (LOMROG) expedition in 2007 (NODC Accession 0093533), Version 1.1, National Oceanographic Data Center, NOAA, Dataset, 2012.
Blayo, É., Bocquet, M., Cosme, E., and Cugliandolo, L. F.: Advanced Data Assimilation for Geosciences, Oxford University Press, Oxford, UK, 584 pp., 2015.
Böhme, L. and Send, U.: Objective Analyses of hydrographic data for referencing profiling float salinities in high variable environments, Deep-Sea Res. Pt. II, 52, 651–664, https://doi.org/10.1016/j.dsr2.2004.12.014, 2005.
Böhme, L., Meredith, M. P., Thorpe, S. E., Biuw, M., and Fedak, M.: Antarctic Circumpolar Current frontal system in the South Atlantic: Monitoring using merged Argo and animal-borne sensor data, J. Geophys. Res., 113, C09012, https://doi.org/10.1029/2007JC004647, 2008.
Boyer, T. P., Antonov, J. I., Baranova, O. K., Coleman, C., Garcia, H. E., Grodsky, A., Johnson, D. R., Locarnini, R. A., Mishonov, A. V., O'Brien, T. D., Paver, C. R., Reagan, J. R., Seidov, D., Smolyar, I. V., and Zweng, M. M.: World Ocean Database 2013, NOAA Atlas NESDIS 72, edited by: Levitus, S. and Mishonov, A., Silver Spring, MD, 209 pp., https://doi.org/10.7289/V5NZ85MT, 2013.
Chu, P. C., Wells, S. K., Haeger, S. D., Szczechowski, C., and Carron, M.: Temporal and spatial scales of the Yellow Sea thermal variability, J. Geophys. Res., 102, 5655–5667, 1997.
Chu, P. C., Guihua, W., and Chen, Y.: Japan Sea Thermohaline Structure and Circulation, Part III: Autocorrelation functions, J. Phys. Oceanogr., 32, 3596–3615, 2002.
Carton, J. A., Chepurin, G., and Cao, X.: A Simple Ocean Data Assimilation Analysis of the Global Upper Ocean 1950–1995, J. Phys. Oceanogr., 30, 294–309, 2000.
Davis, R. E.: Preliminary results from directly measuring middepth circulation in the tropical and South Pacific, J. Geophys. Res., 103, 24619–24639, 1998.
Davis, R. E., Ohman, M. D., Rudnick, D. L., and Sherman, J. T.: Glider surveillance of physics and biology in the southern California Current System, Limnol. Oceanogr., 53, 2151–2168, 2008.
Delcroix, T., McPhaden, M. J., Dessier, A., and Gouriou, Y.: Time and space scales for sea surface salinity in the tropical oceans, Deep-Sea Res. Pt. II, 52, 787–813, https://doi.org/10.1016/j.dsr.2004.11.012, 2005.
Deser, C., Alexander, M. A., and Timlin, M. S.: Understanding the Persistence of Sea Surface Temperature Anomalies in Midlatitudes, J. Climate, 16, 57–72, 2003.
Eden, C.: Eddy length scales in the North Atlantic Ocean, J. Geophys. Res., 112, C06004, https://doi.org/10.1029/2006JC003901, 2007.
Forget, G. and Wunsch, C.: Estimated Grobal Hydrographic Variability, J. Phys. Oceanogr., 37, 1997–2008, https://doi.org/10.1175/JPO3072.1, 2007.
Gandin, L. S.: Objective Analysis of Meteorological Fields, Israel Program for Scientific Translations, Jerusalem, Israel, 242 pp., 1965.
Giles, K. A., Seymour, W., Laxon, A. L., Ridout, Wingham, D. J., and Bacon, S.: Western Arctic Ocean freshwater storage increased by wind-driven spin-up of the Beaufort Gyre, Nat. Geosci., 5, 194–197, https://doi.org/10.1038/NGEO1379, 2012.
Good, S. A., Martin, M. J., and Rayner, N. A.: EN4: Quality controlled ocean temperature and salinity profiles and monthly objective analyses with uncertainty estimates, J. Geophys. Res., 118, 6704–6716, https://doi.org/10.1002/2013JC009067, 2013.
Gronell, A. and Wijffels, S. E.: A semiautomated approach for quality controlling large historical ocean temperature archives, J. Atmos. Ocean. Tech., 25, 990–1003. https://doi.org/doi:10.1175/JTECHO539.1, 2008.
Guéguen, C., Itoh, M., Kikuchi, T., Eert, J., and Williams, W. J.: Variability in dissolved organic matter optical properties in surface waters in the Amerasian Basin, Front. Mar. Sci., 2, 78, https://doi.org/10.3389/fmars.2015.00078, 2015.
Haidvogel, D. B. and Beckmann, A.: Numerical Ocean Circulation Modeling, Imperial College Press, London, UK, 320 pp., 1999.
Hopkins, T. S.: The GIN Sea – A synthesis of its physical oceanography and literature review 1972–1985, Earth-Sci. Rev., 30, 175–318, 1991.
Hosoda, K. and Kawamura, H.: Global space-time statistics of sea surface temperature estimated from AMSR-E data, Geophys. Res. Lett., 31, L17202, https://doi.org/10.1029/2004GL020317, 2004.
Hurrell, J. W.: Decadal trends in the North Atlantic oscillation: Regional temperatures and precipitation, Science, 269, 676–679, 1995.
Ilıcak, M., Drange, H., Wang, Q., et al.: An assessment of the Arctic Ocean in a suite of international CORE-II simulations, Part III: Hydrography and fluxes, Ocean Modell., 100, 141–161, https://doi.org/10.1016/j.ocemod.2016.02.004, 2016.
Ingleby, B. and Huddleston, M.: Quality control of ocean temperature and salinity profiles – Historical and real-time data, J. Mar. Sys., 65, 158–175, https://doi.org/10.1016/j.jmarsys.2005.11.019, 2007.
Ito, S., Uehara, K., Miyao, T., Miyake, H., Yasuda, I., Watanabe, T., and Shimizu, Y.: Characteristics of SSH anomaly based on TOPEX/POSEIDON altimetry and in situ Measured velocity and transport of Oyashio on OICE, J. Oceanogr., 60, 425–437, 2004.
Itoh, M., Shimada, K., Kmoshida, T., McLaughlin, F., Carmack, E., and Nishino, S.: Interannual variability of Pacific Winter Water inflow through Barrow Canyon from 2000 to 2006, J. Oceanogr., 68, 575–592, https://doi.org/10.1007/s10872-012-0120-1, 2012.
Jackson, J. M., Carmack, E. C., McLaughlin, F. A., Allen, S. E., and Ingram, R. G.: Identification, characterization, and change of the near-surface temperature maximum in the Canada Basin, 1993–2008, J. Geophys. Res., 115, C05021, https://doi.org/10.1029/2009JC005265, 2010.
Jakobsson, M., Mayer, L., Coakley, B., et al.: The International Bathymetric Chart of the Arctic Ocean (IBCAO) version 3.0, Geophys. Res. Lett., 39, L12609, https://doi.org/10.1029/2012GL052219, 2012.
Johnson, G. C., Toole, J. M., and Larson, N. G.: Sensor Corrections for Sea-Bird SBE-41CP and SBE-41 CTDs, J. Atmos. Ocean. Tech., 24, 1117–1130, https://doi.org/10.1175/JTEC2016.1, 2007.
Jones, E. P.: Circulation in the Arctic Ocean, Polar Res., 20, 139–146, 2001.
Kantha, L. H. and Clayson, C. A.: Numerical Models of Ocean and Oceanic Processes, Academic Press, London, UK, 940 pp., 2000.
Karcher, M., Smith, J. N., Kauker, F., Gerdes, R., and Smethie J. W. M.: Recent changes in Arctic Ocean circulation revealed by iodine-129 observations and modeling, J. Geophys. Res., 117, C08007, https://doi.org/10.1029/2011JC007513, 2012.
Kendall, M. G.: A new measure of rank correlation, Biometrika, 30, 81–93, 1938.
Kikuchi, T., Uno, H., Hosono, M., and Hatakeyama, K.: Accurate Ocean Current Observation near the magnetic dip pole: compass error estimation, J. Jap. Soc. Mar. Sci. Tech., 16, 19–27, 2004 (in Japanese).
Kim, S. Y. and Kosro, P. M.: Observations of near-inertial surface currents off Oregon: Decorrelation time and length scales, J. Geophys. Res., 118, 3723–3736, https://doi.org/10.1002/jgrc.20235, 2013.
Kolmogorov, A. N.: The local structure of turbulence in incompressible viscous fluid for very large Reynolds numbers, Proc. R. Soc. Lond. A, 434, 9–13, 1991.
Korablev, A., Smirnov, A., and Baranova, O. K.: Climatological Atlas of the Nordic Seas and Northern North Atlantic, edited by: Seidov, D. and Parsons, A. R., NOAA Atlas NESDIS 77, https://doi.org/10.7289/V54B2Z78, 122 pp., 2014.
Krishfield, R., Toole, J., Proshutinsky, A., and Timmermans, M.-L.: Automated Ice-Tethered Profilers for Seawater Observations under Pack Ice in All Seasons, J. Atmos. Ocean. Tech., 25, 2091–2105, https://doi.org/10.1175/2008JTECHO587.1, 2008a.
Krishfield, R., Toole, J., and Timmermans, M.-L.: ITP Data Pro-cessing Procedures, Woods Hole Oceanographic Institution, Hoods Hole, MA, 24 pp., 2008b.
Kuragano, T. and Kamachi, M.: Global statistical space-time scales of oceanic variability estimated from the TOPEX/POSEIDON altimeter data, J. Geophys. Res., 105, 955–974, 2000.
Lammers, R. B., Shiklomanov, A. I., Vörösmarty, C. J., Fekete, B. M., and Peterson, B. J.: Assessment of contemporary Arctic river runoff based on observational discharge records, J. Geophys. Res., 106, 3321–3334, 2001.
Li, J.-G., Killworth, P. D., and Smeed, D. A.: Response of an eddy-permitting ocean model to the assimilation of sparse in situ data, J. Geophys. Res., 108, 3111, https://doi.org/10.1029/2001JC001033, 2003.
Marcinko, C. L. J., Martin, A. P., and Allen, J. T.: Characterizing horizontal variability and energy spectra in the Arctic Ocean halocline, J. Geophys. Res.-Oceans, 120, 436–450, https://doi.org/10.1002/2014JC010381, 2015.
Martins, M. S., Serra, N., and Stammer, D.: Spatial and temporal scales of sea surface salinity variability in the Atlantic Ocean, J. Geophys. Res.-Oceans, 120, 4306–4323, https://doi.org/10.1002/2014JC010649, 2015.
McLaughlin, F. A., Carmack, E. C., Macdonald, R. W., Melling, H., Swift, J. H., Wheeler, P. A., Sherr, B. F., and Sherr, E. B.: The joint roles of Pacific and Atlantic-origin waters in the Canada Basin, 1997–1998, Deep-Sea Res. Pt. I, 51, 107–128, https://doi.org/10.1016/j.dsr.2003.09.010, 2004.
McLaughlin, F. A., Carmack, E. C., Williams, W. J., Zimmermann, S., Shimada, K., and Itoh, M.: Joint effects of boundary currents and thermohaline intrusions on the warming of Atlantic water in the Canada Basin, 1993–2007, J. Geophys. Res., 114, C00A12, https://doi.org/10.1029/2008JC005001, 2009.
Mclean, L. M.: The Determination of Ocean Correlation Scales using Argo float data, University of Southampton, Faculty of Engineering, Science and Mathematics, School of Ocean and Earth Science, PhD Thesis, 210 pp., 2010.
McPhee, M. G., Stanton, T. P., Morison, J. H., and Martinson, D. G.: Freshening of the upper ocean in the Arctic: Is perennial sea ice disappearing?, Geophys. Res. Lett., 25, 1729–1732, 1998.
Meyers, G., Phillips, H., Smith, N., and Sprintall, J.: Space and time scales for optimal interpolation of temperature – Tropical Pacific Ocean, Prog. Oceanogr., 28, 189–218, 1991.
Molinari, R. L. and Festa, J. F.: Effect of subjective choices on the objective analysis of sea surface temperature data in the tropical Atlantic and Pacific Oceans, Oceanol. Ac., 23, 3–14, 2000.
Morison, J., Steele, M., and Falkner, K.: North Pole Environmental Observatory (NPEO) Aerial CTD Survey, Version 1.0. UCAR/NCAR – Earth Observing Laboratory, doi:10.5065/D6QJ7FFT, 2011
Nguyen, A. T., Menemenlis, D., and Kwok, R.: Arctic ice-ocean simulation with optimized model parameters: Approach and assessment, J. Geophys. Res., 116, C04025, https://doi.org/10.1029/2010JC006573, 2011.
Nurser, A. J. G. and Bacon, S.: The Rossby radius in the Arctic Ocean, Ocean Sci., 10, 967–975, https://doi.org/10.5194/os-10-967-2014, 2014.
Oke, P. R. and Sakov, P.: Representaion error of oceanic observations for data assimilation, J. Atmos. Ocean. Tech., 25, 1004–1017, https://doi.org/10.1175/2007JTECHO558.1, 2008.
Oke, P. R., Brassington, G. B., Griffin, D. A., and Schiller, A.: The Bluelink ocean data assimilation system (BODAS), Ocean Modell., 21, 46–70, https://doi.org/10.1016/j.ocemod.2007.11.002, 2008.
Olbers, D., Willebrand, J., and Eden, C.: Ocean Dynamics, Springer, Heidelberg, Germany, 704 pp., 2012.
Ortiz, J. D., Falkner, K. K., Matrai, A. R., and Woodgate, R. A.: The Changing Arctic Ocean: An Introduction to the Special Issue on the International Polar Year (2007–2008), Oceanography, 24, 14–16, https://doi.org/10.5670/oceanog.2011.49, 2011.
Panteleev, G., Ikeda, M., Grotov, A., Nechaev, D., and Yaremchuk, M.: Mass, Heat and Salt Blances in the Eastern Barents Sea obtained by Inversion of Hydrographic Section Data, J. Oceanogr., 60, 613–623, 2004.
Panteleev, G., Proshutinsky, A., Kulakov, M., Nechaev, D. A., and Maslowski, W.: Investigation of the summer Kara Sea circulation employing a variational data assimilation technique, J. Geophys. Res., 112, C04S15, https://doi.org/10.1029/2006JC003728, 2007.
Pedlosky, J.: Geophysical Fluid Dynamics, 2nd edn., Springer, New York, 710 pp., 1987.
Perlta-Ferriz, C. and Woodgate, R. A.: Seasonal and interannual variability of pan-Arctic mixed layer properties from 1979 to 2012 from hydrographic data, and the dominance of stratification for multilyear mixed layer depth shoaling, Prog. Oceanogr., 134, 19–53, https://doi.org/10.1016/j.pocean.2014.12.005, 2015.
Pickart, R. S., Weingartner, T. J., Pratt, L. J., Zimmermann, S., and Torres, D. J.: Flow of winter-transformed Pacific water into the Western Arctic, Deep-Sea Res. Pt. II, 52, 3175–3198, https://doi.org/10.1016/j.dsr2.2005.10.009, 2005.
Proshutinsky, A., Krishfield, R., Timmermans, M.-L., Toole, J., Carmack, E., McLaughlin, F., Williams, W. J., Zimmermann, S., Itoh, M., and Shimada, K.: Beaufort Gyre freshwater reservoir: State and variability from observations, J. Geophys. Res., 114, C00A10, https://doi.org/10.1029/2008JC005104, 2009.
Rabe, B., Karcher, M., Schauer, U., Toole, J. M., Krischfield, R. A., Pisarev, S., Kauker, F., Gerdes, R., and Kikuchi, T.: An assessment of Arctic Ocean freshwater content changes from the 1990s to the 2006–2008 period, Deep-Sea Res. Pt. I, 58185, https://doi.org/10.1016/j.dsr.2010.12.002, 2011.
Rabe, B., Karcher, M., Kauker, F., Schauer, U., Toole, J. M., Krishfield, R. A., Pisarev, S., Kikuchi, T., and Su, J.: Arctic Ocean basin liquid freshwater storage trend 1992–2012, Geophys. Res. Lett., 41, 961–968, https://doi.org/10.1002/2013GL058121, 2014.
Reeve, K. A., Boebel, O., Kanzow, T., Strass, V., Rohardt, G., and Fahrbach, E.: A gridded data set of upper-ocean hydrographic properties in the Weddell Gyre obtained by objective mapping of Argo float measurements, Earth Syst. Sci. Data, 8, 15–40, https://doi.org/10.5194/essd-8-15-2016, 2016.
Reynolds, R. W. and Smith, T. M.: Improved Global Sea Surface Temperature Analyses using Optimum Interpolation, J. Climate, 7, 929–948, 1994.
Rudels, B., Schauer, U., Björk, G., Korhonen, M., Pisarev, S., Rabe, B., and Wisotzki, A.: Observations of water masses and circulation with focus on the Eurasian Basin of the Arctic Ocean from the 1990s to the late 2000s, Ocean Sci., 9, 147–169, https://doi.org/10.5194/os-9-147-2013, 2013.
Sakov, P., Counillon, F., Bertino, L., Lisæter, K. A., Oke, P. R., and Korablev, A.: TOPAZ4: an ocean-sea ice data assimilation system for the North Atlantic and Arctic, Ocean Sci., 8, 633–656, https://doi.org/10.5194/os-8-633-2012, 2012.
Saunders, P. M. Practical conversion of pressure to depth, J. Phys. Oceanogr., 11, 573–574, 1981.
Schlitzer, R.: Ocean Data View, Ver. 4.7.10. available at: http://odv.awi.de, 2015.
SCICEX Science Advisory Committee: SCICEX: Science Ice Exercise Data Collection, Boulder, Colorado USA: National Snow and Ice Data Center, https://doi.org/10.7265/N5930R3Z, 2009 (updated 2014).
Shi, J.: CTD data of the 2nd Chinese National Arctic Research Expedition in 2003, Data-sharing Platform of Polar Science, Chinese Antarctic and Arctic Data Centre, China, 2009a.
Shi, J.: CTD data of the 3rd Chinese National Arctic Research Expedition in 2008, Data-sharing Platform of Polar Science, Chinese Antarctic and Arctic Data Center, China, 2009b.
Shimada, K., Itoh, M., Nishino, S., McLaughlin, F., Carmack, E., and Proshutinsky, A.: Halocline structure in the Canada Basin of the Arctic Ocean, Geophys. Res. Lett., 32, L03605, https://doi.org/10.1029/2004GL021358, 2005.
Smith, G. C. and Haines, K.: Evaluation of the S(T) assimilation method with the Argo dataset, Q. J. Roy. Meteor. Soc., 135, 739–756, 2009.
Somavilla, R., Schauer, U., and Budéus, G.: Increasing amount of Arctic Ocean deep waters in the Greenland Sea, Geophys. Res. Lett., 40, 4361–4366, https://doi.org/10.1002/grl.50775, 2013.
Sprintall, J. and Meyers, G.: An Optimal XBT Sampling Network for the Eastern Pacific Ocean, J. Geophys. Res., 96, 10539–10552, 1991.
Stammer, D.: Global Characteristics of Ocean Variability Estimated from Regional TOPEX/POSEIDON Altimeter Measurements, J. Phys. Oceanogr., 27, 1743–1769, 1997.
Steele, M., Morley, R., and Ermold, W.: PHC: A global Ocean Hydrography with a High-Quality Arctic Ocean, J. Climate, 14, 2079–2087, 2001.
Steele, M., Morison, J., Ermold, W., Rigor, I., Ortmeyer, M., and Shimada, K.: Circulation of summer Pacific halocline water in the Arctic Ocean, J. Geophys. Res., 109, C02027, https://doi.org/10.1029/2003JC002009, 2004.
Thompson, D. W. J. and Wallace, J. M.: The Arctic Oscillation signature in the wintertime geopotential height and temperature fields, Geophys. Res., Rett., 25, 1297–1300, 1998.
Timmermans, M.-L. and Winsor, P.: Scales of horizontal density structure in the Chukchi Sea surface layer, Cont. Shelf Res., 52, 39–45, https://doi.org/10.1016/j.csr.2012.10.015, 2013.
Timmermans, M.-L., Proshutinsky, A., Golubeva, E., Jackson, J. M., Krishfield, R., McCall, M., Platov, G., Toole, J., Williams, W., Kikuchi, T., and Nishino, S.: Mechanisms of Pacific Summer Water variability in the Arctic's Central Canada Basin, J. Geophys. Res.-Oceans, 119, 7523–7548, https://doi.org/10.1002/2014JC010273, 2014.
Todd, R. E., Gawarkiewicz, G. G., and Owens, W. B.: Horizontal Scales of Variability over the Middle Atlantic Bight Shelf Break and Continental Rise from Finescale Observations, J. Phys. Oceanogr., 43, 222–230, https://doi.org/10.1175/JPO-D-12-099.1, 2013.
Toole, J. M., Krishfield, R. A., Timmermans, M.-L., and Proshutinsky, A.: The Ice-Tethered Profiler: Argo of the Arctic, Oceanography, 24, 126–135, https://doi.org/10.5670/oceanog.2011.64, 2011.
Troupin, C., Machin, F., Ouberdous, M., Sirjacobs, D., Barth, A., and Beckers, J.-M.: High-resolution climatology of the northeast Atlantic using Data-Interpolating Variational Analysis (Diva), J. Geophys. Res., 115, C08005, https://doi.org/10.1029/2009JC005512, 2010.
Troupin, C., Barth, A., Sirjacobs, D., Ouberdous, M., Mrankart, J.-M., Brasseur, P., Rixen, M., Alvera-Azcárate, A., Belounis, M., Capet, A., Lenartz, F., Toussaint, M.-E., and Beckers, J.-M.: Generation of analysis and consistent error fields using the Data Interpolating Variational Analysis (DIVA), Ocean Modell., 52–53, https://doi.org/10.1016/j.ocemod.2012.05.002, 2012.
Tzortzi, E., Srokosz, M., Gommenginger, C., and Josey, S. A.: Spatial and temporal scales of variability in Tropical Atlantic sea surface salinity from the SMOS and Aquarius satellite missions, Remote Sens. Environ., 180, 418–430, 2016.
van Leeuwen, P. J.: Representation errors and retrievals in linear and nonlinear data assimilation, Q. J. Roy. Meteor. Soc., 141, 1612–1623, doi: 10.1002/qj2464, 2015.
Wallace, J. M.: North Atlantic Oscillation/annular mode: Two paradigms-one phenomenon, Q. J. Roy. Meteor. Soc., 126, 791–805, 2000.
Walsh, J. E. Temporal and Spatial Scales of the Arctic Circulation, Mon. Wea. Rev., 106, 1532–1544, 1976.
Walsh, J. E. and Chapman, W. L.: Short-Term Climate Variability of the Arctic, J. Climate, 3, 237–250, 1990.
White, W. B. and Meyers, G.: Space/Time Statistics of Short-Term Climate Variability in the Western North Pacific, J. Geophys. Res., 87, 1979–1989, 1982.
White, W. B.: Design of a global observing system for gyre-scale upper ocean temperature variability, Prog. Oceanogr., 36, 169–217, 1995.
Wong, A. P. S., Johnson, G. C., and Owens, W. B.: Delayed-Mode Calibration of Autonomous CTD Profiling Float Salinity Data by θ−S Climatology, J. Atmos. Ocean. Tech., 20, 308–318, 2003.
Woodgate, R. A., Aagaard, K., Swift, J. H., Falkner, K. K., and Smethie Jr., W. M.: Pacific ventilation of the Arctic Ocean's lower halocline by upwelling and diapycnal mixing over the continental margin, Geophys. Res. Lett., 32, L18609, https://doi.org/10.1029/2005GL023999, 2005.
Wunsch, C.: Discrete Inverse and State Estimation Problems, Cambridge University Press, Cambridge, UK, 371 pp., 2006.
Yoshizawa, E., Shimada, K., Ha, H. K., Kim, T. W., Kang, S. H., and Chung, K. H.: Delayed responses of the oceanic Beaufort Gyre to wind and sea ice motions: incluences on variations of sea ice cover in the Pacific sector of the Arctic Ocean, J. Oceanogr., 71, 187–197, https://doi.org/10.1007/s10872-015-0276-6, 2015.
Zhao, M., Timmermans, M.-L., Cole, S., Krishfield, R., Proshutinsky, A., and Toole, J.: Characterizing the eddy field in the Arctic Ocean halocline, J. Geophys. Res.-Oceans, 119, 8800–8817, https://doi.org/10.1002/2014JC010488, 2014.
Zhong, W. and Zhao, J.: Deepening of the Atlantic Water Core in the Canada Basin in 2013–11, J. Phys. Oceanogr., 44, 2353–2369, https://doi.org/10.1175/JPO-D-13-084.1, 2014.
Zuo, H., Mugford, R. I., Haines, K., and Smith, G. C.: Assimilation impacts on Arctic Ocean circulation, heat and freshwater budgets, Ocean Modell., 40, 147–163, https://doi.org/10.1016/j.ocemod.2011.08.008, 2011.
- Abstract
- Introduction
- Data
- Construction of the background mean field
- Decorrelation scale
- Conclusions
- Data availability
- Appendix A: Correspondence to the geostatistical approach
- Appendix B: Error estimates of ITP level-2 data
- Appendix C: Examination of the second peak in spatial autocorrelation functions
- Competing interests
- Acknowledgements
- References
- Supplement
- Abstract
- Introduction
- Data
- Construction of the background mean field
- Decorrelation scale
- Conclusions
- Data availability
- Appendix A: Correspondence to the geostatistical approach
- Appendix B: Error estimates of ITP level-2 data
- Appendix C: Examination of the second peak in spatial autocorrelation functions
- Competing interests
- Acknowledgements
- References
- Supplement





