Effect of nonlinear tide–surge interaction in the Pearl River Estuary during Typhoon Nida (2016)

Storm surge is one of the most significant marine dynamic disasters affecting coastal areas worldwide. A comprehensive study of its mechanisms is vital for improving forecasting capabilities and developing more prevention strategies. In this study, a two-dimensional (2D) numerical model based on the Advanced Circulation Model (ADCIRC) was employed to examine the characteristics of storm surges and the mechanisms of tide–surge interaction in the Pearl River Estuary (PRE) during Typhoon Nida (2016). Three distinct model runs were conducted to differentiate between variations in water levels attributable to astronomical tides, storm surges, and their combined effect. The results indicated that storm tides are primarily modulated by tides through tide–surge interactions. The nonlinear effect of tide–surge interactions is primarily generated by the nonlinear local acceleration term and convection term from the tide–surge interactions in the study area, as derived from mathematical terms. However, in regions of shallow water, such as the northern part of the island of Qi'ao and Shenzhen Bay, they are predominantly governed by the nonlinear wind stress term and the bottom friction term. Furthermore, the variations in the y components of the nonlinear momentum terms are more significant than those in the x components. To investigate the impact of the tidal phase on the storm surge response to Typhoon Nida, the timing of the landfall was altered in order to introduce variations in PRE characteristics. The results demonstrate that the contribution ratio of each nonlinear term remains relatively constant, while the magnitudes exhibit fluctuations contingent on the timing of the landfall. However, further studies on additional typhoon events, especially with onshore winds, are needed, together with a comprehensive consideration of the meteorological processes and mechanisms of tidal-wave propagation inside and outside the estuary. The model system could still be improved in the future.

1 Introduction

Storm surge is defined as an abnormal rise in sea level caused by atmospheric pressure and wind stress from phenomena such as tropical cyclones (TCs) and fronts. TCs, also known as typhoons or hurricanes, have the potential to induce storm surges with extreme water levels, which can result in significant economic losses and human casualties in coastal areas, particularly when they coincide with high astronomical tides (Flather, 1994). The conventional method for forecasting storm surges during TCs involves predicting the water level under a specified wind field and then linearly adding that water level to the predicted astronomical tides (Heaps, 1983). However, numerous studies have demonstrated that the effect of tide–surge interaction is nonlinear (Johns et al., 1985; Bernier and Thompson, 2007; Quinn et al., 2012). A comparison of observations with straightforward linear superposition of astronomical tides and individually calculated storm surges indicates discrepancies of up to 1–2 m (Rego and Li, 2010). During periods of extreme water levels, nonlinear interactions occur within the estuarine area between tides, storm surges, waves, and river streamflow (Hu et al., 2023). For instance, on beaches and barrier islands, the contribution of wave runup to total water levels is significant and cannot be overlooked (Vicens-Miquel et al., 2025).

The total water level can be divided into three main components: the astronomical tide, the storm surge caused by atmospheric forcing, and the nonlinear residual level caused by tide–surge interaction, which represents a significant source of error in the prediction of storm surges (Idier et al., 2012; Xu et al., 2016; Yang et al., 2019). Observations and simulations have indicated that storm surges are influenced by astronomical tides, and the nonlinear effect of the tide–surge interaction can significantly modulate water levels in shallow regions. There are two main characteristics of storm surges due to the nonlinear effect of tide–surge interaction. One characteristic is that the peak storm surge height near high tide is typically lower than that near low tide, which could increase storm surge levels during the rising tide and decrease them at high tide (Rossiter, 1961; Wolf, 1978; Horsburgh and Wilson, 2007; Olbert et al., 2013). Another characteristic is the variation in storm surge intensity, where the storm surge is notably stronger at low tide compared to high tide (Horsburgh and Wilson, 2007; Feng et al., 2016; Song et al., 2020). The tide–surge interaction comprises three nonlinear physical processes: (a) the nonlinear advective effect from the advective terms in the momentum equations, (b) the nonlinear bottom friction effect with quadratic parameterization, and (c) the shallow water effect arising from the nonlinear terms related to the total water depth in both the mass conservation equation and the momentum equations (Zhang et al., 2010; Song et al., 2020; Zheng et al., 2020). Zhang et al. (2010) found that bottom friction was the principal contributor to tide–surge interaction in the Taiwan Strait. Rego and Li (2010) studied the storm surge induced by Hurricane Rita and revealed that the advection terms were dominant over bottom friction terms, with significant spatial–temporal variations in the nonlinear terms. In strong current regions, the nonlinear advection term may also play a key role in the dynamics of nonlinear tide–surge interactions (Wolf, 1978; Rego and Li, 2010; Yang et al., 2019; Hu et al., 2023). Valle-Levinson et al. (2013) found that Coriolis accelerations and local accelerations due to alongshore currents may significantly influence the tidal modulation of storm surges.

The characteristics of storm surges and nonlinear effects in the Pearl River Estuary (PRE) are especially complex, as its topography consists of deep channels, shallow shoals, and tidal flats. This renders the PRE highly susceptible to storm surges induced by intense TCs (Zheng et al., 2020). As a semi-enclosed bay, as shown in Fig. 1c, Lingding Bay is regularly affected by both storm surges and irregular semi-diurnal tides. The trumpet-shaped bay naturally funnels tidal energy, leading to an amplification of the tidal amplitude at the top of the bay. However, specific investigations concerning the variability of typhoon landfall timing in tide–surge interactions and their impact on the temporal and spatial distributions of storm surges within the PRE are still scarce. Due to the strong tidal dynamics and complex topography of the region, tide–surge interactions along the PRE are significant, and the mechanisms are complex, which motivate this work. Therefore, efficient and accurate marine forecasting, achieved through the analysis of mechanisms and precise modeling of storm surges induced by typhoons, is essential for mitigating typhoon-induced disasters in coastal regions.

The maximum storm surge induced by Typhoon Nida, which coincided with the astronomical high tide, resulted in severe economic losses estimated at RMB 112 million. The principal objective of this study is to investigate the nonlinear residual levels associated with the tide–surge interactions caused by Typhoon Nida. Additionally, the objective is to investigate the dynamic mechanisms by establishing mathematical relationships between these nonlinear levels and the nonlinear dynamic terms. In this paper, a storm surge model for the PRE based on ADCIRC is utilized to investigate the mechanism of tide–surge interaction. In order to better characterize these impacts, different contributions to storm surge events can be calculated separately using the nonlinear terms of the two-dimensional theoretical momentum equations (Yang et al., 2019; Song et al., 2020; Hu et al., 2023).

In this paper, we will outline the characteristics of Typhoon Nida and provide a detailed description of the coupled tide–surge model, which is introduced and validated in Sect. 2. This is followed by an examination of the distribution of storm surge levels and nonlinear levels, along with a discussion of the results in Sect. 3. The conclusions derived from this study are detailed in Sect. 4.

2 Materials and methods

In this study, a coupled tide–surge model was built for Typhoon Nida. The typhoon and the associated numerical model are introduced, and the model setup and validations are also described.

2.1 Typhoon Nida

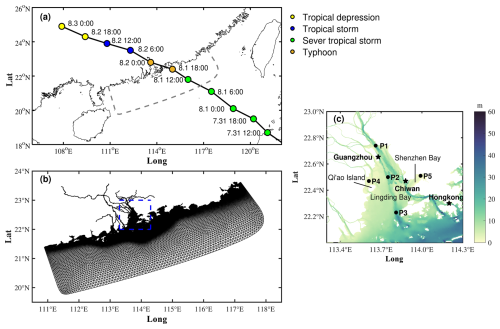
Typhoon Nida was generated in the western North Pacific Ocean on 29 July 2016 and subsequently began to move rapidly westward. As shown in Fig. 1a, Typhoon Nida was classified as a severe tropical storm (STS), passed across the Philippines, and entered the South China Sea (SCS) on 31 July 2016. It continued westward and made landfall as a typhoon (TY) at 19:30 on 1 August in Shenzhen, Guangdong Province, China. Nida had a central pressure of 970 hPa and a maximum wind speed exceeding 42 m s⁻¹. After that, it weakened into a tropical storm (TS). At 00:00 UTC on 3 August, it weakened further into a tropical depression (TD) before dissipating. Notably, the peak water level increase induced by the storm surge of Typhoon Nida coincided with the highest high water (HHW) tidal phase.

Figure 1 (a) The track and intensity of Typhoon Nida. (b) Model domain and grids of the study area. (c) Location and bathymetry of the PRE. The stars represent the tidal gauges, and the dots denote the calculation points of the surge levels.

2.2 The numerical model

The Advanced Circulation Model (ADCIRC) was used to simulate the tide and storm surge in the PRE (Luettich et al., 1992). ADCIRC solves the primitive equations with the finite-element method in space and with the finite-difference method in time (Westerink et al., 1992). Unstructured triangular grids were used in the horizontal plane to resolve dynamics in complex shorelines.

The basic vertically averaged governing equations derived from momentum and continuity are as follows:

$$\begin{array}{}\text{(1)}& \begin{array}{rl}& {\displaystyle \frac{\partial H}{\partial t}}+{\displaystyle \frac{\partial }{\partial x}}\left(UH\right)+{\displaystyle \frac{\partial }{\partial y}}\left(VH\right)=\mathrm{0}\\ & {\displaystyle \frac{\partial U}{\partial t}}+U{\displaystyle \frac{\partial }{\partial x}}U+V{\displaystyle \frac{\partial }{\partial y}}U-fV=\\ & -g{\displaystyle \frac{\partial \left(\mathit{\zeta }+P_{\mathrm{s}}/g{\mathit{\rho }}_{\mathrm{0}}\right)}{\partial x}}+{\displaystyle \frac{{\mathit{\tau }}_{\mathrm{s}x}-{\mathit{\tau }}_{\mathrm{b}x}}{H{\mathit{\rho }}_{\mathrm{0}}}}-{\displaystyle \frac{D_x}{H}}\\ & {\displaystyle \frac{\partial V}{\partial t}}+U{\displaystyle \frac{\partial }{\partial x}}V+V{\displaystyle \frac{\partial }{\partial y}}V+fU=\\ & -g{\displaystyle \frac{\partial \left(\mathit{\zeta }+P_{\mathrm{s}}/g{\mathit{\rho }}_{\mathrm{0}}\right)}{\partial y}}+{\displaystyle \frac{{\mathit{\tau }}_{\mathrm{s}y}-{\mathit{\tau }}_{\mathrm{b}y}}{H{\mathit{\rho }}_{\mathrm{0}}}}-{\displaystyle \frac{D_y}{H}},\end{array}\end{array}$$

where (U,V) are the x and y depth-averaged velocity components, $H=h+\mathit{\zeta }$ is the total water level, ζ is the free surface elevation, h is the water depth, f is the Coriolis force parameter, g is the gravitational acceleration, P_s is the sea surface atmospheric pressure, ρ₀ is the seawater density, (τ_sx,τ_sy) are the x and y components of the surface wind stress, (τ_bx,τ_by) are the x and y components of bottom friction, and (D_x,D_y) are the horizontal momentum diffusion terms.

The surface wind stress parameters (τ_sx,τ_sy) are computed as follows:

$$\begin{array}{}\text{(2)}& {\mathit{\tau }}_{\mathrm{s}x}={\mathit{\rho }}_{\mathrm{a}}{C}_{\mathrm{d}}{W}_x\sqrt{W_x^{\mathrm{2}}+W_y^{\mathrm{2}}},{\mathit{\tau }}_{\mathrm{s}y}={\mathit{\rho }}_{\mathrm{a}}{C}_{\mathrm{d}}{W}_y\sqrt{W_x^{\mathrm{2}}+W_y^{\mathrm{2}}},\end{array}$$

where ρ_a is the air density and (W_x,W_y) are the x and y components of the wind speed. C_d is the wind drag coefficient of Garratt (1977). It is calculated as follows:

$$\begin{array}{}\text{(3)}& C_{\mathrm{d}}=\mathrm{0.001}\times \left(\mathrm{0.75}+\mathrm{0.067}\sqrt{W_x^{\mathrm{2}}+W_y^{\mathrm{2}}}\right).\end{array}$$

The bottom friction (τ_bx,τ_by) is computed using the quadratic equation below:

$$\begin{array}{}\text{(4)}& {\mathit{\tau }}_{\mathrm{b}x}={\mathit{\rho }}_{\mathrm{0}}{C}_{\mathrm{f}}U\sqrt{U^{\mathrm{2}}+V^{\mathrm{2}}},{\mathit{\tau }}_{\mathrm{b}y}={\mathit{\rho }}_{\mathrm{0}}{C}_{\mathrm{f}}V\sqrt{U^{\mathrm{2}}+V^{\mathrm{2}}}.\end{array}$$

The bottom friction drag coefficient C_f is determined by model calibration.

The wind field model is crucial for accurate storm surge calculations. The analytical wind model developed by Holland (1980) was applied in the reconstruction of the wind field during Typhoon Nida. The radial distributions of the pressure and wind are determined as follows:

$$\begin{array}{}\text{(5)}& {\displaystyle }{P}_{\mathrm{s}}\left(r\right)=P_{\mathrm{c}}+\left(P_n-P_{\mathrm{c}}\right)\cdot {\left(-{\displaystyle \frac{R_{max}}{r}}\right)}^{\mathrm{B}},\text{(6)}& {\displaystyle }\begin{array}{rl}& W_g\left(r\right)=\\ & \sqrt{\left(P_n-P_{\mathrm{c}}\right){\displaystyle \frac{B}{{\mathit{\rho }}_{\mathrm{a}}}}{\left({\displaystyle \frac{R_{max}}{r}}\right)}^{\mathrm{B}}\exp {\left(-{\displaystyle \frac{R_{max}}{r}}\right)}^{\mathrm{B}}+{\left({\displaystyle \frac{rf}{\mathrm{2}}}\right)}^{\mathrm{2}}}-{\displaystyle \frac{rf}{\mathrm{2}}}\end{array}\end{array}$$

where r is the distance from the typhoon center, P_n is the ambient pressure (1010 hPa), P_c is the central pressure, R_max is the maximum wind radius, and W_g is the wind speed. The B parameter determines the peak and intensity of the typhoon wind field and is calculated as follows:

$$\begin{array}{}\text{(7)}& B=\mathrm{1.5}+\left(\mathrm{980}-P_{\mathrm{c}}\right)/\mathrm{120}.\end{array}$$

As B increases, the strong wind becomes increasingly localized near the radius of the maximum winds. For larger B, the wind drops off more abruptly both inside and outside the radius of the maximum wind. R_max is calculated as follows:

$$\begin{array}{}\text{(8)}& R_{max}=\mathrm{51.6}\exp \left(-\mathrm{0.0223}{V}_{max}+\mathrm{0.0281}\mathit{\varphi }\right).\end{array}$$

V_max is the maximum wind and φ is the latitude. The inflow angle caused by the friction contributes to the wind field asymmetry, and a constant angle of 25 ° is used in this paper. The central pressure and position data were retrieved from the China Meteorological Administration (CMA) tropical cyclone database (Lu et al., 2021).

2.3 Model setting

The grid resolutions were set at a maximum of 600 m at the open boundaries, while the finest resolution within the PRE region was 100 m. The domain space was discretized into 325 582 triangular cells with 182 048 nodes as shown in Fig. 1b. The model utilized mean sea level as its reference datum and was forced at the open boundaries by eight tidal constituents (M₂, S₂, N₂, K₂, K₁, O₁, P₁, and Q₁) derived from the global tidal model TPXO 9 (Egbert and Erofeeva, 2002). The typhoon wind field was generated using the wind model of Holland (1980). We used a two-dimensional (2D) hydrodynamic model based on ADCIRC for the simulation runs. The vertical current shear in a well-mixed environment at shallow water depth is relatively small. Therefore, the 2D depth-averaged model is sufficient for revealing the physical processes of tide–surge interaction (Idier et al., 2012; Zhang et al., 2017; Song et al., 2020). The model was run with a cold start, setting both the current and water levels to zero at the initial time. The effects of river flow and wind-generated waves were not considered in our model simulation, as the research is primarily focused on tide–surge interactions.

To verify the influence of the tide on storm surges, three simulations were conducted. One was used to obtain the storm surge elevation (ζ_S) by only adding atmospheric forcing, another was used to obtain the tide elevation (ζ_T) by only adding astronomical tidal forcing, and another was used to calculate the storm tide elevation (ζ_TS) using both atmospheric and tidal forcings. The storm tide elevation (ζ_TS) can be written as the sum of the tide elevation (ζ_T), storm surge elevation (ζ_S), and nonlinear residuals (ζ_Non) due to tide–surge interaction, such that ${\mathit{\zeta }}_{\mathrm{TS}}={\mathit{\zeta }}_{\mathrm{T}}+{\mathit{\zeta }}_{\mathrm{S}}+{\mathit{\zeta }}_{\mathrm{Non}}$. Additionally, the practical storm surge elevation ${\mathit{\zeta }}_{\mathrm{PS}}={\mathit{\zeta }}_{\mathrm{TS}}-{\mathit{\zeta }}_{\mathrm{T}}$ was considered in this paper.

3 Results

3.1 Tide and storm tide validation

The correlation coefficient (R), root mean square error (RMSE), and model skill (Skill) were used to validate the computed water level. The definition of the Skill is determined as follows:

$$\begin{array}{}\text{(9)}& \mathrm{Skill}=\mathrm{1}-{\displaystyle \frac{\sum _{n=\mathrm{1}}^N{\left|M_n-C_n\right|}^{\mathrm{2}}}{\sum _{n=\mathrm{1}}^N\left({\left|M_n-\stackrel{\mathrm{‾}}{M_n}\right|}^{\mathrm{2}}+{\left|C_n-\stackrel{\mathrm{‾}}{M_n}\right|}^{\mathrm{2}}\right)}},\end{array}$$

where M_n and C_n are the measurements and model-computed results, respectively, at a discrete point N.

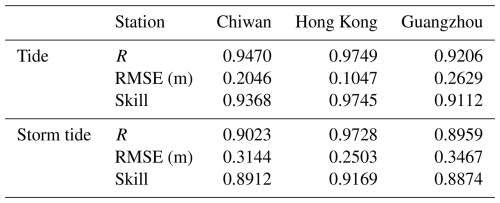
The computed astronomical tides were initially assessed at three hydrological stations, Chiwan, Hong Kong, and Guangzhou, over the period from 2 to 30 July 2016, as shown in Fig. 2. The simulation results demonstrated a close match with the measurements obtained at these three hydrological stations, as detailed in Table 1. The model predictions exhibited excellent agreement with the reconstructed astronomical tide, with RMSE values at all three stations being < 0.27 m. Additionally, both the R values and Skill values are generally above 0.91.

Table 1 Comparisons of the tide and storm tides between the model simulations and observations.

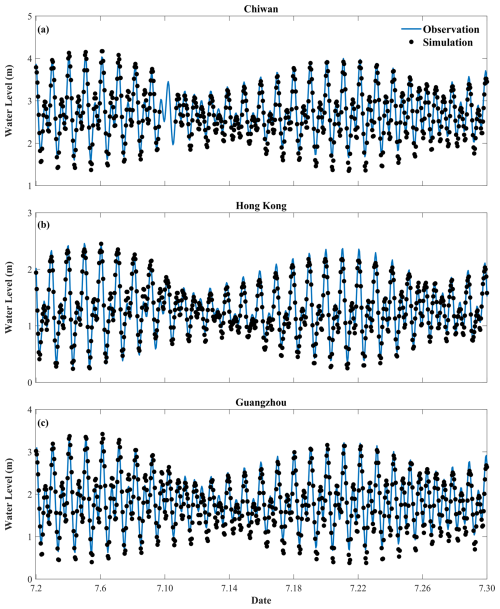
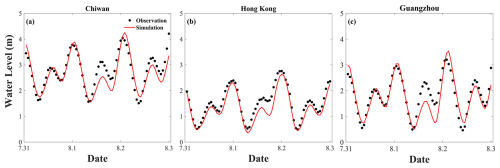
Figure 2 Time series comparisons of measured and modeled astronomical tide levels at the (a) Chiwan gauge, (b) Hong Kong gauge, and (c) Guangzhou gauge.

The model-simulated storm tide levels were further compared with the observed total water levels at the aforementioned three stations, as depicted in Fig. 3. At all three stations mentioned above, the recorded water level reached its maximum (exceeding 2 m) on the evening of 1 August, shortly after Typhoon Nida made landfall. At the Chiwan station, the water level exceeded 4 m, with a positive extreme value error of 0.21 m between the simulated and measured data. At the Hong Kong station, there was a 0.13 m error in the positive extreme value between the simulated data and the measured data. Similarly, at the Guangzhou station, the positive extreme value error between the model-simulated storm tide and the measured data was 0.33 m. As illustrated in Table 1, the R value, RMSE value, and skill value demonstrate that the simulation is functioning effectively.

The numerical results show that, when Nida approached the PRE, the simulation of increased water was underestimated, resulting in significant errors in the storm tide prediction. However, the simulated results for the maximum water levels are in close alignment with the observed values, thereby demonstrating that the model employed in this study is an effective representation of the tide–surge interactions within the study area.

Figure 3 Time series comparisons of measured and modeled storm tide levels at the (a) Chiwan gauge, (b) Hong Kong gauge, and (c) Guangzhou gauge.

3.2 Storm surge characteristics of Typhoon Nida

Typhoon Nida passed through the PRE during a spring tide, coinciding with the maximum storm surge in the HHW tidal phase. Based on this phenomenon, five tidal phases were selected to investigate the evolution of storm surges before or after Typhoon Nida made landfall. The spatial and temporal distribution characteristics of storm tide elevations during various tidal phases in the PRE are illustrated in Fig. 4. Five points were selected for examination within the internal (P1), middle (P2), external (P3), northern Qi'ao (P4), and Shenzhen Bay (P5) regions of the PRE, as shown in Fig. 1c. Notably, the water depths at points P1, P2, and P3 exceed 10 m, while the water depths at points P4 and P5 are less than 10 m. At 09:00 on 1 August, during the lowest low water (LLW) tidal phase, the PRE area showed a decrease in the water level which was affected by the tide (Fig. 4a). The offshore wind exhibited a tendency to decrease the water level, while the nonlinear residuals were positive in Shenzhen Bay and the northern part of Qi'ao (Fig. 4b). At 15:00 on 1 August, which coincides with the lowest high water (LHW) tidal phase, the total water elevation in the PRE exhibited a negative-to-positive trend from northeast to southwest, and the offshore wind made some contribution. The most notable decline in the water level is observed in Shenzhen Bay (Fig. 4d). At the same time, the nonlinear residuals are negative throughout Lingding Bay, with the exception of its upper region (Fig. 4e). At 19:00 on 1 August, during the highest low water (HLW) tidal phase, both offshore wind and tide conditions resulted in a negative trend in the elevation of storm tides in the PRE area, with the most significant negative values occurring from northeast to southwest. Notably, the most substantial decrease in the water level was observed in Shenzhen Bay (Fig. 4g). While the nonlinear residuals are positive, their impact is particularly significant in Shenzhen Bay and the northern part of Qi'ao (Fig. 4h). During the HHW tidal phase, the storm tide elevation in the PRE area exhibits a more substantial increase (Fig. 4j). Conversely, during the same phase, the nonlinear residual levels exhibit a more significant decrease (Fig. 4k). Furthermore, at 10:00 on 2 August, during the LLW tidal phase, the storm tide elevation in the PRE area was negative, which was predominantly attributed to the tide. The onshore wind had a negligible effect on the water level, while the nonlinear residuals were positive.

A comprehensive time series of storm surge elevation (ζ_S), tide elevation (ζ_T), storm tide elevation (ζ_TS), practical storm surge elevation (ζ_PS), and nonlinear residuals (ζ_Non) for each of the five points in the study area is presented in Fig. 4. The positive storm surge elevation at three points (P1, P2, and P3) exhibited a notable increase from the outer to inner regions of Lingding Bay. When Typhoon Nida made landfall, the nonlinear residuals reached their positive extreme value and subsequently reached their negative extreme value before the water elevation experienced its most substantial increase. The nonlinear residuals of P1, P2, and P3 reached their positive extremes of 0.19, 0.14, and 0.04 m, respectively. This resulted in the induction of effects associated with the falling tide. The nonlinear residuals exhibited a decrease after Typhoon Nida made landfall and reached their negative extremes near the times of the positive extremes in storm surge elevation. Specifically, the negative extreme values of the nonlinear residuals at P1, P2, and P3 were −0.43, −0.29, and −0.11 m, respectively. The nonlinear effect within the PRE exhibited a notable increase from the exterior towards the interior. Additionally, the positive extreme values of nonlinear residuals for P4 and P5 were 0.16 and 0.14 m, respectively, while the negative extreme values of nonlinear residuals for P4 and P5 were both −0.29 m each. These findings indicate that the overall impact of Typhoon Nida was characterized by a greater decrease in nonlinear residuals than any increase.

The primary concern is the increase in water level, which exerts the most significant influence on the elevation of the storm tide. The contributions of the storm surge elevation, the tide elevation, the practical surge elevation, and the nonlinear residuals to the storm tide elevation are calculated from five points in the PRE region, as illustrated in Table 2. It is evident from our findings that both the storm surge and the tide make positive contributions to the elevations of storm tides. In contrast, the nonlinear residuals have been demonstrated to exert a negative influence on storm tide elevation. The practical surge contribution at P1 is identified as being the most significant of the five points. The nonlinear effect at P2 especially is the most pronounced one when compared to the other points.

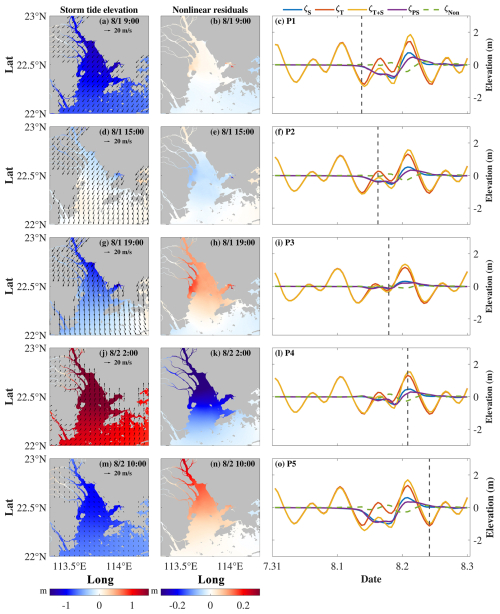
Figure 4 Storm tide elevation and wind vector (left), nonlinear residuals (middle) at different tidal phases, and time series of water elevations (right) for the P1, P2, P3, P4, and P5 locations. The dashed line indicates the time corresponding to the time in the left and middle columns.

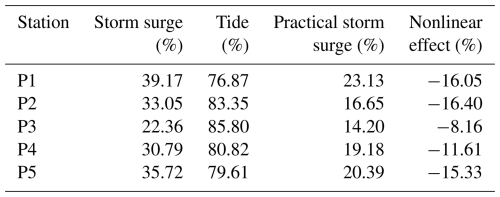
In order to emphasize the importance of the nonlinear effect, the ratio of the nonlinear residuals to the storm surge was calculated and compared with the ratio of the nonlinear residuals to the practical storm surge, as illustrated in Table 3. The ratio of the nonlinear residuals to the storm surge represents the extent to which the nonlinear effect amplifies or diminishes the direct impact of the storm surge. Meanwhile, the ratio of the nonlinear residuals to the practical storm surge provides insight into the extent to which the nonlinear effect contributes to the practical storm surge. It is observed that, of all five points, the influence of storm surges on water elevation is relatively minor at P3 due to nonlinear effects. Nevertheless, the effects in question have an almost 57 % negative impact on practical storm surges. Notably, at P2, there is a markedly negative contribution from nonlinear effects amounting to nearly 98 %. This suggests that, in comparison to other points, P2 is subject to a more pronounced influence from storm surges, which can be considered to be a form of practical storm surge.

Table 2 The contribution to the storm tide elevation at the maximum moment of the storm tide.

Table 3 The contribution of the nonlinear effect to the storm surge and practical storm surge.

3.3 The characteristics of storm surges with different typhoon landfall times

The primary factors contributing to tide–surge interactions are the alteration of tidal phases caused by storm surges and the modulation of storm surges due to tides (Feng et al., 2019; Zheng et al., 2020). Accordingly, the typhoon landfall times were modified in order to examine the characteristics of storm surges occurring during different tidal phases. The nonlinear effects are subject to variation when typhoons make landfall during different tidal phases (Pandey and Rao, 2019). As shown in Fig. 5, the practical storm surge at P1 shows minimal changes with different typhoon landfall times. When the positive increase in water elevation caused by storm surge coincides with the HHW tidal phase, the positive extreme values are smallest at each of the five points. The nonlinear residuals exhibited decreases in both positive and negative extreme values from the inner to outer regions of Lingding Bay. However, when the positive increase in water elevation due to storm surge coincides with the HLW tidal phase, which is equivalent to an advance in landfall time of 6 h, it results in a significantly greater positive extreme value of the practical surge elevation compared to others, as shown in Table 4. The influence of tides on storm tide elevation is more pronounced than that of storm surges, while the nonlinear effect exhibits a negative contribution (see Table 5). When a positive increase in water elevation resulting from a storm surge coincides with the LHW tidal phase, corresponding to an 11 h advance in landfall time, the positive extreme value of the practical storm surge shows minimal variation compared to when it coincides with the HHW tidal phase. It has been demonstrated that both surges and tides have a positive effect on storm tide elevation. However, the increase in water level due to storm surge is greater than that due to the tide. Consequently, the nonlinear effect shows a negative contribution resulting in a reduction in the water level (see Table 6). When the positive increase in water elevation from a storm surge coincides with the LLW tidal phase, occurring at the landfall time of Typhoon Nida advanced by 16 h, the contribution of the practical storm surge to the storm tide elevation is negative. Meanwhile, the contributions from the nonlinear effect are positive (see Table 5).

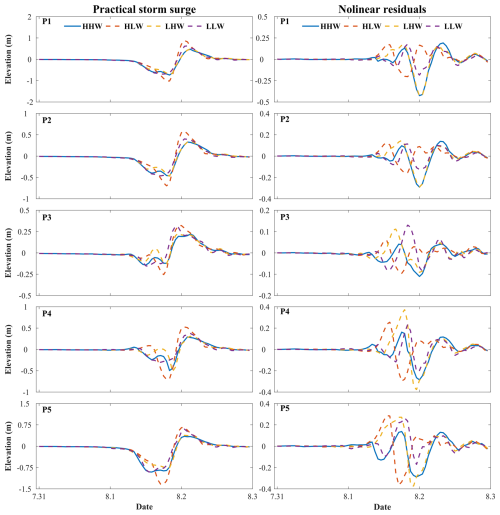
Figure 5 Time series of practical storm surge elevation (left) and nonlinear residuals (right) induced by different landfall time forcings at P1, P2, P3, P4, and P5.

Table 4 Extreme values of practical storm surge elevations caused by different landfall time forcings at P1, P2, P3, P4, and P5. Boldface indicates the highest absolute value of a station class.

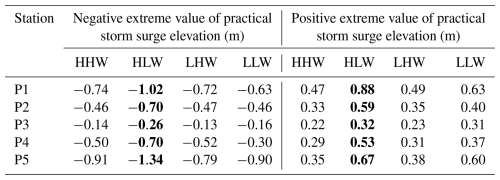
Table 5 Contributions of the practical storm surges and nonlinear effects to storm tide elevations caused by different landfall time forcings at P1, P2, P3, P4, and P5. Boldface indicates the highest absolute value of a station class.

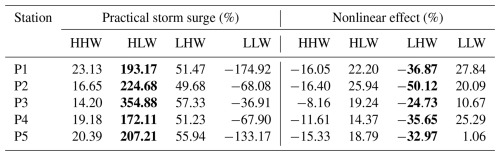
Table 6 Extreme values of nonlinear residuals caused by different landfall time forcings at P1, P2, P3, P4, and P5.

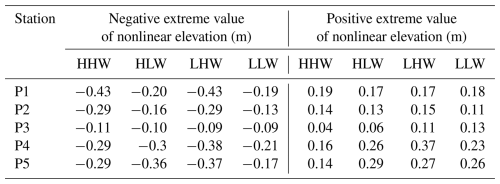
Table 7 Contribution of the nonlinear effect to storm surge and practical storm surge caused by different landfall time forcings at P1, P2, P3, P4, and P5.

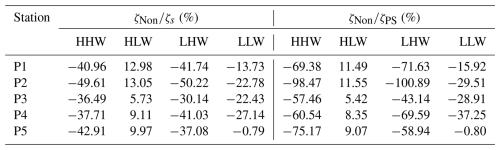
Above all, the practical storm surge elevation and the nonlinear residuals are significantly modulated by tidal forces, particularly in areas of shallow water (Zhang et al., 2017, 2010, 2021). The practical storm surge makes the greatest contribution to the storm tide elevation when the maximum of the storm surge coincides with the HLW tidal phase, as opposed to the other phases. The nonlinear effect is negative at high tides (HHW and LHW) and positive at low tides (HLW and LLW) (Horsburgh and Wilson, 2007). The tidal contribution to the storm tide exceeds the surge contribution when the maximum of storm surges coincides with high tides. Conversely, the contribution of tides is less pronounced than that of the storm surge when the maximum of storm surges coincides with low tides. Notably, when the maximum of storm surges coincides with the LHW tidal phase, the contribution of the nonlinear effect is greatest compared to the other tidal phases (see Table 5). When the landfall time coincides with different tidal phases, the positive extreme value of nonlinear residuals changes little, whereas the negative extreme value of negative nonlinear residuals changes significantly, as demonstrated in Table 6. As shown in Table 5, the practical storm surge makes the greatest contribution when the maximum of the storm surge coincides with the LHW tidal phase, compared to the other tidal phases. The nonlinear effect has the greatest impact when the maximum of the storm surge coincides with the HLW tidal phase. A comparison of the ratios reveals that both the ratio of nonlinear residuals to the storm surge and the ratio of nonlinear residuals to the practical storm surge are positive when their maximum coincides with the HLW tidal phase. Conversely, they are negative during the other tidal phases (see Table 7). This indicates that an increase in water elevation due to nonlinear effects becomes significant only when the maximum of storm surges coincides with the HLW tidal phase.

3.4 Dynamic mechanisms of nonlinear residual levels caused by Typhoon Nida

To further analyze the source of the tide–surge interaction and its nonlinear effects, we utilized the formula proposed by Yang et al. (2019) for calculating these nonlinear terms. As shown in Fig. 2, five representative points were selected to illustrate the nonlinear effects of tide–surge interactions in the PRE.

$$\begin{array}{}\text{(10)}& \begin{array}{r}{\displaystyle \frac{\partial U_{\mathrm{NS}}}{\partial t}}+{\mathit{\psi }}_x\left(U_{\mathrm{NS}},V_{\mathrm{NS}}\right)-f{V}_{\mathrm{NS}}-{\mathit{\tau }}_x^{\mathrm{S}}-{\mathit{\tau }}_x^{\mathrm{B}}=-g{\displaystyle \frac{\partial {\mathit{\zeta }}_I}{\partial x}}\\ {\displaystyle \frac{\partial V_{\mathrm{NS}}}{\partial t}}+{\mathit{\psi }}_y\left(U_{\mathrm{NS}},V_{\mathrm{NS}}\right)+f{U}_{\mathrm{NS}}-{\mathit{\tau }}_y^{\mathrm{S}}-{\mathit{\tau }}_y^{\mathrm{B}}=-g{\displaystyle \frac{\partial {\mathit{\zeta }}_I}{\partial y}}\end{array}\end{array}$$

The calculated results of the nonlinear dynamic terms, i.e., the nonlinear local acceleration terms $\frac{\partial U_{\mathrm{NS}}}{\partial t}$ and $\frac{\partial V_{\mathrm{NS}}}{\partial t}$, the nonlinear convection term ψ_x,ψ_y, the nonlinear Coriolis force terms fU_NS and fV_NS, the nonlinear wind stress term ${\mathit{\tau }}_x^{\mathrm{S}},{\mathit{\tau }}_y^{\mathrm{S}}$, and the nonlinear bottom friction term ${\mathit{\tau }}_x^{\mathrm{B}},{\mathit{\tau }}_y^{\mathrm{B}}$ at each point in the x and y directions, are shown in Fig. 6.

In the eastward direction (x component) at P1, the nonlinear local acceleration term plays a dominant role, with some contribution from the nonlinear bottom friction term. It is important to note that this phenomenon occurs within Lingding Bay. The conclusion is that the effects of nonlinear advection and Coriolis force are deemed negligible. As Typhoon Nida approached Lingding Bay after 18:00 on 1 August 2016, the local acceleration term exhibited an increase, reaching a positive extreme at 00:00 on 2 August 2016, which is similar to the Coriolis term. The advection term reached its positive extreme 1 h later, occurring concurrently with the negative extreme of the nonlinear residuals. Although the wind stress term is minimal, the bottom friction term reached its negative extreme at 02:00 on 2 August 2016, coinciding with the storm surge reaching its positive extreme. In the northward direction (y component), the amplitude of nonlinear local acceleration remains large; however, it is surpassed by the leading role played by the nonlinear advection term, which reached its positive extreme at 02:00 on 2 August 2016.

In the eastward direction at P2, the values of the various nonlinear terms were relatively small, contributing little to the overall nonlinear effect, with the wind stress term playing a minor role in all of the nonlinear terms. However, in the northward direction, the local acceleration term is the dominant factor. The value of this term reached its negative extreme at 22:00 on 1 August 2016 and its positive extreme at 06:00 on 2 August 2016.

In the eastward direction at P3, the nonlinear Coriolis term was the dominant factor, with values reaching their positive extremes at 23:00 on 1 August 2016. Concurrently, both the nonlinear advection term and the local acceleration term reached their positive extremes, with each term making a significant contribution. Of all the nonlinear terms, the wind stress plays a minor role.

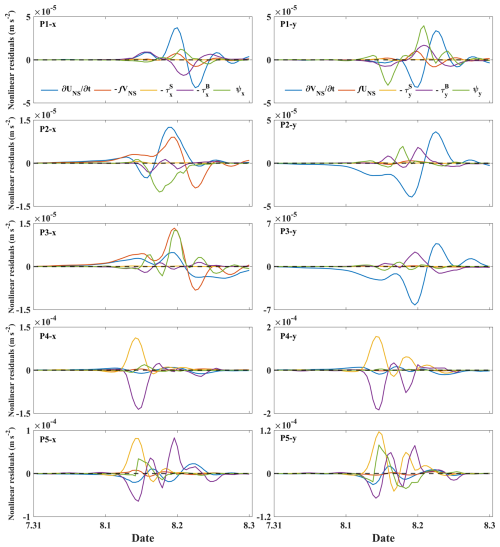
Figure 6 Time series of the nonlinear components of Typhoon Nida at P1, P2, P3, P4, and P5 in the x direction (left) and y direction (right).

Given that P4 is situated in the northern part of Qi'ao and P5 in Shenzhen Bay, these two points represent areas of significant nonlinear effects of tide–surge interaction within the PRE region. As illustrated in Fig. 6, in the eastward direction at P4, the nonlinear wind stress term plays a leading role and reached its positive extreme at 14:00 on 2 August 2016. It is also notable that the nonlinear bottom friction term plays a significant role. In the northward direction at P4, both the nonlinear wind stress and bottom friction terms contribute to the nonlinear effect. In the eastward direction at P5, the significance of the wind stress and bottom friction terms exceeds that of the other terms.

For all of the points, the results indicate that the gradient of the nonlinear residuals was stronger in the northerly direction than in the easterly direction (Hu et al., 2023), with the exception of the nonlinear Coriolis term. This study focuses on analyzing storm surges induced by Typhoon Nida using a two-dimensional (2D) model with a high-regulation unstructured grid, which enhances both the accuracy and robustness of our conclusions. The establishment of direct mathematical relationships between nonlinear residuals and dynamic terms through theoretical derivation provides valuable insights. It was found that the nonlinear acceleration term mainly contributes to the top of the bay, indicating a strong interaction between the tidal current and the storm-induced current (Song et al., 2020). Additionally, wind stress affected the tide–surge interaction since H was in the denominator of the wind stress term, especially in shallow water areas, such as the northern part of Qi'ao and Shenzhen Bay. Furthermore, it is noted that shallow water effects are more pronounced in Shenzhen Bay due to the restricted water depth over tidal flats (Zheng et al., 2020).

3.5 Dynamic mechanisms of the nonlinear residuals influenced by different typhoon landfall times

To investigate the nonlinear momentum characteristics resulting from different tidal forcings, the nonlinear momentum terms were calculated. When the maximum increase in water elevation caused by storm surge coincides with the HLW tidal phase, the temporal changes in the nonlinear residuals are shown in Fig. 7. In the eastward direction at P1, the dominant factor is the nonlinear local acceleration term, with a certain contribution from the nonlinear bottom friction term. Furthermore, the effects of nonlinear advection and the Coriolis force make significant contributions. In the northward direction, while the amplitude of the nonlinear local acceleration term remains considerable, it is surpassed by the influence of the nonlinear advection term. In both the x component and the y component, the wind stress terms exhibit a weak impact and can be neglected. In the eastward direction at P2, the values of the various nonlinear terms were relatively small, with a negligible contribution to the nonlinear effect. Furthermore, the wind stress plays a minor role in all of the nonlinear terms. The nonlinear Coriolis term contributes to positive nonlinear residuals, whereas the advection term and the bottom friction term contribute negatively to the nonlinear residuals. However, in the northward direction, the local acceleration term plays a leading role and reaches its negative extreme in nonlinear residuals at 16:00 on 1 August 2016. In the eastward direction at P3, the nonlinear Coriolis and nonlinear advection terms contribute to the dynamics. However, in the northward direction at P3, the dominant term is the nonlinear local acceleration term, with additional contributions from the bottom friction and nonlinear advection terms. The wind stress plays a minor role in all of the nonlinear terms. In the eastward direction at P4, the nonlinear bottom friction term plays a dominant role, reaching its negative extreme at 18:00 on 1 August 2016. Following closely behind is the nonlinear wind stress term, which reached its positive extreme at 17:00 on 1 August 2016. In the northward direction at P4, both the nonlinear wind stress and bottom friction terms contribute to the nonlinear effect. Specifically, while the bottom friction term makes a negative contribution to the nonlinear residuals, the wind stress contributes positively. The wind stress term reached its positive extreme at 17:00 on 1 August 2016, and the bottom friction term reached its negative extreme at the same time. In the eastward direction at P5, the wind stress and bottom friction terms are of greater significance than the other terms. In the northward direction at P5, the wind stress term and bottom friction term also exerted a dominant influence on the nonlinear residuals. Moreover, the absolute value of the positive extreme of the wind stress term is greater than that of the negative extreme of the bottom friction term. The advection term was so insignificant that it was recorded as negligible, resulting in a discontinuous time series.

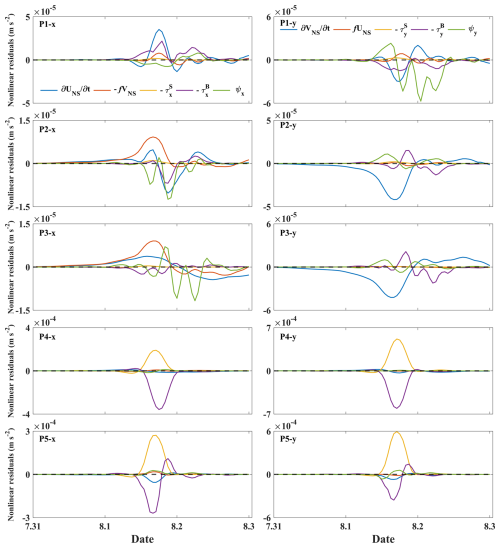
Figure 7 Time series of the nonlinear components at P1, P2, P3, P4, and P5 in the x direction (left) and y direction (right) when the maximum storm surge coincides with the HLW tidal phase.

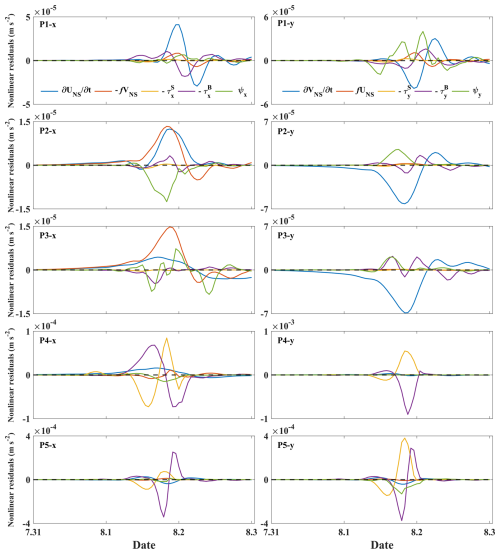
Figure 8 Time series of the nonlinear components at P1, P2, P3, P4, and P5 in the x direction (left) and y direction (right) when the maximum storm surge coincides with the LHW tidal phase.

When the maximum increase in the water level caused by pure storm surge coincides with the LHW tidal phase, Fig. 8 illustrates the time series changes in the nonlinear residuals. In the eastward direction at P1, the nonlinear local acceleration term is also the most significant contributor, followed by the nonlinear bottom friction term, which represents the second-largest contribution. Nonlinear advection and the Coriolis force exert a considerable influence on the nonlinear residuals. In the northward direction, the nonlinear local acceleration term and the nonlinear advection term make major contributions. In both the x component and y component, the wind stress term is weak and can be considered negligible. In the eastward direction at P2, both the bottom friction term and wind stress term are significantly smaller compared to the other terms. The positive nonlinear residuals are contributed by the nonlinear local acceleration term, while the negative ones are a result of contributions from the nonlinear advection term and the bottom friction term. However, in the northward direction at P2, we observe that the nonlinear local acceleration term plays a leading role, reaching its negative extreme value at 20:00 on 1 August 2016. In the eastward direction at P3, the nonlinear Coriolis term exerts the greatest influence on the nonlinear residuals, while the nonlinear local acceleration term and the nonlinear advection term contribute substantially as well. However, in the northward direction at P3, the nonlinear local acceleration term is predominant, with the bottom friction term and the nonlinear advection term exerting influences. The wind stress and Coriolis effects are both minimal. In the eastward direction at P4, the nonlinear bottom friction term and the nonlinear wind stress term exert a greater impact than the other terms. In the northward direction at P4, the nonlinear wind stress term and the bottom friction term contribute significantly to the nonlinear residuals. Notably, the absolute value of the extreme of the bottom friction term is greater than that of the wind stress term. The wind stress term reached its positive extreme at 20:00 on 1 August 2016, while the bottom friction term reached its negative extreme 1 h later. In the eastward direction at P5, the bottom friction term is the primary contributor, with the wind stress term providing a secondary contribution. In the northward direction at P5, the wind stress term and the bottom friction term exert a dominant influence on the nonlinear residuals, with the other terms having a negligible effect.

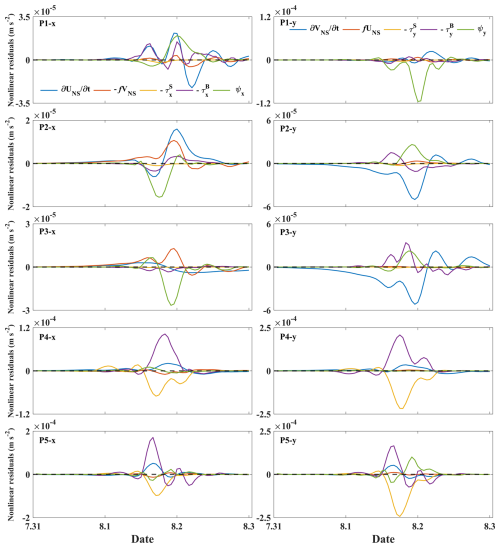
Figure 9 Time series of the nonlinear components at P1, P2, P3, P4, and P5 in the x direction (left) and y direction (right) when the maximum storm surge coincides with the LLW tidal phase.

When the maximum increase in water elevation caused by the storm surge coincides with the LLW tidal phase, the time series changes in the nonlinear residuals are shown in Fig. 9. In the eastward direction at P1, the nonlinear local acceleration term, the advection term, and the bottom friction term make major contributions. In the northward direction, the nonlinear advection term is the most significant contributor. In both the x component and y component, the wind stress term is relatively weak and can be considered negligible. In the eastward direction at P2, major contributions are made by the nonlinear local acceleration term, the Coriolis term, and the nonlinear advection term. However, in the northerly direction at P2, this is primarily influenced by the local acceleration term, which reaches its negative extreme in nonlinear residuals at 23:00 on 1 August 2016. Meanwhile, the advection term exerts a positive influence on the nonlinear residuals, reaching its positive extreme at 22:00 on 1 August 2016. In the eastward direction at P3, the nonlinear advection term exerts the dominant influence, with the nonlinear Coriolis term also making a significant contribution. However, in the northward direction at P3, the nonlinear local acceleration term is predominant, with the bottom friction term and the nonlinear advection term also contributing. The wind stress term and the Coriolis term are negligible by comparison. In the eastward direction at P4, the nonlinear bottom friction term and the nonlinear wind stress term make greater contributions than the other terms, with the nonlinear bottom friction term playing a leading role and making a positive contribution to the nonlinear residuals. In the northward direction at P4, the nonlinear wind stress term and the bottom friction term make significant contributions to the nonlinear effect. The positive contribution of the bottom friction nearly balances the negative contribution of the wind stress. The wind stress reached its negative extreme at 19:00 on 1 August 2016, while the bottom friction term reached its positive extreme 1 h earlier. In the eastward direction at P5, the bottom friction term is the primary contributor, with the wind stress term making the second-largest contribution. In the northward direction at P5, the wind stress term is the most significant contributor, with the other terms making comparatively less impact.

The occurrence of storm surges in the estuary area is subject to the influence of both typhoons and tides. The interaction between these two forces in water levels has been demonstrated in numerous studies. The elevation of storm surges in the PRE varies significantly depending on the tidal phase during which they occur. A comparison of the nonlinear factors at those representative points across the different tidal phases can provide a better understanding of the mechanisms underlying the tide–surge interaction. The analysis of the nonlinear terms in the nonlinear residuals revealed that, when storm surges coincide with high tides (HHW and LHW), the nonlinear acceleration term predominantly affects the y component at P1. Conversely, when storm surges coincide with low tides (HLW and LLW) at P1, the nonlinear advection term is the dominant factor. In the eastward direction, the nonlinear acceleration term consistently plays a dominant role at P1. In the northward direction, both P2 and P3 are characterized by a predominant influence of the nonlinear acceleration term. In instances where storm surges occur concurrently with different tidal phases, the proportionate contribution of each nonlinear term remains almost unchanged, but their magnitudes vary. The results illustrate that the primary sources of the tide–surge interaction nonlinear effects within the PRE are effects of the tide's velocity. In shallow water areas, such as the northern part of Qi'ao and Shenzhen Bay, tide–surge interaction nonlinear effects are predominantly influenced by a combination of wind and bottom friction.

4 Conclusions

An ADCIRC model has been utilized to simulate the storm surges in the PRE induced by Typhoon Nida. Results from several numerical experiments investigating the interaction between tides and storm surges indicate that, when the tidal effect is incorporated, the simulations agree well with observational data.

To study the characteristics of tide–surge interaction in the PRE, three types of model runs were conducted, from which the storm tide, the astronomical tide, the storm surge, the practical storm surge, and the residual elevation due to the tide–surge interaction were obtained. The results show that the storm surge is significantly modulated by the tide due to the tide–surge interaction. A direct mathematical relationship between the nonlinear residuals and dynamic influencing factors has been established. This derivation includes the local acceleration term, the Coriolis force term, the wind stress term, the bottom friction term, and the nonlinear advection term. The nonlinear momentum term can reflect the momentum response of different areas within the estuary to nonlinear effects. The momentum equation facilitates the establishment of a relationship between the nonlinear factors of tide–surge interactions and the underlying physical processes. A comparison of nonlinear factors at representative points from the inner to outer bay has demonstrated that the local acceleration term and the nonlinear advection term exert a predominant influence on the nonlinear dynamics. However, in the case of Shenzhen Bay and the northern part of Qi'ao, it is the wind stress term and the bottom friction term that emerge as the dominant nonlinear factors.

To investigate the relationship between tidal phases and storm surges further, we adjusted the landfall time of Typhoon Nida in our model simulations. The results show that both the practical storm surge level and the nonlinear level are significantly modulated by tidal forces, especially in shallow water areas. For instance, where the maximum of the storm surge coincides with high tides, the contribution of the tide to the storm tide is greater than that of the storm surge. Conversely, the contribution of tides to the storm tide is less than that of the storm surge when the maximum of the storm surge coincides with low tides. The analysis revealed that the nonlinear effect of tide–surge interaction is positive when the maximum of the storm surge coincides with low tidal phases (LLW and HLW). By contrast, this nonlinear effect becomes negative when the maximum of the storm surge coincides with high tidal phases (HHW and LHW). Notably, when the maximum of storm surges coincides with the LHW tidal phase, the contribution of the nonlinear effect is greatest in comparison with other tidal phases. The ratio of the nonlinear residuals to the storm surge and the ratio of the nonlinear residuals to the practical storm surge are both positive when the maximum of the storm surge coincides with the HLW tidal phase, while the ratios during the other tidal phases are negative.

Although similar results were also presented in other studies (Song et al., 2020; Hu et al., 2023), discussions on nonlinear momentum for different tidal phases are still lacking. We calculated the nonlinear terms to discuss the characteristics and mechanisms of tide–surge interaction. When storm surges coincide with different tidal phases, the contribution ratio of each nonlinear term remains almost unchanged, but their magnitudes exhibit notable variation. The results illustrate that the primary source of the tide–surge interaction nonlinear effects within the PRE is the effect of the tide's velocity. In areas of shallow water, such as the northern part of Qi'ao and Shenzhen Bay, the tide–surge interaction nonlinear effects are predominantly influenced by a combination of wind and bottom friction.

Taking Typhoon Nida as a case study, the present research reveals detailed characteristics of tide–surge interaction in the PRE. The present results of this study can provide valuable information for understanding the tide–surge interaction mechanism and improving storm surge prediction within the PRE. However, further studies of additional typhoon events may be needed, along with a comprehensive consideration of meteorological processes and the mechanisms of tidal-wave propagation within and outside the estuary, and the model system could still be improved in the future.