Assessing storm surge model performance: what error indicators can measure the model's skill?

A well-validated storm surge numerical model is crucial, offering precise coastal hazard information and serving as a basis for extensive databases and advanced data-driven algorithms. However, selecting the best model setup based solely on common error indicators like the root-mean-square error (RMSE) or Pearson correlation does not always yield optimal results. To illustrate this, we conducted 34-year high-resolution simulations for storm surge under barotropic (BT) and baroclinic (BC) configurations using atmospheric data from ERA5 and a high-resolution downscaling of the Climate Forecast System Reanalysis (CFSR) developed by the University of Genoa (UniGe). We combined forcing and configurations to produce three datasets: (1) BT-ERA5, (2) BC-ERA5, and (3) BC-UniGe. The model performance was assessed against nearshore station data using various statistical metrics. While RMSE and Pearson correlation suggest BT-ERA5, i.e., the coarsest and simplest setup, is the best model (followed by BC-ERA5), we demonstrate that these indicators are not always reliable for performance assessment. The most sophisticated model (BC-UniGe) shows worse values of RMSE or Pearson correlation due to the so-called “double penalty” effect. Here we propose new skill indicators that assess the ability of the model to reproduce the distribution of the observations. This, combined with an analysis of values above the 99th percentile, identifies BC-UniGe as the best model, while ERA5 simulations tend to underestimate the extremes. Although the study focuses on the accurate representation of storm surge by the numerical model, the analysis and proposed metrics can be applied to any problem involving the comparison between time series of simulation and observation.

1 Introduction

In coastal areas, accurately depicting storm surge is paramount for effective risk assessment, preparedness, and mitigation strategies, as they can lead to coastal erosion, inundation, and infrastructure damage and threaten important cultural heritage sites (Reimann et al., 2018; Vousdoukas et al., 2022). Storm surges arise from the interaction between the atmosphere and the sea. Essentially, the atmosphere exerts forces on the waterbody, causing sea levels to rise due to low-atmospheric-pressure systems and strong wind fields (Pirazzoli and Tomasin, 2022). The atmospheric pressure effect, known as the inverse barometer effect or static amplification, typically contributes 10  % to 15  % of the total storm surge magnitude (World Meteorological Organization, 2011). The second and more significant part of the storm surge, called dynamic amplification or wind setup, arises from tangential wind stress associated with the weather system's wind field acting on the ocean surface (Chaumillon et al., 2017).

Numerical simulations play a pivotal role in unraveling the complexities of physical phenomena such as storm surges (Park et al., 2022). They offer invaluable insights into various processes and greatly contribute to building extensive databases for further analysis and comprehension. Concerning storm surge, this refers to a complex oceanographic phenomenon that demands accurate oceanic and atmospheric data for precise representation. Due to diverse orographic configurations, atmospheric models often exhibit significant errors, necessitating the utilization of local-scale models with high resolution (Umgiesser et al., 2021). Additionally, the intricate coastal and bathymetric features and interactions pose challenges for existing hydrodynamical models to fully capture the relevant dynamics, partly due to their low resolution (Mentaschi et al., 2015; Toomey et al., 2022).

On the other hand, the utilization of unstructured-grid models enables a more accurate portrayal of coastal dynamics, considering the intricacies of bathymetry and shoreline configurations (Federico et al., 2017). This approach offers the advantage of employing a higher resolution at the coastlines while maintaining a more modest resolution in deeper waters (Ferrarin et al., 2019). Unstructured meshes offer flexibility in resolving basin geometry, allowing for local refinement of computational domains to simulate regional dynamics on a global mesh with coarse resolution. This flexibility is particularly valuable for coastal applications, where computational domains encompass complex coastlines and varying scales, ranging from basin size to details of river estuaries or riverbeds (Danilov, 2013). Over recent years, unstructured-grid models have increasingly emerged as alternatives to regular grids for large-scale simulations (e.g., Mentaschi et al., 2020; Muis et al., 2016; Vousdoukas et al., 2018; Fernández-Montblanc et al., 2020; Saillour et al., 2021; Wang et al., 2022; Zhang et al., 2023; Mentaschi et al., 2023), with established circulation unstructured models such as the Advanced Circulation Model for Shelves, Coastal Seas, and Estuaries (ADCIRC, Luettich et al., 1992; Pringle et al., 2021); the Finite-Volume Coastal Ocean Model (FVCOM, Chen et al., 2003); the Semi-implicit Cross-scale Hydroscience Integrated System Model (SCHISM, Zhang and Baptista, 2008; Zhang et al., 2016); the System of HydrodYnamic Finite Element Modules (SHYFEM, Umgiesser et al., 2004; Bellafiore and Umgiesser, 2010; Micaletto et al., 2022); TELEMAC (Hervouet and Bates, 2000); and Delft3D-FM (Deltares: Delft, 2024) being available.

In this study, we developed numerical simulations of storm surge in the northern Adriatic Sea with two main objectives: first we want to generate long-term databases of storm surge with a focus on accurately representing extreme values, and second we want to analyze the ability of different metrics to capture the skill of the model. The northern Adriatic Sea is a semi-enclosed body of water characterized by intricate bathymetry. The region's coastline exhibits distinct features, with the western coastline being relatively smooth and sandy, while the eastern coastline is fragmented and rocky, dotted with numerous islands. Both bathymetry and the configuration of the coastline significantly influence the physical processes occurring along the coast (Bellafiore and Umgiesser, 2010). The semi-enclosed nature of the Adriatic Sea predisposes it to experiencing intense storm surge events, leading to anomalous increases in sea level. These events are typically driven by local low-pressure system cyclogenesis and the associated strong winds, which are influenced by the region's orographic features (Umgiesser et al., 2021).

The application of numerical tools to study storm surge in the northern Adriatic Sea has garnered significant attention over the years, primarily due to its status as a high-risk area with unique cultural and environmental heritage and significant economic activities (Ferrarin et al., 2020). Previous efforts in this field have included predictive models projecting future storm scenarios (Yu et al., 1998), long-term numerical simulations (Lionello et al., 2010), analyses of storm events, use of various atmospheric forcings (De Vries et al., 1995; Zampato et al., 2006; Međugorac et al., 2018), investigations into seiches influence and data assimilation impacts (Bajo et al., 2019), and storm surge ensemble prediction systems for lagoons (Alessandri et al., 2023).

In this study, the numerical simulations are based on a long-term ocean circulation downscaling carried out with the SHYFEM model, which is an unstructured-grid finite-element hydrodynamic open-source code that solves the Navier–Stokes equations with hydrostatic and Boussinesq approximations (Umgiesser et al., 2004; Micaletto et al., 2022). The model has been already implemented in operational (Federico et al., 2017) and relocatable (Trotta et al., 2016) forecasting frameworks and for storm surge events (Park et al., 2022; Alessandri et al., 2023). The choice of SHYFEM is driven by its flexibility in handling complex bathymetry and irregular coastlines through its unstructured-grid framework, allowing for higher resolution in critical areas. Additionally, its successful implementation in operational and relocatable forecasting frameworks and storm surge events confirms its reliability for this study. The simulations consider different setups to explore the influence of different atmospheric forcings and model configurations on the model's skill. Regarding model configurations, both barotropic and baroclinic simulations were conducted to compare potential differences between these two widely used approaches, as covered in the literature for the proper representation of storm surge (e.g., Weisberg and Zheng, 2008; Staneva et al., 2016; Hetzel et al., 2017; Ye et al., 2020; Muñoz et al., 2022). Furthermore, we focus on the use of different metrics and their ability to provide reliable indications of the model's performance, which is an essential aspect in assessing model skill and to select the best model configuration. In addition to classical metrics, such as the Pearson correlation coefficient and root-mean-square error (RMSE), two customized versions of the mean absolute deviation (MAD) are introduced. These tailored metrics incorporate observed and simulated percentiles, ranging from 0 % to 100 %, to ensure accurate representation of extreme values during the performance evaluation.

The paper is organized as follows. Materials and methods are described in Sect. 2, including the description of the two atmospheric databases considered for the simulations, the model setup, and the procedures to carry out the performance evaluation. Section 3 shows the main results of the comparisons between observed and simulated storm surge. The paper continues with a discussion of the results in Sect. 4. Finally, the conclusion in Sect. 5 summarizes the key points of the study.

2 Materials and methods

2.1 Atmospheric forcing

In this study, we utilized two distinct atmospheric databases to force the circulation model, incorporating mean sea level pressure and wind fields. The first database is ERA5, the fifth generation of reanalysis data generated by the European Centre for Medium-Range Weather Forecasts (ECMWF). ERA5 builds upon the Integrated Forecasting System (IFS) Cy41r2, which became operational in 2016, providing hourly output with a horizontal resolution of 0.25° × 0.25° for atmospheric variables (Hersbach et al., 2020). ERA5 is relatively high resolution and accurate for a global reanalysis, although it is known to be affected by negative biases at high percentiles, particularly when compared with measured wind speed (Pineau-Guillou et al., 2018; Vannucchi et al., 2021; Benetazzo et al., 2022; Gumuscu et al., 2023).

Since ERA5 is relatively coarse for local studies and exhibits significant underestimation of extremes, we employed an alternative approach using a high-resolution (3.3 km) atmospheric downscaling developed by the University of Genoa (UniGe). Wind forcing was derived from 10 m wind fields via the Weather Research and Forecast (WRF-ARW) model v3.8.1, allowing for improved representation of small-scale forcings and physics. The computational domains comprised a 10 km resolution grid covering the Mediterranean, northern Africa, and southern Europe (A10) and a 3.3 km grid over the Tyrrhenian Sea basin and northern Adriatic Sea basin (A3) nested within A10. Initial conditions were obtained from the Climate Forecast System Reanalysis (CFSR) data, which are known their for reliability but occasionally underestimate extreme events (Saha et al., 2010). WRF simulations were conducted for 24 h with hourly outputs, employing established physical parameterization schemes to ensure accuracy across various atmospheric conditions. For further details, readers are referred to Mentaschi et al. (2015).

2.2 Model setup

The SHYFEM model utilizes staggered finite elements in an unstructured Arakawa B horizontal grid, with the vertices of the triangle elements referred to as nodes. Vectors (velocity) are calculated at the center of each element, while scalars (temperature, salinity, and water levels) are determined at nodes (Federico et al., 2017). The unstructured grid for the simulations in this study was generated using the OceanMesh2D tool (Roberts et al., 2019) with a horizontal resolution of 3 km on the open-ocean boundary and 50 m in the coastline (Fig. 1.a). The General Bathymetric Chart of the Oceans (GEBCO) dataset (Weatherall et al., 2015) was used, incorporating a high-resolution coastline from the European Environmental Agency. However, due to identified overestimations in water depth in the Venice and Marano lagoons from GEBCO bathymetry, adjustments were made based on the contributions from Fagherazzi et al. (2007), Lovato et al. (2010), and Zaggia et al. (2017) for the Venice lagoon and Petti et al. (2019) and Bosa et al. (2021) the for the Marano lagoon.

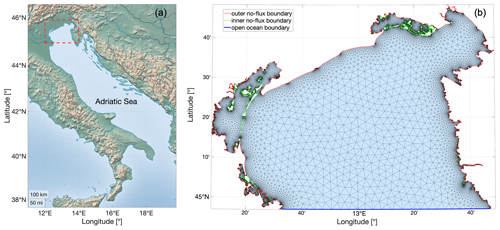
Figure 1 (a) Location of study area, marked with a dashed red line. (b) Unstructured grid for the study area, in which the blue line represents the location of the open boundary condition, the red line the coastline, and the green lines the coastline formed by islands.

Sea level residuals, current velocity, temperature, and salinity from the Copernicus Mediterranean Sea Physics reanalysis (Escudier et al., 2021) were considered as initial and open-ocean boundary conditions. Tides with hourly resolution from the Finite Element Solution (FES) 2014 (Lyard et al., 2021) were also included to account for the total sea level in the simulations. Specifically, the constituents included for the tide reconstruction are SA, SSA, O1, P1, S1, K1, N2, M2, MKS2, S2, R2, K2, M3, M4, and MS4, which were selected based on preliminary harmonic analysis applied to sea level observation data in the locations specified in Sect. 2.2.

Two model configurations were considered: (a) barotropic (BT) and (b) baroclinic (BC), employing 33 vertical levels with a layer thickness of 1 m up to 10 m depth and then 2 m up to a maximum depth of 60 m (BC). To determine vertical viscosities and diffusivities, we utilize a k-ε turbulence scheme derived from the General Ocean Turbulence Model (GOTM) (Burchard and Petersen, 1999). For wind stress at the air–sea interface, a constant wind drag coefficient of $\mathrm{2.5}\times {\mathrm{10}}^{-\mathrm{3}}$ was employed, following the works from Orlić et al. (1994) and Zampato et al. (2007). The bottom stress is determined through the quadratic formulation:

$$\begin{array}{}\text{(1)}& {\mathit{\tau }}_{xz}^{z_N}={\displaystyle \frac{C_{\mathrm{B}}}{H_N^{\mathrm{2}}}}\left|U_N\right|U_N{\mathit{\tau }}_{yz}^{z_N}={\displaystyle \frac{C_{\mathrm{B}}}{H_N^{\mathrm{2}}}}\left|U_N\right|V_N,\end{array}$$

where ${\mathit{\tau }}_{xz}^{z_N}$ and ${\mathit{\tau }}_{yz}^{z_N}$ are the turbulent shear stresses at the bottom interface of the deepest layer, H_N is bottom-layer thickness, and U_N and V_N are the zonal and meridional transports of the bottom layer. C_B is the bottom drag coefficient, which is defined as follows:

$$\begin{array}{}\text{(2)}& C_{\mathrm{B}}={\left({\displaystyle \frac{\mathrm{0.4}}{\ln \left(\frac{{\mathit{\lambda }}_{\mathrm{B}}+\mathrm{0.5}{H}_N}{{\mathit{\lambda }}_{\mathrm{B}}}\right)}}\right)}^{\mathrm{2}},\end{array}$$

where λ_B is the bottom roughness length expressed in meters, which in this study remains constant at 0.01 m. For further details, readers are referred to Maicu et al. (2021).

The simulation period extends from 1987 to 2020 with hourly output. Three combinations of atmospheric forcing and configuration are considered here: (1) barotropic forced by ERA5 (BT-ERA5), (2) baroclinic forced by ERA5 (BC-ERA5), and (3) baroclinic forced by UniGe (BC-UniGe).

2.3 Model performance evaluation

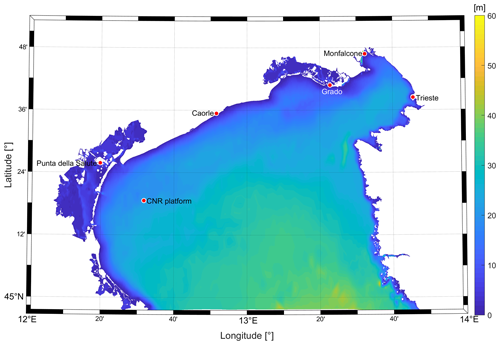
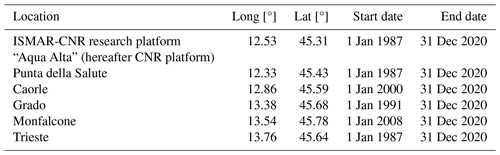
The model output was compared with observations from tide gauges located in the northern Adriatic Sea. The observational data were acquired from the Italian National Institute for Environmental Protection and Research (ISPRA), the Civil Protection of the Friuli-Venezia Giulia Region, and Raicich (2023). Table 1 summarizes the locations considered and the available time spans for comparison that match with the simulation time span. Fig. 2 shows the locations considered for comparison between measured and simulated storm surge, together with the bathymetry used for the simulations.

Table 1 Locations considered for validation, including available start and end dates matching the simulation time span.

Figure 2 Tide gauge locations and bathymetry (depth values on positive).

Both the model output and the observations were processed as follows to enable their intercomparability. To start, both measurement and simulation were centered with a zero mean and then detrended. This approach mitigates possible effects of unmodulated land motion (Chepurin et al., 2014) and ensures that extreme values across the years can be considered as homogeneous and can be compared despite relative sea level changes (Ferrarin et al., 2022). Harmonic analysis was performed for each calendar year on the detrended sea levels using the T-Tide MATLAB package (Pawlowicz et al., 2022), and the non-tidal residual was obtained as the arithmetic difference between sea level and tides (Tiggeloven et al., 2021). Performing yearly harmonic analysis reduces timing errors that could cause tidal energy to seep into the non-tidal residual (Merrifield et al., 2013).

Finally, to obtain the pure storm surge (hereafter also called “surges”), a low-pass filter is applied to the non-tidal residual, following the work of Park et al. (2022). In this study, we consider a cut-off period of 13 h for the filter based on the mixed semidiurnal tidal regime around the northern Adriatic Sea (Lionello et al., 2021).

The performance evaluation of the simulations relies on the computation of statistical metrics of hourly data, which encompass the entire dataset, as well as values exceeding the 99th percentile from the cumulative distribution of measured data at each location. The following metrics are considered.

We first consider the Pearson correlation:

$$\begin{array}{}\text{(3)}& \mathit{\rho }={\displaystyle \frac{\mathrm{1}}{N-\mathrm{1}}}\sum _{i=\mathrm{1}}^N\left({\displaystyle \frac{S_i-{\mathit{\mu }}_S}{{\mathit{\sigma }}_S}}\right)\left({\displaystyle \frac{O_i-{\mathit{\mu }}_O}{{\mathit{\sigma }}_O}}\right),\end{array}$$

where S_i and O_i are the ith simulated and observed data, respectively; N is the sample size; and μ and σ are the mean and standard deviations of S and O, respectively. A value closer to one identifies a better performance.

Second, we consider the root-mean-square error (RMSE):

$$\begin{array}{}\text{(4)}& \mathrm{RMSE}=\sqrt{{\displaystyle \frac{\mathrm{1}}{N}}\sum _{i=\mathrm{1}}^N(S_i-O_i{)}^{\mathrm{2}}},\end{array}$$

where a value closer to zero indicates a better performance.

Third, we consider bias, defined as follows:

$$\begin{array}{}\text{(5)}& \mathrm{Bias}=\stackrel{\mathrm{‾}}{S}-\stackrel{\mathrm{‾}}{O},\end{array}$$

where $\stackrel{\mathrm{‾}}{S}$ and $\stackrel{\mathrm{‾}}{O}$ are the average simulation and observation values, respectively. A value closer to zero identifies a better performance, negative values indicate underestimation, and positive values indicate overestimation from the simulations. Given that both observed and simulated data were detrended and had their mean removed, bias was solely applied to the analysis of values exceeding the 99th percentile.

Fourth, we consider the slope of the linear fit between observations and the simulation:

$$\begin{array}{}\text{(6)}& S=mO+b,\end{array}$$

where the slope is given by the coefficient m. A value closer to one indicates a better performance.

Fifth, we consider mean absolute deviation (MAD):

$$\begin{array}{}\text{(7)}& \mathrm{MAD}=\stackrel{\mathrm{‾}}{\mathrm{|}S-O\mathrm{|}},\end{array}$$

where a value closer to one indicates a better performance.

Additionally, with the aim of considering the representation of extremes by the simulations, we introduce two new metrics based on customized versions of the mean absolute deviation.

The first new metric is the MAD of the percentiles (MADp):

$$\begin{array}{}\text{(8)}& \mathrm{MADp}=\stackrel{\mathrm{‾}}{\mathrm{|}{S}_{\mathrm{prc}}-O_{\mathrm{prc}}\mathrm{|}},\end{array}$$

where S_prc and O_prc are the simulation and observation percentile values, respectively, considered from 0 % to 100 % every 1 %. The MADp metric provides a comprehensive assessment of simulation model performance by comparing percentile values derived from simulations (S_prc) with those observed (O_prc). This evaluation encompasses the entire distribution, from the lowest to the highest percentiles, allowing us to gauge the model's accuracy across a range of scenarios. MADp is particularly valuable for its sensitivity to systematic errors, such as persistent underestimation of high percentiles, which can significantly impact the reliability of simulation results. By penalizing these systematic errors, MADp highlights areas where improvements in the simulation model are necessary to better align with observed data. Lower MADp values indicate closer agreement between simulations and observations.

The second new metric is the corrected MAD (MADc):

$$\begin{array}{}\text{(9)}& \mathrm{MADc}=\stackrel{\mathrm{‾}}{\mathrm{|}S-O\mathrm{|}}+\mathrm{MADp}.\end{array}$$

In this indicator we exploit the ability of the “traditional” MAD to capture the model's skill but reduce its strong penalization of the phase error or timing error (i.e., the reproduction by the model of peaks shifted in space-time) by adding the MAD (MADp) on the percentiles as previously defined. MAD measures the average absolute difference between simulated and observed values, while MADp evaluates the average percentage deviation between them. By combining these two components, MADc provides a comprehensive evaluation of the simulation model's performance, considering both the magnitude and percentage deviations. A lower MADc value indicates better agreement between simulated and observed values, reflecting higher accuracy and reliability of the simulation model.

To quantify phase errors between observations and simulations, peaks in the hourly time series were identified using MATLAB's “find peaks” function for both observed and simulated data. The phase error was then calculated by measuring the time difference (in hours) between the occurrence of each peak in the observations and the corresponding peak in the simulations. This approach provided a direct assessment of the model's accuracy in capturing the timing of key events, such as storm surges.

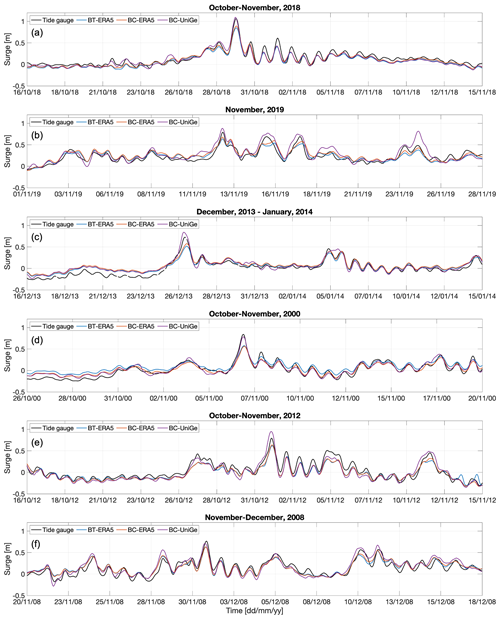
The proposed metrics were also validated using an idealized time series. A sinusoidal time series was generated to represent an observed parameter. Two simulated time series were then created: one with the same amplitude as the observation but shifted in time (introducing a phase error) and the other with the same phase as the observation but with half the amplitude. Various metrics were calculated and plotted as scatter plots (Fig. S1 in the Supplement). The results indicated better performance for the simulation that underestimated the observations when assessed with Pearson correlation, RMSE, and MAD. In contrast, the time series that accurately captured the amplitude was penalized for the phase error, which negatively affected its performance on these metrics. However, the proposed MADp and MADc metrics identified it as the better model.

3 Results

The probability distribution estimates (PDEs) and empirical cumulative distribution functions (ECDFs), available in Figs. S2 to S7, show that BC-UniGe better represents the higher values of storm surge when compared with observations, particularly when considering values above the 99th percentile. However, some overestimations are noticeable for Caorle and Monfalcone with BC-UniGe. In contrast, simulations with ERA5 forcing tend to underestimate these higher values, which is more noticeable for BT-ERA5.

The performance evaluation shows that if the model performance is assessed in terms of Pearson correlation, RMSE, and MAD, the surges simulated with the ERA5 forcing fit better to the measured data (Fig. 3). The Pearson correlation coefficients obtained a range between 0.8 and 0.9 in all locations for the three simulations, with a maximum of 0.842 with BT-ERA5 in Grado (Fig. 3d). Regarding the RMSE, mean values of 0.077 m for BT-ERA5, 0.075 m for BC-ERA5, and 0.079 m for BC-UniGe were obtained, with a minimum of 0.072 m (BT-ERA5 in Grado, Fig. 3d) and a maximum of 0.094 m (BC-UniGe in Monfalcone, Fig. 3e). Similar results are obtained for MAD, which shows better performance for the simulations with ERA5 forcing at all locations. Only in Trieste does BC-UniGe achieve the same performance as BC-ERA5 for this metric. Despite the aforementioned factors, the best performance is achieved by BC-UniGe in the linear fit slope, with values above 0.8 in all locations and a maximum of 0.869 in Monfalcone (Fig. 3e). For this parameter, less favorable performance is obtained with BT-ERA5 at all locations.

For MADp, the best performance is achieved by BC-UniGe at all locations, with a mean value of 0.004 m, while less favorable results are obtained with BT-ERA5, with a mean of 0.011 m. Similar results were obtained for MADc, except in Caorle (Fig. 3c) and Monfalcone (Fig. 3e), where BC-ERA5 showed better performance, likely due to overestimation in the mentioned sites. These results underscore the importance of considering percentiles as part of the performance evaluation. BC-UniGe simulations demonstrate an improvement in representing extreme values, showing a better fit of the highest percentiles, which can be noticed in Figs. 4 and 5. Additionally, these figures indicate that BC-UniGe simulations produce a greater dispersion of data, likely due to a more frequent occurrence of phase error, which was quantified as 3.1 % higher than in BT-ERA5 and 4.5 % higher than in BC-ERA5. However, they also exhibit a better fit of the linear regression and a more accurate representation of extreme values compared to BC-ERA5, which fail to represent the most extreme events in each location.

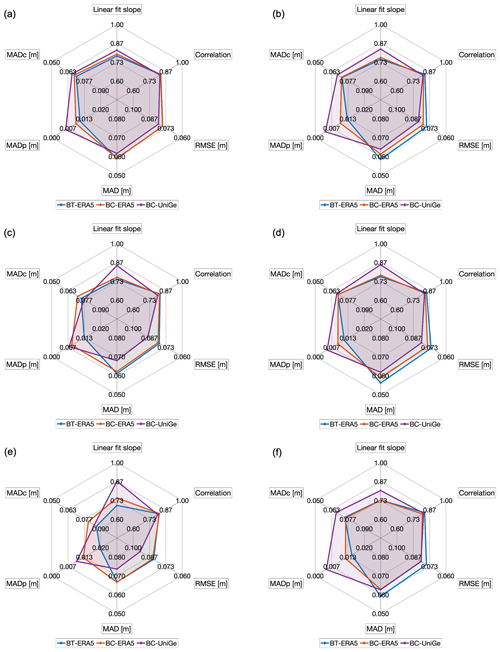
Figure 3 Radar charts of evaluation metrics for the total amount of data in all locations: (a) CNR platform, (b) Punta della Salute, (c) Caorle, (d) Grado, (e) Monfalcone, (f) Trieste. For RMSE, MADp, and MADc a reverse axis is used, this ensures that simulations covering a larger area in each metric represent a better performance (i.e., values on the fringe refer to better performance).

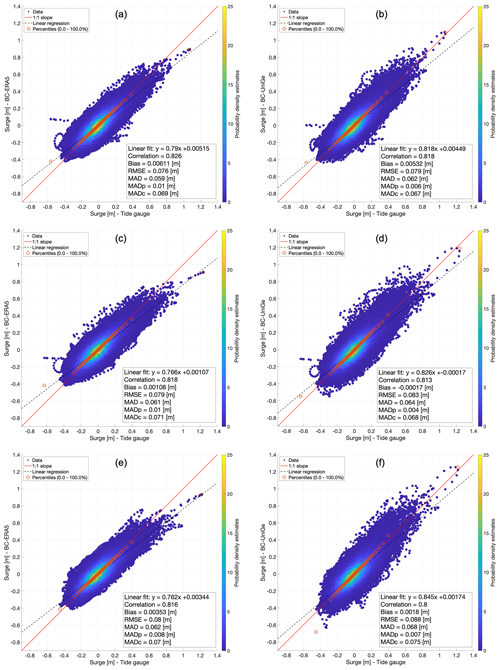
Figure 4 Scatter plots between tide gauges and baroclinic simulations for the CNR platform with BC-ERA5 (a) and BC-UniGe (b), Punta della Salute with BC-ERA5 (c) and BC-UniGe (d), and Caorle with BC-ERA5 (e) and BC-UniGe (f).

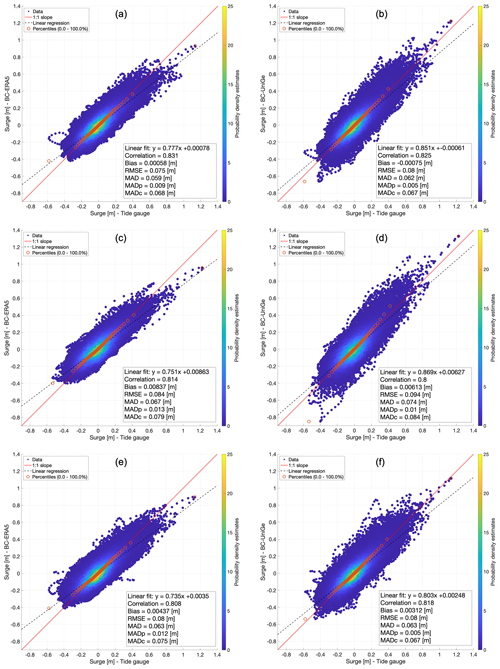
Figure 5 Scatter plots between tide gauges and baroclinic simulations for Grado with BC-ERA5 (a) and BC-UniGe (b), Monfalcone with BC-ERA5 (c) and BC-UniGe (d), and Trieste with BC-ERA5 (e) and BC-UniGe (f).

The results of the error metrics for surge values above the 99th percentile, represented using radar charts (Fig. 6), confirm that, in general, better performance is observed with BC-UniGe, while less favorable results are obtained for BT-ERA5. Although the transition from barotropic to baroclinic configuration indicates an improvement in the representation of extremes (Weisberg and Zheng, 2008; Staneva et al., 2016; Hetzel et al., 2017; Ye et al., 2020; Muñoz et al., 2022), the utilization of UniGe forcing represents the best improvement across practically all metrics. Only in Caorle (Fig. 6c) and Monfalcone (Fig. 6e) does BC-ERA5 show better Pearson correlation, RMSE, and MAD; additionally, at the latter location MADc exhibits better performance for that simulation, likely due to overestimation of the peaks by BC-UniGe in Monfalcone. At the other locations, it is evident that BC-UniGe performs better in representing the highest storm surge values.

In order to show the capacity of the different model configurations to represent certain known storm events at each location, Fig. 7 shows time series of different storm surge events at each location. These extreme events were chosen according to the contributions of Lionello et al. (2012), Međugorac et al. (2018), Ferrarin et al. (2020), Umgiesser et al. (2021), and Giesen et al. (2021). As mentioned before, the incorporation of the UniGe forcing implies a significant improvement in the representation of extreme events, clearly evident in the peak values of the storm surge. Despite this an overestimation of some surge peaks is also observed in the events chosen at Punta della Salute (Fig. 7b), Caorle (Fig. 7c), and Monfalcone (Fig. 7e) with BC-UniGe. On the other hand, a systematic underestimation of extremes obtained in simulations with ERA5 forcing is notable in every surge peak.

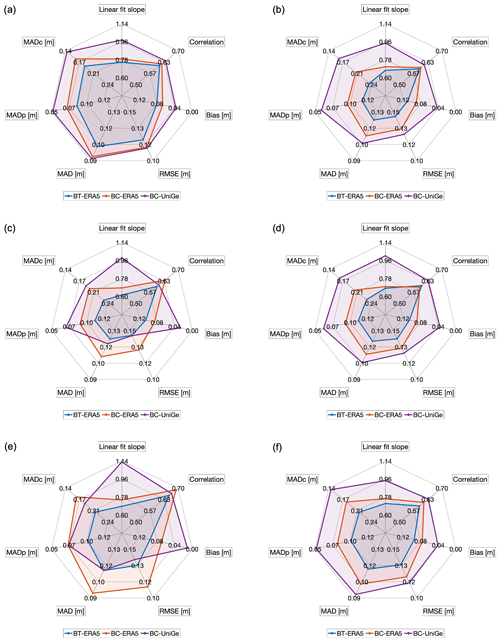
Figure 6 Radar charts of evaluation metrics for surge values above the 99th percentile of the cumulative distribution at each location: (a) CNR platform, (b) Punta della Salute, (c) Caorle, (d) Grado, (e) Monfalcone, and (f) Trieste. Bias is represented by an absolute value. In addition, for RMSE, bias, MADp, and MADc a reverse axis is used. This ensures that simulations covering a larger area for each metric represent a better performance (i.e., values on the fringe refer to better performance).

Figure 7 Time series of different storm surge events in all of the locations, showing the tidal gauge data versus the model data: (a) CNR platform, (b) Punta della Salute, (c) Caorle, (d) Grado, (e) Monfalcone, and (f) Trieste.

4 Discussion

The utilization of different atmospheric forcing databases has revealed significant implications for the representation of storm surge in numerical simulations. Given the direct influence of wind speed and sea level pressure on this phenomenon, as represented in both forcings databases, the resulting model performances present significant differences. While simulations using ERA5 forcing generally show slightly better performance for traditional metrics such as RMSE, MAD, and the Pearson correlation coefficient, a more detailed analysis reveals that using the UniGe forcing results in better performance, especially in terms of the extreme values, when considering additional metrics.

Simulations using ERA5 forcing tend to underestimate the highest surge values, primarily due to a corresponding underestimation of extreme wind speed by this database, a variable crucially linked to surge amplitude (Campos et al., 2022). Despite this, metrics such as the Pearson correlation, RMSE, and MAD generally indicate better performance for ERA5 simulations. Conversely, the utilization of UniGe forcing shows an improvement in representing the peaks of storm surge events (with the noticeable exception of Monfalcone, where the extremes are overestimated, and where MADp present similar values for BC-ERA5 and BC-UniGe). These results demonstrate that the increase in atmospheric forcing resolution does not consistently translate into better values of all the statistical metrics.

It is important to recognize that identifying the optimal model configuration cannot rely solely on a few statistical metrics. As outlined in Sect. 3, no single simulation emerges as superior across all metrics and locations. While ERA5 simulations may demonstrate better performance on RMSE, Pearson correlation, and MAD, BC-UniGe exhibits superior performance in terms of the slope of the linear fit, MADp, and MADc.

From an epistemic point of view, BC-UniGe is a significantly more sophisticated model compared to BT-ERA5. Not only does it employ a higher-resolution forcing, it also takes into account the baroclinicity and the vertical motion within the water column, whereas the barotropic configuration of BT-ERA5 approximates the ocean as a 2D sheet that is only subject to vertically uniform motions and waves. This suggests that widespread indicators such as RMSE, Pearson correlation, and MAD, which in this case identify BT-ERA5 as the best model, should not be considered as the sole source of information in model skill assessment, since a higher-resolution forcing and a baroclinic setup are known in literature to better capture the variability of the sea levels (Weisberg and Zheng, 2008; Hetzel et al., 2017; Muñoz et al., 2022).

Similar results were found by Zampato et al. (2006) using SHYFEM with three different forcings for wind and atmospheric pressure fields: the ECMWF global model, the high-resolution LAMI (Limited Area Model Italy), and satellite QuickSCAT. In this work, the authors found well-correlated sea levels with observations near Venice using the ECMWF forcings but underestimation of the highest values. On the other hand, simulations driven by the high-resolution model (LAMI) succeeded in simulating the storm surge, giving a good reproduction of the sea level peaks. Nevertheless, the correlation with observed data was lower than in the case of ECMWF forcing.

The complexity of simulation performance evaluations is echoed in the work of Mentaschi et al. (2013), who caution against over-reliance on metrics like RMSE, NRMSE (normalized RMSE), and SI (scatter index) as indicators of model performance. These metrics may not fully capture the intricacies of natural processes such as atmospheric dynamics, ocean circulation, or wave generation and propagation. These authors mention that the RMSE and its variations tend to assume typical values of the best performance for simulations that underestimate the physical process of interest. The discrepancy between metrics and the representation of extremes highlights the need for a comprehensive understanding of model performance beyond traditional statistical measures.

These performance evaluation results are usually related to phase error in high-resolution models and RMSE “double penalty”. The phase error refers to a discrepancy between the timing or phase of a simulated event and its actual occurrence on measured data. In the context of atmospheric models, phase errors can manifest as delays or advances in the timing of weather events, such as the onset of precipitation, the movement of storm systems, or the arrival of fronts. Double penalty refers to a situation where the errors in the model output are penalized twice in indicators such as RMSE and MAD, once for missing the observations and again for giving a false alarm (e.g., Gilleland et al., 2009). This is a well-known problem during performance evaluation of numerical models, and different contributions have sought to overcome it with approaches specialized in atmospheric and oceanographic fields (e.g., Ebert and Mcbride, 2000; Zingerle and Nurmi, 2008; Roberts and Lean, 2008; Mittermaier, 2014; Skok and Roberts, 2016; Crocker et al., 2020).

In RMSE, double penalty is further amplified compared to MAD, as the penalizations due to the peak mismatch are squared. This means that phase errors have a disproportionately large impact on RMSE. A more sophisticated model may be better able to capture the magnitude of the peaks, but as it is more prone to phase error compared to low-resolution ones this ability will be doubly penalized. This is the reason why a less sophisticated model employing a low-resolution forcing (BT-ERA5) appears to outperform the other two in terms of RMSE. Conversely, MAD, although it also experiences a form of double penalty, reduces the impact of this effect compared to RMSE. As a result, the performance differences between simulations, particularly above the 99th percentile, are generally more pronounced for MAD than for RMSE, better highlighting the superiority of BC-UniGe. This enhanced differentiation is likely due to MAD's linear weighting of errors, which reduces the inflated impact of large deviations that characterize RMSE.

In other words, RMSE tends to be better for “blurring” models, whereas high-resolution models, known to be more capable of reproducing small-scale dynamics (e.g., BC-UniGe), perform worse in terms of RMSE due to phase error (Crocker et al., 2020). Although in many aspects capturing a peak with a phase error is preferable to missing the peak entirely, this does not lead to a reduction in the RMSE.

This limitation of RMSE also impacts the Pearson correlation. Indeed, RMSE can be decomposed into a bias component and a scatter component that depends solely on the Pearson correlation (Mentaschi et al., 2013, Eq. 8). All of these considerations call for caution when claiming that one model outperforms another simply based on a better value of RMSE, MAD, or Pearson correlation.

The MADc indicator was introduced here as a possible way to correct MAD to make it less prone to the double penalty effect. The incorporation in MADc of a term that takes into account the distribution of the data (the MAD of the percentiles MADp) rewards the ability of a high-resolution and more sophisticated model to reproduce the variability in the observations without systematic errors. In other words, MADc remains more resilient to phase errors compared to other metrics, ensuring that discrepancies in the timing of events do not unduly influence the assessment of model performance. The differences between the simulation metrics are generally in the range of millimeters when considering the overall data, but these differences are significant in relative terms. For the MADc metric, BC-UniGe shows improvements ranging from 1.3 % (Grado) to 9.3 % (Trieste) compared to BT-ERA5 and from 1.6 % (Grado) to 10.3 % (Trieste) compared to BC-ERA5. The improvements are even more notable when focusing on values above the 99th percentile, where BC-UniGe outperforms BT-ERA5 by 12 % (Monfalcone) to 31.6 % (Trieste) and BC-ERA5 by 4.1 % (Caorle) to 20.2 % (Trieste).

As shown in Sect. 3, some discrepancies were observed in Caorle and Monfalcone, where BC-ERA5 achieved better performance in terms of MADc. A possible explanation for this could be related to the location of the tide gauges at these sites. The tide gauge at Caorle is situated in a protected area inside the Livenza River, a location not fully represented by the simulations due to the resolution of the coastline, even though high-resolution model data were used. A similar issue is found in Monfalcone, where the tide gauge is located in front of a breakwater not fully represented by the coastline used in the model. These factors could affect the signals obtained from observations and simulations, primarily due to local effects at the tide gauge locations.

5 Conclusions

In this study we developed high-resolution simulations of storm surge in the northern Adriatic Sea spanning from 1987 to 2020 using the model SHYFEM and employing different forcing data and physical configurations. The comparative analysis of the results highlights nuanced differences in performance metrics, particularly concerning the representation of the extreme values. Traditional metrics like Pearson correlation, RMSE, and MAD favor a simulation (BT-ERA5) forced by a coarser database and employing a less sophisticated setup (barotropic). However, a closer examination and the use of different metrics tell a different story and allow us to identify a baroclinic model forced by a high-resolution dataset (BC-UniGe) as better able to capture the variability of the water levels and, in particular, the extremes. This is because BC-UniGe is more prone to phase error than BT-ERA5 and is thus doubly penalized in indicators such as RMSE, MAD, and Pearson correlation.

The corrected MAD (MADc) introduced in this study comes as a possible way to alleviate the double penalty by adding a term that rewards the ability of a model to capture the distribution of the observations irrespective of the position of the peaks. In this study MADc is successful in identifying BC-UniGe as the best simulation in most locations. Even though this study has focused on the performance evaluation of storm surge, the analysis and proposed customized metrics (MADc and MADp) can be applied to any problem of validating a numerical model with observations by time series comparison.

These findings suggest that simply having a lower RMSE is insufficient evidence to claim that one model is superior to another. RMSE, MAD, and Pearson correlation are valuable indicators but should be used considering their limitations and complemented by other metrics, qualitative assessment, and expert judgment.