TEOS-10 and the climatic relevance of ocean–atmosphere interaction

Unpredicted observations in the climate system, such as recent excessive ocean warming, are often lacking immediate causal explanations and are challenging numerical models. As a highly advanced mathematical tool, the Thermodynamic Equation of Seawater – 2010 (TEOS-10) was established by international bodies as an interdisciplinary standard and is recommended for use in geophysics, such as, and in particular, in climate research. From its very beginning, the development of TEOS-10 was supported by Ocean Science through publishing successive stages and results. Here, the history and properties of TEOS-10 are briefly reviewed. With focus on the air–sea interface, selected current problems of climate research are discussed, and tutorial examples for the possible use of TEOS-10 in the associated context are presented, such as topics related to ocean heat content, latent heat, and the rate of marine evaporation; properties of sea spray aerosol; or climatic effects of low-level clouds. Appended to this article, a list of publications and their metrics is provided for illustrating the uptake of TEOS-10 by the scientific community, along with some continued activities, addressing still pending, connected issues such as uniform standard definitions of uncertainties of relative humidity, seawater salinity, or pH.

This article is dedicated to the jubilee celebrating 20 years of Ocean Science.

This article is also dedicated to the memory of Wolfgang Wagner, who sadly and unexpectedly passed away on 12 August 2024. His contributions to TEOS-10 are truly indispensable constituents; Wolfgang was an essential co-author of various related documents and articles. He will be deeply missed.

All the rivers run into the sea; yet the sea is not full; unto the place from whence the rivers come, thither they return again.

The King James Bible: Ecclesiastes, 450–150 BCE

He wraps up the waters in his clouds, yet the clouds do not burst under their weight.

Holy Bible: New International Version, Job 26:8

Of the air, the part receiving heat is rising higher. So, evaporated water is lifted above the lower air.

Leonardo da Vinci: Primo libro delle acque, Codex Arundel, ca. 1508

Two-thirds of the Sun's energy falling on the Earth's surface is needed to vaporize … water … as a heat source for a gigantic steam engine.

Heinrich Hertz: Energiehaushalt der Erde, 1885

The sea-surface interaction is obviously a highly significant quantity in simulating climate.

Andrew Gilchrist and Klaus Hasselmann: Climate Modelling, 1986

The climate of the Earth is ultimately determined by the temperatures of the oceans.

Donald Rapp: Assessing Climate Change, 2014

1 Introduction

Quite recently in 2024, climate research has published alarming news: “The world's oceans absorbed more heat in 2023 than in any other year since records began in the 1950s. … Data show that the heat stored in the upper 2000 m of oceans increased by 15 zettajoules (1 zettajoule is 10²¹ joules) in 2023 compared with that stored in 2022. This is an enormous amount of energy – for comparison, the world's total energy consumption in 2022 was roughly 0.6 zettajoules” (You, 2024: p. 434). Dividing this value by the global ocean surface area and by the duration of a year, the reported ocean's average warming rate amounts to 1.3 W m⁻², and is apparently even increasing. “Earth's net global energy imbalance (12 months up to September 2023) amounts to +1.9 W m⁻², … ensuring further heating of the ocean” (Kuhlbrodt et al., 2024: p. E474). “Climate models struggle to explain why planetary temperatures spiked suddenly. … No year has confounded climate scientists' predictive capabilities more than 2023. … This sudden heat spike greatly exceeds predictions made by statistical climate models” (Schmidt, 2024: p. 467).

The currently observed ocean heat content (OHC) represents a merely transient maximum after a decade-long systematic warming process in the past (see Fig. 18 in Sect. 6), which may proceed to even higher values in the future. In Sect. 3, thermodynamic aspects of related OHC definitions will be considered. Regarding the long-term period since 1971, “the drivers of a larger Earth energy imbalance in the 2000s than [before] are still unclear. … Future studies are needed to further explain the drivers of this change” (von Schuckmann et al., 2023: p. 1694). Laterally, the observed heat excess is unevenly distributed over the world ocean (Fig. 1), in contrast to what naively may be expected from rising atmospheric CO₂ concentrations. Rather, warming seems to be most pronounced in the cloudy austral and boreal west-wind belts. Selected thermodynamic relations between OHC and cloudiness are briefly discussed in Sect. 6.

Sunlight is the only available heat source of sufficient power to cause the observed warming, while the globally averaged geothermal heat flux is estimated to be just 0.087 W m⁻² (Pollack et al., 1993) and is not expected to suddenly rise recently due to human impact. Irradiation is hampered by clouds; dust and absorbing gases; and water surface reflection such as by whitecaps, waves, or plankton layers (Cahill et al., 2023). Heat absorbed in the water column may effectively exit the ocean again only across the air–sea interface via sensible, radiative, and latent heat flux. All these effects may vary in the climate system in a complicated, mutually interacting manner. Typically, present numerical climate models suffer from an “ocean heat budget closure problem” (Josey et al., 1999) and describe the ocean–atmosphere heat flux only to within uncertainties between 10 and 30 W m⁻² (Josey et al., 2013). According to recent model comparison studies, many of those “models fail to provide as much heat into the ocean as observed” (Weller et al., 2022: p. E1968). Dynamical models, rather than observed correlations, are the most reliable tools for the detection and verification of causal relations (Feistel, 2023); however, such as in this case of air–sea interaction, large uncertainties may prevent any significant conclusions from being drawn regarding the causes of the observed ocean warming rate of 1.3 W m⁻².

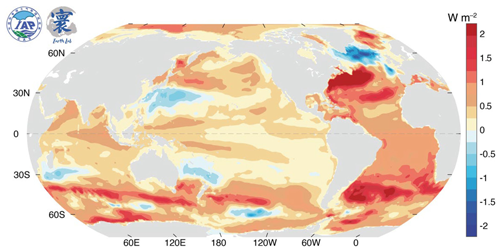
Figure 1 Observed trend 1958 through 2022 of the upper 2000 m ocean heat content (WMO, 2024). Image reproduction permitted by © WMO.

Of the increasing amount of water vapour contained in the global troposphere, 85 % results from ocean evaporation (Gimeno et al., 2013). Corresponding to 1200 mm annual evaporation (Budyko, 1963, 1984; Baumgartner and Reichel, 1975; Peters-Lidard et al., 2019), the associated latent heat flux of about 95 W m⁻² per ocean surface area represents the strongest energy supply for the atmospheric dynamics (Albrecht, 1940) and at the same time the strongest cooling process of the sea. This flux depends sensitively on the relative humidity (RH) at the water surface; an RH increase by 1 % RH can be estimated to reduce evaporation by 5 W m⁻² (Feistel, 2015, 2024; Feistel and Hellmuth, 2021, 2023); therefore, a minor additional 0.2 % RH may already suffice to warm up the ocean by the observed 1.3 W m⁻². Unfortunately, marine RH is observed only with uncertainties between 1 and 5 % RH (Lovell-Smith et al., 2016) or, accordingly, between 5 and 25 W m⁻² of latent heat flux, which is roughly corresponding to unknown variations ranging up to 50–250 mm evaporation per year. It remains unclear as to what extent minor, yet unnoticed changes in marine RH may be responsible for the recent ocean warming.

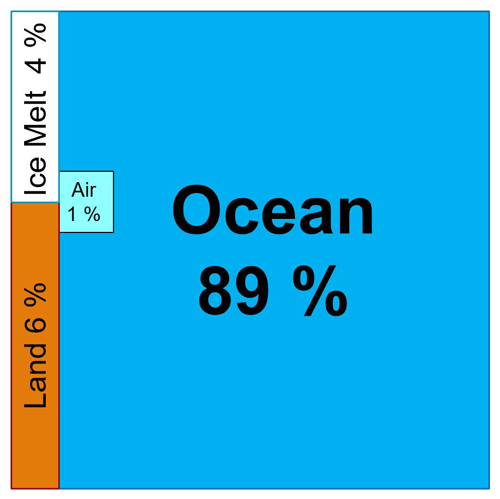
Figure 2 Heat fractions stored additionally in the different parts of the Earth system 1960–2020 (values from von Schuckmann et al., 2023), represented graphically by partial areas. Obviously, the oceans dominate global warming.

According to Fig. 2, a paramount share of 94 % of global warming occurs in different phases and geophysical mixtures of water, in particular in seawater. Considering this situation, the Scientific Committee on Oceanic Research (SCOR) in cooperation with the International Association for the Physical Sciences of the Oceans (IAPSO) decided at its 2005 Cairns meeting on the establishment of the SCOR/IAPSO Working Group 127 on Thermodynamics of Seawater (WG127) (Millero, 2010; Pawlowicz et al., 2012; Smythe-Wright et al., 2019), which held its inaugural meeting in 2006 at Warnemünde (Fig. 3). It had been recognized that “modelling of the global heat engine needs accurate expressions for the entropy, enthalpy, and internal energy of seawater so that heat fluxes can be more accurately determined in the ocean” (Millero, 2010: p. 28), while such properties were not available from the thermodynamic seawater standard at that time, the 1980 equation of state of seawater (EOS-80) (Fofonoff and Millard Jr., 1983).

Figure 3 Participants of the 2006 kick-off meeting of SCOR/IAPSO WG127 at the Leibniz Institute for Baltic Sea Research (IOW) in Warnemünde, Germany. From left to right: Chen-Tung Arthur Chen (Taiwan), Frank Millero (USA), Brian King (UK), Rainer Feistel (WG vice chair, Germany), Daniel Wright (Canada, deceased 2010), Trevor McDougall (WG chair, Australia) and Giles Marion (USA).

Figure 4 Participants of the BIPM–IAPWS meeting in February 2012 at the Pavillon de Breteuil, Sèvres. From left to right: Dan Friend (IAPWS), Karol Daučik (IAPWS president), Jeff Cooper (IAPWS), Alain Picard (BIPM, deceased 2015), Petra Spitzer (WG127), Rainer Feistel (WG127), Michael Kühne (director BIPM), Andy Henson (BIPM), and Robert Wielgosz (BIPM).

The foundation of WG127 happened almost coincidently with the establishment of the Ocean Science journal of the European Geosciences Union (EGU) in 2004–2005. The development of the new standard by WG127, the Thermodynamic Equation of Seawater – 2010 (TEOS-10), was very successfully supported by Ocean Science, publishing the Special Issue No. 14 on “Thermophysical properties of seawater” with 16 articles between 2008 and 2012 (Feistel et al., 2008a). Appendix A reports the current metrics of this special issue. Also in 2008, at its conference in Berlin, Germany, the International Association for the Properties of Water and Steam (IAPWS) established the new Subcommittee on Seawater (SCSW) that cooperated closely with WG127. In the form of carefully verified mathematical formulations for properties of water, ice, seawater, and humid air, IAPWS adopted nine fundamental documents related to TEOS-10 (IAPWS AN6-16, 2016); see Appendix A.

With respect to problems still pending after the official adoption of TEOS-10, especially for the preparation of future novel international definitions of seawater salinity, seawater pH, and atmospheric relative humidity (Feistel et al., 2016; Pawlowicz et al., 2016; Dickson et al., 2016; Lovell-Smith et al., 2016), the standing IAPSO/SCOR/IAPWS Joint Committee on the Properties of Seawater (JCS) was established in 2012. In 2011, IAPWS also extended its cooperation with the International Bureau for Weights and Measures (BIPM); see Fig. 4. Further details on TEOS-10 (IOC et al., 2010; McDougall et al., 2013; Feistel, 2018; Wikipedia, 2024) are available from the TEOS-10 home page (https://www.teos-10.org, last access: 23 October 2024) and are briefly reviewed in Sect. 2 and Appendix B.

In the context of the predecessor EOS-80, ocean heat content (OHC) was defined in terms of potential temperature (Abraham et al., 2013). Improving this method, TEOS-10 entropy and enthalpy of seawater provided a proper quantitative basis for a novel, thermodynamically rigorous definition of the OHC in the form of seawater potential enthalpy (McDougall, 2003; McDougall et al., 2013, 2021; Graham and McDougall 2013), equivalently defined as Conservative Temperature and briefly discussed in Sect. 3.

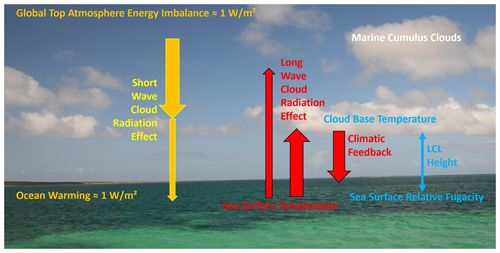
Figure 5 Schematic of cloud radiation effects (CREs). The shortwave effect (SW CRE) controls the downward flux of solar irradiation, while the longwave effect governs the infrared radiation balance between water surface and cloud base. By thermal convection, cumulus clouds emerge at the isentropic lifted condensation level (LCL). Figure from Feistel and Hellmuth (2024b).

Currently implemented parameterizations of marine evaporation rates in the form of historical Dalton equations (Stewart, 2008; Josey et al., 1999, 2013) may be replaced by TEOS-10 chemical potentials, which provide the proper quantitative basis for a thermodynamically rigorous formulation of non-equilibrium Onsager forces and fluxes in terms of relative fugacity (RF) of humid air (Kraus and Businger, 1994; Feistel and Lovell-Smith, 2017; Feistel and Hellmuth, 2023, 2024a), as described in Sect. 4. Relative humidity (RH) is defined relative to the saturation state of moist air, which in turn is controlled by the chemical potentials of water in the gas and liquid phase. It is only natural, therefore, to define RH in terms of chemical potentials, which in fact is performed by RF. The uncertainty of latent heat flux with respect to the uncertainty of surface RH observation is shown to be significantly larger than the observed warming of 1.3 W m⁻²; therefore this unpredicted warming may or may not be caused by a minor RH increase that has been ignored so far.

The conceptual model of sea air as a two-phase composite thermodynamic system is outlined in Sect. 5. The roles of enthalpy, chemical potential, and entropy are explained by means of explicit theoretical descriptions of three simplified tutorial examples: (i) for the latent heat of evaporation, (ii) for the heat capacity of humid air containing sea spray, and (iii) for the entropy production of irreversible evaporation.

Clouds do not only release the latent heat which water vapour has carried away from the ocean; they also interfere substantially in the global radiation balance, cooling the surface by reflecting shortwave solar irradiation and warming the surface by sending back down longwave thermal radiation; see Fig. 5. In the course of global warming, cloudiness has been found to exhibit a systematic trend of reduction (see Sect. 6), which affects the ocean heat content in a non-trivial, non-uniform manner. Marine cumulus clouds arise by isentropic uplift of thermal convection. Their height controls their temperature and their thermal downward radiation, affecting the ocean's energy balance. Updating previous results (Romps, 2017) for the lifted condensation level (LCL) of marine cumulus clouds to thermodynamically rigorous TEOS-10 standard equations (Feistel and Hellmuth, 2024b), the radiative effect of those clouds can be estimated from sea-surface temperature (SST) and surface relative humidity. This effect turns out to be weakly cooling and cannot provide a reasonable explanation for the strong ocean warming that is still unclear. The effect of increasing SST in the past decades has turned out to be minor in comparison to that caused by RH uncertainty.

Section 7 provides a summary of this paper. Appendix A reports collections of publications with respect to TEOS-10 as well as their metrics, and Appendix B gives a short introduction to the concept of thermodynamic potentials.

2 Thermodynamic Equation of Seawater – 2010 (TEOS-10)

In the climate system, the omnipresent and dominant substance is water in various phases and mixtures. For example, “water vapor is by far the most important greenhouse gas, in the sense that it absorbs more irradiance from the Earth than all other greenhouse gases combined” (Rapp, 2014: p. 381). Textbooks and other publications offer numerous collections of various different property equations for water, ice, seawater, or moist air, but uncertainties and mutual consistencies of those equations are often unclear. To improve this situation, the novel Thermodynamic Equation of Seawater – 2010 (TEOS-10) was developed by the members of the SCOR/IAPSO Working Group 127 (WG 127) in close cooperation with the International Association for the Properties of Water and Steam (IAPWS). TEOS-10 is described in a detailed manual (IOC et al., 2010) and has been adopted and recommended by IOC-UNESCO (2009) in Paris and by the IUGG (2011) in Melbourne; see also Feistel (2008b, 2012, 2018), Valladares et al. (2011), and Pawlowicz et al. (2012). Starting in 2008 with a special issue of Ocean Science (Feistel et al., 2008a), a large number of scientific publications have appeared in the meantime, supporting, extending, or exploiting TEOS-10. A collection of selected papers related to TEOS-10 is summarized in Appendix A, together with metrics that illustrate the growing uptake of TEOS-10 by the scientific community.

The development of the first numerical thermodynamic Gibbs potentials (see Appendix B) for seawater (Feistel, 1991, 1993; Feistel and Hagen, 1995) was based on the works of Millero and Leung (1976) and Millero (1982, 1983), together with high-pressure background data of the previous EOS-80 standard (Unesco, 1981). Independently of that, a Helmholtz potential for pure fluid water had been adopted by IAPWS in 1996 at Fredericia (Harvey, 1998; Wagner and Pruß, 2002). These were the key activities which eventually culminated in the formulation of TEOS-10 about 2 decades later. By combining those equations for pure and seawater, some known pending problems of EOS-80 (Fofonoff and Millard Jr., 1983) could incidentally be resolved (Feistel, 2003). In the end, TEOS-10 has been assembled from four basic thermodynamic potentials derived from the mutually consistent, most comprehensive, and most accurate datasets of measured properties available at that time. Those potentials are as follows (IAPWS R6-95, 2016; IAPWS R10-06, 2009; IAPWS R13-08, 2008; IAPWS G8-10, 2010; respectively):

• i.

  A Helmholtz function of fluid water. $f^{\mathrm{F}}\left(T,\mathit{\rho }\right)\equiv f^{\mathrm{W}}\left(T,\mathit{\rho }\right)\equiv f^{\mathrm{V}}\left(T,\mathit{\rho }\right)$, known as the IAPWS-95 formulation (Wagner and Pruß, 2002), which is identical for liquid water, f^W(T,ρ), and for water vapour, f^V(T,ρ). It describes de-aerated water of a fixed isotopic composition, termed Standard Mean Ocean Water (SMOW), with density ρ and temperature T.

• ii.

  A Gibbs function of ambient hexagonal ice I. This is the g^Ih(T,p) or IAPWS-06 formulation (Feistel and Wagner, 2006) (see Tables A2 and A3 of Appendix A), depending on pressure p.

• iii.

  A Gibbs function of IAPSO Standard Seawater. This is the $g^{\mathrm{SW}}\left(S,T,p\right)$ or IAPWS-08 formulation (Feistel, 2008a); see Tables A2 and A3 of Appendix A. The variable S, at which a subscript A is omitted here for simplicity, is the specific or Absolute Salinity, the mass fraction of dissolved salt in seawater, which differs from Practical Salinity, S_P, measured by present-day oceanographic instruments, as well as from various other obsolete salinity scales (Millero et al., 2008). Throughout this paper, the term “salinity” is exclusively shorthand for TEOS-10 Absolute Salinity. Sea salt is assumed to have stoichiometric Reference Composition. The pure-water limit, $g^{\mathrm{SW}}\left(\mathrm{0},T,p\right)=g^{\mathrm{W}}\left(T,p\right)$, is the Gibbs function of liquid water computed from the IAPWS-95 Helmholtz function f^W(T,ρ). For brackish seawater, g^SW has implemented Debye's root law of dilute electrolyte solutions (Landau and Lifschitz, 1966; Falkenhagen et al., 1971).

• iv.

  A Helmholtz function of humid air. This is the $f^{\mathrm{AV}}\left(A,T,\mathit{\rho }\right)$ or IAPWS-10 formulation (Feistel et al., 2010a); see Tables A1 and A2 of Appendix A. The variable A is the mass fraction of dry air admixed with water vapour, so $q=\mathrm{1}-A$ is the specific humidity. The dry-air limit $f^{\mathrm{AV}}\left(\mathrm{1},T,\mathit{\rho }\right)=f^{\mathrm{A}}\left(T,\mathit{\rho }\right)$ equals, up to modified reference-state conditions, the equation of state of Lemmon et al. (2000). The air-free limit $f^{\mathrm{AV}}\left(\mathrm{0},T,\mathit{\rho }\right)=f^{\mathrm{V}}\left(T,\mathit{\rho }\right)$ equals the IAPWS-95 Helmholtz function of water vapour. In f^AV, the interaction of water vapour with dry air is described by second and third virial coefficients.

Thermodynamic potentials include certain adjustable constants expressing the absolute energies and entropies of the particular substances, which are not available from measurement (Planck, 1906; Feistel, 2019b) and have, in turn, no effect on measurable properties derived from those potentials. In fact, among the comprehensive experimental datasets from which the TEOS-10 equations were derived, none of those are suitable for fitting the empirical coefficients that represent absolute energies and entropies of those equations. For this reason, the International Conference on the Properties of Steam in London in 1967 defined the common triple point of water as the reference state at which those absolute values were arbitrarily set. Since then, no evidence has appeared for putative conflicts caused by such settings with any technical or scientific applications of the equations. Despite this, Feistel and Wagner (2006) and Feistel et al. (2008b) discuss the implementation of alternative residual entropies of water, if that should be of interest in exceptional applications of TEOS-10. For recent discussions of Pauling's absolute “residual” entropy at 0 K and Nernst's Third Law of Thermodynamics, see Kozliak and Lambert (2008), Gutzow and Schmelzer (2011), Takada et al. (2015), Schmelzer and Tropin (2018), Feistel (2019b), or Shirai (2023).

The TEOS-10 reference states (Feistel et al., 2008b, 2010a) are the triple point of water, T_TP=273.16 K, p_TP=611.654771 Pa, where the conditions

$$\begin{array}{}\text{(1)}& {\mathit{\eta }}_{\mathrm{TP}}^{\mathrm{W}}=\mathrm{0},e_{\mathrm{TP}}^{\mathrm{W}}=\mathrm{0},\end{array}$$

are imposed, as well as the standard-ocean state at Absolute Salinity, $S_{\mathrm{SO}}=\mathrm{35.16504}\mathrm{g}{\mathrm{kg}}^{-\mathrm{1}}$; absolute temperature, T_SO=273.15 K; and absolute pressure, p_SO=101 325 Pa, with the conditions for sea salt,

$$\begin{array}{}\text{(2)}& {\mathit{\eta }}_{\mathrm{SO}}^{\mathrm{SW}}=\mathrm{0},h_{\mathrm{SO}}^{\mathrm{SW}}=\mathrm{0},\end{array}$$

and for dry air,

$$\begin{array}{}\text{(3)}& {\mathit{\eta }}_{\mathrm{SO}}^{\mathrm{A}}=\mathrm{0},h_{\mathrm{SO}}^{\mathrm{A}}=\mathrm{0}.\end{array}$$

Here, η, e, and h, respectively, are specific entropy, internal energy, and enthalpy of water (superscript W), seawater (superscript SW), and dry air (superscript A). The TEOS-10 potential functions and properties thereby derived are numerically implemented in two different libraries, the Sea-Ice-Air (SIA) and the Gibbs-SeaWater (GSW) libraries; see Table A4 in Appendix A.

The SIA library only includes empirical coefficients in the four fundamental potentials (Feistel, 2010d; Wright et al., 2010). All other potential functions and properties are derived strictly by mathematical operations to ensure consistent results, even at the cost of low computation speeds as a result of stacked iteration procedures. All quantities are exclusively expressed in basic SI units such as kilograms (kg), metres (m), joules (J), or pascals (Pa). A more recent extension of SIA code is reported in Feistel et al. (2022) for the computation of relative fugacity.

The GSW library is tailored for oceanographic models, optimized in computation speed (Roquet et al., 2015). For fast numerical evaluation, GSW procedures contain new empirical coefficients determined from the SIA library functions by regression. Units and variables are adjusted to common oceanographic practice such as pressure in decibars relative to surface pressure or temperatures in degrees Celsius (°C). Conservative Temperature (CT) is used as a new preferred thermal variable. An additional thermodynamic potential has been constructed (McDougall et al., 2023) that supports the use of CT universally as an independent variable.

3 Potential enthalpy and ocean heat content (OHC)

Thermodynamically, the term “ocean heat content” (OHC) is sloppy wording. “Content” means a state quantity of a body or volume, while, by contrast, “heat” is an exchange quantity rather than a state quantity. “We have … a right to speak of heat as a measurable quantity, … however, … we have no right to treat heat as a substance” (Maxwell, 1888: p. 7). “The obsolete hypothesis of heat being a substance is excluded” (Sommerfeld, 1988: p. 6). “Heat is not a substance! More formally: Heat is not a thermodynamic function of state” (Romer, 2001: p. 107). This distinction is qualitatively fundamental (Feistel, 2023). Physical conservation quantities such as energy or mass have the key property that the change of that quantity in a volume equals the flux of that quantity across the boundary (Landau and Lifschitz, 1966; Glansdorff and Prigogine, 1971), but this does not apply to heat. For example, a heat engine receives a permanent net heat flux without getting permanently hotter. While asking how much heat is contained in the ocean may find ambiguous answers, it is correct to say how much heat has entered or left the ocean across its boundary by a specified process that transfers the ocean from a certain state of reference to the current state of interest. In this section, based upon TEOS-10, related states and processes are described which may properly specify what is commonly termed OHC. This consideration intrinsically connects OHC with ocean–atmosphere exchange processes relevant to climate change.

Since a long time, measuring and calculating the ocean's “heat” has been a question of central interest to oceanography. Recently, this issue has become even more important and urgent in the context of climate change. “The total energy imbalance at the top of atmosphere is best assessed by taking an inventory of changes in energy storage. The main storage is in the ocean” (Abraham et al., 2013: p. 450). The conventional approach is a formally defined mathematical procedure based on potential temperatures. “Changes to ocean heat content (OHC) can be calculated from measurements of the temperature evolution of the ocean. The OHC is attained from the difference of the measured potential temperature profile and the potential temperature climatology. This difference is integrated over a particular reference depth (for instance, 700 m) and is multiplied by a constant ocean density reference and heat capacity” (Abraham et al., 2013: p. 468). However, in representing a kind of “heat substance”, this OHC definition has no rigorous thermodynamic justification, and the relation to processes of ocean–atmosphere heat fluxes is not entirely clear. If a sea–air heat flux of 1 W m⁻² warms up the atmosphere, by what rate exactly will that OHC decrease?

Making the seawater properties entropy and enthalpy quantitatively available, TEOS-10 has offered a thermodynamically improved option for defining OHC (McDougall et al., 2021), in the form of the integral over the ocean volume,

$$\begin{array}{}\text{(4)}& \mathrm{OHC}=\int h^{\mathrm{SW}}\left(S,\mathit{\eta },p_{\mathrm{0}}\right){\mathit{\rho }}^{\mathrm{SW}}\left(S,\mathit{\eta },p\right)\mathrm{d}V.\end{array}$$

Here, $h^{\mathrm{SW}}\left(S,\mathit{\eta },p_{\mathrm{0}}\right)$ is the potential enthalpy (McDougall, 2003) relative to the surface pressure, p₀, and ${\mathit{\rho }}^{\mathrm{SW}}\left(S,\mathit{\eta },p\right)$ is the in situ mass density at the pressure p of a parcel with salinity and entropy equal to those before. This definition can be understood in terms of both a specified process of heat exchange and a reference state relative to which OHC is counted, as follows (Feistel, 2024):

• i.

  A virtual heat exchange process supporting the definition (4) is sketched in Fig. 6. In turn, each ocean parcel with in situ properties $\left(S,\mathit{\eta },p\right)$ is lifted to the surface pressure p₀, keeping its salinity and entropy constant. There, it reversibly exchanges heat, dh=Tdη, with a measuring device until the parcel's entropy has reached a certain reference value, η_ref, while the parcel's salinity remains unchanged. Subsequently, the heat is reversibly put back to the parcel which is then returned to its original location. The work required to lift and lower the parcel is balanced because the parcel's thermodynamic state is exactly the same before and after the balanced reversible heat exchange across the surface. The heat content defined this way for a single parcel is added up then over all ocean parcels to result in its total OHC value.

• ii.

  The reference state relative to which OHC is measured may freely be specified at will but beneficially be chosen with respect to its convenience or usefulness. In the case of Eq. (4), the OHC reference state is zero potential enthalpy (or zero Conservative Temperature; McDougall 2003) of all ocean parcels.

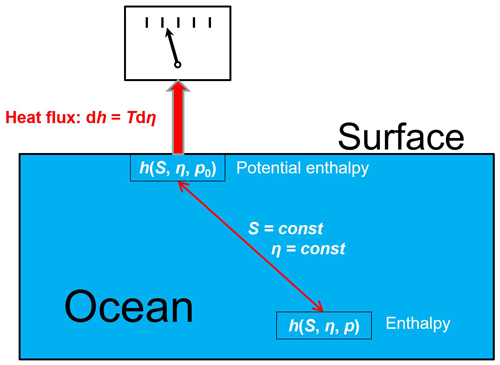
Figure 6 Schematic of a conceptual process defining the ocean heat content (OHC) by measuring heat flux across the ocean boundary according to Eqs. (4) and (5).

The process depicted in Fig. 6 measures the total heat flux $\int \mathrm{d}h=\int T\mathrm{d}\mathit{\eta }$, which changes the entropy of the given sample from the current value, η, to some arbitrary reference value, η_ref, and this way, the process also changes the parcel's enthalpy from $h^{\mathrm{SW}}\left(S,\mathit{\eta },p_{\mathrm{0}}\right)$ to $h^{\mathrm{SW}}\left(S,{\mathit{\eta }}_{\mathrm{ref}},p_{\mathrm{0}}\right)$. Integration over all ocean samples results in an OHC value of

$$\begin{array}{}\text{(5)}& \begin{array}{rl}{\mathrm{OHC}}^{*}& =\int \left[h^{\mathrm{SW}}\left(S,\mathit{\eta },p_{\mathrm{0}}\right)-h^{\mathrm{SW}}\left(S,{\mathit{\eta }}_{\mathrm{ref}},p_{\mathrm{0}}\right)\right]{\mathit{\rho }}^{\mathrm{SW}}\\ & \left(S,\mathit{\eta },p\right)\mathrm{d}V.\end{array}\end{array}$$

While the choice of the OHC reference state is – in principle – entirely arbitrary, such as simply putting η_ref=0, it is reasonable to better adapt this selection to the purpose of the OHC definition. The main purpose of estimating OHC is keeping track of the ocean's long-term energy balance, in particular of the ocean's share of global warming. Three conditions appear immediately plausible in order to achieve this goal:

• i.

  The OHC definition should ensure that OHC differences represent a suitable spatial integral over the heat fluxes crossing the ocean's boundaries. As discussed in more detail in Sect. 5.3, production of entropy, d_iη, caused by irreversible processes between different parcels within the ocean, does not affect the ocean's total enthalpy budget. This is quite in contrast to entropy exchange, d_eη, of the given sample in the form of reversible heat flux across its boundary. Such irreversible processes affect the ocean's total potential enthalpy much less than its total entropy (McDougall et al., 2021). For this reason the OHC reference state should explicitly be defined in terms of potential enthalpy, $h^{\mathrm{SW}}\left(S,{\mathit{\eta }}_{\mathrm{ref}},p_{\mathrm{0}}\right)$, and this way only implicitly in terms of entropy by specifying η_ref(S).

• ii.

  Provided that the ocean's mass remains the same between any two ocean states (1) and (2), the difference OHC(1) − OHC(2) should depend only on the surface heat flux balance during the time in between. In particular, differences OHC(1) − OHC(2) should not depend on the OHC reference state. For this reason, the OHC reference value should be independent of changes occurring in the density distribution, ${\mathit{\rho }}^{\mathrm{SW}}\left(S,\mathit{\eta },p\right)$. This can be achieved by assigning to each ocean parcel the same reference potential enthalpy, $h^{\mathrm{SW}}\left(S,{\mathit{\eta }}_{\mathrm{ref}},p_{\mathrm{0}}\right)=\mathrm{const}$, even though such a state may hardly ever be observed in the real ocean.

• iii.

  Quantitatively, OHC values estimated at different times or places should be mutually comparable without estimation bias resulting from possibly changing methods of OHC calculation. For this reason, resulting OHC values should be independent of the inevitable arbitrary, physically irrelevant reference-state conditions imposed on energy and entropy, such as Eqs. (1)–(3). This can be achieved by assigning to each ocean parcel the same standard-ocean enthalpy as its reference potential enthalpy, $h^{\mathrm{SW}}\left(S,{\mathit{\eta }}_{\mathrm{ref}},p_{\mathrm{0}}\right)=h_{\mathrm{SO}}$. In the special case of TEOS-10 enthalpy, this value is defined by Eq. (2), h_SO=0. This choice is implicitly made by the definition (4) but needed to be considered explicitly as soon as alternative equations for seawater enthalpy or entropy are employed, such as those of Millero and Leung (1976) and Millero (1982, 1983).

In a sense consistent with the previous OHC definition (Abraham et al., 2013), also a climatological average state could in principle be chosen as the OHC reference. However, this option includes the problem that the salinity distribution of the current ocean may differ from the reference ocean, and that thermodynamically properly treating the required salt exchange processes at the surface may turn the issue unnecessarily complicated. A detailed comparison of the OHC definition (4) with its precursor prior to TEOS-10 is provided by McDougall et al. (2021). OHC as a part of the total energy balance of the ocean is analysed by Tailleux (2010, 2018) and Tailleux and Dubos (2024).

4 Relative fugacity and ocean evaporation rate

“The global water cycle and the exchange of freshwater between the atmosphere and ocean is poorly understood. … It has been predicted that increasing global temperatures will lead to an enhanced global water cycle” (Holliday et al., 2011: p. 34). In the past, several climate researchers have argued that along with global warming the marine evaporation has or will be “amplified” or “intensified” (Feistel and Hellmuth, 2021). However, it was not always made clear whether this may mean that (a) in the course of a year, more water vapour is transferred from the global ocean to the atmosphere; (b) the global-mean evaporation rate remains unchanged while locally or temporally, evaporation is more intense; or (c) any combination of the two variants occurs. Conclusions of kind (a) were drawn by renowned climatologists such as Budyko (1984), Flohn et al. (1992), Yu (2007), Randall (2012), Francis (2021), or Zhang et al. (2021).

By contrast, in favour of option (b), the currently observed ocean warming at a rate about 1 W m⁻² does not support assumptions of an enhanced hydrological cycle with related latent heat cooling, rather, it more likely suggests a slight reduction of evaporation. Held and Soden (2006: p. 5687–5689) already clearly stated 2 decades ago that “it is important that the global-mean precipitation or evaporation, commonly referred to as the strength of the hydrological cycle, does not scale with Clausius–Clapeyron. … We can, alternatively, speak of the mean residence time of water vapor in the troposphere as increasing with increasing temperature.” Subsequent observations have underpinned their statement.

Between 1979 and 2022, annual mean global precipitation values (see Fig. 7) fluctuated by about $\pm \mathrm{10}\mathrm{mm}{\mathrm{yr}}^{-\mathrm{1}}$, in particular due to La Niña events, but do not exhibit a significant long-term trend (Vose et al., 2023). Under the common assumption that global precipitation is balanced against evaporation, no substantial strengthening of the hydrological cycle may be observed yet.

Probably, the minor trend of 0.06 mm yr⁻² of the data displayed in Fig. 7 is statistically insignificant. Associated with this apparent trend, the latent heat transferred to the troposphere can be estimated to a negligible putative warming rate of an additional 0.5 mW m⁻² yr⁻¹, which could explain only 10 % of observed atmospheric warming by 1.7 °C per century (Morice et al., 2012; Feistel and Hellmuth, 2021).

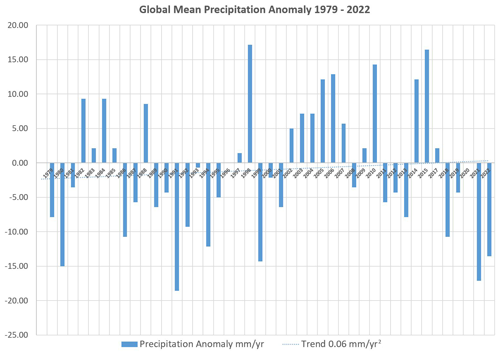
Figure 7 Global-mean precipitation anomaly 1979–2022 in mm yr⁻¹. The values displayed exhibit a minor increasing trend (dotted line) of 0.06 mm yr⁻². Data from Vose et al. (2023).

The thermodynamic driving force for evaporation is the difference between the chemical potentials of water in humid air and in seawater at the two sides of the sea–air interface (Kraus and Businger, 1994). TEOS-10 has made this difference numerically available in the form of the water mass evaporation rate (Feistel and Hellmuth, 2023, 2024a)

$$\begin{array}{}\text{(6)}& J_{\mathrm{W}}=-D_{\mathrm{f}}\left(u\right)\ln {\displaystyle \frac{{\mathit{\psi }}_{\mathrm{f}}}{x_{\mathrm{W}}}}.\end{array}$$

Here, x_W is the mole fraction of water in seawater. Consistent with Wüst (1920), for the standard ocean with Reference Composition, this fraction is (Millero et al., 2008: Table 4)

$$\begin{array}{}\text{(7)}& x_{\mathrm{W}}={\displaystyle \frac{\mathrm{53.556}\mathrm{514}\mathrm{4}}{\mathrm{54.6762838}}}=\mathrm{0.97952},\ln x_{\mathrm{W}}=-\mathrm{0.0206926}.\end{array}$$

In Eq. (6), D_f(u), the Dalton coefficient, is an empirical transfer coefficient as a function of the wind speed, u, as a parameterization of the turbulent transport processes of water in the vicinity of the interface. Applications of the Monin–Obukhov similarity theory (MOST) in order to estimate the Dalton coefficient are reviewed by Liu et al. (1979), Foken and Richter (1991), and Foken (2004, 2016) and in the digital supplement of Feistel and Hellmuth (2024a). A review of empirical Dalton coefficients is given by Debski (1966); historical evaporation experiments are summarized by Biswas (1969).

In Eq. (6), the sea-surface humidity is expressed by the relative fugacity (RF), ψ_f, defined by the ratio of the water-vapour fugacity in humid air, f_V, to the fugacity at saturation, $f_{\mathrm{V}}^{\mathrm{sat}}$ (Feistel and Lovell-Smith, 2017); see Eq. (49). In ideal-gas approximation, RF equals conventional RH (Lovell-Smith et al., 2016):

$$\begin{array}{}\text{(8)}& {\mathit{\psi }}_{\mathrm{f}}\equiv {\displaystyle \frac{f_{\mathrm{V}}}{f_{\mathrm{V}}^{\mathrm{sat}}}}\approx {\mathit{\psi }}_x\equiv {\displaystyle \frac{x}{x^{\mathrm{sat}}}}.\end{array}$$

Here, the mole fraction of water vapour in humid air is x, and its value at saturation is x^sat. Further, ψ_x is the conventional definition of RH in metrology and meteorology which, however, is inconsistent with alternative definitions such as the one employed in climatology (Lovell-Smith et al., 2016). Independent of ideal-gas conditions, but sufficiently close to saturation, such as near the sea surface, RF can be estimated in excellent approximation from the Clausius–Clapeyron formula (Feistel et al., 2022),

$$\begin{array}{}\text{(9)}& {\mathit{\psi }}_{\mathrm{f}}\approx \exp \left\{{\displaystyle \frac{L\left(T_{\mathrm{dp}},p\right)}{R_{\mathrm{W}}}}\left({\displaystyle \frac{\mathrm{1}}{T}}-{\displaystyle \frac{\mathrm{1}}{T_{\mathrm{dp}}}}\right)\right\}.\end{array}$$

The evaporation enthalpy of pure water (IAPWS SR1-86, 1992) at the dewpoint T_dp is L, and $R_{\mathrm{W}}=\mathrm{461.523}\mathrm{J}{\mathrm{kg}}^{-\mathrm{1}}{\mathrm{K}}^{-\mathrm{1}}$ is the specific gas constant of water. The typical marine RF is

$$\begin{array}{}\text{(10)}& {\mathit{\psi }}_{\mathrm{f}}\approx \mathrm{80}\mathit{\%}\mathrm{RH}\end{array}$$

and is fairly independent of region, season or global warming (Dai, 2006; Randall, 2012; Rapp, 2014; MetOffice, 2020). Indeed, observed ocean surface RH has no significant climatological trend (Willett et al., 2023). Similarly, observed ocean wind speeds seem to be unaffected by global warming (Azorin-Molina et al., 2023). Equation (6) for the evaporation rate depends only on wind speed and RF; therefore it may be concluded that the global-mean evaporation rate also has no significant climatic trend. In turn, as far as the release of latent heat is the main driving force of marine tropospheric dynamics, without increase in that release, the mean wind speed is not expected to grow. “Latent heat is the main fuel that powers hurricanes, thunderstorms and normal bouts of lousy weather” (Francis, 2021). Hence, the TEOS-10 approach in the form of Eq. (6) appears to be consistent with the prediction of Held and Soden (2006) that the global evaporation does not increase along with temperature.

Various empirical evaporation equations, commonly known as Dalton equations, are found in the literature (Wüst, 1920; Sverdrup, 1936, 1937; Montgomery, 1940; Debski, 1966; Biswas, 1969; Baumgartner and Reichel, 1975). Several numerical climate models estimate evaporation from the formula (Stewart, 2008; Pinker et al., 2014)

$$\begin{array}{}\text{(11)}& J_{\mathrm{W}}=D_q\left(u\right)\left(q_{\mathrm{0}}-q_{\mathrm{10}}\right),\end{array}$$

where q₀ is the specific humidity at the sea surface and q₁₀ is that at 10 m height, or from (Josey et al., 1999, 2013) the formula

$$\begin{array}{}\text{(12)}& J_{\mathrm{W}}=D_q\left(u\right)\left(\mathrm{0.98}{q}^{\mathrm{sat}}-q\right).\end{array}$$

Here, q is the near-surface specific humidity, and q^sat is the saturation value at the same temperature and pressure. The factor 0.98 accounts for the salinity; see Eq. (7). After a few approximation steps (Feistel and Hellmuth, 2023), these Dalton equations can be derived from the TEOS version (Eq. 6); however, there is an important qualitative difference. At constant RH, due to global warming, specific humidities such as q and q^sat, as well as their difference, are increasing following the Clausius–Clapeyron saturation formula. Accordingly, Eq. (12) implies that the evaporation rate J_W is also growing this way, by contrast to Eq. (6). This virtual acceleration of the hydrological cycle is evidently inconsistent with the prediction of Held and Soden (2006). This parameterization-caused additional latent heat flux implies a spurious ocean cooling that may contribute to the finding that many numerical climate models tend to underestimate the observed ocean warming (Weller et al., 2022).

From Eq. (6), the sensitivity of the latent heat flux, LJ_W, with respect to RH variations is easily estimated. For a mean evaporation rate of 1200 mm yr⁻¹, the corresponding mass flux is about $J_{\mathrm{W}}\approx \mathrm{3.8}\times {\mathrm{10}}^{-\mathrm{5}}\mathrm{kg}{\mathrm{m}}^{-\mathrm{2}}{\mathrm{s}}^{-\mathrm{1}}$ and the related heat flux is $L{J}_{\mathrm{W}}\approx \mathrm{95}\mathrm{W}{\mathrm{m}}^{-\mathrm{2}}$ with respect to the ocean surface area and a specific evaporation enthalpy of $L=\mathrm{2}\mathrm{501}\mathrm{kJ}{\mathrm{kg}}^{-\mathrm{1}}$. At a surface humidity of ψ_f=0.8, a value of $D_{\mathrm{f}}\left(u\right)\approx \mathrm{1.87}\times {\mathrm{10}}^{-\mathrm{4}}\mathrm{kg}{\mathrm{m}}^{-\mathrm{2}}{\mathrm{s}}^{-\mathrm{1}}$ can be concluded for the mass transfer coefficient and of $L{D}_f\left(u\right)\approx \mathrm{468}\mathrm{W}{\mathrm{m}}^{-\mathrm{2}}$ for that of latent heat. Then, from

$$\begin{array}{}\text{(13)}& \mathrm{\Delta }\left(L{J}_{\mathrm{W}}\right)=L{\displaystyle \frac{\partial J_{\mathrm{W}}}{\partial {\mathit{\psi }}_{\mathrm{f}}}}\mathrm{\Delta }{\mathit{\psi }}_{\mathrm{f}}=-L{D}_{\mathrm{f}}\left(u\right){\displaystyle \frac{\mathrm{\Delta }{\mathit{\psi }}_{\mathrm{f}}}{{\mathit{\psi }}_{\mathrm{f}}}}\end{array}$$

it follows that an increase by Δψ_f=1 % RH results in a heat flux reduction by $\mathrm{\Delta }\left(L{J}_{\mathrm{W}}\right)=\mathrm{5.85}\mathrm{W}{\mathrm{m}}^{-\mathrm{2}}$. So, the currently observed ocean warming (Cheng et al., 2024) of 1.3 W m⁻² could theoretically be caused already by a minor marine humidity increase in Δψ_f=0.2 %rh, a value far below the present measurement uncertainty between 1 and 5 % RH. The resolution of climate models and observations still seems to be insufficient to identify the possible role of RH in the unclear explanation of the warming ocean.

5 Sea air as a two-phase composite

The method of Gibbs (1873a, b) of using potential functions can be applied to any systems possessing stable thermodynamic equilibria and obeying energy conservation, without being restricted to merely homogeneous or single-phase samples. The intentionally strict mutual consistency of the different TEOS-10 potential functions permits a mathematical description of multi-phase composites such as sea ice, consisting of ice with included brine pockets (Feistel and Hagen, 1998; Feistel and Wagner, 2005), or clouds, where liquid water or ice is floating in saturated humid air (Hellmuth et al., 2021). Another important model is that of sea air, a sample consisting of a mass m^SW of seawater in thermodynamic equilibrium with a mass m^AV of humid air (Feistel et al., 2010d; Feistel and Hellmuth, 2023). Such a model may serve as a mathematical description for certain thermodynamic properties of ocean–atmosphere interaction.

Extensive thermodynamic functions such as Gibbs energy or enthalpy are additive with respect to the two separate phases of the sample. Equilibrium between those parts requires equal temperatures and pressures. For this reason, a Gibbs function of sea air is an appropriate potential for the composite system, with the TEOS-10 Gibbs functions $g^{\mathrm{SW}}\left(S,T,p\right)$ describing the liquid part and $g^{\mathrm{AV}}\left(A,T,p\right)$ the gas part. Let the masses of the substances in the parts be m^W of liquid water, m^S of dissolved salt, m^A of dry air, and m^V of water vapour. Note that TEOS-10 neglects solubility of dry-air constituents in liquid water. From combinations of the partial masses follow the liquid mass, $m^{\mathrm{SW}}=m^{\mathrm{S}}+m^{\mathrm{W}}$; the gas mass, $m^{\mathrm{AV}}=m^{\mathrm{A}}+m^{\mathrm{V}}$; the total mass, $m=m^{\mathrm{SW}}+m^{\mathrm{AV}}$; the total water mass, $m^{\mathrm{WV}}=m^{\mathrm{W}}+m^{\mathrm{V}}$; the salinity, $S=m^{\mathrm{S}}/m^{\mathrm{SW}}$; and the dry-air fraction, $A=\mathrm{1}-q=m^{\mathrm{A}}/m^{\mathrm{AV}}$.

The Gibbs energies of the two phases of sea air are additive,

$$\begin{array}{}\text{(14)}& G^{\mathrm{SA}}=G^{\mathrm{SW}}+G^{\mathrm{AV}}=m{g}^{\mathrm{SA}},\end{array}$$

and, accordingly, the Gibbs function of sea air, g^SA, may be constructed from that of seawater, $g^{\mathrm{SW}}\left(S,T,p\right)$, with a liquid mass fraction of $w^{\mathrm{SW}}=m^{\mathrm{SW}}/m$ and that of humid air, $g^{\mathrm{AV}}\left(A,T,p\right)$, with a gaseous mass fraction of $w^{\mathrm{AV}}=m^{\mathrm{AV}}/m=\mathrm{1}-w^{\mathrm{SW}}$,

$$\begin{array}{}\text{(15)}& \begin{array}{rl}{g}^{\mathrm{SA}}& \left(S,A,w^{\mathrm{SW}},T,p\right)=w^{\mathrm{SW}}{g}^{\mathrm{SW}}\left(S,T,p\right)\\ & +\left(\mathrm{1}-w^{\mathrm{SW}}\right)g^{\mathrm{AV}}\left(A,T,p\right).\end{array}\end{array}$$

If the two phases are assumed to be at mutual equilibrium, they possess the same temperature, pressure, and chemical potentials (see Eq. (B11) in Appendix B), ${\mathit{\mu }}_{\mathrm{W}}^{\mathrm{SW}}={\mathit{\mu }}_{\mathrm{V}}^{\mathrm{AV}}$, namely that of water in seawater,

$$\begin{array}{}\text{(16)}& {\mathit{\mu }}_{\mathrm{W}}^{\mathrm{SW}}\left(S,T,p\right)=g^{\mathrm{SW}}-S{\left({\displaystyle \frac{\partial g^{\mathrm{SW}}}{\partial S}}\right)}_{T,p},\end{array}$$

equalling that of water vapour in humid air,

$$\begin{array}{}\text{(17)}& {\mathit{\mu }}_{\mathrm{V}}^{\mathrm{AV}}\left(A,T,p\right)=g^{\mathrm{AV}}-A{\left({\displaystyle \frac{\partial g^{\mathrm{AV}}}{\partial A}}\right)}_{T,p}.\end{array}$$

5.1 Sea air as a model for latent heat of evaporation

Water evaporated from the ocean surface drives the climate system. “The by far largest part of heat conveyed to the air is in the form of latent heat during subsequent condensation along with cloud formation. The heat budget over the sea is mainly controlled by the latent heat released to the air” (Albrecht, 1940). It is the “heat source for a gigantic steam engine”, as Heinrich Hertz put it in his 1885 inaugural lecture at Karlsruhe (Mulligan and Hertz, 1997). The latent heat of evaporation of pure liquid water into pure water vapour is numerically well known from experiments (IAPWS SR1-86, 1992; Harvey, 1998; Wagner and Pruß, 2002). Slightly differing values are reported in various textbooks on hydrology (Debski, 1966: p. 332), meteorology (Linke and Baur, 1970), or geophysics (Gill, 1982; Kraus and Businger, 1994). TEOS-10, however, permits the computation of evaporation properties from seawater into humid air, based on the first-time availability of standard equations for enthalpies and chemical potentials of those non-ideal mixtures.

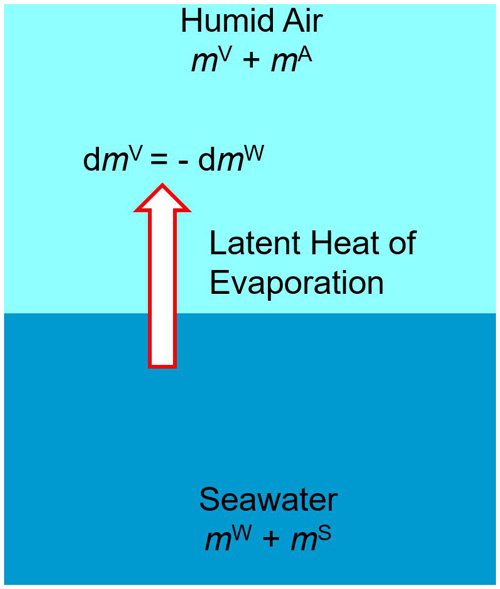
Figure 8 Conceptual thermodynamic “sea air” model of ocean–atmosphere interaction as a two-phase composite of seawater and humid air.

“Latent heat is the quantity of heat which must be communicated to a body in a given state in order to convert it into another state without changing its temperature” (Maxwell, 1888: p.73). If an infinitesimal amount of water is transferred from the liquid to the gas phase (Fig. 8), while temperature and pressure remain at their equilibrium values, and the total masses of salt (m^S), dry air (m^A), and water (m^WV) are not affected, the isobaric–isothermal latent heat of evaporation may be defined by

$$\begin{array}{}\text{(18)}& L^{\mathrm{SA}}\equiv {\left({\displaystyle \frac{\partial H^{\mathrm{SA}}}{\partial m^{\mathrm{V}}}}\right)}_{T,p,m^{\mathrm{S}},m^{\mathrm{A}},m^{\mathrm{WV}}}.\end{array}$$

This latent heat accounts for the loss of total heat of the sea-air sample associated with the loss of liquid water and equal gain of water vapour,

$$\begin{array}{}\text{(19)}& {\displaystyle \frac{\partial m^{\mathrm{V}}}{\partial T}}=-{\displaystyle \frac{\partial m^{\mathrm{W}}}{\partial T}}.\end{array}$$

Here, H^SA is the enthalpy of sea air, available from the Gibbs function (15) through the sum

$$\begin{array}{}\text{(20)}& H^{\mathrm{SA}}\equiv m^{\mathrm{SW}}{h}^{\mathrm{SW}}+m^{\mathrm{AV}}{h}^{\mathrm{AV}}.\end{array}$$

Here, the specific enthalpies of seawater,

$$\begin{array}{}\text{(21)}& h^{\mathrm{SW}}=g^{\mathrm{SW}}-T{\left({\displaystyle \frac{\partial g^{\mathrm{SW}}}{\partial T}}\right)}_{S,p},\end{array}$$

and of humid air,

$$\begin{array}{}\text{(22)}& h^{\mathrm{AV}}=g^{\mathrm{AV}}-T{\left({\displaystyle \frac{\partial g^{\mathrm{AV}}}{\partial T}}\right)}_{A,p},\end{array}$$

are defined in terms of the related Gibbs functions.

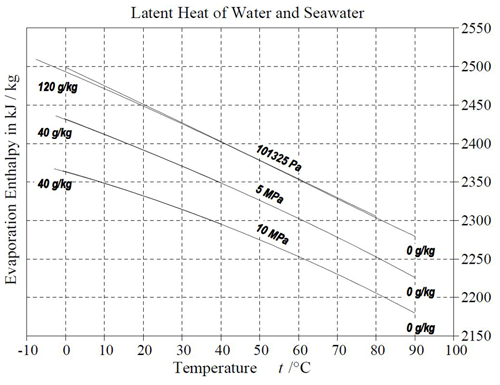
Figure 9 Evaporation enthalpy (Eq. 24) of seawater in equilibrium with humid air at different temperatures, pressures, and salinities. The dependence on salinity is very weak; graphically, the related curves are hardly distinguishable. The nonlinear dependence on temperature is more pronounced at elevated pressures. Figure from Feistel et al. (2010a: p. 105).

The derivative (18) is carried out in the form

$$\begin{array}{}\text{(23)}& \begin{array}{rl}{L}^{\mathrm{SA}}& =-h^{\mathrm{SW}}-m^{\mathrm{SW}}{\left({\displaystyle \frac{\partial h^{\mathrm{SW}}}{\partial S}}\right)}_{T,p}{\left({\displaystyle \frac{\partial S}{\partial m^{\mathrm{V}}}}\right)}_{m^{\mathrm{S}},m^{\mathrm{WV}}}\\ & +h^{\mathrm{AV}}+m^{\mathrm{AV}}{\left({\displaystyle \frac{\partial h^{\mathrm{AV}}}{\partial A}}\right)}_{T,p}{\left({\displaystyle \frac{\partial A}{\partial m^{\mathrm{V}}}}\right)}_{m^{\mathrm{A}}},\end{array}\end{array}$$

which results in the TEOS-10 latent heat equation (Feistel et al., 2010a; Feistel and Hellmuth, 2023),

$$\begin{array}{}\text{(24)}& L^{\mathrm{SA}}=h^{\mathrm{AV}}-A{\left({\displaystyle \frac{\partial h^{\mathrm{AV}}}{\partial A}}\right)}_{T,p}-h^{\mathrm{SW}}+S{\left({\displaystyle \frac{\partial h^{\mathrm{SW}}}{\partial S}}\right)}_{T,p},\end{array}$$

with typical values shown in Fig. 9. If seawater is in mutual equilibrium with humid air at given temperature and pressure, salinity and humidity of the parts of sea air satisfy the condition ${\mathit{\mu }}_{\mathrm{W}}^{\mathrm{SW}}={\mathit{\mu }}_{\mathrm{V}}^{\mathrm{AV}}$, given by Eqs. (16) and (17),

$$\begin{array}{}\text{(25)}& \mathrm{\Delta }\mathit{\mu }\equiv g^{\mathrm{SW}}-S{\left({\displaystyle \frac{\partial g^{\mathrm{SW}}}{\partial S}}\right)}_{T,p}-g^{\mathrm{AV}}+A{\left({\displaystyle \frac{\partial g^{\mathrm{AV}}}{\partial A}}\right)}_{T,p}=\mathrm{0}.\end{array}$$

At given masses of salt (m^S), of dry air (m^A), and of total water ($m^{\mathrm{WV}}=m^{\mathrm{W}}+m^{\mathrm{V}}$), Eq. (25) controls the value of either m^W or m^V and this way also of S and A as functions of T, p, m^S, m^A, and m^WV. Related numerical solutions are readily implemented in the TEOS-10 SIA library; the latent heat of sea air can be computed by calling the function sea_air_enthalpy_evap_si(); see Wright et al. (2010).

Latent heat of Eq. (24) is valid regardless of the equilibrium condition (Eq. 25) being satisfied or not. The non-equilibrium case is considered separately in Sect. 5.3.

5.2 Sea air as a model of sea spray

As a special form of air–sea interaction, sea spray is typically ejected from the crest of a breaking wave, which may happen all along oceanic coasts but also wherever whitecaps are produced from swell or a stormy sea state; see Fig. 10. In contrast to fresh-water haze, droplets of sea spray cannot completely evaporate because of the salt they contain and rather develop into a floating persistent Köhler (1936) equilibrium between droplet size, droplet salinity, and ambient relative fugacity (Hellmuth and Shchekin, 2015; Pöhlker et al., 2023). This equilibrium can be described by the TEOS-10 model of sea air if the additional kelvin pressure caused by the surface tension is allowed for.

In the infrared spectral range, sea spray as well as other aerosols (Carlon, 1970, 1980) may be considered a black absorber and emitter of thermal radiation. The resulting “grey atmosphere” is a conveniently simple conceptual model for the longwave radiative effects of dust or haze in the climate system (Emden, 1913). When heated from below, as in the case of the clear-sky marine troposphere, a theoretical finding is that the thermally stratified grey troposphere exhibits a special critical value of the isobaric heat capacity at c_p=4R (Pierrehumbert, 2010: p. 201), R being the molar gas constant. Vertical stability may be lost at c_p>4R, and turbulent mixing is expected to commence (Feistel, 2011b: Eq. 58 therein). Such a kinetic phase transition could substantially modify the thermal radiation balance between the troposphere and ocean surface.

The terrestrial atmosphere is dominated by the diatomic gases N₂ and O₂ with heat capacities about 3.5 R, which prevent the putative radiative vertical instability from occurring. This situation may change, however, in the presence of haze or sea spray. To investigate this effect theoretically, in this section a TEOS-10 equation for the heat capacity of equilibrium sea air is derived from the definition

$$\begin{array}{}\text{(26)}& c_p^{\mathrm{SA}}\equiv {\displaystyle \frac{\mathrm{1}}{m}}{\left({\displaystyle \frac{\partial H^{\mathrm{SA}}}{\partial T}}\right)}_{p,m^{\mathrm{S}},m^{\mathrm{A}},m^{\mathrm{WV}}}.\end{array}$$

The enthalpy of sea air is given by Eq. (20). Taking into account water conservation upon evaporation, m^WV=const, that is,

$$\begin{array}{}\text{(27)}& {\displaystyle \frac{\partial m^{\mathrm{V}}}{\partial T}}=-{\displaystyle \frac{\partial m^{\mathrm{W}}}{\partial T}},\end{array}$$

and Eq. (24), the isobaric heat capacity of sea air is concluded to be

$$\begin{array}{}\text{(28)}& c_p^{\mathrm{SA}}=w^{\mathrm{SW}}{c}_p^{\mathrm{SW}}+w^{\mathrm{AV}}{c}_p^{\mathrm{AV}}+L^{\mathrm{SA}}{\displaystyle \frac{\mathrm{1}}{m}}{\displaystyle \frac{\partial m^{\mathrm{V}}}{\partial T}}.\end{array}$$

In addition to the additive contributions of the partial heat capacities of the liquid and the gas part, there appears the latent heat of the water mass that evaporates from the liquid as vapour. This evaporation rate is governed by the mutual equilibrium between seawater and humid air.

Figure 10 Sea spray ejection from a breaking wave crest of Atlantic swell. Photo taken at Cabo Trafalgar in March 2011.

During the temperature change, mutual sea–air equilibrium (Eq. 25), is assumed to be maintained by water transfer between the phases, changing S and A along with T,

$$\begin{array}{}\text{(29)}& {\left({\displaystyle \frac{\partial \mathrm{\Delta }\mathit{\mu }}{\partial T}}\right)}_{p,m^{\mathrm{S}},m^{\mathrm{A}},m^{\mathrm{WV}}}=\mathrm{0}.\end{array}$$

Carrying out the derivative, this condition reads

$$\begin{array}{}\text{(30)}& \begin{array}{rl}{\left({\displaystyle \frac{\partial g^{\mathrm{SW}}}{\partial T}}\right)}_{S,p}& -S{\left({\displaystyle \frac{{\partial }^{\mathrm{2}}{g}^{\mathrm{SW}}}{\partial S\partial T}}\right)}_p-S{\left({\displaystyle \frac{{\partial }^{\mathrm{2}}{g}^{\mathrm{SW}}}{\partial S^{\mathrm{2}}}}\right)}_{T,p}{\left({\displaystyle \frac{\partial S}{\partial T}}\right)}_{m^{\mathrm{S}}}\\ & ={\left({\displaystyle \frac{\partial g^{\mathrm{AV}}}{\partial T}}\right)}_{A,p}-A{\left({\displaystyle \frac{{\partial }^{\mathrm{2}}{g}^{\mathrm{AV}}}{\partial A\partial T}}\right)}_p\\ & -A{\left({\displaystyle \frac{{\partial }^{\mathrm{2}}{g}^{\mathrm{AV}}}{\partial A^{\mathrm{2}}}}\right)}_{T,p}{\left({\displaystyle \frac{\partial A}{\partial T}}\right)}_{m^{\mathrm{A}}}.\end{array}\end{array}$$

On the other hand, from combining Eq. (24) with Eq. (25), it follows that the latent heat may be expressed by

$$\begin{array}{}\text{(31)}& \begin{array}{rl}{L}^{\mathrm{SA}}& =T\left\{{\left({\displaystyle \frac{\partial g^{\mathrm{SW}}}{\partial T}}\right)}_{S,p}-S{\left({\displaystyle \frac{{\partial }^{\mathrm{2}}{g}^{\mathrm{SW}}}{\partial S\partial T}}\right)}_p\right.\\ & \left.-{\left({\displaystyle \frac{\partial g^{\mathrm{AV}}}{\partial T}}\right)}_{A,p}+A{\left({\displaystyle \frac{{\partial }^{\mathrm{2}}{g}^{\mathrm{AV}}}{\partial A\partial T}}\right)}_p\right\}.\end{array}\end{array}$$

Therefore, Eq. (30) may be written as

$$\begin{array}{}\text{(32)}& \begin{array}{rl}{L}^{\mathrm{SA}}& =T\left\{S{\left({\displaystyle \frac{{\partial }^{\mathrm{2}}{g}^{\mathrm{SW}}}{\partial S^{\mathrm{2}}}}\right)}_{T,p}{\left({\displaystyle \frac{\partial S}{\partial T}}\right)}_{m^{\mathrm{S}}}\right.\\ & \left.-A{\left({\displaystyle \frac{{\partial }^{\mathrm{2}}{g}^{\mathrm{AV}}}{\partial A^{\mathrm{2}}}}\right)}_{T,p}{\left({\displaystyle \frac{\partial A}{\partial T}}\right)}_{m^{\mathrm{A}}}\right\}.\end{array}\end{array}$$

Further, the total water mass balance (Eq. 27) implies that

$$\begin{array}{}\text{(33)}& {\left({\displaystyle \frac{\partial S}{\partial T}}\right)}_{m^{\mathrm{S}}}={\left({\displaystyle \frac{\partial S}{\partial m^{\mathrm{W}}}}\right)}_{m^{\mathrm{S}}}{\displaystyle \frac{\partial m^{\mathrm{W}}}{\partial T}}={\displaystyle \frac{S}{m^{\mathrm{SW}}}}{\displaystyle \frac{\partial m^{\mathrm{V}}}{\partial T}},\end{array}$$

and similarly,

$$\begin{array}{}\text{(34)}& {\left({\displaystyle \frac{\partial A}{\partial T}}\right)}_{m^{\mathrm{A}}}={\left({\displaystyle \frac{\partial A}{\partial m^{\mathrm{V}}}}\right)}_{m^{\mathrm{A}}}{\displaystyle \frac{\partial m^{\mathrm{V}}}{\partial T}}=-{\displaystyle \frac{A}{m^{\mathrm{AV}}}}{\displaystyle \frac{\partial m^{\mathrm{V}}}{\partial T}}.\end{array}$$

Inserting those expressions into Eq. (32), the equation for the isobaric evaporation rate of sea air is

$$\begin{array}{}\text{(35)}& {\displaystyle \frac{\partial m^{\mathrm{V}}}{\partial T}}={\displaystyle \frac{L^{\mathrm{evap}}}{T}}{\left\{{\displaystyle \frac{S^{\mathrm{2}}}{m^{\mathrm{SW}}}}{\left({\displaystyle \frac{{\partial }^{\mathrm{2}}{g}^{\mathrm{SW}}}{\partial S^{\mathrm{2}}}}\right)}_{T,p}+{\displaystyle \frac{A^{\mathrm{2}}}{m^{\mathrm{AV}}}}{\left({\displaystyle \frac{{\partial }^{\mathrm{2}}{g}^{\mathrm{AV}}}{\partial A^{\mathrm{2}}}}\right)}_{T,p}\right\}}^{-\mathrm{1}}.\end{array}$$

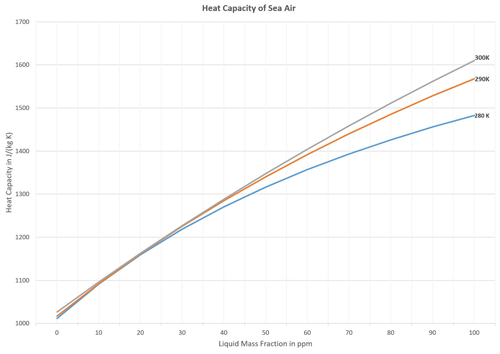
Figure 11 TEOS-10 values for the isobaric specific heat capacity (Eq. 36) of sea air at atmospheric pressure and sea spray standard-ocean salinity, S=35.16504 g kg⁻¹, at temperatures of 280 K (lower curve), 290 K (middle curve), and 300 K (upper curve) as functions of the liquid mass fraction, w^SW, up to 100 ppm.

Together with Eq. (35), the desired formula for the isobaric heat capacity (28) of sea air finally becomes (Feistel et al., 2010a: Eq. 6.22 therein)

$$\begin{array}{}\text{(36)}& \begin{array}{rl}{c}_p^{\mathrm{SA}}& =w^{\mathrm{SW}}{c}_p^{\mathrm{SW}}+\left(\mathrm{1}-w^{\mathrm{SW}}\right)c_p^{\mathrm{AV}}+{\displaystyle \frac{{\left(L^{\mathrm{SA}}\right)}^{\mathrm{2}}}{T}}\\ & {\left\{{\displaystyle \frac{S^{\mathrm{2}}}{w^{\mathrm{SW}}}}{\left({\displaystyle \frac{{\partial }^{\mathrm{2}}{g}^{\mathrm{SW}}}{\partial S^{\mathrm{2}}}}\right)}_{T,p}+{\displaystyle \frac{A^{\mathrm{2}}}{\left(\mathrm{1}-w^{\mathrm{SW}}\right)}}{\left({\displaystyle \frac{{\partial }^{\mathrm{2}}{g}^{\mathrm{AV}}}{\partial A^{\mathrm{2}}}}\right)}_{T,p}\right\}}^{-\mathrm{1}}.\end{array}\end{array}$$

Of the liquid water content, expressed in form of the liquid mass fraction, w^SW, realistic values may typically range between 10⁻⁶ and 10⁻⁴ in the troposphere. Growing along with this fraction, related heat capacities of sea air (Eq. 36) may substantially exceed those of liquid-free humid air, $c_p^{\mathrm{AV}}$; see Fig. 11.

5.3 Sea air as a model for irreversible evaporation

The climate system functions far from thermodynamic equilibrium, permanently producing and exporting entropy at an average rate about 1 W m⁻² K⁻¹ per global surface area (Ebeling and Feistel, 1982; Feistel and Ebeling, 2011). By contrast, TEOS-10 is a mathematical description of equilibrium properties (Appendix B). The latter is applicable to states away from thermodynamic equilibrium under the assumption of local equilibrium as introduced by Prigogine (1947, 1978). This assumption means that spatially extended substances such as the ocean or atmosphere consist of sufficiently small volume elements that may reasonably be described as macroscopic equilibrium states, homogeneous in temperature, pressure, and chemical potentials. TEOS-10 thermodynamic potentials can be used to describe those local states.

By definition, if a volume at equilibrium is divided into partial volumes, each of those parts is at equilibrium itself, and each pair of those is at mutual equilibrium also. By contrast, the combination of several local-equilibrium elements forms a non-equilibrium state if pairs of elements exist that are out of mutual equilibrium. Extensive properties such as mass, energy, entropy, or enthalpy can be added up to give correct values of the entire system. When exchange processes between those elements occur, gains and losses of masses, energies, or enthalpies are mutually balanced by conservation laws; however, this is not the case for entropy.

A tutorial case of a local equilibrium system may be the model of sea air (Feistel and Hellmuth, 2024a) depicted in Fig. 8. It consists of a mass $m^{\mathrm{SW}}=m^{\mathrm{S}}+m^{\mathrm{W}}$ of seawater in contact with a mass $m^{\mathrm{AV}}=m^{\mathrm{A}}+m^{\mathrm{A}}$ of humid air. Both fluids are assumed to be at internal equilibrium themselves but not necessarily in mutual equilibrium with one another. This is a natural geophysical situation – marine RH has typical values of 80 % RH, while the equilibrium of humid air with seawater (Eq. 25) is established at about 98 % RH. For simplicity, let all parts have equal temperatures and pressures.

If evaporation takes place, the partial water masses involved will change by a mass flux across the sea surface,

$$\begin{array}{}\text{(37)}& J_m\equiv {\displaystyle \frac{\mathrm{d}{m}^{\mathrm{AV}}}{\mathrm{d}t}}={\displaystyle \frac{\mathrm{d}{m}^{\mathrm{V}}}{\mathrm{d}t}}=-{\displaystyle \frac{\mathrm{d}{m}^{\mathrm{SW}}}{\mathrm{d}t}}=-{\displaystyle \frac{\mathrm{d}{m}^{\mathrm{W}}}{\mathrm{d}t}}.\end{array}$$

The change of the total enthalpy of the sea-air sample is available from Eqs. (18) and (24),

$$\begin{array}{}\text{(38)}& {\displaystyle \frac{\mathrm{d}{H}^{\mathrm{SA}}}{\mathrm{d}t}}={\left({\displaystyle \frac{\partial H^{\mathrm{SA}}}{\partial m^{\mathrm{V}}}}\right)}_{T,p,m^{\mathrm{S}},m^{\mathrm{A}},m^{\mathrm{WV}}}{\displaystyle \frac{\mathrm{d}{m}^{\mathrm{V}}}{\mathrm{d}t}}=L^{\mathrm{SA}}{J}_m.\end{array}$$

This expression of energy conservation, the first law of thermodynamics, is similarly valid for equilibrium and non-equilibrium conditions of the sample. For comparison, for the total entropy defined by

$$\begin{array}{}\text{(39)}& N^{\mathrm{SA}}\equiv m^{\mathrm{SW}}{\mathit{\eta }}^{\mathrm{SW}}+m^{\mathrm{AV}}{\mathit{\eta }}^{\mathrm{AV}},\end{array}$$

the change is given by

$$\begin{array}{}\text{(40)}& {\displaystyle \frac{\mathrm{d}{N}^{\mathrm{SA}}}{\mathrm{d}t}}={\left({\displaystyle \frac{\partial N^{\mathrm{SA}}}{\partial m^{\mathrm{V}}}}\right)}_{T,p,m^{\mathrm{S}},m^{\mathrm{A}},m^{\mathrm{WV}}}{\displaystyle \frac{\mathrm{d}{m}^{\mathrm{V}}}{\mathrm{d}t}}.\end{array}$$

In terms of its two parts (Eq. 39), this change takes the form

$$\begin{array}{}\text{(41)}& {\displaystyle \frac{\mathrm{d}{N}^{\mathrm{SA}}}{\mathrm{d}t}}=\left[{\mathit{\eta }}^{\mathrm{AV}}-A{\left({\displaystyle \frac{\partial {\mathit{\eta }}^{\mathrm{AV}}}{\partial A}}\right)}_{T,p}-{\mathit{\eta }}^{\mathrm{SW}}+S{\left({\displaystyle \frac{\partial {\mathit{\eta }}^{\mathrm{SW}}}{\partial S}}\right)}_{T,p}\right]J_m.\end{array}$$

In oceanography, the symbol N for entropy was suggested by Fofonoff (1962) to avoid confusion with salinity S. Making use of their local equilibria, specific entropy of each part can be expressed by the difference (Eq. B6),

$$\begin{array}{}\text{(42)}& \mathit{\eta }={\displaystyle \frac{h-g}{T}},\end{array}$$

between specific enthalpy, h, and specific Gibbs energy, g. Therefore, the entropy change (41) becomes

$$\begin{array}{}\text{(43)}& T{\displaystyle \frac{\mathrm{d}{N}^{\mathrm{SA}}}{\mathrm{d}t}}=\left(L^{\mathrm{SA}}+\mathrm{\Delta }\mathit{\mu }\right)J_m.\end{array}$$

Here, the latent heat, L^SA, is given by Eq. (24) and the distance from mutual equilibrium, Δμ, by Eq. (25).

The first term,

$$\begin{array}{}\text{(44)}& T{\displaystyle \frac{{\mathrm{d}}_{\mathrm{e}}{N}^{\mathrm{SA}}}{\mathrm{d}t}}\equiv L^{\mathrm{SA}}{J}_m,\end{array}$$

is the external entropy change (subscript e) in the form of the heat flux required to maintain the sample's temperature, in the sense of Maxwell's (1888) definition of latent heat, compensating for the storage of latent heat by emitting water vapour.

The second term,

$$\begin{array}{}\text{(45)}& T{\displaystyle \frac{{\mathrm{d}}_{\mathrm{i}}{N}^{\mathrm{SA}}}{\mathrm{d}t}}\equiv J_m\mathrm{\Delta }\mathit{\mu },\end{array}$$

is the internal entropy change (subscript i), or entropy production, of the non-equilibrium sea-air sample. It represents the additional entropy gain of humid air compared to the entropy loss of seawater. This production happens at the air–sea interface and disappears as soon as mutual equilibrium, Δμ=0, is approached.

It is important to be aware that the external part, $\frac{{\mathrm{d}}_{\mathrm{e}}{N}^{\mathrm{SA}}}{\mathrm{d}t}$, always constitutes a contribution to the system's energy balance, while, by contrast, the internal part, $\frac{{\mathrm{d}}_{\mathrm{i}}{N}^{\mathrm{SA}}}{\mathrm{d}t}$, never constitutes any such contribution. The irreversible production of entropy is an internal conversion or redistribution of energy rather than a change in it. This implies that irreversible processes violate Gibbs' fundamental equation (Eq. B8) in the sense that

$$\begin{array}{}\text{(46)}& \begin{array}{rl}{\displaystyle \frac{\mathrm{d}{H}^{\mathrm{SA}}}{\mathrm{d}t}}& =-T{\displaystyle \frac{{\mathrm{d}}_{\mathrm{e}}{N}^{\mathrm{SA}}}{\mathrm{d}t}}+V^{\mathrm{SA}}{\displaystyle \frac{\mathrm{d}p}{\mathrm{d}t}}+\sum _i{\mathit{\mu }}_i{\displaystyle \frac{\mathrm{d}{m}_i}{\mathrm{d}t}}>\\ & -T{\displaystyle \frac{\mathrm{d}{N}^{\mathrm{SA}}}{\mathrm{d}t}}+V^{\mathrm{SA}}{\displaystyle \frac{\mathrm{d}p}{\mathrm{d}t}}+\sum _i{\mathit{\mu }}_i{\displaystyle \frac{\mathrm{d}{m}_i}{\mathrm{d}t}},\end{array}\end{array}$$

even though each of its local-equilibrium elements strictly satisfies the related fundamental equation (Eq. B13), valid for reversible processes only:

$$\begin{array}{}\text{(47)}& \mathrm{d}h=-T\mathrm{d}\mathit{\eta }+v\mathrm{d}p+\sum _{i=\mathrm{1}}^{n-\mathrm{1}}\left({\mathit{\mu }}_i-{\mathit{\mu }}_{\mathrm{0}}\right)\mathrm{d}{w}_i.\end{array}$$

Entropy production appears wherever a flux is passing its driving gradient. Near equilibrium, this flux is proportional to its driving force (Glansdorff and Prigogine, 1971; Landau and Lifschitz, 1974; Kraus and Businger, 1994; Feistel and Hellmuth, 2024a), usually termed Onsager force. For example, the evaporation mass flux of water (Eq. 6),

$$\begin{array}{}\text{(48)}& J_m=C\mathrm{\Delta }\mathit{\mu },\end{array}$$

may be assumed as being proportional to the difference between the chemical potentials of water across the air–sea interface. The related Dalton equation (Eq. 6) was discussed in Sect. 4. The associated entropy production (Eq. 45) obeys the second law of thermodynamics by the inequality

$$\begin{array}{}\text{(49)}& {\displaystyle \frac{{\mathrm{d}}_{\mathrm{i}}{N}^{\mathrm{SA}}}{\mathrm{d}t}}=C{\left(\mathrm{\Delta }\mathit{\mu }\right)}^{\mathrm{2}}\ge \mathrm{0},\end{array}$$

while the total entropy change (Eq. 43) may possess any sign. In other words, the second law forbids that Onsager fluxes may be directed against their causing Onsager forces. The Prigogine theorem predicts that in linear irreversible thermodynamics, entropy production approaches minimum values at steady states (Glansdorff and Prigogine, 1971).

Processes accompanied by entropy production are termed irreversible ones, since entropy that has once been created may never be destroyed again. Related processes cannot be reversed unless lasting changes are left behind in the external world. By contrast, processes which transform an equilibrium state into another equilibrium state may reversibly be performed without producing entropy. Entropy production is only possible under non-equilibrium conditions.

Under typical marine circumstances, the entropy production density of ocean evaporation can be estimated to about 4 mW K⁻¹ m⁻², contributing roughly 0.4 % to the global entropy production (Feistel and Ebeling, 2011; Feistel and Hellmuth, 2024a).

6 Cloudiness and ocean warming

“Cloud feedback on climate represents the largest uncertainty in our ability to understand the sensitivity of the planet to radiative forcing” (Gettelman and Sherwood, 2016). On the long-term average, cloudiness is particularly strong in the low-pressure belts of the global tropospheric circulation, where air is ascending and its humidity is condensing; see Fig. 12. Except for the equatorial zone, those spatial cloudiness patterns correlate visibly with those of recent ocean warming; compare Fig. 1. It is a plausible working hypothesis that this correlation could also indicate a causal relation between the two phenomena. However, such correlations imply chicken-and-egg problems (Rapp, 2014): putative causality relations between those trends cannot be derived from observations but only be concluded from reliable prediction models (Feistel, 2023). May the observed systematic reduction of global cloudiness (Fasullo and Trenberth, 2012) actually be responsible for the currently recorded excessive ocean warming (You, 2024)? Unfortunately, and somewhat surprisingly, this assumption can apparently not be underpinned yet by closer investigation. Some related issues will be discussed in this section.

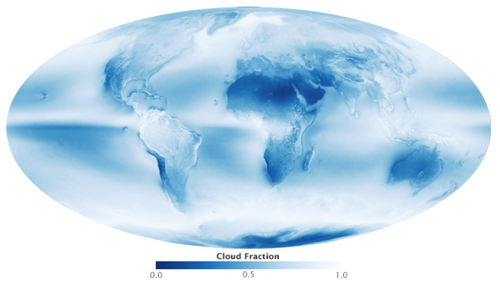
Figure 12 Global distribution of cloudiness July 2002–April 2015 (Allen and Ward, 2015). Image reproduction permitted by © NASA.

6.1 Cloudiness trend

The global cloud-covered surface area fraction C systematically reduced by about 6 % per century (see Fig. 13) from C≈67.5 % in 1980 to C≈65 % in 2022 (Foster et al., 2023; Phillips and Foster, 2023). Observed cloudiness values depend strongly on the way clouds are defined (Spänkuch et al., 2022) and on the measurement technology applied. For example, Rapp (2014: Fig. 6.20) reported a decrease in cloudiness in 30 years from 70 % in 1983 down to 63.5 % in, likely, 2013. This reduction rate of more than 20 % per century is 3 times faster than that given in Fig. 13 and may result from different observation techniques.

Assuming that this shrinking occurred in a similar way above both land and sea, the ocean is expected to receive increasingly more solar irradiation. This phenomenon is known as the shortwave cloud radiative effect (SW CRE); see Fig. 14.

On the other hand, clouds are opaque with respect to oceanic upward thermal radiation and emit themselves downward infrared radiation. This phenomenon is known as the longwave cloud radiative effect (LW CRE); see Fig. 15. Radiation models show that on average, globally, these two effects cancel each other out almost completely up to a minor residual of −1 mW m⁻² yr⁻¹; therefore the continuously shrinking cloudiness may be assumed to have practically no net effect on the ocean's radiation balance (Phillips and Foster, 2023; Feistel and Hellmuth, 2024b). However, more detailed investigations in the future may reveal more rigorous results for the ocean than this simplified picture.

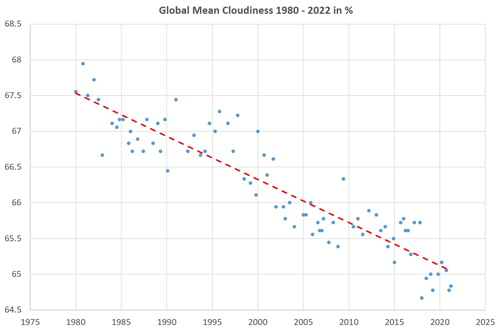
Figure 13 Dots: satellite-derived global-mean cloud area fractions 1980–2022 in percent. Data from Foster et al. (2023). Dashed line: present cloudiness is 65 % with a climatological linear shrinking trend of −6.2 % per century.

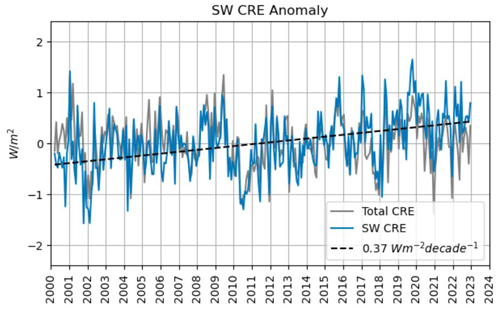
Figure 14 Shortwave cloud radiative effect (SW CRE) of increasing solar irradiation. Image kindly provided by Coda Phillips (personal communication, 2024), with minor correction compared to the similar previous publication (Phillips and Foster, 2023). Total CRE is the net effect of SW and LW CRE; see Fig. 15.

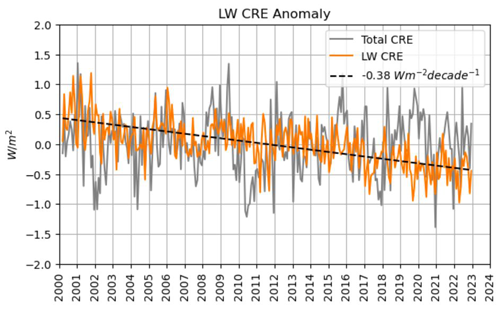
Figure 15 Longwave cloud radiative effect (LW CRE) of decreasing net thermal radiation. Image kindly provided by Coda Phillips (personal communication, 2024), with minor corrections compared to the similar previous publication (Phillips and Foster, 2023). Total CRE is the net effect of SW and LW CRE; see Fig. 14.

6.2 Cumulus clouds

Cumulus clouds are often formed in the course of diurnal convection by isentropic uplift of humid air parcels from the sea surface to the condensation level, mostly located at low heights between 200 and 500 m. This process permits a thermodynamic description of such clouds (Romps, 2017) by calculating the lifted condensation level (LCL) as the cumulus cloud base. In distinction to previous studies, as the first such international geophysical standard, TEOS-10 provides explicit equations for entropy, enthalpy, and chemical potentials of humid air, which may be used to derive reference equations and values of the LCL (Feistel and Hellmuth, 2024b).

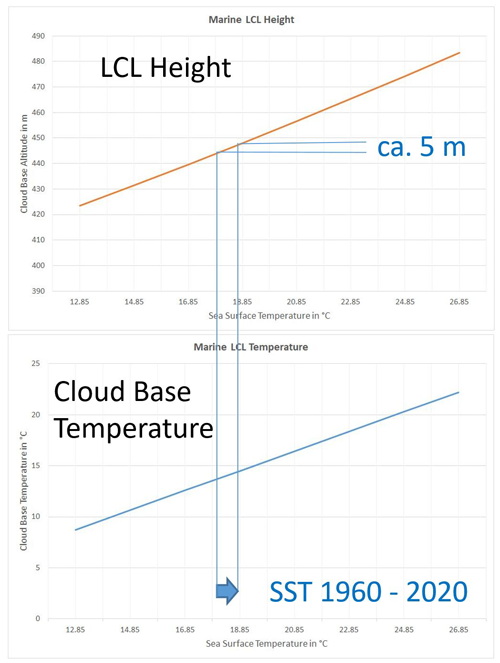
Figure 16 As a function of typical low-latitude sea-surface temperatures, LCL height (top) and LCL temperature (bottom) are computed from the TEOS-10 equations (Eqs. 50–53) at a typical marine surface RH of 80 %. The added interval indicates the global-mean SST change between 1960 and 2020 which has resulted in an increase in the cloud-base altitude by about 5 m.

At the sea-surface pressure, p_SS, the air parcel may possess the temperature T_SS and the relative fugacity ψ_f, which is a real-gas definition of relative humidity (Feistel and Lovell-Smith, 2017) in terms of the chemical potential of water vapour in humid air, ${\mathit{\mu }}_{\mathrm{V}}^{\mathrm{AV}}$, and that of liquid water, μ_W,

$$\begin{array}{}\text{(50)}& R_{\mathrm{W}}{T}_{\mathrm{SS}}\ln {\mathit{\psi }}_{\mathrm{f}}={\mathit{\mu }}_{\mathrm{V}}^{\mathrm{AV}}\left(A,T_{\mathrm{SS}},p_{\mathrm{SS}}\right)-{\mathit{\mu }}_{\mathrm{W}}\left(T_{\mathrm{SS}},p_{\mathrm{SS}}\right).\end{array}$$

Here, $R_{\mathrm{W}}=\mathrm{461.523}\mathrm{J}{\mathrm{kg}}^{-\mathrm{1}}{\mathrm{K}}^{-\mathrm{1}}$ is the specific gas constant of water, and $A=\mathrm{1}-q$ is the dry-air mass fraction of the parcel, to be determined from ψ_f by this condition.

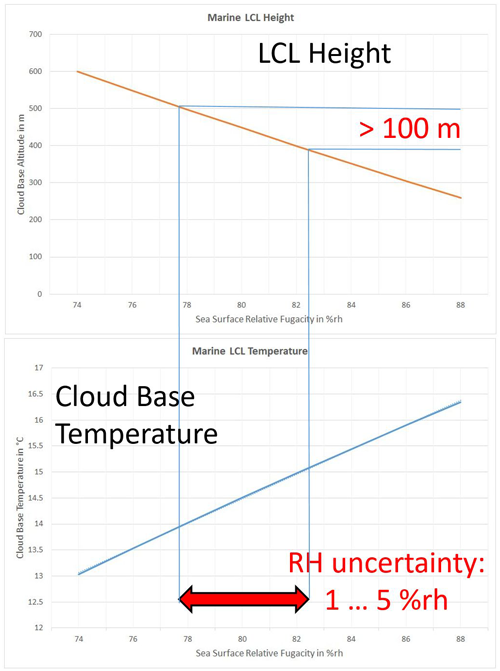
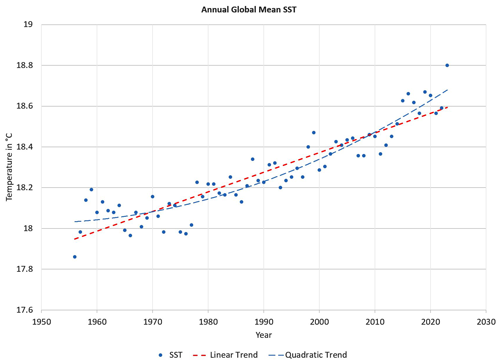
Figure 17 As a function of typical marine RH values, LCL height (top) and LCL temperature (bottom) are computed from the TEOS-10 Eqs. (50)–(53) at a sea-surface temperature of 292 K, close to the current global-mean SST of 18.8 °C; see Fig. 18. The added interval indicates the observation uncertainty of sea-surface RH, which corresponds to an uncertainty of the cloud-base altitude of more than 100 m.

At the LCL, the parcel is saturated at ψ_f=1, i.e.

$$\begin{array}{}\text{(51)}& \mathrm{0}={\mathit{\mu }}_{\mathrm{V}}^{\mathrm{AV}}\left(A,T_{\mathrm{LCL}},p_{\mathrm{LCL}}\right)-{\mathit{\mu }}_{\mathrm{W}}\left(T_{\mathrm{LCL}},p_{\mathrm{LCL}}\right).\end{array}$$

During uplift, A is assumed to remain constant, as well as the parcel's entropy, η^AV,

$$\begin{array}{}\text{(52)}& {\mathit{\eta }}^{\mathrm{AV}}\left(A,T_{\mathrm{SS}},p_{\mathrm{SS}}\right)={\mathit{\eta }}^{\mathrm{AV}}\left(A,T_{\mathrm{LCL}},p_{\mathrm{LCL}}\right).\end{array}$$

Finally, the LCL altitude, z_LCL, above sea level follows from the isentropic integral of the hydrostatic equation in terms of the enthalpy, h^AV, of humid air,

$$\begin{array}{}\text{(53)}& z_{\mathrm{LCL}}={\displaystyle \frac{\mathrm{1}}{g_{\mathrm{E}}}}\left[h^{\mathrm{AV}}\left(A,{\mathit{\eta }}^{\mathrm{AV}},p_{\mathrm{SS}}\right)-h^{\mathrm{AV}}\left(A,{\mathit{\eta }}^{\mathrm{AV}},p_{\mathrm{LCL}}\right)\right].\end{array}$$

The gravity acceleration is $g_{\mathrm{E}}=\mathrm{9.81}\mathrm{m}{\mathrm{s}}^{-\mathrm{2}}$. The functions ${\mathit{\mu }}_{\mathrm{V}}^{\mathrm{AV}}$, η^AV, h^AV, and μ_W can be expressed by partial derivatives of the TEOS-10 thermodynamic potentials of humid air and liquid water and are numerically available from the Sea-Ice-Air (SIA) library (Feistel et al., 2010d; Wright et al., 2010). Solving Eqs. (50)–(53) numerically, the LCL properties $\left(A,T_{\mathrm{LCL}},p_{\mathrm{LCL}},z_{\mathrm{LCL}}\right)$ are obtained from the given surface properties, $\left({\mathit{\psi }}_f,T_{\mathrm{SS}},p_{\mathrm{SS}}\right)$.

Table 1 LCL cloud-base temperatures, T_LCL, pressures, p_LCL, and heights, z_LCL, as functions of the SST, T_SS, at marine surface relative fugacity of ψ_f=80 %rh, computed from TEOS-10 equations (Eqs. 49–52). In addition, climatic LCL sensitivities, $\mathit{\alpha },\mathit{\beta },\mathit{\gamma }$, Eq. (53), with respect to increasing SST (Feistel and Hellmuth, 2024b), are shown. The row printed in bold approximates the current global-mean SST; see Fig. 18.

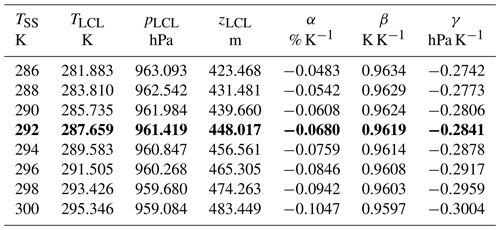
As solutions of Eqs. (50)–(53), height and base temperature of marine cumulus clouds, as a function of the sea-surface temperature T₀ at a sea-surface relative fugacity of ψ_f=80 %rh, are displayed in Fig. 16. Similarly, height and base temperature, as a function of the sea-surface relative fugacity RF of ψ_f at a sea-surface temperature T_SS=292 K, close to the current global-mean SST, are displayed in Fig. 17. It is obvious that the LCL effect of the range of RF uncertainty exceeds the effect caused by global SST rise significantly; therefore unknown minor systematic RF changes may easily disguise the thermal effects on marine cumulus clouds.

Global-mean sea-surface temperature rose from about 17.9 °C in 1956 to 18.8 °C in 2023 (Cheng et al., 2024); see Fig. 18. This pronounced climatic trend is expected to let the cumulus cloud base lift up while at the same time warming it (see Fig. 16), but not as much as the SST itself is increasing. The related climatic sensitivities possess complicated dependencies but may directly be derived by taking the related derivatives,

$$\begin{array}{}\text{(54)}& \begin{array}{rl}\mathit{\alpha }& \equiv {\left({\displaystyle \frac{\partial A}{\partial T_{\mathrm{SS}}}}\right)}_{p_{\mathrm{SS}},{\mathit{\psi }}_{\mathrm{f}}}=-{\left({\displaystyle \frac{\partial q}{\partial T_{\mathrm{SS}}}}\right)}_{p_{\mathrm{SS}},{\mathit{\psi }}_{\mathrm{f}}},\\ \mathit{\beta }& \equiv {\left({\displaystyle \frac{\partial T_{\mathrm{LCL}}}{\partial T_{\mathrm{SS}}}}\right)}_{p_{\mathrm{SS}},{\mathit{\psi }}_{\mathrm{f}}}\mathrm{and}\mathit{\gamma }\equiv {\left({\displaystyle \frac{\partial p_{\mathrm{LCL}}}{\partial T_{\mathrm{SS}}}}\right)}_{p_{\mathrm{SS}},{\mathit{\psi }}_{\mathrm{f}}},\end{array}\end{array}$$

of the TEOS-10 LCL equations (Eqs. 50–53) with respect to the surface temperature while keeping surface RH fixed (Feistel and Hellmuth, 2024). Selected results for those sensitivities are given in Table 1 relative to 1 °C rise in SST, similar to that in the past 70 years (Fig. 16). Here, $\mathit{\alpha }\approx -\mathrm{0.07}\mathit{\%}{\mathrm{K}}^{-\mathrm{1}}$ describes the rate of increase in specific humidity at the sea surface, often dubbed the “Clausius–Clapeyron effect”. The value of β≈0.96 indicates that the cumulus cloud base warms up more slowly than the ocean by about 4 %, and $\mathit{\gamma }\approx -\mathrm{0.28}\mathrm{hPa}{\mathrm{K}}^{-\mathrm{1}}$ is the LCL pressure lowering caused by ocean warming, corresponding to ascending clouds. The value β<1 implies that the thermal downward radiation from the cloud base does not keep pace with the ocean upward radiation; therefore the net climatic feedback of cumulus clouds is negative and acts against ocean warming. These clouds do not provide a physical explanation for the observed enhanced ocean warming.

Figure 18 Estimated increase 1957–2023 of global annual mean sea-surface temperatures (source: Cheng et al., 2024). The linear trend (red) is $t/\mathit{°}\mathrm{C}\approx \mathrm{18}+\mathrm{0.01}\times$ (year − 1961). The quadratic trend curve (blue) suggests an acceleration of warming.

6.3 Stratocumulus and other clouds

“Marine low clouds strongly cool the planet” (Myers et al., 2021). Over the Atlantic, “the strongest surface longwave cloud effects were shown in the presence of low level clouds” (Kalisch and Macke, 2012). “Low-cloud feedbacks are also a leading cause of uncertainty in future climate prediction because even small changes in cloud coverage and thickness have a major impact on the radiation budget” (Wood, 2012: p. 2373).

Generally, however, the dominating cloud type over the ocean is stratocumulus (Eastman et al., 2011). “They are common over the cooler regions of subtropical and midlatitude oceans where their coverage can exceed 50 % in the annual mean” (Wood, 2012: p. 2373) with a typical thickness of about 320 m and “a tendency for thicker clouds (median 420 m) in mid- and high latitudes” (Wood, 2012: p. 2378). “Stratocumuli tend to form under statically stable lower-tropospheric conditions” (Wood, 2012: p. 2374). On average, annually, stratocumulus is particularly frequent (up to 60 % coverage) in the subtropical coastal upwelling regions such as the cold Benguela, Humboldt, and California currents (Wood, 2012: Fig. 4a, Muhlbauer et al., 2014: Fig. 2). However, in those areas there is no obvious correlation of cloud cover with ocean warming (Fig. 1). Stratocumulus also forms large cloud cover (about 20 % coverage) in the boreal and austral west-wind bands (Wood, 2012: Fig. 4a) where the ocean is strongly warming up (Fig. 1).

“Only small changes in the coverage and thickness of stratocumulus clouds are required to produce a radiative effect comparable to those associated with increasing greenhouse gases” (Wood, 2012: p. 2374). Marine stratocumulus cloud feedback is still a major challenge and source of uncertainty of climate models (Hirota et al., 2021). However, “similar to other low-cloud types in the marine boundary layer, the impact of stratocumulus clouds on the outgoing longwave radiation is marginal due to the lack of contrast between the temperature of stratocumulus cloud tops and the temperature of the sea surface over which they form. Thus, the net radiative effect of stratocumulus clouds is primarily controlled by factors influencing their shortwave cloud forcing such as the cloud albedo and the cloud coverage” (Muhlbauer et al., 2014: p. 6695).

Following this argumentation and assuming that the shortwave cloud effect of stratocumuli on the ocean radiation balance by far outweighs their longwave effects, then the shortwave warming effect (Fig. 14) of decreasing cloudiness may dominate over the longwave cooling (Fig. 15). Possibly, this could make stratocumulus a potential candidate for causing the unclear recent ocean warming.

Similarly, in the diurnal cycle, shortwave effects (Fig. 14) have an impact at daytime only, while longwave effects (Fig. 15) are present all 24 h. In this respect, Luo et al. (2024) report that low-level cloudiness has an asymmetric day–night trend, which enhances ocean warming. Regionally, where in spring the days get longer, and the heavy cloudiness of the west-wind belt becomes replaced by fewer subtropical clouds (see Fig. 12), the systematic reduction in cloudiness may be expected to produce local excess warming such as near the subtropical fronts (see Fig. 1). Only dedicated future model studies, however, may reliably verify such speculations. As a recent example for the complexity of SST warming “by suppressing the evaporative cooling” of the ocean, Wang et al. (2024) explain dramatic but yet elusive warming events in the northeast Pacific by changes in ocean–atmosphere mechanisms caused by reduced Chinese aerosol emissions. Also, Berthou et al. (2024) describe cloud cover feedback over the sea during an unprecedented marine heatwave off northwest Europe in 2023. Excess water vapour emitted from a 2022 submarine volcano eruption may have contributed to the observed 2023 heat anomaly as well (Vömel et al., 2022; Jucker et al., 2024).

7 Summary

Substantial uncertainties of estimated heat fluxes at the ocean–atmosphere interface, such as the “ocean heat budget closure problem”, prevent reliable model predictions and causal explanations of climate phenomena that may take place within the range of those uncertainties. Among such “surprises” is the currently registered excessive ocean warming but also the subsequent consequences of this warming, such as those expected for global weather processes. Intending to reduce model uncertainties of thermal energies and heat fluxes in the climate system associated with the global circulation of water in its different phases and mixtures, the new geophysical thermodynamic standard TEOS-10 was adopted internationally in 2009 and 2011. Meanwhile, the uptake of TEOS-10 by the scientific community is mainly focussed on ocean observations and modelling, as the related publication metrics are suggesting (Appendix A).

TEOS-10 is advanced over previous similar standards and various collections of tailored empirical property equations by (i) its completeness in describing all thermodynamic properties of seawater, humid air, and ice, including their entropies, enthalpies, and chemical potentials; by (ii) its perfect mutual consistency between different phases and mixtures; and by (iii) its minimum uncertainty over maximum ranges of validity. Among its particularly favourable fields of application are composite systems with internal phase boundaries such as air sea interaction or cloud formation.

In addition to entropies, enthalpies, and chemical potentials, TEOS-10 has made certain new quantities for the description and modelling of climate processes available, such as (i)  Absolute Salinity of the ocean with a specified Reference Composition, (ii) Conservative Temperature as a measure of Potential Enthalpy of seawater representing a definite heat content, and (iii) Relative Fugacity as the thermodynamic driving force of evaporation, suggesting an improved full-range definition of relative humidity as a substitute for such mutually inconsistent and restricted definitions in practical use in climatology, meteorology, and physical chemistry.

This paper explains some tutorial examples for the application of TEOS-10 to selected current climate problems. There is (i) the two-phase conceptual model of “sea air” which provides rigorous equations for the latent heat of evaporation, for the heat capacity of humid air including salty aerosols (sea spray), and for the irreversible production of entropy by evaporation into the marine troposphere. There is also (ii) the formation of low marine cumulus clouds by isentropic thermal convection up to their condensation level and their climatic feedback to surface temperature and humidity concerning their infrared radiation effects.

It is currently unclear why and how the ocean warming is intensifying and when and how the related enormous amount of heat may transfer to the atmosphere. The observed systematic reduction of cloudiness may play an important role in this process, but details of reasons and theoretical causes are unknown. Marine surface relative humidity is an important and rather sensitive “control valve” for the supply of the troposphere with latent heat; however, the common assumption of constant relative humidity during climate change lacks rigorous explanation and leaves open the question of its possible trends below the insufficiently high level of observational uncertainty. TEOS-10 may further assist climate modellers to address such issues.

Ocean Science has proved to be a scientifically well-reputable, reliable, and successful partner journal for the publication of advanced results and methods in oceanography and geophysics. Cooperation with international bodies such as IUGG, UNESCO/IOC, IAPSO, SCOR, IAPWS, and BIPM has made the development and international introduction of TEOS-10 possible. The established standing committee JCS remains active with respect to related fundamental problems yet to be solved. It is hoped and expected that TEOS-10 may constitute a reliable long-term thermodynamic basis for interdisciplinary climate research.

Appendix A: Summary and metrics of selected publications related to TEOS-10

Between December 2008 and December 2012, supporting the activities of SCOR/IAPSO WG127, Ocean Science published 16 articles open-access in the Special Issue No. 14, “Thermophysical properties of seawater” (Feistel et al., 2008a). From February 2013 on, monthly metrics have been recorded by the journal. Table A1 reports these metrics of the last decade.

For comparison, metrics – as far as published elsewhere by 4 April 2024 – of selected TEOS-10 articles listed at https://www.teos-10.org (last access: 23 October 2024) are reported in Table A2.

Table A1 Metrics of articles in the Ocean Science Special Issue No. 14, “Thermophysical properties of seawater” (Feistel et al., 2008a), from February 2013 till March 2024. “SIA” stands for the TEOS-10 Sea-Ice-Air open-source code library.

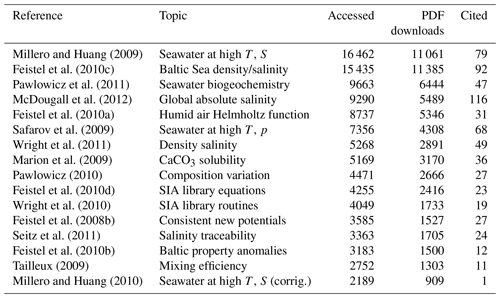
Table A2 Metrics published by March 2024 of selected TEOS-10 related articles apart from the Ocean Science Special Issue No. 14. “Ice Ih” is the ambient, hexagonal ice I phase of water.

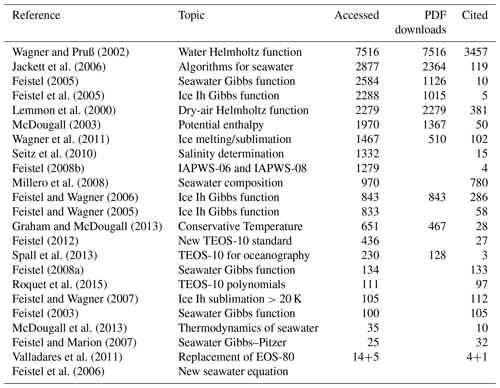
Table A3 IAPWS documents supporting TEOS-10, openly accessible at https://www.iapws.org (last access: 23 October 2024). IAPWS documents are independently and painstakingly verified before they may become adopted at an annual meeting. No metrics available.

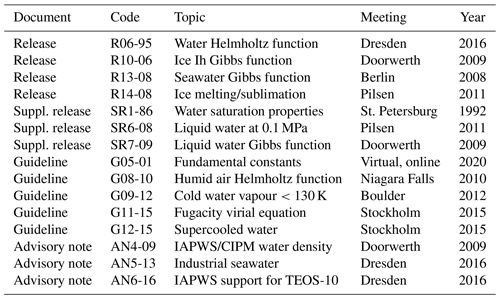
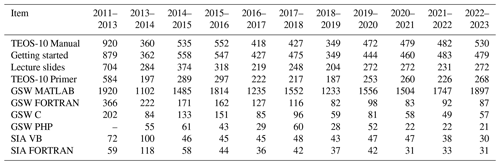
Table A4 Numbers of unique internet downloads 2011–2023 of supporting material from the TEOS-10 home page at https://www.teos-10.org (last access: 23 October 2024). “GSW” stands for the TEOS-10 Gibbs Seawater open-source code library. Data from Pawlowicz (2023).

Table A5 Selected additional TEOS-10 related readings, metrics by March 2024.

Appendix B: Thermodynamic potentials

This appendix provides a short introduction to thermodynamic potentials, supporting the equations and topics discussed in this article. Alternative presentations from different perspectives are available from numerous textbooks such as Guggenheim (1949), Margenau and Murphy (1964), Landau and Lifschitz (1966), or Kittel (1969). For seawater, the use of a Gibbs thermodynamic potential was first suggested theoretically by Fofonoff (1958, 1962); see also Craig (1960).

A key theoretical tool for the physical investigation of the globally warming climate and the related energy balances is thermodynamics. It is known from experience that there exists a distinguished state of various ambient substances that is known as a thermodynamic equilibrium state. If a sample of matter is in this state, it may never spontaneously alter its measurable macroscopic properties unless it becomes disturbed by external contact and exchange of energy or matter with its surrounding. Typical properties which characterize a particular equilibrium state are the total mass of a sample, m; its volume, V; its temperature, T; or its pressure, p. Of a given sample, different equilibrium states may exist that differ in those quantities, but there is a specific relation between those variables, known as an equation of state, which is characteristic of the given substance and remains universally valid at any of its possible equilibrium states. The most general and comprehensive equation of state of a given substance is a thermodynamic potential of that substance.

Thermodynamics is a mathematical theory for the construction and exploitation of equations of state and of properties derived therefrom for the prediction or verification of observations or experiments. Depending on the properties of interest, equations of state may be formulated in various different mathematical forms. It was discovered by J. Willard Gibbs (1873a, b) that from a suitable thermodynamic potential all thermodynamic properties of a given substance at any of its equilibrium states can be derived by appropriate mathematical methods.

For theoretical reasons (namely, the statistical so-called canonical ensemble, Landau and Lifschitz 1966: Sect. 31; Kittel, 1969: Chap. 18), a preferred thermodynamic potential of a pure substance is its Helmholtz energy, or free energy, $F\left(m,T,V\right)$, expressed in terms of the sample's mass, m; its temperature; and its volume. For mixtures, the single mass must be replaced by the set of partial masses of the species involved. Here, mass is used as a measure for the amount of substance, rather than particle or mole numbers, for the practical reason that in oceanography masses are easier measured than moles, and so TEOS-10 is following that tradition and is a mass-based description. Classical empirical thermodynamics of Clausius and Gibbs was formulated independently of the existence and properties of atoms or molecules, which presently define the mole (BIPM, 2019). The Helmholtz energy is related to the internal energy E of the sample by the Helmholtz differential equation,

$$\begin{array}{}\text{(B1)}& E=F-T{\left({\displaystyle \frac{\partial F}{\partial T}}\right)}_{m,V}.\end{array}$$

Note that IOC et al. (2010) use the symbol U for the internal energy rather than E in Eq. (B1). This replacement is done here for denoting the wind speed with u (Eq. 6) rather than specific internal energy, which is defined here by $e=E/m$ (Eqs. 1 and B3). The symbol E is frequently used in the thermodynamic literature, for example, by Gibbs (1873a) and Landau and Lifschitz (1966).

The potential function F is extensive, which means that for instance $F\left(\mathrm{2}m,T,\mathrm{2}V\right)=\mathrm{2}F\left(m,T,V\right)$ is valid for an equilibrium sample of twice the mass. It follows that the mass-specific Helmholtz function, $F/m\equiv f\left(T,\mathit{\rho }\right)$, depends on two variables only, T and the mass density, $\mathit{\rho }\equiv m/V$, and is mathematically simpler and more convenient than F, which may always be retrieved from a given f by

$$\begin{array}{}\text{(B2)}& F\left(m,T,V\right)=m\times f\left(T,{\displaystyle \frac{m}{V}}\right).\end{array}$$

The quantitative description of a substance of interest in the form of a thermodynamic potential such as f(T,ρ) has axiomatic properties. The description is complete (i.e. all thermodynamic properties of that substance are available), it is consistent (i.e. for any property one and only one result can be derived), and it is independent (i.e. no part of this description may be omitted without loosing the completeness). It is obvious that such axiomatic properties are very desirable for the description of geophysical substances; however, such thermodynamic potentials are rarely found in the corresponding literature. In particular, in climate research, which combines results and data from different disciplines, such as meteorology and oceanography, from research carried out all over the globe and over the years by subsequent generations of specialists, international binding standards such as the International System of Units (SI) are required that ensure mutual consistency and metrological comparability of any involved data produced from experiments, observations, and models.

The original potential function by Gibbs (1873a) was (internal) energy, $e=E/m$. It is known that a sample's energy can be increased by compression, −pdv, where $v=\mathrm{1}/\mathit{\rho }$ is the specific volume, or by input of heat, Tdη, where $\mathit{\eta }=N/m$ is the specific entropy. As an extensive quantity, entropy introduced by Clausius (1865, 1976) is denoted here by N to avoid confusion with seawater salinity, S. Energy conservation implies that

$$\begin{array}{}\text{(B3)}& \mathrm{d}e=T\mathrm{d}\mathit{\eta }-p\mathrm{d}v.\end{array}$$

Any such change between different equilibrium states of the same sample takes place along a definite, substance-specific surface e(η,v) so that de in Eq. (B3) is mathematically an exact differential and the partial derivatives of e possess the physical meanings that

$$\begin{array}{}\text{(B4)}& T={\left({\displaystyle \frac{\partial e}{\partial \mathit{\eta }}}\right)}_v,-p={\left({\displaystyle \frac{\partial e}{\partial v}}\right)}_{\mathit{\eta }}.\end{array}$$

Gibbs (1873b) also demonstrated that for several equilibrium samples in contact with one another, in absence of gravity or accelerated motion, the samples are in mutual equilibrium only if they have equal values of the coefficients T and p of Eq. (2.3).

In geophysical practice, the quantities η and v are difficult to measure, in contrast to, say, T or p. Mathematically equivalent to e(η,v), thermodynamic potentials in terms of the three other possible pairs of independent variables are formally obtained from so-called Legendre transforms (Alberty, 2001), namely the Helmholtz function $f\left(T,v\right)\equiv e-T\mathit{\eta }$ with the differential

$$\begin{array}{}\text{(B5)}& \mathrm{d}f=-\mathit{\eta }\mathrm{d}T-p\mathrm{d}v,\end{array}$$

the Gibbs function $g\left(T,p\right)\equiv f+pv=e-T\mathit{\eta }+pv$ with

$$\begin{array}{}\text{(B6)}& \mathrm{d}g=-\mathit{\eta }\mathrm{d}T+v\mathrm{d}p,\end{array}$$

and the specific enthalpy $h\left(\mathit{\eta },p\right)\equiv g+T\mathit{\eta }=f+T\mathit{\eta }+pv=e+pv$ with

$$\begin{array}{}\text{(B7)}& \mathrm{d}h=T\mathrm{d}\mathit{\eta }+v\mathrm{d}p.\end{array}$$

Depending on the application purpose, each of these potential functions has certain advantages and disadvantages, and having all of them optionally at hand in mutually consistent versions is most useful.

Gibbs (1874–1878) also considered a situation in which a given sample may exchange substance with its surrounding. If the exchanged mass of substance i is dm_i, the related change of the sample's (extensive) energy E at constant entropy and volume is termed the chemical potential μ_i of that substance,

$$\begin{array}{}\text{(B8)}& \mathrm{d}E=T\mathrm{d}N-p\mathrm{d}V+\sum _i{\mathit{\mu }}_i\mathrm{d}{m}_i.\end{array}$$

Therefore, this exact differential implies that the chemical potential is obtained from

$$\begin{array}{}\text{(B9)}& \begin{array}{rl}{\mathit{\mu }}_i\equiv & {\left({\displaystyle \frac{\partial E}{\partial m_i}}\right)}_{N,V,m_{j\ne i}}={\left({\displaystyle \frac{\partial F}{\partial m_i}}\right)}_{T,V,m_{j\ne i}}\\ & ={\left({\displaystyle \frac{\partial G}{\partial m_i}}\right)}_{T,p,m_{j\ne i}}={\left({\displaystyle \frac{\partial H}{\partial m_i}}\right)}_{N,p,m_{j\ne i}}.\end{array}\end{array}$$

Equilibrium of a spatially extended substance, in absence of gravity or accelerated motion, requires that in addition to T and p, the chemical potential μ_i also needs to possess the same value anywhere in the volume separately for each present substance. “The potential for each component substance must be constant throughout the whole mass” (Gibbs, 1874–1978: p. 119).

As intensive properties, the specific energies cannot depend on the total mass but only on the mass fractions, $w_i\equiv m_i/m$. Because by definition $\sum w_i=\mathrm{1}$, only (n−1) different fractions may be independent variables describing the n components of a mixture. For example, one of the components may be chosen as a master species, “0”, such as a solvent, and the remaining ones, $i=\mathrm{1},\mathrm{\dots },n-\mathrm{1}$, may denote the solutes.

In terms of T and p, chemical potentials are computed from the Gibbs function, g, through the Gibbs energy, G, of Eq. (B9). Because the Gibbs function only depends on the independent intensive variables, $g\left(w_{\mathrm{1}},\mathrm{\dots },w_{n-\mathrm{1}},T,p\right)$, the solutes' chemical potentials, i>0, are

$$\begin{array}{}\text{(B10)}& \begin{array}{rl}{\mathit{\mu }}_i& ={\left({\displaystyle \frac{\partial G}{\partial m_i}}\right)}_{T,p,m_{j\ne i}}={\left({\displaystyle \frac{\partial \left(mg\right)}{\partial m_i}}\right)}_{T,p,m_{j\ne i}}\\ & =g+{\left({\displaystyle \frac{\partial g}{\partial w_i}}\right)}_{T,p,w_{j\ne i}}\\ & -\sum _{j=\mathrm{1}}^{n-\mathrm{1}}{w}_j{\left({\displaystyle \frac{\partial g}{\partial w_j}}\right)}_{T,p,w_{k\ne j}}.\end{array}\end{array}$$

Similarly, the solvent's chemical potential is

$$\begin{array}{}\text{(B11)}& \begin{array}{rl}{\mathit{\mu }}_{\mathrm{0}}& ={\left({\displaystyle \frac{\partial G}{\partial m_{\mathrm{0}}}}\right)}_{T,p,m_{j>\mathrm{0}}}={\left({\displaystyle \frac{\partial \left(mg\right)}{\partial m_{\mathrm{0}}}}\right)}_{T,p,m_{j>\mathrm{0}}}\\ & =g-\sum _{j=\mathrm{1}}^{n-\mathrm{1}}{w}_j{\left({\displaystyle \frac{\partial g}{\partial w_j}}\right)}_{T,p,w_{k\ne j}}.\end{array}\end{array}$$

Therefore, the relative chemical potentials of the solutes are simply the partial derivatives,

$$\begin{array}{}\text{(B12)}& {\mathit{\mu }}_i-{\mathit{\mu }}_{\mathrm{0}}={\left({\displaystyle \frac{\partial g}{\partial w_i}}\right)}_{T,p,w_{j\ne i}}\end{array}$$

For mixtures, n>1, the differential (B6) of the Gibbs function takes the more general form

$$\begin{array}{}\text{(B13)}& \mathrm{d}g=-\mathit{\eta }\mathrm{d}T+v\mathrm{d}p+\sum _{i=\mathrm{1}}^{n-\mathrm{1}}\left({\mathit{\mu }}_i-{\mathit{\mu }}_{\mathrm{0}}\right)\mathrm{d}{w}_i.\end{array}$$

It follows straightforwardly from Eqs. (B10) and (B11) that the sum,

$$\begin{array}{}\text{(B14)}& \sum _{i=\mathrm{0}}^{n-\mathrm{1}}{\mathit{\mu }}_i{m}_i=mg=G,\end{array}$$

equals the Gibbs energy itself (Gibbs, 1874–1978: Eq. (96) therein, Guggenheim, 1949; Landau and Lifschitz, 1966; Kittel, 1969). In particular, if n=1, the Gibbs function g of a pure substance represents its chemical potential,

$$\begin{array}{}\text{(B15)}& g=\mathit{\mu }.\end{array}$$

Where two phases of a pure substance are in contact at mutual equilibrium, such as saturated water vapour at the liquid water surface, the mathematically distinct Gibbs functions of those phases take equal values. This indispensable condition for mutual consistency between the thermodynamic potentials of TEOS-10 is rigorously obeyed by virtue of appropriate reference-state conditions (Feistel et al., 2008b).