North Atlantic Subtropical Mode Water properties: intrinsic and atmospherically forced interannual variability

This study investigates the contributions of the ocean's chaotic intrinsic variability (CIV) and atmospherically forced variability to the interannual fluctuations in the North Atlantic Subtropical Mode Water (STMW) properties. Utilizing a 0.25° regional 50-member ocean–sea-ice ensemble simulation driven by an original surface forcing method and perturbed initially, the forced variability in STMW properties is estimated from ensemble mean fluctuations, while CIV is determined from deviations around the ensemble mean within each member. The model successfully captures the main features of STMW, showing correct agreement with observation-based ARMOR3D data in terms of location, seasonality, mean temperature and volume, as well as interannual variance of STMW's main properties. CIV significantly impacts STMW, explaining 10 %–13 % and 28 %–44 % of the interannual variance of its geometric and thermohaline mean properties, respectively, with a maximum imprint on STMW temperature. Observation-based and simulated intrinsic-to-total variance ratios are mostly consistent, dispelling concerns about a signal-to-noise paradox. This study also illustrates the advantages of ensemble simulations over single simulations in understanding oceanic fluctuations and attributing them to external drivers, while also cautioning against overreliance on individual simulation assessments.

1 Introduction

The North Atlantic Subtropical Mode Water (STMW), also called Eighteen Degree Water (EDW), is an abundant water mass located in the North Atlantic subtropical gyre.

It is a weakly stratified, homogeneous water mass sitting on top of the permanent pycnocline with constant temperature near 18 °C (Worthington, 1958; Feucher et al., 2016). STMW plays a notable role in climate and ecosystems, most notably because it is a significant heat and anthropogenic carbon reservoir (e.g., Dong and Kelly, 2004; Bates et al., 2002; Bates, 2007; Kelly et al., 2010; Pérez et al., 2013) that further supplies oxygen and nutrients to or depletes them in the subtropical gyre and the western boundary current system (e.g., Jenkins and Doney, 2003; Palter et al., 2005). Worthington (1958) first described a possible formation mechanism for STMW, later completed in Worthington (1976): surface buoyancy loss during the winter deepens the mixed layer in the Gulf Stream area. Part of this newly formed water mass is advected eastward by the North Atlantic Current, but most of it is subducted in spring to the south and isolated from the atmosphere below the summer thermocline. This subduction process forms the weakly stratified core of STMW, which is partially renewed each year. Maze et al. (2009), Forget et al. (2011), Billheimer and Talley (2013, 2016), Joyce et al. (2013), and Joyce (2013), among others, have shown that the seasonal fluctuations in STMW are governed by air–sea fluxes that form the deep winter mixed layer feeding the STMW reservoir and by vertical diffusion together with isopycnal eddy-driven mixing to the south of the Gulf Stream that erodes the STMW reservoir. More recently, Wenegrat et al. (2018) have shown that submesoscale eddies through near-surface restratification (mixed layer instability) can significantly erode the STMW reservoir. However, Sinha et al. (2023) have shown that mesoscale-resolving numerical simulations can capture this impact without fully resolved submesoscales (i.e.,  buoyancy fluxes insensitive to finer grid resolution).

Mode waters are associated with minima in Ertel potential vorticity (PV), where relative vorticity ζ is generally omitted when the available data have coarse spatial resolution. Forget et al. (2011) and Joyce (2013) have noted that while PV minima are very often used to detect STMW, there is no unique definition of this water mass in the literature. Depending on their available data, authors use working definitions that identify STMW well enough for their purposes. Drawing on the impermeability theorem laid out by Haynes and McIntyre (1990), Marshall et al. (2001) showed that there can be no PV flux across isopycnals within the water column and that any PV flux along isopycnals can only take place at the air–sea interface or at the interface with topography. Since STMW is formed in the winter mixed layer, it is visible as a pool of low PV relative to its surroundings once isolated from the atmosphere below the seasonal thermocline, and any erosion of this low-PV pool must be isopycnal. Using three-dimensional data obtained from observations or numerical simulations, it is possible to combine PV and density to identify and describe STMW (e.g., Maze and Marshall, 2011).

Kwon and Riser (2004) have shown that the observed interannual to decadal fluctuations in STMW properties are strongly correlated to the North Atlantic Oscillation (NAO) index. Dong and Kelly (2013) used a combination of observations and proxies for key processes (e.g., Gulf Stream path length for mixing) to further investigate these low-frequency fluctuations and highlighted the dominant role of surface heat fluxes, with Ekman advection playing a smaller but non-negligible role. Evans et al. (2017) and Li et al. (2022) further demonstrated that STMW interannual volume variations are indeed driven by a combination of diabatic and adiabatic atmospheric forcing but that the NAO-related adiabatic forcing (Ekman-driven) is a key player in explaining local extreme anomalies.

However, model studies have shown that STMW interannual fluctuations are not fully explained by the atmospheric variability when oceanic nonlinearities are explicitly simulated. Hazeleger and Drijfhout (2000) showed from shallow-water eddying simulations that the horizontal distribution of the STMW thickness exhibits modes of interannual variability under climatological atmospheric forcing devoid of interannual fluctuations. Dewar (2003) further showed from quasi-geostrophic eddying simulations that interannual to multidecadal modes of variability also emerge under stochastic atmospheric forcing in the region of STMW. These low-frequency modes emerge in the absence of any low-frequency atmospheric variability and may thus be labeled intrinsic. More realistic primitive-equation ocean simulations confirmed the emergence and persistence in the eddying regime of substantial low-frequency intrinsic variability under seasonal forcing (Penduff et al., 2011), with marked imprints on the North Pacific STMW as well (Douglass et al., 2012). Various nonlinear oceanic processes have been invoked to explain this phenomenon. Sérazin et al. (2018) for instance showed that an inverse cascade of kinetic energy from mesoscale turbulence toward larger scales can drive intrinsic variability up to interannual timescales, regardless of the atmospheric variability; Hochet et al. (2020) showed from eddying simulations that large-scale baroclinic instabilities may also directly generate interannual to decadal intrinsic variability with no direct contribution of mesoscale turbulence. However, Penduff et al. (2011) and Grégorio et al. (2015) showed that the interannual to multidecadal intrinsic variability becomes negligible when the resolution of their global ocean model is coarsened from 0.25° to 2°.

The large ensemble of global ocean–sea-ice simulations performed during the OceaniC Chaos – ImPacts, strUcture, predicTability (OCCIPUT) project (Penduff et al., 2014) has shown that at 0.25° resolution, intrinsic variability can compete with, and locally exceed, its atmospherically forced counterpart at interannual to decadal timescales, with substantial imprints on many large-scale oceanic indices: the Atlantic Meridional Overturning Circulation (AMOC; Leroux et al., 2018), the global meridional heat transport (Zanna et al., 2019), the latitude and velocity of the Kuroshio extension (Fedele et al., 2021), Southern Ocean eddy kinetic energy (Hogg et al., 2022), ocean heat content variability and long-term trends (Sérazin et al., 2017; Llovel et al., 2022), etc. These studies highlight the random phase of intrinsic ocean fluctuations developing within individual ensemble members around the atmospherically paced ensemble mean evolution. This nonlinearly driven random ocean variability will thus be referred to here as chaotic intrinsic variability (CIV).

Since Hazeleger and Drijfhout (2000) and Dewar (2003), no study has been published on the North Atlantic STMW chaotic intrinsic variability. During the last 20 years, however, model studies have confirmed in idealized and realistic setups that mid-latitude ocean dynamics are strongly impacted by low-frequency CIV, in particular within western boundary current systems and their associated recirculation gyres, where STMW is found. The major contribution of nonlinear and mesoscale processes in STMW formation and erosion is also well established. It is thus time to revisit and quantify the relative contributions of CIV and of atmospheric fluctuations in the interannual STMW variability; this is the aim of the present study, performed with a primitive-equation ensemble simulation, whose realism will be assessed against an observational reference.

Section 2 describes the simulated and observation-based datasets used in this study, our definitions of STMW and of its features, and the methods we used to process the data. Section 3 compares the simulated and observation-based STMW interannual variabilities and assesses their forced and chaotic intrinsic components with an emphasis on ensemble simulation benefits. Our results are summarized and discussed in Sect. 4.

2 Datasets and processing

2.1 The OCCIPUT regional ocean–sea-ice ensemble simulation

2.1.1 Ensemble modeling strategy

Our 5-daily model dataset was produced during the OCCIPUT project using a 50-member regional ensemble of forced oceanic hindcasts performed with the NEMO v3.5 ocean–sea-ice model implemented on the North Atlantic with 0.25° horizontal resolution and 46 vertical levels. This regional ensemble simulation, referred to as NATL025-GSL301 in the OCCIPUT database, is similar to the E-NATL025 simulation described in Bessières et al. (2017), with two differences: its size (50 members instead of 10) and its atmospheric forcing function, as described below. Its southern and northern boundaries at 20° S and 80° N are treated as solid walls with 28-grid-point buffer zones where simulated tracers are restored to monthly climatological conditions (Levitus et al., 1998), with a restoring coefficient decreasing inward toward zero; intrinsic variability is therefore solely generated inside the domain, without any influence from the surrounding ocean, and damped in the buffer zones.

The 50 ensemble members are initialized on 1 January 1993 from the final state of a single-member 19-year spin-up and are further integrated for 20 years until the end of 2012. The ensemble dispersion is triggered by applying a slight stochastic perturbation to each member during 1993; this perturbation scheme is described in Brankart (2013) and is designed to simulate the impact of subgrid-scale uncertainty on geostrophic velocities. The perturbations are turned off at the end of 1993, and the spread that they have introduced is then fully controlled by nonlinear ocean processes during the rest of the run. The realistic DRAKKAR Forcing Set 5.2 (DFS5.2) described in Dussin et al. (2016) is used between 1993 and 2012 to derive the atmospheric forcing, which is applied identically to all ensemble members: the (atmospherically) forced variability is thus estimated from the variability of the ensemble mean, and CIV is given by deviations around the ensemble mean within each ensemble member. The technical implementation of OCCIPUT ensembles is described in more detail in Bessières et al. (2017).

2.1.2 The ensemble-averaged forcing function and its impact on ensemble statistics

Besides its regional extension and shorter duration, this simulation differs from the 56-year global OCCIPUT ensemble described in earlier papers (e.g., Bessières et al., 2017) by its surface forcing: all members are forced by identical air–sea fluxes in our regional ensemble, rather than by identical atmospheric conditions in the global ensemble. At each time step, bulk formulae are used within each of the 50 regional members to compute air–sea fluxes based on the current DFS5.2 atmospheric state and on each member's surface state. The ensemble average of these air–sea fluxes is then computed at each time step and applied uniformly to all members in order to compute the next time step.

Figure 1 compares in the STMW pool the behavior of the present ensemble to ensemble-averaged air–sea fluxes with a smaller 10-member ensemble, where each member was driven by air–sea fluxes computed from its own surface state; the latter 10-member ensemble run is referred to as E-NATL025 and is described in Bessières et al. (2017). The left panel in Fig. 1 shows that the shallowest maximum of model stratification (on ensemble and temporal average) sits at the depth (about 50 m) of the seasonal pycnocline and above the pool of weakly stratified STMW found between about 150 and 300 m. The second stratification maximum locates the permanent pycnocline at about 450 m on average, and the stratification decreases toward greater depths. This profile is not only consistent with the observed mean stratification of the region (e.g., Feucher et al., 2016, 2019), but also almost identical in both ensembles: these two results show the equal consistency and realism of both forcing methods regarding the main STMW structure and of the ensemble mean (forced) long-term model state.

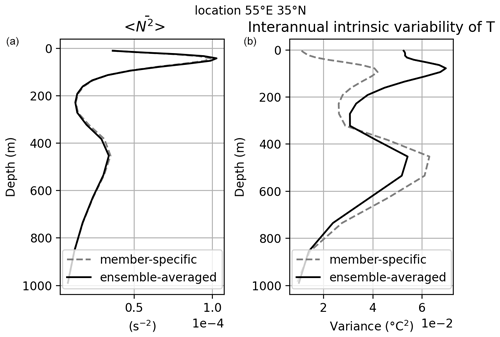
Figure 1 Vertical profiles of the time- and ensemble-averaged Brunt–Väisälä frequency (a) and of the time average of the ensemble variance of yearly mean temperature (b). Results are shown for the run where ensemble-averaged air–sea fluxes are applied to all members (thick line) and for the run where member-specific air–sea fluxes are applied to each member (dashed line). All profiles are taken at the same location within the formation zone of STMW.

The vertical profile of interannual intrinsic variance of temperature (varT(z), right panel in Fig. 1) has the same general shape as the averaged stratification in both ensembles, with the shallowest varT maximum sitting slightly below the seasonal pycnocline. However, varT at the surface increases by a factor of 5 when member-specific air–sea fluxes are replaced by ensemble-averaged fluxes; this factor is about 1.75 near the seasonal pycnocline.¹ In other words, using ensemble-averaged instead of member-specific air–sea fluxes does not adversely affect the atmospherically forced oceanic state and evolution, and it enhances the ensemble dispersion of yearly temperatures in the upper 300 m. We explain this latter enhancement and argue that this ensemble-averaged forcing method is preferable as follows.

The classical (member-specific) computation of turbulent air–sea fluxes through bulk formulae in ocean-only simulations induces an implicit relaxation of sea surface temperature (SST) toward a prescribed and fluctuating equivalent air temperature T_a, with a timescale on the order of 40 d in our region of interest (see Fig. 6 in Barnier et al., 1995). This relaxation is arguably overestimated in such simulations, where the heat capacity of the atmosphere is assumed infinite despite it being much smaller than that of the ocean in nature. In an ensemble simulation driven with member-specific fluxes, this results in SSTs being over-relaxed toward the same T_a within all members; this in turns yields an excessive damping of ensemble SST dispersion on these long timescales in particular and of intrinsic variability in general. Indeed, previous 0.25° resolution NEMO simulations driven by classical (member-specific) forcing have been shown to underestimate surface intrinsic variability at all scales compared to observations (see, for example, Penduff et al., 2010). The use of ensemble-averaged fluxes enhances surface intrinsic variability and compensates for this bias.

The ensemble-averaged forcing method avoids this excessive damping of surface CIV and lets intrinsic temperature anomalies reach up to the surface. Such behavior is arguably expected in coupled ocean–atmosphere simulations, where the ocean's thermal inertia overwhelms that of the atmosphere; estimating the strength of interannual CIV in eddying coupled models would help verify this hypothesis. Nevertheless, the use of ensemble-averaged instead of member-specific fluxes removes this unphysical imbalance between the oceanic and atmospheric heat capacities and compensates for the lack of simulated intrinsic variability.

Intrinsic thermal anomalies are not damped with the ensemble-averaged forcing approach; such anomalies in the real ocean may be slightly damped by air–sea interactions but much less strongly than in the member-specific approach. We thus hypothesize that the amplitude of upper-ocean-temperature interannual CIV in nature sits between those amplitudes simulated with both forcing strategies, and we argue that the ensemble-averaged forcing method lets it evolve in a more physically consistent and realistic way.

2.2 The ARMOR3D gridded observational product

We use ARMOR3D over its first 34 vertical levels (i.e., down to about 800 m) to assess the model simulation over our region of interest and the whole simulation period. ARMOR3D is a global analysis based on observational datasets including satellite sea surface temperature (SST), altimeter-derived sea surface height, in situ temperature and salinity profiles from the Argo array, and conductivity–temperature–depth (CTD) and expendable bathythermograph (XBT) profiles. These observations were processed to provide temperature (T), salinity (S) and geostrophic velocity (u,v) fields on a 3-D grid at 0.25° resolution using optimal interpolation and multiple linear regression methods as explained in Guinehut et al. (2012) and Mulet et al. (2012). This latter study presents how gridded T and S fields are used to provide consistent 3-D velocity fields via the thermal wind relation, with a surface reference level where geostrophic velocities are derived from altimetry.

ARMOR3D has some uncertainties and limitations, as is the case for any gridded product constrained by observations. Episodic spurious density inversions have been detected in ARMOR3D near the surface (Etienne Pauthenet, personal communication, 2022), but these artifacts do not affect the subsurface where most of the STMW is found. The interannual variability (in particular of salinity) is also known to be somewhat underestimated in ARMOR3D (Guinehut et al., 2012), partly since the coverage of in situ data is relatively coarse and since optimal interpolation has a tendency to smooth solutions.

The ARMOR3D dataset also has strengths despite its limitations, and it was chosen as our observation-based reference for three main reasons, the first two of which are documented in Balmaseda et al. (2015): (i) ARMOR3D compares well with independent observations at the local and large scale in our region of interest, with a skill that is similar to ocean reanalyses. (ii) The ARMOR3D fields are independent of multiple and complex modeling choices, which produce substantial differences between reanalyses. (iii) Perhaps more decisively, ARMOR3D is the only available model-independent T, S, u and v dataset that yields the full Ertel PV (including ζ) at a spatiotemporal resolution that is close to that of our model. As in all comparisons between simulations and any observation-based gridded dataset, the specificities of ARMOR3D will be taken into account in the comparisons discussed below.

2.3 ARMOR3D and simulated mean seasonal STMW structure

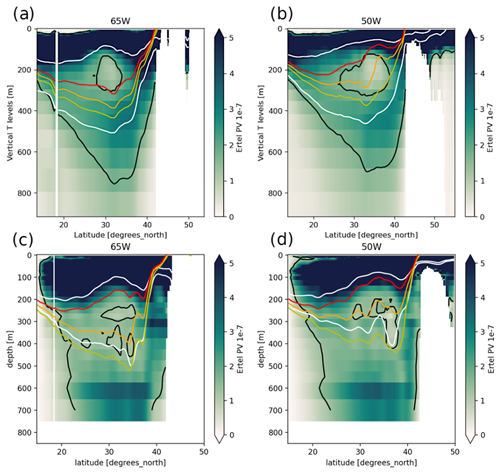
Ertel PV (Ertel, 1942) is defined as $Q=\frac{\mathrm{1}}{{\mathit{\rho }}_{\mathrm{0}}}(\mathit{\zeta }+f)\cdot \frac{\partial \mathit{\rho }}{\partial z}$, where f is the Coriolis parameter, ρ is potential density, ρ₀ is a reference density and ζ is relative vorticity; given the relatively fine resolution (0.25°) of our multivariate datasets, we do not neglect this latter term. In the rest of this paper, figures and numerical values express PV as ρ₀Q (in $\mathrm{kg}{\mathrm{m}}^{-\mathrm{4}}{\mathrm{s}}^{-\mathrm{1}}$), which is Ertel PV normalized by ρ₀=1020 kg m⁻³. Figures 2 and 3 show meridional sections of seasonally averaged PV in one randomly chosen ensemble member and in ARMOR3D. We verified that the behavior of this particular member is representative of all members in the ensemble and that the following results are robust.

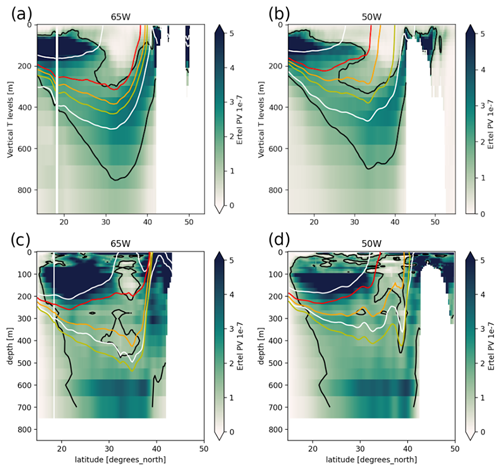
Figure 2 Sections at 65° W (a, c) and 50° W (b, d) of the winter Ertel PV, averaged over February–March–April from 1993 to 2012, in one ensemble member (a, b) and in ARMOR3D (c, d). Yellow, orange and red lines show the 17, 18 and 19 °C isotherms, respectively. White lines show the STMW density bounds in the model ($\mathrm{25.2}\le \mathit{\gamma }\le \mathrm{26.4}$ kg m⁻³) and in ARMOR3D ($\mathrm{25.8}\le \mathit{\gamma }\le \mathrm{26.4}$ kg m⁻³). Black lines show the STMW PV upper bound in the model ($\text{PV}<\mathrm{1.7}\times {\mathrm{10}}^{-\mathrm{7}}$ $\mathrm{kg}{\mathrm{m}}^{-\mathrm{4}}{\mathrm{s}}^{-\mathrm{1}}$) and in ARMOR3D ($\text{PV}<\mathrm{1.32}\times {\mathrm{10}}^{-\mathrm{7}}$ $\mathrm{kg}{\mathrm{m}}^{-\mathrm{4}}{\mathrm{s}}^{-\mathrm{1}}$).

Figure 3 The same as Fig. 2 but for summer months (July–August–September).

Two mean biases appear in these sections: the simulated STMW is about 80 m shallower and 0.4 kg m⁻³ lighter than in ARMOR3D, and its density range is wider (i.e., its PV is larger). This may be explained by a 0.4 psu fresh bias in the simulated STMW on temporal and ensemble average and by the usual tendency of this class of models to overestimate vertical mixing.

However, multi-year animations of these fields in various ensemble members and in ARMOR3D confirm that in both datasets the wintertime deepening of the mixed layer feeds the STMW reservoir, which is then shielded from the atmosphere in summer. The main features of the simulated STMW seasonal cycle (location, properties, time of formation and subduction, etc.) in the simulation are thus consistent with ARMOR3D and with those described in Maze et al. (2009), Kelly and Dong (2013), Billheimer and Talley (2016), and many other studies.

2.4 STMW definitions and properties

As mentioned in the Introduction, various authors define STMW in different ways given the data available to them, typically using one or a combination of the criteria listed in Table 1. In the present study, simulated and ARMOR3D STMW are defined using three criteria: PV maximum, geographic boundaries and density range (see Table 2). This definition is commonly used; see, for example, Forget et al. (2011). The PV maximum and geographical boundaries select weakly stratified waters in the region of interest, and the density range excludes those located outside the layer located between the seasonal and main thermoclines. The PV maximum and density range have different values in the model ensemble and the observational product to account for their differences (see Sect. 2.3). The ARMOR3D gridding algorithm also yields some uncertainty as to which exact criteria should be chosen to identify STMW. This uncertainty was evaluated using various sets of values for PV and density: three of these are presented here, defined in Table 2 as A, B and C, with increasingly larger bounds. Section 3 evaluates the effect of the different values used in setting the boundaries of STMW in both datasets.

Worthington (1958)Speer and Tziperman (1992)Joyce (2013)Forget et al. (2011)Maze and Marshall (2011)Kwon and Riser (2004)Worthington (1976)

Table 1 Criteria used in the literature to define STMW and associated references. This list is non-exhaustive since similar criteria are used in other studies.

Table 2 Definition of STMW in the present study. A, B and C correspond to sensitivity choices in ARMOR3D.

2.5 Computation and processing of STMW property time series

The above criteria are used within both datasets to label grid cells corresponding to STMW; their individual volumes are summed up at each time step to estimate the time-varying enclosed volume of STMW in “Sverdrup-years” (Svy; i.e., volume arising from a 1 Sv flux sustained for 1 year: 31.536×10¹² m³). Model and ARMOR3D fields in labeled grid cells are then averaged to estimate the volume-weighted mean temperature (T), salinity (S), neutral density (γ) and PV of the simulated and ARMOR3D STMW. The mean depth of the water mass is finally given by the volume-weighted average of the immersions of labeled grid points.

The resulting time evolution of these six STMW properties may exhibit geophysical trends and variability for periods greater than the 20 years of available data and potential numerical trends in the case of the simulation. Variability for periods longer than 20 years and possible trends were finally removed from each ensemble member and from ARMOR3D over the 20-year period using the locally weighted regression scatterplot smoothing (LOWESS) nonlinear detrending method (Cleveland, 1979), yielding the evolution of STMW properties over the range of timescales τ that is properly resolved in the datasets ($\mathrm{10}\mathrm{d}<\mathit{\tau }<\mathrm{10}\mathrm{years}$).

These 50+1 time series of each STMW property were further split over two ranges of timescales: (i) interannual time series ($\mathrm{18}\mathrm{months}<\mathit{\tau }<\mathrm{10}\mathrm{years}$) were obtained by removing the mean seasonal cycle from the 51 time series and applying a low-pass Lanczos filter with a cutoff period of 18 months; (ii) so-called subannual time series ($\mathrm{10}\mathrm{d}<\mathit{\tau }<\mathrm{18}\mathrm{months}$, including seasonal cycles) were obtained by subtracting the interannual time series from the detrended time series.

2.6 Total, forced and chaotic intrinsic variances

We hereafter focus on the contributions of the atmospherically forced and chaotic intrinsic components of the STMW total interannual variability. The forced, intrinsic and total variances (${\mathit{\sigma }}_{\mathrm{F}}^{\mathrm{2}}$, ${\mathit{\sigma }}_{\mathrm{I}}^{\mathrm{2}}$ and ${\mathit{\sigma }}_{\mathrm{T}}^{\mathrm{2}}$, respectively) of any variable X are computed as in Leroux et al. (2018):

$$\begin{array}{}\text{(1)}& {\displaystyle }{\mathit{\sigma }}_{\mathrm{F}}^{\mathrm{2}}& {\displaystyle }={\text{var}}_t(\langle X_m(t)\rangle ),\text{(2)}& {\displaystyle }{\mathit{\sigma }}_{\mathrm{I}}^{\mathrm{2}}& {\displaystyle }=\stackrel{\mathrm{‾}}{{\text{var}}_m\left(X_m\right(t\left)\right)},\text{(3)}& {\displaystyle }{\mathit{\sigma }}_{\mathrm{T}}^{\mathrm{2}}& {\displaystyle }=\langle {\text{var}}_t\left(X_m\right(t\left)\right)\rangle .\end{array}$$

In the latter expressions, $\stackrel{\mathrm{‾}}{\cdot }=\frac{\mathrm{1}}{T}{\sum }_{t=\mathrm{1}}^T$ is the temporal average over T time steps, $\langle \cdot \rangle =\frac{\mathrm{1}}{M}{\sum }_{m=\mathrm{1}}^M$ is the ensemble average of M members, ${\text{var}}_m\left(X_m\right(t\left)\right)=\frac{\mathrm{1}}{M}{\sum }_{m=\mathrm{1}}^M\left(X_m\right(t)-\langle X_m(t)\rangle {)}^{\mathrm{2}}$ is the ensemble variance at time t and ${\text{var}}_t\left(X_m\right(t\left)\right)=\frac{\mathrm{1}}{T}{\sum }_{t=\mathrm{1}}^T\left(X_m\right(t)-\stackrel{\mathrm{‾}}{X_m\left(t\right)}{)}^{\mathrm{2}}$ is the temporal variance for member m. It can be shown that with this choice of biased variance estimates, ${\mathit{\sigma }}_{\mathrm{T}}^{\mathrm{2}}={\mathit{\sigma }}_{\mathrm{F}}^{\mathrm{2}}+{\mathit{\sigma }}_{\mathrm{I}}^{\mathrm{2}}$ if $\stackrel{\mathrm{‾}}{X_m\left(t\right)}=\mathrm{0}$; this property is very well verified in our case since $\left|\frac{{\mathit{\sigma }}_{\mathrm{T}}^{\mathrm{2}}-({\mathit{\sigma }}_{\mathrm{F}}^{\mathrm{2}}+{\mathit{\sigma }}_{\mathrm{I}}^{\mathrm{2}})}{{\mathit{\sigma }}_{\mathrm{T}}^{\mathrm{2}}}\right|<{\mathrm{10}}^{-\mathrm{3}}$. Finally, we estimate the intrinsic fraction of the total variance of STMW properties from the ratio $R_{\mathit{\sigma }}=\mathrm{100}\mathit{\%}\cdot {\mathit{\sigma }}_{\mathrm{I}}^{\mathrm{2}}/{\mathit{\sigma }}_{\mathrm{T}}^{\mathrm{2}}$.

3 Results

The interannual anomalies of integrated STMW properties defined in Sect. 2.5 are shown in Fig. 4 for both datasets. The ensemble and temporal mean values of the STMW properties are given at the bottom of each panel for the simulation and for each of the three definitions in the observational product. Definition B in the observational product (green) yields a mean volume of 28 Svy that is very close to the 30.5 Svy in the ensemble and will thus be retained in the following to identify STMW in ARMOR3D. The colored lines in this figure also show that in ARMOR3D, the three definitions of STMW yield very similar interannual evolutions: this confirms the robustness of our criteria despite their partial arbitrariness.

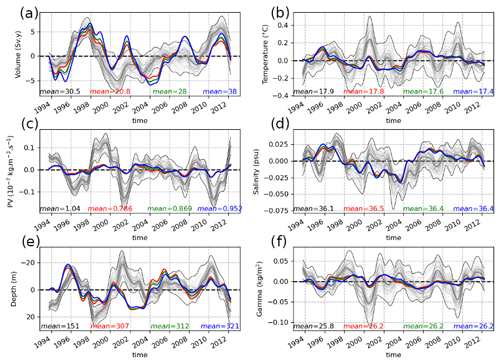
Figure 4 Interannual evolution of the six STMW property anomalies. Thin grey lines shows individual ensemble members and thick grey lines ensemble averages. Thin black lines show the maximum and minimum values of the entire ensemble at each time step. The colored lines show the same quantities in ARMOR3D using the three definitions given in Sect. 2.2: criteria A, B and C correspond to red, green and blue lines, respectively. The text at the bottom gives the 1993–2012 mean value of STMW properties computed before detrending and filtering in the ensemble mean (black) and in the ARMOR3D data (the same three colors as above).

Simulated STMW properties vary around their ensemble mean within individual ensemble members due to the random phase of intrinsic variability in the 50 realizations. Throughout most of the integration period, the ARMOR3D-derived STMW interannual variability remains within the simulated envelope, providing a first indication of correct model–ARMOR3D agreement in terms of variability, which is assessed more precisely in the following.

3.1 Forced and chaotic intrinsic components of the STMW variability

3.1.1 Intrinsic fraction of STMW properties' simulated variance

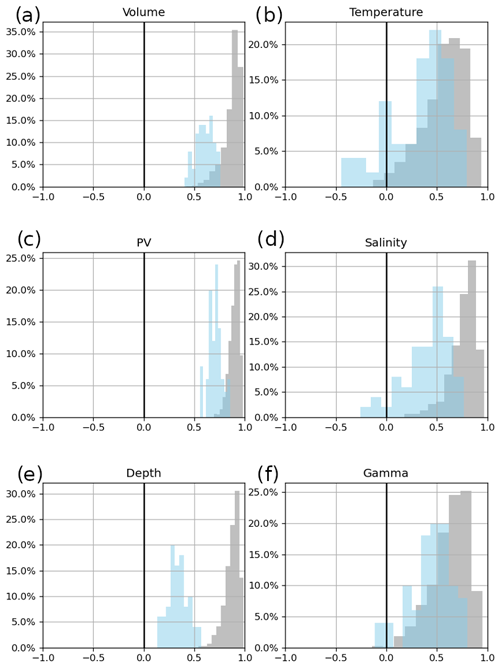
Using the definitions outlined in Sect. 2.4, we computed the intrinsic fraction R_σ of the variances of each simulated STMW property within the three ranges of timescales introduced in Sect. 2.5: all resolved periods (10 d to 10 years) and annual–subannual periods (10 d to 18 months), both of which include seasonal cycles, and interannual periods (18 months to 10 years). Results are shown in Table 3.

Table 3 Intrinsic fraction of interannual variances (percentage $R_{\mathit{\sigma }}=\mathrm{100}\mathit{\%}\cdot {\mathit{\sigma }}_{\mathrm{I}}^{\mathrm{2}}/{\mathit{\sigma }}_{\mathrm{T}}^{\mathrm{2}}$) of STMW properties in three ranges of timescales τ.

When all resolved timescales are considered ($\mathrm{10}\mathrm{d}<\mathit{\tau }<\mathrm{10}\mathrm{years}$), the contribution of intrinsic processes to the variance of STMW properties reaches a modest maximum of 13 % for temperature. This intrinsic fraction is even smaller at annual–subannual timescales with a maximum of 4.94 % for temperature; the atmospheric forcing thus explains most of the variability in STMW properties at these relatively short timescales, consistently with the large control exerted by the atmospheric annual cycle on STMW (see Sect. 1).

Nonetheless, the intrinsic fraction becomes much larger at interannual timescales. Even the smallest contributions of CIV (10.6 % for PV and about 13 % for volume and depth) cannot be neglected for $\mathrm{18}\mathrm{months}<\mathit{\tau }<\mathrm{10}\mathrm{years}$. Interannual fluctuations in STMW thermohaline properties are most strongly impacted by CIV: about one-fourth, one-third and one-half of the interannual variance of STMW salinity, density and temperature, respectively, is controlled by intrinsic processes and is random in phase. Explaining why interannual CIV has a weaker impact on “geometric” STMW properties (volume, PV and depth) would require additional analyses, which are left for future studies.

3.1.2 Simulated and ARMOR3D STMW fluctuations

STMW interannual fluctuations simulated in each member are compared to their ARMOR3D counterparts using Taylor diagrams (Taylor, 2001) in Fig. 5. The reference for each simulated STMW property is the corresponding ARMOR3D interannual anomaly (based on definition B; see Sect. 2.4): comparisons between each ensemble member and this reference yield 50 black dots in each panel.

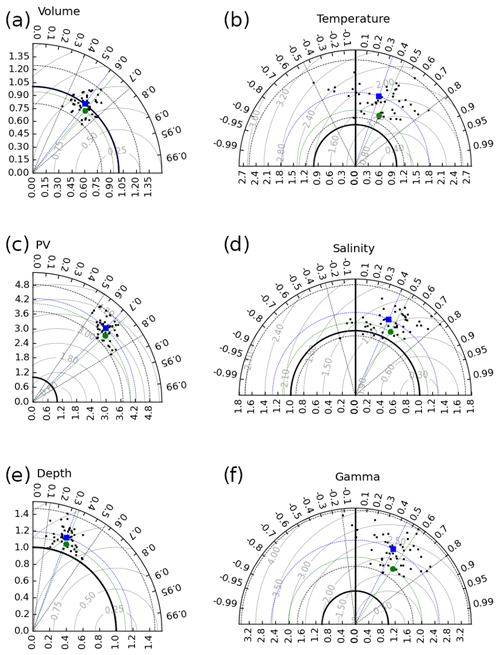
Figure 5 Taylor diagrams comparing the interannual fluctuations in STMW properties in the reference (ARMOR3D time series) and in each ensemble member (total variabilities, black dots) and in their ensemble mean (forced variabilities, green circles). Blue squares show the center of gravity of the black dots. The distance between each dot and the origin gives the ratio of simulated and reference SDs; the angle between the latter line and the horizontal axis gives the temporal correlation between simulated and reference time series; the distance between dots and the (1,0) point gives the rms difference between the latter time series. Thick black lines show unity SD ratios; dashed grey lines show the range of correlations and SD ratios for black dots; dashed blue and green lines show the coordinates of blue squares and green circles.

The center of gravity (COG, blue square) of the black dots in the top-left subpanel of Fig. 5 sits very close to the unit radius circle: the ensemble-averaged total interannual SD of STMW volume compares very well with its ARMOR3D counterpart. In other words, the model remarkably simulates the interannual SD of the STMW volume in ARMOR3D in an ensemble-averaged sense.

For the five other simulated STMW properties, ensemble-averaged interannual SDs exceed their ARMOR3D counterparts by a factor of 1.2 for depth to 4.2 for PV. That our 0.25° ensemble may overestimate STMW fluctuations would come as a surprise, since most NEMO simulations at this resolution tend instead to underestimate interannual fluctuations (see, for example, Penduff et al., 2010). In fact, interannual fluctuations in simulated STMW properties are more in line than ARMOR3D estimates with previous observational studies (see, for example, Fig. 2 in Kwon and Riser, 2004, and Figs. 2 and S1 in Stevens et al., 2020). It is therefore very likely that we found here an illustration of ARMOR3D underestimating STMW fluctuations (especially for PV), which is consistent with the fact that ARMOR3D is known to substantially underestimate the actual interannual ocean variability (Guinehut et al., 2012).

We now focus on the ensemble dispersion of black dots around their COG in these panels. By design, all ensemble members are driven by the same atmospheric evolution and simulate equally likely evolutions of STMW properties: inter-member differences in STMW evolutions and in their agreement with ARMOR3D are thus due to different CIV realizations. Accordingly, Fig. 5 reveals a substantial angular dispersion of black dots with respect to the x axis, corresponding to differences in correlations of individual ensemble members with ARMOR3D time series. For STMW volume for instance, certain ensemble members have good phase agreement with the observational reference (up to 0.75 correlation) and almost the same interannual SD, while other members have poorer correlations (as low as 0.4) and under- or overestimate the ARMOR3D SD by 20 %. The CIV-related diversity of correlations and SD ratios is even larger for STMW temperature, whose interannual variance is the most affected by CIV (Sect. 3.1): member–ARMOR3D correlations range from −0.45 to 0.79 and their SD ratios from 1.2 to 2.6.

These large dispersions indicate that slightly different initial conditions can strongly affect the skill of eddying ocean simulations driven by the same realistic forcing for decades, yielding a wide range of model–ARMOR3D correlations of either sign depending on the member considered. This demonstrates a specific value of ensemble experiments for model evaluation: this approach gives a direct measure of the CIV-related uncertainty in simulated time series and allows for a much more robust model skill assessment.

For the six STMW properties under consideration, the green circles indicate how the ensemble mean (forced) variability compares with the ARMOR3D reference. These circles show that the forced variability has smaller SD but is better correlated with the reference than individual members on ensemble average (ensemble COG, blue squares). This is consistent with the fact that the phase of CIV-related “noise” is random within each ensemble member: this noise is strongly attenuated in the ensemble mean evolution, hence explaining the position of green dots relative to blue squares. On the other hand, the phase of CIV in certain members may happen to correlate favorably (unfavorably) with the observational reference, explaining that certain black dots sit right (left) of the green lines; the same behavior was reported by Leroux et al. (2018) from the analysis of AMOC fluctuations in the global OCCIPUT ensemble.

These results globally show relatively good agreement between the simulated and ARMOR3D data. The average and SD of STMW volume are very similar in both datasets; other variables have an SD within the same order of magnitude (knowing the probable underestimation of ARMOR3D-derived estimates), and most ensemble means of STMW properties are in correct phase agreement with ARMOR3D.

3.1.3 Possibility of a signal-to-noise paradox

We finally assess whether the simulated variability in STMW properties are affected by the so-called “signal-to-noise paradox”, as discussed in Leroux et al. (2018). This concept has been proposed to characterize ensemble climate simulations where ensemble mean fluctuations are strongly correlated to observations, while most individual members are more closely correlated to other members than to observations (see, for example, Eade et al., 2014; Scaife and Smith, 2018; Christiansen, 2019). When this paradox is met, the ensemble mean (forced) variability is correctly simulated but the model is over-dispersive (overestimated contribution of CIV).

Figure 6 exhibits an overlap between the distributions of member–ARMOR3D correlations (blue) and member–member correlations (grey) for most interannual STMW properties. Member–ARMOR3D and member–member correlations overlap over the range of 0.5–0.75 for STMW volume for instance and over much wider ranges for STMW thermohaline properties. In particular, member–member correlations do not largely fall below member–ARMOR3D correlations, suggesting that the ensemble is not clearly over-dispersive. The opposite is found however for STMW depth, for which the ensemble seems to be under-dispersive. Besides this main exception though, we conclude that it is unlikely that a signal-to-noise paradox contaminates the statistics of STMW properties in our simulation. In other words, the simulated partition between forced and intrinsic interannual variabilities in STMW properties is consistent with their counterpart in ARMOR3D.

Figure 6 Distributions of various correlation coefficients using the interannual fluctuations in STMW properties in the 50 ensemble members as references. The distributions show their correlations with the corresponding time series in all other ensemble members (grey) and in ARMOR3D (blue).

4 Discussion and conclusion

We have investigated the contributions of the ocean's chaotic intrinsic variability (CIV) and of the atmospherically forced variability in the interannual fluctuations in the North Atlantic Subtropical Model Water (STMW) main properties. We made use of a 0.25° regional 50-member ocean–sea-ice ensemble simulation with perturbed initial conditions and of the ARMOR3D observation-based product. The forced variability in simulated STMW properties was estimated from the fluctuations of the ensemble mean, and its chaotic intrinsic variability was estimated from the deviations around the ensemble mean within each ensemble member. This regional ensemble simulation is driven through bulk formulae by a realistic atmospheric evolution, each member being forced by the same time-varying air–sea fluxes computed online via an ensemble average. We showed that this forcing approach avoids excessive damping of the interannual CIV (i.e., ensemble spread) of upper-ocean temperature, without impacting the mean state and forced variability.

Following the literature (Table 1), we identified STMW in all ensemble members and in ARMOR3D using the same combination of physical criteria, i.e., all water parcels with low potential vorticity values within a geographical area and a density range. Parameters were adjusted to fit differences between the ARMOR3D and simulated mean states (Table 2). Geometric (volume, Ertel potential vorticity, depth) and thermohaline (temperature, salinity, density) properties of the STMW core were estimated from the simulation and from ARMOR3D over the period 1993–2012. We found that although the simulated STMW is slightly more buoyant, its main features are in agreement with ARMOR3D, in particular its location, seasonality, mean temperature, mean volume and interannual volume variance (Figs. 2 and 3).

The CIV contribution to the STMW properties' variance was estimated in different frequency bands via the intrinsic fraction R_σ. We found that STMW is substantially impacted by interannual CIV, which in particular explains 44 % of its low-frequency temperature variance. Explaining why thermohaline STMW properties are more impacted by interannual CIV than geometric STMW properties (R_σ=28 %–44 % vs. 10 %–13 %, Table 3) would require a detailed analysis of the atmospheric and oceanic processes that control the water mass interannual evolution, which lies beyond the scope of the present paper and is left for the future. These results nevertheless provide a new context for the attribution of observed STMW fluctuations to external (atmospheric) and internal (oceanic) drivers: a non-negligible part (10 %–44 %) of STMW fluctuations is ocean-driven, is random in phase and cannot be explained by atmospheric fluctuations only.

We verified at interannual timescales that our analysis is not plagued by the so-called signal-to-noise paradox, meaning that intrinsic-to-total variance ratios are compatible in the ensemble simulation and in ARMOR3D (except for STMW depth, whose sensitivity to CIV may be underestimated in the model). These findings suggest that the contribution of CIV to the variance of real STMW properties is genuine and globally consistent with its simulated contribution.

Building upon a few earlier studies (e.g., Leroux et al., 2018; Fedele et al., 2021), our present analysis illustrates the benefit of ensemble simulations over single hindcasts for model evaluation in the eddying regime. The random phase of CIV noise can result in either high or low and even negative model–ARMOR3D correlations (from −0.45 to 0.8 for STMW temperature) depending on the ensemble member. Assessing a single eddying ocean simulation against observational references should thus be done with care, all the more so since such references also contain random components, with an amplitude that is specific to the object of study.

The quantitative results of the present study may somewhat depend on certain model parameters and on our analysis technique. In particular, it is difficult to predict whether a finer model resolution may enhance STMW's intrinsic fractions R_σ (as found for sea level; see Sérazin et al., 2015) or barely impact them (as shown for AMOC; see Grégorio et al., 2015). We also made the classical assumption that the forced and intrinsic variabilities in STMW properties may be separated and quantified using ensemble means and ensemble anomalies; other approaches have been recently proposed to avoid this separation (see, for example, Fedele et al., 2021). More generally, alternative ensemble simulations and diagnostics could help refine the present results.

The impacts of CIV on STMW properties at eddy-permitting resolution are likely to also exist in coupled ocean–atmosphere simulations, although experimental strategies allowing the quantification of CIV impacts in a coupled context are not yet clear. In the meantime, prescribing the atmospheric forcing of an eddying ocean ensemble simulation as done here provides a natural and efficient means to study forced and intrinsic variabilities. In this forced ocean modeling context, the ensemble mean forcing technique that we propose is designed to let CIV behave as freely as it may in an eddying ocean model coupled to the atmosphere by removing excessive damping of upper-ocean thermal intrinsic variability up to long timescales.

Previous studies have shown that beyond STMW properties, the interannual to multidecadal variability in several other climate-relevant oceanic indices is influenced by oceanic CIV, which is strongly underestimated in coarse-resolution ocean models such as those used in most CMIP-class climate models. The physical consistency of climate models may thus be improved by taking CIV into account, either explicitly using higher-resolution ocean components or by parameterizing the impacts of CIV in coarse ocean components.