Seasonal extrema of sea surface temperature in CMIP6 models

CMIP6 model sea surface temperature (SST) seasonal extrema averaged over 1981–2010 are assessed against the World Ocean Atlas (WOA18) observational climatology. We propose a mask to identify and exclude regions of large differences between three commonly used climatologies (WOA18, WOCE-Argo Global Hydrographic climatology (WAGHC) and the Hadley Centre Sea Ice and Sea Surface Temperature data set (HadISST)). The biases in SST seasonal extrema are largely consistent with the annual mean SST biases. However, the amplitude and spatial pattern of SST bias vary seasonally in the 20 CMIP6 models assessed. Large seasonal variations in the SST bias occur in eastern boundary upwelling regions, polar regions, the North Pacific and the eastern equatorial Atlantic. These results demonstrate the importance of evaluating model performance not simply against annual mean properties. Models with greater vertical resolution in their ocean component typically demonstrate better representation of SST extrema, particularly seasonal maximum SST. No significant relationship of SST seasonal extrema with horizontal ocean model resolution is found.

1 Introduction

Seasonal extrema of sea surface temperature (SST) are important for the global climate system. SST seasonal maxima influence the formation and intensity of tropical cyclones (Palmen, 1948; Dare and McBride, 2011; Holland, 1997; Sun et al., 2017) and may be associated with marine heatwaves, which can cause damage to marine ecosystems worldwide, including biomass decrease, bleaching of coral reefs and deaths of marine animals (Cheung and Frölicher, 2020; Hughes et al., 2018; Jones et al., 2018). SST seasonal minima are closely linked to the formation of sea ice and determine the properties of intermediate and deep water. Heat loss in winter allows surface water to subduct into the deep ocean, important for thermohaline circulation. Therefore, future projections of tropical cyclones, heatwaves, water mass formation and sea ice extent require our models to have a realistic representation of SST seasonal extrema.

Typically, however, evaluations of climate model historical runs focus on annual or long-term mean SST, revealing common biases across many models (Wang et al., 2014; Flato et al., 2013). Assessments of model performance in simulating SST seasonal cycles are less common and are often only regional. For example, a marked seasonal variability of SST warm bias in the eastern tropical Atlantic has been documented in Coupled Model Intercomparison Project Phase 5 (CMIP5) and CMIP6 (CMIP Phase 6) models (Prodhomme et al., 2019; Richter et al., 2014; Richter and Tokinaga, 2020). In these models, the eastern tropical Atlantic warm bias is at a maximum in boreal summer (June–July–August), which has been attributed to the largest wind biases occurring during spring (Richter et al., 2012; Richter and Tokinaga, 2020). Similarly, CMIP6 model SST cold biases in the North Pacific subtropics vary seasonally (Zhu et al., 2020). Song and Zhang (2020) suggested that the CMIP5 multi-model mean has seasonally dependent SST biases in the northeastern Pacific Ocean, with a warm bias during summer and a cold bias during winter, which they argued was caused by poorly simulated North American monsoon winds. Wang et al. (2014) showed that the amplitude of CMIP5 multi-model mean SST biases varies seasonally and therefore an accurate annual mean SST does not guarantee accurate seasonal extrema or seasonal cycle. Here we evaluate the seasonal cycle globally in 20 state-of-the-art CMIP6 climate models, to provide a foundation for model SST bias identification and future reduction. By presenting maps of SST bias in seasonal extrema for each model, we highlight the care needed in selecting these models for future climate projections in particular regions.

Bi et al. (2020)Law et al. (2017)Semmler et al. (2020)Wu et al. (2019)Wu et al. (2020)Danabasoglu et al. (2020)Swart et al. (2019)Golaz et al. (2019)Held et al. (2019)Kelley et al. (2020)Kelley et al. (2020)Andrews et al. (2020)Andrews et al. (2020)Volodin et al. (2017)Boucher et al. (2020)Tatebe et al. (2019)Müller et al. (2018)Seland et al. (2020)Park et al. (2019)Sellar et al. (2019)

Table 1 The 20 CMIP6 models used in this study; the horizontal resolution of their ocean component; ocean vertical coordinate (z: traditional height coordinate; z^∗: rescaled height coordinate for more accurate representation of free-surface variations; ρ: isopycnic coordinate; σ: terrain-following sigma coordinate; multiple symbols refer to a hybrid coordinate); total number of ocean vertical levels; thickness of the ocean top grid cell; and references.

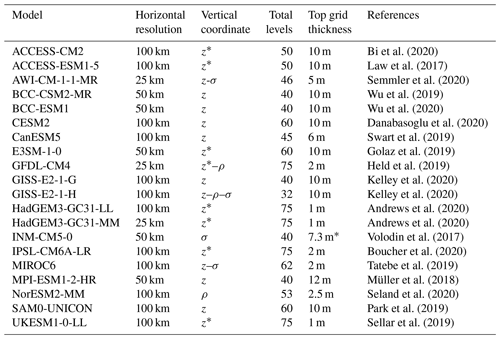
^∗ The global averaged thickness of top grid cell in INM-CM5-0 was calculated using the sigma coordinates and bottom topography obtained from E. M. Volodin (personal communication, 2021).

2 Data and methods

The historical runs of 20 models (Table 1) were averaged over 1981–2010 to create monthly mean climatologies for each model. The first ensemble member (r1i1p1f1) is used where available; we choose r1i1p1f3 for HadGEM3-GC3-LL and HadGEM3-GC3-MM and r1i1p1f2 for UKESM1-0-LL. The models include those incorporating biogeochemical cycling (earth system models) as well as conventional climate models. The ocean vertical coordinate is typically z level (or the related z^∗), but some models use isopycnal, sigma or hybrid coordinates (Table 1). The total number of levels and thickness of top grid cell are used as proxies for ocean vertical resolution.

To examine the seasonal cycle of SST, most studies picked specific months to represent summer and winter (e.g. Zhang and Zhao, 2015; Liu et al., 2020). However, model seasonal cycles may be out of phase with observations and observed maxima and minima occur in different months in different regions. Instead, here we take the maximum and minimum SST of the monthly mean climatologies (T_max and T_min) at each grid point, identifying which months they occur in, for both model and observation. T_max and T_min, plus the annual mean SST (T_mean) and the range of the seasonal cycle ($T_{\text{cycle}}=T_{max}-T_{min}$) from the model climatologies are compared with the World Ocean Atlas 2018 (WOA18) observational climatology on a grid spacing of 0.25^∘ × 0.25^∘ (Locarnini et al., 2018), which covers the period from 1981 to 2010. The model fields were interpolated to the same grid as WOA18. Biases are defined as model values minus WOA18 values. For the multi-model mean, at each grid point we average T_max, T_min, T_mean and T_cycle across the 20 CMIP6 models. To quantify the performance of CMIP6 models, we calculated the area-weighted root mean square error of T_max, T_min, T_mean and T_cycle of the model against WOA18 (henceforth RMSE) for global SST.

Since there is some uncertainty in observational climatologies because of sparse sampling, instrumental error, quality control or gridding techniques, we compared three recent climatologies: WOA18, WOCE-Argo Global Hydrographic Climatology (WAGHC) (Gouretski, 2018a) (covering the time period 1985–2016) and HadISST (Rayner et al., 2003) (covering the time period 1981–2010). Any grid points where the maximum difference in T_max or T_min between the three climatologies is larger than 2 ^∘C are considered uncertain for that variable, and these grid points are excluded from our assessment. Any grid points which did not have values for all 12 months for at least two climatologies are also excluded. For T_mean and T_cycle, we exclude any points where either T_max or T_min is excluded. The excluded grid points are mostly located in coastal areas, a few regions in the Arctic, and around the Antarctic Circumpolar Current (ACC), Agulhas Current and Benguela Current. In total, 4 %, 3 %, 4 % and 4 % of the ocean's surface area are excluded for T_max, T_min, T_mean and T_cycle, respectively. Similarly, for the timing of T_max and T_min, any grid points which did not have values for at least two climatologies or whose maximum difference between climatologies in timing is larger than 2 months are excluded. In our global maps, these points are masked, and in calculations of global and regional metrics, these points are excluded.

3 Results and discussion

3.1 Model representation of SST extrema

For the multi-model mean, T_max and T_min have larger global RMSEs than T_mean (Fig. 1), as SST biases with opposite signs in different seasons compensate each other when calculating the annual mean. Similarly, the T_max and T_min global RMSEs of the multi-model mean are smaller than the RMSEs of individual models (Figs. 1b and c, 2 and 3). Therefore, a small bias in T_mean does not guarantee a realistic T_max or T_min.

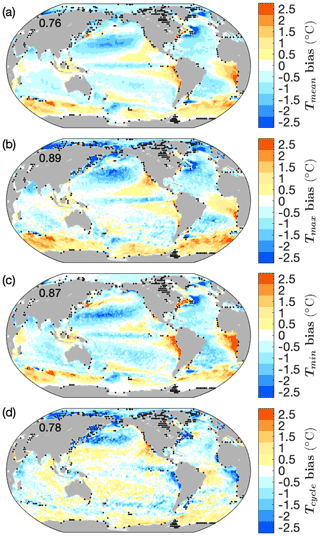
Figure 1 Biases (model minus climatology) of multi-model mean in (a) T_mean, (b) T_max, (c) T_min and (d) T_cycle. Black dots mark grid points excluded from our analysis, as described in Sect. 2. The numbers indicate the global RMSE (^∘C).

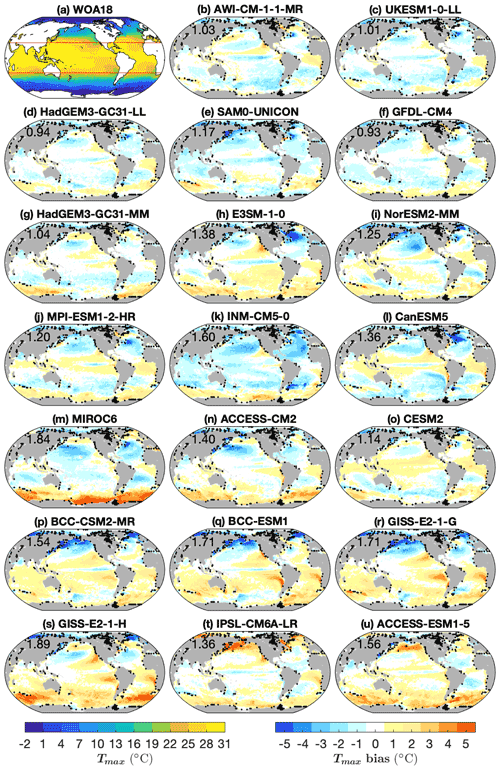
Figure 2 (a) T_max in WOA18 and (b–u) T_max model biases. Black dots mark grid points excluded from our analysis, as described in Sect. 2. The numbers in (b–u) indicate the global RMSE of T_max. Red lines in (a) are 30^∘ N and 30^∘ S. Note that the range of the bias colour bar is twice as much as in Fig. 1.

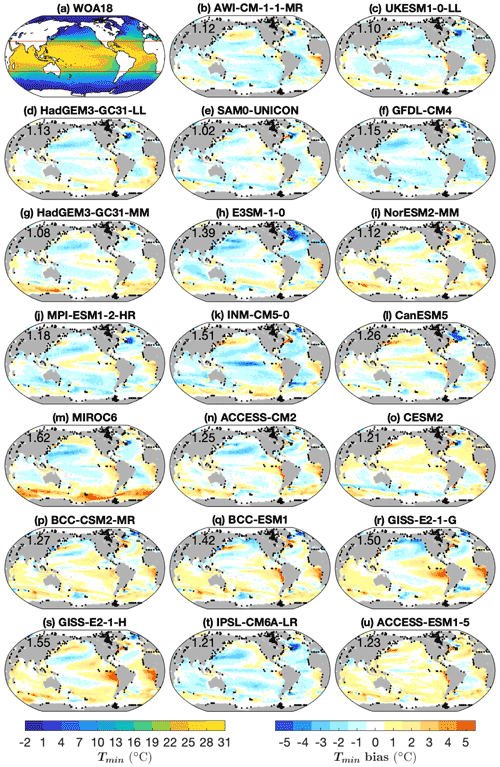
Figure 3 As in Fig. 2 but for T_min.

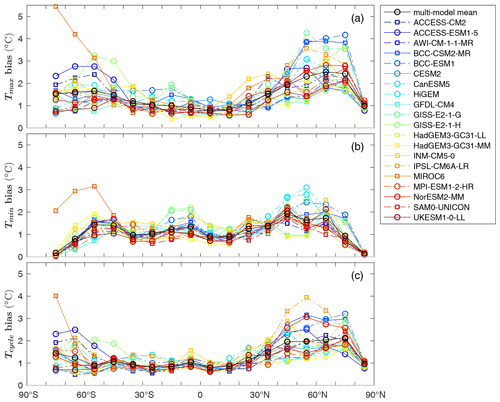
The magnitudes of biases in T_max and T_min vary from model to model (Figs. 2, 3 and 7). The multi-model mean has an RMSE of less than 1 ^∘C in both T_max and T_min (0.89 and 0.87 ^∘C, respectively). Most models have T_max and T_min RMSEs between 1 and 2 ^∘C. Only HadGEM3-GC31-LL and GFDL-CM4 have a T_max RMSE of less than 1 ^∘C (0.94 and 0.93 ^∘C, respectively). GISS-E2-1-H has the largest T_max RMSE of 1.89 ^∘C, and MIROC6 has the largest T_min RMSE of 1.62 ^∘C (Figs. 2 and 3). To test the dependence of the biases found on the realisation of models, we compared the first and second ensemble members (except for SAM0-UNICON and GFDL-CM4 as they have only one ensemble member). The differences between ensemble members are very small compared with the model biases (Figs. S1–S4 in the Supplement), and thus the model biases we report are robust.

In most of the models the global RMSE is larger in T_max than in T_min (Fig. 7a). As the bias in T_max and T_min is largely consistent with T_mean bias, the T_cycle RMSE is small compared to T_max and T_min RMSEs in most models. Different biases in T_max, T_min, T_cycle and T_mean suggest that models have different performances in simulating SST seasonal variation and annual mean. The “best” and “worst” models depend on whether you choose SST seasonal extrema or an annual mean as your metric. For example, GFDL-CM4 and HadGEM-GC31-MM have the smallest RMSE in T_max, and thus they are best for simulating tropical cyclones and heatwaves; SAM0-UNICON has the smallest RMSE in T_min, and thus it is best for simulating the properties of intermediate and deep waters.

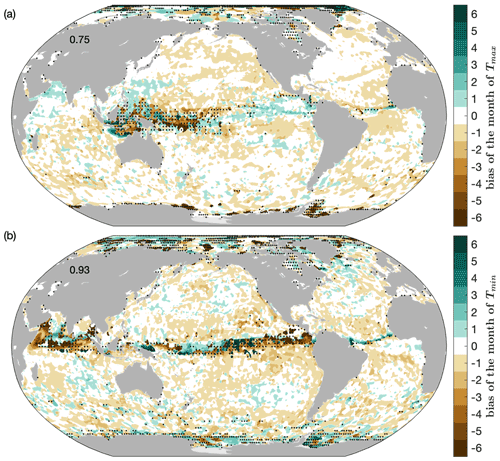
Figure 4 Biases in the timing of (a) T_max and (b) T_min in the multi-model mean. Black dots mark grid points excluded from our analysis, as described in Sect. 2.

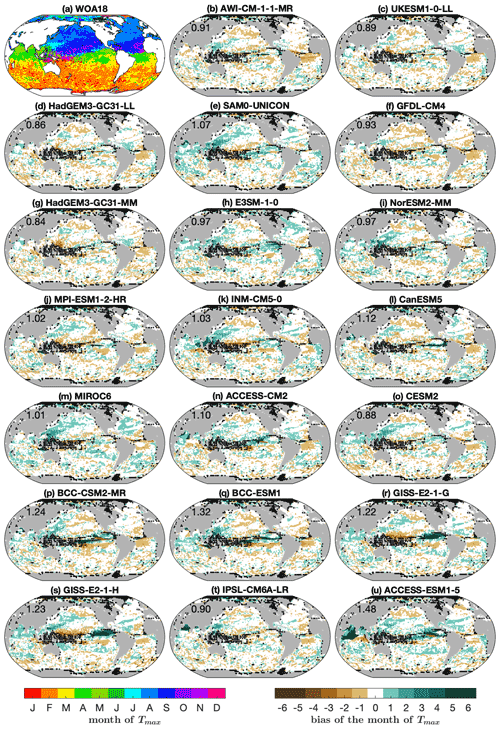
Figure 5 (a) Timing of T_max in WOA18 and (b–u) biases in the timing of T_max in models. Black dots mark grid points excluded from our analysis, as described in Sect. 2.

Figure 6 As in Fig. 5 but for the timing of T_min.

The bias in the timing of T_max and T_min is within 1 month in most of the global ocean in most models (Figs. 4, 5 and 6). In the multi-model mean, T_max and T_min occur 1 month earlier than in WOA18 for most of the global ocean, whereas in some parts of the Arabian Sea and equatorial regions, they occur 1 month later (Fig. 4). The bias in the timing of T_max and T_min demonstrates that the seasonal cycles in CMIP6 models are out of phase with observations. In regions where monsoon prevails (e.g. the northwestern Indian Ocean), the timing bias suggests a bias in the onset of summer monsoon.

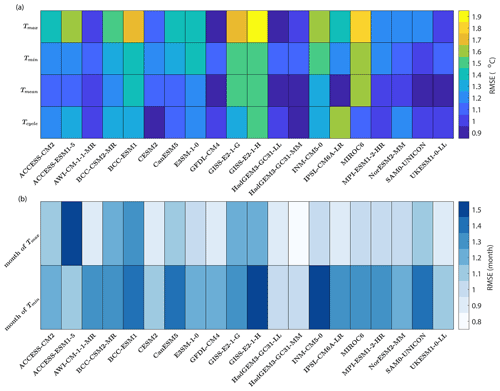
Figure 7 The global area-weighted RMSE of the biases in (a) T_max, T_min, T_mean and T_cycle and (b) the timing of T_max and T_min.

Models have different performance in simulating the timing of T_max and the timing of T_min. All the models except ACCESS-ESM1-5 have a smaller global RMSE in the timing of T_max than in the timing of T_min (Fig. 7b). HadGEM3-GC31-MM has the smallest global RMSE in the timing of T_max, whereas HadGEM3-GC31-LL and HadGEM3-GC31-MM have the smallest global RMSE in the timing of T_min.

Figure 8 Area-weighted RMSE in 10^∘ bands for (a) T_max, (b) T_min and (c) T_cycle.

T_max and T_min biases vary with latitude (Figs. 1b, c, 2, 3 and 8a, b). High latitudes show larger biases than low latitudes. Typically, the RMSE of T_max at 30–80^∘ is 1–2 ^∘C larger than at low latitudes (between 30^∘ N and 30^∘ S) (Fig. 8a). For GISS-E2-1-H, GISS-E2-1-G, BCC-CSM2-MR, BCC-ESM1 and IPSL-CM6A-LR, T_max RMSEs at 30–80^∘ N are about 3 ^∘C larger than at low latitudes. A similar pattern is seen for T_min, but the variation in biases with latitude is much smaller than for T_max (Figs. 1c and 8b). Flato et al. (2013) found a similar result for some CMIP5 models, with larger zonal mean biases in T_mean between 30 and 70^∘ than at other latitudes. The larger biases, and greater difference between T_max and T_min, at mid–high latitudes (greater than 30^∘ in both hemispheres) may be explained by the large seasonal cycle of mixed-layer depth there. Shallower summer mixed layers have a smaller heat capacity; thus a small error in heat fluxes or mixing processes can result in a large bias for T_max, though this will be modulated by any seasonal biases in mixed-layer depth. The larger inter-model biases in T_max than in T_min can be explained by the shallower mixed layer in summer, which can amplify SST biases due to biases in surface heat flux. The difference between biases in T_max and T_min leads to biases in T_cycle (Fig. 1d). The RMSE of T_cycle at low latitudes is typically 1 ^∘C, whereas at mid–high latitudes it is larger, particularly in the Northern Hemisphere (Fig. 8c). The T_cycle RMSE in IPSL-CM6A-LR and MIROC6 reaches 4 ^∘C at high latitudes (Fig. 8c).

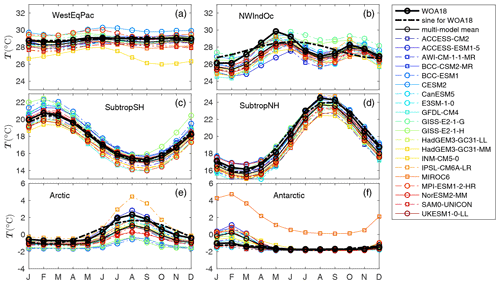
Figure 9 Monthly time series of area-weighted mean SST over the (a) western equatorial Pacific (5^∘ S–5^∘ N, 140^∘ E–160^∘ W), (b) northwestern Indian Ocean (10–20^∘ N, 60–70^∘ E), (c) subtropical Southern Hemisphere (30–40^∘ S), (d) subtropical Northern Hemisphere (30–40^∘ N), (e) Arctic (70–80^∘ N) and (f) Antarctic (70–80^∘ S). The y-axis range is same for (a–f).

In polar regions, there are very small T_min biases (Figs. 1c, 3 and 8b) except for MIROC6 in the Antarctic. Winter SSTs are close to freezing but cannot go below freezing because sea ice forms instead. If models have realistic freezing points, T_min biases will be small. Some models have salinity-dependent freezing points (Beaumet et al., 2019), in which case a salinity bias could cause a bias in temperature. T_min biases in the Arctic are larger than in the Antarctic (Figs. 1c and 9e, f), which suggests larger salinity biases in the Arctic.

In the subtropical North Pacific, the SST cold bias is typically 0.5–1 ^∘C smaller in T_max than T_min, which leads to too large a T_cycle (Figs. 1b–d, 2 and 3). Zhu et al. (2020) showed a similar seasonal SST cold bias in the CMIP6 multi-model mean but not in the CMIP5 multi-model mean. Underestimated surface shortwave radiation and too strong westerly winds in the CMIP6 multi-model mean (Lyu et al., 2020; Li et al., 2020) are possible reasons for the year-round cold bias. The shortwave radiation bias is likely related to the bias of low-level cloud in the subtropics (Burls et al., 2017; Li and Xie, 2012), and its associated cold bias is smaller in winter when there is less solar radiation. The westerly winds cool the surface through latent heat flux and southward ocean advection due to Ekman transport. The latent heat loss shows a maximum in summer (Yu, 2007), while the ocean heat advection shows a maximum in winter when meridional SST gradients are greatest.

SST biases are seasonally dependent in the northeastern Pacific Inter Tropical Convergence Zone (ITCZ) (Figs. 1b, c, 2 and 3). For the multi-model mean, there is a warm bias in T_max which exceeds 2 ^∘C and a cold bias in T_min of 0.5–1.5 ^∘C. Similar seasonal biases exist in CMIP5 models and were linked to an easterly wind bias throughout the year there (Song and Zhang, 2020). A coarse atmospheric model resolution smooths out the elevation difference between mountains and oceans, which allows easterly trade winds to cross the mountains, leading to the easterly wind bias (Song and Zhang, 2020). An easterly bias of annual mean wind was found in the CMIP6 multi-model mean (Li et al., 2020; Lyu et al., 2020). If the easterly bias exists throughout the year, it can explain the seasonal SST bias we found. During winter–spring, the northeastern Pacific ITCZ is dominated by easterly winds, so overly strong easterly winds enhance surface evaporation and lead to cold biases. In contrast, during summer–autumn when westerly winds dominate, the simulated wind is too weak, which causes the warm bias. The northeastern Pacific is a region where tropical cyclones and heatwaves occur (Gilford et al., 2017; Frölicher and Laufkötter, 2018), so a warm bias of over 2 ^∘C in T_max may lead to the overprediction of tropical cyclones and heatwaves.

The multi-model mean has a cold bias in T_max and a warm bias in T_min over the northwest Pacific, leading to too small a T_cycle (bias of more than 2 ^∘C) (Fig. 1b–d). The warm bias in winter can be seen in many models, especially in ACCESS-ESM1-5, BCC-ESM1, CanESM5 and INM-CM5-0 (Fig. 3). The winter warm bias east of Japan was also found in a CMIP5 multi-model mean (Wang et al., 2018), but from our results the warm bias extends further east (Fig. 1c).

The large cold biases at Northern Hemisphere high latitudes in BCC-CSM2-MR, BCC-ESM1, GISS-E2-1-G and GISS-E2-1-H are typically 2–5 ^∘C smaller in T_min than in T_max (Figs. 2, 3 and 8a, b). These cold biases are likely to be linked to cloud biases due to the cooling radiative effect of low cloud (Myers et al., 2021). The negative cloud radiative forcing is excessive in BCC-CSM2-MR (Wu et al., 2019) and BCC-ESM1 (cloud simulation likely to be similar to BCC-CSM2-MR), while overestimated low-cloud cover in GISS-E2-1-G and GISS-E2-1-H (Kelley et al., 2020) blocks more of the incoming solar radiation. As solar radiation is negligible at high latitudes in winter, the SST cold bias due to cloud bias is much smaller in winter than in summer, consistent with our results. Deep winter mixed-layer depths and SSTs close to freezing likely also contribute to the smaller cold biases in T_min than in T_max at high latitudes.

In most models there is a warm T_mean bias in the Southern Ocean, commonly attributed to excessive shortwave radiation linked to cloud process representation deficiencies (Hyder et al., 2018). MIROC6 has an underestimated mid-level cloud cover (Tatebe et al., 2019); GISS-E2-1-G and GISS-E2-1-H have an underestimated shortwave cloud radiative forcing (Kelley et al., 2020), and hence they have pronounced warm biases in the Southern Ocean (Figs. 2, 3). The warm bias is larger for T_max than T_min (Figs. 1b, c, 2, 3 and 8a, b) because the lack of incoming solar radiation in winter means cloud biases have minimal effect on surface solar insolation. Shallower mixed-layer depths in summer will also tend to enhance any bias in incoming solar insolation. The larger warm bias in T_max than T_min results in a sea ice extent that is too small in most CMIP6 models, especially in summer (Beadling et al., 2020; Shu et al., 2020). As mode and intermediate waters primarily form within the winter mixed layer of the Antarctic Circumpolar Current (Talley, 1999), the T_min warm bias can influence global ocean stratification.

MIROC6 stands out with the largest warm bias in the Southern Ocean (Figs. 2m and 3m), with a T_max RMSE between 3 and 5 ^∘C and T_min RMSE between 2 and 3 ^∘C at 50–80^∘ S (Fig. 8a and b). The largest biases in MIROC6 occur in regions where there should be sea ice and where the deep ocean is ventilated. Beadling et al. (2020) found that MIROC6 has the lowest Southern Ocean sea ice extent among CMIP6 models in both summer and winter, and Tatebe et al. (2019) revealed annual warm biases exceeding 2 ^∘C in the intermediate and deep layers of MIROC6.

In eastern boundary upwelling regions (especially the Benguela and Humboldt currents), most models have a seasonal warm bias that is 1–5 ^∘C smaller in T_max than T_min (Figs. 1b, c, 2 and 3). Richter (2015) suggested that underestimation of stratocumulus cloud and insufficient upwelling due to overly weak winds contribute to the warm bias in eastern boundary upwelling regions. The warm bias we found therefore is likely associated with the underestimated surface shortwave radiation and overly weak, upwelling-favourable winds in CMIP6 models identified by Li et al. (2020). The warm bias may lead to excessive precipitation in the Atlantic Ocean off Angola and Namibia as shown by Rouault et al. (2003). Letelier et al. (2009) showed that in the Humboldt Current coastal region the cooling effect of upwelling is strongest in austral summer, which is consistent with the peak of upwelling-favourable wind in December and January. A poor simulation of the seasonal cloud and upwelling processes will contribute to the seasonality of SST biases in eastern boundary upwelling regions.

Most models have a seasonal warm SST bias in the eastern equatorial Atlantic (Figs. 1b, c, 2 and 3). The T_min multi-model mean bias can be more than 2 ^∘C larger than the T_max multi-model mean bias. Richter and Tokinaga (2020) showed a similar seasonal warm bias in the CMIP6 multi-model mean, which is about 1–2 ^∘C larger during June–July–August than March–April–May. Richter et al. (2012) argued that the warm SST bias in the eastern equatorial Atlantic during June–July–August is linked to overly deep thermoclines caused by overly weak easterlies during March–April–May. Therefore, the warm bias can be attributed to overly weak easterlies in the CMIP6 multi-model mean (Li et al., 2020; Lyu et al., 2020). GISS-E2-1-G and GISS-E2-1-H have the largest seasonality of SST warm bias in the eastern equatorial Atlantic, with T_min biases up to 5 ^∘C. Richter and Tokinaga (2020) illustrated that warmer than observed SSTs in the equatorial Atlantic lead to excessive precipitation. Roxy (2014) quantified the SST–precipitation relationship: a 1 ^∘C SST increase corresponds to a 2 mm d⁻¹ precipitation increase. Therefore, the 5 ^∘C T_min warm bias in GISS-E2-1-G and GISS-E2-1-H could cause a 10 mm d⁻¹ increase in precipitation.

Although the amplitudes of biases are different in T_max and T_min, the global patterns and signs of T_max and T_min biases are similar to each other in most models (Figs. 2 and 3). Wang et al. (2014) indicated that the SST bias of the CMIP5 multi-model mean has a pattern independent of season but did not analyse the seasonality in bias in individual models. Our results show two exceptions: E3SM-1-0 and IPSL-CM6A-LR, which both have an overall warm bias in T_max but an overall cold bias in T_min (Figs. 2h, t and 3h, t), which tend to cancel out in the annual means. The T_max RMSE is 1.38 ^∘C for E3SM-1-0 and 1.36 ^∘C for IPSL-CM6A-LR, and the T_min RMSE is 1.39 ^∘C for E3SM-1-0 and 1.21 ^∘C for IPSL-CM6A-LR, whereas the T_mean RMSE is only 1.17  ^∘C for E3SM-1-0 and 0.94 ^∘C for IPSL-CM6A-LR. In E3SM-1-0, the global annual average mixed-layer depth is generally too shallow (Golaz et al., 2019), which can contribute to the summer SST warm bias and winter SST cold bias, and a similar process may be affecting IPSL-CM6A-LR. These results illustrate the risks involved in assessing only annual means, as models may have greater biases than assumed, so tropical cyclone formation, for example, may be overpredicted.

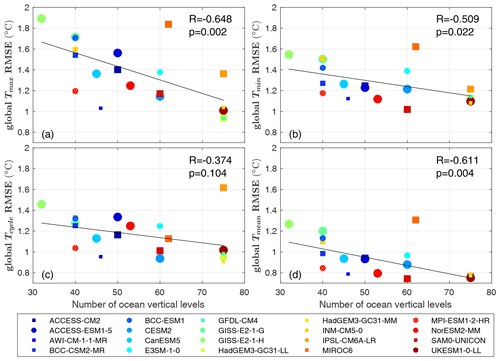
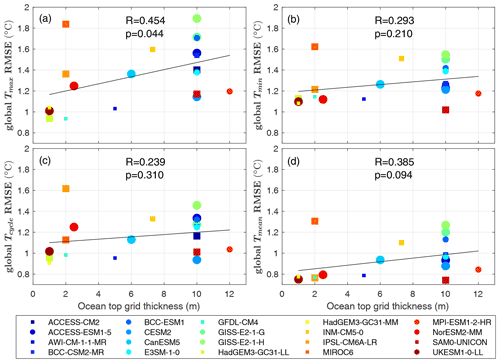
Figure 10 Global RMSE of (a) T_max, (b) T_min, (c) T_cycle and (d) T_mean, all against the total number of vertical levels in the ocean. Circles represent earth system models, while squares represent non-earth system models. The size of the markers represents the ocean horizontal resolution for that model, with larger markers for models with lower horizontal resolution. The black line is the line of best fit (with the least sum of squared errors). The inter-model correlation R and p value are shown in each panel.

In midlatitudes the SST seasonal cycle is well represented by an annual sinusoid, whereas in equatorial and polar regions an annual sinusoid explains little of the total SST seasonal variance (Trenberth, 1983; Yashayaev and Zveryaev, 2001). In regions with fairly sinusoidal SST annual cycles such as the subtropics (sinusoidal signal explains 87 % of the observed variances in the subtropical Northern Hemisphere and 89 % of the observed variances in the subtropical Southern Hemisphere), models have realistic SST seasonal cycles with well-simulated amplitude and phase of the annual cycle (Fig. 9c and d). Phase biases are mainly within 1 month (Figs. 4, 5 and 6). In subtropical regions, seasonal SST biases are consistent with biases in T_mean. Differences between the T_max and T_min biases are smaller than those in non-sinusoidal regions (Fig. 9). In regions with non-sinusoidal SST seasonal cycles such as the western equatorial Pacific, northwestern Indian Ocean, the Arctic and the Antarctic (sinusoidal signal explains 33 %, 23 %, 58 % and 46 % of the observed variances), models tend to have biases in amplitudes or phases of their SST seasonal cycles (Figs. 4, 5, 6 and 9a–b, e–f).

In the western equatorial Pacific, the SST seasonal cycle in WOA18 is modest (less than 1 ^∘C), whereas in some models such as MPI-ESM1-2-HR, GISS-E2-1-G, GISS-E2-1-H and especially INM-CM5-0, the seasonal cycle is much larger (Fig. 9a). In INM-CM5-0, the T_cycle is about 2 ^∘C and there is a cold SST bias throughout the year, reaching 3 ^∘C during September–October–November (Fig. 9a). Similar to our analysis, Volodin et al. (2017) noted that INM-CM5-0 has a cold bias of more than 4 ^∘C in annual mean temperature in the upper 700 m of the western equatorial Pacific. The cold bias could limit the skills of models in simulations of the El Niño–Southern Oscillation (ENSO) and ENSO-induced teleconnections. For example, a cold bias in the western equatorial Pacific results in a rising branch of the Walker circulation that is too far west in many coupled climate models leading to too weak an ocean–atmosphere coupling and unrealistic ENSO dynamics (Bayr et al., 2018). The associated convective response along the Equator during ENSO events is too far west leading to a westward shift in the sea level pressure response in the North Pacific and precipitation response in the subtropics (Bayr et al., 2019).

In the northwestern Indian Ocean where the monsoon system prevails, SST has a semi-annual cycle, but most models are unable to reproduce this with the correct amplitude and phase (Figs. 4, 5, 6 and 9b). Most CMIP6 models have SST cold biases in this region throughout the year, while the biases are generally larger during March–April–May than other months and the multi-model mean fails to simulate the primary maximum SST (Fig. 9b). Cold SST biases in the northwestern Indian Ocean lead to a significant reduction in the monsoon rainfall over the Indian subcontinent (Prodhomme et al., 2014; Levine and Turner, 2012). Thus the cold biases in the CMIP6 models are likely to lead to overly weak monsoon precipitation. Consistent with our result, McKenna et al. (2020) found a cold SST bias over the northwestern Indian Ocean in the CMIP6 multi-model mean. Fathrio et al. (2017) showed that the SST cold bias over the western Indian Ocean in the CMIP5 multi-model mean has a seasonal cycle, with the coldest SST bias occurring in April, whereas the coldest SST bias in our CMIP6 multi-model mean occurs in May. GISS-E2-1-G and GISS-E2-1-H fail to simulate a realistic second minimum SST in August (Fig. 9b), which would lead to overly intense tropical cyclones. SST in the northwestern Indian Ocean determines the onset of the summer monsoon (Sijikumar and Rajeev, 2012; Jiang and Li, 2011). The primary maximum SST is 2 months later in ACCESS-ESM1-5 than in WOA18 (Fig. 9b), which suggests a delayed summer monsoon onset in projections using that model.

3.2 Impact of model characteristics on SST seasonal extrema

We have shown that biases in T_max, T_min and T_cycle are different between models. We now use the diversity in the 20 CMIP6 models to explore the effects of different model characteristics on the magnitude of these biases as quantified by global area-weighted RMSE for T_max, T_min, T_cycle and T_mean.

No significant correlation was found between the models' seasonal biases and horizontal ocean resolution (Fig. S5 in the Supplement). Chassignet et al. (2020) used four pairs of matched low-resolution and high-resolution ocean simulations from FSU-HYCOM, AWI-FESOM, NCAR-POP and IAP-LICOM to isolate the effect of ocean horizontal resolution and compared their representation of global SST. They found that enhanced horizontal resolution does not deliver unambiguous SST bias improvement in all regions for all models, which is consistent with our finding. Nor did we find any correlation of seasonal biases with atmospheric resolution (Figs. S6 and S7 in the Supplement), ocean grid type, ocean vertical coordinate and inclusion (or not) of biogeochemical processes (circles or squares in Figs. 10 and 11).

Figure 11 As in Fig. 10 but against the thickness of top grid in ocean.

The only characteristic yielding a statistically significant relationship was the ocean vertical resolution (Figs. 10 and 11). The importance of vertical resolution for reducing seasonal biases is not unexpected: SST is influenced by ocean stratification and ocean vertical mixing processes, whose representation depends upon the vertical resolution. It has been found that high resolution in the upper ocean is important for the representation of diurnal and intraseasonal SST variability in ocean general circulation models (Misra et al., 2008; Xavier et al., 2008; Ge et al., 2017). Ideally we would have considered the number of vertical levels in the upper ocean. However, the number of vertical levels in the upper ocean (e.g. upper 200 m) cannot be unambiguously determined for models using an isopycnal or sigma vertical coordinate (6 out of 20 in our study) as their level depths vary with location and time (Bleck, 2002; Shchepetkin and McWilliams, 2005). Excluding the isopycnal and sigma models, the remaining high vertical-resolution models are mainly from the Met Office Hadley Centre family, and hence any relationship between SST biases and vertical resolution in the upper ocean might have been overly influenced by that particular family. Hence we use the total number of vertical levels and top grid cell thickness (Table 1) as proxies for the vertical resolution. Our study emphasises the importance of vertical resolution for simulating seasonal extreme SST and annual mean SST.

For the 20 models, there is a decrease in bias with increasing total number of vertical levels (Fig. 10). We calculated the inter-model correlation between global RMSE and the total number of vertical levels following the method of Wang et al. (2014). The relationship between SST biases and the total number of vertical levels is significant for T_max, T_min and T_mean (p values < 0.05), with the largest correlation of −0.648 for T_max. The higher correlation between the global T_max RMSE and ocean vertical resolution is likely linked to shallower mixed-layer depths in summer than in winter. RMSE is also correlated with top grid thickness (but with a smaller correlation than the total number of vertical levels): models with a smaller top grid thickness tend to have smaller biases (Fig. 11).

The impact of ocean vertical resolution on SST biases varies with latitude and season. Ocean vertical resolution is most important for T_max at low latitudes (Figs. S8 and S9 in the Supplement). SST biases decrease with the number of vertical levels in the Benguela, Humboldt and California upwelling regions (Figs. S10–S12 in the Supplement). Only the Canary upwelling region, which has the smallest SST bias among the main four eastern boundary upwelling regions, does not have a good inter-model correlation between SST biases and ocean vertical resolution (Fig. S13 in the Supplement).

4 Conclusions

Using the newly released CMIP6 models, this study provides a global view of the biases in SST extrema, identifies regions with large seasonal bias and suggests a future direction to reduce these biases. To study the seasonal cycle of SST, we focus on T_max and T_min whenever they occur, rather than particular months. Global area-weighted T_max, T_min and T_cycle RMSEs are typically 1–2 ^∘C. Most models have T_max and T_min biases of the same sign at most locations, apart from IPSL-CM6A-LR and E3SM-1-0, which have an overall warm bias in T_max and an overall cold bias in T_min. When averaged across the whole globe, the bias in T_mean is typically consistent with T_max and T_min biases, but certain regions (eastern boundary upwelling regions, polar regions, the eastern equatorial Atlantic, the North Pacific) show significant differences between winter and summer biases. The seasonal variation in the SST bias demonstrates the importance of evaluating model performance on T_max and T_min, not just T_mean. Seasonal processes related to wind and cloud could be the main reasons for seasonal SST biases but depend upon region. Further investigations of wind and cloud biases in CMIP6 models for different seasons could be undertaken to better understand the causes of seasonal SST biases. In regions with non-sinusoidal SST seasonal cycles, models tend to have biases in amplitudes and/or phases of their SST seasonal cycles. If there is a substantial change in the climate, it should be considered that the pattern of biases in T_max and T_min may change. For the models we examined, those with increased vertical resolution in the ocean generally had a better representation of SST extrema, particularly T_max. This is likely related to the ability of the higher-resolution models to better represent the surface mixed layer and particularly shallow mixed layers in summer. For improving the accuracy of future climate projections, we suggest that as much priority (or possibly more) should be given to increasing vertical ocean model resolution as is given to increasing horizontal resolution.