the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Tracer and observationally derived constraints on diapycnal diffusivities in an ocean state estimate
Caitlin B. Whalen
Thomas W. N. Haine
Amy F. Waterhouse
An T. Nguyen
Arash Bigdeli
Matthew Mazloff
Patrick Heimbach
Use of an ocean parameter and state estimation framework – such as the Estimating the Circulation and Climate of the Ocean (ECCO) framework – could provide an opportunity to learn about the spatial distribution of the diapycnal diffusivity parameter (κρ) that observations alone cannot due to gaps in coverage. However, we show that the inclusion of misfits to observed physical variables – such as in situ temperature, salinity, and pressure – currently accounted for in ECCO is not sufficient, as κρ from ECCO does not agree closely with any observationally derived product. These observationally derived κρ products were inferred from microstructure measurements, derived from Argo and conductivity–temperature–depth (CTD) data using a strain-based parameterization of fine-scale hydrographic structure, or calculated from climatological and seafloor data using a parameterization of tidal mixing. The κρ products are in close agreement with one another but have both measurement and structural uncertainties, whereas tracers can have relatively small measurement uncertainties. With the ultimate goal being to jointly improve the ECCO state estimate and representation of κρ in ECCO, we investigate whether adjustments in κρ due to inclusion of misfits to a tracer – dissolved oxygen concentrations from an annual climatology – would be similar to those due to inclusion of misfits to observationally derived κρ products. We do this by performing sensitivity analyses with ECCO. We compare multiple adjoint sensitivity calculations: one configuration uses misfits to observationally derived κρ, and the other uses misfits to observed dissolved oxygen concentrations. We show that adjoint sensitivities of dissolved oxygen concentration misfits to the state estimate's control space typically direct κρ to improve relative to the observationally derived values. These results suggest that the inclusion of oxygen in ECCO's misfits will improve κρ in ECCO, particularly in (sub)tropical regions.
- Article
(24916 KB) - Full-text XML
- BibTeX
- EndNote
We consider the challenges with using observational data in the context of a parameter and state estimation framework to infer the global distribution of ocean mixing. Ocean models must parameterize the unresolved, turbulent diffusion of oceanic tracers. Ocean mixing is typically conceptualized in terms of diffusion along and across isopycnal surfaces. Subgrid-scale transport of isopycnal thickness (or bolus) – which is effectively an advective contribution to tracer budgets – must also be parameterized. Ocean models often represent these unresolved processes with three parameters: the across-isopycnal mixing parameter (diapycnal diffusivity; Munk and Wunsch, 1998), the along-isopycnal mixing parameter (Redi coefficient; Redi, 1982), and the eddy isopycnal thickness transport parameter (Gent–McWilliams coefficient; Gent and McWilliams, 1990). Diapycnal mixing is an essential component in explaining the observed oceanic stratification (Munk and Wunsch, 1998; Gnanadesikan, 1999; Scott and Marotzke, 2002). Changes in the background diapycnal diffusivity (Dalan et al., 2005; Krasting et al., 2018; Hieronymus et al., 2019; Sinha et al., 2020), Redi coefficient (Gnanadesikan et al., 2015; Ehlert et al., 2017), and Gent–McWilliams coefficient (Danabasoglu and McWilliams, 1995) are known to have a profound influence on climate simulations through alterations in the response to surface flux perturbations and changes in ventilation rates.
The spatiotemporal variabilities suggested in previous studies of the Redi coefficient (Abernathey and Marshall, 2013; Bates et al., 2014; Forget et al., 2015b; Cole et al., 2015; Busecke and Abernathey, 2019; Groeskamp et al., 2020) and Gent–McWilliams coefficient (Forget et al., 2015b; Katsumata, 2016; Bachman et al., 2020) fields are virtually absent in ocean models. There is also a dearth of independent observations with which to assess their observationally derived values (Cole et al., 2015; Katsumata, 2016; Roach et al., 2018; Groeskamp et al., 2020), and these values cannot be easily compared with those in models. For instance, it is unclear how to compare Redi coefficients derived from observations with those from models because they are expected to vary with horizontal resolution. Also, the formulations of the perpendicular and parallel components of the eddy advection tensor relative to isopycnal surfaces are not the same in many models as in the observationally derived Gent–McWilliams coefficient product (Katsumata, 2016). To gain deeper insight into the issues with model representation of ocean mixing, we focus on the diapycnal diffusivity field – κρ hereafter – in this study.
Parameterizations for κρ (Gaspar et al., 1990; Large et al., 1994; Reichl and Hallberg, 2018) have allowed for a spatiotemporally varying κρ field, but assessing the performance of these parameterizations has been challenging due to a profound lack of observations. Until recently, the only available observational information about κρ came from tracer release experiments (Ledwell and Watson, 1991; Polzin et al., 1997; Messias et al., 2008) and microstructure (i.e., the scales over which molecular viscosity and diffusion are important) measurements of velocity shear (e.g., Waterhouse et al., 2014) or temperature variability (e.g., Gregg, 1987). These data are infrequently sampled and cover a relatively small portion of the ocean but are independent observations with which to compare the more recent global mixing data products calculated from Argo (Whalen et al., 2015), conductivity–temperature–depth (CTD) (Kunze, 2017), and climatological and seafloor (de Lavergne et al., 2020) observations. While our understanding of the global distribution of κρ has been transformed by the use of theories to derive κρ from limited observations (MacKinnon et al., 2017; Whalen et al., 2020), none of the observationally derived κρ products have been used to date in ocean models to assess whether corresponding simulations would be improved over globally uniform values or those based on theory. (Here, by “constrain,” we refer to using new data to change the level of agreement between the model and an observational product – not necessarily to achieve a perfect match.)
Currently, the only information about κρ comes from temperature, salinity, and pressure observations in ocean parameter and state estimation or data assimilation systems. If these observations were collected at every location and depth of the ocean, there could be sufficient information to accurately derive κρ (Groeskamp et al., 2017), but there are spatiotemporal gaps. This work explores the use of a parameter and state estimation framework to invert for global fields of κρ using incomplete observations and theories.
We use the Estimating the Circulation and Climate of the Ocean (ECCO) parameter and state estimation framework to evaluate how nearly global, observationally derived κρ can be used to inform ocean models. The aim of the ECCO framework is to reconstruct the recent history of the ocean (the “state estimate”) by filling in the gaps between incomplete observations, which are often sparse and aliased, through dynamical techniques. The state estimate is related to a reanalysis product (Heimbach et al., 2019), but the state estimation framework overcomes some serious shortcomings (see the Appendix) by requiring dynamical and kinematical consistency (Stammer et al., 2016) of the estimated state throughout its full period of estimation (here, 1992 to 2015). Version 4 release 3 of the ECCO (ECCOv4r3; Fukumori et al., 2017) state estimate – like previous versions and releases – is achieved by fitting a general circulation model to available observations in a weighted least-squares sense (Wunsch, 2006; Forget et al., 2015a). The model–data misfit (objective or “cost function”) is minimized by varying (i.e., inverting for) a set of uncertain control variables, all of which are independent inputs to the model equations being solved. These control variables can be iteratively improved by running the model in forward plus backward – its “adjoint” – mode, which enables the calculation of gradients in the cost function. Each of these runs maintains dynamical and kinematical consistency because, in contrast to filter-based data assimilation systems (see the Appendix for an example), the only ocean variables that get adjusted are the control variables – not the dynamically active – or prognostic – variables. These control variables are determined using the entire length of the state estimate – as opposed to introducing temporal discontinuities by periodically adjusting them. Importantly for our goal of parameter estimation, the set of control variables may consist not only of initial and boundary conditions, but also of (spatially varying) model parameters, such as the three used to represent ocean subgrid-scale transport or mixing (Liu et al., 2012; Forget et al., 2015a). Inaccuracies in variables such as κρ in any ocean model can make physical inference less grounded in reality – e.g., the differences in the importance of diapycnal mixing in steric sea level budgets of models used in this study (Piecuch and Ponte, 2011; Palter et al., 2014) – and could make the ECCO state estimate itself less accurate – e.g., errors in κρ will influence vertical tracer transport and mixed layer depths. Since it remains underexplored how well κρ, in particular, is estimated with ECCOv4r3, this is one subject of the current study.
The other goal of the present study is to examine how we can provide additional information about κρ using either observational estimates of κρ itself or a tracer – e.g., oxygen – from observations in ECCO's misfits. κρ products have been shown to agree well with each other (Whalen et al., 2015; de Lavergne et al., 2020). However, because κρ is derived and not measured, a parameter and state estimation system would need to account for both their structural and measurement errors, and their structural uncertainties are not yet well-understood. This is a potential problem because it is not clear how to weight these data when constraining the model, and conservatively large uncertainties would place little to no constraints on the model. An alternative approach to constraining κρ is to find a quantity measured with in situ observations – e.g., a tracer, as proposed here – that provides information about κρ. Passive transient tracers are known to provide information about ocean mixing (Mecking et al., 2004; Trossman et al., 2014; Shao et al., 2016). However, their concentrations tend to be difficult to detect below a couple thousand meters of depth and are not monitored, in addition to biogeochemical tracers such as dissolved oxygen. Dissolved oxygen has vertical gradients that can be resolved by most ocean models in the open ocean. Through altering oxygen saturation and ventilation rates, mixing likely plays an important role in controlling the dissolved oxygen concentrations and volumes of tropical oxygen minimum zones (OMZs) (Brandt et al., 2015; Lévy et al., 2021; Ito et al., 2022), the rate of future global deoxygenation (Duteil and Oschlies, 2011; Palter and Trossman, 2018; Couespel et al., 2019), the abyssal–shadow zone overturning connectivity (Holzer et al., 2021), and the upwelling of low-latitude waters as part of the meridional overturning circulation (Talley, 2013). Oxygen utilization rates within subtropical mode water in the North Atlantic Ocean strongly depend upon vertical mixing (Billheimer et al., 2021). Along with temperature and salinity observations, oxygen concentrations help identify particular water masses because oxygen utilization often reflects how recently water has been ventilated by the thermocline (Jenkins, 1987). Oxygen concentrations are less numerous than temperature and salinity observations, but tracers have different sources and sinks, are in varying degrees of disequilibrium, and require different amounts of time to equilibrate – similar in argument to why multiple tracers are needed to best constrain transit-time distributions (Waugh et al., 2003). Thus, we assess the information that dissolved oxygen concentrations provide about κρ with ECCOv4r3 – which has already incorporated information about temperature and salinity – in the present study.
Our two primary objectives are (1) to test whether κρ calculated using ECCO agrees with κρ from observations given incomplete temperature, salinity, and pressure observations and (2) to assess whether dissolved oxygen concentrations and κρ from observations provide similar information about how to improve the agreement between κρ from ECCO and observations. In the Appendix, we present κρ from one example sequential data assimilation framework in order to contrast its potential issues with those of ECCO. We use κρ inferred from microstructure (Waterhouse et al., 2014), derived from Argo floats (Whalen et al., 2015) and CTD profiles (Kunze, 2017), and calculated from climatological and seafloor data (de Lavergne et al., 2020) to determine whether the ECCO framework needs to improve its κρ using observational constraints (Sects. 3.1 and 3.2). We then perform model experiments in forward plus adjoint mode to determine whether dissolved oxygen concentration data and observationally derived κρ provide similar information about how to adjust κρ (Sect. 3.3). This will help determine whether κρ could be improved by including tracer data in the misfits of a future iterative ocean parameter and state estimation procedure.
2.1 Observationally derived data products and measured data
2.1.1 Diapycnal diffusivities
κρ is routinely inferred from the velocity shear measured using microstructure profilers (Waterhouse et al., 2014). We use microstructure-inferred κρ – referred to as κρ,micro hereafter (Osborn, 1980; Lueck et al., 1997; Gregg, 1989; Moum et al., 2002; Waterhouse et al., 2014) – to evaluate a model's κρ. (We distinguish between “observations” that are measured quantities using in situ instruments and observationally derived values, which use measured quantities and a theory to derive values. The former data have only measurement uncertainties, while the latter data have both measurement and structural uncertainties. We further distinguish “observationally inferred” values, which are from the currently accepted method of observing a quantity such as κρ but are not measured, and “observationally derived” values because the latter data depend on a method that requires additional assumptions. These terms only apply to values calculated making use of observations.) κρ,micro is based on an expression for the isotropic turbulence field, which is proportional to the viscosity of water and the velocity shear resolved to dissipative scales (Thorpe, 2007, and references therein). The depth ranges of the data collected by Waterhouse et al. (2014) go from the upper several hundred meters to the full water column. The profiles are seasonally biased at higher latitudes and span decades. There are thousands of vertical profiles from 24 different campaigns that comprise this dataset, with samples being taken in North Pacific Ocean, North Atlantic Ocean, tropical Pacific, near Drake Passage, near the Kerguelen Plateau, and in the South Atlantic Ocean. Many of the profiles were taken in regions with both smooth and rough bottom topography. To compare the microstructure profiles with model output, the nearest neighbors to each model's grid are selected. A geometric average is taken for each profile because this is more representative than an arithmetic average for a small sample size and when the data are not normally distributed (Manikandan, 2011), like the lognormal distribution of κρ (Whalen, 2021).
We make use of multiple datasets for κρ derived from observations. Two of these datasets – listed in Table 1 – are derived using a fine-scale parameterization; they contain values equatorwards of 75∘ S and 75∘ N and deeper than about 250 m because the theory does not yield accurate results in the presence of strong upper-ocean density variability (e.g., D'Asaro, 2014). κρ values are derived from fine-structure observations of temperature, salinity, and pressure using a strain-based fine-scale parameterization, which has been developed and implemented in different ways (Henyey et al., 1986; Gregg, 1989; Polzin et al., 1995, 2014) but typically assumes a mixing efficiency of 0.2 (St. Laurent and Schmitt, 1999; Gregg et al., 2018). The fine-scale parameterization assumes that (1) the production of turbulent energy at small scales is due to an energy transfer driven by wave–wave interactions down to a wave breaking scale; (2) nonlinearities in the equation of state, double diffusion, downscale energy transports, and mixing associated with boundary layer physics and hydraulic jumps are neglected; and (3) stationary turbulent energy balance exists where production is matched by dissipation and a buoyancy flux in fixed proportions (Polzin et al., 2014). The implementation by Whalen et al. (2015) uses Argo data, assumes a shear-to-strain variance ratio of 3 and a flux Richardson number of Rif=0.17, and determines the fraction of turbulent production that goes into the buoyancy flux (and the rest for dissipation). The fine-structure method is not expected to be valid in equatorial regions of the ocean, but nevertheless, the κρ product compares well with microstructure near the Equator (Whalen et al., 2015). We use the 2006–2014 climatology of Whalen et al. (2015) – referred to as κρ,Argo hereafter – which is a gridded product on an approximately horizontal grid and has three vertical levels: 250–500, 500–1000, and 1000–2000 m depth. Whalen et al. (2015) found that 81 % (96 %) of their κρ,Argo product is within a factor of 2 (3) of the microstructure measurements. We use this as the basis for the factor of 2–3 uncertainty we cite hereafter.
Table 1The latitude and depth ranges of each observationally derived product from a parameterization used in this study. The longitude range for each dataset spans (180∘ E, 180∘ W). Also listed are the time period of the observations each product is based on and the range of values in each product (to the nearest order of magnitude in units of m2 s−1).

In addition to the Argo-derived κρ,Argo product, there is ship-based CTD hydrography-derived κρ (Kunze, 2017) – referred to as κρ,CTD hereafter – that uses the same fine-structure parameterization as in the calculation of the κρ,Argo product (see Sect. 2.2). The vertical resolution of the κρ,CTD product is 256 m, and the horizontal resolution is the spacing between each CTD profile. Data are only included in the κρ,CTD product when the square of the buoyancy frequency is greater than 10−7 rad2 s−2 and greater than the square of the Coriolis frequency, m2 s−1 is positive, and the depth is deeper than 400 m.
One last product we use for observationally derived κρ – referred to as κρ,tides hereafter – is based on theory, a spectral parameterization for abyssal hills, and climatological products (de Lavergne et al., 2020). This scheme accounts for the local breaking of high-mode internal tides and remote dissipation of low-mode internal tides. The four processes contributing to the mixing from this scheme include wave–wave interactions that attenuate low-mode internal tides, shoaling that breaks low-mode internal tides, dissipation of low-mode internal tides at critical slopes, and scattering of low-mode internal tides combined with generation of high-mode internal tides via abyssal hills. Note that these tidally induced mixing process are not equivalent to the suite of internal wave-induced mixing processes that κρ,Argo and κρ,CTD account for. The gridded κρ,tides product is global, nominally horizontal resolution, and ranges from 10 to 250 m in vertical resolution. A stratification field is provided in this product, which is the one we use for the remainder of this study (Sect. 2.1.3).
2.1.2 Dissolved oxygen
Because we have annual mean κρ products, we use the annual mean dissolved oxygen concentration climatology from the World Ocean Atlas (Garcia et al., 2013) for the remainder of our analysis. Any potential information that oxygen concentrations provide about κρ is likely through oxygen's vertical gradients because water masses – which tend to be relatively homogenous in oxygen concentrations – are eroded via diapycnal mixing along their peripheries. Thus, we show oxygen's vertical gradients, , here. We compare (Fig. 1a, c, and e) with the dissipation rates, , for stratification N2 through the Osborn (1980) relationship from the Whalen et al. (2015) product (Fig. 1b, d, and f) at the same depth-averaged bins. is generally smaller in magnitude in many high-latitude and tropical regions (Fig. 1a, c, and e), whereas the Argo-derived dissipation rates can be relatively large in these regions, with the exception of locations in the Southern Ocean (Fig. 1b, d, and f). is relatively large and positive landward of the Gulf Stream, in the Chukchi Sea and Beaufort Sea, near the Norwegian coast, off the southern coast of India, near the Equator in the Atlantic Ocean and western Pacific Ocean, and in the Southern Hemisphere's subtropical gyres of the Pacific Ocean and Indian Ocean between 250 and 500 m depth (Fig. 1a). The largest positive values are between the subpolar regions and the Equator at deeper depths (Fig. 1c and e). The dissipation rates are relatively small in many of these regions (Fig. 1b, d, and f). Exceptions to the inverse relationship between and the dissipation rates tend to be in the vicinity of intensified jets, likely because lateral exchanges of oxygen concentrations become more important in these regions. Where data exist for both data products, the spatial correlation between and the dissipation rates is about −0.2 and increases in magnitude on coarser grids. This indicates a possibly nonlocal relationship between and dissipation rates. The spatial correlation between and κρ,Argo is smaller in magnitude – about −0.1 – which motivates further consideration of the information provided by N2.
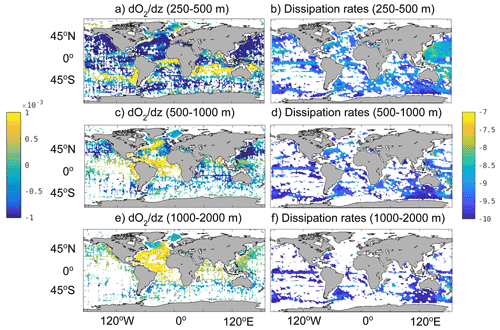
Figure 1Shown are the vertical gradients of oxygen concentrations (units in ) from the World Ocean Atlas (2013) (panels a, c, and e) and the base-10 logarithms of the dissipation rates (units in W kg−1) from Whalen et al. (2015) (panels b, d, and f). Panels (a) and (b) show an average over 250–500 m depth. Panels (c) and (d) show an average over 500–1000 m depth. Panels (e) and (f) show an average over 1000–2000 m depth. White areas in the ocean indicate insufficient data.
2.1.3 Stratification
We use an observational climatology for N2, as provided by the de Lavergne et al. (2020) dataset. N2 is generally about 10−7–10−5 s−2, with lower values in high-latitude and deeper regions and higher values in the thermocline and in shallow water areas – which skew its global average (standard deviation) below the mixed layer to about () s−2. The vertical gradients in N2 are typically between and 10−5 and have an average value (standard deviation) of about () , with its largest magnitudes on continental shelves – high-latitude ones in particular – and in the eastern equatorial Pacific Ocean. The spatial correlation between the annual mean vertical gradients in oxygen (Fig. 1a, c, and e) and the annual mean vertical gradients in N2 is about 0.25, which suggests that stratification is one candidate factor in explaining why oxygen concentrations are correlated with κρ and ϵ. However, we do not test this with model experiments that incorporate information about N2 – which directly compare N2 from our model and observations – because the vertical resolution of our ocean model is so much coarser than that of observations. Instead, we run a set of model experiments that compare oxygen concentrations, κρ, or ϵ. We perform these model experiments to further explore the potential information that oxygen concentrations provide about κρ and indirectly infer – via the Osborn (1980) relation – the possible role of stratification.
2.2 Modeling system
We use the Estimating the Circulation and Climate of the Ocean (ECCO) framework in our analysis. ECCO uses a time-invariant but spatially varying background κρ field – κρ,bg hereafter – calculated with a parameter and state estimation procedure, and κρ associated with temperature and salinity are assumed to be identical. Details about the model simulations we perform are summarized in Table 2.
Table 2Listed are the ECCO simulations performed and analyzed in the present study as well as the observationally derived data or measured data included in each simulation. Either observationally derived data or measured data are included in the experiments through a misfit calculation (Eq. 1). Here, κρ,obs denotes an observationally derived κρ product derived from a parameterization (κρ,Argo and κρ,CTD or κρ,tides) or inferred from microstructure (κρ,micro), indicates an observationally derived dissipation rate (N2 is the stratification from the World Ocean Atlas or WOA, 2013), and O2 is the climatology of measured oxygen concentrations from WOA (2013). The misfits for the experiments with κρ and ϵ are calculated using Eq. (2).

2.2.1 ECCO
The modeling system used here is ECCOv4r3 (Fukumori et al., 2017). The underlying ocean–sea ice model is based on the Massachusetts Institute of Technology general circulation model (MITgcm), which is a global finite-volume model. The ECCOv4r3 global configuration uses curvilinear Cartesian coordinates (Forget et al., 2015a – see their Figs. 1–3) at a nominal 1∘ (0.4∘ at the Equator) resolution and rescaled height coordinates (Adcroft and Campin, 2004) with 50 vertical levels and a partial cell representation of bottom topography (Adcroft et al., 1997). The MITgcm uses a dynamic–thermodynamic sea ice component (Menemenlis et al., 2005; Losch et al., 2010; Heimbach et al., 2010) and a nonlinear free surface with freshwater flux boundary conditions (Campin et al., 2004). The wind speed and wind stress are specified as 6-hourly varying input fields over 24 years (1992–2015). Average adjustments to the wind stress, wind speed, specific humidity, shortwave downwelling radiation, and surface air temperature are re-estimated and then applied over 14 d periods. These adjustments are based on estimated prior uncertainties for the chosen atmospheric reanalysis (Chaudhuri et al., 2013), which is ERA-Interim (Dee et al., 2011). The net heat flux is then computed via a bulk formula (Large and Yeager, 2009). The ocean variables, on the other hand, do not get periodically adjusted. A parameterization of the effects of geostrophic eddies (Gent and McWilliams, 1990) is used. Mixing along isopycnals is accounted for according to the framework provided by Redi (1982). Vertical mixing is the sum of diapycnal mixing and the vertical component of the along-isopycnal tensor, with diapycnal mixing determined according to the Gaspar et al. (1990) mixed layer turbulence closure and estimated κρ,bg. Convective adjustment does not act through κρ in the MITgcm. Here, κρ represents a combination of processes, including – but potentially not limited to – internal wave-induced mixing. κρ,bg, the Redi coefficient, and the Gent–McWilliams coefficient are time-independent because of the underdetermined problem of inverting for initial conditions, and model parameters would be even more underdetermined if they were allowed to vary in time – explained below. In order to simulate oxygen concentrations, tracers are carried using the Biogeochemistry with Light, Iron, Nutrients and Gases (BLING) model (Galbraith et al., 2015). BLING is an intermediate-complexity biogeochemistry model that uses eight prognostic tracers and parameterized, implicit representations of iron, macronutrients, and light limitation and photoadaptation. BLING has been shown to compare well with the Geophysical Fluid Dynamics Laboratory's full-complexity biogeochemical model, TOPAZ (Galbraith et al., 2015), and has been adapted for use in the MITgcm with its adjoint (Verdy and Mazloff, 2017).
Initial conditions and model parameters for the runs performed here are from ECCOv4r3. The least-squares problem solved by the ECCO model uses the method of Lagrange multipliers through iterative improvement, which relies upon a quasi-Newton gradient search (Nocedal, 1980; Gilbert and Lemarechal, 1989). Algorithmic (or automatic) differentiation tools (Griewank, 1992; Giering and Kaminski, 1998) have allowed for the practical use of Lagrange multipliers in a time-varying nonlinear inverse problem such as ocean modeling, eliminating the need for discretized adjoint equations to be explicitly hand-coded. Contributions of observations to the model–data misfit function are weighted by the best available estimated data and model representation error variance (Wunsch and Heimbach, 2007). The observational data included in the ECCO state estimation procedure are discussed in Forget et al. (2015a) and Fukumori et al. (2017). These data include satellite-derived ocean bottom pressure anomalies, sea ice concentrations, sea surface temperatures, sea surface salinities, sea surface height anomalies, and mean dynamic topography, as well as profiler- and mooring-derived temperatures and salinities (Fukumori et al., 2017). No ocean subgrid-scale transport parameter, mixing parameter, or biogeochemical tracer data are included in the model's misfits during the parameter and state estimation procedure. The control variables that are inverted for iteratively by ECCO are listed in Table 3, which include the ocean subgrid-scale transport and mixing parameters – e.g., κρ,bg. The error covariances for each of the ocean subgrid-scale transport and mixing parameters are specified by imposing a smoothness operator (Weaver and Courtier, 2001) at the scale of three grid points – which corresponds to a decorrelation length scale diameter of ∼100 km – which allows the dynamical model to regionally adjust from the information provided by observations (Forget et al., 2015b). A total of 59 iterations of the parameter and state estimation procedure – referred to as the “optimization” run hereafter – were performed to arrive at the ECCOv4r3 solution we start from for our experiments. The resulting κρ,bg field in the ECCOv4r3 solution – plus the Gaspar et al. (1990) contribution – will be referred to as κρ,ECCO hereafter and is shown in Fig. 2 depth-averaged below the model's average mixed layer depth. Note that the initial guess for κρ,bg in ECCO is 10−5 m2 s−1, and in the absence of observation-driven adjustments, κρ,bg in ECCO remains at or is close to its initial value in the ECCOv4r3 solution, at least in its depth average. Also note that in regions away from ocean boundary layers, κρ,ECCO is approximately κρ,bg in ECCO. κρ,ECCO is elevated in regions that undergo deep convection, near the margins of continental shelves and intensified jets, and in the Indonesian Throughflow. We will later compare κρ,ECCO with κρ from the first iteration of the same optimization run with ECCO, which will be referred to as hereafter. If is in closer agreement with κρ from observational products than κρ,ECCO, then errors in κρ,ECCO are likely being compensated for by errors in other control variables beyond the first iteration of the model's optimization run.
(Redi, 1982)(Gent and McWilliams, 1990)Table 3The control variables that ECCO inverts for and optimizes. Some of these control variables are initial conditions only (indicated in the “initial condition” column). Other control variables are time-varying (indicated in the “time-varying” column). The rest are not initial conditions but also are time-independent. Also noted is whether the control variable's field is two-dimensional or three-dimensional – there are no control variables that vary in both time and over all locations and depths of the ocean.
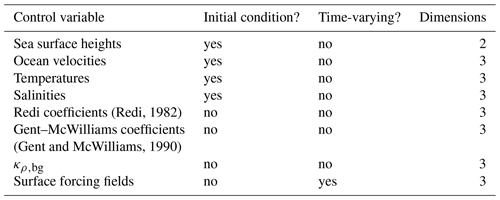
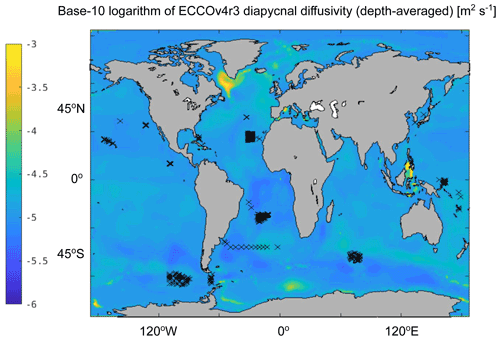
Figure 2Shown is the base-10 logarithm of κρ,ECCO (units in m2 s−1), depth-averaged over all depths below the average mixed layer depth to exclude very large values within the mixed layer. Black X marks indicate locations where there are microstructure measurements used in this study.
We run ECCO in two configurations: (1) a “re-run,” wherein all control variables are set to their estimated values from ECCOv4r3 in forward mode – sometimes referred to as an ocean-only free run – and (2) an “adjoint sensitivity” run of the parameter and state estimate in forward plus adjoint modes, wherein data are included in the model's misfits but not technically “assimilated” because the model input parameters do not change as the model runs. An adjoint sensitivity is essentially the sensitivity of one variable to another, computed by making use of the model's adjoint. Formally, an adjoint sensitivity is , where the cost function J is a sum of weighted misfits to observations and a control variable X is a variable that the model estimates by making use of its adjoint and observations – see Sect. 2.2.2. The adjoint sensitivities provide information about which directions the model's input parameters should change X in order to minimize J. Masuda and Osafune (2021) showed some examples of adjoint sensitivities of several model parameters in their ocean state estimate to a vertical mixing parameter (slightly different from κρ). We also compute adjoint sensitivities in the present study, but using ECCO with respect to X=κρ.
The following is a summary of the ECCO experiments we run (Table 2).
-
E-CTRL is a forward ECCOv4 simulation that uses the parameters from ECCOv4r3; this simulation can be referred to as a re-run.
-
EO is an adjoint sensitivity (with respect to X=κρ) experiment in which only oxygen concentrations from the World Ocean Atlas (2013) climatology are included in the misfit function J.
-
Eκ is an adjoint sensitivity (with respect to X=κρ) experiment in which only the base-10 logarithm of the κρ,micro dataset, κρ,Argo and κρ,CTD products, or κρ,tides product is included in the misfit function J.
-
Eϵ is an adjoint sensitivity (with respect to X=ϵ) experiment in which only the base-10 logarithm of the and products or the product is included in the misfit function J.
The difference between experiment Eκ and Eϵ is that the latter uses observationally derived dissipation rates, instead of κρ, in the misfit function via Eq. (2). We do not perform experiment Eϵ with microstructure data included in the model's misfit function because of the sparsity of those data. We analyze the adjoint sensitivities with dissipation rates in the misfit function (Eϵ in Table 2) in order to assess whether the stratification – a multiplying factor between κρ and the dissipation rates according to Osborn (1980) – provides information about κρ. Due to the relatively coarse vertical resolution of ECCO compared with observations, we do not directly compare N2 from ECCO with N2 from observations in another adjoint sensitivity experiment.
We take the ECCOv4r3 solution as the reference state for each of our simulations. We perform an adjoint calculation in each experiment, except for E-CTRL. The adjoint sensitivities are accumulated and averaged over the full integration period. Only 1 year was run for each of the adjoint simulations, but our results are not qualitatively sensitive to the run length – which is at least partially because we use time-invariant climatologies. The time dependence of the κρ sensitivities from Eκ is weak due to the lack of time dependence of the observations included in the misfits – κρ and oxygen concentrations; initial condition sensitivities are stronger. Thus, our simulations will suffice to demonstrate whether the inclusion of a biogeochemical tracer in the model's misfits can reduce the bias in κρ.
We begin EO from a previously derived product that has been spun up from an initial climatology (Fig. 3a) derived from World Ocean Atlas (2013). Thus, disagreements with the World Ocean Atlas (2013) are due to model drift. The depth-averaged differences between the uninterpolated World Ocean Atlas (2013) product and the initial conditions for oxygen concentrations in our ECCO run using BLING are shown in Fig. 3b. The differences are largest in the Arctic Ocean, northeastern Pacific Ocean, and near the coasts, particularly on the eastern side of the American continent, the southwestern side of the African continent, around the Kuroshio and Sea of Japan region, along almost every coastline of Oceania, and in the Mediterranean Sea (Fig. 3b). Pointwise differences between the initial conditions for oxygen concentrations in ECCO and the World Ocean Atlas (2013) product are shown in Fig. 3c, which suggests that there is strong agreement between the two fields. Where there are disagreements, the initial conditions for oxygen concentrations in ECCO are more often too small (particularly in the Atlantic Ocean, as shown in Fig. 3b) than too large. These differences are likely due to the deficiencies in model resolution, the sparse observations in regions such as the Arctic Ocean, the locations of sea ice (Bigdeli et al., 2017), and the parameterization of the tracer air–sea fluxes (e.g., Atamanchuk et al., 2020). We need to consider the spatial patterns shown in Fig. 3b when interpreting the signs of the adjoint sensitivities.
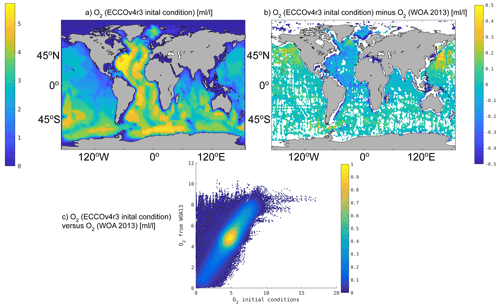
Figure 3Shown are (a) the depth-averaged oxygen concentrations' initial conditions in ECCO (units in mL L−1), (b) the depth-averaged oxygen concentrations' initial conditions in ECCO minus the depth-averaged observational climatologies from the World Ocean Atlas (2013) (units in mL L−1) at locations where observations were sampled, and (c) the pointwise comparisons between the oxygen concentrations' initial conditions and the observational climatologies from the World Ocean Atlas (2013) (units in mL L−1), which are used for the ECCO adjoint sensitivity experiments in the model's cost function. White areas in panel (b) in the ocean indicate insufficient data to calculate a depth average.
2.2.2 ECCO adjoint sensitivity analyses
Short of including a particular dataset (e.g., dissolved oxygen concentrations) in the misfits of a new optimization run of ECCO, we assess whether the inclusion of a particular dataset in the model's misfits could lead to a more accurate estimate of a control variable that can be observed (e.g., κρ). In order to understand whether κρ could be estimated more accurately through the inclusion of oxygen concentrations in the model's misfit, we need to further explain the details of our adjoint sensitivity experiments with ECCO. We define the objective (or cost) function here to more formally explain what the adjoint sensitivity is. ECCO calculates the cost function to be minimized, J (Stammer et al., 2002) – focusing here only on the observational misfit terms while omitting regularization terms for the control variables – as
where tf is the final time step, is the model-based estimate of the state vector x, S is the observation matrix that relates the model state vector to observed variables y (such that is the model-based estimate of the observables y), and W is the weight (inverse square of approximate uncertainties accounting for measurement and representation errors) of the observations. In each of our adjoint sensitivity experiments, the data vector y only contains the dataset specific to the experiment (see Table 2), so we emphasize here that J is different for each of our experiments. The uncertainties in κρ,ECCO in Eκ are set to be 3 times the values of the observationally derived κρ because of the level of agreement between κρ,Argo and κρ,micro (Whalen et al., 2015). The uncertainties in oxygen concentrations in EO are set to be 2 % of the values of the measured dissolved oxygen concentrations.
The adjoint sensitivities computed in this study are the derivatives of J in Eq. (1) with respect to κρ. We consider evaluating directions in the control space in which to improve κρ through improvement of κρ,bg, given the control vector from the ECCOv4r3 solution. While the adjoint sensitivities of J to the control space in experiment EO must be computed online, those in Eκ can either be computed online or offline using an analytical equation (see below). The adjoint sensitivity run with κρ included in the misfit calculation of experiment Eκ can be calculated offline using output from the E-CTRL run instead of being calculated online as follows:
Here, X=κρ is the control variable, Xobs is the observationally derived value of X described in the previous section, Xmodel is the value that ECCO estimates for X, and σX is taken to be (or the base-10 logarithm of this in the case of κρ) due to the factor of 3 uncertainty corresponding to an approximate 95 % confidence interval in Whalen et al. (2015). For Xmodel, we use the offline values calculated from the E-CTRL run following Eq. (2). While this assumes a diagonal W and minimal impact of the smoothing operator applied over a decorrelation length scale diameter of ∼100 km, the offline Eq. (2) and online sensitivities have been verified to be in agreement.
Because the observations of κρ here are not direct measurements, we first need to show that observationally derived κρ has a smaller bias with respect to independent observations than the model's estimate of κρ. We devote the first portion of our study to determining whether (and, by extension, κρ,CTD in place of κρ,Argo) is true. We do this because κρ,micro is limited in its spatial coverage compared to κρ,Argo, κρ,CTD, and κρ,tides. Also, κρ,Argo and κρ,CTD are still limited in spatial coverage relative to dissolved oxygen concentrations. While κρ,tides has global spatial coverage, its measurement and structural uncertainties are not well-known compared to dissolved oxygen concentrations. The data product with higher accuracy (dissolved oxygen concentrations) will have larger weights (W in Eq. 1) and will thus exert more influence in constraining κρ,ECCO – bringing it closer to microstructure values. So if we can show that the adjustments to κρ in ECCO are similar, whether we provide information from observationally derived κρ or a measured tracer with relatively small uncertainties (dissolved oxygen concentrations), then we would include the tracer in the misfits.
One problem with doing a direct comparison of the adjustments is that the uncertainties in observationally derived κρ products are large, so we first quantify the extent to which the adjoint sensitivities from two runs (here, Eκ and EO) have the same sign at each location and depth. Specifically, we inspect whether has the same sign in Eκ and EO, where is significantly different from zero (i.e., κρ,Argo is more than a factor of 3 greater or less than a factor of 3 smaller than κρ,ECCO). We are interested in regions where κρ is significantly erroneous and where the errors in oxygen are due to errors in the physics (e.g., κρ), not initial conditions: hence, these choices. We perform these comparisons in regions where the difference between the observationally derived κρ products and κρ,ECCO exceeds 3 times the observational products' magnitudes (i.e., statistically distinguishable from zero). Because model errors unrelated to κρ can confound the correlations between the adjoint sensitivities from Eκ and EO, we additionally look at regions where the difference between oxygen concentrations from the model and the World Ocean Atlas (2013) is relatively small to determine whether oxygen concentrations guide the state estimate's control space to improve the magnitude of κρ. In this subset of regions, we calculate the correlations between the adjoint sensitivities from Eκ and EO – despite the difficulty with determining their significance.
To investigate whether the results are sensitive to our assumptions about the signal-to-noise ratio of our data – through W in Eq. (1) – we additionally perform Monte Carlo simulations for the adjoint sensitivities from Eκ – using three different datasets for κρ: κρ,micro, κρ,Argo together with κρ,CTD, and κρ,tides. In the Monte Carlo simulations, at each location and depth, we randomly sample κρ values within its uncertainty – σκ – simultaneously with randomly sampled values of σκ between a factor of 2–3 of κρ. This accounts for the uncertainties in the κρ products in both the numerator – corresponding to uncertainties in the observationally derived estimates – and denominator of Eq. (2) – corresponding to the weights. With each of the 10 000 samples of κρ and σκ, we recompute the adjoint sensitivity for Eκ and then its correlation with that for EO. With these Monte Carlo simulations, we report the maximum possible correlation between each experiment's adjoint sensitivities.
We first show that the disagreements between κρ from ECCO and κρ from various observations are larger than the observations' approximate 95 % confidence intervals. Then we analyze results from pairs of adjoint sensitivity runs: one with misfits to observed κρ derived from the fine-scale parameterization and the other with misfits to observed O2. We use these results to investigate the potential to use O2 as a constraint for improving κρ,ECCO in a future optimization. We then compare the results of the adjoint sensitivity runs using misfits in κρ with ones using misfits in ϵ to infer a potential role of stratification in any information that O2 provides about κρ. In the Appendix, we show there is general agreement between κρ from observations and a free-running Earth system model that calculates a physically motivated parameterization for κρ, but there is poor agreement between κρ from observations and a sequential ocean data assimilation system based on the same Earth system model (Fig. A1a).
3.1 Model-inverted vs. microstructure-inferred κρ comparisons
We compare the average κρ,micro profile that is comprised of 24 campaigns' worth of data (Waterhouse et al., 2014) (see their Fig. 6; black curves in Figs. 4a and 5) with average κρ,ECCO profiles from two different iterations and the κρ,Argo product (Whalen et al., 2015). The locations of the microstructure measurements are shown in Fig. 2 (black X marks). We also compare the average κρ,tides profile (de Lavergne et al., 2020) (see their Fig. 2e; black curve in Fig. 4b) with the average κρ,ECCO profile from the final iteration.
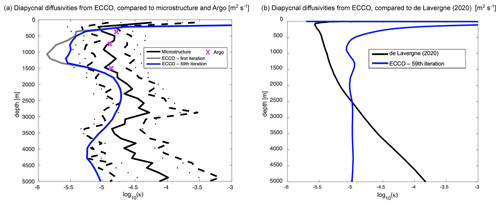
Figure 4(a) κρ profiles averaged over all microstructure observation locations (shown in Fig. 2) from the first iteration of the optimization (E-CTRL0 – grey curve) and from the (final) 59th iteration of the optimization (E-CTRL – blue curve). Also shown is the average of κρ profiles from the full-depth microstructure observations (black curve) presented in Waterhouse et al. (2014) (see their Fig. 6; also see Fig. 5 of the present study) with 1 spatial standard deviation flanking the average (dashed black curves) and an approximate factor of 3 uncertainty flanking the average (dotted black curves), as well as the average of κρ (magenta X marks) at each of the depth bins in the Whalen et al. (2015) product. At each location, the simulated profiles are extracted and the base-10 logarithms of the geometric averages of the observed and ECCO-estimated κρ (units in m2 s−1) are shown. (b) κρ profiles averaged over the entire ocean from the 59th iteration of the optimization (E-CTRL – blue curve) and from the de Lavergne et al. (2020) tidal mixing product (black curve).
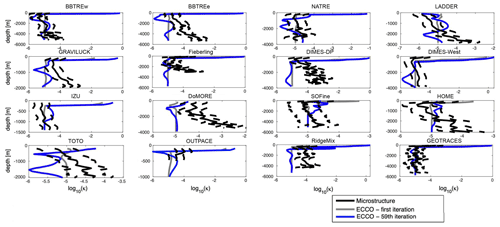
Figure 5In each panel, κρ profiles are shown averaged over 16 example microstructure observation campaigns (see Fig. 2): from the first iteration of the optimization (E-CTRL0 – grey curve), from the (final) 59th iteration of the optimization (E-CTRL – blue curve), and from the full-depth microstructure observations (black curve) presented in Waterhouse et al. (2014) (see their Fig. 6). Approximate factor of 3 uncertainties flanking the κρ profiles from microstructure are shown with dashed black curves.
The average profile – i.e., the first adjusted initial guess of κρ,ECCO – is typically smaller than the microstructure profile, particularly at 1000 m where the difference is approximately an order of magnitude (Fig. 4a). At iteration 59 (which is the ECCOv4r3 solution), the difference between κρ,ECCO and κρ,micro decreases. However, agreement between the average profiles of κρ,ECCO and κρ,micro is still worse than the agreement between κρ,Argo and κρ,micro. The agreement between κρ,Argo and κρ,micro at each of the three depth bins is well within a factor of 3 (dotted black curves in Fig. 4a) and the spatial standard deviation of κρ,micro (dashed black curves in Fig. 4a). The agreement between the average profiles of κρ,ECCO and κρ,tides is poor, with κρ,ECCO typically too small, notably so at deeper depths (Fig. 4b). κρ,ECCO includes internal-wave-induced mixing as well as potentially numerical diffusion. However, numerical diffusion cannot explain the errors in κρ,ECCO, where κρ is too small in the model relative to the observationally derived products because numerical diffusion would increase κρ,ECCO. In these regions, one likely explanation is that errors in other model parameters (e.g., the Redi coefficients) compensate for the errors in κρ,bg.
We also compare κρ,ECCO and profiles with κρ,micro from 16 example campaigns in Fig. 5. In some regions, the κρ,ECCO and profiles are constant (10−5 m2 s−1, the default background value) because ECCO does not sufficiently resolve the bathymetry, so we exclude those from Fig. 5. We also exclude some others, for example, in the subpolar North Atlantic Ocean because temporal variations in κρ can be large there (Fig. A1b). The κρ,ECCO profiles (blue curves in Fig. 5) and profiles (grey curves in Fig. 5) are often within the approximate (factor of 3) uncertainties in the κρ,micro profiles (dashed black curves in Fig. 5), but not always. Without taking an average over all of the campaigns, there can be large regional disagreements between the model and observations. Also, the κρ,ECCO profiles are not always closer to the κρ,micro profiles than the profiles. This suggests that performing more iterations of the optimization of ECCO is not necessarily going to lead to more accurate representation of κρ with the current data constraints.
3.2 Model-inverted vs. fine-scale parameterization-derived κρ comparisons
We next show κρ,Argo and κρ,tides as well as how they contrast with κρ,ECCO because this highlights the spatial patterns of the adjoint sensitivities in Eκ (see later). The ratio between the κρ,Argo product (Fig. 6a, c, and e) and κρ,ECCO varies throughout the globe (Fig. 6b, d, and f). Red (blue) areas in Fig. 6b, d, and f indicate locations where Argo-derived κρ,Argo is smaller (larger) than κρ,ECCO. The percent of volume for which κρ,ECCO is at least an order of magnitude different from κρ,Argo is 43.8 %. The values of κρ,ECCO are smaller than those in the Argo- and hydrography-derived observational product in the Kuroshio Extension (500–1000 m depth), subpolar North Atlantic Ocean (500–1000 m depth), Southern Ocean, equatorial regions in the Atlantic Ocean, and shallow (250–500 m depth) Indian Ocean and eastern Pacific Ocean (Fig. 6b, d, and f). In contrast, κρ,ECCO tends to be too large relative to the κρ,tides product (Fig. 7a, c, and e) in the Atlantic Ocean below 500 m depth as well as in many near-equatorial and subpolar regions, and κρ,ECCO tends to be too small everywhere else (Fig. 7b, d, and f). Regardless of the observational product, the κρ,ECCO field is comparatively large in many of the model's near-equatorial regions, where the intermittency of strong mixing events is likely not captured – even in a time-mean sense – because the ECCO framework uses a smoother. However, the fidelity of each observational product is unknown near the Equator. The fact that κρ,ECCO and each observational product disagree within the deep mixed layers at high latitudes is not consequential for tracer transport. The errors in κρ,bg could be partially compensating for errors in the vertical component of the along-isopycnal diffusivity tensor, erroneous air–sea fluxes due to inconsistencies between the sea surface and atmospheric forcing fields, and/or the presence of numerical diffusion.
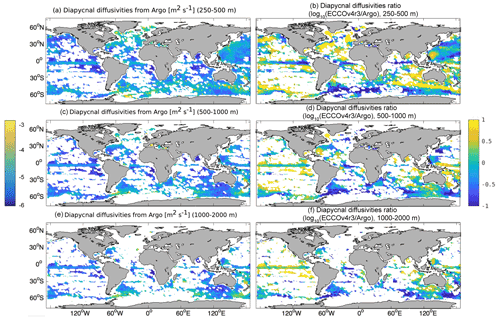
Figure 6Shown are (a, c, and e) the base-10 logarithms of κρ,Argo (units in m2 s−1) and (b, d, and f) the base-10 logarithms of the ratios of the time-averaged κρ,ECCO to κρ,Argo. Panels (a) and (b) show an average over 250–500 m depth. Panels (c) and (d) show an average over 500–1000 m depth. Panels (e) and (f) show an average over 1000–2000 m depth. White areas in the ocean indicate insufficient Argo data to derive κρ,Argo.
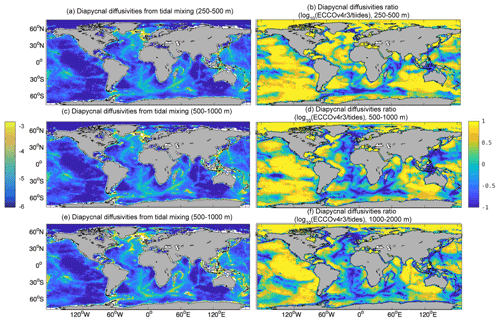
Figure 7Shown are (a, c, and e) the base-10 logarithms of κρ,tides (units in m2 s−1) and (b, d, and f) the base-10 logarithms of the ratios of the time-averaged κρ,ECCO to κρ,tides. Panels (a) and (b) show an average over 250–500 m depth. Panels (c) and (d) show an average over 500–1000 m depth. Panels (e) and (f) show an average over 1000–2000 m depth.
Incomplete historical observations – of temperature, salinity, and pressure – are currently insufficient to accurately estimate κρ,bg – approximately κρ,ECCO away from the boundary layers, where we compare with observational products. Even the abundance of Argo data in the upper 2000 m has not been enough to calculate a realistic κρ,ECCO in the upper 2000 m. The sparsity of the observations below 2000 m depth, in high-latitude regions, and in some near-coastal areas – where internal wave-induced mixing can be important – is relevant because complete observational coverage of the ocean's temperature, salinity, and pressure could, in principle, better constrain κρ,bg using inverse modeling (Groeskamp et al., 2017). However, the lack of time dependence of κρ,bg, the presence of numerical mixing, and joint estimation of many underdetermined parameters in ECCO could also lead to erroneous κρ,ECCO. These are some reasons why values of κρ,ECCO do not agree well with κρ from observations – κρ,micro, κρ,Argo, κρ,CTD, or κρ,tides.
3.3 Adjoint sensitivities in ECCO
Because the data that are currently included in ECCO's misfits are insufficient for κρ,ECCO to match κρ,micro, κρ,Argo, κρ,CTD, or κρ,tides, including additional variables controlled by mixing in the model's misfits may assist in further improving the modeled mixing parameters. Oxygen is a candidate since its distribution is, in part, determined by the local κρ. To test this, we run multiple adjoint sensitivity experiments in which either observationally derived κρ or oxygen is included in the misfit calculation to guide constraints on κρ. We expect the signs of sensitivities to agree most in regions away from where air–sea fluxes and transport of oxygen – e.g., by intensified jets – are large. One of these regions is the subtropical North Atlantic Ocean, away from the Gulf Stream Extension. Further, we expect to find more agreement between the signs of sensitivities in tropical OMZs and other (sub)tropical regions because of the known importance of diapycnal mixing in these regions.
We show the adjoint sensitivity calculations using Eq. (2) for κρ misfits (experiment Eκ in Table 2) in Fig. 8 using κρ,Argo and κρ,CTD; these are later compared with the sensitivities for oxygen concentration misfits in experiment EO. A positive adjoint sensitivity implies that the misfit can be reduced by decreasing κρ,ECCO. The signs of using κρ,Argo and κρ,CTD (Fig. 8a) are consistent with the signs of local disagreement with microstructure (Figs. 4a and 5) and Argo-derived observations (Fig. 6b, d, and f) by construction. Because κρ,ECCO tends to be very large inside mixed layers, tends to be positive and larger at many locations in the subpolar latitudes where there are deep mixed layers in the model but possibly not in the real ocean; conversely, can be negative where the mixed layer depth is too shallow in ECCO, but this is not the only reason for . The large positive values of within the mixed layer and some other regions overwhelm the zonal averages in favor of positive values (Fig. 8c). κρ,ECCO needs to be decreased in many regions at depths shallower than 500 m to agree better with κρ,Argo and κρ,CTD (yellow regions in Fig. 6b, d, and f), but microstructure measurements (X marks in Fig. 2) were often taken in locations where κρ,ECCO should be increased (blue regions in Fig. 6b, d, and f) or stay the same. Microstructure measurements tend to be regions where there are prominent topographic features and where the centers of subtropical gyres are found, which – judging from the predominant signs of disagreement in Figs. 4a and 5 versus Fig. 6b, d, and f – are not representative of the ocean where Argo measurements were taken.
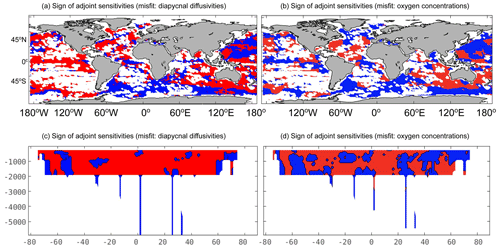
Figure 8Adjoint sensitivity sign comparisons: results from Eκ – using the Whalen et al. (2015) and Kunze (2017) products – (panels a and c) and EO (panels b and d) are shown for the adjoint sensitivities (units in s m−2) with respect to κρ averaged over 250–2000 m depth (panels a and b) and zonally averaged (panels c and d). The red regions indicate that the adjoint sensitivities are positive (), and blue regions indicate negative adjoint sensitivities. κρ,Argo and κρ,CTD are the only quantities used in the misfit calculation of an adjoint run shown in panels (a) and (c). The climatological oxygen concentrations from the World Ocean Atlas (2013) are the only observations used in the misfit calculation of a separate adjoint run shown in panels (b) and (d). The adjoint sensitivities in panels (a) and (c) are computed offline (i.e., not using ECCO, but by plugging in the value the model reads in for the base-10 logarithm of κρ and comparing that with the above observationally derived base-10 logarithm of the κρ products using the fine-scale parameterization via Eq. 2). The adjoint sensitivities in panels (b) and (d) are computed online (i.e., using ECCO, which uses the base-10 logarithm of κρ as a control variable). The white regions are locations with bathymetry or insufficient observations. The adjoint sensitivities are calculated over just 1 year (1992).
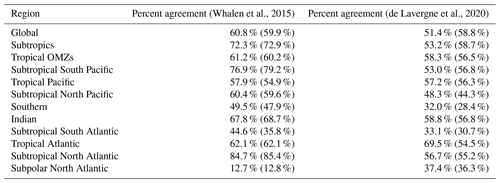
We next compare from Eκ using κρ,Argo and κρ,CTD with from EO. In EO, is generally negative in subtropical regions (Fig. 8b and d). Overall, the locations of the positive and negative signs of are not the same everywhere between the Eκ and EO experiments, but they agree in many regions (Fig. 8a and c and Fig. 8b and d) using κρ,Argo and κρ,CTD, which account for nearly two-thirds (three-fourths) of the ocean's volume where they can be compared (in the subtropics, between 20 and 50∘ N and S; Fig. 9 and Table 4). The ocean basin with the highest percent volume of agreement in adjoint sensitivity signs between Eκ and EO is the subtropical North Atlantic Ocean, with nearly 85 % volume agreement. The subtropical South Atlantic Ocean is the only subtropical basin with less than half of its volume in agreement in adjoint sensitivity sign. In general, the tropical regions (between 20∘ S and 20∘ N) have adjoint sensitivity signs in lesser agreement than the subtropical regions, and the subpolar regions (poleward of 50∘ N and S) are the regions with the lowest percent volume agreements in adjoint sensitivity signs.
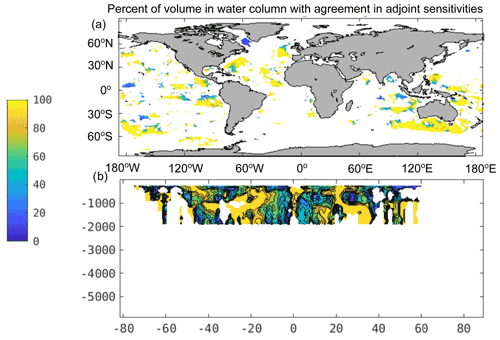
Figure 9Adjoint sensitivity sign comparisons: shown are the percents of volume over the water column for each horizontal location (panel a) and percent of volume over all longitudes for each depth and latitude (panel b) where the sign of agrees between Eκ – using the Whalen et al. (2015) and Kunze (2017) products – and EO. The white areas are locations where the disagreements between κρ,ECCO and κρ,Argo supplemented with κρ,CTD are within 3 times the value of the observationally derived κρ, so these were excluded.
Table 4Listed are the percent volumes for which the signs of the adjoint sensitivities agree between Eκ – for both the Whalen et al. (2015) and de Lavergne et al. (2020) products – and EO for different regions of the ocean. The boundaries of subtropical–equatorial regions are set to be at 20∘ N and S. The boundaries of subtropical–subpolar and subtropical–Southern Ocean regions are set to be 50∘ N and S. The tropical oxygen minimum zones (OMZs) are where oxygen concentrations are less than 2 mL L−1 between 20∘ S and 20∘ N. The percentages are only calculated when sufficient observations are available to derive κρ and when the difference between the model-calculated and observationally derived κρ is greater than the uncertainty (i.e., 3 times the observationally derived κρ). In parentheses are the same, except for the dissipation rates, , where N2 is the stratification and 0.2 is an empirical coefficient (see, e.g., Gregg et al., 2018).
We also show the adjoint sensitivity calculations using Eq. (2) for κρ misfits (experiment Eκ in Table 2) in Fig. 10 using κρ,tides and compare from Eκ using κρ,tides with from EO. The signs of using κρ,tides (Fig. 10a) are consistent with the signs of local disagreement with the de Lavergne et al. (2020) product (Figs. 4b and 7b, d, and f) by construction. The positive values of outside the Atlantic Ocean and in the vicinity of intensified jets overwhelm the zonal averages in favor of positive values at most depths (Fig. 10c). κρ,ECCO needs to be decreased in many regions at depths shallower than about 2500 m to agree better with κρ,tides (Fig. 4b; yellow regions in Fig. 7b, d, and f). The regions where κρ,ECCO needs to be increased become dominant closer to the seafloor, particularly in the Atlantic Ocean. The signs of from Eκ agree with from EO in fewer regions (Fig. 10a and c and Fig. 10b and d) using κρ,tides instead of κρ,Argo and κρ,CTD. The regions with agreement in signs of sensitivities using κρ,tides account for just over half of the ocean's volume where they can be compared globally (Fig. 11 and Table 4); this is also true for the subtropics. The equatorial regions have the highest percent volume of agreement in signs of sensitivities using κρ,tides over all depths, but the North Atlantic Ocean also has fairly high agreement (Fig. 11a). There is high agreement in the regions of the Arctic Ocean that are north of the Greenland and Barents seas too. Compared with shallower depths, regions below 3000 m depth tend to be derived from Antarctic Bottom Water (Marshall and Speer, 2012 – see their Fig. 1) and therefore have different oxygen concentration characteristics such as weaker vertical gradients. They also have differences between κρ,ECCO and observationally derived κρ that are more commonly statistically indistinguishable and have less overwhelmingly positive adjoint sensitivities from Eκ using κρ,tides (Fig. 10c). As a result, all of the depths with the highest levels of agreement in signs of sensitivities using κρ,tides are between the mixed layer depth and 3000 m depth (Fig. 11b). Most differences in the spatial distribution of agreements between the signs of sensitivities across different observationally derived products (Figs. 9 and 11) are at least partially due to their spatial coverage – Argo versus global – and the <100 % overlap in processes accounted for by the various κρ products. Thus, the level of agreement in signs of sensitivities from Eκ and EO is high over many regions and is qualitatively consistent in its spatial distribution across the different observationally derived products for κρ.
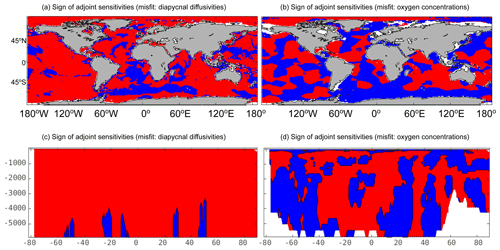
Figure 10Adjoint sensitivity sign comparisons: same as Fig. 8, but with the de Lavergne et al. (2020) product, κρ,tides.
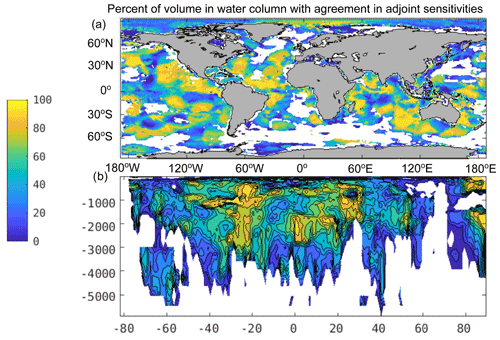
Figure 11Adjoint sensitivity sign comparisons: same as Fig. 10, except using the de Lavergne et al. (2020) product, κρ,tides.
We need to address whether any of the agreement in signs of sensitivities is random – as their correlation is due to the large uncertainties in observationally derived κρ – or underpinned by physical reasons. We first focus on the locations with statistically indistinguishable errors in κρ,ECCO. These regions and those where there can be significant differences between oxygen concentrations in ECCO and the World Ocean Atlas (2013) product correspond to the white regions in Fig. 9 that are red or blue in Fig. 8 – likewise for Fig. 11 versus Fig. 10. The vast majority of the locations where disagreements occur in sensitivity signs are in places with statistically indistinguishable differences between κρ,ECCO and observationally derived κρ. The regions with statistically indistinguishable differences in κρ account for 56.2 % (24.1 %) of the volume of the ocean where the adjoint sensitivities from EO and Eκ can be compared using κρ,Argo and κρ,CTD (κρ,tides). Thus, we exclude a large portion of the ocean from the remainder of our analysis because we cannot determine whether agreements in signs of sensitivities are by random chance in these regions.
We next inspect the sensitivity sign patterns in regions with statistically significant κρ misfits. The regions where the signs of agree from the two experiments and have large differences between κρ,ECCO and the combined κρ,Argo and κρ,CTD product tend to have relatively small oxygen concentration misfits (Fig. 3b). This is also true when using the κρ,tides product. For example, when only regions with less than 1 standard deviation above the average oxygen concentration misfits are selected, the signs of the adjoint sensitivities agree between EO and Eκ over 60.8 % (50.5 %) of the volume with sufficient data using κρ,Argo and κρ,CTD (κρ,tides). However, the larger the oxygen concentration misfits, the more often the signs of the sensitivities agree. When only regions with more than 3 standard deviations above the average oxygen concentration misfits are selected, the signs of the sensitivities always agree. Thus, the regions with the largest disagreements in oxygen concentrations can always decrease their oxygen misfits by changing κρ,ECCO with a sign consistent with decreasing its disagreement with observationally derived κρ, wherever differences in κρ are detectable.
Where there are statistically significant differences in κρ, we still need to determine whether there is a physical basis for the agreements in signs of sensitivities. We next show results that are consistent with our hypothesis that tropical OMZs and other (sub)tropical regions are where oxygen concentrations can inform κρ in the model such that there is better agreement with observationally derived κρ products. The regions with the highest percent volume agreement in sensitivity signs, regardless of which observationally derived κρ product is used, include tropical OMZs and other (sub)tropical regions below several hundred meters of depth (Figs. 9b and 11b). Differences between the signs of the sensitivities tend to be more common in locations where κρ is not expected to dominate the variability in oxygen. These regions include, for example, the open subpolar North Atlantic Ocean (e.g., the Labrador Sea in Figs. 9a and 11a), where Atamanchuk et al. (2020) present observational evidence that air–sea fluxes mediated by bubble injection – not represented by ECCO – dominate the variability in oxygen down to 1000 m depth. While there can be a high percent volume agreement in sensitivity signs in the equatorial Pacific Ocean and Atlantic Ocean, these are also regions where Palter and Trossman (2018) and Brandt et al. (2021) point out that ocean circulation changes significantly influence long-term changes in oxygen. This suggests that changes in both ocean circulation and κρ could be important in explaining oxygen concentration variations in the tropics. When the tropical and subpolar regions (outside the 20–50∘ N and S bands) are excluded, the percent volume of the ocean where the signs of the adjoint sensitivities agree between Eκ and EO increases, regardless of which observationally derived κρ product we use. Given that there are known physical processes not dominated by κρ causing variations in oxygen concentrations in regions outside tropical OMZs and other (sub)tropical regions, our interpretation of the patterns shown in Figs. 8–11 is that κρ controls much of the variability in oxygen concentrations in large portions of tropical OMZs and other (sub)tropical regions. This is one indication that dissolved oxygen concentrations could provide information about κρ, at least for some regions of the ocean.
We further address whether the potential information dissolved oxygen concentrations provide about κρ is due to the information oxygen contains about stratification. To determine whether oxygen provides information about stratification – and through stratification, about κρ – we use the adjoint sensitivity results obtained from experiment Eϵ with observationally derived dissipation rates, (e.g., Fig. 1b, d, and f) instead of κρ (e.g., Fig. 6b, d, and f), in the misfit function via Eq. (2) and multiply the adjoint sensitivity of EO by so that their sensitivities are each taken with respect to ϵ (parentheses in Table 4). We find approximately equal agreement between the signs of the adjoint sensitivities from EO (scaled by ) and Eϵ as we do between those from EO and Eκ in every region, regardless of which observationally derived product we use. Because ϵ is related to κρ through the stratification, we suggest that the information oxygen concentrations provide about κρ is likely independent of the stratification field.
Lastly, given that the general agreement in signs of sensitivities between Eκ and EO is likely underpinned by physical reasons unrelated to stratification, we pursue whether there is a statistically significant relationship between the adjoint sensitivities from Eκ and EO. We again focus on the regions where the difference between κρ,ECCO and observational κρ products (from tides, Argo/CTD, and microstructure) is statistically significant (greater than a factor of 3), but also filter out the adjoint sensitivities when the differences between oxygen concentrations from ECCO and those from the World Ocean Atlas (2013) are statistically significant. The simple correlations between the adjoint sensitivities from Eκ and EO in the remaining regions tend to be small but positive (Fig. 12). In addition to taking simple correlations, we performed Monte Carlo simulations to get a maximum possible correlation between each experiment's adjoint sensitivities. The maximum correlations from the Monte Carlo simulations are larger than the simple correlations. This is particularly the case when the adjoint sensitivities are both negative (Fig. 12a, c, and e) but is also true when the adjoint sensitivities are both positive (Fig. 12b, d, and f). If we only consider comparing locations where we have both observationally derived κρ data and oxygen data, our results are qualitatively the same and the correlations increase to as much as 0.47 in the case of the κρ,tides product using a Monte Carlo approach. If we further only consider regions where the vertical gradients in stratification are less than their global mean and where the vertical gradients in oxygen concentrations are greater than their global mean, the correlations are approximately the same, indicating that the information oxygen provides about κρ is not conditional on the stratification. This suggests that κρ,ECCO may be constrained by the information provided by oxygen concentrations. That is, oxygen concentrations inform adjoint sensitivities that typically direct κρ,ECCO to improve relative to observationally derived κρ. However, inclusion of accurately known oxygen concentrations in the model's misfits is not a perfect substitute for the inclusion of accurately known κρ itself in the model's misfits.
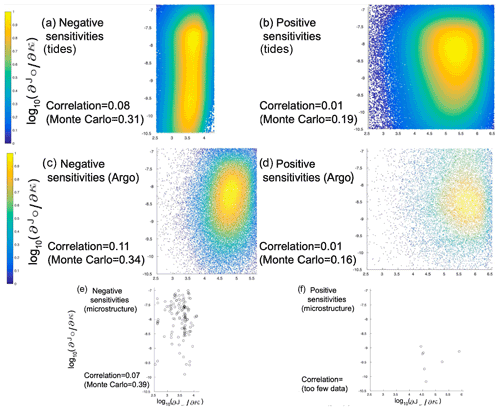
Figure 12Shown are scatterplots between the adjoint sensitivities from EO and Eκ where they are both negative (panels a, c, and e) and where they are both positive (panels b, d, and f). Eκ has its adjoint sensitivities calculated with the tidal mixing product κρ,tides (panels a and b), Argo-derived κρ (κρ,Argo and κρ,CTD; panels c and d), or microstructure-inferred κρ (panels e and f). Only the adjoint sensitivities for which the differences between κρ,ECCO and observational κρ products are statistically significant (greater than a factor of 3) and when the differences between oxygen concentrations from ECCO and those from the World Ocean Atlas (2013) are statistically insignificant (within 2 % of the latter) are included. The correlations for all of the data points shown in each panel are listed. Also listed below each panel are the maximum possible correlations from a Monte Carlo-based approach in which 10 000 random samples of κρ within the uncertainties of the observational κρ products are used to recompute the adjoint sensitivities for Eκ.
4.1 Discussion
This study evaluated the potential to improve the diapycnal diffusivities (κρ) in the ECCOv4 ocean parameter and state estimation framework. We assessed the fidelity of κρ,ECCO by first comparing the average vertical profiles of κρ,ECCO with those inferred from microstructure. The comparison was not favorable. In regions where we compare with observational products, κρ,ECCO is approximately κρ,bg in ECCO, which is inverted for through constraints of vertical profiles of temperature and salinity – e.g., from Argo profiles. Model choices – e.g., the initial guess of background m2 s−1 everywhere – can lead to errors in κρ,ECCO even in the presence of globally complete hydrographic observations (see Sect. 4.2), but we investigated whether κρ,ECCO can benefit from new information.
We then investigated which additional observations can be used as new constraints to improve the fidelity of the inverted κρ,ECCO. The products we used were observationally derived κρ based on Argo and ship-based CTD hydrographic data, observationally derived κρ based on climatological and seafloor data, and climatological oxygen concentrations. To justify the use of the observationally derived κρ products, we also evaluated them by comparing them with the microstructure-inferred product. κρ,Argo and κρ,CTD have better agreement with the microstructure-inferred data than κρ,ECCO does.
We inspected the misfit of the model parameter κρ,ECCO with respect to κρ,Argo and κρ,CTD as well as to κρ,tides and motivated the use of dissolved oxygen concentration data as a potential constraint in ECCO. One drawback of the observationally derived data products for κρ is that they have large uncertainties – here approximated by a factor of 3. Observed oxygen concentrations, on the other hand, have relatively small uncertainties. More importantly, we showed that vertical oxygen gradients have geographical patterns similar to energy dissipation rates. We therefore performed an additional adjoint sensitivity experiment with oxygen concentration data as the only data in the misfit function. Adjoint sensitivity results were compared between the experiment with measured oxygen in the misfit function and observationally derived κρ in the misfit function. Regions where the sensitivities agree in signs between the two experiments are locations where adjustments in κρ, as informed by these data, can potentially help improve κρ,ECCO. These regions include well over half of the volume of comparable seawater in the (sub)tropical regions – including tropical OMZs. These spatial patterns are consistent with where we expected κρ to explain much of the variability in oxygen concentrations. Correlations between adjoint sensitivities from each experiment are positive when differences between the oxygen concentrations in the model and observations are relatively small. These findings suggest that dissolved oxygen concentrations could be used to more accurately estimate κρ through κρ,bg in a newly optimized ECCO solution. However, given the magnitudes of the correlations between the adjoint sensitivities, inclusion of observationally derived κρ in the model's misfits could (additionally) be necessary, especially if their uncertainties are reduced.
4.2 Caveats and future directions
Many factors – including a significant absence of independent observations for assessment, a combination of measurement and structural errors, numerical diffusion in our simulations, and unconstrained parameters in the biogeochemical modules – have stymied progress in state estimation of ocean subgrid-scale transport and mixing parameters. First, the observational measurement errors used here are only approximate. We assumed uncertainties equal to a factor of 3 of the observationally derived κρ and 2 % of the oxygen concentrations. These do not account for interpolation and/or averaging errors that entered the data prior to our calculations but are conservative estimates nonetheless. The observational uncertainties affect the weights given in the misfits that enter the adjoint sensitivity calculations, and our Monte Carlo simulations of the correlations between the adjoint sensitivities account for the possibility that these weights are misspecified. Second, only one ocean subgrid-scale transport or mixing parameter – namely, κρ – has been compared with independent observational data microstructure. This is the primary reason why we focused on κρ in our study. Third, the ECCO-estimated κρ,bg accounts for other model errors – e.g., structural ones suggested by Polzin et al. (2014) – which explains some of the model biases relative to microstructure observations. For instance, the ECCO-estimated κρ,bg should be time-dependent as well as spatially varying, but it is only spatially varying. In the presence of other estimated model parameters and initial conditions, some parameters could be compensating for errors in κρ,bg. The ECCO-estimated κρ,bg can also be sensitive to the a priori estimate of κρ,bg, and we showed how one particular initial guess – 10−5 m2 s−1 everywhere – can evolve from the first optimization iteration to the final one. Additionally, there is numerical diffusion in the model, which could confound some physical inferences about the model – e.g., regarding how sensitive the model's state is to κρ,bg relative to along-isopycnal diffusion. Numerical errors could remain and result in the primary source of error in the ocean state estimate even if additional constraints are placed on κρ,bg in ECCO. Retaining a parameter which absorbs structural model errors that are not expressed in the model's functional form may be necessary to improve the ECCO state estimate itself, but minimizing numerical errors would be beneficial to improve the ECCO-estimated κρ,bg. Lastly, there are several unconstrained parameters in biogeochemical modules used to calculate biogeochemical tracers (Verdy and Mazloff, 2017), so some of the disagreements in signs of the adjoint sensitivities found here could be associated with other inaccurate parameters.
These challenges can continue to be overcome by allowing models and observations to inform each other. First, the observationally derived κρ from the fine-scale parameterization could be further scrutinized using ship-based CTD data taken concurrently with microstructure velocity shear data. A preliminary analysis suggests that the percent difference between the full depth-averaged CTD-derived κρ from the fine-scale parameterization and the microstructure-inferred κρ at the same locations is 1.68 %, which is indistinguishable from zero, but the quality of the CTD data taken concomitantly with microstructure has not been fully assessed. Second, we can potentially overcome several computational challenges to improve κρ,bg. One example of this is to account for the time dependence of κρ,bg in a future ocean state estimate, but the underdetermined nature of the parameter estimation procedure makes this difficult. These efforts would also benefit from minimizing spurious mixing due to numerical diffusion (e.g., Holmes et al., 2021) through choosing a different advection scheme, but this would add computational expense. If the goal is to improve the other control variables and the state estimate itself – instead of estimating κρ,bg with ECCO – then we could potentially reduce the influence of numerical diffusion and other confounding factors in the estimation of κρ,bg by no longer treating κρ,bg as a control variable. Using an observationally derived κρ, such as the de Lavergne et al. (2020) product, would make the estimation of other control variables less underdetermined, but this would not resolve the problem with a lack of time dependence of κρ,bg nor would it assuage potential problems with model drift. One potential solution to this is to use the de Lavergne et al. (2020) product for κρ,bg and use the Prandtl number as a control variable to help determine the vertical viscosities. This would help with the problem of neither the estimation of underdetermined parameters nor time dependence of κρ,bg, but it could help with numerical issues. Third, we could potentially circumvent the issue of unconstrained parameters in the biogeochemical modules. One potential way to do this is by including preformed oxygen – i.e., oxygen without any biological influence, making it a passive tracer – in the model's misfits instead of oxygen concentrations. Observationally derived transit-time distributions with a maximum entropy-based method from previous studies (e.g., Khatiwala et al., 2009; Zanna et al., 2019) or from a tracer-informed ocean state estimate (DeVries and Holzer, 2019) can help derive preformed oxygen from oxygen concentration observations. Fourth, we could optimize the information from existing oxygen observations with the purpose of constraining κρ. One way to do this is to run observing system experiments. A complementary approach that uses the effective proxy potential framework of Loose and Heimbach (2021) could also help indicate whether measurements of oxygen concentrations in particular locations are redundant or more informative of κρ than in other locations. We did not pursue this in the present study because our adjoint runs use a global misfit. If we perform an ensemble of adjoint sensitivity runs with a single observation in each run, then we could calculate the effective proxy potential at each of these observation locations. Lastly, the (imperfectly known) initial conditions of biogeochemical tracers will also need to be included in the input control vector during optimization of the ocean state estimate. If biogeochemical tracers are included in the misfit calculation in an optimization run, their impact on variables such as κρ would depend upon how they are weighted relative to the physical variables – e.g., temperature, salinity, and pressure. A more complete representation and understanding of κρ are possible through these analyses and methods.
A1 GEOS-5 and the GMAO S2S Ocean Analysis
To demonstrate a problem with κρ in a sequential data assimilation framework, we present example output from a reanalysis product and output from an identical ocean model hindcast without any data assimilation. GEOS-5 includes a global, finite-volume atmospheric general circulation model that is used for numerical weather prediction, seasonal to decadal forecasts, and as the background field for atmospheric reanalyses (Molod et al., 2015). The ocean is represented by the GFDL Modular Ocean Model (Griffies et al., 2015) version 5 (MOM5) and the Los Alamos Community Ice CodE sea ice model (Hunke et al., 2013) version 4.1 (CICE4.1). We use a configuration of the GEOS-5 modeling system with a 1∘ (0.5∘ at the Equator) resolution on a tripolar (Murray, 1996) staggered Arakawa B-grid (Mesinger and Arakawa, 1976) and 50 geopotential levels for MOM5, 2∘ resolution and 24 pressure levels for the atmospheric model, and 1∘ resolution and three layers for CICE4.1. Historical aerosols (sulfate, dust, and sea salt) and biomass burning emissions (black and organic carbon) updated from the Goddard Chemistry Aerosol Radiation and Transport (GOCART) model (Chin et al., 2002) are used over the time period 1992 through 2016. Initial conditions are based on a long spin-up that used MOM4 coupled to one version of the GEOS-5 atmosphere model (Molod et al., 2012) and hundreds of additional years of spin-up that used MOM4 coupled to a slightly different version of the GEOS-5 atmosphere model. The differences between the two versions of the GEOS-5 atmospheric model used in the two phases of spin-up include developments in cloud microphysics and atmospheric chemistry.
κρ, Redi coefficients, and Gent–McWilliams coefficients are determined in MOM5 as follows. κρ in MOM5 – κρ,GEOS5 hereafter – is represented by the K-Profile Parameterization (KPP; Large et al., 1994) and a parameterization for mixing due to internal tides (Simmons et al., 2004). Shear-driven mixing, gravitational instabilities that can cause vertical convection, and double-diffusive processes, which can cause the temperature diffusivity to be different from the salinity diffusivity, are accounted for in the interior (Large et al., 1994). The resulting κρ,GEOS5 field spatiotemporally varies. However, this combination of parameterizations does not make use of an explicit energy budget that accounts for conversion between kinetic and potential energy when determining κρ,GEOS5. The Redi coefficients (Redi, 1982) and Gent–McWilliams coefficients of the (Gent and McWilliams, 1990) parameterization for mesoscale eddies are, by default, prescribed to be 600 m2 s−1 everywhere, except for some variation in western boundary current regions for the Gent–McWilliams coefficients. The Redi coefficients and Gent–McWilliams coefficients are thus constant in time and in most locations. A mixed layer instability scheme for the submesoscale transport by Fox-Kemper et al. (2011) is used.
We use a reanalysis product, which uses the same underlying modeling system as the GEOS-5 coupled Earth system model, called the Global Modeling and Assimilation Office sub-seasonal to seasonal (GMAO S2S) Ocean Analysis. The output of the GMAO S2S Ocean Analysis highlights how κρ can behave due to the disruption of dynamical balance that can be the result of the use of a sequential data assimilation system (Stammer et al., 2016; Pilo et al., 2018). The GMAO S2S Ocean Analysis only assimilates hydrographic information to constrain κρ and relies on the same parameterizations as GEOS-5's ocean component to calculate κρ.
The NASA GMAO has recently updated their GEOS-5 sub-seasonal to seasonal forecast system (S2S-v2.1; https://gmao.gsfc.nasa.gov/cgi-bin/products/climateforecasts/geos5/S2S_2/index.cgi, last access: 23 August 2019). This new system is the current contribution of the GMAO to the North American Multi-Model project (http://www.cpc.ncep.noaa.gov/products/NMME/about.html, last access: 23 August 2019) and NOAA's experimental sub-seasonal ensemble project (http://cola.gmu.edu/kpegion/subx/index.html, last access: 23 August 2019). A configuration of the modeling system is used that is nominally 0.5∘ resolution on a tripolar (Murray, 1996) staggered Arakawa B-grid (Mesinger and Arakawa, 1976) with 40 geopotential levels for MOM5 as well as 0.5∘ resolution and five layers for CICE4.1 with atmospheric forcing from the MERRA-2 (Modern-Era Retrospective analysis for Research and Applications version 2) reanalysis (Gelaro et al., 2017). The GMAO S2S Ocean Analysis (Molod et al., 2020) is a reanalysis product that uses a system similar to the local ensemble transform Kalman filter (LETKF) data assimilation procedure described by Penny et al. (2013), but the background error is calculated offline using ensemble members of freely coupled simulations. The background error does not explicitly account for uncertainties in any of the ocean subgrid-scale transport or mixing parameters, as it is only a function of the observed and background temperatures and salinities. The temperature and salinity would change and so would the calculated covariances if the mixing parameterizations were changed, but each of the 21 background free-running simulations have the same mixing parameterization, as they only differ in their initialization.
The following datasets were used by the GMAO S2S data assimilation modeling system. A relaxation procedure, or update, is applied to the MERRA-2 sea surface temperatures and sea ice fraction from the NASA TEAM-2 product (Markus and Cavalieri, 2009) at a 5 d assimilation cycle. No ocean subgrid-scale transport or mixing parameter data are assimilated. Assimilated in situ observational data that provide temperatures and salinities come from TAO, PIRATA, RAMA, XBT, CTD, and Argo instruments. Satellite altimetry data that provide sea level anomalies come from TOPEX, ERS-1+2, Geosat FO, Jason-1, Jason-2, Jason-3, Envisat, Cryosat-2, Saral, HY-2A, and Sentinel 3A. The absolute dynamic topography is calculated as the sum of the sea level anomaly and the mean dynamic topography, which is estimated using GOCE and GRACE data, all available altimetry, and in situ data. Absolute dynamic topography data are assimilated into the model system using the same method as for the in situ data, except these data are thinned along-track and a Gaussian-weighted mean using a decorrelation scale of 1000 km is calculated prior to assimilation. In addition, the global trend was removed from the absolute dynamic topography before assimilation and zero net input of water was applied. Precipitation is corrected using the Global Precipitation Climatology Project version 2.1 (GPCPv2.1, provided by the NASA/Goddard Space Flight Center's Laboratory for Atmospheres, which calculates the dataset as a contribution to the GEWEX Global Precipitation Climatology Project) and Climate Prediction Center (CPC) Merged Analysis of Precipitation (CMAP, provided by the NOAA/OAR/ESRL PSD, Boulder, Colorado, USA, from their website at http://www.esrl.noaa.gov/psd/, last access: 22 April 2019), as described by Reichle et al. (2011) except for MERRA-2 instead of MERRA data. All other atmospheric forcing fields used in the construction of the reanalysis came from MERRA-2. The GMAO S2S modeling system is an update to the one described in Borovikov et al. (2019). As such, the model only ran for the period May 2012 to March 2019.
A2 Steric sea level budget framework
In order to examine whether the analysis increments can dynamically impact κρ, we analyze a model's buoyancy budget, which is broken down into heat and salt budgets and used to calculate the steric sea level budget. The tracer tendency equation terms required for the heat and salt budgets were computed online and saved as the reanalysis was running. The tracer equations can be broken down into individual contributions (Palter et al., 2014),
where is the material derivative, v is the resolved velocity field, v* is the eddy-induced or quasi-Stokes velocity field that represents parameterized motions, Θ is the potential temperature, S is the salinity, ρ is the locally referenced potential density, JΘ and JS are the parameterized along-isopycnal and diapycnal mixing fluxes associated with potential temperature and salinity, QΘ and QS are the sums of sources and sinks of potential temperature and salinity, and AΘ and AS are the analysis increments for potential temperature and salinity due to the assimilation of data by a sequential filter-based data assimilation ocean modeling system. The analysis increments in a sequential filter-based data assimilation system can obscure the physics, as AΘ and AS effectively correspond to unphysical, time-varying, three-dimensional fluxes of heat and salt.
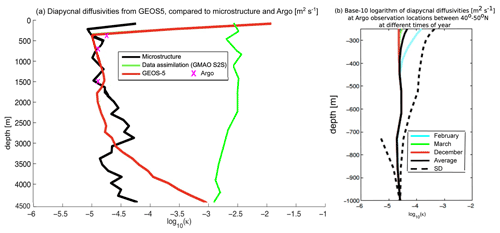
Figure A1κρ profiles (panel a; units in m2 s−1) averaged over the full-depth microstructure locations from the observations (black curve) presented in Waterhouse et al. (2014) (see their Fig. 6), the Whalen et al. (2015) Argo-derived product for three depth bins (magenta X marks), the temporally averaged output of a free-running coupled Earth system model simulation (GEOS-5 – red curve), and the temporally averaged output of an equivalent run with data assimilation (GMAO S2S – green curve). Also shown are (panel b) κρ profiles from the free-running GEOS-5 simulation averaged over 40–50∘ N in the North Atlantic Ocean and averaged over all January months (lighter colors) and all December months (darker colors). The base-10 logarithms of the geometric averages are shown in each panel.
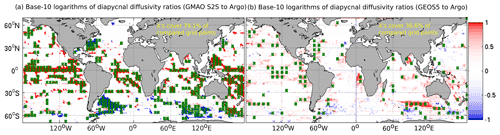
Figure A2Shown are (a) the base-10 logarithms of the ratios of the time-averaged κρ,GMAO to κρ,Argo and (b) the base-10 logarithms of the ratios of the time-averaged κρ,GEOS5 to κρ,Argo. Each panels shows an average over 250–2000 m depth. White areas in the ocean indicate insufficient Argo data to derive κρ,Argo. The green X marks indicate regions where the disagreement between κρ,GMAO or κρ,GEOS5 and κρ,Argo is greater than a factor of 3.
Figure A3Scatterplots between several of the most locally dominant tendency terms in the steric sea level budget of the GMAO S2S Ocean Analysis, averaged over the entire runtime period (2012–2017): shown are (panel a) the analysis increment (abscissa) versus the resolved advection (ordinate) terms, (panel b) the analysis increment (abscissa) versus the vertical diffusion (ordinate) terms, and (panel c) the surface flux (abscissa) versus the vertical diffusion (ordinate) terms. The more yellow colors indicate a greater density of dots in the scatterplots. The more blue colors indicate a lower density of dots in the scatterplots. Also listed in each panel are the correlations between each of the comparisons.
The heat and salt budget terms summarized by Eq. (A1) are computed as follows. The resolved, mesoscale, and submesoscale transports are accounted for in the material derivatives Θ and S, the neutral and diapycnal diffusion of Θ and S is accounted for by JΘ and JS, and the analysis increments of Θ and S are accounted for by AΘ and AS. The neutral diffusion term includes cabbeling, thermobaricity, and a dianeutral contribution that mixes properties by providing for the exponential transition to horizontal diffusion in regions of steep isoneutral slopes according to Treguier (1992) and Ferrari et al. (2008, 2010) where the surface boundary layer is encountered and following Gerdes et al. (1990) next to solid walls. The diapycnal diffusion term is not added to the vertical component of the along-isopycnal diffusion term but because of convention (e.g., Palter et al., 2014) is nevertheless referred to as the vertical diffusion term hereafter. The vertical diffusion term also includes penetrating shortwave radiation flux. The sources and sinks of Θ and S accounted for by QΘ and QS include nonlocal convection (the transport for which turbulent fluxes do not depend upon local gradients in Θ or S because buoyant water gets entrained into the mixed layer when the surface buoyancy forcing drives convection above a stratified water column), surface buoyancy fluxes (latent, sensible, shortwave, longwave, and frazil heat fluxes), precipitation minus evaporation, runoff mixing (mixes properties associated with river outflows); downslope mixing (mixes properties downslope to represent the overflow of dense waters from marginal seas), sigma diffusion (mixing properties along terrain-following coordinates in regions with partial bottom cells), numerical smoothing of the free surface (intended to reduce B-grid checkerboard noise), numerical sponge (intended to absorb the Kelvin waves set off by the assimilation of some data), calving of land ice, and frazil ice formation. The runoff mixing, downslope mixing, and sigma diffusion terms are considered sources or sinks here because they are associated with numerical schemes that aim to resolve problems created by coarse model resolution, the vertical coordinate system used near boundary layers, and imperfect bathymetry. There is no geothermal heating included in the GMAO S2S Ocean Analysis. The vertical diffusion term includes a subsurface shortwave heating contribution to a function of the κρ field, the mesoscale transport term assumes constant Gent–McWilliams coefficients, and the neutral diffusion term assumes constant Redi coefficients.
At each time step, the model evaluates a tendency term for every process that contributes to Eq. (A1) from their parameterized or dynamically calculated values, their units are converted to W m−2 and for Θ and S, and their monthly averages are saved to the output files used in this analysis. Implicit in these output tendency terms is that each term is weighted by the thicknesses of each layer as the model runs and writes the output to file. The heat and salt budget terms saved to file are used to calculate the steric sea level budget as follows. The steric sea level budget terms are computed by scaling the heat tendency terms by and the salt tendency terms by −1000β, where Cp (units in ) is the specific heat of seawater, (units in K−1) is the thermal expansion coefficient, and (units in kg g−1) is the haline contraction coefficient. In order to get a longitude–latitude map of the terms that depend upon depth shown here, we integrate over depth by summing over the depth dimension. We analyze part of the steric sea level budget of the GMAO S2S Ocean Analysis to examine the relationships between different terms.
B1 Assessments of κρ from models
First, we compare the average κρ,micro profile that is comprised of data from 24 campaigns (Waterhouse et al., 2014) (see their Fig. 6; black curve in Fig. A1a) with the average model-calculated κρ profiles and κρ,Argo. A geometric average is taken for each profile because a geometric average is more representative than an arithmetic average for a small sample size and when the data are not normally distributed (Manikandan, 2011), like the lognormal distribution of κρ (Whalen, 2021).
We compare microstructure (black curve in Fig. A1a) with GEOS-5 (red curve in Fig. A1a). κρ,GEOS5, on average, is in close agreement with microstructure over the upper 250–2000 m. On average, the disagreement with microstructure and Argo is approximately the same as the disagreement between microstructure and GEOS-5. All three κρ values are well within the uncertainty of the Argo product. The profiles are also within the temporal variability in κρ,GEOS5 below the mixed layer depths (Fig. A1b; also see Fig. 9 in Whalen et al., 2015). The temporal variability in κρ is only large near regions with active deep convection (e.g., between 40 and 50∘ N in the North Atlantic Ocean, as shown in Fig. A1b). The blue and green diamonds in Fig. 1c of Waterhouse et al. (2014) show that there are only a few microstructure profiles are within the 40–50∘ N band in the North Atlantic Ocean. These are all near the east coast of North America and not in regions that experience deep convection, so the temporal variability in microstructure is not expected to be large enough that the disagreements in κρ can be explain by temporal sampling and/or aliasing.
While the average κρ,GEOS5 profile is fairly accurate, particularly below 500 m depth (red curve in Fig. A1), κρ,GMAO is in much worse agreement with microstructure (green curves in Fig. A1). The large values of κρ,GMAO are not due to a few isolated locations. κρ,GMAO is too large below about 250 m depth (solid green curve in Fig. A1). The average profile of κρ,GMAO is generally constant or decreases with depth, as opposed to the average profiles of κρ,GEOS5 and microstructure, which generally increase with depth. Potential reasons for the large disagreements between κρ,GMAO and microstructure include dynamical adjustments due to the GMAO S2S Ocean Analysis increments, inconsistencies between the model's atmosphere and ocean due to the strong relaxation to sea surface temperatures, fixed zero net water input for global sea level, and numerics such as the techniques applied to damp the waves created from assimilating some observations.
B2 Model- vs. fine-scale parameterization-derived κρ comparisons
While comparisons with microstructure reveal general agreement with the average profile of κρ,GEOS5 – except near the surface and at deep depths – we also want to assess whether there are deficiencies in the average geographic distribution of κρ,GEOS5 by comparing the output of GEOS-5 with the κρ,Argo product. Comparing the κρ,GEOS5 field with the κρ,Argo product results in better agreement than the similar comparisons between κρ,GMAO and κρ,Argo. For example, κρ,GEOS5 only disagrees with κρ,Argo by more than a factor of 3 over 36.6 % of grid points with available data (Fig. A2b), while the disagreement doubles in percentage (79.1 %) for κρ,GMAO (Fig. A2a). The errors in κρ,GEOS5 are smaller than κρ,GMAO. Thus, when the objective of the GMAO S2S Ocean Analysis is to minimize the misfit between the model and observations of temperature, salinity, and some surface characteristics, κρ can be better represented without any observational constraints; i.e., the GMAO S2S Ocean Analysis improves temperature and salinity misfits for the wrong reasons.
The regions with the largest disagreement between κρ,GEOS5 and κρ,Argo are along the Equator, in the Southern Ocean, in the Labrador and Irminger seas, and in the Gulf Stream and Kuroshio extensions (Fig. A2b). Along the Equator the values of κρ,GEOS5 tend to be larger than the observational product, but the discrepancy changes sign slightly poleward in the tropics near the Equator. Inadequate resolution and parameterization of diapycnal mixing can cause too little mixing to occur in these regions as well as in the Southern Ocean and along mid-ocean ridges (MacKinnon et al., 2017). The values of κρ,GEOS5 are smaller than the observations both in regions where deep convection is prevalent and in the vicinity of the Antarctic Circumpolar Current (ACC). In the Gulf Stream Extension region, the Malvinas Current region, part of the Kuroshio Extension region, and the Indian Ocean sector of the ACC above 500 m depth, the values of κρ,GEOS5 are too large. This is because κρ,GEOS5 can be greatly increased inside the mixed layer depth, which can be deeper than 250 m due to vertical convection. One possible source of these errors in the abyssal κρ is the improper treatment of remote internal tide-induced mixing, discussed in Melet et al. (2016), but several other processes can impact κρ in the upper water column. For example, the wind-driven nearly inertial waves (Alford et al., 2016) can be important near the surface in many locations, and internal tide breaking is important near the seafloor at low latitudes in the Northern Hemisphere (Arbic et al., 2004; Nycander, 2005; Melet et al., 2013; MacKinnon et al., 2017) and beneath the ACC, where lee wave breaking is important (Nikurashin and Ferrari, 2011; Scott et al., 2011; Naveira Garabato et al., 2013; Melet et al., 2014; Wright et al., 2014; Trossman et al., 2013, 2016; Yang et al., 2018). MacKinnon et al. (2017) discuss other candidates for more accurate representation of κρ. Identifying the sources of errors in κρ,GEOS5, particularly in the abyss, is beyond the scope of the present study. We emphasize the much greater errors in κρ,GMAO and next examine whether the analysis increments could be one source of these larger errors (either directly or by way of altering the velocity field).
B3 Relationships between steric sea level budget terms
There are distortions in temperature and salinity fields from applying analysis increments, violating conservation principles and potentially causing the model to undergo baroclinic adjustment (Stammer et al., 2016). Thus, we examine whether the velocity field itself changes because of the analysis increments. To do this, we show the relationship between the analysis increments and resolved advection terms in the steric sea level budget for the GMAO S2S Ocean Analysis in Fig. A3a. The Pearson correlation coefficient between the analysis increments and resolved advection terms in the steric sea level budget is about −0.3. The magnitudes of the analysis increments are determined by the temperature, salinity, and sea surface height fields, and the analysis increments and the resolved advection term in the GMAO S2S Ocean Analysis are comparable in size for both heat and salt tendencies – the largest terms in each budget in their zonal averages at most latitudes. However, previous studies have shown that analysis increments induce changes in the velocity field via dynamic adjustment (Stammer et al., 2016; Pilo et al., 2018). The correlation between the analysis increments and resolved advection terms shown in Fig. A3a is consistent with the findings of these previous studies. The analysis increments, by a similar argument, could induce physically inconsistent air–sea exchanges through changing the temperature and salinity fields in the top model layer. We next show that these factors at least partially cause errors in κρ,GMAO. The Pearson correlation coefficients between the diapycnal diffusion terms and the analysis increment terms in the heat and salt budgets over all locations are about 0.7 (Fig. A3b), suggesting that the analysis increments are associated with errors in κρ,GMAO. Problems with the physical consistency of air–sea exchanges – due to relaxation of sea surface temperatures and requiring net zero water input – could also contribute to the errors in κρ,GMAO. However, it is possible that instead of the air–sea exchanges impacting the diapycnal diffusivities directly, the analysis increments affect both the air–sea exchanges and diapycnal diffusivities, as the changes in temperature and salinity at depth also change the mixed layer depths, which perturb the diapycnal diffusivity profiles and therefore their contribution to steric sea level through the altered thermal expansion and/or haline contraction coefficients. The surface flux and diapycnal diffusion terms in the heat and salt tendency budgets are fairly well-correlated with a Pearson correlation coefficient of about −0.4 (Fig. A3c), suggesting that there is an association between the surface flux errors and errors in κρ,GMAO. Given these correlations and the way analysis increments and physical inconsistencies of air–sea exchanges are implemented in the GMAO S2S Ocean Analysis, errors in κρ,GMAO must be caused by analysis increments (and possibly adjustments of air–sea exchanges) rather than the other way around.
The data used in this are available at https://doi.org/10.5281/zenodo.6576835 (Trossman et al., 2022). Also, the GMAO S2S Ocean Analysis output is available at ftp://gmaoftp.gsfc.nasa.gov/pub/data/kovach/S2S_OceanAnalysis/ (last access: 23 August 2019, Molod et al., 2012) thanks for Robin Kovach. The hydrography-derived diapycnal diffusivities from the fine-scale parameterization used in this study, courtesy of Eric Kunze, are available by logging in as a guest at ftp://ftp.nwra.com/outgoing/kunze/iwturb/ (Kunze, 2017). The microstructure data used in this study are available at https://microstructure.ucsd.edu/ (Waterhouse et al., 2014).
DST conceived of the idea, did the ECCO and GEOS-5 simulations, performed the analyses, and wrote up the paper. CW provided the Argo-derived data and helped with their use as well as the writing. TH helped with the interpretation of the results and the writing. AW provided the microstructure data and helped with their use as well as the writing. AN helped with the interpretation of the ECCO results and the writing. AB provided help with getting the adjoint to work with ECCO. PH provided help with getting the forward MITgcm runs set up correctly on the TACC machines. MM helped with the interpretation of the results and the writing.
The contact author has declared that neither they nor their co-authors have any competing interests.
Publisher's note: Copernicus Publications remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
The authors thank the reviewers of this paper for their suggestions. The authors acknowledge the Texas Advanced Computing Center (TACC) at the University of Texas at Austin for providing HPC resources for the ECCO simulations (URL: http://www.tacc.utexas.edu, last access: 10 March 2020) and the NASA Center for Climate Simulation (NCCS) for the computer time spent on the GEOS-5 simulations that contributed to the research results reported within this paper.
This research has been supported by the National Aeronautics and Space Administration, Earth Sciences Division (GESTAR cooperative agreement with Johns Hopkins University, grant no. 80NSSC17K0675, and ECCO project through JPL/CalTech subcontract), the National Oceanic and Atmospheric Administration, NOAA Research (grant no. NA15OAR4310172), and the National Science Foundation, Directorate for Geosciences (grant nos. OCE-1338814, OCE-0968721, OCE-1923558, OPP-1603903, and OPP-1708289).
This paper was edited by Ilker Fer and reviewed by three anonymous referees.
Abernathey, R. P. and Marshall, J.: Global surface eddy diffusivities derived from satellite altimetry, J. Geophys. Res.-Oceans, 118, 901–916, https://doi.org/10.1002/jgrc.20066, 2013. a
Adcroft, A. and Campin, J.-M.: Rescaled height coordinates for accurate representation of free-surface flows in ocean circulation models, Ocean Model., 7, 269–284, 2004. a
Adcroft, A., Hill, C., and Marshall, J.: The representation of topography by shaved cells in a height coordinate model, Mon. Weather Rev., 125, 2293–2315, 1997. a
Alford, M. H., MacKinnon, J. A., Simmons, H. L., and Nash, J. D.: Near-inertial internal gravity waves in the ocean, Annu. Rev. Mar. Sci., 8, 95–123, 2016. a
Arbic, B. K., Garner, S. T., Hallberg, R. W., and Simmons, H .L.: The accuracy of surface elevations in forward global barotropic and baroclinic tide models, Deep-Sea Res. Pt. II, 51, 3069–3101, https://doi.org/10.1016/j.dsr2.2004.09.014, 2004. a
Atamanchuk, D., Koelling, J., Send, U., and Wallace, D. W. R.: Rapid transfer of oxygen to the deep ocean mediated by bubbles, Nat. Geosci., 13, 232– 237, https://doi.org/10.1038/s41561-020-0532-2, 2020. a, b
Bachman, S. D., Fox-Kemper, B., and Bryan, F. O.: A diagnosis of anisotropic eddy diffusion from a high-resolution global ocean model, J. Adv. Model. Earth Sy., 12, e2019MS001904, https://doi.org/10.1029/2019MS001904, 2020. a
Bates, M., Tulloch, R., Marshall, J., and Ferrari, R.: Rationalizing the spatial distribution of mesoscale eddy diffusivity in terms of mixing length theory, J. Phys. Oceanogr., 44, 1523–1540, https://doi.org/10.1175/jpo-d-13-0130.1, 2014. a
Bigdeli, A., Loose, B., Nguyen, A. T., and Cole, S. T.: Numerical investigation of the Arctic ice–ocean boundary layer and implications for air–sea gas fluxes, Ocean Sci., 13, 61–75, https://doi.org/10.5194/os-13-61-2017, 2017. a
Billheimer, S. J., Talley, L. D., and Martz, T. R.: Oxygen seasonality, utilization rate, and impacts of vertical mixing in the eighteen degree water region of the sargasso sea as observed by profiling biogeochemical floats, Global Biogeochem. Cy., 35, e2020GB006824, https://doi.org/10.1029/2020GB006824, 2021. a
Borovikov, A., Cullather, R., Kovach, R., Marshak, J., Vernieres, G., Vikhliaev, Y., Zhao, B., and Li, Z.: GEOS-5 seasonal forecast system, Clim. Dynam., 53, 7335–7361, https://doi.org/10.1007/s00382-017-3835-2, 2019. a
Brandt, P., Bange, H. W., Banyte, D., Dengler, M., Didwischus, S.-H., Fischer, T., Greatbatch, R. J., Hahn, J., Kanzow, T., Karstensen, J., Körtzinger, A., Krahmann, G., Schmidtko, S., Stramma, L., Tanhua, T., and Visbeck, M.: On the role of circulation and mixing in the ventilation of oxygen minimum zones with a focus on the eastern tropical North Atlantic, Biogeosciences, 12, 489–512, https://doi.org/10.5194/bg-12-489-2015, 2015. a
Brandt, P., Hahn, J., Schmidtko, S., Tuchen, F. P., Kopte, R., Kiko, R., Bourlés, B., Czeschel, R., and Dengler, M.: Atlantic equatorial undercurrent intensification counteracts warming-induced deoxygenation, Nat. Geosci., 14, 278–282, https://doi.org/10.1038/s41561-021-00716-1, 2021. a
Busecke, J. J. M. and Abernathey, R. P.: Ocean mesoscale mixing linked to climate variability, Science Advances, 5, eaav5014, https://doi.org/10.1126/sciadv.aav5014, 2019. a
Campin, J.-M., Adcroft, A., Hill, C., and Marshall, J.: Conservation of properties in a free surface model, Ocean Model., 6, 221–244, 2004. a
Chaudhuri, A. H., Ponte, R. M., Forget, G., Heimbach, P.: A comparison of atmospheric reanalysis surface products over the ocean and implications for uncertainties in air-sea boundary forcing, J. Climate, 26, 153–170, 2013. a
Chin, M., Ginoux, P., Kinne, S., Holben, B. N., Duncan, B. N., Martin, R. V., Logan, J. A., Higurashi, A., and Nakajima, T.: Tropospheric aerosol optical thickness from the GOCART model and comparisons with satellite and sunphotometer measurements, J. Atmos. Sci., 59, 461–483, 2002. a
Cole, S. T., Wortham, C., Kunze, E., and Owens, W. B.: Eddy stirring and horizontal diffusivity from argo float observations: Geographic and depth variability, Geophys. Res. Lett., 42, 3989–3997, https://doi.org/10.1002/2015GL063827, 2015. a, b
Couespel, D., Lévy, M., and Bopp, L.: Major contribution of reduced upper ocean oxygen mixing to global ocean deoxygenation in an earth system model, Geophys. Res. Lett., 46, 12239–12249, https://doi.org/10.1029/2019GL084162, 2019. a
Dalan, F., Stone, P. H., and Sokolov, A. P.: Sensitivity of the ocean's climate to diapycnal diffusivity in an EMIC. Part II: Global warming scenario, J. Climate, 18, 2482–2496, 2005. a
Danabasoglu, G. and McWilliams, J. C.: Sensitivity of the global ocean circulation to parameterizations of mesoscale tracer transports, J. Climate, 8, 2967–2987, 1995. a
D'Asaro, E.: Turbulence in the upper-ocean mixed layer, Annu. Rev. Mar. Sci., 6, 101–115, https://doi.org/10.1146/annurev-marine-010213-135138, 2014. a
Dee, D. P., Uppala, S. M., Simmons, A. J., Berrisford, P., Poli, P., Kobayashi, S., Andrae, U., Balmaseda, M. A., Balsamo, G., Bauer, P., Bechtold, P., Beljaars, A. C. M., van de Berg, L., Bidlot, J., Bormann, N., Delsol, C., Dragani, R., Fuentes, M., Geer, A. J., Haimberger, L., Healy, S. B., Hersbach, H., Hólm, E. V., Isaksen, L., Kållberg, P., Köhler, M., Matricardi, M., McNally, A. P., Monge-Sanz, M., Morcrette, J.-J., Park, B.-K., Peubey, C., de Rosnay, P., Tavolato, C., Thépaut, J.-N., and Virtart, F.: The ERA-Interim reanalysis: configuration and performance of the data assimilation system, Q. J. Roy. Meteor. Soc., 137, 553–597, 2011. a
de Lavergne, C., Vic, C., Madec, G., Roquet, F., Waterhouse, A. F., Whalen, C. B., Cuypers, Y., Bouruet-Aubertot, P., Ferron, B., and Hibiya, T.: A parameterization of local and remote tidal mixing, J. Adv. Model. Earth Sy., 12, e2020MS002065, https://doi.org/10.1029/2020MS002065, 2020. a, b, c, d, e, f, g, h, i, j, k, l, m
DeVries, T. and Holzer, M.: Radiocarbon and helium isotope constraints on deep ocean ventilation and mantle-3He sources, J. Geophys. Res.-Oceans, 124, 3036–3057, https://doi.org/10.1029/2018JC014716, 2019. a
Duteil, O. and Oschlies, A.: Sensitivity of simulated extent and future evolution of marine suboxia to mixing intensity, Geophys. Res. Lett., 38, L06607, https://doi.org/10.1029/2011GL046877, 2011. a
Ehlert, D., Zickfeld, K., Eby, M., and Gillett, N.: The sensitivity of the proportionality between temperature change and cumulative CO2 emissions to ocean mixing, J. Climate, 30, 2921–2935, 2017. a
Ferrari, R., McWilliams, J. C., Canuto, V. M., and Dubovikov, M.: Parameterization of eddy fluxes near oceanic boundaries, J. Climate, 21, 2770–2789, 2008. a
Ferrari, R., Griffies, S. M., Nurser, A. J. G., and Vallis, G. K.: A boundary-value problem for the parameterized mesoscale eddy transport, Ocean Model., 32, 143–156, 2010. a
Forget, G., Campin, J.-M., Heimbach, P., Hill, C. N., Ponte, R. M., and Wunsch, C.: ECCO version 4: an integrated framework for non-linear inverse modeling and global ocean state estimation, Geosci. Model Dev., 8, 3071–3104, https://doi.org/10.5194/gmd-8-3071-2015, 2015a. a, b, c, d
Forget, G., Ferreira, D., and Liang, X.: On the observability of turbulent transport rates by Argo: supporting evidence from an inversion experiment, Ocean Sci., 11, 839–853, https://doi.org/10.5194/os-11-839-2015, 2015b. a, b, c
Fox-Kemper, B., Danabasoglu, G., Ferrari, R., Griffies, S. M., Hallberg, R. W., Holland, M. M., Maltrud, M. E., Peacock, S., and Samuels, B. L.: Parameterization of mixed layer eddies. III: Implementation and impact in global ocean climate simulations, Ocean Model., 39, 61–78, 2011. a
Fukumori, I., Wang, O., Fenty, I., Forget, G., Heimbach, P., and Ponte, R. M.: ECCO version 4 release 3, DSpace MIT, http://hdl.handle.net/1721.1/110380, last access: 10 March 2017. a, b, c, d
Galbraith, E. D., Dunne, J. P., Gnanadesikan, A., Slater, R. D., Sarmiento, J. L., Dufour, C. O., de Souza, G. F., Bianchi, D., Claret, M., Rodgers, K. B., and Marvasti, S. S.: Complex functionality with minimal computation: Promise and pitfalls of reduced-tracer ocean biogeochemistry models, J. Adv. Model. Earth Sy., 7, 2012–2028, https://doi.org/10.1002/2015MS000463, 2015. a, b
Garcia, H. E., Boyer, T. P., Locarnini, R. A., Antonov, J. I., Mishonov, A. V., Baranova, O. K., Zweng, M. M., Reagan, J. R., Johnson, D. R., and Levitus, S.: World ocean atlas 2013, Vol. 3, Dissolved oxygen, apparent oxygen utilization, and oxygen saturation, NOAA Atlas NESDIS 75, https://doi.org/10.7289/V55X26VD, 2013.
Gaspar, P., Grégoris, Y., and LeFevre, J.-M.:. A simple eddy kinetic energy model for simulations of the oceanic vertical mixing: tests at station papa and long-term upper ocean study site, J. Geophys. Res., 95, 16179–16193, 1990. a, b, c
Gelaro, R., McCarty, W., Suárez, M. J., Todling, R., Molod, A., Takacs, L., Randles, C. A., Darmenov, A., Bosilovich, M. G., Reichle, R., Wargan, K., Coy, L., Cullather, R., Draper, C., Akella, S., Buchard, V., Conaty, A., da Silva, A. M., Gu, W., Kim, G. K., Koster, R., Lucchesi, R., Merkova, D., Nielsen, J. E., Partyka, G., Pawson, S., Putman, W., Rienecker, M., Schubert, S. D., Sienkiewicz, M., and Zhao, B.: The modern-era retrospective analysis for research and applications, version 2 (MERRA-2), J. Climate, 30, 5419–5454, https://doi.org/10.1175/JCLI-D-16-0758.1, 2017. a
Gent, P. R. and McWilliams, J. C.: Isopycnal mixing in ocean circulation models, J. Phys. Oceanogr., 20, 150–155, https://doi.org/10.1175/1520-0485(1990)020<0150:IMIOCM>2.0.CO;2, 1990. a, b, c
Gerdes, R., Köberle, C., and Willebrand, J.: The influence of numerical advection schemes on the results of ocean general circulation models, Clim. Dynam., 5, 211–226, 1990. a
Giering, R. and Kaminski, T.: Recipes for adjoint code construction, ACM T. Math. Software, 24, 437–474, 1998. a
Gilbert, J. C. and Lemarechal, C.: Some numerical experiments with variable-storage quasi-newton algorithms, Math. Program., 45, 407–435, 1989. a
Gnanadesikan, A.: A simple predictive model for the structure of the oceanic pycnocline, Science, 283, 2077, 1999. a
Gnanadesikan, A., Pradal, M.-A., and Abernathey, R.: Isopycnal mixing by mesoscale eddies significantly impacts oceanic anthropogenic carbon uptake, Geophys. Res. Lett., 42, 4249–4255, https://doi.org/10.1002/2015GL064100, 2015. a
Gregg, M. C.: Diapycnal mixing in the thermocline: A review, J. Geophys. Res., 92, 5249–5286, https://doi.org/10.1029/JC092iC05p05249, 1987. a
Gregg, M. C.: Scaling turbulent dissipation in the thermocline, J. Geophys. Res., 94, 9686–9698, 1989. a, b
Gregg, M. C., D'Asaro, E. A., Riley, J. J., and Kunze, E.: Mixing efficiency in the ocean, Annu. Rev. Mar. Sci., 10, 443–473, 2018. a, b
Griewank, A.: Achieving logarithmic growth of temporal and spatial complexity in reverse automatic differentiation, Optim. Method. Softw., 1, 35–54, https://doi.org/10.1080/10556789208805505, 1992. a
Griffies, S. M., Winton, M., Anderson, W. G., Benson, R., Delworth, T. L., Dufour, C. O., Dunne, J. P., Goddard, P., Morrison, A. K., Rosati, A., Wittenberg, A. T., Yin, J., and Zhang, R.: Impacts on ocean heat from transient mesoscale eddies in a hierarchy of climate models, J. Climate, 28, 952–977, 2015. a
Groeskamp, S., Sloyan, B. M., Zika, J. D., and McDougall, T. J.: Mixing inferred from an ocean climatology and surface fluxes, J. Phys. Oceanogr., 47, 667–687, https://doi.org/10.1175/jpo-d-16-0125.1, 2017. a, b
Groeskamp, S., LaCasce, J. H., McDougall, T. J., Rogé, M.: Full-depth global estimates of ocean mesoscale eddy mixing from observations and theory, Geophys. Res. Lett., 47, e2020GL089425. https://doi.org/10.1029/2020GL089425, 2020. a, b
Heimbach, P., Menemenlis, D., Losch, M., Campin, J.-M., and Hill, C.: On the formulation of sea-ice models. Part 2: Lessons from multi-year adjoint sea ice export sensitivities through the Canadian Arctic archipelago, Ocean Model., 33, 145–158, https://doi.org/10.1016/j.ocemod.2010.02.002, 2010. a
Heimbach, P., Fukumori, I., Hill, C. N., Ponte, R. M., Stammer, D., Wunsch, C., Campin, J.-M., Cornuelle, B., Fenty, I., Forget, G., Köhl, A., Mazloff, M., Menemenlis, D., Nguyen, A. T., Piecuch, C., Trossman, D., Verdy, A., Wang, O., and Zhang, H.: Putting it all together: Adding value to the global ocean and climate observing systems with complete self-consistent ocean state and parameter estimates, Frontiers in Marine Science, 6, 55, https://doi.org/10.3389/fmars.2019.00055, 2019. a
Henyey, F. S., Wright, J., and Flatté, S. M.: Energy and action flow through the internal wave field: an Eikonal approach, J. Geophys. Res., 91, 8487–8495, 1986. a
Hieronymus, M., Nycander, J., Nilsson, J., Döös, K., and Hallberg, R.: Oceanic overturning and heat transport: the role of background diffusivity, J. Climate, 32, 701–716, 2019. a
Holmes, R. M., Zika, J. D., Griffies, S. M., Hogg, A. M., Kiss, A. E., and England, M. H.: The geography of numerical mixing in a suite of global ocean models, J. Adv. Model. Earth Sy., 13, e2020MS002333, https://doi.org/10.1029/2020MS002333, 2021. a
Holzer, M., DeVries, T., and de Lavergne, C.: Diffusion controls the ventilation of a Pacific Shadow Zone above abyssal overturning, Nat. Commun., 12, 4348, https://doi.org/10.1038/s41467-021-24648-x, 2021. a
Hunke, E. C., Lipscomb, W. H., Turner, A. K., Jeffery, N., and Elliott, S.: CICE: the Los Alamos sea ice model documentation and software user's manual version 5.0, Los Alamos National Laboratory, LA-CC-06-012, 2013. a
Ito, T., Takano, Y., Deutsch, C., and Long, M. C.: Sensitivity of global ocean deoxygenation to vertical and isopycnal mixing in an ocean biogeochemistry model, Global Biogeochem. Cy., 36, e2021GB007151, https://doi.org/10.1029/2021GB007151, 2022. a
Jenkins, W. J.: 3H and 3He in the Beta triangle: observations of gyre ventilation and oxygen utilization rates, J. Phys. Oceanogr., 27, 763–783, 1987. a
Katsumata, K.: Eddies observed by Argo floats. Part I: Eddy transport in the upper 1000 dbar, J. Phys. Oceanogr., 46, 3471–3486, https://doi.org/10.1175/JPO-D-16-0150.1, 2016. a, b, c
Khatiwala, S., Primeau, F., and Hall, T. M.: Reconstruction of the history of anthropogenic CO2 concentrations in the ocean, Nature, 462, 346–349, https://doi.org/10.1038/nature08526, 2009. a
Krasting, J., Stouffer, R., Griffies, S., Hallberg, R., Malyshev, S., Samuels, B., and Sentman, L.: Role of ocean model formulation in climate response uncertainty, J. Climate, 31, 9313–9332, 2018. a
Kunze, E.: Internal-wave-driven mixing: Global geography and budgets, J. Phys. Oceanogr., 47, 1325–1345, 2017 (data available at: ftp://ftp.nwra.com/outgoing/kunze/iwturb/, last access: 20 August 2019). a, b, c, d, e, f
Large, W. G. and Yeager, S. G.: The global climatology of an interannually varying air-sea flux data set, Clim. Dynam., 33, 341–364, 2009. a
Large, W. G., McWilliams, J. C., and Doney, S. C.: Oceanic vertical mixing: a review and a model with a nonlocal boundary layer parameterization, Rev. Geophys., 32, 363–403, 1994. a, b, c
Ledwell, J. R. and Watson, A. J.: The Santa Monica basin tracer experiment: A study of diapycnal and isopycnal mixing, J. Geophys. Res., 96, 8695–8718, https://doi.org/10.1029/91JC00102, 1991. a
Lévy, M., Resplandy, L., Palter, J. B., Couespel, D., and Lachkar, Z.: The crucial contribution of mixing to present and future ocean oxygen distribution, in: Ocean Mixing, edited by: Naveira Garabato, A. C. and Meredith, M. P., Elsevier, https://doi.org/10.1016/B978-0-12-821512-8.00020-7, 2021. a
Liu, C., Kohl, A., and Stammer, D.: Adjoint-based estimation of eddy-induced tracer mixing parameters in the global ocean, J. Phys. Oceanogr., 42, 1186–1206, 2012. a
Loose, N. and Heimbach, P.: Leveraging uncertainty quantification to design ocean climate observing systems, J. Adv. Model. Earth Sy., 13, e2020MS002386, https://doi.org/10.1029/2020MS002386, 2021. a
Losch, M., Menemenlis, D., Campin, J.-M., Heimbach, P., and Hill, C.: On the formulation of sea-ice models. Part 1: Effects of different solver implementations and parameterizations, Ocean Model., 33, 129–144, https://doi.org/10.1016/j.ocemod.2009.12.008, 2010. a
Lueck, R. G., Huang, D., Newman, D., and Box, J.: Turbulence measurement with a moored instrument, J. Atmos. Ocean. Tech., 14, 143–161, https://doi.org/10.1175/1520-0426(1997)014<0143:TMWAMI>2.0.CO;2, 1997. a
MacKinnon, J., Zhao, Z., Whalen, C. B., Waterhouse, A. F., Trossman, D. S., Sun, O. M., St. Laurent, L. C., Simmons, H. L., Polzin, K., Pinkel, R., Pickering, A., Norton, N. J., Nash, J. D., Musgrave, R., Merchant, L. M., Melet, A. V., Mater, B., Legg, S., Large, W. G., Kunze, E., Klymak, J. M., Jochum, M., Jayne, S. R., Hallberg, R. W., Griffies, S. M., Diggs, S., Danabasoglu, G., Chassignet, E. P. Buijsman, M. C., Bryan, F. O., Briegleb, B. P., Barna, A., Arbic, B. K., Ansong, J. K., and Alford, M. H.: Climate process team on internal-wave driven ocean mixing, B. Am. Meteorol. Soc., 98, 2429–2454, https://doi.org/10.1175/BAMS-D-16-0030.1, 2017. a, b, c, d
Manikandan, S.: Measures of central tendency: The mean, Journal of Phamacol. Pharmacother., 2, 140–142, 2011. a, b
Markus, T. and Cavalieri, D. J.: The AMSR-E NT2 sea ice concentration algorithm: its basis and implementation, Journal of The Remote Sensing Society of Japan, 29, 216–225, https://doi.org/10.11440/rssj.29.216, 2009. a
Marshall, J. and Speer, K.: Closure of the meridional overturning circulation through Southern Ocean upwelling, Nat. Geosci, 5, 171–180, https://doi.org/10.1038/ngeo1391, 2012.
Masuda, S. and Osafune, S.: Ocean state estimations for synthesis of ocean-mixing observations, J. Oceanogr., 77, 359–366, https://doi.org/10.1007/s10872-020-00587-x, 2021. a
Mecking, S., Warner, M. J., Greene, C. E., Hautala, S. L., and Sonnerup, R. E.: Influence of mixing on CFC uptake and CFC ages in the North Pacific thermocline, J. Geophys. Res., 109, C07014, https://doi.org/10.1029/2003JC001988, 2004. a
Melet, A., Nikurashin, M., Muller, C., Falahat, S., Nycander, J., Timko, P. G., Arbic, B. K., and Goff, J. A.: Internal tide generation by abyssal hills using analytical theory, J. Geophys. Res.-Oceans, 118, 6303–6318, 2013. a
Melet, A., Hallberg, R., Legg, S., and Nikurashin, M.: Sensitivity of the ocean state to lee wave-driven mixing, J. Phys. Oceanogr., 44, 900–921, 2014. a
Melet, A., Legg, S., and Hallberg, R.: Climatic impacts of parameterized local and remote tidal mixing, J. Climate, 29, 3473–3500, https://doi.org/10.1175/JCLI-D-15-0153.1, 2016. a
Menemenlis, D., Fukumori, I., and Lee, T.: Using Green's functions to calibrate and ocean general circulation model, Mon. Weather Rev., 133, 1224–1240, https://doi.org/10.1175/MWR2912.1, 2005. a
Mesinger, F. and Arakawa, A.: Numerical methods used in atmospheric models, WMO/ICSU Joint Organizing Committee, GARP Publ. Series, 64, 1976. a, b
Messias, M.-J., Watson, A. J., Johannessen, T., Oliver, K. I. C., Olsson, K. A., Fogelqvist, E., Olafsson, J., Bacon, S., Balle, J., Bergman, N., Budéus, G., Danielsen, M., Gascard, J.-C., Jeansson, E., Olafsdottir, S. R., Simonsen, K., Tanhua, T., Van Scoy, K., and Ledwell, J. R.: The Greenland sea tracer experiment 1996–2002: Horizontal mixing and transport of Greenland sea intermediate water, Prog. Oceanogr., 78, 85–105, https://doi.org/10.1016/j.pocean.2007.06.005, 2008. a
Molod, A., Takacs, L., Suarez, M., Bacmeister, J., Song, I. S., and Eichmann, A.: The GEOS-5 atmospheric general circulation model: Mean climate and development from MERRA to Fortuna, Technical Report Series on Global Modeling and Data Assimilation, 28, NASA/TM-2012-104606-VOL-28, 2012 (data available at: ftp://gmaoftp.gsfc.nasa.gov/pub/data/kovach/S2S_OceanAnalysis/, last access: 23 August 2019). a, b
Molod, A., Takacs, L., Suarez, M., and Bacmeister, J.: Development of the GEOS-5 atmospheric general circulation model: evolution from MERRA to MERRA2, Geosci. Model Dev., 8, 1339–1356, https://doi.org/10.5194/gmd-8-1339-2015, 2015. a
Molod, A., Hackert, E., Vikhliaev, Y., Zhao, B., Barahona, D., Vernieres, G., Borovikov, A., Kovach, R. M., Marshak, J., Schubert, S., Li, Z., Lim, Y.-K., Andrews, L. C., Cullather, R., Koster, R., Achuthavarier, D., Carton J., Coy, L., Friere, J. L. M., Longo, K. M., Nakada, K., and Pawson, S.: GEOS-S2S version 2: The GMAO high-resolution coupled model and assimilation system for seasonal prediction, J. Geophys. Res.-Atmos., 125, e2019JD031767, https://doi.org/10.1029/2019JD031767, 2020. a
Moum, J. N., Caldwell, D. R., Nash, J. D., and Gunderson, G. D.: Observations of boundary mixing over the continental slope, J. Phys. Oceanogr., 32, 2113–2130, https://doi.org/10.1175/1520-0485(2002)032<2113:OOBMOT>2.0.CO;2, 2002. a
Munk, W. and Wunsch, C.: Abyssal recipes II: Energetics of tidal and wind mixing, Deep-Sea Res. Pt. I, 45, 1977–2010, 1998. a
Murray, R. J.: Explicit generation of orthogonal grids for ocean models, J. Comput. Phys., 126, 251–273, 1996. a, b
Naveira Garabato, A. C., Nurser, A. G., Scott, R. B., and Goff, J. A.: The impact of small-scale topography on the dynamical balance of the ocean, J. Phys. Oceanogr., 43, 647–668, 2013. a
Nikurashin, M. and Ferrari, R.: Global energy conversion rate from geostrophic flows into internal lee waves in the deep ocean, Geophys. Res. Lett., 38, L08610, https://doi.org/10.1029/2011GL046576, 2011. a
Nocedal, J.: Updating quasi-newton matrices with limited storage, Math. Comput., 35, 773–782, 1980. a
Nycander, J.: Generation of internal waves in the deep ocean by tides, J. Geophys. Res., 110, C10028, https://doi.org/10.1029/2004JC002487, 2005. a
Osborn, T. R.: Estimates of the local rate of vertical diffusion from dissipation measurements, J. Phys. Oceanogr., 10, 83–89, 1980. a, b, c, d
Palter, J. B. and Trossman, D. S.: The sensitivity of future ocean oxygen to changes in ocean circulation, Global Biogeochem. Cy., 32, 738–751, https://doi.org/10.1002/2017GB005777, 2018. a, b
Palter, J. B., Griffies, S. M., Galbraith, E. D., Gnanadesikan, A., Samuels, B., and Klocker, A.: The driving processes of the deep ocean buoyancy budget and their temporal variability, J. Climate, 27, 551–573, 2014. a, b
Penny, S. G., Kalnay, E., Carton, J. A., Hunt, B. R., Ide, K., Miyoshi, T., and Chepurin, G. A.: The local ensemble transform Kalman filter and the running-in-place algorithm applied to a global ocean general circulation model, Nonlin. Processes Geophys., 20, 1031–1046, https://doi.org/10.5194/npg-20-1031-2013, 2013. a
Piecuch, C. G. and Ponte, R. M.: Mechanisms of interannual steric sea level variability, Geophys. Res. Lett., 38, L15605, https://doi.org/10.1029/2011GL048440, 2011. a
Pilo, G. S., Oke, P. R., Coleman, R., Rykova, T., and Ridgway, K.: Impact of data assimilation on vertical velocities in an eddy resolving ocean model, Ocean Model., 131, 71–85, 2018. a, b
Polzin, K. L., Toole, J. M., and Schmitt, R. W.: Finescale parameterizations of turbulent dissipation, J. Phys. Oceanogr., 25, 306–328, 1995. a
Polzin, K. L., Toole, J. M., Ledwell, J. R., and Schmitt, R. W.: Spatial variability of turbulent mixing in the abyssal ocean, Science, 276, 93–96, https://doi.org/10.1126/science.276.5309.93, 1997. a
Polzin, K. L., Naveira Garabato, A. C., Huussen, T. N., Sloyan, B. N., and Waterman, S.: Finescale parameterizations of turbulent dissipation, J. Geophys. Res.-Oceans, 119, 1383–1419, https://doi.org/10.1002/2013JC008979, 2014. a, b, c
Redi, M. H.: Oceanic isopycnal mixing by coordinate rotation, J. Phys. Oceanogr., 12, 1154–1158, 1982. a, b, c
Reichl, B. G. and Hallberg, R.: A simplified energetics based planetary boundary layer (ePBL) approach for ocean climate simulations, Ocean Model., 132, 112–129, https://doi.org/10.1016/j.ocemod.2018.10.004, 2018. a
Reichle, R., Koster, R., De Lannoy, G., Forman, B., Liu, Q., Mahanama, S., and Touré, A.: Assessment and enhancement of MERRA land surface hydrology estimates, J. Climate, 24, 6322–6338, https://doi.org/10.1175/JCLI-D-10-05033.1, 2011. a
Roach, C. J., Balwada, D., and Speer, K.: Global observations of horizontal mixing from Argo float and surface drifter trajectories, J. Geophys. Res.-Oceans, 123, 4560–4575, https://doi.org/10.1029/2018JC013750, 2018. a
Scott, J. R. and Marotzke, J.: The location of diapycnal mixing and the meridional overturning circulation, J. Phys. Oceanogr., 32, 3578–3595, 2002. a
Scott, R. B., Goff, J. A., Naveira-Garabato, A. C., and Nurser, A. J. G.: Global rate and spectral characteristics of internal gravity wave generation by geostrophic flow over topography, J. Geophys. Res.-Oceans, 116, C09029, https://doi.org/10.1029/2011JC007005, 2011. a
Shao, A. E., Mecking, S., Thompson, L., and Sonnerup, R. E.: Evaluating the use of 1-D transit time distributions to infer the mean state and variability of oceanic ventilation, J. Geophys. Res.-Oceans, 121, 6650–6670, https://doi.org/10.1002/2016JC011900, 2016. a
Simmons, H. L., Jayne, S. R., St. Laurent, L. C., and Weaver, A. J.: Tidally driven mixing in a numerical model of the general circulation, Ocean Model., 6, 245–263, 2004. a
Sinha, B., Sévellec, F., Robson, J., and Nurser, G.: Surging of global surface temperature due to decadal legacy of ocean heat uptake, J. Climate, 33, 8025–8045, https://doi.org/10.1175/JCLI-D-19-0874.1, 2020. a
Stammer, D., Wunsch, C., Giering, R., Eckert, C., Heimbach, P., Marotzke, J., Adcroft, A., Hill, C. N., and Marshall, J.: Global ocean circulation during 1992–1997, estimated from ocean observations and a general circulation model, J. Geophys. Res., 107, 3118, https://doi.org/10.1029/2001JC000888, 2002. a
Stammer, D., Balmaseda, M., Heimbach, P., Köhl, A., and Weaver, A.: Ocean data assimilation in support of climate applications: status and perspectives, Annu. Rev. Mar. Sci., 8, 491–518, https://doi.org/10.1146/annurev-marine-122414-034113, 2016. a, b, c, d
St. Laurent, L. and Schmitt, R.: The contribution of salt fingers to vertical mixing in the north Atlantic tracer release experiment, J. Phys. Oceanogr., 29, 1404–1424, 1999. a
Talley, L. D.: Closure of the global overturning circulation through the Indian, Pacific, and Southern Oceans: Schematics and transports, Oceanography, 26, 80–97, https://doi.org/10.5670/oceanog.2013.07, 2013. a
Thorpe, S.: In An introduction to ocean turbulence, Cambridge University Press, https://doi.org/10.1017/CBO9780511801198, 2007. a
Treguier, A. M.: Kinetic energy analysis of an eddy resolving, primitive equation model of the North Atlantic, J. Geophys. Res., 97, 687–701, 1992. a
Trossman, D. S., Arbic, B. K., Garner, S. T., Goff, J. A., Jayne, S. R., Metzger, E. J., and Wallcraft, A. J.: Impact of parameterized lee wave drag on the energy budget of an eddying global ocean model, Ocean Model., 72, 119–142, 2013. a
Trossman, D. S., Thompson, L., Mecking, S., Warner, M. J., Bryan, F., and Peacock, S.: Evaluation of oceanic transport parameters using transient tracers from observations and model output, Ocean Model., 74, 1–21, 2014. a
Trossman, D. S., Arbic, B. K., Richman, J. G., Garner, S. T., Jayne, S. R., and Wallcraft, A. J.: Impact of topographic internal lee wave drag on an eddying global ocean model, Ocean Model., 97, 109–128, 2016. a
Trossman, D. S., Whalen, C., Haine, T. W. N., Waterhouse, A. F., Bigdeli, A., Nguyen, A. T., Mazloff, M., and Heimbach, P.: Tracer and Observationally-Derived Constraints on Diapycnal Diffusivities in an Ocean State Estimate, Zenodo [data set], https://doi.org/10.5281/zenodo.6576835, 2022. a
Verdy, A. and Mazloff, M. R.: A data assimilating model for estimating Southern Ocean biogeochemistry, J. Geophys. Res.-Oceans, 122, 6968–6988, https://doi.org/10.1002/2016JC012650, 2017. a, b
Waterhouse, A. F., MacKinnon, J. A., Nash, J. D., Alford, M. H., Kunze, E., Simmons, H. L., Polzin, K. L., St. Laurent, L. C., Sun, O. M., Pinkel, R., Talley, L. D., Whalen, C. B., Huussen, T. N., Carter, G. S., Fer, I., Waterman, S., Naveira Garabato, A. C., Sanford, T. B., and Lee, C. M.: Global patterns of diapycnal mixing from measurements of the turbulent dissipation rate, J. Phys. Oceanogr., 44, 1854–1872, 2014 (data available at: https://microstructure.ucsd.edu/, last access: 19 August 2019). a, b, c, d, e, f, g, h, i, j, k, l
Waugh, D. W., Hall, T. M., and Haine, T. W. N.: Relationships among tracer ages, J. Geophys. Res., 108, 3138, https://doi.org/10.1029/2002JC001325, 2003. a
Weaver, A. T. and Courtier, P.: Correlation modeling on a sphere using a generalized diffusion equation, Q. J. Roy. Meteor. Soc., 127, 1815–1846, 2001. a
Whalen, C. B.: Best Practices for Comparing Ocean Turbulence Measurements across Spatiotemporal Scales, J. Atmos. Ocean. Tech., 38, 837–841, 2021. a, b
Whalen, C. B., MacKinnon, J. A., Talley, L. D., and Waterhouse, A. F.: Estimating the mean diapycnal mixing using a finescale strain parameterization, J. Phys. Oceanogr., 45, 1174–1188, 2015. a, b, c, d, e, f, g, h, i, j, k, l, m, n, o, p, q, r, s
Whalen, C. B., de Lavergne, C., Naveira Garabato, A. C., Klymak, J. M., MacKinnon, J. A., and Sheen, K. L.: Internal wave-driven mixing: governing processes and consequences for climate, Nature Reviews Earth and Environment, 1, 606–621, https://doi.org/10.1038/s43017-020-0097-z, 2020. a
Wright, C. J., Scott, R. B., Ailliot, P., and Furnival, D.: Lee wave generation rates in the deep ocean, Geophys. Res. Lett., 41, 2434–2440, https://doi.org/10.1002/2013GL059087, 2014. a
Wunsch, C.: In The ocean circulation inverse problem, Cambridge University Press, https://doi.org/10.1017/CBO9780511629570, 2006. a
Wunsch, C. and Heimbach, P.: Practical global oceanic state estimation, Physica D, 230, 197–208, https://doi.org/10.1016/j.physd.2006.09.040, 2007. a
Yang, L., Nikurashin, M., Hogg, A. M., and Sloyan, B. M.: Energy loss from transient eddies due to lee wave generation in the Southern Ocean, J. Phys. Oceanogr., 48, 2867–2885, 2018. a
Zanna, L., Khatiwala, S., Gregory, J. M., Ison, J., and Heimbach, P.: Global reconstruction of historical ocean heat storage and transport, P. Natl. Acad. Sci. USA, 116, 1126–1131, https://doi.org/10.1073/pnas.1808838115, 2019. a
- Abstract
- Introduction
- Methods
- Results
- Discussion and concluding remarks
- Appendix A: Model with a sequential data assimilation framework
- Appendix B: Results for the sequential data assimilation framework
- Data availability
- Author contributions
- Competing interests
- Disclaimer
- Acknowledgements
- Financial support
- Review statement
- References
- Abstract
- Introduction
- Methods
- Results
- Discussion and concluding remarks
- Appendix A: Model with a sequential data assimilation framework
- Appendix B: Results for the sequential data assimilation framework
- Data availability
- Author contributions
- Competing interests
- Disclaimer
- Acknowledgements
- Financial support
- Review statement
- References





