Net community production in the northwestern Mediterranean Sea from glider and buoy measurements

The Mediterranean Sea comprises just 0.8 % of the global oceanic surface, yet considering its size, it is regarded as a disproportionately large sink for anthropogenic carbon due to its physical and biogeochemical characteristics. An underwater glider mission was carried out in March–April 2016 close to the BOUSSOLE and DyFAMed time series moorings in the northwestern Mediterranean Sea. The glider deployment served as a test of a prototype ion-sensitive field-effect transistor pH sensor. Dissolved oxygen (O₂) concentrations and optical backscatter were also observed by the glider and increased between 19 March and 1 April, along with pH. These changes indicated the start of a phytoplankton spring bloom, following a period of intense mixing. Concurrent measurements of CO₂ fugacity and O₂ concentrations at the BOUSSOLE mooring buoy showed fluctuations, in qualitative agreement with the pattern of glider measurements. Mean net community production rates (N) were estimated from glider and buoy measurements of dissolved O₂ and inorganic carbon (DIC) concentrations, based on their mass budgets. Glider and buoy DIC concentrations were derived from a salinity-based total alkalinity parameterisation, glider pH and buoy CO₂ fugacity. The spatial coverage of glider data allowed the calculation of advective O₂ and DIC fluxes. Mean N estimates for the euphotic zone between 10 March and 3 April were ($-\mathrm{17}\pm \mathrm{36}$) for glider O₂, (44±94) for glider DIC, (17±37) for buoy O₂ and (49±86) $\mathrm{mmol}{\mathrm{m}}^{-\mathrm{2}}{\mathrm{d}}^{-\mathrm{1}}$ for buoy DIC, all indicating net metabolic balance over these 25 d. However, these 25 d were actually split into a period of net DIC increase and O₂ decrease between 10 and 19 March and a period of net DIC decrease and O₂ increase between 19 March and 3 April. The latter period is interpreted as the onset of the spring bloom. The regression coefficients between O₂ and DIC-based N estimates were 0.25 ± 0.08 for the glider data and 0.54 ± 0.06 for the buoy, significantly lower than the canonical metabolic quotient of 1.45±0.15. This study shows the added value of co-locating a profiling glider with moored time series buoys, but also demonstrates the difficulty in estimating N, and the limitations in achievable precision.

1 Introduction

Around a quarter of anthropogenic carbon dioxide (CO₂) emitted between 2011 and 2020 was absorbed by the oceans (Friedlingstein et al., 2022). On timescales of less than a day to many months, CO₂ in the ocean is influenced by biological (photosynthesis, respiration) and physical processes (air-sea gas exchange, mixing and advection) (Hood and Merlivat, 2001; Takahashi et al., 2002; Copin-Montégut et al., 2004; Hall et al., 2004; Alkire et al., 2014). Understanding the processes affecting export of carbon from the surface to the interior ocean is key for quantifying the effects of a future warmer climate (Bauer et al., 2013). Whether a location is predominantly autotrophic (dominated by photosynthesis) or heterotrophic (dominated by respiration) determines the sign of net community production, which is defined as gross primary production (by phytoplankton) minus total respiration (by phytoplankton, zooplankton and bacteria) (Alkire et al., 2012).

The surface of the Mediterranean Sea (2.5×10⁶ km²) represents just 0.8 % of oceans globally, but relative to its size, it is regarded as an important sink for anthropogenic carbon dioxide emissions due to higher levels of anthropogenic carbon than in the Atlantic and Pacific oceans (Lee et al., 2011; Schneider et al., 2010). This is due to a low Revelle factor (Broecker et al., 1979) related to relatively warm, salty and high-alkalinity waters, encouraging a net flux of carbon dioxide from the atmosphere to the ocean. Carbon dioxide dissolved in water (CO₂(aq) and H₂CO₃) dissociates to bicarbonate (HCO${}_{\mathrm{3}}^{-}$) and carbonate (CO${}_{\mathrm{3}}^{\mathrm{2}-}$), releasing H⁺ ions (Zeebe and Wolf-Gladrow, 2001). CO₂(aq), H₂CO₃, HCO${}_{\mathrm{3}}^{-}$ and CO${}_{\mathrm{3}}^{\mathrm{2}-}$ make up total dissolved inorganic carbon (DIC), with HCO${}_{\mathrm{3}}^{-}$ accounting for 90 % of DIC. Carbon dioxide absorbed by the ocean is thought to reach the interior via deep water formation and biological processes (Álvarez et al., 2014; Arrigo et al., 2008).

The northwestern Mediterranean Sea displays strong seasonal variability. At the surface, temperatures remain at around 13 to 14 ^∘C during winter, increasing to maxima of 26 to 28 ^∘C during summer. Wind-driven vertical mixing occurs during autumn and winter, whilst surface stratification is common during summer as a result of solar heating (Copin-Montégut et al., 2004; D’Ortenzio et al., 2008). Vertical mixing can transport nutrients from greater depths to oligotrophic surface waters (Marty and Chiavérini, 2002; de Fommervault et al., 2015). A combination of nutrient availability and increased stability driven by surface warming of 0.2 ^∘C can trigger phytoplankton blooms (Yao et al., 2016; Copin-Montégut et al., 2004). The onset of the spring bloom in the northwestern Mediterranean Sea varies from March to April, as observed between 2013 and 2015 at the BOUSSOLE buoy (Bouée pour l'acquisition de Séries Optiques à Long Terme, http://www.obs-vlfr.fr/Boussole/, last access: 20 August 2022) close to the DyFAMed (Dynamique des Flux Atmospheriques en Mediterraneé) site in the Ligurian–Provençal basin (Merlivat et al., 2018). Significant increases in particulate and dissolved organic carbon (POC and DOC) concentrations have been observed during bloom events (e.g. Carlson et al., 1998). POC and DOC export from the ocean surface constitutes the “biological carbon pump” (Carlson et al., 1998; Van Der Loeff et al., 1997; Alkire et al., 2014).

Quantifying these processes in detail requires sufficient data coverage in space and time. Few DIC time series have been maintained continuously, among them the DyFAMed mooring, which is complemented by monthly ship hydrocasts (Copin-Montégut et al., 2004; Antoine et al., 2008; Taillandier et al., 2012). The DyFAMed site is considered an open-ocean location as it is roughly 52 km from the coast in >2000 m deep water. The mooring is useful for studying processes occurring at specific depth levels at one location (Merlivat et al., 2018; Copin-Montégut et al., 2004; Hood and Merlivat, 2001), but a lack of vertical and horizontal spatial information is a limiting factor when quantifying mass and energy budgets. Autonomous underwater gliders have been used to survey the northwestern Mediterranean Sea since 2005 (Niewiadomska et al., 2008; Cyr et al., 2017). They are useful platforms for a range of physical and biogeochemical sensors and can operate autonomously for many months in up to 1000 m deep water using battery power (Eriksen et al., 2001; Piterbarg et al., 2014; Queste et al., 2012). The deployment of autonomous platforms, such as underwater gliders, complements fixed-depth time series by enabling observations of biogeochemical and physical horizontal and vertical gradients. This paper aims to estimate net community production (N) at the DyFAMed site using in situ continuous measurements from a mooring and an underwater glider deployed in March–April 2016. The additional glider data help overcome limitations of the single-depth mooring data in terms of both vertical data coverage and the contribution of horizontal advection. Furthermore, the glider mission served as a test for a prototype ion-sensitive field-effect transistor (ISFET) pH sensor, which complemented the standard temperature, salinity and c(O₂) sensors, to provide both O₂- and DIC-based net community production.

2 Data collection and quality

2.1 Ship measurements

Ship CTD and water sample profiles were collected by RV Téthys II on 7 March and 16 April 2016 at the DyFAMed site (Fig. 1). Ship hydrocast profiles of temperature and salinity (Sea-Bird Scientific SBE 9 CTD), and c(O₂) (Sea-Bird Scientific SBE 43 sensor), were supplemented by discrete Niskin bottle samples for c(O₂), c(DIC), total alkalinity (A_T) and concentrations of total oxidised nitrogen (NO${}_x^{-}$, i.e. the total of NO${}_{\mathrm{3}}^{-}$ and NO${}_{\mathrm{2}}^{-}$), silicate (Si(OH)₄) and phosphate (PO${}_{\mathrm{4}}^{\mathrm{3}-}$); see Appendix A for details. Implausible outliers in the CTD profiles (<1 % of values) were flagged and excluded from further analysis.

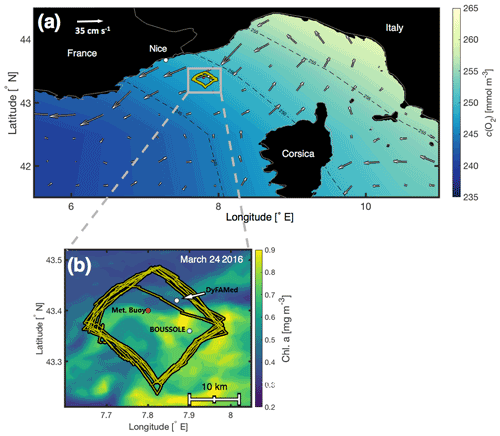
Figure 1 (a) The northwestern Mediterranean Sea and glider deployment area (small grey box) superimposed on the World Ocean Atlas 2013 surface c(O₂) March climatology (https://www.nodc.noaa.gov/OC5/woa13/woa13data.htm, last access: 20 August 2022), with accompanying AVISO satellite absolute mean surface currents (cm s⁻¹, white arrows) for 6 March–6 April 2016 (http://marine.copernicus.eu/services-portfolio/access-to-products, last access: 20 August 2022). (b) A close-up of the deployment area at the DyFAMed/BOUSSOLE site. The positions of the glider's track (yellow), the DyFAMed mooring (43.36^∘ N, 7.90^∘ E) (white), the BOUSSOLE buoy (43.42^∘ N, 7.87^∘ E), and the meteorological buoy “Côte D'Azur” (43.38^∘ N, 7.83^∘ E) are superimposed on surface chlorophyll a concentrations (https://oceancolor.gsfc.nasa.gov/products, last access: 20 August 2022) on 24 March 2016 (Hu et al., 2012). The bathymetry is flat and greater than 2000 m depth.

2.2 BOUSSOLE and meteorological buoy measurements

At BOUSSOLE, CO₂ fugacity f(CO₂) (Wanninkhof and Thoning, 1993) at 10 m depth was measured spectrophotometrically via a CARIOCA sensor using the thymol blue pH indicator. Inside an exchanger cell, dissolved CO₂ equilibrates with the pH indicator across a silicon membrane. The change in the optical absorbance of the pH indicator is converted to hourly readings of f(CO₂) (Hood and Merlivat, 2001), with an accuracy of 3 µatm (Copin-Montégut et al., 2004). The CARIOCA sensor is replaced roughly every 6 months with a newly calibrated instrument (Merlivat et al., 2018). To remove temperature effects, we show f₁₃(CO₂), normalised to a temperature of 13 ^∘C (Takahashi et al., 1993).

Temperature and salinity were measured hourly using two Sea-Bird Scientific SBE 37-SM MicroCAT sensors at 3 and 10 m depth. The 10 m MicroCAT failed on 15 March 2016. Up to that point, the mean temperature difference between 10 and 3 m was $(-\mathrm{0.01}\pm \mathrm{0.03})$ ^∘C. The corresponding mean practical salinity S(PSS-78) difference was $-\mathrm{0.069}\pm \mathrm{0.004}$. The 10 m MicroCAT had the same salinity offset to the ship CTD cast on 7 March. The 3 m MicroCAT agreed to within 0.007 ^∘C with temperature and to within 0.006 with salinity of the ship CTD cast on 7 March. A total of 3 d before the ship CTD cast on 16 April, the 3 m MicroCAT also failed. However, its final salinity reading was within 0.01 of the ship value. We therefore used the 3 m MicroCAT temperature and salinity readings for calculating buoy-related results.

c(O₂) was measured at BOUSSOLE using Aanderaa oxygen optodes at 3 and 10 m. Only nighttime optode measurements were used because the daytime readings were affected by light-induced spikes (Binetti et al., 2020). Winkler titration samples taken during the ship visits on 7 March and 16 April were used to calibrate optode c(O₂) (Coppola et al., 2018).

The meteorological buoy “Côte D'Azur” maintained by Météo-France is located close to the BOUSSOLE buoy (Fig. 1). This meteorological buoy measures wind speed at 3.8 m height above sea level (which is extrapolated to 10 m by adding 10 % of the value), wind direction, air temperature, atmospheric pressure, relative humidity, precipitation and sea surface salinity. Data are archived in the database “SErvice de DOnnées de l'OMP (SEDOO) Mistrals” (http://mistrals.sedoo.fr/Data-Download, last access: 20 August 2022). Wind speed and sea level pressure were used in this study.

2.3 Glider measurements

An iRobot Seaglider model 1KA (sg537; named “Fin”) with an ogive fairing was deployed close to the DyFAMed mooring site. A total of 147 dives (294 profiles) were completed by the glider between 7 March and 5 April 2016, covering a diamond-shaped pattern at 43.22–43.50^∘ N, 7.64–8.00^∘ E (Fig. 1). The glider completed seven circumnavigations of the survey pattern, each in approximately 4 d, with each of the four sides of the pattern taking approximately 1 d to complete. The glider was equipped with a non-pumped SBE model CTD sensor, an Aanderaa model 4330F oxygen optode sensor, a WET Labs Eco Puck sensor measuring optical backscatter at two wavelengths (470 and 700 nm) and two paired prototype ISFET pH and p(CO₂) sensors (Shitashima et al., 2013; Hemming et al., 2017).

Conductivity, temperature and pressure were used to derive potential temperature (θ) and practical salinity (S). Glider c(O₂) was calibrated against ship-based c(O₂) profiles (Fig. 2a, Appendix B1). Outliers (<1 % of values) outside specified standard deviation ranges (3.5 standard deviations for depths >400 m; 10 standard deviations for depths <400 m) were flagged and discarded from further analysis.

The deployment offered a second opportunity to trial prototype ISFET sensors, previously tested on a glider during the REP14–MED experiment in the Sardinian Sea (Hemming et al., 2017; Onken et al., 2018). ISFET pH was corrected (Fig. 2b) for drift and pressure effects, similar to the steps undertaken by Hemming et al. (2017). The drift- and pressure-corrected ISFET pH was calibrated by linear regression against ship pH on 7 March and 16 April 2016 (Appendix B2).

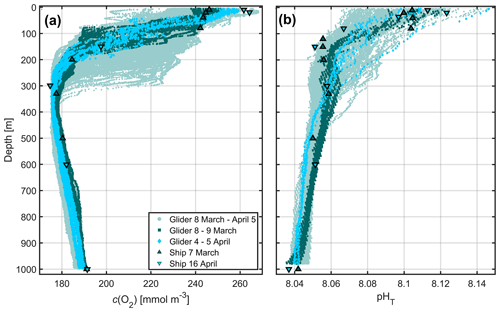
Figure 2 Calibrated glider (a) c(O₂) and (b) ISFET pH_T over the whole deployment (pale green), 8–9 March (dark green) and 4–5 April (light blue). Ship samples were collected on 7 March (dark green upward-pointing triangles) and on 16 April (light blue downward-pointing triangles).

Figure 3 Glider pH_T against glider c(O₂) and coloured by time for all points within the mean euphotic layer (top 46 m). The linear fit and corresponding equation between c(O₂) and pH_T−8 are also shown.

3 Development of a spring bloom

The spring bloom at the DyFAMed site is characterised by a decrease in surface f₁₃(CO₂) due to photosynthesis. Its onset varies from year to year (e.g. April 2013, March 2014) and usually occurs after a period of deep mixing (Merlivat et al., 2018). The glider deployment in March–April 2016 provided horizontal and vertical context to the fixed-depth near-surface mooring sensors when the spring bloom was expected to occur.

Sea surface temperature (SST) remained relatively stable below 13.5 ^∘C between 7 and 19 March whilst surface f₁₃(CO₂) increased by 40 µatm (Fig. 4a), and surface salinity increased by 0.13 (Fig. 4b). The higher-f₁₃(CO₂), higher-salinity waters were likely the results of wind-induced deep mixing and increased convection (Fig. 4a). These waters originate from 50–150 m depth where high-salinity (Fig. 5b), high-f₁₃(CO₂), low-c(O₂) (Fig. 5c) Levantine Intermediate Water (LIW) exists (Knoll et al., 2017). SST increased by up to 0.6 ^∘C between 19 and 20 March and continued to increase intermittently to a maximum of 14.3 ^∘C on 5 April (total increase of 1 ^∘C over the deployment period).

Whilst SST increased between 19 March and 1 April, f₁₃(CO₂) decreased by 85 µatm. This was the start of the spring bloom, associated with increased surface c(O₂), pH_T and optical backscatter (Figs. 4b, 5c, d, e). O₂ is produced by photosynthesis. The pH_T increase reflects biological CO₂ uptake altering the carbonate equilibria (Cornwall et al., 2013; Copin-Montégut and Bégovic, 2002), and increases in temperature. Optical backscatter relates to predominantly POC (Stramski et al., 2004), with minor contributions from mineral particles and gas bubbles at this site. Therefore, all of these observations suggested an increase in biological production.

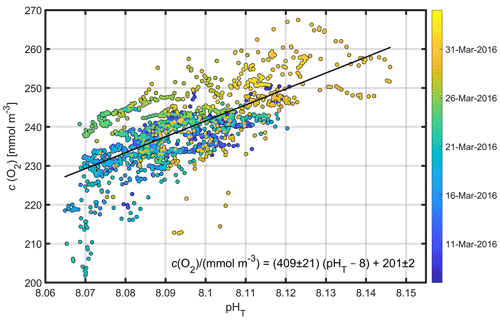
A clear relationship between potential temperature (θ), c(O₂) and pH_T existed within the euphotic layer (mean depth: $z_{\mathrm{eu}}=\mathrm{46}\pm \mathrm{7}$ m) (Figs. 3, 5a, c, e), with higher potential temperature associated with higher pH_T and c(O₂). The stronger surface stratification resulting from calmer meteorological conditions (e.g. reduced wind speed after 19 March, Fig. 4a) enhanced light supply and stability and caused productivity to increase (Sverdrup, 1953; Pingree et al., 1977). As a result of increased photosynthesis, surface waters became O₂-supersaturated by 27 March (Figs. 4b, 5c).

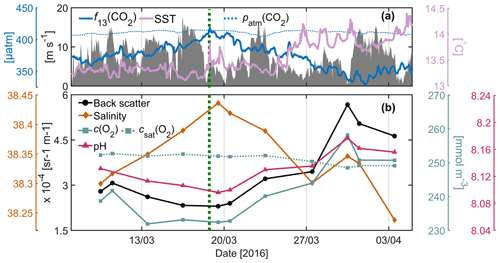
Figure 4 (a) Wind speed at 10 m above sea level at the meteorological buoy (dark grey shading), sea surface temperature (pale pink) and CO₂ fugacity normalised to 13 ^∘C (blue) at 10 m depth at the BOUSSOLE buoy. The partial pressure of atmospheric CO₂ in March 2016 (dotted blue) at Lampedusa, Italy, is shown. The onset of the spring bloom (dashed green), determined using buoy f(CO₂) measurements, is plotted for comparison. (b) Glider measurements of salinity (orange), optical backscatter at 700 nm (black), dissolved oxygen concentrations (c(O₂)) (turquoise) and calibrated pH_T (pink) binned at 10 m. The oxygen concentration at saturation (dashed turquoise; parameterisation of García and Gordon (1992) based on Benson and Krause, 1984) is plotted for comparison.

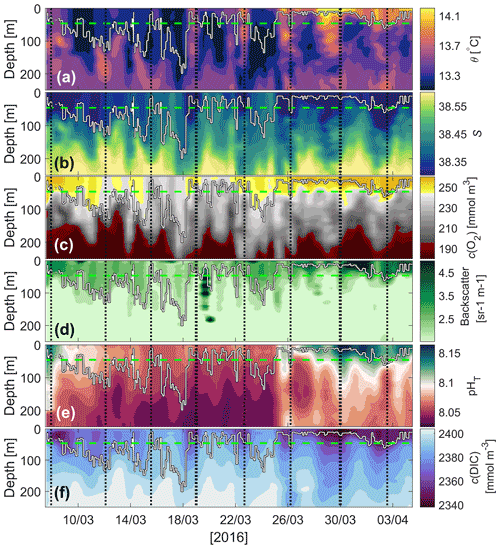
Figure 5 Glider (a) potential temperature (θ), (b) salinity, (c) dissolved oxygen concentration (c(O₂)), (d) optical backscatter, (e) pH_T and (f) dissolved inorganic carbon concentration (c(DIC)). The mean euphotic depth used for calculating N (green dashed line, z_lim=46 m) and mixed-layer depth (white line; derived using the potential density criteria of the hybrid scheme of Holte and Talley, 2009) are superimposed. The vertical dashed black lines represent the glider reaching the most northerly point of its transects.

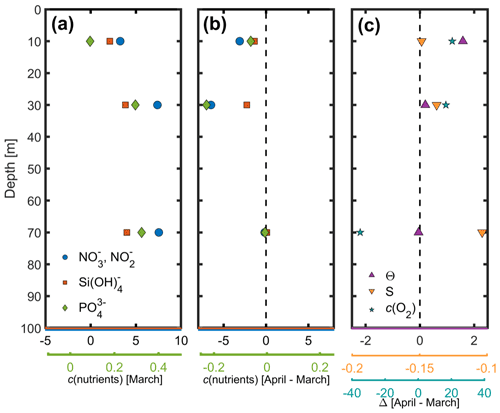
Nutrient concentrations obtained by ship hydrocasts for depths of 10–90 m on 7 March were generally highest at 90 m where there is increased remineralisation and lowest at the surface where there is increased usage by phytoplankton (Fig. 6a). Clear differences can be seen in nutrient samples obtained before and after the spring bloom (Fig. 6b). NO${}_x^{-}$ concentrations decreased by 7 mmol m⁻³, Si(OH)₄ by 2.5 mmol m⁻³ and PO${}_{\mathrm{4}}^{\mathrm{3}-}$ by 0.22 mmol m⁻³ at 30 m depth, associated with biological production during the spring bloom period. A deep chlorophyll a maximum is often found around this depth (Estrada, 1996) later in the season but was not apparent in our data. At 70 and 90 m depth, nutrient concentrations did not vary much between March and April, while there was a significant decrease in c(O₂) and a small change in potential temperature (Fig. 6c). This corresponded to increased stratification with a stronger potential temperature gradient within the top 70 m.

Figure 6 (a) Nutrient concentrations (mmol m⁻³) in March 2016, (b) change in nutrient concentrations between March and April 2016, and (c) changes in potential temperature (θ), practical salinity (S) and c(O₂) (mmol m⁻³) between March and April 2016.

4 Estimating net community production from O₂ and DIC mass budgets

Net community production N is estimated based on mass budgets using the method described by Alkire et al. (2014):

$$\begin{array}{}\text{(1)}& \underset{\mathrm{0}}{\overset{z_{\lim }}{\int }}\left({\displaystyle \frac{\partial c}{\partial t}}+u{\displaystyle \frac{\partial c}{\partial x}}+v{\displaystyle \frac{\partial c}{\partial y}}\right)\mathrm{d}z=-F_{\mathrm{ase}}+N\left({\mathrm{O}}_{\mathrm{2}}\right)+F_{\mathrm{e}}+F_{\mathrm{v}}.\end{array}$$

This equation applies to N(O₂). For DIC, the N(O₂) term is replaced with −N(DIC) because during photosynthesis, DIC is consumed and O₂ is produced, and vice versa for respiration.

The following diagnostic equations are therefore used to calculate N based on O₂ and DIC mass budgets.

$$\begin{array}{}\text{(2)}& {\displaystyle }\begin{array}{rl}N\left({\mathrm{O}}_{\mathrm{2}}\right)& ={\displaystyle \frac{\mathrm{\Delta }I\left({\mathrm{O}}_{\mathrm{2}}\right)}{\mathrm{\Delta }t}}+F_{\mathrm{ase}}\left({\mathrm{O}}_{\mathrm{2}}\right)+F_{\mathrm{adv}}\left({\mathrm{O}}_{\mathrm{2}}\right)-F_{\mathrm{e}}\left({\mathrm{O}}_{\mathrm{2}}\right)\\ & -F_{\mathrm{v}}\left({\mathrm{O}}_{\mathrm{2}}\right)\end{array}\text{(3)}& {\displaystyle }\begin{array}{rl}N\left(\mathrm{DIC}\right)& =-{\displaystyle \frac{\mathrm{\Delta }I\left(\mathrm{DIC}\right)}{\mathrm{\Delta }t}}-F_{\mathrm{ase}}\left(\mathrm{DIC}\right)-F_{\mathrm{adv}}\left(\mathrm{DIC}\right)\\ & +F_{\mathrm{e}}\left(\mathrm{DIC}\right)+F_{\mathrm{v}}\left(\mathrm{DIC}\right)\end{array}\end{array}$$

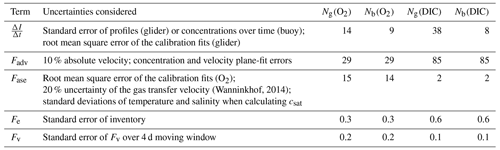
$\frac{\mathrm{\Delta }I}{\mathrm{\Delta }t}$ is the integrated column inventory change over time, F_adv is horizontal advection, F_ase is the air–sea flux (positive for the direction ocean to atmosphere), F_e is the entrainment flux due to mixed-layer deepening and F_v is the diapycnal eddy diffusion flux. The time period chosen to derive the fluxes required to calculate N spanned 25 d between 10 March and 3 April and included 285 individual profiles (glider dives 10 to 147) spanning the entire survey domain. The first nine dives were omitted because they were used for glider flight trimming. Table 1 gives the uncertainties considered for each budget term. Mean values over the 25 d period are shown in Table 2.

4.1 Inventory change $\mathrm{\Delta }I/\mathrm{\Delta }t$

Daily mean column inventories were integrated between surface and z_lim for all glider profiles within a 4 d moving window centred on each date. As integration depth z_lim, we used the mean euphotic depth of 46 m, derived from satellite measurements using the method described by Lee et al. (2007). Inventory changes ($\frac{\mathrm{\Delta }I}{\mathrm{\Delta }t}$) were calculated from the day-to-day inventory differences.

$$\begin{array}{}\text{(4)}& {\displaystyle \frac{\mathrm{\Delta }I}{\mathrm{\Delta }t}}={\displaystyle \frac{{\int }_{\mathrm{0}}^{z{}_{\lim }}{c}_{t+\mathrm{1}\mathrm{d}}\left(z\right)\mathrm{d}z-{\int }_{\mathrm{0}}^{z{}_{\lim }}{c}_t\left(z\right)\mathrm{d}z}{\mathrm{1}\mathrm{d}}}\end{array}$$

4.2 Advection F_adv

The glider measured within an Eulerian framework, sampling geographic locations over time. In contrast to a Lagrangian framework, estimates of F_adv are needed to close the budget. Advection was calculated following Alkire et al. (2014) using zonal and meridional mean horizontal concentration gradients and current velocities within z_lim using a moving time window of 8 d. This longer time window of 8 d was chosen to reduce the error in the mean gradients (Fig. 7). Mean horizontal concentration gradients A_c(z) and B_c(z) were calculated for each 5 m depth bin using robust plane fits of all concentration measurements in the 8 d time window:

$$\begin{array}{}\text{(5)}& c_{\mathrm{fit}}\left(z\right)=A_{\mathrm{c}}\left(z\right)x+B_{\mathrm{c}}\left(z\right)y+d_{\mathrm{c}}\left(z\right),\end{array}$$

where d_c(z) is a constant (not used), and x and y are Cartesian coordinates calculated using zonal and meridional distances, respectively. Bisquare weights were applied when determining the fit coefficients (Gross, 1977) to limit the effect of outliers.

The zonal (east–west) concentration gradients were small for both O₂ and DIC (Fig. 8). Opposing meridional (north–south) gradients for O₂ and DIC indicate biological patchiness. However, interestingly the positive gradient for O₂ (corresponding to higher concentrations in the north) is opposite to the pattern seen in the satellite-derived ocean colour (Fig. 1b), which shows lower chlorophyll a concentrations in the north (implying that the bloom propagates from south to north). This highlights that primary production and net community production are not always directly correlated.

To estimate the absolute geostrophic currents within the survey domain, the dynamic height anomaly (Ψ) was calculated relative to the surface using glider salinity, temperature and pressure (Roquet et al., 2015), and planes were fitted for a moving time window of 8 d:

$$\begin{array}{}\text{(6)}& {\mathit{\Psi }}_{\mathrm{fit}}\left(z\right)=A_{\mathit{\Psi }}\left(z\right)x+B_{\mathit{\Psi }}\left(z\right)y+d_{\mathit{\Psi }}\left(z\right).\end{array}$$

Using these plane fits, the meridional and zonal components of geostrophic shear were derived and referenced to the 8 d running means of the meridional and zonal components of OSCAR velocities (Bonjean and Lagerloef, 2002). Referencing the geostrophic shear with glider dive-averaged currents (DACs) was initially explored, but when compared with satellite data products (Fig. 8c, d) it was clear that the meridional velocities (v) were unrealistic (see Sect. 7).

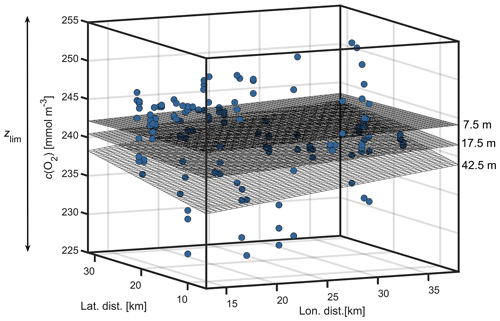
Figure 7 Plane fits of dissolved oxygen concentrations (c(O₂)) at 7.5, 17.5 and 42.5 m depth within z_lim for 25 March 2016.

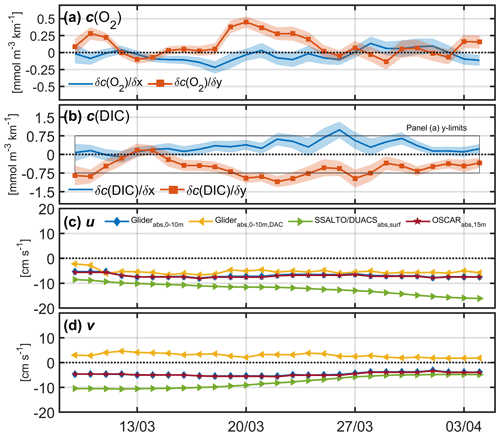
Figure 8 Zonal and meridional mean horizontal concentration gradients for (a) c(O₂) and (b) c(DIC) estimated using robust plane fits. The black box in panel (b) highlights the y limits for panel (a) for reference. (c) Absolute mean u velocity and (d) v velocity using glider measurements in the top 10 m referenced to OSCAR velocities (blue), and referenced to dive-averaged currents (DACs, yellow), absolute surface mean currents from satellite products SSALTO/DUACS (green) and OSCAR (red).

(Wanninkhof, 2014)

Table 1 The uncertainties considered for each flux term when estimating total propagated error. The mean errors for N using glider (N_g) and buoy (N_b) measurements are listed for both c(O₂) and c(DIC) in $\mathrm{mmol}{\mathrm{m}}^{-\mathrm{2}}{\mathrm{d}}^{-\mathrm{1}}$.

The advection flux (F_adv) was calculated from the horizontal concentration gradients and the absolute geostrophic velocities:

$$\begin{array}{}\text{(7)}& F_{\mathrm{adv}}\left(z\right)=A_{\mathrm{c}}\left(z\right)u\left(z\right)+B_{\mathrm{c}}\left(z\right)v\left(z\right).\end{array}$$

The mean gradients using measurements binned every 5 m between the surface and z_lim were averaged at each time step and used for estimating advection (Fig. 8a, b).

4.3 Air–sea gas exchange F_ase

Air–sea gas exchange (negative for fluxes from atmosphere to ocean) was estimated for O₂ and DIC using

$$\begin{array}{}\text{(8)}& \begin{array}{rl}{F}_{\mathrm{ase}}\left({\mathrm{O}}_{\mathrm{2}}\right)& =k\left({\mathrm{O}}_{\mathrm{2}}\right)\left[c_{\mathrm{surf}}\left({\mathrm{O}}_{\mathrm{2}}\right)-\left(\mathrm{1}+{\mathit{\Delta }}_{\mathrm{bubble}}\right)c_{\mathrm{sat}}\left({\mathrm{O}}_{\mathrm{2}}\right)\right]\\ & {\displaystyle \frac{\min (z_{\lim },z_{\mathrm{mix}})}{z_{\mathrm{mix}}}},\end{array}\end{array}$$

with the equilibrium bubble correction ${\mathit{\Delta }}_{\mathrm{bubble}}=\mathrm{0.01}[w_{\mathrm{10}}/(\mathrm{9}\mathrm{m}{\mathrm{s}}^{-\mathrm{2}}){]}^{\mathrm{2}}$ (Woolf and Thorpe, 1991) and

$$\begin{array}{}\text{(9)}& \begin{array}{rl}{F}_{\mathrm{ase}}\left(\mathrm{DIC}\right)& =k\left({\mathrm{CO}}_{\mathrm{2}}\right)\left[c_{\mathrm{surf}}\left({\mathrm{CO}}_{\mathrm{2}}\right)-c_{\mathrm{sat}}\left({\mathrm{CO}}_{\mathrm{2}}\right)\right]\\ & {\displaystyle \frac{\min (z_{\lim },z_{\mathrm{mix}})}{z_{\mathrm{mix}}}}.\end{array}\end{array}$$

The gas transfer velocity k is calculated according to Wanninkhof (2014). c_surf is the mean concentration in the top 10 m over a moving 4 d time window. The mixed-layer depth z_mix was estimated using the potential density criteria of the algorithm of Holte and Talley (2009), with a threshold of 0.03 kg m⁻³ and gradient of 0.0005 $\mathrm{kg}{\mathrm{m}}^{-\mathrm{3}}{\mathrm{dbar}}^{-\mathrm{1}}$. These criteria are sensitive enough to detect the actual mixed-layer depth relevant for gas exchange fluxes (Brainerd and Gregg, 1995). c_sat(O₂) is the O₂ air-saturation concentration of García and Gordon (1992), corrected to actual sea-level pressure, p_baro. c_sat(CO₂)=χ(CO₂)p_baroF(CO₂) is the CO₂ air-saturation concentration, calculated using the dry mole fraction of atmospheric CO₂, χ(CO₂), at the nearest NOAA Carbon Cycle network station Lampedusa, Italy, in March 2016 (ftp://aftp.cmdl.noaa.gov/data/trace_gases/co2/flask/surface, last access: 20 August 2022, site code: LMP, Dlugokencky et al., 2021). F(CO₂) is the CO₂ solubility function in $\mathrm{mol}{\mathrm{dm}}^{-\mathrm{3}}{\mathrm{atm}}^{-\mathrm{1}}$ (Weiss and Price, 1980). The last term of the equations is a scaling factor that apportions the air–sea exchange flux to the depth layer of interest (z_lim=46 m) when z_mix is deeper than z_lim.

4.4 Entrainment F_e

When the mixed layer deepens to depths greater than z_lim, water from below with different concentrations mixes with water within the layer. As a result, there is either a reduction or an increase in mean concentration within z_lim depending on the vertical concentration distribution. To account for this, F_e was estimated following Binetti et al. (2020):

$$\begin{array}{}\text{(10)}& F_{\mathrm{e}}={\displaystyle \frac{I_{\mathrm{1}}\left(z_{\mathrm{mix}}\right(t_{\mathrm{2}}\left)\right)\frac{z_{\lim }}{z_{\mathrm{mix}}\left(t_{\mathrm{2}}\right)}-I_{\mathrm{1}}\left(z_{\lim }\right)}{t_{\mathrm{2}}-t_{\mathrm{1}}}},\end{array}$$

where I₁(z_mix(t₂)) is the inventory at time t₁ within the mixed-layer depth z_mix at time t₂, I₁(z_lim) is the inventory at t₁ within z_lim and t₂−t₁ represents the time difference. Mean values of z_mix and c averaged over a 4 d moving time window were used.

The mean F_e(O₂) was ($-\mathrm{65}\pm \mathrm{1}$) $\mathrm{mmol}{\mathrm{m}}^{-\mathrm{2}}{\mathrm{d}}^{-\mathrm{1}}$ and the mean F_e(DIC) was ($-\mathrm{74}\pm \mathrm{1}$) $\mathrm{mmol}{\mathrm{m}}^{-\mathrm{2}}{\mathrm{d}}^{-\mathrm{1}}$ for the 7 d in the 25 d period when entrainment (mixed-layer deepening) occurred and z_mix>z_lim.

4.5 Vertical diapycnal eddy diffusion F_v

Vertical diapycnal eddy diffusion across the base of z_lim was estimated using the measured concentration–density gradients (Copin-Montégut, 2000) and an estimate of the turbulence energy dissipation rate ϵ:

$$\begin{array}{}\text{(11)}& F_{\mathrm{v}}={\displaystyle \frac{\mathrm{0.25}\mathit{ϵ}\mathit{\rho }}{g}}{\displaystyle \frac{\partial c}{\partial \mathit{\rho }}},\end{array}$$

where the concentration gradient was evaluated using centred finite differences at z_lim±5 m. $\mathit{ϵ}=\mathrm{1.5}\times {\mathrm{10}}^{-\mathrm{9}}$ m² s⁻³ was taken from measurements in the Mediterranean bottom pycnoline (Cuypers et al., 2012). Copin-Montégut (2000) guessed a 33 times higher value of $\mathrm{5}\times {\mathrm{10}}^{-\mathrm{8}}$ m² s⁻³ in her study of net community production at DyFAMed, but this value was probably an overestimate because even in the presence of eddies, Cuypers et al. (2012) estimate ϵ to be only $\mathrm{8.5}\times {\mathrm{10}}^{-\mathrm{9}}$ m² s⁻³. Concentration gradients were calculated for each profile within a 4 d moving window and then averaged to get one gradient per time step.

The mean F_v(O₂) was ($-\mathrm{0.8}\pm \mathrm{0.2}$) $\mathrm{mmol}{\mathrm{m}}^{-\mathrm{2}}{\mathrm{d}}^{-\mathrm{1}}$ and the mean F_v(DIC) was ($-\mathrm{0.1}\pm \mathrm{0.1}$) $\mathrm{mmol}{\mathrm{m}}^{-\mathrm{2}}{\mathrm{d}}^{-\mathrm{1}}$ over the 25 d period. With the higher ϵ value of $\mathrm{8.5}\times {\mathrm{10}}^{-\mathrm{9}}$ m² s⁻³ found in eddies, these fluxes would be 5.7 times higher, but still negligible with respect to the other four terms in the mass budget.

4.6 Buoy measurements

We calculate N from c(O₂) and c(DIC) at the BOUSSOLE buoy (N_b) for comparison with N_g estimates. N_b was estimated similarly to N_g, in that we follow the budget approach defined in Sect. 4, and equations defined thereafter. Inventory changes were calculated from surface observations multiplied by z_lim because depth profiles are not measured at the buoy. When z_mix<z_lim, this most likely results in an overestimate of the actual inventory change because N decreases with depth. Also, F_ase was scaled in the same way as the glider-based estimates when z_mix>z_lim. Finally, F_adv, F_e and F_v could not be derived from the single-depth measurements at BOUSSOLE. Instead, the glider-derived fluxes were also used to compute N_b.

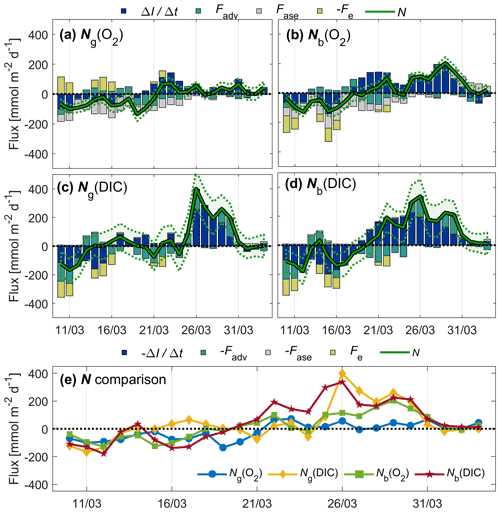
Figure 9 Inventory change ($\mathrm{\Delta }I/\mathrm{\Delta }t$), advection (F_adv), air–sea exchange (F_ase), entrainment (F_e) fluxes, and net community production (N) of O₂ (a, b; top legend) and DIC (c, d; bottom legend) related to glider (a, c) and buoy (b, d) measurements. Uncertainty intervals are shown as dotted lines. All N estimates are compared in panel (e).

5 Net community production N

Prior to 21 March, N_g and N_b were negative or close to zero most of the time (Fig. 9e). This could be a sign of local net heterotrophic conditions, but could also be due to underestimated entrainment (F_e) or vertical eddy diffusion fluxes (F_v). This observation cannot be explained by physical undersaturation driven by recent cooling because temperatures decreased by only 0.2 ^∘C between 1 and 21 March, explaining at most 0.4 % undersaturation. After 21 March, N exceeds zero until the end of the deployment period. The approximate start of the spring bloom was 19 March as evidenced by the buoy c(DIC) (Fig. 4), which is also the time when N_b(DIC) becomes positive, lasting until the end of the deployment period.

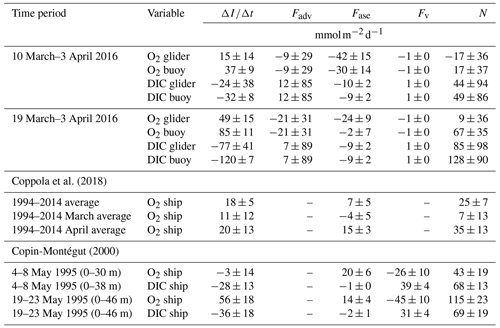
Coppola et al. (2018)Copin-Montégut (2000)

Table 2 Comparison of $\mathrm{\Delta }I/\mathrm{\Delta }t$ , F_adv, F_ase, F_v and N estimates using c(O₂) and c(DIC) and the corresponding flux terms used in this study with others in the literature. The N estimates of Copin-Montégut (2000) are based on $\mathrm{\Delta }I/\mathrm{\Delta }t$, F_ase and F_v (calculated with a turbulence energy dissipation rate of $\mathit{ϵ}=\mathrm{5.0}\times {\mathrm{10}}^{-\mathrm{8}}{\mathrm{m}}^{\mathrm{2}}{\mathrm{s}}^{-\mathrm{3}}$).

N_g(O₂) peaks on 22–23 and 31 March at around 70 $\mathrm{mmol}{\mathrm{m}}^{-\mathrm{2}}{\mathrm{d}}^{-\mathrm{1}}$, matching periods of high c(O₂) (Fig. 5c). In contrast, N_b(O₂) is highest between 25 and 31 March at ≥80 $\mathrm{mmol}{\mathrm{m}}^{-\mathrm{2}}{\mathrm{d}}^{-\mathrm{1}}$. The total range of N(DIC) is larger than for N(O₂). N_g(DIC) and N_b(DIC) reach similar peak values on 26 and 29–30 March.

The contributions of F_adv and F_e are significant at times. $F_{\mathrm{e}}\left({\mathrm{O}}_{\mathrm{2}}\right)<-\mathrm{80}$ $\mathrm{mmol}{\mathrm{m}}^{-\mathrm{2}}{\mathrm{d}}^{-\mathrm{1}}$ on days when wind is high and the surface mixed layer is deepening (Fig. 9), and there are periods when absolute F_adv(O₂)>50 $\mathrm{mmol}{\mathrm{m}}^{-\mathrm{2}}{\mathrm{d}}^{-\mathrm{1}}$. Absolute F_adv(DIC) is on average 34 $\mathrm{mmol}{\mathrm{m}}^{-\mathrm{2}}{\mathrm{d}}^{-\mathrm{1}}$ higher than F_adv(O₂), and on some days absolute F_adv(DIC)>100 $\mathrm{mmol}{\mathrm{m}}^{-\mathrm{2}}{\mathrm{d}}^{-\mathrm{1}}$. F_e(DIC) is generally of similar magnitude to absolute F_e(O₂). Surface waters are undersaturated with O₂ prior to 29 March (negative F_ase) and then oversaturated until the end of the deployment period (positive F_ase). Surface waters are undersaturated in CO₂ throughout the deployment period (negative F_ase).

Between 10 March and 3 April we estimate an average N of between ($-\mathrm{17}\pm \mathrm{36}$) and (49±86) $\mathrm{mmol}{\mathrm{m}}^{-\mathrm{2}}{\mathrm{d}}^{-\mathrm{1}}$, depending on the variable used (Table 2). Between 19 March and 3 April, N was positive most of the time and on average ranged between (9±36) and (128±90) $\mathrm{mmol}{\mathrm{m}}^{-\mathrm{2}}{\mathrm{d}}^{-\mathrm{1}}$.

6 Stoichiometric relationship

Dividing N(O₂) by N(DIC) provides the photosynthetic quotient Q_P, previously estimated as 1.45±0.15 (Laws, 1991; Anderson and Sarmiento, 1995; Anderson, 1995). The average Q_P in this study using N_g(O₂) and N_g(DIC) between 10 March and 3 April was 0.14±0.81, excluding periods when N_g(DIC)<30 $\mathrm{mmol}{\mathrm{m}}^{-\mathrm{2}}{\mathrm{d}}^{-\mathrm{1}}$ (i.e. close to zero within its uncertainty). When using N_b(O₂) and N_b(DIC) over the same time period, average Q_P was 0.49±0.60. Using linear regression of N(O₂) against N(DIC) provides another way to derive Q_P. The resulting slopes are 0.25±0.06 for the glider and 0.54±0.06 for the buoy N estimates. These Q_P values therefore do not match the canonical values of 1.45±0.15, but similarly low values of 0.63±0.30 were observed by Copin-Montégut (2000) in early May 1995 at the same site (Table 2).

The change of nutrient concentrations provides an alternative to estimating net community production. Assuming the observed NO${}_x^{-}$ drawdown of 7 mmol m⁻³ and the PO${}_{\mathrm{4}}^{\mathrm{3}-}$ drawdown of 0.22 mmol m⁻³ occurred over a period of 15 to 25 d (with 15 d corresponding to the period 19 March to 3 April; the exact period is not known because we only have observations on 7 March and 16 April) and extends over the same depth horizon (46 m) as used for the O₂- and DIC-based N calculations, and neglecting any additional contribution to net community production fuelled by diapycnal mixing, this corresponds to rates of 13 to 21 mmol $\mathrm{mmol}{\mathrm{m}}^{-\mathrm{2}}{\mathrm{d}}^{-\mathrm{1}}$ for nitrogen and 0.4 to 0.7 mmol $\mathrm{mmol}{\mathrm{m}}^{-\mathrm{2}}{\mathrm{d}}^{-\mathrm{1}}$ for phosphorus. Assuming a Redfield $\mathrm{C}:\mathrm{N}:\mathrm{P}$ stoichiometric ratio of $\mathrm{106}:\mathrm{16}:\mathrm{1}$ (Redfield et al., 1963), this corresponds to carbon fluxes of 85 to 142 $\mathrm{mmol}{\mathrm{m}}^{-\mathrm{2}}{\mathrm{d}}^{-\mathrm{1}}$ (based on nitrogen) and 43 to 72 $\mathrm{mmol}{\mathrm{m}}^{-\mathrm{2}}{\mathrm{d}}^{-\mathrm{1}}$ (based on phosphorus). The values are in reasonable agreement with the N(DIC) values derived for the bloom period between 19 March and 3 April of (85±98) to (128±90) $\mathrm{mmol}{\mathrm{m}}^{-\mathrm{2}}{\mathrm{d}}^{-\mathrm{1}}$, indicating nutrient consumption in line with the assumed stoichiometric ratio.

The discrepancy between Redfield and observed stoichiometry is larger for the O₂-based net community production, especially for the glider-based values. Non-Redfield ratios have been documented before, including at the same site. For example, Copin-Montégut (2000) found non-Redfield ratios for O₂ and DIC-derived N at DyFAMed. Hull et al. (2021) found non-Redfield ratios for O₂- and nitrate-derived N in the North Sea. We do not have a physiological explanation for such large deviations from the canonical stoichiometric values. It is unlikely to be due to a calibration error in the O₂ concentration because it would have to be of the order of 20 mmol m⁻³, and our observations at depths >400 m agree to within 3 mmol m⁻³ with the record of historic measurements.

7 Discussion

Quantifying net community production helps us to understand the role of biological production and consumption on carbon export from the surface to deep waters. If the rate of carbon export is known, the rate of atmospheric CO₂ drawdown into the ocean can be better quantified, and the accuracy of future climate projections might improve. Using underwater gliders as tools to observe the water column on timescales of less than a month over a wider area allows us to estimate physical processes (e.g. mixing, advection) that affect biogeochemical tracer concentrations and estimates of net community production derived therefrom.

During the spring bloom (19 March to 3 April) we estimate N between (9±36) and (128±90) $\mathrm{mmol}{\mathrm{m}}^{-\mathrm{2}}{\mathrm{d}}^{-\mathrm{1}}$ on average, with maxima >300 $\mathrm{mmol}{\mathrm{m}}^{-\mathrm{2}}{\mathrm{d}}^{-\mathrm{1}}$ at times. Few studies have estimated N at the DyFAMed site, and there are currently no N estimates that incorporate F_adv using concentrations over a larger area surrounding DyFAMed.

Another study at this site estimated an annual mean N(O₂) of (25±7) $\mathrm{mmol}{\mathrm{m}}^{-\mathrm{2}}{\mathrm{d}}^{-\mathrm{1}}$ (equivalent to 9.2 $\mathrm{mol}{\mathrm{m}}^{-\mathrm{2}}{\mathrm{a}}^{-\mathrm{1}}$) and monthly mean O₂ production of (7±13) $\mathrm{mmol}{\mathrm{m}}^{-\mathrm{2}}{\mathrm{d}}^{-\mathrm{1}}$ and (35±13) $\mathrm{mmol}{\mathrm{m}}^{-\mathrm{2}}{\mathrm{d}}^{-\mathrm{1}}$ in March and April, respectively, using excess O₂ above 100 % saturation over a period of 20 years (Coppola et al., 2018). Furthermore, Copin-Montégut (2000) estimated N(O₂) as (43±19) $\mathrm{mmol}{\mathrm{m}}^{-\mathrm{2}}{\mathrm{d}}^{-\mathrm{1}}$ in the top 30 m from 4–8 May 1995 and as (115±23) $\mathrm{mmol}{\mathrm{m}}^{-\mathrm{2}}{\mathrm{d}}^{-\mathrm{1}}$ in the top 46 m from 19–23 May 1995. A direct comparison is not possible between this study, Coppola et al. (2018) and Copin-Montégut (2000) because each study is based on different timescales (from years to days), different vertical integration horizons and different seasons. Keeping this in mind, our range of N estimates is similar to those of Coppola et al. (2018) and Copin-Montégut (2000).

We can compare our study with other studies elsewhere that estimate N using glider measurements. Alkire et al. (2014) estimated mean N(O₂) as (65±25) $\mathrm{mmol}{\mathrm{m}}^{-\mathrm{2}}{\mathrm{d}}^{-\mathrm{1}}$ over a 23 d period in June 2008 in the North Atlantic. Like our study, they estimated N(O₂) incorporating F_adv derived using horizontal gradients measured by a glider. Further, Hull et al. (2021) estimated N(O₂) as (154±2) $\mathrm{mmol}{\mathrm{m}}^{-\mathrm{2}}{\mathrm{d}}^{-\mathrm{1}}$ in the North Sea in April 2019.

Uncertainties for N(DIC) are generally higher than those for N(O₂), and the highest uncertainties are associated with F_adv. F_adv uncertainties are high because the uncertainties associated with the concentration plane fits are high due to c(DIC) variability within the time-centred window. For example, c(DIC) within z_lim varied over 33 mmol m⁻³ for the time-centred window on 16 March, leading to low standard errors (Fig. 8b), while c(DIC) varied over 40 mmol m⁻³ for the time-centred window on 26 March, leading to high standard errors. For this latter window centred on 26 March, the decrease in c(DIC) over time between 25 and 30 March caused this high uncertainty. We use an 8 d time-centred moving window to reduce the potential effect of biologically related concentrations on the mean gradients, typically seen on short timescales. However, as demonstrated here, a trade-off is the higher uncertainty. Additional gliders deployed in future missions could potentially decrease the uncertainty associated with F_adv by combination of alternative sampling strategies, leading to more measurements in horizontal space and thus improving the robustness of the plane fits.

We initially explored using the glider DACs to reference geostrophic shear, required to estimate F_adv. However, DAC v velocities were positive throughout most of the deployment period in an area where negative v velocity is expected, as seen in satellite data products (Fig. 8). We think the erroneous DAC v velocities relate to the glider's roll during flight, which was consistently $>\mathrm{100}{}^{\circ }$ starboard. The disadvantage of using OSCAR velocities to derive velocity profiles relates to resolution; OSCAR velocities are derived every 8 d on a grid with 0.25^∘ resolution.

The N_b estimates incorporate measurements at a depth of approximately 10 m that we extrapolate over the average euphotic depth (z_lim=46 m), while N_g estimates account for the vertical variability between the surface and z_lim. This means that the glider-based N estimates should in principle be more accurate. It also explains why the buoy-based inventory changes are larger than for the glider, due to concentrations varying more near the surface than at depth.

We chose z_lim=46 m as the integration depth for estimating N. We investigated the sensitivity of the integration depth to N estimates by estimating N over the top 36 m and top 56 m of the water column. We found that N estimates are not very sensitive to the integration depth; e.g. using z_lim=36 m, we obtain N values between (11±28) and (113±75) $\mathrm{mmol}{\mathrm{m}}^{-\mathrm{2}}{\mathrm{d}}^{-\mathrm{1}}$ for the period 19 March to 3 April. Using z_lim=56 m, we obtain N values between (3±44) and (147±109) $\mathrm{mmol}{\mathrm{m}}^{-\mathrm{2}}{\mathrm{d}}^{-\mathrm{1}}$.

8 Conclusions

The spring bloom started in this area of the northwestern Mediterranean Sea around 19 March 2016. We identified the spring bloom through a decrease in the DIC concentration (inferred from a pH increase) and an increase in the oxygen concentration. The spring bloom followed a period of high winds and a well-mixed higher nutrient water column. The glider also detected increased optical backscatter with spikes on 19 and 20 March, an indication of increased particle concentrations. The spring bloom start date fell into the time frame of phytoplankton blooms in previous years according to buoy-based sensors. However, this was the first time that high-resolution glider profiles were available, providing insights into the biogeochemical and physical processes at depth and in waters horizontally surrounding the DyFAMed mooring.

This study demonstrates the potential of using autonomous glider measurements for estimating net community production (N). It is the first study of this kind in the northwestern Mediterranean Sea. Both oxygen and dissolved inorganic carbon concentrations were used to derive mass budgets, taking into account N, air–sea gas exchange, horizontal advection, vertical entrainment and diapycnal eddy diffusion. Estimating N using different data sets was challenging, which is reflected in the range of N estimates and their uncertainties presented here. We found that day-to-day variations in derived N estimates were dominated by net inventory changes, air–sea exchange and horizontal advection. Entrainment only came into play on 7 out of 25 d, i.e. during periods when the mixed-layer depth deepened beyond the integration limit of the mean euphotic zone depth of 46 m. Diapycnal eddy diffusion was negligible at all times. Over the duration of the deployment from 10 March to 3 April, we estimate N over the mean euphotic zone depth to be ($-\mathrm{17}\pm \mathrm{36}$) $\mathrm{mmol}{\mathrm{m}}^{-\mathrm{2}}{\mathrm{d}}^{-\mathrm{1}}$ based on glider O₂, (44±94) $\mathrm{mmol}{\mathrm{m}}^{-\mathrm{2}}{\mathrm{d}}^{-\mathrm{1}}$ based on glider DIC, ($-\mathrm{17}\pm \mathrm{37}$) $\mathrm{mmol}{\mathrm{m}}^{-\mathrm{2}}{\mathrm{d}}^{-\mathrm{1}}$ based on buoy O₂ and (49±86) $\mathrm{mmol}{\mathrm{m}}^{-\mathrm{2}}{\mathrm{d}}^{-\mathrm{1}}$ based on buoy DIC. Within their uncertainties these values agree and show net metabolic balance. Unlike previous studies in this region of the northwestern Mediterranean Sea, our results and their uncertainties explicitly consider the role of horizontal advection.

We showed that advection can potentially be significant in the area of our study, bearing in mind that the associated uncertainty was high. Daily mean N values estimated from point measurements typical of fixed moorings were affected by advection on some days. Advection may also be relevant on timescales longer than 1 month, but the current study was too short to explore this. However, when the advection flux was averaged over the 25 d period, there was less of an effect on N, suggesting that at least in this region, its importance might diminish for longer integration periods. To better resolve the influence of advection on shorter timescales and reduce its uncertainty, similar future studies should increase the number of gliders circumnavigating the central mooring so that averaging intervals can be reduced and the time resolution can be enhanced.

This was the second test deployment of the prototype ISFET sensors on gliders, following our first test in 2014 (Hemming et al., 2017). There were still considerable problems with drift and a need for calibration. Since then, Saba et al. (2018) and Takeshita et al. (2021) had more success with a Sea-Bird Scientific ISFET sensor and a Deep-Sea-DuraFET sensor, respectively. However, these sensors are not yet commercially available for gliders.

Appendix A: Discrete water samples

Water samples used to measure c(O₂) were collected at the DyFAMed site on 7 March (n=10) and 16 April 2016 (n=8) using 12 L Niskin bottles (General Oceanics 1010X) from the top 1000 m of the water column; four samples each were from the top 100 m (Fig. B1b). Reagents needed for the fixation of oxygen were added to the samples at the time of water sample collection on board the ship. An automated Winkler titration method with endpoint detection was used after each cruise in the laboratory at the Observatoire Océanologique de Villefranche-sur-Mer, France, to determine c(O₂). Replicates were obtained to determine precision. c(O₂) measured by the rosette-mounted SBE43 sensor within the top 150 m was 15 mmol m⁻³ higher than the Winkler measurements (Fig. B1b). SBE 43 sensor c(O₂) was corrected by regressing against the Winkler c(O₂) values. The resulting regression coefficients were 0.892 ± 0.009 for slope and $(\mathrm{18.7}\pm \mathrm{2.0})\mathrm{mmol}{\mathrm{m}}^{-\mathrm{3}}$ for intercept on 7 March (r²=0.9993; σ=0.9 mmol m⁻³). The corresponding values on 16 April were 0.920 ± 0.008 and $(\mathrm{11.8}\pm \mathrm{1.6})\mathrm{mmol}{\mathrm{m}}^{-\mathrm{3}}$ (r²=0.9997; σ=0.7 mmol m⁻³).

A Marianda Versatile INstrument for the Determination of Titration Alkalinity (VINDTA 3C; https://www.marianda.com, last access: 20 August 2022) was used to measure c(DIC) and A_T at 10 depth levels. A total of 19 bottles of certified reference material (CRM) supplied by Scripps Institution of Oceanography (San Diego, California, USA) were run to calibrate the instrument. Coulometry following standard operating procedure SOP 2 was used to measure c(DIC) (Dickson et al., 2007; Johnson et al., 1985), and potentiometric titration following SOP 3b was used to measure A_T (Dickson et al., 2007).

Nutrients at DyFAMed were measured using water collected in the same Niskin bottles as those used for c(O₂), c(DIC) and A_T. Samples were analysed via a standard automated colorimetry system (Seal Analytical continuous flow AutoAnalyser III) at Observatoire Océanologique de Villefranche-sur-Mer for NO${}_x^{-}$ (nitrate NO${}_{\mathrm{3}}^{-}$ and nitrite NO${}_{\mathrm{2}}^{-}$ combined) (Bendschneider and Robinson, 1952), Si(OH)₄ (Murphy and Riley, 1962) and PO${}_{\mathrm{4}}^{\mathrm{3}-}$ (Strickland and Parsons, 1972), with detection limits of 0.01, 0.02 and 0.02 mmol m⁻³, respectively (de Fommervault et al., 2015).

Appendix B: Glider calibrations

B1 O₂ measurements

Glider c(O₂) values were calibrated to take into account the response time (τ) of the sensor, which is dependent on the thickness, and usage of the sensor foil (McNeil and D'Asaro, 2014), as well as temperature, and to account for the difference between the glider measurements and c(O₂) obtained by the ship (Fig. B1b) (Binetti et al., 2020; Hemming et al., 2017). To correct c(O₂) measured by the glider sensor, the sensor-related oxygen engineering parameters TCPhase and CalPhase were used. A mean τ of 8 s was applied to correct measurements for the sensor time lag. This mean τ value was determined from the lowest root mean square difference between descending and ascending TCPhase profiles shifted in time by values of τ ranging from 0 to 50 s. After lag correction of the glider TCPhase, the relationship between the ship sensor pseudo-CalPhase measured on 7 March and on 16 April and the glider TCPhase measured on 8 March and on 4 April was determined (Fig. B1a). The ship sensor pseudo-CalPhase was calculated from the calibrated ship sensor c(O₂) by inverting the set of equations normally used to obtain c(O₂) from glider optode TCPhase and CalPhase. The slope and offset coefficients obtained from the relationship between the glider TCPhase over the entire deployment time period and ship sensor pseudo-CalPhase on 7 March and 16 April (Fig. B1a) were linearly interpolated over the duration of the deployment. The interpolated coefficients were matched with glider measurements in time and used to correct all glider CalPhase profiles obtained during the deployment, allowing a calibration of glider c(O₂) (Fig. B1b). After calibration, the glider c(O₂) agreed with buoy c(O₂) (Fig. B1c), as would be expected because the same Winkler samples were used to calibrate ship and buoy oxygen sensors.

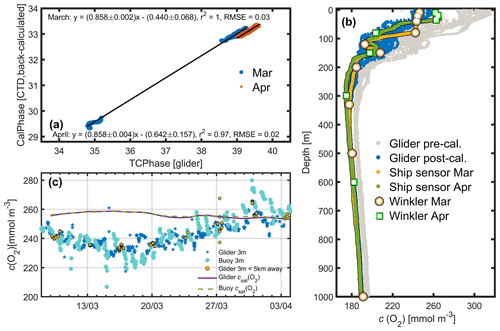
Figure B1 Calibration of the glider dissolved oxygen concentration (c(O₂)) sensor. (a) The linear regression fit using back-calculated ship pseudo-CalPhase and glider TCPhase for 7 March (blue) and 16 April (orange), along with the corresponding linear equations, r² and root-mean-squared errors (RMSE). The 95 % confidence bounds are also shown. (b) Glider c(O₂) measured on 8–9 March and on 3–4 April before (grey), and after (blue) calibration, the ship sensor c(O₂) on 7 March (yellow) and on 16 April (green), and the c(O₂) Winkler samples on 7 March (white with orange border) and on 16 April (white with green border). (c) All glider sensor c(O₂) at 3 m depth (blue stars), <5 km away from the BOUSSOLE buoy only (turquoise spots) and glider c_sat (purple line) are compared with the BOUSSOLE buoy sensor c(O₂) measurements (orange spots) at 3 m depth and buoy c_sat (green dashed line).

B2 ISFET pH measurements

The deployment offered a second opportunity to trial two prototype ISFET pH–p(CO₂) sensor pairs, previously tested on an underwater glider in the Sardinian Sea during the REP14–MED experiment (Hemming et al., 2017; Onken et al., 2018). The sensors are custom-built non-commercially by Kiminori Shitashima's group at Tokyo University of Marine Science and Technology, Japan. ISFET sensors measure pH using the interface potential between a reference chlorine electrode (Cl-ISE) and a semiconducting ion sensing transistor (Hemming et al., 2017).

One pH–p(CO₂) sensor pair was stand-alone, meaning measurements were logged and stored by the sensor and retrieved after the deployment. Another sensor pair was integrated into the glider electronics, allowing measurements to be sent remotely by satellite in near-real time. Both the stand-alone and integrated sensors were positioned on the underside of the glider to limit the effect of sunlight on measurements, and backup batteries were provided to supply power in between sampling (Hemming et al., 2017). Unfortunately, the stand-alone sensor ceased operating after less than 3 d around 07:00 CET on 10 March because of an issue with its power supply. For this reason, pH_T obtained by the stand-alone sensor was not used. The sensors were placed in a bucket of locally collected coastal surface seawater for a period of 10 h before deployment. Several weeks of pre-deployment conditioning have been recommended (Bresnahan et al., 2014; Takeshita et al., 2014), but this was not possible due to time constraints.

A comparison of sensor measurements with pH_T calculated from discrete c(DIC) and A_T measurements both during the deployment and with archived data from between 1998 and 2013 at the DyFAMed site (http://mistrals.sedoo.fr/Data-Download, last access: 20 August 2022) indicated problems in accuracy and stability (Fig. B2). The pH_T of the integrated sensor drifted by 0.8 over the course of the 29 d deployment, with a depth-dependent range in pH_T of 1.

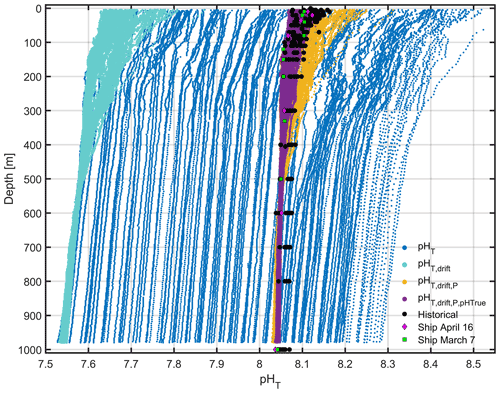
Figure B2 A comparison of glider pH_T after various corrections have been applied. Raw pH_T (blue) is corrected for drift (turquoise) and subsequently for pressure effects (yellow). Finally pH_T is compared with “true” ship pH_T and corrected (purple). Historical pH_T anomalies (black) collected in March and April between 1998 and 2013 are shown for comparison, alongside the ship pH_T on 7 March (green squares) and 16 April (pink diamonds).

pH_T measurements were corrected for drift using the mean difference (offset) between dive 10 pH_T measured between 350 and 950 m and pH_T measured at the same depths during each subsequent dive. This method assumes that pH_T variations over the 29 d deployment between 350 and 950 m are negligible with respect to the sensor precision. The offsets were added to the full-depth glider pH_T profiles, and the range of pH_T was reduced 3-fold to approximately 0.3 (Fig. B2).

After correcting pH_T for drift, pH_T was corrected for pressure using a pressure coefficient of $+\mathrm{5.6}\times {\mathrm{10}}^{-\mathrm{5}}$ dbar⁻¹. After adding this correction term, the range of pH_T was reduced to approximately 0.2 (Fig. B2).

Finally, integrated ISFET pH_T values were corrected relative to “true” discrete pH_T. Regression coefficients calculated using glider drift- and pressure-corrected pH_T and ship pH_T collected on 7 March and on 16 April were used to correct glider pH_T. The range of glider pH_T was now matched with that of historical discrete samples (Fig. B2).

Appendix C: Deriving parameters using CO2SYS

The CO2SYS software package (Van Heuven et al., 2011; Orr et al., 2015) was used to derive discrete pH_T for correcting glider ISFET pH_T, using discrete measurements of c(DIC), A_T, in situ temperature, salinity, pressure, and Si(OH)₄ and ${\mathrm{PO}}_{\mathrm{4}}^{\mathrm{3}-}$ concentrations. Equilibrium constants (Mehrbach et al., 1973; Dickson and Millero, 1987), sulfate acid dissociation constant (Dickson, 1990) and total borate concentration (Uppström, 1974) were used, as recommended by previous Mediterranean-based studies (Álvarez et al., 2014; Key et al., 2010). c(DIC) and A_T had an uncertainty of 3.5 and 3.2 µmol kg⁻¹, respectively, determined from CRM measurements, representing a combined uncertainty of 0.008 in derived pH_T.

The A_T–S relationship was determined using A_T and salinity measurements from discrete ship samples collected in spring 2016 above the salinity maximum (n=20). This parameterisation, $A_{\mathrm{T}}/\mathrm{\mu }\mathrm{mol}{\mathrm{kg}}^{-\mathrm{1}}=(\mathrm{80.72}\pm \mathrm{10})(S-\mathrm{38})+\mathrm{2551}\pm \mathrm{4}$ (r²=0.88; σ=5.7 µmol kg⁻¹), was used to obtain A_T from glider and buoy salinity.

Calibrated glider pH_T and A_T were used to derive glider f(CO₂) and c(DIC) using CO2SYS. The mean uncertainties of derived f(CO₂) and c(DIC) were 5.3 µatm and 4.1 µmol kg⁻¹, respectively, calculated as the mean of the absolute differences of f(CO₂) and c(DIC) derived using single values of A_T and pH (including the margin of error associated with the A_T–S relationship and the pH_T pressure correction, respectively).

To obtain buoy c(DIC), observed f(CO₂) at 10 m was used with A_T calculated from S. The uncertainty of derived buoy c(DIC) was 6.6 µmol kg⁻¹, calculated as the absolute difference between the ship c(DIC) sample collected on 7 March at 10 m depth and average c(DIC) measured by the buoy on the same day.