Tidal variability in the Hong Kong region

Mean sea level (MSL) is rising worldwide, and correlated changes in ocean tides are also occurring. This combination may influence future extreme sea levels, possibly increasing coastal inundation and nuisance flooding events in sensitive regions. Analyses of a set of tide gauges in Hong Kong reveal complex tidal behavior. Most prominent in the results are strong correlations of MSL variability to tidal variability over the 31-year period of 1986–2016; these tidal anomaly correlations (TACs) express the sensitivity of tidal amplitudes and phases (M₂, S₂, K₁, O₁) to MSL fluctuations and are widely observed across the Hong Kong region. At a few important harbor locations, time series of approximations of the parameter δ-HAT, computed from combinations of the major tidal constituents, are found to be highly sensitive to MSL variability, which may further increase local flood levels under future MSL rise. Other open-water locations in Hong Kong only show TACs for some individual tidal constituents but not for combined tidal amplitudes, suggesting that the dynamics in enclosed harbor areas may be partially frequency dependent and related to resonance or frictional changes. We also observe positive correlations of the fluctuations of diurnal (D₁) tides to semidiurnal (D₂) tides at most locations in the region, which may lead to further amplified tidal ranges under MSL. It is demonstrated here that tidal changes in the Hong Kong coastal waters may be important in combination with MSL rise in impacting future total water levels.

1 Introduction

Ocean tides have long been thought of as a stationary process as they are driven by the gravitational forcing of the Sun and Moon whose motions are complex but highly predictable (Cartwright and Tayler, 1971). Yet, long-term changes in the tides have been observed recently on regional (Ray, 2006; Jay, 2009; Zaron and Jay, 2014; Rasheed and Chua, 2014; Feng et al., 2015; Ross et al., 2017) and global spatial scales (Woodworth, 2010; Müller et al., 2011; Haigh et al., 2014; Mawdsley et al., 2014), concurrent with long-term global mean sea level (MSL) rise (Church and White, 2006, 2011). Since gravitational changes are not the reason for this, the tidal changes are likely related to terrestrial factors such as changes in water depth – which can alter friction (Arbic et al., 2009), coastal morphology, and resonance changes in harbor regions (Cartwright, 1972; Bowen and Gray, 1972; Amin, 1983; Vellinga et al., 2014; Jay et al., 2011; Chernetsky et al., 2010; Familkhalili and Talke, 2016) – or stratification changes induced by increased upper-ocean warming (Domingues et al., 2008; Colosi and Munk, 2006; Müller, 2012; Müller et al., 2012), all of which are also related to sea level rise.

Tides can also exhibit short-term variability correlated to short-term fluctuations in MSL (Devlin et al., 2014, 2017a, b). These variabilities may influence extreme water level events, such as storm surge or nuisance flooding (Sweet and Park, 2014; Cherqui et al., 2015; Moftakhari et al., 2015, 2017; Ray and Foster, 2016; Buchanan et al., 2017). Such short-term extreme events are obscured when only considering long-term linear trends. Any significant additional shorter-term positive correlation between tides and sea level fluctuations may amplify this variability and would imply that flood risk based only on the superposition of present-day tides and surge onto a higher baseline sea level will be inaccurate in many situations. The analysis of the correlations between tides and sea level at a local or regional scale can indicate locations where tidal evolution should be considered a substantial complement to sea level rise. Moreover, since storm surge is a long-wave process, factors affecting tides can also alter storm surge (Familkhalil and Talke, 2016; Arns et al., 2017). Hong Kong is often subject to typhoons, with some recent storms yielding anomalously high storm surges, so this issue is of critical interest if all such factors are undergoing change.

Recent works surveyed tidal anomaly correlations (TACs) at multiple locations in the Pacific; a TAC quantifies the sensitivity of tides to short-term sea level fluctuations (Devlin et al., 2014, 2017a); they found that over 90 % of tide gauges analyzed exhibited some measure of correlation in at least one tidal component. In a related work (Devlin et al., 2017b), the combined TACs of the four largest tidal components was calculated as a proxy for what can be described as changes in the highest astronomical tide (δ-HAT), with 35 % of gauges surveyed exhibiting a sensitivity of δ-HATs to sea level fluctuations of at least ±50 mm under a 1 m sea level change (∼5 %). A step-by-step description of the TAC and δ-HAT methods, including the details of the calculations of the regressions and statistics, can be found in the supplementary materials of Devlin et al. (2017a, b), and in this paper we summarize the meaning and interpretations of the TACs and the δ-HATs in the Appendix.

A recent paper performed a similar analysis in the Atlantic Ocean, finding comparable results to the Pacific (Devlin et al., 2019). Comparing all worldwide locations found that the greatest (positive) δ-HAT response was seen in Hong Kong (+650 mm m⁻¹). A probability distribution function analysis revealed that an extreme sea level exceedance which includes tidal changes can be nearly double (+150 mm) that which only considers MSL exceedance alone (+78 mm) over the past 50 years (Devlin et al., 2017b). However, this approach did not consider water level extremes due to nontidal or non-MSL factors, such as storm surge, which may further complicate extreme water levels. Yet, even without storm surge included, it was demonstrated that the nonstationarity of tides can be a significant contributor to total (non-storm) water levels in this region and warrants closer examination. Furthermore, tides and storm surge are both long-wave processes and may be sensitive to the same forcing factors, so the behavior of tides may be a possible instructor of the future behavior of storm surge events.

Hong Kong and Pearl River Delta (PRD) regions contain many densely populated areas with extensive coastal infrastructure and significant and continuous recent land reclamation projects. Sea level rise in the region has exhibited a variable rate in the region over the past 50 years (Li and Mok, 2012; Ip and Wai, 1990) but a common feature of all sea level records in the South China Sea (SCS) is a steep increase in the late 1990s with a subsequent decrease in the early 2000s, followed by a sustained increase to the present day. In addition to this variable MSL behavior, there are also anomalous tidal events observed at gauges in semi-enclosed harbor regions during the late 1990s and early 2000s (shown and discussed below), corresponding to times of both rapidly changing sea level and aggressive land reclamation. In this study, we perform a spatial and temporal analysis of tidal sensitivity to MSL variations in Hong Kong using the tidal anomaly correlation (TAC) method at 12 closely located tide gauges.

2 Methods

2.1 Data sources

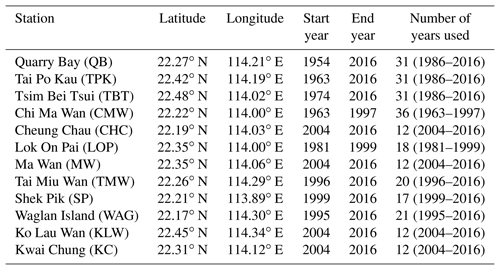
A set of 12 tide gauge records in the Hong Kong region was provided by the Hong Kong Observatory (HKO) and the Hong Kong Marine Department (HKMD), spanning from 12 to 63 years in length, including two gauges that are “historical” (i.e., no longer operational). The longest record is the North Point/Quarry Bay tide gauge, located in Victoria Harbour, established originally in 1952 and relocated from North Point to Quarry Bay in 1986. The datums were adjusted and quality controlled by HKO to provide a continuous record (Ip and Wai, 1990). Another long and continuous record is located at Tai Po Kau inside Tolo Harbour. Gauge locations in Hong Kong are shown in Fig. 1, with the gauges from HKO indicated by green markers, gauges from HKMD by light blue, and historical (nonoperational) gauges by red. Four of six of the HKO gauges (Quarry Bay, Tai Po Kau, Tsim Bei Tsui, and Waglan Island) are sea level pressure transducer types, and the other two (Shek Pik and Tai Miu Wan) are pneumatic-type tide gauges. The Quarry Bay gauge was recently updated from a float-type gauge (2017), and the Tai Po Kau gauge was also updated from a float gauge in 2006, and all gauges operated by the HK Marine Department were set up in 2004 as sea level pressure transducers (https://www.hko.gov.hk/publica/pubsmo.htm, last access: 1 June 2019).

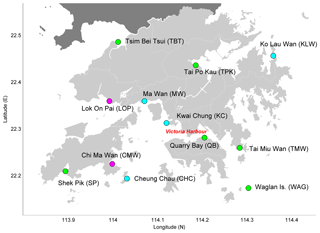
Figure 1 Tide gauge locations in Hong Kong used in this study. Green markers indicate active gauges provided by the Hong Kong Observatory (HKO), light blue markers indicate gauges provided by the Hong Kong Marine Department (HKMD), and red markers indicate historical gauges (once maintained by HKO) that are no longer operational.

Figure 2 shows the geographical setting of the South China Sea, with the location of Hong Kong indicated by the red box. Table 1 lists the metadata for all locations, including station name and station code, latitude, etc., and the ranges of the data records used in this study.

Figure 2 Location of Hong Kong in the South China Sea shown by the red box with some major oceanographic features labeled. Depth is given by the color bar in units of meters.

Table 1 Metadata for all tide gauge locations, giving the station names and station codes, latitude/longitude, year of the available records, and the range of data analyzed.

2.2 Tidal admittance calculations

Our investigations of tidal behavior use a tidal admittance method. The tidal admittance is the unitless ratio of an observed tidal constituent to the corresponding tidal constituent in the astronomical tide-generating force expressed as a potential, V. This potential can then be divided by the acceleration due to gravity, g, to yield $Z_{\mathrm{pot}}\left(t\right)=V/g$, with units of length that can be compared to tidal elevations, Z_obs(t). Yearly harmonic analyses are performed on both Z_obs(t) and Z_pot(t) at each location using the R_T_TIDE package for MATLAB (Leffler and Jay, 2009), a robust analysis suite based on T_TIDE (Pawlowicz et al., 2002). The tidal potential is determined based on the methods of Cartwright and Tayler (1971).

The result from a single harmonic analysis of Z_obs(t) or Z_pot(t) determines an amplitude, A, and phase, θ, at the central time of the analysis window for each tidal constituent, with error estimates. A moving analysis window (e.g., at mid-year) produces an annual time series of amplitude, A(t), and phase, θ(t), with the complex amplitude, Z(t), given by

$$\begin{array}{}\text{(1)}& Z\left(t\right)=A\left(t\right)e^{i\mathit{\theta }\left(t\right)}.\end{array}$$

The tidal admittance (A) and phase lag (P) are formed using Eqs. (2) and (3)

$$\begin{array}{}\text{(2)}& {\displaystyle }& {\displaystyle }A\left(t\right)=\mathrm{abs}∥{\displaystyle \frac{Z_{\mathrm{obs}}\left(t\right)}{Z_{\mathrm{pot}}\left(t\right)}}∥,\text{(3)}& {\displaystyle }& {\displaystyle }P\left(t\right)={\mathit{\theta }}_{\mathrm{obs}}\left(t\right)-{\mathit{\theta }}_{\mathrm{pot}}\left(t\right).\end{array}$$

Nodal variabilities are typically present with similar strengths in both the observed tidal record and in the tidal potential. Therefore, when the observed data (harmonically analyzed in 1-year windows) are divided by the potential (also analyzed in 1-year windows), nodal effects are mostly constrained in the resulting admittance time series. This may not always hold true in shallow-water areas (Amin, 1983) but does seem valid for the locations and tides analyzed in Hong Kong. The harmonic analysis procedure also provides an annual MSL time series. For each resultant dataset (MSL, A and P), the mean and trend are removed from the time series to allow direct comparison of their covariability. The magnitude of the long-term trends is typically much less than the magnitude of the short-term variability, which is more apparent in the datasets used here (Devlin et al., 2017a, b).

Tidal sensitivity to sea level fluctuations is quantified using tidal anomaly correlations (TACs), the relationships of detrended tidal variability to detrended MSL variability (see Appendix). With the use of the TACs we determine the sensitivity of the amplitude and phase of individual constituents (M₂, S₂, K₁, O₁) to sea level perturbations at the yearly-analyzed scale. We also consider a proxy for the change in the approximate highest astronomical tide (δ-HAT; see Appendix for details). The approximation δ-HAT reflects the maximum tide-related water level that would be obtained in a year from a combination of time-dependent amplitudes and phases of the four largest tidal constituents (M₂, S₂, K₁, and O₁) extracted by the admittance method, typically ∼75 % of the full tidal range.

The detrended time series of the year-to-year change in the δ-HATs are compared to detrended yearly MSL variability in an identical manner as the TACs, and both are expressed in units of millimeter change in tidal amplitude per 1 m fluctuation in sea level (mm m⁻¹). These units are adopted for convenience, though in practice the observed fluctuations in MSL are on the order of ∼0.25 m. The phase TACs are reported in units of degree change per 1 m fluctuation in sea level. The TAC methodology can also be used to examine correlations between different parts of the tidal spectrum. We additionally examine the sensitivity of combined diurnal (D₁: K₁+O₁) tidal amplitudes to semidiurnal (D₂: M₂+S₂) tidal amplitudes (D₁∕D₂ TACs). The units of the D₁∕D₂ TACs are dimensionless (i.e., mm mm⁻¹) and statistics are calculated as above.

The use of a window of a year in a harmonic analysis may have an influence on the value of the TAC or δ-HAT, e.g., calendar year (January–December) vs. water year (October–September). To provide a better estimate of the overall correlations for all data we take a set of determinations of the correlations using 12 distinct year definitions (i.e., 1-year windows running from January–December, February–January, …, December–January). We take the average of the set of significant determinations (i.e., p values of <0.05) as the magnitude of the TAC or δ-HAT. For an estimate of the confidence interval of the TAC or δ-HAT, the interquartile range (middle 50 % of the set) is used.

For the very long record stations (e.g., Quarry Bay and Tai Po Kau), we only consider the past 31 years for TAC and δ-HAT determinations (Table 1). The TAC values may change over time so we adopt a common epoch to better match the rest of the Hong Kong tide gauge networks, which are typically ∼12–31 years long. Finally, we highlight some anomalous tidal events observed at certain Hong Kong gauges and discuss the temporal evolution of the tidal characteristics in Hong Kong.

3 Results

The individual TACs for amplitude and phase in Hong Kong are discussed first, followed by the δ-HATs and the D₁∕D₂ TACs. In all figures, significant positive results will be reported by red markers, significant negative results by blue markers, and insignificant values are shown as black markers. The relative size of the markers will indicate the relative magnitude of the TAC or δ-HAT according to the legend scale on each plot. All numerical results for the major amplitude TACs (M₂, S₂, K₁, and O₁) are listed in Table 2, and the δ-HATs and D₁∕D₂ TACs are listed in Table 3. Phase TACs of the individual constituents are reported in Table S1 of the Supplement.

Table 2 Amplitude TACs for M₂, S₂, K₁, and O₁ for the period of 1986–2016. All values given are in units of millimeter change in tidal amplitude for a 1 m fluctuation in sea level (mm m⁻¹). Statistically significant positive values are given in bold text.

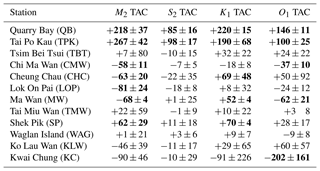
Table 3 The δ-HAT and D₁∕D₂ TACs for the period of 1986–2016. The δ-HAT values given are in units of millimeter change in tidal amplitude for a 1 m fluctuation in sea level (mm m⁻¹). D₁∕D₂ TACs are in unitless ratios (i.e., mm mm⁻¹). Statistically significant values are given in bold text.

3.1 Tidal anomaly correlations (TACs)

The strongest positive M₂ TACs are seen at Quarry Bay ($+\mathrm{218}\pm \mathrm{37}$ mm m⁻¹) and at Tai Po Kau ($+\mathrm{267}\pm \mathrm{42}$ mm m⁻¹) with a smaller positive TAC seen at Shek Pik (Fig. 3). In the waters west of Victoria Harbour, all other gauges except Kwai Chung exhibit moderate negative TACs. The semidiurnal phase TACs in Hong Kong (shown in the Supplement, Fig. S1) show an earlier M₂ tide under higher MSL at Quarry Bay and Tai Po Kau and a later tide west of Victoria Harbour. The S₂ results in Hong Kong (Fig. 4) show that only Quarry Bay and Tai Po Kau have significant amplitude TAC values (though smaller than M₂) and the S₂-phase TACs in Hong Kong (Fig. S2) also show an earlier tide at Quarry Bay and Tai Po Kau under higher MSL.

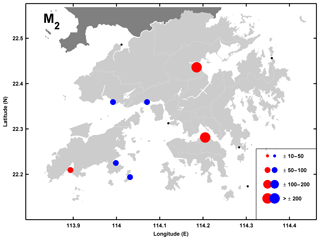
Figure 3 Tidal anomaly correlations (TACs) of detrended M₂ amplitude to detrended MSL in Hong Kong with the marker size showing the relative magnitude according to the legend in units of mm m⁻¹. Red/blue markers indicate positive/negative TACs and black markers indicate TACs which are not significantly different from zero.

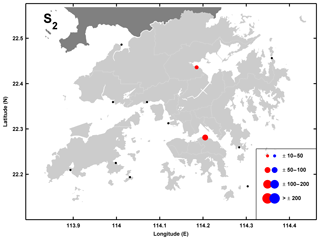
Figure 4 Tidal anomaly correlations (TACs) of detrended S₂ amplitude to detrended MSL in Hong Kong with the marker size showing the relative magnitude according to the legend in units of mm m⁻¹. Red/blue markers indicate positive/negative TACs and black markers indicate TACs which are not significantly different from zero.

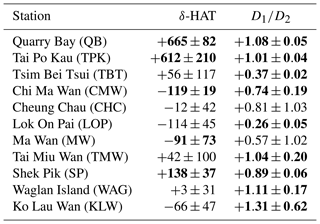
The diurnal TACs in Hong Kong generally exhibit a larger-magnitude and more spatially coherent response than semidiurnal TACs. Like M₂, the strongest K₁ values in Hong Kong (Fig. 5) are seen at Quarry Bay ($+\mathrm{220}\pm \mathrm{15}$ mm m⁻¹) and Tai Po Kau ($+\mathrm{190}\pm \mathrm{68}$ mm m⁻¹). The O₁ results in Hong Kong (Fig. 6) are like the M₂ results showing positive TACs at Quarry Bay ($+\mathrm{146}\pm \mathrm{11}$ mm m⁻¹) and Tai Po Kau ($+\mathrm{100}\pm \mathrm{25}$ mm m⁻¹) and strongly negative TACs west of Quarry Bay. However, unlike the semidiurnal constituents, the phase TACs for K₁ are mostly insignificant in Hong Kong (Fig. S3) and O₁ phase TACs (Fig. S4) are only significant at Quarry Bay.

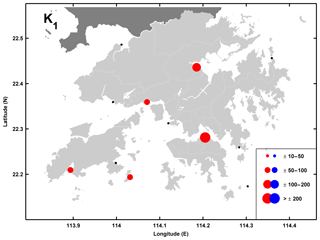
Figure 5 Tidal anomaly correlations (TACs) of detrended K₁ amplitude to detrended MSL in Hong Kong with the marker size showing the relative magnitude according to the legend in units of mm m⁻¹. Red/blue markers indicate positive/negative TACs and black markers indicate TACs which are not significantly different from zero.

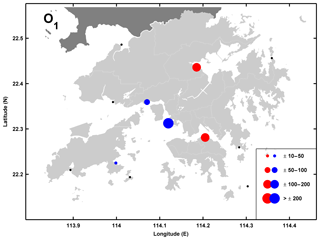
Figure 6 Tidal anomaly correlations (TACs) of detrended O₁ amplitude to detrended MSL in Hong Kong with the marker size showing the relative magnitude according to the legend in units of mm m⁻¹. Red/blue markers indicate positive/negative TACs and black markers indicate TACs which are not significantly different from zero.

3.2 Combined tidal variability (δ-HATs) and tidal covariability

The TACs are widely observed in Hong Kong but the δ-HATs are only of significance at particular locations (Fig. 7). Five stations exhibit significant δ-HAT values with Quarry Bay and Tai Po Kau having very large positive magnitudes ($+\mathrm{665}\pm \mathrm{85}$ mm m⁻¹ and $+\mathrm{612}\pm \mathrm{210}$ mm m⁻¹, respectively) and Shek Pik having a lesser magnitude of $+\mathrm{138}\pm \mathrm{47}$ mm m⁻¹. Conversely, Ma Wan and Chi Ma Wan exhibit moderate negative δ-HAT values ($\sim -\mathrm{100}$ mm m⁻¹). The remainder of gauges (which are mainly open-water locations) have statistically insignificant results for the combined tidal amplitudes, even where some large individual TACs were observed. This shows that the combined tidal amplitude effect as expressed by the δ-HATs is most important in semi-enclosed harbors. The D₁∕D₂ TACs are also important in Hong Kong and are seen at almost every location. All significant D₁∕D₂ TACs results are positive (Fig. 8) and at most locations the correspondence is nearly 1 to 1, indicating that a change in D₁ can yield a nearly identical magnitude change in D₂, and vice versa. Smaller magnitude relations are seen in the western areas of the Hong Kong region.

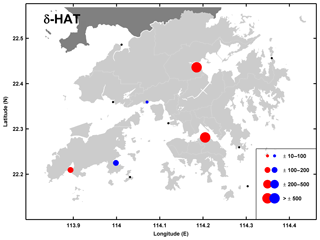
Figure 7 The tidal anomaly correlation computed from the combination of the four largest tidal constituent amplitudes (given by the detrended sum of $M_{\mathrm{2}}+S_{\mathrm{2}}+K_{\mathrm{1}}+O_{\mathrm{1}}$) as a proxy for the change in the approximate highest astronomical tide (δ-HAT) relative to detrended MSL in Hong Kong with the marker size showing the relative magnitude according to the legend in units of mm m⁻¹. Red/blue markers indicate positive/negative TACs and black markers indicate TACs which are not significantly different from zero.

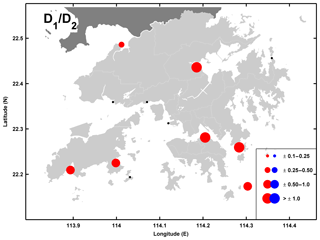
Figure 8 The D₁∕D₂ TACs; the relations of detrended diurnal tidal amplitude sum (D₁: K₁+O₁) to detrended semidiurnal tidal amplitude sum (D₂: M₂+S₂) in Hong Kong with the marker size showing the relative magnitude according to the legend in dimensionless units. Red/blue markers indicate positive/negative TACs and black markers indicate TACs which are not significantly different from zero.

3.3 Anomalous tidal events at Hong Kong harbor locations

The overall temporal behavior of the tidal spectrum at enclosed harbor locations in Hong Kong (Quarry Bay and Tai Po Kau) is especially interesting. In Fig. 9, the time series of water level spectrum components are shown for Quarry Bay and Tai Po Kau, presenting the D₁ (K₁+O₁) band (Fig. 9a), the D₂ (M₂+S₂) band (Fig. 9b), and mean sea level (MSL) (Fig. 9c), given as normalized amplitudes with mean values shown in the legends. The magnitude of MSL is given in relation to the Hong Kong Chart Datum as defined by the Hong Kong Observatory. The Chart Datum is defined as 0.146 m below the Hong Kong Principal Datum (HKPD). The HKPD determined for the years 1965–1983 was approximately 1.23 m below MSL. The HKPD has been recently redetermined using data from 1997–2015 to be 1.30 m below MSL. Therefore, all MSL values reported here are given relative to the HKPD for the epoch 1965–1985 (https://www.hko.gov.hk/contente.htm, last access: 1 March 2019).

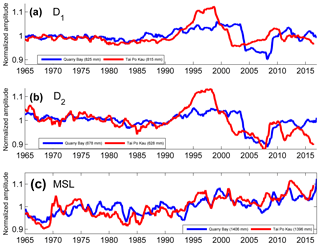
Figure 9 Time series of water level spectrum components at Quarry Bay (QB; blue) and Tai Po Kau (TPK; red) tide gauges in Hong Kong, showing the D₁ band (a), the D₂ band (b), and mean sea level (MSL) (c). Components are plotted as a function of normalized amplitudes to show relative variability with mean values given in the legend.

Some very notable features of the tides are clear. At Quarry Bay, the early part of the record shows nearly constant tidal amplitudes in D₁, while D₂ amplitudes show a slight decrease, and MSL exhibits a slight positive trend. In the late 1980s, however, both D₁ and D₂ increase until around the year 2003 at which time both tidal bands undergo a rapid decrease in amplitude of ∼15 %, sustaining this diminished magnitude for about 5 years before increasing nearly as rapidly. The MSL record is also highly variable at Quarry Bay, with a nearly zero trend during the increase in tides seen in the 1980s followed by a strong increase from ∼1993–2000, and then a steep decrease concurrent with the time of diminished tides before increasing again. The gauge at Tai Po Kau shows a similar tidal behavior, although the timing and magnitudes are different. The increase in D₁ and D₂ at Tai Po Kau in the 1980s is much larger and peaks earlier than Quarry Bay, reaching a maximum around 1996, and then decreasing around 1998, about 5 years before the drop at Quarry Bay. Both locations experience an absolute minimum around 2007 in D₂ but the D₁ minimum at TPK leads the Quarry Bay minimum by a few years. These observed anomalies are only observed at these two gauges; other locations in Hong Kong did not reveal similar behavior.

4 Discussion

4.1 Summary of observed tidal variability

This survey has identified several types of tidal variability in Hong Kong. The individual TACs are significant at many Hong Kong locations, while the TACs of the approximate δ-HATs appear to be more locally important, as the strongest responses are mainly concentrated at specific locations (e.g., Quarry Bay and Tai Po Kau). The M₂ response (Fig. 3) is negative at gauges just west of Quarry Bay and positive at Shek Pik, with a similar pattern seen for the O₁ TACs (Fig. 6). Conversely, the K₁ TAC results are generally positive (Fig. 5). At both Quarry Bay and Tai Po Kau, the positive reinforcements of individual tidal fluctuations lead to very large δ-HATs, though moderately negative δ-HATs are seen near Quarry Bay at Chi Ma Wan and Ma Wan (Fig. 7). The spatial similarity in the semi-enclosed center harbor regions suggest a connected mechanism; this area is where most recent Hong Kong coastal reclamation projects have occurred, including the construction of a new island for an airport, shipping channel deepening, and other coastal morphology changes. Such changes in water depth and coastal geometry strongly suggest a relation to frictional or resonance mechanisms.

The D₁∕D₂ TAC relations (Fig. 8) are a more regionally relevant phenomenon, being significant nearly everywhere in Hong Kong. The majority of significant D₁∕D₂ TACs are positive with most being nearly 1 to 1 (i.e., a ∼1 mm change in D₁ will yield a ∼1 mm change in D₂), confirmed by the close similarity of temporal tidal trends of the D₁ and D₂ tidal bands in Hong Kong (Fig. 9). This aspect of tidal variability in Hong Kong may be related to the dynamics near the Luzon Strait, where large amounts of baroclinic conversion in both D₁ and D₂ tides may tend to couple the variabilities (Jan et al., 2007, 2008; Lien et al., 2015; Xie et al., 2008, 2011, 2013). The D₁ and D₂ internal tides may interact with each other as well as with processes at other frequencies, such as at the local inertial frequency, f, via parametric subharmonic instability (PSI) interactions (McComas and Bretherton, 1977; MacKinnon and Winters, 2005; Alford, 2008; Chinn et al., 2012), a form of resonant triad interactions (Craik, 1985). The low-mode baroclinic energy can travel great distances, being enhanced upon arrival at the shelf and leading to the further generation of baroclinic energy. In the western part of Hong Kong, the D₁∕D₂ relationships are less than 1 to 1 (∼0.33 to ∼0.25 at TBT and LOP, respectively). This may be partially influenced by effects of the Pearl River, which discharges part of its flow along the Lantau Channel. The flow of the river is highly seasonal and ejects a freshwater plume at every ebb tide that varies with prevailing wind conditions and with the spring–neap cycle (Pan et al., 2014). The plumes may affect turbulence and mixing in the region and can dissipate tidal energy, which may “decouple” the correlated response of D₁ and D₂ seen in the rest of the Hong Kong coastal waters.

4.2 Effects of local dynamics on tidal variability

Hong Kong has had a long history of land reclamation to accommodate an ever-growing infrastructure and population, including the building of a new airport island (Chep Lap Kok); new land connections, channel deepening to accommodate container terminals; and many bridges, tunnels, and “new cities” built on reclaimed land. All of these may have changed the resonance and/or frictional properties of the region. Tai Po Kau has also had some land reclamation projects that have changed the coastal morphology and may have modulated the tidal response. Both locations also show coherent D₁∕D₂ TACs, as well as having the largest positive δ-HATs, and large tidal anomalies (Fig. 9). Other locations in Hong Kong did not show such extreme variations so these variations appear to only be amplified in harbor areas. Decreases in friction associated with sea level rise may lead to larger tides and those changes may also be amplified by the close correlations of D₁ and D₂ variability or local harbor development, which may further decrease local friction. Hence, a small change in friction due to a small sea level change may induce a significant change in tidal constituents. The positive reinforcement of multiple tidal constituent correlated with regional sea level adjustments may amplify the risks of coastal inundation and coastal flooding, as evidenced by the gauges that had the largest δ-HAT values.

4.3 Limitations of this study and future steps

The analysis of tides in the Hong Kong tide gauge network revealed new dynamics and spatial connections in the area. However, some records are of shorter length and/or have many gaps, making a full analysis of the area problematic. For example, the Tsim Bei Tsui gauge covers a long period but there are significant gaps in the record, which complicated our analysis. This gauge is located within a harbor region (Deep Bay, bordered to the north by Shenzhen, PRC, which has also grown and developed its coastal infrastructure in past decades; therefore, one might expect similar dynamics as was seen at Quarry Bay and Tai Po Kau. While there were moderately significant D₁∕D₂ correlations at Tsim Bei Tsui, no significant TACs or δ-HATs were observed. The large anomalies seen at Quarry Bay and Tai Po Kau around 2000 are suggested by the data at Tsim Bei Tsui but some data are missing around this time, making any conclusions speculative. The Deep Bay region is ecologically sensitive, being populated by extensive mangrove forests which may be disturbed by rapidly changing sea levels (Zhang et al., 2018), so accurate determination of future sea levels is of utmost importance to the vitality of these important ecosystems. Future studies considering highly accurate digital elevation models will employ simple analytical models as well as high-resolution three-dimensional numerical ocean models to simulate the changing impacts on coastlines under a variety of sea level, tidal forcing, and anthropogenic change scenarios (historical and future) to better understand the tidal dynamics in Hong Kong, and to try to separate the relative importance of local and regional effects. Lastly, we briefly mention the instrumental changes at two of the HKO gauges. The Quarry Bay gauge was recently updated from a float-type gauge (2017) and the Tai Po Kau gauge was also updated from a float gauge in 2006. Neither of these times correspond to any obvious anomalies in the tidal admittance records (the large changes at Tai Po Kau predate this by a few years at least, and are consistent before and after the gauge change) so we conclude that the instrumental changes were not a factor in the observed variability.

5 Conclusions

This study has presented new information about the tidal variability in Hong Kong, based on observations of a set of closely located tide gauges in Hong Kong. The TACs, D₁∕D₂ relations, δ-HATs, and the anomalous events in tidal amplitudes seen at the Quarry Bay and Tai Po Kau gauges show an amplified tidal response to MSL fluctuations in these harbor regions as opposed to more open-water locations, where individual TACs were sometimes significant but the δ-HAT changes were less significant. The reason for the observed behavior may be due to changing friction or resonance induced by coastal engineering projects that are only significant at highly local (i.e., individual harbor) scales. Alternatively, the observed behavior could be related to regional South China Sea changes due to climate change (such as increased upper-ocean warming and/or regional stratification and internal tide generation). It is difficult to separate the local engineering changes from regional climatic changes without closer investigations. However, even without exact knowledge of the relevant mechanisms, these anomalies do suggest that a pronounced change in tidal properties occurred around the year 2000 in Hong Kong, with the effect being most pronounced at gauges in semi-enclosed harbors. Overall, the tidal variability in Hong Kong documented here may have significant impacts on the future of extreme sea level in the region, especially if the strong positive reinforcements hold or increase in coming decades. Short-term inundation events, such as nuisance flooding, may be amplified under scenarios of higher sea levels that lead to corresponding changes in the tides, which may amplify small changes in water levels and/or reductions in friction due to harbor improvements. The δ-HAT and D₁∕D₂ TAC results illustrate that the tidal variability in multiple constituents may be additive and may reinforce MSL changes at some locations, which may further aggravate coastal flooding under MSL future rise. Since tides and storm surge are both long-wave processes, the locations of strong tidal response may also experience an exaggerated storm surge in the near future.

Appendix A: Methodology details

A1 Tidal anomaly correlations (TACs)

Tidal admittances are constructed as described above, employing the use of the tidal potential and Eqs. (2) and (3) to constrain the nodal variation present in the observed tidal amplitudes and phases. Our primary interest in this paper is the interannual to decadal variations and not the long-term trends in mean values. Therefore, we first remove the long-term trends and mean values using the MATLAB “detrend” function. The detrended time series of residual variations in A and P, and the residual variations in MSL, can now be examined for coherence, using scatter plots, cross correlations, and regression statistics. We define the tidal anomaly correlation (TAC) as the slope between detrended tidal properties (amplitude and phase) and detrended MSL, expressed as the millimeter change in tidal amplitude per meter of sea level rise (mm m⁻¹). The same approach is used with the phase difference time series to provide phase anomaly trends, with the trends expressed as degree change in tidal phase per meter of sea level rise (deg m⁻¹). The errors of the TAC determinations are defined as the 95 % confidence interval (CI) of the linear trend determination. Trends are deemed significant if the signal-to-noise ratio (SNR) of the linear trend to the associated error is greater than 2.0.

A2 Approximate change in the highest astronomical tide (δ-HAT)

We also construct a proxy quantity as an approximate change in the highest astronomical tide (δ-HAT) using an extension of the TAC method. To do this, we combine the tidal admittance amplitudes of the (typically) four largest astronomical tides (M₂, S₂, K₁, and O₁) then detrend the resultant combined time series as above. Next, we perform a similar scatter plot and regression approach against the detrended MSL time series as was done with the TACs. The benefit of this approach is to give a clear picture of the overall changes in tides related to sea level changes. Some locations may show that the variability in multiple tidal constituents partially cancel each other (e.g., semidiurnal tides may have a large positive tendency compared to MSL variability while diurnal tides may have a large negative tendency, resulting in an offsetting of variabilities under MSL changes, and a smaller overall magnitude δ-HAT), while other locations may show a reinforced variability (e.g., both diurnal and semidiurnal tides have positive tendencies compared to MSL changes, resulting in an amplified δ-HAT). Thus, the accurate interpretation of the δ-HAT is that it reflects the maximum tide-related water level that would be obtained in a given analysis period (here, 1 year) from a chosen set of time-dependent amplitudes extracted from the admittance method.

Two details about the δ-HAT parameter should be noted here. First, only the amplitude of the tidal admittance can be combined in this manner, as combining the phase variability in multiple frequencies may be inaccurate at worst and at best is not very helpful. Second, we acknowledge that the use of the term “δ-HAT” may be somewhat confusing as previous literature about tidal analysis uses the term “Highest Astronomical Tide” (HAT) to denote the highest water level that can be expected to occur under average meteorological conditions due purely to astronomical forcing in a given epoch. This typical period is 19 years, which considers the full nodal cycle. This definition of HAT does not reflect the highest possible water level at a given location, since storm surge or other non-average meteorological conditions may amplify water levels far above this level on a shorter timescale than a 19-year determination can reveal. The intention behind our chosen nomenclature of the “approximate change in the highest astronomical tide” (δ-HAT) attempts to expand on this concept by considering the full tidal variability (not strictly true since the four largest tides are only about 75 % of the full tidal range but these tidal components are nearly always stable in 1-year analyses, so it is a dependable and easily comparable metric) at timescales shorter than a nodal period (∼19 years), but longer than a storm surge (∼2–5 d) or other meteorological anomalies. Furthermore, our interest is the changes in tidal components that is not due to astronomy or to meteorology. Rather, we show possible changes to tide-related water level modifications due to MSL modifications, which may be important on seasonal to decadal timescales, induced by mechanisms associated with global climate change (e.g., steric sea level rise due to ice melt, thermal sea level rise due to upper-ocean warming) or to more local effects (such as rapid harbor modifications or land reclamation that adjusts tidal resonance at a particular location).

The changes shown by the δ-HATs are important to consider since a full understanding of the changes in all components and timescales of the tides may better instruct future coastal planning and engineering. The δ-HAT method used here can give important information about possible future water level inundation in coastal locations that are not storm related, such as nuisance flooding (or sometimes called “sunny day flooding”). These may be obscured by longer-term analyses of the classical HAT (i.e., 19 years) if changes are more rapid (i.e., year to year or season to season). However, it should also be reiterated that a good understanding of changes in tides due to changing background water levels may also be instructive for future storm-surge-related inundation at a location; both tides and storms are long-wave processes so changes in one aspect of water level variability (i.e., a large positive δ-HAT) may also indicate future increase in storm surge levels at the same location.