On the role of the seawater absorption-to-attenuation ratio in the radiance polarization above the southern Baltic surface

Information about polarization of light leaving the ocean surface has the potential to improve the quality of bio-optical parameter retrieval from ocean color remote sensing (OCRS). This improvement can be applied in numerous ways, such as limiting of Sun glints and obtaining information about atmospheric aerosol properties for atmospheric correction as well as increasing the accuracy of the algorithms based on the water-leaving signal. Polarization signals at the top of the atmosphere (ToA) that include the water-leaving signal are strongly influenced by atmospheric molecular scattering and by direct Sun and sky reflections from the sea surface. For these reasons, it is necessary to better understand the factors that change the polarization of light in the atmosphere–ocean system, especially in coastal zones affected by dynamic changes. In this paper, the influence of seasonal variability of light absorption and scattering coefficients (inherent optical properties; IOPs) of seawater, wind speed and solar zenith angle (SZA) on the polarization of upwelling radiance over the sea surface in the visible light bands is discussed. The results come from a polarized radiative transfer model based on the Monte Carlo code and applied to the atmosphere–ocean system using averaged IOPs as input data. The results, presented in the form of polar plots of the total upwelling radiance degree of polarization (DoP), indicate that regardless of the wavelength of light and type of water, the highest value of the above-water DoP is strongly correlated with the absorption-to-attenuation ratio. The correlation is a power function that depends on both the SZA and the wind speed. The correlation versatility for different wavelengths of light is very unusual in optics of the sea and is therefore worth emphasizing.

1 Introduction

Satellite ocean color radiometry has been developed for decades to study the interaction of a light field within the visible part of the spectrum (i.e., 400–700 nm) with the different optically significant constituents of seawater. The research has been focusing on information coming from the intensity of water-leaving light – its measurement, retrieval, correlations and interpretation (e.g., Volpe et al., 2012; Zibordi et al., 2013; Sammartino et al., 2015). However, in addition to the light intensity, consideration of light polarization has been demonstrated to improve the accuracy of the information from a variety of remote sensing applications, i.e., in remote radar measurements (Hajnsek et al., 2003; Soloviev et al., 2012; Benassai et al., 2013) and in atmospheric correction algorithms (Chowdhary et al., 2002).

Vector radiative transfer simulations have shown that the polarization of the underwater light field is sensitive to the nature of the suspended marine particles. Ibrahim et al. (2012) and Ibrahim et al. (2016) demonstrated that the attenuation-to-absorption ratio influences the polarization of upwelling radiance below the sea surface. Polarized measurements have also been performed near and above the sea surface. Reduction of Sun glints to improve the ocean color retrieval has been studied by He et al. (2014), Zhou et al. (2017) or Shaw and Vollmer (2017), and limitation of sky reflections by observation of sea surface at the Brewster angle from the shipboard has been examined by Wood and Cunningham (2001) and Cunningham et al. (2002). Polarization distribution of skylight reflected off the rough sea surface has been recently examined in many independent studies, e.g., by Zhou et al. (2013), Harmel et al. (2012), Mobley (2015), Hieronymi (2016), Foster and Gilerson (2016) and D'Alimonte and Kajiyama (2016). Zhou et al. (2013) simulated the degree of polarization as well as the angle of polarization (AoP) for reflected parts of upwelling radiance and discussed its variability with solar zenith angle (SZA) for 0, 30, 60 and 90^∘. Moreover, Zhou et al. (2013) showed the influence of wind speed and direction on the polarization pattern of reflected radiance. Harmel et al. (2012) showed that knowledge of the polarization field of the diffuse skylight significantly improves above-water radiometry estimates, in particular in the blue part of the spectrum where the reflected skylight is dominant. Mobley (2015) and Hieronymi (2016) applied polarized radiative transfer in order to show the role of sky polarization in the retrieval of radiance and irradiance reflectance of the windblown sea surface. Likewise, D'Alimonte and Kajiyama (2016) discussed joint effect of polarization and the sea-surface statistics on the in situ water-leaving radiance. Foster and Gilerson (2016) provided transfer functions for surface-reflected polarized skylight and upward transmission of light through the sea surface and estimated the sensitivity of polarized components to environmental conditions. Furthermore, polarized radiative transfer simulations have shown the effect of marine suspensions on the polarization of light recorded above the sea surface (see Chami, 2007; Chami et al., 2015). Further studies have also shown the possibility of knowing the composition of the suspension, i.e., the ratio of mineral to organic suspension, using polarization properties of water-leaving radiance (see Gilerson et al., 2006; Chami, 2007; Tonizzo et al., 2011). The intent of the authors was to show the seasonal variability of polarization of the upwelling radiance above the sea surface.

The most challenging part in the analysis of the signal registered by passive radiometric sensors at the top of the atmosphere is to remove the contribution of the reflected photons at the air–sea interface as well as the contribution of the atmosphere. To assess the water-leaving radiance, L_w(λ), on the level of accuracy required to derive accurate estimates of the desired water components, other characteristics and methods that support the advanced atmospheric correction and parameter retrieval have been searched, i.e., the black pixel assumption (Siegel et al., 2000), using near-infrared and shortwave infrared bands (Wang et al., 2007), using unpolarized top of the atmosphere (ToA) reflectance (Frouin et al., 1994), or using polarized water-leaving radiance (Zhai et al. 2017). The latter showed that, in general, the polarized signal at the ToA is 2–3 times higher than its water-leaving part because of the influence of molecular scattering in the atmosphere. Discussions on the use of remote polarization measurements to determine the aerosol properties that can then be used for atmospheric correction are included in Chowdhary et al. (2002), Mishchenko and Travis (1997) and Hasekamp and Landgraf (2005). Harmel and Chami (2013) demonstrated that polarization-based atmospheric correction improves the retrieval of the aerosol properties over open ocean waters. Pust et al. (2011) showed that measurements of the degree of polarization of the sky (made from the ground) can also be helpful in obtaining aerosol parameters. He et al. (2014) proposed to measure the parallel polarization radiance (PPR) instead of radiance intensity at ToA. According to them, such measurements would enhance the ocean color remote sensing (OCRS) capability. Liu et al. (2017), based on radiative transfer modeling and laboratory measurement, showed that the concentration of particulate matter influences the PPR measured at ToA.

Polarized signal can be measured from the satellite sensors, e.g., POLarization and Directionality of the Earth's Reflectances sensor (POLDER-2), above water using a polarization imaging camera (Freda et al., 2015) or underwater as by Loisel et al. (2008) and Harmel et al. (2011). The measurements are often supported by numerical modeling. Although there are many ongoing numerical radiative transfer models applied to ocean–atmosphere system, only some of them include light polarization (e.g., Schulz et al., 1999; Ota et al., 2010; Piskozub and Freda, 2013; Chami et al., 2015, Korkin et al., 2017). Kokhanovsky (2010) compared several vector radiative transfer models.

The polarized radiative transfer has been applied for the open ocean–atmospheric system since the 1970s (see, for example, Kattawar et al., 1973); however, its significance in coastal zone remote sensing has been highlighted in the last decade. Chami et al. (2015) applied the polarized radiative transfer to retrieve the polarizing properties of the marine phytoplankton and minerals for different water conditions. Their analysis revealed that the application of the polarization of light in ocean color algorithms might significantly improve the retrieval of hydrosol properties, especially in coastal waters. Piskozub and Freda (2013) applied their polarized radiative transfer model to the Baltic Sea. They examined how scattering properties of seawater represented by a single scattering albedo affected the polarization of water-leaving radiance. They demonstrated the impact of air bubble layers of various concentrations on the degree of polarization of water-leaving light. They also concluded that polarization remote sensing should be performed on a plane tilted approximately 90^∘ from the solar azimuth angle to avoid Sun glints. The involvement of polarization in radiative transfer analysis seems to be especially important in coastal areas, knowing that they undergo dynamic changes due to human proximity (Drozdowska et al., 2017), river inflows and the occurrence of pollution, including optically significant oil pollution (Drozdowska et al., 2013). There has been several significant studies performed in coastal zones of New York Harbor (Tonizzo et al., 2009), Long Island Sound (Harmel et al., 2012) or a selected few places from the East Coast and Gulf of Mexico (Tonizzo et al., 2011). Nevertheless, little attention has been paid to the measurement and modeling of light polarization in some coastal areas and closed water basins like the Baltic Sea characterized by optically complex waters. The Baltic Sea represents a region of a great economic importance, extremely high marine traffic and the impact of inflows from nine different surrounding countries. Inherent optical properties of Baltic seawater and its constituents have been in the spotlight for oceanographers for two decades. In addition to regular measurements of depth profiles of absorption and attenuation coefficients, measurements for different components of seawater have been performed. Colored dissolved organic matter (CDOM) is known to be the primary absorber in the Baltic Sea (Kowalczuk et al., 2006, 2010), and its impact on the total absorption coefficient for blue light can reach up to 80 % (Kowalczuk et al., 2005). Kowalczuk (1999) and Kowalczuk and Kaczmarek (1996) found that the high absorption of CDOM in spring and low absorption in winter is due to the biological cycle as well as the seasonal variability of the inlet with river water and its mixing. The aim for a better correlation of the spectral remote sensing reflectance R_rs ratio with the absorption coefficient of CDOM has been intensively researched within the SatBaltic system (Meler et al., 2016a). Measurements of suspended matter inherent optical properties (IOPs) in the Baltic, i.e., particle absorption and particle scattering coefficients, have been compared with biogeochemical characteristics of suspended matter such as concentrations of suspended particulate matter, particulate organic matter, particulate organic carbon and chlorophyll a (Woźniak et al., 2011). Meler et al. (2016b) concluded that absorption properties of non-algal particles undergo larger regional than seasonal variability. In addition to the absorption and attenuation coefficients, the volume scattering functions (VSFs) were also measured in the waters of the southern Baltic (Freda et al., 2007; Freda and Piskozub, 2007; Freda, 2012). Unique measurements have been performed by the prototype volume scattering meter, characterized by an angular resolution of 0.3^∘ and a range of scattering angles from 0.6 to 177.9^∘, described by Lee and Lewis (2003). The same instrument has also been used by Chami et al. (2005) in the Black Sea and by Berthon et al. (2007) in the Adriatic Sea. Baltic Sea waters are often affected by small-scale oil pollution (Rudź et al., 2013). The influence of dispersed oil droplets on the absorption coefficient of seawater was researched by Otremba (2007) as well as Haule and Freda (2016), while their influence on scattering properties has been tested by Freda (2014). The consequences of changes in IOPs for remote detection of dispersed oil pollution have been discussed by Otremba et al. (2013), Otremba (2016) and Haule et al. (2017) based on radiative transfer modeling. Knowledge and datasets collected in the Baltic throughout the past two decades helped us to perform a unique study on polarized radiation above the southern Baltic sea surface. This study shows the application of a polarized radiative transfer model in three optically different regions, two seasons and two different sea states. The study highlights the possibilities and consequences of including polarization information in bio-optical models of seawater.

2 Methods

The difficulty of comparison of upwelling radiance degree of polarization (DoP) over a wind-roughened southern Baltic surface for various seasons is caused by the small number of sunny days in winter and too many variable weather factors that would make it difficult to explain the differences. These undesirable weather factors are different aerosol optical depths, sky overcast and changing speed and direction of wind relative to the position of the Sun. For those reasons, we applied a polarized radiative transfer model based on the Monte Carlo code to describe the effect of seasonal changes on the polarization of upwelling radiance. The simulations involved seasonally averaged measurements of inherent optical properties from the southern Baltic basin and were run for constant weather conditions. For a detailed description of the inputs and conditions under which the simulation is performed, see the following subsections.

2.1 Polarized radiative transfer model – theoretical background

Numerical simulations were carried out using the Monte Carlo algorithm created by Jacek Piskozub and applied previously in Piskozub and Freda (2013). The algorithm solves the vector radiative transfer equation for the atmosphere–ocean system using the successive orders of scattering method and the Stokes formalism to track the polarization of photons. The algorithm collects information about virtual photons involved statistically in optical processes: reflection at the rough sea surface, refraction at the air–water interface, scattering and absorption within the water body and reaching the ToA. Moreover, the original Monte Carlo algorithm has been modified to track polarization changes of each photon during these processes. The unmodified version of the algorithm was successfully used, with results published in Piskozub et al. (2001), Stramski and Piskozub (2003), McKee et al. (2008, 2013) or Piskozub and McKee (2011).

Polarization information is described by four elements of the Stokes vector: $\mathit{S}=[I,Q,U,V{]}^T$, where I is the total radiance of light, Q describes the radiance of linearly polarized light (vertical to horizontal), U describes the radiance of linearly polarized light (diagonal right skewed to left skewed), V describes the circular polarization (clockwise to counterclockwise), and T denotes the transposition. Three elements (Q, U and V) of the Stokes vector may be both positive or negative. The single quantity that characterizes these properties is the degree of polarization:

$$\begin{array}{}\text{(1)}& \mathrm{DoP}={\displaystyle \frac{\sqrt{Q^{\mathrm{2}}+U^{\mathrm{2}}+V^{\mathrm{2}}}}{I}}.\end{array}$$

The defined degree of polarization is often replaced by the degree of linear polarization (DoLP).

$$\begin{array}{}\text{(2)}& \mathrm{DoLP}={\displaystyle \frac{\sqrt{Q^{\mathrm{2}}+U^{\mathrm{2}}}}{I}}\end{array}$$

The latter hardly differs from DoP because circular polarization is relatively rare in nature (Cronin and Marshall, 2011). The circular polarization represented by the V element of the Stokes vector does not appear in seawater as a result of scattering; see off-diagonal Mueller matrix elements in Voss and Fry (1984). It is measurable in light internally reflected from the underside of the sea's surface (Ivanoff and Watermann, 1958).

Our polarized radiative transfer model involves a virtual light source to send randomly polarized photons and track their pathways in the means of the probability of occurrence of the processes mentioned above. Reflection and refraction processes are described by Fresnel equations, and the slopes of the sea surface are characterized by the wind-dependent distribution of Cox and Munk (1956). The algorithm does not take into account additional depolarization due to enhanced whitecap fraction, described by Hu et al. (2008) – that is likely for high wind speed. The probability of processes within the water body is determined by the corresponding coefficients of absorption and scattering (including multiple scattering). Angular distribution of scattered photons is described by phase functions that, for both atmosphere and sea depth, are characterized separately for molecular scattering and particle scattering. Polarization properties of particle scattering are described by Mueller matrices that for seawater are taken from Voss and Fry (1984) and for atmospheric aerosol particles from Volten et al. (2001). The model outputs the angular distribution of the upwelling radiance and its degree of polarization at any desired level, which are presented in form of polar plots. Some of the results are additionally specified in the principal plane.

2.2 Polarized radiative transfer model – input parameters

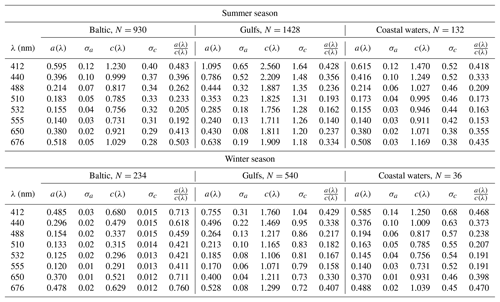
This section reports the input parameters used in the computations. The dataset of the absorption and attenuation coefficients of seawater constituents come from in situ measurements in the southern Baltic contained in Sagan (2008). It is the largest dataset of ac-9 (WET Labs, Inc.) measurements in the southern Baltic that was published in a tabular form of average values, extreme values and standard deviations. The instrument was calibrated in ultrapure water and routinely checked for stability with air readings. The standard recommended data processing was performed (Zaneveld et al., 1994). Absolute precision of measurement is 0.005 m⁻¹, while relative precision is estimated from 4 % in clear waters to 12 % in the areas of turbid waters. The data have been recorded during cyclical cruises aboard R/V Oceania in 1999 and 2003 to 2005. Measurements were made in different months of the year. The dataset was divided into two seasons, here called “winter”, for the months from November to March, and “summer”, for the months from April to October. The summer season is characterized by strong phytoplankton growth and the winter season by low biological activity. In addition, Sagan (2008) distinguished three regions: open Baltic, gulfs (Gulf of Gdańsk and Pomeranian Gulf) and coastal waters. The measuring stations, divided into these three types of water, are shown in Fig. 1. For defined regions – open Baltic and coastal areas – those two datasets are statistically significantly different for all optical parameters (t test for means) at the level p<0.05 by Sagan (2008).

Total absorption coefficient taken to the simulation is a sum $a_{\mathrm{t}}=a_{\mathrm{pg}}+a_{\mathrm{w}}$, where a_pg is an average absorption coefficient (particle and dissolved fraction) of the N number of measured depth profiles (see Table 1) made with the ac-9 after Sagan (2008), and a_w is the pure water absorption coefficient and comes from Pope and Fry (1997). Similarly, the total attenuation coefficient is defined as $c_{\mathrm{t}}=c_{\mathrm{pg}}+a_{\mathrm{w}}+b_{\mathrm{w}}$, where the component c_pg comes directly from Sagan (2008), but to get the total attenuation coefficient, it was enlarged by clean water components of absorption a_w and scattering b_w (Smith and Baker, 1981). According to Sagan (2008), the highest values of IOPs and their highest variability are observed for the water of gulfs and estuaries of rivers that are located nearby. The simulations are carried out at nine wavelengths, namely, 412, 440, 488, 510, 532, 555, 650, 676 and 715 nm, which correspond to the ac-9 and are commonly dedicated to ocean color analysis.

Solar zenith angles in the southern Baltic region depend strongly on the season. In months described by Sagan (2008) as the summer season, the highest Sun position over the horizon, which means the minimum of SZA during Sun culmination, varies between 31^∘ in June (the longest day of the year) and 69^∘ at the end of October. In the modeling, a single value of 45^∘ was chosen as a summer SZA. For months of the winter season, the minimum of SZA varies between 50^∘ in the end of March and 78^∘ in December (the shortest day). Given values are reached at approximately noon and are higher in the rest of the days. That is why SZA of 75^∘ is chosen as a representative for the winter season. Computations are performed for the direction of wind twisted by 45^∘ from the Sun reflection plane, chosen arbitrarily. Two wind speeds of 5 and 15 m s⁻¹ are considered. Aerosol optical thickness of 0.12, independent of the wavelength and the same for both seasons, was applied to all simulations. This allowed us to observe DoP variations and correlations that were not affected by aerosol changes.

Here and in the following figures, the celestial hemisphere and its reflection patterns are represented in a two-dimensional coordinate system. The zenith and the nadir are at the origin and the horizon is represented by the outermost circle. The zenith angle and azimuth angle are measured radially and tangentially, respectively. The solar azimuth angle is always set to 0.

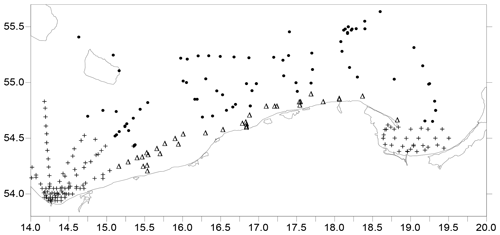
Figure 1 The area of the southern Baltic Sea, on which the positions of measurement stations are marked, divided into three areas: Pomeranian Gulf and Gulf of Gdańsk (+), coastal water (Δ) and open Baltic water (•).

Table 1 Average values of total absorption coefficients, total attenuation coefficients, their standard deviations and their ratios. All values measured by Sagan (2008) in southern Baltic in 1999 and 2003 to 2005 are averaged for depths 0 to 5 m and then averaged for N measuring stations.

3 Results and discussion

3.1 Extreme values of the degree of polarization

The full set of simulation results is available in the repository Freda (2019). It contains tables of Stokes vector elements for sectors marked with zenith–azimuth coordinates, which allows one to calculate the DoP. Examples of simulation results are presented in Fig. 2a and b in the form of polar plots of the degree of polarization of upwelling radiance just above the sea surface. Figure 2a shows the DoP for the average IOPs measured in the open waters of the Baltic Sea for a wavelength of 412 nm in the summer season, while Fig. 2b depicts an analogous case for the winter season. These two plots are characterized by one of the highest values of the peak of DoP of 0.88 for summer and 0.84 for winter. The azimuth position of the Sun is 0^∘ in all cases. Corresponding values of computed upwelling radiance I (in units of Wm⁻² sr⁻¹ nm⁻¹) are shown on the plots of Fig. 2c and d on the logarithmic scale (due to their high angular variability).

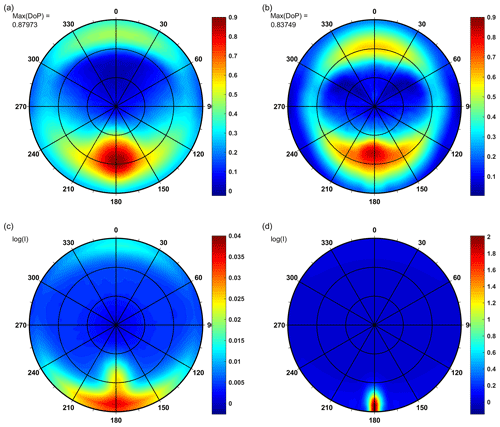
Figure 2 Simulation results of above-water upwelling radiance for average IOPs of open waters of the southern Baltic, wavelength 412 nm, for wind speed of 5 m s⁻¹: (a) DoP in the summer season, SZA 45^∘, (b) DoP in the winter season, SZA 75^∘, (c) decimal logarithm of upwelling radiance in the summer season, SZA 45^∘, (d) decimal logarithm of upwelling radiance in the winter season, SZA 75^∘. Concentric circles inside mean zenith angles of 30 and 60^∘, respectively.

The small SZA of the summer season (45^∘) resulted in low values of upwelling radiance that are stretched from the direct reflection point to the horizon, where it is extended both left and right from the azimuth of 180^∘. The high SZA of the winter season (75^∘) resulted in much higher values of reflected light, which are also stretched from reflection point to the horizon.

Examples of the lowest values of the maximum DoP, referred to as max(DoP), are shown in Fig. 3a and b. They were obtained for the regions of Gulf of Gdańsk and Pomeranian Gulf, simulated for the spectral band of 555 nm, for the summer season (Fig. 3a) and for the winter season (Fig. 3b).

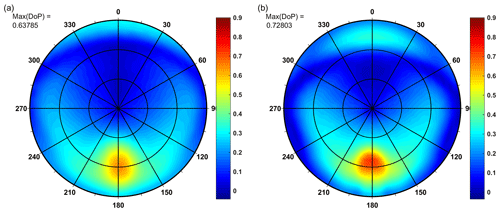
Figure 3 Simulation results of above-water upwelling radiance for average IOPs of gulf waters of the southern Baltic, wavelength 555 nm, for speed of wind of 5 m s⁻¹: (a) DoP in the summer season, SZA 45^∘, (b) DoP in the winter season, SZA 75^∘. Concentric circles inside mean zenith angles of 30 and 60^∘, respectively.

The maximum values of DoP presented in Fig. 2a (summer season, open Baltic waters) are visible for azimuth angles close to 180^∘ (direction of reflected Sun) and a zenith angle of approximately 55^∘ although the solar zenith angle is 45^∘, while the max(DoP) in Fig. 3a (summer season, waters of gulfs) is visible for a zenith angle of approximately 60^∘. In contrast to the summer season case, the maximum DoPs in the winter season are close to the zenith angle of 48^∘ (Fig. 2b) and 54^∘ (Fig. 3b), while SZA is 75^∘. The lower position of the Sun results in a higher position of the maximum DoP of upwelling radiation than its reflection angle, and a higher position of the Sun results in a lower position of the maximum DoP. Another interesting effect is the higher DoP observed for directions close to the incident rays of the Sun (azimuth of 0^∘). In general, in the winter season, the values of DoP are higher than in summer, and zenith angles of this effect are lower in the winter than in the summer season.

3.2 Spectral variability of the degree of polarization

The results of Monte Carlo simulations of angular characteristics of DoP of upwelling radiance are presented in Fig. 4. These results are obtained for average IOPs of open Baltic waters for wind speed of 5 m s⁻¹ for three wavelengths (440, 555, 650 nm) and for both seasons. Vertical cross-sections of such polar plots for the same type of water (open Baltic Sea) but additionally for all examined wavelengths and for two speeds of wind, 5 and 15 m s⁻¹, are presented in Fig. 5. Such cross-sections show the DoP in the principal plane, including the direction of incident Sun beam (on the left side of the plot), zenith and direction of Sun reflection beam for calm sea surface (on the right side). The azimuth direction of the Sun position, described as 0^∘ in the polar plots, is marked by negative zenith angles in Fig. 5, while azimuth directions of 180^∘ that include the Sun reflection beam are marked by positive zenith angles.

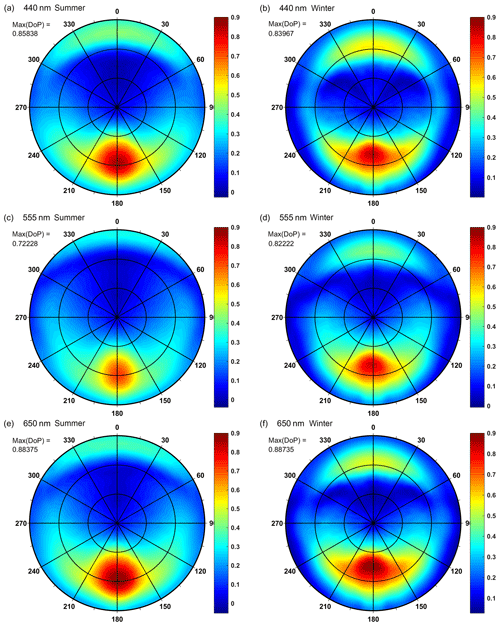
Figure 4 Simulation results of above-water upwelling radiance for average IOPs of open Baltic Sea water, for speed of wind of 5 m s⁻¹: (a) DoP in the summer season, λ=440 nm, SZA 45^∘, (b) DoP in the winter season, λ=440 nm, SZA 75^∘, (c) DoP in the summer season, λ=555 nm, SZA 45^∘, (d) DoP in the winter season, λ=555 nm, SZA 75^∘, (e) DoP in the summer season, λ=650 nm, SZA 45^∘, (f) DoP in the winter season, λ=650 nm, SZA 75^∘. Concentric circles inside mean zenith angles of 30 and 60^∘, respectively.

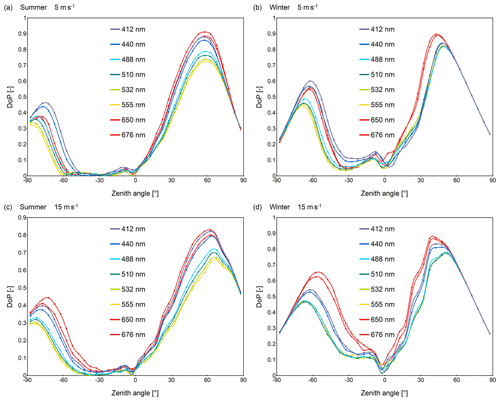
Figure 5 Degree of polarization plotted for the principal plane, e.g., plane containing both the incident ray of the Sun and zenith direction (cross-section through polar plots for azimuths 0 and 180^∘). Azimuth of 0^∘ is the azimuth of Sun position is marked by negative zenith angles, while azimuth 180^∘, which contains the Sun reflection, is marked by positive zenith angles. Simulation results for open Baltic Sea water: (a) summer season, SZA 45^∘, wind speed 5 m s⁻¹, (b) winter season, SZA 75^∘, wind speed 5 m s⁻¹, (c) summer season, SZA 45^∘, wind speed 15 m s⁻¹, (d) winter season, SZA 75^∘, wind speed 15 m s⁻¹.

The analysis of individual spectral bands shows that high values of DoP correspond to the high absorption-to-attenuation ratio for the total of visible light domain (see Table 1). High values of absorption coefficient for 650–676 nm wavelengths (in the red spectral region) are caused by pure water (see Pope and Fry, 1997), while high absorption coefficients for wavelengths of the blue–green range are caused mainly by CDOM (Kowalczuk et al., 2005). The lowest values of max(DoP) for each type of water and for each season are observed for the 555 nm spectral band. The lowest values of absorption and weak spectral variability of the scattering coefficient imply that the wavelength of 555 nm is characterized by the lowest absorption-to-attenuation ratios due to the existence of a minimum of absorption for seawater containing phytoplankton. Algae cells, depending on the composition of their pigments, may have a minimum of absorption in a wide range of spectral bands from 550 nm to 660 nm (Bricaud et al., 2004). Considering the absorption of pure water that is increasing with wavelength (Pope and Fry, 1997), the minimum of the absorption in Baltic waters for the spectral band of 555 nm results.

The spectral shape of the DoP cross-sections contains two maxima, and their angular positions depend on the absorption-to-attenuation ratio, the season and the wind speed. The angular position of the higher maximum depends mostly on the season, varying from approximately 60^∘ in the summer to 35–50^∘ in the winter (see Fig. 5). The lower maximum is observed at the zenith angles between −70 and −90^∘ in the summer as well as between −55 and −70^∘ in the winter. Higher wind speed of 15 m s⁻¹, in comparison to 5 m s⁻¹, causes the irregular shape of peaks. Moreover, the higher wind speed causes an increase of the DoP value for a lower maximum in the 650 and 676 nm spectral bands and its shift to a higher position (toward the zenith). At the same time, the DoP values for shorter wavelength bands are decreased and shifted to a lower position (toward horizon).

3.3 Regional variability of the degree of polarization

Computations of DoP were carried out in three optically different regions of the southern Baltic. Such a division is justified in previous studies of optical and hydrological properties of the south Baltic waters (Olszewski et al., 1992). They showed a relationship between the measured values of IOPs and their location in relation to river estuaries, distance from the shore or bathymetry of the bottom.

Comparison of water type influence on the DoP is shown in Fig. 6 for two wavelengths: 440 (Fig. 6a) and 555 nm (Fig. 6b). The type of water has less influence on the DoP than the season and its representative SZA.

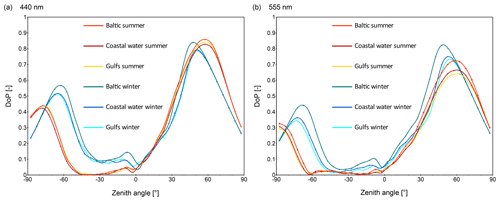
Figure 6 Degree of polarization plotted for the principal plane, i.e., plane containing both incident ray of the Sun and zenith direction (cross-section through polar plots for azimuths 0 and 180^∘). Azimuth of 0^∘ is marked by negative zenith angles. Simulation results are for wind speed of 5 m s⁻¹ for all types of water and two seasons: (a) 440 and (b) 555 nm.

However, the highest values of DoP for most zenith angles and the highest values of its peak max(DoP) for each season are observed for open Baltic Sea water. Coastal waters and gulfs are characterized by similar values of DoP in each season. For the wavelength of 440 nm, in the summer, the differences of max(DoP) between the open Baltic and other regions reach 0.02–0.04, while in the winter those differences exceed 0.05. For the 555 nm band, in the summer, the differences of max(DoP) between the open Baltic and other regions reach 0.06–0.09 and in the winter these differences reach 0.07–0.09, respectively. We also observed another regional difference in the angular position of the maxima of DoP that is noticeable in the winter season only. Two maxima of the DoP cross-sections are closer for open Baltic waters than for gulfs and coastal waters.

In the following section, we explain that the degree of polarization depends on the absorption-to-attenuation ratio, and all its regional changes are the result of the absorption-to-attenuation ratio variability.

The results of our simulations are in qualitative agreement with the measurements of above-water DoLP of the total upwelling radiance presented by Freda et al. (2015). This agreement is the similarity of the peak of degree of polarization on the polar plots, which are stretched along the azimuth angles. Freda et al. (2015) obtained lower values of measured DoLP with a maximum of 30 %–40 % (see Figs. 1 and 2 in Freda et al., 2015), which is presumably caused by different weather conditions and unknown environmental parameters during measurements, such as a high absorption coefficient in the waters of the river mouth, different aerosol optical depth or other parameters. However, despite the differences in the maximum degree of polarization, the angular distribution patterns are similar, with the peak in the vicinity of the Sun reflection azimuth angle.

3.4 DoP dependence on the absorption-to-attenuation ratio

This section contains the comparison of the degree of polarization for summer and winter seasons as a function of the absorption-to-attenuation ratio.

The total a(λ)∕c(λ) ratio (see Table 1) is higher in the open Baltic water than in other regions because of the low scattering coefficients (Sagan, 2008). The value of the latter is determined mainly by the concentration of suspended matter, which in open waters is significantly lower than in gulfs or coastal/nearshore waters. According to Sagan (2008), the average particle scattering coefficient does not depend strongly on wavelengths, and in open Baltic waters in the winter season it varies between 0.15 (for 676 nm) and 0.19 (for 412 nm). In the same season, but in the waters of gulfs, the average particle scattering coefficient varies between 0.77 (for 676 nm) and 1.00 (for 412 nm). For the influence of water type on DoP, regardless of the wavelength and wind speed, the lowest max(DoP) values in winter are observed in the waters of gulfs. These waters are characterized by the highest scattering coefficients because of the high inflow of particulate matter with river waters. However, in the summer season, the lowest peak of DoP is observed for spectral bands from 412 to 532 nm in coastal waters and in wavelengths from 555 to 676 nm in gulfs. The values of a(λ)∕c(λ) for these types of water differ by less than 5 % except for the 650 and 676 nm spectral bands.

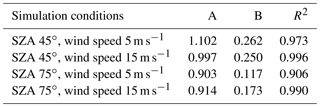
All the values of maximum DoP of above-water upwelling radiance obtained for each absorption-to-attenuation ratio are collected in Fig. 7. The summer season case is depicted in Fig. 7a, while the winter case is depicted in Fig. 7b. The water types are marked with different symbols, and two wind speeds are marked with different colors. The correlations of the max(DoP) to the ratio of a(λ)∕c(λ) are approximately linear. However, correlation coefficient analysis has shown that the power functions are better matched. The reason for the nonlinearity of this correlation may be related to the potential obtaining or even exceeding one by the value of DoP for certain combinations of absorption and attenuation coefficients. The trend line for the plot depicted in Fig. 7a shows the relationship of the maximum of DoP to the ratio of a(λ)∕c(λ) for the summer season and in Fig. 7b for the winter season, respectively. The trend lines presented may be described by the following power functions:

$$\begin{array}{}\text{(3)}& max\left(\mathrm{DoP}\right)=A{\left({\displaystyle \frac{a\left(\mathit{\lambda }\right)}{c\left(\mathit{\lambda }\right)}}\right)}^B,\end{array}$$

whose parameters are collected in Table 2. These correlations are obtained for various spectral channels. Hence, they are wavelength-independent for the examined visible spectral range.

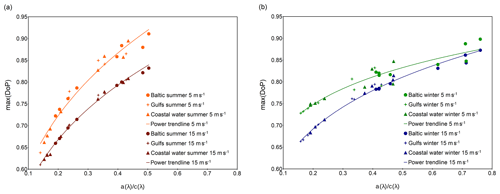
Figure 7 Values of maximum of degree of polarization against absorption-to-attenuation ratios a(λ)∕c(λ) for average values of IOPs presented in Table 1, plotted for (a) the summer season and (b) the winter season.

Table 2 Parameters of Eq. (3), which describes the power trend lines in Fig. 4a and b.

An analysis of all collected data shows that higher values of maximum DoP are observed for lower wind speed. Moreover, max(DoP) has a higher range of variability in the summer season than in the winter. Figure 7a (summer season) shows that values of max(DoP) are between 0.64 and 0.91 for the wind speed of 5 m s⁻¹ and between 0.61 and 0.83 for the wind speed of 15 m s⁻¹. However, in Fig. 7b (winter season), the values are between 0.73 and 0.9 for the wind speed of 5 m s⁻¹ and between 0.66 and 0.87 for the wind speed of 15 m s⁻¹. Power trend lines for the same wind speed for summer and winter seasons (in Fig. 7a and b) intersect. For a wind speed of 5 m s⁻¹, by a(λ)∕c(λ) equal to 0.26, both power functions reach the same max(DoP) of 0.77. For a wind speed of 15 m s⁻¹, by a(λ)∕c(λ) equal to 0.32, both power functions reach the same value of 0.75. For lower absorption-to-attenuation ratios, winter DoPs have higher values than summer and for higher a(λ)∕c(λ) values, the summer DoPs are higher.

The reason for the correlation of the maximum DoP with the absorption-to-attenuation ratio is the occurrence of multiple scattering in water depth. The degree of polarization tends to decrease after multiple scattering events. A high absorption-to-attenuation ratio means simply low scattering-to-attenuation impact and hence shallow penetration of light in the water column and low participation in multiple scattering that decreases the DoP. Such conclusion is in accordance with Piskozub and Freda (2013), who examined the influence of single scattering albedo on the polarization of water-leaving radiance. Their results show that in the Sun reflection plane, the highest value of DoP is observed when the total scattering coefficient is the lowest (see Fig. 3 in Piskozub and Freda, 2013).

The influence of wind speed on the DoP values shown in Fig. 7a and b is very clear: sea-surface roughness depolarizes the reflected light. Zhou et al. (2013) demonstrated that wind speed and wind direction can change the polarization patterns of reflected skylight from a rough sea surface to a certain extent. Our study shows, in particular, that high wind speed results in lower values of max(DoP) of the total upwelling radiance. Such regularity is filled for all types of water and all spectral bands.

Our algorithm does not consider possible additional depolarization, which is likely especially for high wind speeds (15 m s⁻¹). This can be caused by whitecaps (Hu et al., 2008), air bubble entrainment and possibly more sea spray generation. Moreover, additional factors that may decrease the DoP value for high SZA (winter season) are wave-shadowing effects of incident and multiple reflected rays (see Hieronymi, 2016), which are not considered in this paper.

The results of the correlation of the maximum DoP with the absorption-to-attenuation ratio seem to be coincident with the results of Ibrahim et al. (2012), who studied the degree of linear polarization just below the air–water interface. Their correlation of attenuation-to-absorption ratio with DoLP displays a hyperbolic shape (see Figs. 5 to 8 in Ibrahim et al., 2012). Therefore, for an inverted absorption-to-attenuation ratio, it would be near linear. The modeling results of Ibrahim et al. cannot be compared directly to the results presented in this paper because they received DoLP just below the sea surface, and we focused on DoP just above the surface. However, our choice of seawater absorption-to-attenuation ratio, which can be called the relative absorption value (to total attenuation), as a parameter correlated to degree of polarization seems to be more suitable.

4 Conclusions

In this paper, we have investigated the relationship between the seawater absorption-to-attenuation ratio and the degree of radiance polarization above the rough sea surface. Using a Monte Carlo polarized radiative transfer model, we compared simulated polarization patterns in three optically different regions in the southern Baltic (i.e., open Baltic, gulfs, coastal waters), two seasons (defined by their typical solar zenith angles: 45^∘ for summer and 75^∘ for winter) and two wind speeds of 5 and 15 m s⁻¹, each for nine visible spectral bands (412, 440, 488, 510, 532, 555, 650, 676, 715 nm). The use of the modeling tool allowed us to exclude unwanted and unpredictable variables (such as weather conditions and aerosol optical thickness) and to conduct undisturbed comparison of the DoPs of combined water-leaving and reflected components of upwelling radiance.

We found that the variability of the maximum of DoP depends more on seasonal than regional changes and can be explained to a large degree by the absorption-to-attenuation ratio. A thorough analysis has shown that there is a strong correlation between max(DoP) and the ratio mentioned previously. The correlation is well described (R²>0.90) by a power function with factor A close to 1 and factor B depending more on SZA than on the wind speed. In our study, seasonal variability of the degree of polarization is higher/more significant than regional variability. However, this may be true only in the southern Baltic region due to the characteristically different SZA ranges in the winter and summer seasons.

For the ocean color remote sensing application, only the water-leaving part of the upwelling radiance carries useful information about bio-optical parameters of seawater, although it is a small fraction of the total upwelling radiance. Polarized radiative transfer modeling makes it possible to separate the water-leaving part and, in this case, the noise-inducing reflected part and therefore to enhance the quality of information on the seawater optically active components retrieved by above-water sensors – airborne or satellites. Our study is a step toward inclusion of polarization properties in the bio-optical models in the Baltic Sea. However, the conclusions from the research, in our opinion, should be universal and apply also to other water bodies.