the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
The wave spectrum in archipelagos
Jan-Victor Björkqvist
Heidi Pettersson
Kimmo K. Kahma
Sea surface waves are important for marine safety and coastal engineering, but mapping the wave properties at complex shorelines, such as coastal archipelagos, is challenging. The wave spectrum, E(f), contains a majority of the information about the wave field, and its properties have been studied for decades. Nevertheless, any systematic research into the wave spectrum in archipelagos has not been made. In this paper we present wave buoy measurements from 14 locations in the Finnish archipelago. The shape of the wave spectrum showed a systematic transition from a single-peaked spectrum to a spectrum with a wide frequency range having almost constant energy. The exact shape also depended on the wind direction, since the fetch, island, and bottom conditions are not isotropic. The deviation from the traditional spectral form is strong enough to have a measurable effect on the definitions of the significant wave height. The relation between the two definitions in the middle of the archipelago was , but the ratio varied with the spectral width (Hs was defined using the variance). At this same location the average value of the single highest wave, Hmax∕Hs, was only 1.58. A wider archipelago spectrum was also associated with lower confidence limits for the significant wave height compared to the open sea (6 % vs. 9 %). The challenges caused by the instability of the peak frequency for an archipelago spectrum are presented, and the mean frequency, weighted with E(f)4, is proposed as a compromise between stability and bias with respect to the peak frequency. The possibility of using the frequency and width parameters of this study as a starting point for a new analytical parameterisation of an archipelago type spectrum is discussed.
- Article
(6440 KB) - Full-text XML
- BibTeX
- EndNote
Since the 1950s the wave spectrum has been the central way to define the properties of random sea-surface wind waves (Pierson and Marks, 1952). Although the exact power law describing the high-frequency part of the spectrum is still an open question (e.g. Phillips, 1958; Toba, 1973; Kitaigorodskii, 1983; Kahma, 1981; Banner, 1990; Lenain and Melville, 2017), the central determining feature has been the location of the spectral maximum, which then consequently determines the total wave energy (Hasselmann et al., 1973; Donelan et al., 1985). From a practical perspective of derived wave parameters the spectral features translate into the peak frequency, fp, and the significant wave height, Hs. The evolution of these two parameters, as a function of the fetch and the wind speed, has been extensively studied by laboratory and field experiments (e.g. Pierson and Moskowitz, 1964; Toba, 1972; Hasselmann et al., 1973; Kahma, 1981; Donelan et al., 1985; Kahma and Calkoen, 1992).
In the coastal region, waves are important for coastal engineering, erosion, small-vessel safety, and biological processes. Coastal waves deviate from deep-water open-sea waves, but their exact properties depend on the shoreline structure. On sloping beaches the limitation by the water depth is a major factor shaping the wave properties through bottom friction, depth-induced wave breaking, and shallow-water non-linear wave interactions (SPM, 1984; Eldeberky, 1996). Coastal coral reefs shape the wave spectrum away from the deep-water form (Hardy and Young, 1996); the same thing can be said for tidal inlets where the waves are also affected by strong currents (van der Westhuysen et al., 2012).
One of the most complex nearshore conditions can be found in coastal archipelagos where islands, the irregular shoreline, the slanting fetch, and the decreasing depth affect the attenuation and local growth of the waves. Collections of large islands, in the scale of kilometres, can be found in, for example, the Gulf of Mexico, outside of Louisiana, or between Vancouver and Seattle (the San Juan Islands). In Europe an example is the Aegean Sea, which separates parts of Turkey and Greece from the Mediterranean Sea. Denser archipelagos, where the island sizes are of the order of hundreds of metres, are even more complex. An archipelago made up of a large number of small islands has a strong effect on the wave field by attenuating the waves and diffracting the remaining wave energy behind them. At the same time groups of islands practically define new fetches for local wave systems to grow from, thus giving birth to unique wave conditions. Examples of such archipelagos are the Thousand Islands at the US–Canadian border or the coastline of Maine. In Europe dense coastal archipelagos can be found especially in the Baltic Sea, with examples being the Stockholm archipelago and the Archipelago Sea. Also the coastline near the Finnish capital, Helsinki, has a characteristic archipelago with heavy commercial and recreational marine traffic.
Although coastal archipelagos are usual – almost typical – in the Baltic Sea, there is a limited amount of data available on their effect on waves. Kahma (1979) presented measurements of wave spectra in the archipelago that showed an almost complete absence of the traditional spectral peak. Single measurements like these have proven the shape of the wave spectrum to differ significantly from both open-sea observations and theoretical spectral models. Nevertheless, there exists no broader methodological study into the different spectral shapes and the transition between the two extremes, not least because of the limited amount of available observational data. Efforts to simulate the wave field in the archipelagos have been made (Soukissian et al., 2004; Mazarakis et al., 2012; Tuomi et al., 2014; Anderson et al., 2015; Björkqvist et al., 2019a), but, while fairly successful, they are still not a substitute for measurements.
The shape of the wave spectrum is of pure theoretical interest. Still, it also has direct and indirect consequences for practical applications, such as for estimating the expected height of single waves. An atypical spectral shape also affects the applicability and reliability of engineering formulas using integrated wave parameters and alters the sampling variability in standard wave buoy measurements. The spectral shape can be atypical at any location because of swell or decaying and turning winds. Nonetheless, in the archipelago an atypical spectral shape forms even under steady wave conditions, thus giving the wave field inside the archipelago its prevailing properties. These properties need to be identified and quantified in order to fundamentally understand waves in archipelagos.
This paper aims to fill the knowledge gap regarding the properties of the wave field inside dense coastal archipelagos. The study relied on spatially extensive wave buoy measurements; all data were collected in the Helsinki archipelago, which is located in the Gulf of Finland, the Baltic Sea. The data and methods are introduced in Sect. 2, while Sect. 3 presents and quantifies the transformation of the mean spectral shape in the archipelago. Section 4 is dedicated to studying what implications the results have for the determination of derived wave parameters, such as the significant wave height, the maximum height of a single wave, and the peak frequency. One candidate for a characteristic frequency, suitable for a wide range of wave conditions, is proposed. We end the paper by discussing and concluding our findings.
2.1 Wave measurements
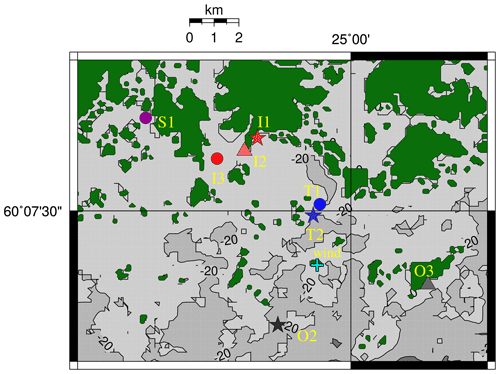
We conducted wave measurements at 14 locations off Helsinki in the Gulf of Finland (GoF). An overview of the sites can be found in Fig. 1 and Table 1. All observations were made with Datawell Directional Waverider buoys. Some of the data originate from smaller 40 cm GPS-based DWR-G4 buoys (henceforth G4), which use the Doppler shift of the GPS signal to measure the surface elevation. Measurements from larger (70–90 cm) accelerometer-based Mk-III and DWR4/ACM buoys (henceforth Mk-III and DWR4) were available from two operational wave buoys: one is located in the centre of the GoF (Fig. 1), while the other is deployed in the middle of the archipelago outside of the island Suomenlinna (T2, Fig. 2).
The nearshore measurements with the G4 buoys – conducted as part of a commissioned work by the city of Helsinki – were made for about a month at each location between 2012 and 2014 (Table 1). The exceptions are the Berggrund (O1) and Harmaja (O2) sites, where measurements were made for research purposes in 2015 and 2012. The shortest deployment time was 11 d (at Länsikari, T1) and the longest 39 d (at Isosaari, O2). Except for the July campaign at O1, the measurements were made between August and November to capture the harshest wave conditions before the areas froze. While observations at 12 out of the 14 locations were made with the smaller G4 buoys, most of the data originate from the long time series of the operational Mk-III and DWR4 wave buoys at GoF and Suomenlinna (T2). Data from the Suomenlinna (T2) wave buoy were available from 2016–2018. Operational wave measurements from the GoF have been conducted for every year in this study (2012–2018), but the results are based only on the years 2016–2018 to coincide with the Suomenlinna (T2) data.
Both the G4 and the Mk-III use a sampling frequency of 1.28 Hz and calculate the spectrum up to 0.58 Hz. A DWR4 buoy was used at the GoF site in 2018 and part of the year 2016. The DWR4 has a sampling frequency of 2.56 Hz and the 90 cm version calculates the spectrum up to 1 Hz. Nevertheless, only data up to 0.58 Hz were used to keep all results comparable, since the change in upper frequency would affect the calculations of higher spectral moments. No parametric tail was added to the observed spectra.
For the G4 buoys, the low-frequency artefacts, which have later been identified to be caused by the filter response to a missing GPS signal, were corrected following Björkqvist et al. (2016). Since the authors found that the correction can affect the high-frequency part of the spectrum, the corrected spectrum was only used for frequencies below 0.8fm, where fm is the mean frequency (see Eq. 4). For frequencies above 1.2fm Hz, the original spectrum was used, while a linear combination was used for intermediate frequencies to avoid discontinuities.
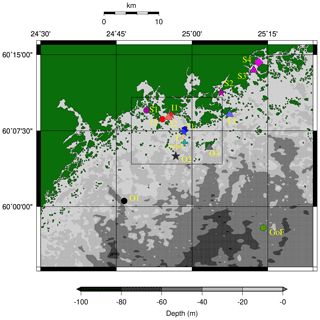
Figure 1The bathymetry and the measurement locations. GoF (green) is the open-sea wave buoy. The stations are divided into groups: outer archipelago (O1–O3), transition zone (T1–T3), inner archipelago (I1–I3), and sheltered archipelago (S1–S4). The plus (+) marks the Harmaja weather station. The Kalbådagrund weather station is outside of the map. The black box marks the area of Fig. 2.
2.2 Wind measurements
We used wind measurements from two of the Finnish Meteorological Institute's operational automatic weather stations. Harmaja (measuring height 17.5 m) is located less than 10 km from the Helsinki shoreline, about 2 km from the Suomenlinna wave buoy (T2, Fig. 2). The Kalbådagrund station (measuring height 31.8 m) is located in the middle of the Gulf of Finland, about 20 km east of the operational GoF wave buoy. Both stations have been active during the entire period of the study, but there are long gaps in the Kalbådagrund data in August and September 2018.
The weather stations provided the wind speed and direction averaged over 10 min. We calculated the 30 min averages from these data to coincide with the time series used to compute a single wave spectrum. The mean wind speed at Harmaja and Kalbådagrund for the years 2016–2018 were 6.1 and 7.8 m s−1. The 80th percentiles were 8.7 and 11.0 m s−1, respectively. The corresponding values calculated from the data coinciding with the wave measurements at each location are given in Table 1.
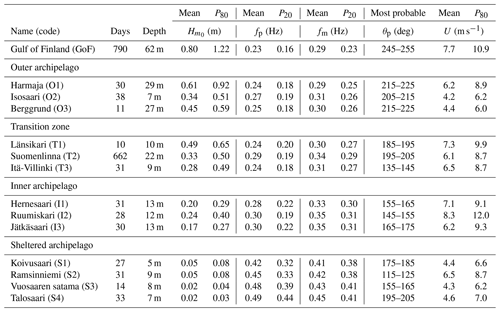
Table 1The measurement time and depth at the different sites (see Fig. 1 for an overview). The mean and 80th and 20th percentiles are shown for the significant wave height (), the peak frequency (fp), the mean frequency (fm), and the 30 min wind speed (U). The most probable value of the mean direction at the spectral peak (θp) is also shown. All available spectra between 2016 and 2018 (and the coinciding wind data) were used to compile these statistics.
2.3 Wave parameters and definitions
2.3.1 Spectral wave parameters
The wave buoys calculated the wave spectrum E(f) (m2 Hz−1), where f (Hz) is the frequency. The nth order moment of the wave spectrum is
All integrals were evaluated up to 0.58 Hz without adding a parametric tail. Using these moments we defined most of the relevant wave parameters. The significant wave height was defined as
A spectral version of the zero down-crossing period was defined as
while the mean frequency was given by
We defined the peak frequency as
i.e. the frequency where the wave spectrum has its maximum value. Because of the discrete frequency intervals and statistical variations in the spectrum, several methods for calculating the peak frequency have been proposed. In this paper we calculated fp using a parabolic fit. We, however, also applied an integrated definition (Young, 1995):
where q in a positive integer. Note that for q=1, Eq. (6) equals the mean period fm given by Eq. (4).
2.3.2 Wave parameters from time series
We also determined wave parameters directly from the 30 min vertical displacement time series, η(t).
The significant wave height, Hs, was defined as
where σ is the standard deviation. This definition is identical to Eq. (2) with the exception of the statistical variability introduced by the window tapering of the time series before calculating the spectrum.
The traditional definition of the significant wave height is the mean height of the highest one-third of the individual waves in the time series. To distinguish it from the significant wave height calculated using the variance, we will denote this parameter H1∕3. The individual waves were determined between two zero down-crossings, sorted in descending order, and the mean was calculated as
where Hi is the height of a single wave and N is their total number.
The zero down-crossing period, Tz, was calculated as
where T is the length of the time series η(t).
Assuming that η(t) is Gaussian, ; assuming that Hi values are Rayleigh distributed, .
2.3.3 Spectral width parameters
Several parameters to quantify the spectral width have been proposed. The width parameter ε (Cartwright and Longuet-Higgins, 1956) depends on the fourth moment, m4, and is therefore sensitive to noise in the higher frequencies.
Longuet-Higgins (1975) defined a spectral width parameter, ν, as
which, to a certain degree, suffers from similar issues as ε. Two other width (narrowness) parameters were used in this study. The first was the κ2 parameter of Battjes and van Vledder (1984):
where . This parameter was used as the main way to quantify the width of different spectral shapes. The other parameter was the Goda peakedness parameter (Goda, 1970), defined as
The Goda peakedness parameter was needed in the definition of the Benjamin–Feir index (BFI; Janssen, 2003), which is essentially the wave steepness divided by the spectral width. We used the BFI to quantify its possible connection with single waves that are high compared to the significant wave height, i.e. so called “rogue waves”, where . The formulation given by Serio et al. (2005) is
where the peak wavenumber, kp, is estimated from fp using linear wave theory. The coefficients α0,αBFI, and βBFI depend on the dimensionless depth, kph. Their exact expressions are given by, for example, Serio et al. (2005).
2.4 Choosing wave spectra and spectral scaling
Data were available from more locations than the 14 presented in this paper (Kahma et al., 2016). We, however, excluded some stations based on the following: (i) very small maximum wave heights, meaning that the wave buoy was often unable to measure the entire spectrum; (ii) the location was not even remotely exposed to open-sea waves (a determining factor for the archipelago type spectrum); or (iii) the location was too exposed to external disturbances, such as wave reflection or ship wakes.
As a loose definition of well defined wave conditions we used the 80th percentile of the significant wave height as a cut-off for each location. The 80th percentiles for the 13 coastal locations were determined using all available data. For the GoF, only data from the years 2016–2018 were used to keep the measurement period comparable with the Suomenlinna (T2) observations. In addition we used a cut-off of U≥5 m s−1, where U is the 30 min average wind speed. For the GoF wave buoy, we used the Kalbådagrund data, while Harmaja wind data were used for all other locations. For the nearshore locations, only onshore winds were considered (), while no restrictions on the wind direction was set for the GoF. Henceforth, we will call this data set the P80 data set.
The choice of the 80th percentile was a compromise between (i) removing the smallest wave heights, e.g. Hs<0.5 at Suomenlinna (T2), since they are bound to be noisy, and (ii) not excluding too much data from the limited data sets available from the short measurements. Using a different cut-off for the significant wave height (60–90th percentiles) resulted in very similar results. We also tried setting restrictions with respect to the steadiness of the wind direction and the wind speed, but imposing these additional restrictions resulted in very similar results and identical conclusions. To avoid adding unnecessary complexity, these additional constraints were dropped. Also, some of the highest wave heights at the GoF buoy were measured during a time when no wind data were available (August–September 2018). Cases with missing wind data were therefore included if they fulfilled the conditions set for the significant wave height.
Because the short waves are generated by the shortest fetch, they are least affected by the varying spectral shape inside the archipelago. The chosen spectra were therefore normalised using the values at the high frequencies (f>0.4 Hz). The scaled spectra were calculated as
where
f0 is any fixed frequency, and the brackets signify a mean value over frequencies f>f1. We chose Hz for simplicity, but the two frequencies need not be the same. The exact value of f1 is unimportant as long as the spectrum follows some kind of power law for higher frequencies. If an f−4 power law exists, the frequency f1 can even change between spectra and still provide a consistent normalisation. Nevertheless, since we had no reliable way of determining the starting point of the power laws in the spectra, we chose a frequency that was sufficiently high for the strong wind conditions that are represented in the P80 data set.
The frequencies were then normalised with respect to the mean frequency and the spectra, , were interpolated to a common set of dimensionless frequencies, . This resulted in the final scaled spectra . The mean frequency was chosen instead of the peak frequency because it is more stable. Using this same data set Björkqvist et al. (2019a) found that the peak frequency can be highly noisy in the archipelago, and this parameter is therefore unusable to scale the spectra. The choice of a good characteristic frequency for archipelago conditions will be studied in Sect. 4.5.
2.5 Determining groups
The 13 measurement stations in the archipelago were divided into four groups based on a visual estimation of the geographical conditions. The attenuation coefficients for the significant wave height compared to the GoF wave buoy were used as a crude check to ensure that the visual determination of the amount of sheltering was reasonable. The attenuation coefficients, K, were determined by a linear fit using the effective variance method (Orear, 1982). The different groups, visible in Fig. 1, can be described as follows.
Outer archipelago (O1–O3). The locations are not inside the archipelago, but the effect of the finite depth and/or the limited fetch caused by the irregular shoreline might be visible in the wave spectrum. Although the O2 station (Harmaja) seems to be very exposed, Björkqvist et al. (2017a) have shown that the wave field here is already restricted by the peninsula of Porkkalanniemi for south-westerly winds. The attenuation coefficients for the significant wave height were K=0.6–0.7.
Transition zone (T1–T3). The sheltering of the islands plays a significant role in shaping the wave field, but the longer waves propagating from the GoF are still somewhat dominant. The attenuation coefficients for the significant wave height were all K=0.4.
Inner archipelago (I1–I3). There is a clearly defined local fetch, but there is still a significant contribution from longer propagating waves. The attenuation coefficients for the significant wave height were K=0.2.
Sheltered archipelago (S1–S4). These locations should be dominated by the locally generated waves. Residuals of longer waves can, however, still be present. The attenuation coefficients for the significant wave height were very small (all K<0.10).
The common denominator throughout the archipelago is that the waves travel slower than the wind. Thus, the longer waves propagating from the open sea are not swell. In this paper we will show that the sheltering effect of the archipelago is a continuum and several reasonable classifications could therefore be made. The main purpose of the classification was to make the results more presentable.
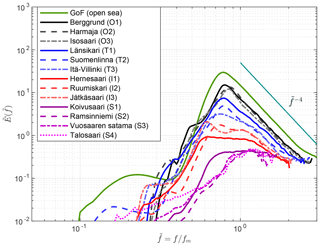
3.1 Transition from peaked to flat spectra
The main result of this section is that the wave spectrum transitioned from a, more traditional, single-peaked spectrum to a flat spectrum inside the archipelago. The transition was continuous, as readily seen in Fig. 3. In the outer archipelago (black) the mean spectrum had a very similar shape to the open-sea conditions observed at the GoF wave buoy (green). Namely, it had a single peak even if it lacked the overshooting of an even more peaked fetch-limited spectrum.
When moving closer towards the coast the spectral shape started to flatten out in the transition zone (blue). Länsikari (T1) and Suomenlinna (T2) are located very close to each other (Fig. 2), and the similar spectral shapes give confidence to the fact that we captured the shape of the mean spectrum even with the shorter measurement time series. Although the mean spectral profiles in the transition zone were still peaked, the rear face of the spectrum was starting to collapse. In contrast to the outer archipelago, the mean spectra in the transition zone decayed slower than just above the spectral peak. Especially T3 was showing a clear collapse towards a flat spectral shape.
In the inner archipelago (red) the spectral shape had collapsed around the peak and exhibited a constant energy in a broad frequency interval (). Even if the peak frequency could be reliably determined – which is challenging because of the statistical variability – it is obvious that it would not characterise the spectrum in a similar fashion as the spectral peak in, for example, the outer archipelago. There were, however, small low-frequency peaks, most notably at Jätkäsaari (I3). Relying on the directional spectrum from this same site presented by Björkqvist et al. (2017b), we concluded that these peaks were caused by refracted narrowband waves. These kinds of peaks are therefore expected to be specific to the bathymetrical conditions of the area.
In the sheltered archipelago (magenta) even these attenuated low-frequency peaks were no longer visible. The mean spectrum at Koivusaari (S1) was still flat (in a similar fashion to sites I1–I3), but for the other sheltered locations the spectra almost transitioned back to a single-peaked shape – the local fetch was starting to dominate over the very attenuated longer waves. The tail of the spectrum was not determined reliably, since these short waves were often not captured by the wave buoy.
3.2 Quantifying the spectral width
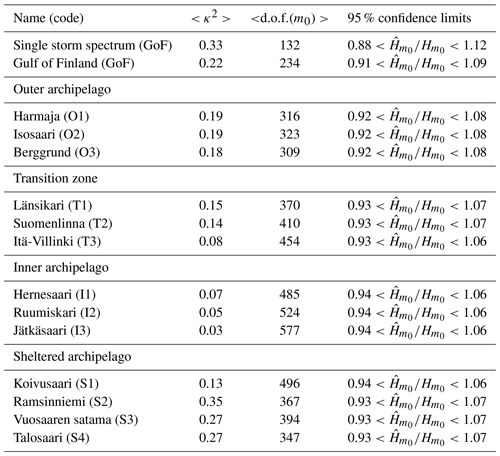
We quantified the change in width (or more exactly, narrowness) of the spectrum using the κ2 narrowness parameter (Eq. 11) of Battjes and van Vledder (1984). The mean width of the wave spectrum changed when moving into the archipelago, with κ2 being 0.03–0.07 in the inner archipelago (signalling a wide spectrum), while being 0.18–0.19 in the outer archipelago (Table 2). The values in the outer archipelago were close to the one at the open-sea location in the GoF. As an example, we also calculated the κ2 parameter for the single storm spectrum of the measured maximum 5.2 m significant wave height during the easterly Antti storm in 2012. The value of κ2=0.33 was higher than the average value at the GoF, but this storm spectrum is affected by the narrow fetch geometry of the GoF, which leads to a less peaked spectrum (Pettersson, 2004). Higher values (up to κ2=0.46) were found at the GoF.
The spectral width in the transition zone was in between those of the outer and inner archipelago (). The almost identical width of T1 and T2, and the wider shape of T3, was in good agreement with what was determined visually from Fig. 3. The κ2 values for the sheltered archipelago sites (S1–S4) were variable, which was a consequence of the wave buoys' issues with resolving the entire spectrum. The results from sites S1–S4 can therefore not be considered entirely reliable.
Quantifying the spectral width is no trivial matter, but the good agreement between the κ2 parameter and the obvious visual changes suggests that the parameter is applicable over a wide range of conditions.
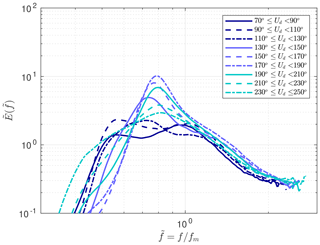
3.3 Directional dependence
Although the mean spectral profiles were shown to change when moving through the archipelago towards the shore, the spectral shape also varied with the wind direction because of the anisotropic fetch conditions. We used the wind direction because the instability of the spectral peak at Suomenlinna (T2) made it hard to define the dominant wave direction. The wave direction at the GoF buoy, again, collapses to be aligned with the gulf, thus causing a misalignment of up to 50∘ between the direction of the wind and the dominant waves (Pettersson et al., 2010). Nevertheless, the local fetch at Suomenlinna (T2) would still vary significantly within this large wind sector. Suomenlinna (T2) is the only location in the archipelago with enough data to partition it further with respect to the wind direction. This section will therefore be based on data from Suomenlinna (T2) only.
The most peaked spectra at Suomenlinna (T2) were generated by southerly winds (Fig. 4), since only small islands block the wave propagation in this direction (Fig. 1). For easterly winds, the spectral shape was flat, resembling the profiles of the inner archipelago (I1–I3, Fig. 3). Such a variation was identified already by Björkqvist et al. (2019a) when studying wave model performance against the Suomenlinna (T2) wave data, but our results showed a systematic behaviour. Importantly, the eastern wind directions showed a very flat mean spectrum even though the average shape over all wind directions was peaked. This discrepancy is explained by easterly winds not being dominant ( of the times). Nevertheless, strong easterly winds are possible in the GoF; the maximum significant wave height of 5.2 m at the GoF wave buoy has been measured twice, both during south-westerly winds (in 2001; Tuomi et al., 2011) and easterly winds (in 2012; Pettersson et al., 2013).
This section presents some implications of the results of Sect. 3. The quantification of the spectral narrowness, κ2, revealed that the measurements from the sheltered archipelago (S1–S4) did not capture all the properties of the wave field reliably enough. The issue was connected to low wave heights that were not captured entirely by the 40 cm wave buoys, as seen in Fig. 3. The shorter measurements from the slightly more exposed transition zone, and inner and outer archipelago, showed consistent results, and they were deemed reliable.
When appropriate, the results make use of all available data. Nonetheless, especially Sect. 4.2–4.4 will rely only on the long time series from Suomenlinna in the transition zone (T2) and the GoF. Such an analysis was possible because these data captured a variety of spectral shapes depending on the amount of sheltering for different wind directions (Fig. 4). The advantages of using data from only T2 were that (i) the analysis was based on a long time series coinciding with open-sea wave measurements from the GoF, (ii) the water depth was constant for all spectral shapes, and (iii) the spectral tail was captured equally well for all different spectral shapes, because they were all measured at the same location with an identical device.
4.1 Confidence limits of significant wave height
The confidence limits of observed wave spectra follow a distribution, where k is the degrees of freedom determined by the number of averaged elementary bins. The confidence limits of the spectrum propagate to its integral, which is also the total variance of the wave field, m0. By Eq. (2) the confidence limits of the observed significant wave height follow from those of m0.
The final degrees of freedom (d.o.f.) of the integral of a measured spectrum depend on the shape of the spectrum in the following way (Donelan and Pierson, 1983):
It immediately follows that d.o.f.(m0)=kN for a white noise spectrum (E(f)≡ const.), while d.o.f.(m0)=k for an infinitely peaked spectrum (). Thus, a broader spectrum will have more d.o.f., leading to smaller confidence limits for the significant wave height.
In Sect. 3.2 we quantified the spectral width using the κ2 parameter. The change in spectral width should also be seen in the d.o.f. calculated at the different locations. This was, indeed, the case: the d.o.f. in the inner archipelago were roughly 500–600, while the corresponding values in the outer archipelago were around 300 (Table 2). The transition zone, again, had values falling in between the inner and outer archipelago, with the d.o.f at site T3 being closest to the inner archipelago. In the open-sea location (GoF) the d.o.f. values of the variance were lower than anywhere in the archipelago, and the low d.o.f. of the single GoF storm spectrum went hand in hand with the large κ2 value.
The increase in the d.o.f. in the archipelago had a direct implication for the confidence limits of the significant wave height: the confidence limits at the GoF wave buoy were 50 % larger than at the inner archipelago points (Table 2). The confidence limits of the single storm spectrum was twice that of the average value in the inner archipelago (12 % vs. 6 %).
Because the spectral shape depended strongly on the wind direction at Suomenlinna (T2), the confidence limits for easterly winds were close to those of the inner archipelago, while south-westerly – and especially southerly – winds resulted in confidence limits in line with the open sea (Fig. 5a). By comparing the d.o.f. to the κ2 parameter it is obvious that they were both quantifying a similar property of the spectrum (Fig. 5b). The correlation between these two parameters was , and also the Goda peakedness parameter (Eq. 12) was correlated () with the d.o.f. of the spectrum (Fig. 5c).
The correlation between the d.o.f. and the spectral width parameter ν by Longuet-Higgins (1975) was only r=0.2 (Fig. 5d), and the correlation was equally low for the spectral width parameter ε proposed by Cartwright and Longuet-Higgins (1956) (not shown).
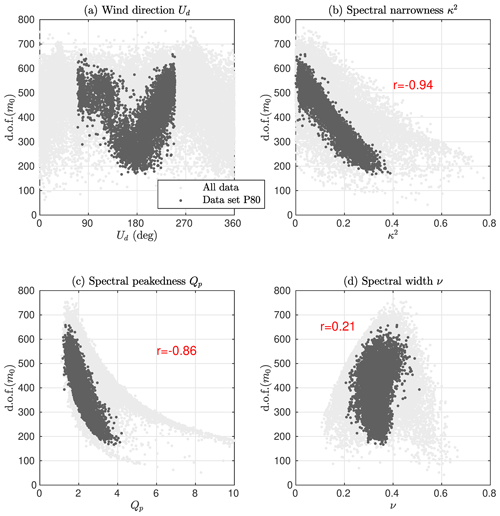
Figure 5The degrees of freedom of the Suomenlinna (T2) wave variance as a function of the wind direction (a) and the different spectral width and narrowness parameters (b–d).
4.2 The significant wave height: H1∕3 vs. Hs
The significant wave height is the most central and widely used wave parameter. Still, it can be defined in a couple of different ways. The connection between the definition using the mean height of the highest one-third of the single waves and the definition based on the variance of the vertical displacement was made based on the assumption of a narrowband spectrum, deep water, and that the height of single waves are Rayleigh distributed with the parameter . These conditions lead to a proportionality constant of 4 in the equality,
Studies have shown, however, that the assumption of a Rayleigh distribution (with a parameter ) for the height of individual waves predicts higher values of compared to observations (Forristall, 1978; Longuet-Higgins, 1980; Casas-Prat and Holthuijsen, 2010). The discrepancy has been solved, for example, by assuming a Weibull distribution (Forristall, 1978) or by simply scaling the Rayleigh parameter as (Longuet-Higgins, 1980). The use of a scaled Rayleigh distribution modifies Eq. (17) to
Longuet-Higgins (1980) determined α as a function of the spectral width:
where ν is the spectral width parameter of Longuet-Higgins (1975) (Eq. 10). Since the original derivation of Eq. (17) assumed a narrowband spectrum with symmetrical Gaussian water level displacements, we expected that the two definitions for the significant wave height would vary even more in the archipelago than previously observed for open-sea conditions.
We determined the fit between H1∕3 (Eq. 8) and Hs (Eq. 7) that was calculated from the vertical displacement time series. The fit to the Suomenlinna (T2) P80 data set was (Fig. 6a), which is a stronger deviation from Eq. (17) than found by previous studies (Table 3). The coefficient depended on the wind direction in a similar fashion as the spectral shape shown in Fig. 4; the more peaked spectral shapes of the southerly winds resulted in a proportionality constant of 0.90, while the corresponding value for the flat easterly spectra was around 0.86 (Fig. 6c).
Vandever et al. (2008) found that depended on the spectral width and determined a best fit of from Doppler wave gauge data. We note that calculating the ratio α from Eq. (19) using ν, as proposed by Longuet-Higgins (1980), increased the disagreement with our data for both Suomenlinna (T2) and GoF (Table 3). The value determined empirically by Longuet-Higgins (1980) using the data of Forristall (1978) (0.925) was, however, in very close agreement with 0.927 determined from our GoF data. The issue might have been caused by the reliable determination of ν; the mean value of ν=0.36 (GoF) is lower than ν=0.41–0.83 reported by Vandever et al. (2008), although their data had swell present. We instead determined a linear fit using the narrowness parameter κ2 and our Suomenlinna (T2) data, which resulted in (Fig. 7a). For an infinitely narrow spectrum (ν=0, κ2=1), both fits result in approximately unity, which is in accordance with the narrowband assumption used to derive Eq. (17).
Even for the southerly waves at Suomenlinna (T2) was no higher than 0.90. It is therefore possible that the finite water depth (22 m at Suomenlinna) affected the results to a certain degree. The ratio , however, showed a negative correlation () with the dimensionless depth, kph, meaning that the largest deviations from deep-water values are found for the cases where the water is deepest (relative to the waves). This is the opposite of what we would expect if the deviation from Eq. (17) was indeed caused by the finite depth effects. The apparent correlation was created by more sheltering simultaneously leading to both shorter waves (i.e. higher kph) and a wider wave spectrum. The wider spectrum can then explain the discrepancy through the κ2 parameter as outlined above. We concluded that the deviation from Eq. (17) was mainly caused by the spectral shape, not the finite depth at the measurement site.
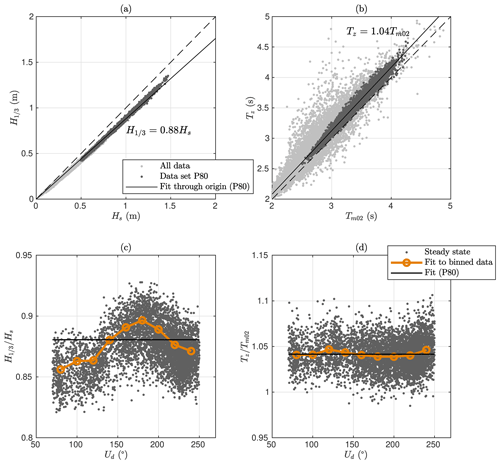
Figure 6Comparison of H1∕3 and Tz with respect to Hs and at Suomenlinna (T2). In panels (c) and (d) the ratios are given as a function of the wind direction.
Table 3The different wave height and crest height parameters at the Gulf of Finland (GoF) and Suomenlinna (T2). The values have been determined using a linear fit through the origin of the P80 data set. The ratio was taken as reported in the literature. The single wave statistics for the distributions given in the literature have been determined using the individual number of waves for each wave record and the mean value of the spectral width parameter ν (when given).
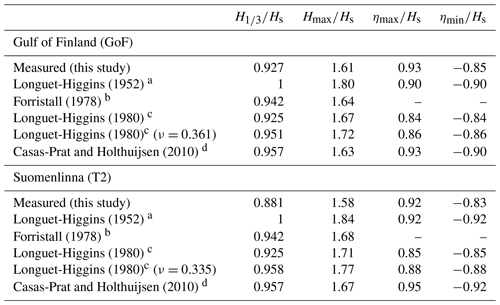
a Assuming a narrowband spectrum in deep water, Gaussian water level elevations with respect to the still water level, and a Rayleigh distribution for the heights of single waves. b Empirical Weibull fit to storm data. c Empirical Rayleigh fit to the storm data of Forristall (1978). d Empirical Rayleigh fit based on 15 years of measurements from four wave buoys.
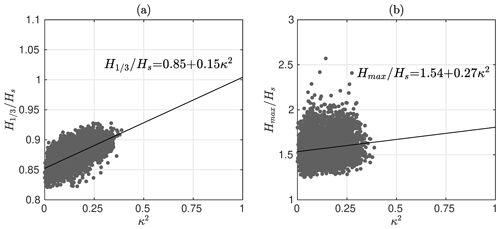
Figure 7H1∕3 (a) and Hmax (b) at Suomenlinna (T2) relative to the significant wave height. The ratios are plotted against the spectral narrowness κ2. For an infinitely narrow spectrum (κ2=1), the linear regressions ( and ) are in good agreement with the theoretical predictions that Longuet-Higgins (1952) derived for a narrowband spectrum (Table 3).
4.3 Single wave statistics: Hmax∕Hs
The highest expected single wave is often of considerable interest, and usually this single wave is given relative to the significant wave height. The estimate is made based on the assumption that the height of the single waves are either Rayleigh or Weibull distributed. The estimated highest single wave thus depends on the assumed distribution and the number of waves encountered during the measurement period (N).
We determined the highest single wave from the vertical displacement time series of the P80 data sets. For the GoF, the connection between the single wave height and the significant wave height was determined to be Hmax=1.61Hs using a linear fit. The coefficient 1.61 was lower than assuming the Rayleigh distribution of Longuet-Higgins (1952), but it was in good agreement with the prediction of Forristall (1978) and Casas-Prat and Holthuijsen (2010) (Table 3). The maximum crest height at the GoF were well predicted by Casas-Prat and Holthuijsen (2010), but the wave troughs (ηmin) agreed better with Longuet-Higgins (1980).
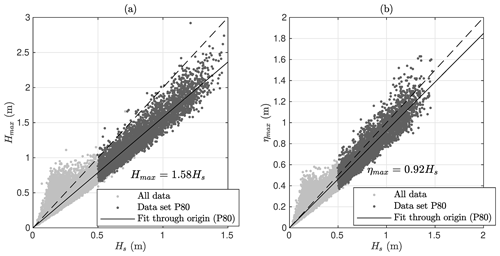
The linear regression to the Suomenlinna (T2) data was Hmax=1.58Hs (Fig. 8a). The ratio was lower compared to the GoF even though we would expect the higher N at Suomenlinna (caused by shorter waves) to result in a higher single wave Hmax∕Hs. The disagreement with previous studies was also more pronounced (Table 3). We determined a linear fit with the spectral narrowness to be (Fig. 7b). This regression results in for a theoretical infinitely peaked spectrum (κ2=1), which is in good agreement with the theoretical derivations of Longuet-Higgins (1952) that assumed a narrowband spectrum (Table 3). Nevertheless, the very low correlation between the variables (r=0.15) limits the confidence in this specific result. Vandever et al. (2008) found no connection between and ν. The correlation between and κ2 was zero also in our data, most probably because of the self-scaling nature of .
The maximum crest height, ηmax∕Hs, at Suomenlinna (T2) was only slightly lower than at the GoF (Table 3). If symmetry would be assumed, the maximum crest heights would be in perfect agreement with the estimates from the Rayleigh distribution of Longuet-Higgins (1952), which was also found by Casas-Prat and Holthuijsen (2010). The troughs were slightly shallower in our data compared to, for example, Casas-Prat and Holthuijsen (2010), but they were well described by the scaled Rayleigh distribution of Longuet-Higgins (1980). There was no correlation between ηmax∕Hs (or ηmin∕Hs) and the spectral narrowness κ2 (r=0.0).
None of the aforementioned dimensionless wave or crest heights had any correlation with the dimensionless depth, kph (r=0.0). Together these results suggests that the main factor controlling the magnitude of the highest single waves was the spectral shape. Thus, the differences from previous results were mainly caused by the violation of the assumption of a narrowband spectrum, not the assumption of deep water. The exceptions were the crest and trough heights, which exhibited no connection to the spectral width.
The maximum single wave measured at Suomenlinna (T2) was Hmax=2.92 m (1), having a crest height of ηmax=1.54 m. This wave was measured during south-easterly winds (Ud=152∘). It is evident from Fig. 7b that a ratio over 2 was not a rare occurrence, since it happened 45 times during the 3-year deployment period of the buoy. Still, the criterion of (roughly) is often taken as a definition for “rogue waves” (e.g. Onorato et al., 2002). Also Casas-Prat and Holthuijsen (2010) found thousands of single waves exceeding twice the significant wave height. The generation of rogue waves has been proposed to be controlled by modulation instability (Janssen, 2003), which is quantified using the Benjamin–Feir index (Eq. 13). Nevertheless, the correlation between BFI and Hmax∕Hs (or ηmax∕Hs) was only 0.1 for the Suomenlinna (T2) P80 data set (not shown). The lack of descriptive power of the BFI is expected, because the modulation instability is strongest for narrowband spectra – the exact opposite of the conditions that we have observed in the archipelago.
4.4 The zero-crossing period, Tz
As for the significant wave height, the zero-crossing period, Tz, is one of the oldest wave parameters. Based on theoretical arguments about the Gaussian distribution of the water level displacement, it can be calculated from the spectral moments as (Eq. 3). Since this connection is based on theoretical assumptions, it might not be valid for atypical spectral shapes, such as the ones found in the archipelago.
We compared these two definitions of the zero-crossing period using a linear fit to the P80 data sets. For the GoF data, the two definitions agreed well, with a linear fit giving a proportionality coefficient of 1.02. For the Suomenlinna (T2) data, the linear fit was (Fig. 6c), meaning that the traditional definition of the zero-crossing period was quite robust and coincided well with the one calculated from the spectral moments over a wide range of spectral shapes. In the Suomenlinna (T2) data the ratio was only weakly correlated with the κ2 narrowness parameter (). A linear fit () still gave almost unity for a theoretical narrowband spectrum (κ2=1).
The ratio at Suomenlinna (T2) was also correlated with the dimensionless depth kph (). The explanation for this, possibly spurious, correlation might be the same as for the significant wave height, namely that more sheltering results in both a wider spectrum and a deeper dimensionless depth. Nonetheless, the sign of the correlation was what would be expected if the variations were really explained by the variations in dimensionless depth. The reason for the slight 4 % bias at Suomenlinna (T2) was therefore left undetermined.
4.5 Finding a characteristic frequency, fc
Often the full spectrum is not available, and the characteristics of the wave field are described using a limited set of integrated parameters. If directionality is ignored, the choice is usually a measure for the height and a measure for the length, or equally well the frequency. A unimodal spectrum, for example, is quite well described by the significant wave height and the peak frequency. Nevertheless, the flat spectral shape in the archipelago leads to a low stability of the peak frequency. The mean frequency, again, is stable but biased compared to the peak frequency for the more unimodal spectra in the outer archipelago.
Young (1995) proposed a definition for the peak frequency, , that is based on a weighted mean integral of the spectrum (Eq. 6). This expression has a free parameter, q, that needs to be determined. We set out to study if any exponent of q could produce a characteristic frequency (henceforth, fc) that would be more stable than simply taking the argument maximum of the spectrum but still would not be as biased as fm compared to the peak frequency. The challenge in choosing a value for q is that minimising the scatter suggests low values for q (with q=1 resulting in fm), while minimising the bias compared to fp requires a high value for q. To determine a best estimate, we defined an error function:
where 〈⋅〉 denotes the mean and σ is the standard deviation. In other words, it is the norm of the bias and the standard deviation of .
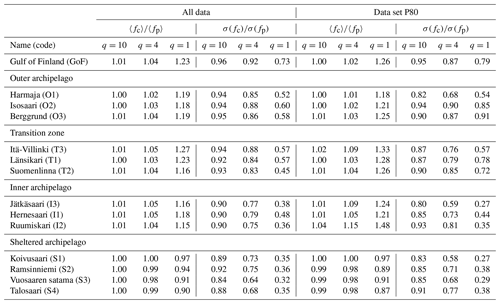
We determined this error function for each location separately using the P80 data set. The minimum was achieved between q=3 and q=5, with the exception of the sheltered archipelago sites (q=2–3). These values are in line with q=4 of Young (1995) but lower than q=8 of Sobey and Young (1986), which the authors recommended for an alternative definition of the peak frequency.
In addition to a best estimate of q=4 we compared the peak frequency to using the values q=1 and q=10. As a metric quantifying how different candidates for fc characterise the spectrum, we determined the relative amount of energy that is carried by waves below the characteristic frequency, i.e.
In the GoF data roughly 65 % of the energy was below the mean frequency regardless to the wind direction (E0(fm)≈0.65, Fig. 9c). For the peak frequency, the respective value was 29 %, but it varied with the wind direction, being as high as 40 % for southerly winds. The southerly wind sector produces waves that are unaffected by the narrow fetch geometry of the gulf. They should therefore most closely resemble classic fetch-limited spectra, although they might still be affected by swell propagating along the gulf, especially from the Baltic Proper in the west. With a choice of q=4 the integrated parameter agreed well with the peak frequency for southerly winds in the GoF data set (Fig. 9c). For other wind directions, where the narrow fetch effects came into play, resulted in slightly higher frequency estimates compared to fp (Fig. 9c). Since the most dominant wind directions are along the axis of the Gulf, it is clear that does not produce an unbiased estimate in a general sense. A choice of q=10 introduced practically no bias, and it can therefore be used as an alternative definition for the peak frequency (Table , Fig. 9c).
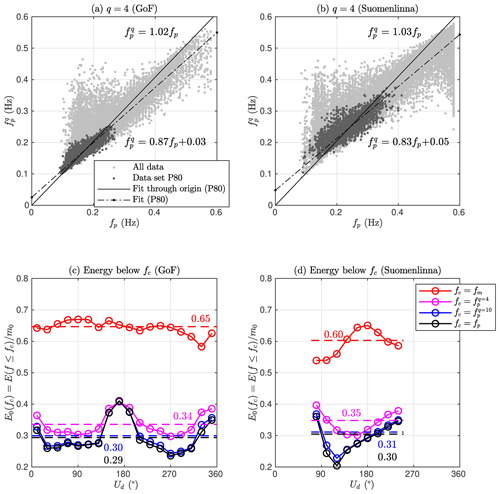
Figure 9The characteristic wave frequency compared to fp for different values of q at the open sea (GoF, left column) and in the middle of the archipelago (Suomenlinna (T2), right column). Note that fm is identical to .
For Suomenlinna (T2), also showed a good general agreement with the peak frequency, and the mean value of was almost identical (35 % vs. 34 %) to the one determined for the GoF (Fig. 9b and d). The energy below the mean frequency was, on average, only 60 %, but this value depended strongly on the wind direction. For the southerly winds – where the spectral shape was most peaked – E0(fm) agreed with the GoF data. For the wider spectra of the other wind directions, the two sites disagreed; especially for eastern winds the amount of energy below the mean frequency was only slightly above 50 %, which would be the value for a theoretical white noise spectrum. Also varied with the wind direction for both q=4 and q=10. Even though a similar variation was seen also in the GoF, the easterly wind directions at Suomenlinna (T2) produced wave spectra where, on average, only 20 % of the energy was below the peak frequency – a situation that was not possible at the GoF.
Choosing q=4 resulted in E0(fc) being roughly between 30 % and 40 % at both in the open sea (GoF) and in the archipelago (Suomenlinna, T2). While the integrated definition using q=4 was not identical to the peak frequency, it had the advantage of describing a similar characteristic feature in both locations. Namely, in a mean sense, 30 %–40 % of the wave energy was contained by waves with a frequency lower than fc. A consistency in this respect might be important for constructing an accurate analytical parameterisation of the archipelago spectrum. Using q=10 is attractive as its bias with respect to the peak frequency was small at all locations (Table ). On the other hand, the scatter (as measured by the standard deviation) was only reduced slightly compared to the peak frequency.
Table 4The mean values and the scatter (standard deviation) of the characteristic wave frequency for three different values of q (see Eq. 6) compared to that of the peak frequency, fp. Note that for q=1.
5.1 Direct implications
The spectral shape affected the relation between the different definitions of the significant wave height (H1∕3 vs. Hs). The ratio varied, in a mean sense, as a function of the spectral narrowness κ2 (Fig. 7a). Regardless of the scatter, this connection suggested a decreased height of the highest single waves compared to the total variance for a wider spectrum. The highest single wave Hmax∕Hs was, indeed, statistically lower at Suomenlinna (T2) compared to the open sea (Table 3). A connection to κ2 was also found (Fig. 7b), although with a very weak correlation (r=0.15). The low correlation between the highest single wave and the spectral width might partly be explained by the higher number of waves associated with a wider spectrum: a wide spectrum would suggest a low maximum wave, while the accompanying increase in the number of single waves in the time series (N) has an opposite effect. If the average values at Suomenlinna (T2) are viewed as a function of the wind direction (as d.o.f.(m0) in Fig. 6a), the relevant parameters had a variation of and (not shown). Assuming a single Rayleigh distribution, the variation in N would cause a difference of 1.1 % in estimates for Hmax∕Hs, which is a similar order of magnitude to the observed variation in the average value of Hmax∕Hs (3.9 %).
The reduction of the single highest wave in a wider spectrum has been explained by the de-correlation of the following crests and troughs: a deep trough is less likely to be followed by a high wave crest, even if the maximum and minimum water levels are not affected (e.g. Tayfun, 1983). This is also supported by our data, since we found no connection between the crest (or trough) heights and the spectral width. Goda (1970) found that in computer-simulated data the height of the single waves followed a Rayleigh distribution regardless of the spectral width (as quantified by ε of Cartwright and Longuet-Higgins, 1956). Nevertheless, based on a very extensive data set, Casas-Prat and Holthuijsen (2010) pointed out that the use of other distributions can have an advantage over the Rayleigh distribution for large numbers of N. Further research is needed to resolve the open questions regarding the affect of spectral width on the distribution of the height of single waves.
The d.o.f. of the wave variance (m0) closely reflected the spectral width, and they seemed to correlate well with the narrowness parameter κ2 (Fig. 5). Wider (flatter) spectra had more degrees of freedom, which lead to smaller confidence limits for the measured significant wave height (Table 2). It follows that when evaluating a wave model in archipelago conditions, a constant performance will lead to a smaller scatter index (or normalised root-mean-square error) inside the archipelago compared to the open sea. The peak frequency, again, is a very noisy parameter for the flat spectral shape found in the archipelago. This noise is connected to the sampling variability of a spectrum that has a wide frequency range with an almost constant variance density – the peak frequency is determined by the variability of the peaks in this region. A theoretical perfect model would therefore show an increased accuracy for the significant wave height when moving through the archipelago, while conversely showing a decrease in the accuracy in the peak frequency. We do, however, want to point out that the latter effect is much stronger.
5.2 Parameterising the spectrum
Section 4.5 was dedicated to finding a good characteristic frequency for the varying wave conditions encountered in the archipelago. Equation (6) with q=4 was proposed as a balanced choice between the mean frequency's stability and the peak frequency's skill in identifying the energy-dominated part of the spectrum. Nonetheless, simply redefining the peak frequency in traditional spectral parameterisation (such as JONSWAP; Hasselmann et al., 1973) does not make archipelago wave spectra comparable with traditional unimodal open-sea spectra. Especially engineering approaches that are a function of (Hs, fp) or (Hs, fm) will not be reasonable for any choice of a characteristic frequency.
The overall results of this study showed that general archipelago conditions need to be quantified using at least three parameters. If the total energy is known, a frequency will give – in some sense – the location where the energy of the wave spectrum is concentrated. The spectral width, again, quantifies how narrowly the energy is distributed around this frequency. Traditionally the variation in spectral width has been relatively small, but in an archipelago setting it is dominant. Clearly, advancing our knowledge of waves in archipelagos hinges on the development of an analytical parameterisation for the archipelago type spectrum. Both fc and κ2 have shown desirable properties in regards to stability and descriptive power. The triplet (Hs, fc, κ2) can therefore serve as a starting point for further studies, and the analytical expression can then consequently be used to derive practical formulas for wave bottom interaction. Even before a parameterisation of the archipelago wave spectrum has been established, wave model studies (and other comparative analyses) can benefit by expanding the validation to cover the aforementioned triplet.
5.3 Limitations of the data set
This study was done using the most extensive wave data set that is available from dense archipelago areas. Still, since the material was not primarily collected for fundamental research purposes, it has a few limitations. The first limitation is the sheltered archipelago locations (S1–S4), where the standard 40 cm wave buoy was unable to capture the entire spectrum because of the very low wave conditions. Visually, the spectra from the sheltered archipelago are qualitatively consistent with the rest of the data (Fig. 3). The missing spectral tail, however, rendered quantitative metrics – such as the degrees of freedom or the κ2 narrowness parameter – unreliable (Table 2). The challenges caused by low wave heights inside the archipelago were mitigated by appropriately analysing the long time series at Suomenlinna (T2), since these data contained almost the full range of the different spectral shapes. Instead of actual geographical sites, we could then use the wind direction as a proxy for different amounts of sheltering (Fig. 4).
The second limitation is the short duration of the measurements in 12 of the 14 locations (Table 1). Since the measurements were mostly made during the autumn, they are comparable to each other, and also representative of the harsher wave conditions of the area. While short, the data show a consistent transition of the spectral shape throughout the archipelago (Fig. 3). Also, the shortest time series (T1) is in close proximity to the longest time series (T2), and the results from the two locations agree well, both visually (Fig. 3) and quantitatively (Table 2). All in all, the quality of the available data was sufficient to reach the objectives of the study and to support our conclusions.
An extensive field measurement campaign consisting of wave buoy measurements from 14 locations was performed in the Helsinki archipelago during 2012–2018. Multi-year time series were available from two operational wave buoys in the middle of the Gulf of Finland (GoF) and in the middle of the archipelago (Suomenlinna, T2). Measurements from the other sites in the archipelago lasted for about a month. These measurements were used to study the shape of the wave spectrum in the archipelago and the consequences that the variations in the spectrum have for derived wave parameters.
The mean spectral shape in the middle of the GoF was unimodal with a distinct peak. No peak was identifiable close to the shoreline, where the spectrum was best described by a wide energy-carrying range with almost constant variance density. At Suomenlinna (T2), located in between these two extremes, the spectral shape varied strongly with the wind direction because of the anisotropic fetch conditions. For south-westerly, and especially southerly, winds, the spectral shape was peaked. For easterly winds, the spectral shape was wide, being close to that of the sites near the shore. The wide spectral shape in the archipelago was not created by swell, since even the longer waves travelled slower than the wind. Rather, the spectra reflected complex wind sea conditions where waves grow from different fetches and are attenuated by the islands.
The mean shape of the spectra was well quantified by the spectral narrowness parameter (κ2) of Battjes and van Vledder (1984), but a scatter still persisted. The width parameter ν of Longuet-Higgins (1975) had no predictive value, possibly because of the challenges imposed by measuring the short waves in the archipelago with wave buoys. The spectral width was also connected to the degrees of freedom of the wave variance (m0), with a wider spectrum having more degrees of freedom. As a direct consequence, the confidence limits for the measured significant wave height are lower inside the archipelago compared to the open sea (Table 2).
The spectral shape affected the ratio , with a wider spectrum resulting in a lower ratio (Hs was defined using the variance). The ratio between the two definitions of significant wave height was determined to be at Suomenlinna (T2), but the ratio varied as a function of the spectral narrowness κ2 (Fig. 7a). The effect of the spectral shape on the ratio was weak.
The highest single wave Hmax∕Hs was, on average, 1.58 at Suomenlinna (T2), which is lower both compared to the open-sea measurements at GoF (1.61) and to estimates using the literature (1.67–1.84, Table 3). Our results suggest that the deviation in Hmax∕Hs from previous studies is mainly caused by a wider spectral shape (Fig. 7b), not by the finite water depth. Nevertheless, the weak correlation found in the data can offer no solid conclusions, and the issue warrants further research.
The traditional peak frequency, fp, was practically undefinable in the archipelago. As a compromise between scatter and bias with respect to fp, the integrated frequency weighted by E(f)4 was proposed as a characteristic frequency, fc. This definition was applicable over a wide range of wave conditions, and it functioned as a non-biased estimate for fp in a wide fetch geometry. Nevertheless, a proper parameterisation of the archipelago wave field cannot be obtained using only two parameters (e.g. Hs and fc), but the triplet (Hs, fc, κ2) seems like a promising candidate for developing an analytical form of a wave spectrum that covers also archipelago conditions.
The data are available through the following DOI: https://doi.org/10.5281/zenodo.3482304 (Björkqvist et al., 2019b).
JVB initiated the study based on previous conceptualisations of KK and HP. KK and JVB took part in designing the field measurements. JVB produced the methodology and performed the analysis. JVB did the visualisation. JVB wrote the article with contributions from HP and KK. HP supervised the study.
The authors declare that they have no conflict of interest.
We want to acknowledge the work done by the technical staff at FMI, namely Tuomo Roine, Heini Jalli, and Riikka Hietala. The efforts of Hannu Jokinen in processing the raw wave buoy data are also gratefully acknowledged. Most of the wave buoy observations in this study have been collected through work commissioned by the city of Helsinki. The data is used in this paper with their kind permission. We thank the anonymous reviewers for their constructive critique and comments. They helped us improve our article.
This research has been supported by the University of Helsinki and the Svenska Kulturfonden (grant no. 17/103386).
This paper was edited by Judith Wolf and reviewed by two anonymous referees.
Anderson, J. D., Wu, C. H., and Schwab, D. J.: Wave climatology in the Apostle Islands, Lake Superior, J. Geophys. Res.-Oceans, 120, 4869–4890, https://doi.org/10.1002/2014JC010278, 2015. a
Banner, M. L.: Equilibrium Spectra of Wind Waves, J. Phys. Oceanogr., 20, 966–984, https://doi.org/10.1175/1520-0485(1990)020<0966:ESOWW>2.0.CO;2, 1990. a
Battjes, J. A. and van Vledder, G. P.: Verification of Kimura’s Theory for Wave Group Statistics, in: Proc. 19th Int. Conf. Coastal Engineering, 642–648, ASCE, New York, https://doi.org/10.1061/9780872624382.044, 1984. a, b, c
Björkqvist, J.-V., Pettersson, H., Laakso, L., Kahma, K. K., Jokinen, H., and Kosloff, P.: Removing low-frequency artefacts from Datawell DWR-G4 wave buoy measurements, Geosci. Instrum. Method. Data Syst., 5, 17–25, https://doi.org/10.5194/gi-5-17-2016, 2016. a
Björkqvist, J.-V., Tuomi, L., Fortelius, C., Pettersson, H., Tikka, K., and Kahma, K. K.: Improved estimates of nearshore wave conditions in the Gulf of Finland, J. Mar. Syst., 171, 43–53, https://doi.org/10.1016/j.jmarsys.2016.07.005, 2017a. a
Björkqvist, J.-V., Vähäaho, I., and Kahma, K. K.: Spectral field measurements of wave reflection at a steep shore with wave damping chambers, in: WIT Transactions on the Built Environment, 170, 185–191, https://doi.org/10.2495/CC170181, 2017b. a
Björkqvist, J.-V., Vähä-Piikkiö, O., Alari, V., Kuznetsova, A., and Tuomi, L.: WAM, SWAN and WAVEWATCH III in the Finnish archipelago – the effect of spectral performance on bulk wave parameters, J. Oper. Oceanogr., 1–16, https://doi.org/10.1080/1755876X.2019.1633236, 2019a. a, b, c
Björkqvist, J.-V., Pettersson, H., and Kahma, K.: Wave and wind data from the Helsinki archipelago and Gulf of Finland (Version Version1) [Data set], Zenodo, https://doi.org/10.5281/zenodo.3482304, 2019b. a
Cartwright, D. and Longuet-Higgins, M. S.: The Statistical Distribution of the Maxima of a Random Function, P. R. Soc. London, 237, 212–232, 1956. a, b, c
Casas-Prat, M. and Holthuijsen, L. H.: Short-term statistics of waves observed in deep water, J. Geophys. Res.-Oceans, 115, 1–20, https://doi.org/10.1029/2009JC005742, 2010. a, b, c, d, e, f, g, h, i
Donelan, M. A. and Pierson, W. J.: The Sampling Variability of Estimates of Spectra of Wind-Generated Gravity Waves, J. Geophys. Res., 88, 4381–4392, https://doi.org/10.1029/JC088iC07p04381, 1983. a
Donelan, M. A., Hamilton, J., and Hui, W. H.: Directional Spectra of Wind-Generated Waves, Philos. T. Roy. Soc. A, 315, 509–562, https://doi.org/10.1098/rsta.1985.0054, 1985. a, b
Eldeberky, Y.: Nonlinear transformation of wave spectra in the nearshore, PhD thesis, Delft University of Technology, 1996. a
Forristall, G. Z.: On the statistical distribution of wave heights in a storm, J. Geophys. Res., 83, 2353, https://doi.org/10.1029/JC083iC05p02353, 1978. a, b, c, d, e, f, g
Goda, Y.: Numerical experiments on wave statistics with spectral simulation, Report of the Port and Harbour Research Institute, Ministry of Transport, Nagase, Yokosuka, Japan, 9, 3–57, 1970. a, b
Hardy, T. A. and Young, I. R.: Field study of wave attenuation on an offshore coral reef, J. Geophys. Res., 101, 14311–14326, https://doi.org/10.1029/96JC00202, 1996. a
Hasselmann, K., Barnett, T. P., Bouws, E., Carlson, H., Cartwright, D. E., Enke, K., Ewing, J. A., Gienapp, H., Hasselmann, D. E., Kruseman, P., Meerburg, A., Muller, P., Olbers, D. J., Richter, K., Sell, W., and Walden, H.: Measurements of Wind-Wave Growth and Swell Decay during the Joint North Sea Wave Project (JONSWAP), Ergnzungsheft zur Deutschen Hydrographischen Zeitschrift Reihe, A(8), p. 95, 2710264, 1973. a, b, c
Janssen, P. A. E. M.: Nonlinear Four-Wave Interactions and Freak Waves, J. Phys. Oceanogr., 33, 863–884, https://doi.org/10.1175/1520-0485(2003)33<863:NFIAFW>2.0.CO;2, 2003. a, b
Kahma, K. K.: On a two-peak structure in steady-state fetch-limited wave spectra, Licentiate thesis in Geophysics, University of Helsinki, p. 75, 1979. a
Kahma, K. K.: A Study of the Growth of the Wave Spectrum with Fetch, J. Phys. Oceanogr., 11, 1503–1515, https://doi.org/10.1175/1520-0485(1981)011<1503:ASOTGO>2.0.CO;2, 1981. a, b
Kahma, K. K. and Calkoen, C. J.: Reconciling Discrepancies in the Observed Growth of Wind-generated Waves, J. Phys. Oceanogr., 22, 1389–1405, https://doi.org/10.1175/1520-0485(1992)022<1389:RDITOG>2.0.CO;2, 1992. a
Kahma, K. K., Björkqvist, J.-V., Johansson, M. M., Jokinen, H., Leijala, U., Särkkä, J., Tikka, K., and Tuomi, L.: Turvalliset rakentamiskorkeudet Helsingin rannoilla 2020, 2050 ja 2100, Tech. rep., 96, City of Helsinki, Real Estate Department, Geotechnical Division, available at: http://www.hel.fi/static/kv/turvalliset-rakentamiskorkeudet.pdf (last access: 11 November 2019), 2016. a
Kitaigorodskii, S. A.: On the Theory of the Equilibrium Range in the Spectrum of Wind-Generated Gravity Waves, J. Phys. Oceanogr., 13, 816–827, https://doi.org/10.1175/1520-0485(1983)013<0816:OTTOTE>2.0.CO;2, 1983. a
Lenain, L. and Melville, W. K.: Measurements of the directional spectrum across the equilibrium-saturation ranges of wind-generated surface waves, J. Phys. Oceanogr., 47, 2123–2138, https://doi.org/10.1175/JPO-D-17-0017.1, 2017. a
Longuet-Higgins, M. S.: On the Statistical Distribution of the Heights of Sea Waves, J. Mar. Res., 11, 245–266, 1952. a, b, c, d, e, f
Longuet-Higgins, M. S.: On the Join Distribution of the Periods and Amplitudes of Sea Waves, J. Geophys. Res., 80, 2688–2694, https://doi.org/10.1029/JC080i018p02688, 1975. a, b, c, d
Longuet-Higgins, M. S.: On the distribution of the heights of sea waves: Some effects of nonlinearity and finite band width, J. Geophys. Res., 85, 1519, https://doi.org/10.1029/JC085iC03p01519, 1980. a, b, c, d, e, f, g, h, i, j, k
Mazarakis, N., Kotroni, V., Lagouvardos, K., and Bertotti, L.: High-resolution wave model validation over the Greek maritime areas, Nat. Hazards Earth Syst. Sci., 12, 3433–3440, https://doi.org/10.5194/nhess-12-3433-2012, 2012. a
Onorato, M., Osborne, A. R., and Serio, M.: Extreme wave events in directional, random oceanic sea states, Phys. Fluids, 14, 3–6, https://doi.org/10.1063/1.1453466, 2002. a
Orear, J.: Least squares when both variables have uncertainties, American J. Phys., 50, 912–916, https://doi.org/10.1119/1.12972, 1982. a
Pettersson, H.: Wave growth in a narrow bay, PhD thesis, University of Helsinki, 2004. a
Pettersson, H., Kahma, K. K., and Tuomi, L.: Wave Directions in a Narrow Bay, J. Phys. Oceanogr., 40, 155–169, https://doi.org/10.1175/2009JPO4220.1, 2010. a
Pettersson, H., Lindow, H., and Brüning, T.: Wave climate in the Baltic Sea 2012, Tech. rep., available at: http://www.helcom.fi/Documents/Baltic sea trends/Environment fact sheets/Wave_climate_in_the_Baltic_Sea_2012_BSEFS2013.pdf (last access: 11 November 2019), 2013. a
Phillips, O. M.: The equilibrium range in the spectrum of wind-generated waves, J. Fluid Mech., 4, 426–434, https://doi.org/10.1017/S0022112058000550, 1958. a
Pierson, W. J. and Marks, W.: The power spectrum analysis of ocean‐wave records, EOS T. Am. Geophys. Un., 33, 834–844, https://doi.org/10.1029/TR033i006p00834, 1952. a
Pierson, W. J. and Moskowitz, L.: A proposed spectral form for fully developed wind seas based on the similarity theory of S. A. Kitaigorodskii, J. Geophys. Res., 69, 5181–5190, https://doi.org/10.1029/JZ069i024p05181, 1964. a
Serio, M., Onorato, M., Osborne, A. R., and Janssen, P. A. E. M.: On the computation of the Benjamin-Feir Index, Nuovo Cimento C, 28, 893–903, https://doi.org/10.1393/ncc/i2005-10134-1, 2005. a, b
Sobey, R. J. and Young, I. R.: Hurricane Wind Waves–A Discrete Spectral Model, in: Journal of Waterway, Port, Coastal and Ocean Engineering, 112, 370–389, ASCE, https://doi.org/10.1061/(ASCE)0733-950X(1986)112:3(370), 1986. a
Soukissian, T. H., Prospathopoulos, A. M., and Diamanti, C.: Wind and Wave Data Analysis for the Aegean Sea – Preliminary Results, J. Atmos. Ocean Sci., 8, 163–189, https://doi.org/10.1080/1023673029000003525, 2004. a
SPM: Shore Protection Manual, Vol. I, Dept. of the Army, Waterways Experiment Station, Corps of Engineers, Coastal Engineering Research Center,, available at: http://www.biodiversitylibrary.org/item/102420 (last access: 11 November 2019), 1984. a
Tayfun, M. A.: Effects of spectrum band width on the distribution of wave heights and periods, Ocean Eng., 10, 107–118, https://doi.org/10.1016/0029-8018(83)90017-3, 1983. a
Toba, Y.: Local balance in the air-sea boundary processes – I. on the growth process of wind waves, J. Oceanogr. Soc. Jpn., 28, 109–120, https://doi.org/10.1007/BF02109772, 1972. a
Toba, Y.: Local balance in the air-sea boundary processes – III. On the Spectrum of Wind Waves, J. Oceanogr. Soc. Jpn., 29, 209–220, https://doi.org/10.1007/BF02108528, 1973. a
Tuomi, L., Kahma, K. K., and Pettersson, H.: Wave hindcast statistics in the seasonally ice-covered Baltic Sea, Boreal Environ. Res., 16, 451–472, 2011. a
Tuomi, L., Pettersson, H., Fortelius, C., Tikka, K., Björkqvist, J.-V., and Kahma, K. K.: Wave modelling in archipelagos, Coast. Eng., 83, 205–220, https://doi.org/10.1016/j.coastaleng.2013.10.011, 2014. a
van der Westhuysen, A. J., van Dongeren, A. R., Groeneweg, J., van Vledder, G. P., Peters, H., Gautier, C., and van Nieuwkoop, J. C.: Improvements in spectral wave modeling in tidal inlet seas, J. Geophys. Res.-Oceans, 117, 1–23, https://doi.org/10.1029/2011JC007837, 2012. a
Vandever, J. P., Siegel, E. M., Brubaker, J. M., and Friedrichs, C. T.: Influence of Spectral Width on Wave Height Parameter Estimates in Coastal Environments, J. Waterw. Port Coast., 134, 187–194, https://doi.org/10.1061/(ASCE)0733-950X(2008)134:3(187), 2008. a, b, c
Young, I. R.: The determination of confidence limits associated with estimates of the spectral peak frequency, Ocean Eng., 22, 669–686, https://doi.org/10.1016/0029-8018(95)00002-3, 1995. a, b, c