The influence of dissolved organic matter on the marine production of carbonyl sulfide (OCS) and carbon disulfide (CS₂) in the Peruvian upwelling

Oceanic emissions of the climate-relevant trace gases carbonyl sulfide (OCS) and carbon disulfide (CS₂) are a major source to their atmospheric budget. Their current and future emission estimates are still uncertain due to incomplete process understanding and therefore inexact quantification across different biogeochemical regimes. Here we present the first concurrent measurements of both gases together with related fractions of the dissolved organic matter (DOM) pool, i.e., solid-phase extractable dissolved organic sulfur (DOS_SPE, n=24, 0.16±0.04 µmol L⁻¹), chromophoric (CDOM, n=76, 0.152±0.03), and fluorescent dissolved organic matter (FDOM, n=35), from the Peruvian upwelling region (Guayaquil, Ecuador to Antofagasta, Chile, October 2015). OCS was measured continuously with an equilibrator connected to an off-axis integrated cavity output spectrometer at the surface (29.8±19.8 pmol L⁻¹) and at four profiles ranging down to 136 m. CS₂ was measured at the surface (n=143, 17.8±9.0 pmol L⁻¹) and below, ranging down to 1000 m (24 profiles). These observations were used to estimate in situ production rates and identify their drivers. We find different limiting factors of marine photoproduction: while OCS production is limited by the humic-like DOM fraction that can act as a photosensitizer, high CS₂ production coincides with high DOS_SPE concentration. Quantifying OCS photoproduction using a specific humic-like FDOM component as proxy, together with an updated parameterization for dark production, improves agreement with observations in a 1-D biogeochemical model. Our results will help to better predict oceanic concentrations and emissions of both gases on regional and, potentially, global scales.

1 Introduction

Oceanic emissions play a dominant role in the atmospheric budget of the climate-relevant trace gases carbonyl sulfide (OCS) and carbon disulfide (CS₂) (Chin and Davis, 1993; Kremser et al., 2016). OCS is the most abundant sulfur gas in the atmosphere, and CS₂ is its most important precursor. Both gases influence the climate directly (OCS) or indirectly (CS₂ by oxidation to OCS in the atmosphere), as OCS is a major supplier of stratospheric aerosols (Brühl et al., 2012; Crutzen, 1976), which exert a cooling effect on the atmosphere and can foster ozone depletion (Junge et al., 1961; Kremser et al., 2016). Furthermore, OCS has been suggested as a proxy to constrain global terrestrial gross primary production (Campbell et al., 2008; Montzka et al., 2007; Berry et al., 2013). The oceanic emissions of both gases have recently attracted interest because they are suggested to account for a missing source of atmospheric OCS (Berry et al., 2013; Kuai et al., 2015; Glatthor et al., 2015; Launois et al., 2015). In situ measurements of OCS in surface seawater are still limited, but those available suggest that oceanic emissions are too low to fill the proposed gap of 400–600 Gg S yr⁻¹ in the atmospheric budget (Lennartz et al., 2017). Still, oceanic emission estimates are associated with high uncertainties (ca. 50 %) (Kremser et al., 2016; Whelan et al., 2018). Reducing these uncertainties for present and future emission estimates requires (i) increasing the existing field data across various biogeochemical regimes and (ii) increasing process understanding and quantification in the whole water column to facilitate model approaches.

Most of the in situ observations of OCS and CS₂ in seawater were reported from the Atlantic Ocean and adjacent seas and mainly represent surface ocean measurements (see Whelan et al., 2018, for an overview). Here we report the first concurrent measurements in the surface ocean and the water column for both gases from the Peruvian upwelling. This region is one of the most biologically productive regions in the global ocean due to the upwelling of nutrient-rich water. The upwelling influences the pool of dissolved organic matter (DOM) exposed to sunlight by transporting DOM from the deep ocean to the surface. The DOM pool is relevant in this context because it contains the precursors and photosensitizers for the photochemical production of OCS and CS₂ (Pos et al., 1998; Flöck et al., 1997; Uher and Andreae, 1997). Here we show measurements of chromophoric and fluorescent DOM as well as solid-phase extractable dissolved organic sulfur (DOS_SPE) in order to further specify drivers of production processes and improve parameterizations of production rates in biogeochemical models.

Chromophoric DOM (CDOM) is the fraction that absorbs light in the UV and visible range. CDOM contains photosensitizers that absorb light and facilitate photochemical reactions, and it can undergo photodegradation itself (Coble, 2007). A part of the CDOM fraction fluoresces (FDOM), i.e., emits absorbed light at a shifted wavelength. Distinct groups of molecules have a specific fluorescence pattern, enabling the molecule classes such as humic substances or proteins (FDOM components) to be differentiated (Coble, 2007; Murphy et al., 2013). DOS_SPE is operationally defined as the dissolved organic sulfur retained by solid-phase extraction (Dittmar et al., 2008). The method favors the retention of polar molecules, which comprise approximately 40 % of the total dissolved organic carbon (DOC) in marine waters (Dittmar et al., 2008). Due to the operational definition, no direct comparison to the CDOM and FDOM pools is possible (Wünsch et al., 2018).

OCS is produced in the surface ocean by the interaction of UV radiation with CDOM (Uher and Andreae, 1997), making coastal and shelf regions a hot spot for OCS production (Cutter and Radford-Knoery, 1993). A reaction pathway through an acyl radical intermediate in addition to a thiyl (organic RS⋅) or sulfhydryl (inorganic SH⋅, from bisulfide) radical pathway has been proposed by Pos et al. (1998) based on incubation experiments. Indeed, the amount of OCS produced has been shown to depend on CDOM, more specifically the absorption coefficient at 350 nm (a₃₅₀), and a variety of organic sulfur-containing precursors, such as methionine or glutathione (Zepp and Andreae, 1994; Flöck et al., 1997). a₃₅₀ has previously been used as a proxy to calculate the photochemical production of OCS (Preiswerk and Najjar, 2000). In addition, von Hobe et al. (2003) suggested a relationship between the photoproduction rate constant and a₃₅₀, making the overall photoproduction rate quadratic with respect to a₃₅₀. This dependency is based on the assumption that a₃₅₀ can serve as a proxy for both photosensitizers and organic sulfur precursors on large spatial scales. Accordingly, a global parameterization for photochemical production was developed based on a₃₅₀ by integrating data from the Atlantic, Pacific, and Indian oceans (Lennartz et al., 2017). To improve this parameterization on a regional scale, we tested whether the precursors can be further specified by an easily measurable fraction of the DOM pool (FDOM components, DOS_SPE), without performing costly and potentially incomplete analysis on the molecular level. In addition, OCS is produced in a light-independent reaction termed dark production (Flöck and Andreae, 1996; Von Hobe et al., 2001). Two hypotheses exist to date: an abiotic reaction involving thiyl radicals formed by O₂ or metal complexes (Pos et al., 1998; Flöck et al., 1997; Flöck and Andreae, 1996) and a coupling to microbial processes during organic matter remineralization (Radford-Knoery and Cutter, 1994). Dark production is parameterized based on temperature and a₃₅₀ derived from field data in the Atlantic Ocean and the Mediterranean Sea (Von Hobe et al., 2001). It is still unclear whether this parameterization is valid on a global scale. Furthermore, OCS is degraded by hydrolysis, yielding CO₂ and hydrogen sulfide (H₂S) or bisulfide (SH⁻), in the following summarized as sulfide. The hydrolysis degradation rate increases strongly with temperature and has been well quantified by a comprehensive laboratory study over a wide temperature range (Elliott et al., 1989) and by seawater incubation studies (Radford-Knoery and Cutter, 1994). Oceanic OCS concentrations have been modeled using surface box models on regional (von Hobe et al., 2003) and global scales (Lennartz et al., 2017), in the water column (von Hobe et al., 2003), and with a global 3-D circulation model (Preiswerk and Najjar, 2000; Launois et al., 2015) based on the same or similar parameterizations as described above. Here we test whether subsurface concentrations can be numerically simulated by coupling the box model to a physical 1-D water column host model.

Production and loss processes for CS₂ are less well constrained. Photochemical incubation studies indicate that the photoproduction of CS₂ has a similar wavelength dependence (spectrally resolved apparent quantum yield, AQY) but only a quarter of the magnitude compared to OCS (Xie et al., 1998). It is currently unclear whether the in situ photoproduction rates of both gases covary on larger spatial scales. A covariation is expected only when identical drivers limit production for both gases. Evidence for biological production comes from incubation studies (Xie et al., 1999), indicating varying CS₂ production for different phytoplankton species. Outgassing to the atmosphere appears to be the most important sink for CS₂ in the mixed layer (Kettle, 2000). Although CS₂ is hydrolyzed and oxidized by H₂O₂, the corresponding lifetimes are too long to rival emission to the atmosphere at the surface (Elliott, 1990). In addition to the known sinks, namely air–sea exchange, hydrolysis, and oxidation, Kettle (2000) proposed a sink with a lifetime on the order of weeks to match observed concentrations with a surface box model. No underlying mechanism for such a sink is currently known, hampering further model approaches.

Table 1 Model experiments with 1-D GOTM–FABM modules for OCS and CS₂. AQY: apparent quantum yield.

The goal of this study is to quantify production rates for both gases in the Peruvian upwelling and to further specify their drivers. Surface concentrations and emissions to the atmosphere from the cruise presented here are discussed in Lennartz et al. (2017). Here, we focus on processes in the water column. We use the comprehensive dataset together with simple biogeochemical models to increase the understanding and quantification of the cycling of both gases in the water column and to improve model capability to predict OCS and CS₂ seawater concentrations.

2 Material and methods

2.1 Study area

The cruise ASTRA-OMZ on RV Sonne started in Guayaquil, Ecuador, on 5 October 2015 and reached Antofagasta on 22 October 2015 (Fig. 1). It covered several regimes from the open ocean to the coastal shelf between 5^∘ N and 17^∘ S. The hydrographic conditions encountered during this cruise have been described elsewhere (Stramma et al., 2016). The area off Peru is associated with one of the four major global eastern boundary upwelling systems (Chavez et al., 2008). A large oxygen minimum zone expands into the Pacific Ocean at depths between 100 and 900 m, resulting from weak ventilation and strong respiration (Karstensen et al., 2008). The cruise covered areas of open ocean with warm sea surface temperatures (SSTs) between 22 and 27 ^∘C (stations 1–6) and regions with colder SSTs below 20 ^∘C closer to the coast (stations 7–18). Upwelling occurred at the southernmost transects indicated by the lowest SSTs (15–18 ^∘C) encountered during that cruise (stations 15–18).

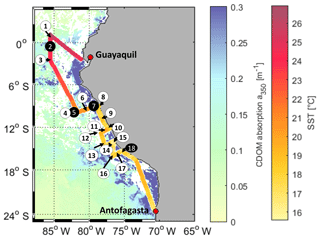
Figure 1 Cruise track of ASTRA-OMZ with stations 1–18 (in black circles: stations where OCS profiles were taken). The cruise track shows sea surface temperature (SST) measured onboard. For visualization only, the background is composed of MODIS Aqua satellite data for the absorption of CDOM and detritus corrected from 443 to 350 nm with the mean slope of our in situ measurements (0.0179, 300–450 nm; MODIS Aqua composite for October 2015). Note: as a monthly composite does not necessarily reflect the exact conditions during the cruise, in situ measurements are illustrated in Fig. 2e. White areas: no satellite data available.

2.2 Measurement of trace gases

Carbonyl sulfide concentrations were determined with an off-axis integrated cavity output spectrometer (OA-ICOS; Los Gatos Inc., USA) coupled to a Weiss-type equilibrator (Lennartz et al., 2017). The Weiss-type equilibrator was supplied with 2–4 L min⁻¹ of seawater from the hydrographic shaft of the ship 5 m below the surface. The sample gas stream from the headspace of the equilibrator was filtered (Pall Acro Filter, 0.2 µm) and dried (Nafion^® drier, Gasmet Perma Pure) before entering the cavity of the OCS analyzer. The outlet of the OCS analyzer was connected to the Weiss equilibrator, as this recirculation method kept the concentration gradient between the water and gas phases small, enabling rapid equilibration. OCS calibrations using standards from permeation tubes (Fine Metrology, Italy) were performed before and after the cruise, showing good agreement. Details on the OA-ICOS can be found in Schrade (2011). The precision of this setup is 15 ppt for 2 min averages of 1 Hz measurement frequency and was experimentally determined (running a standard for >60 min). The limit of detection is 180 ppt (corresponding to 4 pmol L⁻¹ at 20 ^∘C), defined by the instrument's internal 1 s spectra. Additionally, independent samples for comparison measured with GC-MS (Schauffler et al., 1998; de Gouw et al., 2009) reflected a <2 % difference between the NOAA scale (Montzka et al., 2007) and the perm tube standards. A corrected calibration led to a minor change in absolute concentrations of OCS compared to Lennartz et al. (2017), which was on average +2 pmol L⁻¹. Marine boundary layer air was measured every hour for 10 min by pumping air from the ship's deck (ca. 35 m a.s.l.) through a metal tube (Decabon) with a chemically inert pump (KNF Neuberger). Resulting emissions are reported in Lennartz et al. (2017).

OCS depth profiles were obtained using a newly developed submersible pumping system. A rotary pump (Lowara, Xylem) connected to a 1” PTFE hose supplied the Weiss equilibrator with 2–4 L seawater min⁻¹. The pump inlet was held at a constant depth for 10–15 min to ensure full equilibration at four to six depths during each profile.

CS₂ was measured with a purge-and-trap system attached to a gas chromatograph and mass spectrometer (GC–MS; Agilent 7890A, Agilent 5975C; inert XL MSD with triple axis detector) running in single-ion mode (Lennartz et al., 2017); 50 mL samples were taken in 1 to 3 h intervals from the same underway system as for continuous OCS measurements. After purging for 15 min with helium (70 mL min⁻¹), the gas stream was dried with a Nafion^® membrane drier (Gasmet Perma Pure) and trapped with liquid nitrogen for preconcentration. Hot water was used to heat the trap and inject CS₂ into the GC–MS. The retention time for CS₂ ($\frac{m}{z}=\mathrm{76}$, 78) was 4.9 min. The analyzed data were calibrated daily using gravimetrically prepared liquid CS₂ standards in ethylene glycol. During purging, 500 µL gaseous deuterated dimethyl sulfide (d3-DMS) and isoprene (d5-isoprene) were added to each sample as an internal standard to account for possible sensitivity drift between calibrations. The limit of detection was 1 pmol L⁻¹. Discrete samples from depth profiles were obtained from the rosette sampler connected to a conductivity–temperature–depth (CTD) sensor. Note that OCS and CS₂ profiles were not obtained at the same time but up to 7 h apart. The stations were defined by geographical location and not by a Lagrangian experiment following the same water mass, which explains temperature changes between OCS and CS₂ profiles, for example at station 2 (see Fig. 2c, Table S2).

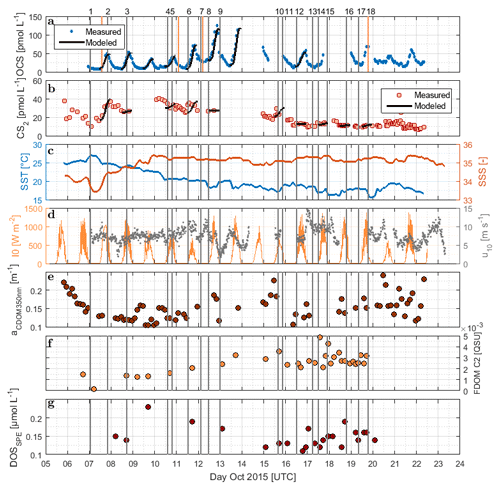
Figure 2 Time series of (a) OCS, (b) CS₂, (c) SST and sea surface salinity (SSS), (d) I0 and wind speed at 10 m, (e) absorption coefficient of CDOM at 350 nm, (f) humic-like FDOM component 2, and (g) DOS_SPE sampled from the underway system along the cruise track of ASTRA-OMZ from 5 to 23 October 2018. Vertical lines indicate stations of ASTRA-OMZ for comparison with locations (see Fig. 1).

2.3 Chromophoric dissolved organic matter (CDOM)

The spectral absorption coefficient of CDOM (a₃₅₀) was determined for samples collected from CTD Niskin bottles or from the underway system, here in a 3 h interval. The sampled water was filtered through a sample-washed 0.2 µm membrane (GWSP, Millipore) after prefiltration through a combusted glass-fiber filter (GFF, Whatman). The optical density of the CDOM in the filtrate was analyzed using a spectrophotometric setup with a liquid waveguide capillary cell (LWCC, WPI; path length: 2.5 m) (Miller et al., 2002). Spectra were recorded for wavelengths between 270 and 700 nm at 2 nm spectral resolution for the sample filtrate and purified water as the reference, with the sample and reference at room temperature. The absorption coefficient is determined from the obtained optical density using the Lambert–Beer law and corrected for the salinity effect (see Lefering et al., 2017, for details).

2.4 Fluorescent dissolved organic matter (FDOM)

Fluorescent dissolved organic matter (FDOM) was recorded in excitation–emission matrices (EEMs) with a UV–Vis spectrofluorometer (Hitachi F2700) from filtered seawater samples (0.2 µm, <200 mbar below atmospheric pressure) directly onboard. Excitation wavelengths ranged from 220 to 550 nm with a resolution of 10 nm. Emission wavelengths were recorded from 250 to 550 nm in 1 nm resolution at a photomultiplier voltage of 400 or 800 V due to a change in method during the campaign (from 10 October 2015 onwards). For both voltages, calibration curves with quinine sulfate (5 to 30 ppb) in sulfuric acid were measured with R² of 0.9991 and 0.9971, respectively. EEMs were blank subtracted and Raman normalized (Murphy et al., 2013). The values are reported here in quinine sulfate units (QSUs). A parallel factor analysis (PARAFAC) was performed using the drEEM toolbox (Murphy et al., 2013; Stedmon and Bro, 2008) to separate the superimposed optical signals of different fluorophores (“components”) in the EEMs. FDOM concentrations are reported here in quinine sulfate units (Murphy et al., 2013); the conversion factor between QSUs and Raman units is 0.3540 and 0.4256 for each of the QS calibrations (i.e., before and after the change in photomultiplier voltage, respectively). The components were compared to the database OpenFluor (Murphy et al., 2014) to identify similar components from previous studies in other environments.

2.5 Solid-phase extractable dissolved organic sulfur (DOS_SPE)

DOS_SPE was sampled from the underway system or from submersible pump profiles directly into glass bottles and filtered through precombusted GF/F filters (Whatman, 450 ^∘C for >5 h) at a maximum of 200 mbar below atmospheric pressure; 450 mL of each filtered sample was acidified to pH 2 (hydrochloric acid, Suprapur; Merck), extracted according to Dittmar et al. (2008) (PPL, 1 g, Mega Bond Elut; Varian), and stored at −20 ^∘C until further analysis. For analysis, the PPL cartridges were eluted with 5 mL of methanol (LiChrosolv, Merck). DOS_SPE was quantified with an inductively coupled plasma–optical emission spectrometer (ICP-OES; iCAP 7400, Thermo Fisher Scientific), and 100 µL of the extract was evaporated with N₂ and redissolved in 1 mL nitric acid (1 M, double distilled; Merck); 1 mL of yttrium (2 µg L⁻¹ in the spike solution) was added as an internal standard. The sulfur signal was detected at a wavelength of 182.034 nm. Nitric acid (1 M, double distilled, Merck) was used for an analysis blank. Calibration standards were prepared from a stock solution (1000 mg L⁻¹ sulfur ICP standard solution; Carl Roth). To assess the accuracy and precision of the method, the SLRS-5 reference standard was analyzed five times during the run. Although sulfur is not certified for SLRS-5, a previous study (Yeghicheyan et al., 2013) reported S concentrations of 2347–2428 µg S L⁻¹, which is in agreement with our findings. The limit of detection (according to German industry standard DIN 32645) was 1.36 µmol L⁻¹ S, corresponding to 0.015 µmol L⁻¹ DOS_SPE in original seawater (average enrichment factor of 89.4).

2.6 Shortwave radiation in the water column

Underwater shortwave radiation was assessed through downwelling irradiance profiles obtained with the hyperspectral radiometer RAMSES ACC-VIS (TriOS GmbH, Germany). This instrument covers a wavelength range of 318 to 950 nm with an optical resolution of 3.3 nm and a spectral accuracy of 0.3 nm. Measurements were collected with sensor-specific automatically adjusted integration times (between 4 ms and 8 s). Radiometric profiles were collected down to the maximum at which light could be recorded prior to or after CDOM–FDOM sampling except at station 7 where sampling took place at night only. Shortwave radiation was approximated at this station with the shortwave radiation profile at station 6, which had similar properties in chlorophyll a distribution in the water column.

Following NASA protocols (Mueller et al., 2003), all downwelling irradiance profiles were corrected for incident sunlight (e.g., changing due to varying cloud cover) using simultaneously obtained downwelling irradiance at the respective wavelength, measured above the surface with another hyperspectral RAMSES irradiance sensor. Finally, these data were interpolated on discrete intervals of 1 m.

As surface waves strongly affect measurements in the upper few meters, deeper measurements that are more reliable can be further extrapolated to the sea surface. Each profile was checked and an appropriate depth interval was defined (ranging 4–25 for station 2 and 2–25 m for the other three stations) to calculate the vertical attenuation coefficients for downwelling irradiance (i.e., K_d(λ, z')) for the upper surface layer. With K_d(λ, z') the subsurface irradiance $E_{\mathrm{d}}^{-}$(λ, 0 m) was extrapolated from the profiles of E_d(λ, z) within the respective depth interval. Finally, shortwave radiation rad(z) and photosynthetically active radiation PAR(z) were calculated as the integral over $E_{\mathrm{d}}^{-}$(λ, z) for λ=318 to 398 nm and for λ=400 to 700 nm, respectively, for the depths above the lower limit of the respective depth interval and the originally measured $E_{\mathrm{d}}^{-}$(λ, z) for the depths below. Finally, the euphotic depth Z_eu at each station was calculated from the in situ PAR profiles as the 1 % light depth at which PAR(z) 0.01 of PAR(z=0 m).

2.7 Determination of gas diffusivity with microstructure profiles

Diapycnal diffusive gas fluxes, i.e., fluxes of dissolved gas compounds caused by turbulent mixing in a direction perpendicular to the stratification, were calculated for the four stations 2, 5, 7, and 18. The diapycnal diffusive flux of a compound, φ_dia (pmol m⁻² s⁻¹), is estimated as

$$\begin{array}{}\text{(1)}& {\mathrm{\Phi }}_{\mathrm{dia}}\approx \mathit{\rho }\cdot K_{\mathit{\rho }}\cdot {\displaystyle \frac{\partial c}{\partial z}},\end{array}$$

where $\frac{\partial c}{\partial z}$ (pmol kg⁻¹ m⁻¹) is the vertical gradient of gas concentration across a layer of ideally constant stratification and constant diffusivity, K_ρ (m² s⁻¹) is the diapycnal turbulent diffusivity, and ρ(kg m⁻³) is the water density. Fluxes can be estimated for depth ranges that are limited above and below by concentration measurements and that do not vary systematically in stratification and turbulent mixing within. Particular focus is on fluxes to and from the mixed layer (ML), which cause particular issues because of the sudden changes in stratification and mixing intensity at the mixed layer depth (MLD). That is why we approximate ML fluxes by fluxes through a transition zone at 5 to 15 m below the MLD, following Hummels et al. (2013), because stratification there is typically strong and relatively constant. MLD was defined here as the depth at which the density has increased by an amount equivalent to a 0.5 K temperature decrease compared to the surface (Schlundt et al., 2014). The diapycnal turbulent diffusivity K_ρ was estimated from the average dissipation rate of turbulent kinetic energy, which in turn was estimated from profiles of velocity microstructure. Details on the methodology to estimate the diapycnal fluxes of dissolved substances from microstructure measurements and concentration profiles can be found in Fischer et al. (2013) and Schlundt et al. (2014). The microstructure profiles were obtained with a tethered profiler (type MSS 90D, Sea & Sun Technology).

The depths at which fluxes could be estimated were then used as the upper and lower bounds of budget volumes. The difference of the diapycnal fluxes in and out of each volume determines convergence or divergence of the diapycnal flux. If other transport processes are negligible and if steady state is assumed, sources–sinks to compensate for the flux divergence–convergence can be determined.

Uncertainties of fluxes have been calculated by error propagation from measurement uncertainties of the gas concentrations and the average K_ρ values. There are additional uncertainties not quantified, e.g., from the approximation of the average gas gradient or from the neglect of gas transport processes other than diapycnal mixing. It should be noted that the diffusivity profile only represents current conditions during profiling and can change on a daily basis due to varying stratification and/or surface winds among other factors.

2.8 Determination of OCS dark production rates

Dark production rates were determined from hourly averaged measured seawater concentrations shortly before sunrise (i.e., ca. 12–14 h after the concentration maximum of the previous day) or at depths below the euphotic zone. Concentration data from this study and a previous study from the Indian Ocean (Lennartz et al., 2017) were used to calculate dark production rates. The determination of dark production rates relies on the principle that in the absence of light, an equilibrium between dark production and loss by hydrolysis results in stable concentrations (Von Hobe et al., 2001). To ensure approximately steady-state conditions, we averaged the concentrations 1 h before sunrise and compared to the average of the previous hour. We only considered instances when the concentration before sunrise deviated less than 1 pmol L⁻¹ from the previous hour for further calculation. These conditions were met at the beginning of the cruise (7 to 12 October), when water temperatures ranged between 21 and 26 ^∘C and the corresponding e-folding lifetimes of OCS due to hydrolysis ranged from 6 h (7 October) to 12 h (12 October). In steady state (early morning or below the euphotic zone), dark production P_D (pmol L⁻¹ s⁻¹) equals loss by hydrolysis L_H (pmol L⁻¹ s⁻¹), the latter being the product of the steady-state concentration (OCS; pmol L⁻¹) and the rate constant k_h (s⁻¹) according to Eq. (2):

$$\begin{array}{}\text{(2)}& P_{\mathrm{D}}=L_{\mathrm{H}}=\left[\mathrm{OCS}\right]\cdot {\mathrm{k}}_h.\end{array}$$

The rate constant for hydrolysis, k_h (s⁻¹), was calculated according to Elliott et al. (1989) with Eqs. (3) and (4):

$$\begin{array}{}\text{(3)}& {\displaystyle }{\mathrm{k}}_h=e^{(\mathrm{24.3}-\frac{\mathrm{10450}}{T})}+e^{(\mathrm{22.8}-\frac{\mathrm{6040}}{T})}\cdot {\displaystyle \frac{K_{\mathrm{w}}}{a\left[H^{+}\right]}},\text{(4)}& {\displaystyle }-{\log }_{\mathrm{10}}{K}_{\mathrm{w}}={\displaystyle \frac{\mathrm{3046.7}}{T}}+\mathrm{3.7685}+\mathrm{0.0035486}\cdot \sqrt{S},\end{array}$$

with temperature T, salinity S, a[H]⁺ the proton activity, and K_w the ion product of seawater (Dickinson and Riley, 1979).

The temperature dependency of the reaction rate P_D (pmol L⁻¹ s⁻¹) can be described with an Arrhenius relationship, resulting in the following equation (Eq. 5) in its linearized form:

$$\begin{array}{}\text{(5)}& \ln \left({\displaystyle \frac{P_{\mathrm{D}}}{a_{\mathrm{350}}}}\right)={\displaystyle \frac{a}{T}}+b,\end{array}$$

with a₃₅₀ being the absorption coefficient of CDOM at 350 nm (m⁻¹), T the temperature (K), and a and b coefficients describing the temperature dependency of the reaction (–). The production rate P_D is normalized to a₃₅₀ (von Hobe et al., 2001). The parameters a and b in Eq. (5) were derived from P_D (Eq. 5) in the Arrhenius plot to obtain a parameterization for dark production rate in relation to temperature and a₃₅₀.

Biases can potentially be introduced in two ways: (1) neglecting other sinks like air–sea exchange can lead to underestimations of the production rate. With wind speeds of 8 m s⁻¹ and MLD on the order of 20–40 m, lifetimes due to air–sea exchange are on the order of days to weeks and hence negligible. (2) Sampling fewer than two half-lives after the maximum concentrations can lead to overestimations of the production rate. For 11 and 12 October, samples considered for the calculation of dark production rates were taken fewer than two half-lives after the concentration maximum of the previous day. Since the concentration changed less than 1 pmol L⁻¹ within 2 h prior to this sampling, we consider the bias to be within the range of the given uncertainty.

2.9 Surface box models to estimate photoproduction rate constants

The surface box model for OCS has already been used in Lennartz et al. (2017) to estimate OCS photoproduction rate constants. The model consists of parameterizations for the four processes of hydrolysis (Elliott et al., 1989), dark production (Von Hobe et al., 2001), photoproduction (Lennartz et al., 2017), and air–sea exchange (Nightingale et al., 2000). In situ measurements of meteorological, physical, and biogeochemical parameters are used as model forcing. Photochemical production was calculated according to Eq. (6):

$$\begin{array}{}\text{(6)}& {\displaystyle \frac{\mathrm{d}{c}_{\mathrm{photo}}}{\mathrm{d}t}}=\underset{\mathrm{MLD}}{\overset{\mathrm{0}}{\int }}\mathrm{UV}\cdot a_{\mathrm{350}}\cdot p,\end{array}$$

with $\frac{\mathrm{d}{c}_{\mathrm{photo}}}{\mathrm{d}t}$ being the change in concentration due to photoproduction (pmol L⁻¹ s⁻¹), UV the irradiance in the UV range (W m⁻²), a₃₅₀ the absorption coefficient of CDOM at 350 nm (m⁻¹), and p the photoproduction rate constant (pmol J⁻¹). The model was set up in an inverse mode constrained by time series of OCS measurements $\left(\frac{\mathrm{d}c}{\mathrm{d}t}\right)$ to optimize the photoproduction rate constant p during each daylight period (13:00 to 23:00 h UTC) with a Levenberg–Marquardt routine (MATLAB version 2015a, MathWorks, Inc.). The scaling of the rate constant p can be seen as the contribution of the precursors varying in concentration, as detailed in von Hobe et al. (2003).

An analogous model setup was developed for CS₂, including only the processes of air–sea exchange and photoproduction. The estimated production rate hence compensates for the sink of air–sea exchange. Processes without known parameterizations, such as possible biotic production and a potential (chemical) sink, are excluded at this stage (see the Discussion section). More information on the model forcing parameters can be found in the Supplement (Tables S1 and S2).

2.10 1-D water column modules for OCS and CS₂

The Framework for Aqueous Biogeochemical Modelling (FABM) was used to couple the box model to a 1-D water column model (Bruggeman and Bolding, 2014) and compare simulated concentrations to observations at stations 2, 5, 7, and 18. FABM provides the frame for a physical host model and a biogeochemical model, wherein the physical host is responsible for tracer transport and the biogeochemical model provides local source and sink terms. The physical host used here is the General Ocean Turbulence Model (GOTM), which is a 1-D water column model simulating hydrodynamic and thermodynamic processes related to vertical mixing (Umlauf and Burchard, 2005). GOTM derives solutions for the transport equations of heat, salt, and momentum.

In situ measurements of radiation, temperature, salinity, CDOM, and meteorological parameters were used as model forcing to represent conditions under which the concentration profiles were taken. Diurnal radiation cycles and constant meteorological conditions, salinity, and water temperature were repeated for 5 d for OCS to obtain stable diurnal concentration cycles and 21 d for CS₂ due to its longer lifetime.

The same process parameterizations as for the box models were used as local source and sink terms in the 1-D water column modules for OCS and CS₂ in FABM. Photochemical production was calculated in the wavelength-integrated approach (300–400 nm) described above in Eq. (6) and, in addition, in a wavelength-resolved approach. For this purpose, we used in situ measured, wavelength-resolved downwelling irradiance profiles together with in situ wavelength-resolved CDOM absorption coefficients to model the photoproduction of both gases in the water column based on previously published apparent quantum yields (AQYs) by Weiss et al. (1995) for OCS and by Xie et al. (1998) for CS₂. We use the AQYs by Weiss et al., since they were measured at the location closest to our study region (i.e., South Pacific). We assume they reflect the DOM composition in our study region best due to their similarity in a₃₅₀. We note other observed AQYs (Zepp and Andreae, 1994; Cutter et al., 2004), which vary by up to 2 orders of magnitude. In addition, the photoproduction rate constant p of OCS in Eq. (6) was calculated based on the relationship with FDOM component 2 developed in this study.

In addition, sensitivity tests were performed to further constrain production and consumption processes for CS₂. Here we assessed the sensitivity of the general shape of the profiles and did not focus on exact production rates, since both sink and source processes are too poorly constrained to derive reaction rates from single concentration profiles. Profiles were initialized with the lowest subsurface concentration of the respective measured profile: low enough to be able to assess whether in situ photoproduction can explain concentration peaks below the mixed layer, but high enough to keep diapycnal fluxes out of the mixed layer in a reasonable range (in contrast to initializing with 0 pmol L⁻¹). The same meteorological conditions that occurred on the day of measurement were repeated for 21 d, i.e., ∼2–3 times longer than the lifetime due to air–sea exchange. These sensitivity tests demonstrate (1) the sensitivity of surface CS₂ concentrations against diurnal mixed layer variations (simulations X98, X98d, X98s) and (2) the sensitivity of the subsurface CS₂ peak against the photoproduction rate constant and wavelength resolution (simulations X98x2, pfit, psfit). Testing the sensitivity against diurnal mixed layer variations is important because surface CS₂ concentrations depend on the amount of photochemical production occurring within the mixed layer. Air–sea exchange as the major sink for CS₂ within the mixed layer led to relatively long lifetimes on the order of days to weeks during this cruise, so the conditions during the days prior to the CS₂ profile measurements became important. Simulations with adjusted temperature and salinity profiles with a diurnally varying mixed layer between 10–25 m (“shallow” simulation X98s) and 25–50 m (“deep” simulation X98d) were performed. For the second test, demonstrating the sensitivity of the subsurface peak, we chose station 5. This station provides the unique opportunity to assess a profile in which the photic zone reaches below the ML; hence, photoproduction might occur at depths at which the sink of air–sea exchange is absent due to the bottom of the mixed layer acting as a barrier. We used two scenarios to assess the subsurface concentrations with one photoproduction rate constant p across the profile, which is consistent with surface concentrations: (1) a scenario during which the AQY by Xie et al. (1998) is scaled by a factor of 2 to match the surface concentration in a wavelength-resolved approach and (2) a scenario in which p is fitted with a wavelength-integrated approach (Eq. 6) with (simulation psfit) and without (simulation pfit) allowing for an additional chemical first-order sink.

An overview of the model experiments is listed in Table 1, and more information on the model forcing and setup can be found in the Supplement (Table S2).

3 Results

3.1 CDOM, FDOM, and DOS_SPE

DOM showed strong spatial variability in FDOM but less in the DOS_SPE concentration and CDOM absorbance. CDOM, here shown as the absorption coefficient at 350 nm, was on average $a_{\mathrm{350}}=\mathrm{0.15}\pm \mathrm{0.03}$ m⁻¹ (coefficient of variation – CV: 0.2 m⁻¹). The highest absorption coefficients were found closest to the continent and in the upwelling-influenced region between 17 and 20^∘ S (Fig. 2e), as expected in upwelling regions (Nelson and Siegel, 2013). This spatial pattern was consistent with the monthly composite of satellite data (Fig. 1).

Four different components of FDOM, representing groups of similarly fluorescing molecules, were isolated and validated with PARAFAC analysis. Components C1 (average ± standard deviation 0.015±0.0119 QSU, CV: 0.79) and C4 (0.0091±0.0158 QSU, CV: 1.74) have their fluorescence peak in the UV part of the EEM (see the Supplement, Fig. S1). They resemble the naturally occurring amino acids tryptophane and tyrosine (Coble, 2007). Components C2 (0.0032±0.0027 QSU, CV: 0.84) and C3 (0.0032±0.0158 QSU, CV: 0.91) fluoresce in the visible range (Vis-FDOM) of the EEM. Their fluorescence pattern showed characteristics of humic-like substances and they were abundant, especially in the southern part of the cruise closer to the continent and upwelling region (C2 in Figs. 2f and S1).

Surface DOS_SPE only showed minor variations along the cruise track with concentrations of 0.16±0.05 µmol L⁻¹ (CV: 0.31). The highest surface DOS_SPE concentrations were found in the 16^∘ S transect connected to an active upwelling cell and in the open-ocean part of the cruise (Fig. 2g). DOS_SPE concentrations in the water column (not shown) decreased with depth, as also found in the eastern Atlantic Ocean and the Sargasso Sea (Ksionzek et al., 2016). Concentrations decreased from 0.76 (5 m depth) to 0.33 µmol L⁻¹ in 100 m at station 7, from 0.62 (25 m) to 0.49 µmol L⁻¹ (125 m) at station 7, and from 0.49 (20 m) to 0.28 µmol L⁻¹ (115 m) at station 18. At station 2, concentrations of 0.89–0.91 µmol L⁻¹ were measured at a depth of 50–100 m; no surface data are available.

3.2 Carbonyl sulfide (OCS)

3.2.1 Horizontal and vertical distribution

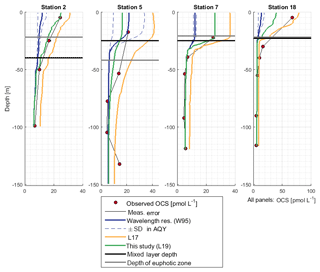
OCS surface water concentrations ranged from 6.4 to 144.1 pmol L⁻¹ (average 30.5 pmol L⁻¹) with strong diurnal cycles as described in Lennartz et al. (2017). Surface concentrations increased towards the shelf and coast, were the highest along a shelf transect from 8 to 12^∘ S, and were connected to a fresh upwelling patch around 16^∘ S (Fig. 2a). Surface concentrations and emissions to the atmosphere are described in detail in Lennartz et al. (2017). The concentrations in the water column decreased with depth at stations 2, 7, and 18 to ca. 10 pmol L⁻¹ below the euphotic zone with varying gradients. Profiles at stations 7 and 18 ranged down to the oxygen minimum zone, but the concentration profiles did not show any corresponding discontinuity. The shape of the concentration profile for station 5 differed from the other stations: here the profile had a convex shape down to 75 m, and it was the only station where a subsurface concentration peak was recorded at a depth of 136 m (Fig. 3).

Figure 3 Profile measurements of OCS concentrations and 1-D model results for the OCS model experiments described in Table 1.

3.2.2 Dark production

The dark production rates at the surface varied between 0.86 and 1.81 pmol L⁻¹ h⁻¹ along the northern part of the cruise track and between 0.16 and 0.81 pmol L⁻¹ h⁻¹ in the four depth profiles below 50 m. The Arrhenius-type temperature dependency showed significantly increasing dark production rates with increasing temperature (Pearson's test, $p=\mathrm{5.66}\times {\mathrm{10}}^{-\mathrm{10}}$). Dark production P_D at both the surface and at depth along the cruise track (Fig. 4) is described by the following Arrhenius equation:

$$\begin{array}{}\text{(7)}& P_{\mathrm{D}}=a_{\mathrm{350}}\cdot \exp \left(-{\displaystyle \frac{\mathrm{15182}}{T}}+\mathrm{53.1}\right).\end{array}$$

The Arrhenius fit could not be improved using FDOM, DOS_SPE, or O₂ instead of a₃₅₀ (not shown). At station 5, the dark production rates at 50 and 136 m were larger than predicted for the temperature and the a₃₅₀ (Fig. 4).

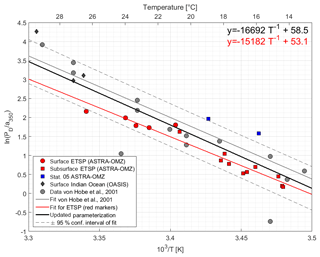
Figure 4 Arrhenius plot of dark production rates from ASTRA-OMZ (this study, red and blue markers), data from the Indian Ocean (OASIS cruise; Lennartz et al., 2017), and previously published rates (von Hobe et al., 2001; grey markers; note that P_D was converted from original units of pmol m⁻³ s⁻¹ to pmol L⁻¹ h⁻¹; for reconversion subtract 1.28). The red linear fit and equation show the parameterization for ASTRA-OMZ only, whereas the black fit and equation represent an updated parameterization including dark production rates from this and previous studies (see Von Hobe et al., 2001).

The parameterization for dark production, previously including only dark production rates from the North Atlantic, Mediterranean, and North Sea (Von Hobe et al., 2001), was updated with the data from the Peruvian upwelling and the Indian Ocean; it yields the following semiempirical equation (Eq. 8) (Fig. 4):

$$\begin{array}{}\text{(8)}& P_{\mathrm{D}}=a_{\mathrm{350}}\cdot \exp \left(-{\displaystyle \frac{\mathrm{16692}}{T}}+\mathrm{58.5}\right).\end{array}$$

3.2.3 Diapycnal fluxes

The diapycnal fluxes of OCS within the water column were derived from measured concentration and diffusivity profiles. OCS produced at the surface was mixed downwards in all four profiles. Diapycnal fluxes out of the mixed layer were always 2 or 3 orders of magnitude smaller than emissions to the atmosphere at stations 2, 5, and 7 with diapycnal fluxes of $\mathrm{8.2}\times {\mathrm{10}}^{-\mathrm{4}}$, $\mathrm{2.4}\times {\mathrm{10}}^{-\mathrm{4}}$, and $\mathrm{3.8}\times {\mathrm{10}}^{-\mathrm{3}}$ pmol s⁻¹ m⁻². An exception is station 18, where diapycnal fluxes (0.48 pmol s⁻¹ m⁻²) were almost half of the air–sea flux (−1.0 pmol s⁻¹ m⁻²).

3.2.4 Photoproduction

The photoproduction rate constants according to Eq. (6) were previously derived from a surface box model and have already been discussed in Lennartz et al. (2017). For days with concurrent measurements of FDOM (7, 8, 9, 10, 13, 16 October 2015), the correlation between photoproduction rate constant and humic-like FDOM C2 was significant (Pearson's test, p=0.014, R²=0.81; Fig. 5a). Measurements of FDOM (and a₃₅₀) during the period used for optimization of the photoproduction rate constant p (i.e., daylight period) were averaged for this correlation. The relationship was quantified by Eq. (9):

$$\begin{array}{}\text{(9)}& p=\mathrm{85.8}\cdot \left[\mathrm{FDOM}\mathrm{C}\mathrm{2}\right]+\mathrm{828.76},\end{array}$$

with the photoproduction rate constant p (pmol J⁻¹) and the concentration of the FDOM component C2 (QSU). The correlation with a₃₅₀ only explains a variance of R²=0.01 (n=7, i.e., 7, 8, 9, 10, 12, 13, 16 October 2015). R² increases to 0.3 when the respective days for FDOM C2 correlations are considered (p>0.25). C2 and a₃₅₀ were not significantly correlated during these days (p>0.2, R²=0.36) but showed a similar spatial trend over the entire cruise track (Fig. 2). Although our experiment was not strictly Lagrangian, a₃₅₀ only changed <0.05 m⁻¹ within each respective fitting period. For FDOM C2, only one to two measurements per daylight period were available during the days when photoproduction rate constants were fitted, but variations of only 0.003 QSU per day were encountered during high-frequency sampling towards the end of the cruise. This relationship thus carries some uncertainties and will benefit from additional data from other regions.

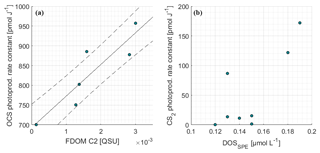
Figure 5 Correlations of the photoproduction rate constant from inverse surface box modeling for (a) OCS and FDOM component C2 as well as (b) CS₂ and DOS_SPE.

OCS concentrations in the water column were simulated with the new module in the model environment of GOTM–FABM. While the AQY of Weiss et al. (1995) yielded surface concentrations a factor of 3–6 too small compared to observations, the L17 simulation overestimated concentrations in all cases up to twofold (Fig. 3). Deviations between simulations and measurements were reduced by using the updated dark production rate of this study and the linear correlation between FDOM C2 and p shown in Fig. 5a (Eq. 9; see Sect. 3.2.2). At station 18, surface concentrations were simulated lower than observed. The shapes of the concentration profiles were well reflected in the simulations except at station 5, where the subsurface concentration peaks at 55 and 136 m were not adequately reproduced. Despite the different magnitude of the wavelength-resolved (W95) and wavelength-integrated (L17, L19) approaches, the shape of the photoproduction profile in the water column did not show major differences.

3.3 Carbon disulfide (CS₂)

3.3.1 Horizontal and vertical distribution

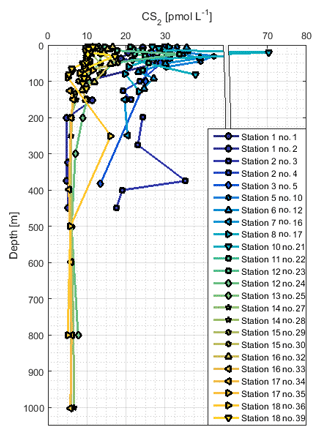
The surface concentration of CS₂ during ASTRA-OMZ was in the lower picomolar range, with an average of 17.8±8.9 pmol L⁻¹, and displayed diurnal cycles only on some days (e.g., 7 October 2015) but not on the majority (Fig. 3). The spatial pattern of sea surface concentrations was opposite to that of OCS, with the highest concentrations distant from the shelf and the lowest closer to the shore. The highest surface concentrations of CS₂ coincided with warm temperatures (Fig. 2b and c). Surface temperatures T (^∘) and concentrations of CS₂ (pmol L⁻¹) were binned for daily averages and yielded the following relationship (p=0.0026, R²=0.61) of (Eq. 10):

$$\begin{array}{}\text{(10)}& \left[{\mathrm{CS}}_{\mathrm{2}}\right]=\mathrm{2.3}T-\mathrm{27.2}.\end{array}$$

The concentration profiles of CS₂ did not show a steep decrease with depth like OCS, but they were more homogeneous (Fig. 6) apart from subsurface peaks below the mixed layer that occurred, for example, at stations 2, 5, and 18. The concentration in CS₂ profiles down to about 200 m was distinctly higher in profiles on which upwelling did not occur (stations 1 to 13; ∼20 pmol L⁻¹) compared to stations in the southern part of the cruise track (stations 15 to 18; ∼10 pmol L⁻¹). This difference in concentrations throughout the water column reflected the pattern observed at the surface, where high concentrations coincide with high temperatures.

Figure 6 Concentration depth profiles for discrete measurements of CS₂ for open-ocean regions (stations 1–5, blueish colors) and stations closer to the shelf (stations 6–13, green–yellow colors).

3.3.2 Diapycnal fluxes

The diapycnal fluxes of CS₂ within the water column revealed the highest production at the surface except for station 18. Within the water column, CS₂ was redistributed downwards. Small in situ sinks (stations 2, 7, and 18) and in situ sources at different water depths (stations 2 and 18) within the water column were required to maintain convergences–divergences under a steady-state assumption. Fluxes out of the ML were $\mathrm{7.6}\times {\mathrm{10}}^{-\mathrm{4}}$, $\mathrm{3.3}\times {\mathrm{10}}^{-\mathrm{4}}$, $\mathrm{1.9}\times {\mathrm{10}}^{-\mathrm{3}}$, and 0.98 pmol s⁻¹ m⁻² at stations 2, 5, 7, and 18 and thus 1–3 orders of magnitude smaller than fluxes to the atmosphere. At station 18, diapycnal fluxes out of the ML and emissions to the atmosphere were at a similar magnitude (0.98 and −1.0 pmol s⁻¹ m⁻², respectively).

3.3.3 Photoproduction of CS₂

Photoproduction rate constants for CS₂ were determined using an inverse setup of the surface box model analogous to OCS, but including only photoproduction and air–sea exchange as source and sink terms. The resulting photoproduction rate constants were between 5 and 70 times smaller than those of OCS. Opposite to OCS, the rate constants did not covary significantly with any FDOM component (p≫0.05). A weak trend was detected for DOS_SPE (p=0.08, Spearman's r²=0.44, n=8; Fig. 5), and all other tested parameters did not show any correlation (FDOM C1-C4, CDOM).

The shape of the CS₂ concentration profiles was modeled for four stations (Fig. S2) with the scenarios described in Table 1. Concentrations in the mixed layer of stations 2, 5, and 7 using the wavelength-resolved AQY from Xie et al. (1998) yielded concentrations 4–6 times lower than observed (simulation X98).

The influence of mixed layer depth variations was tested in simulations X98d and X98s. Surface concentrations differed from the reference simulation X98 by <2.5 pmol L⁻¹ (Fig. 7). The shape of the concentration profile, however, was sensitive to mixed layer variations, as indicated by the sensitivity simulations X98d and X98s. In these artificially created test scenarios, concentrations accumulated below the bottom of the deepest mixed layer during the simulation period.

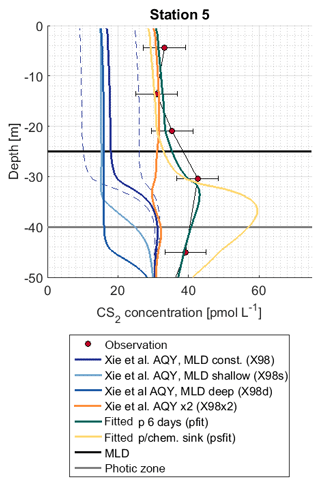
Figure 7 Observation and model sensitivity simulations at station 5. AQY: apparent quantum yield, MLD: mixed layer depth. Simulation names in brackets refer to Table 1. Dashed lines indicate the confidence interval of AQY as reported in Xie et al. (1998).

The subsurface concentration peak was investigated with (1) simulation X98x2, with the wavelength-dependent AQY by Xie et al. (1998) scaled by a factor of 2 so that it matches CS₂ concentrations in the mixed layer, and (2) simulations pfit and psfit in which a photoproduction rate constant in an integrated wavelength approach (Eq. 6) was fitted to observed profiles (corresponding to an evenly distributed AQY across wavelengths of 300–400 nm). Simulation X98x2 does not reproduce the subsurface peak, whereas simulations pfit and psfit are two possible scenarios to reproduce the observed peak (Fig. 7). Photoproduction rates for these simulations are shown in Fig. S3.

4 Discussion

4.1 Carbonyl sulfide

The four profiles at stations 2, 5, 7, and 18 represent the first observations of OCS profiles in the upwelling area off Peru. They do not indicate any connection to a significant redox-sensitive process, as most profiles show a continuous decreasing shape as expected for photochemically produced compounds with a short lifetime in seawater. The independence from dissolved oxygen concentrations is in line with previous findings (Zepp and Andreae, 1994; Uher and Andreae, 1997). Station 5 was the only profile that differed in shape. This profile was measured in an eddy in which downward mixing occurred (Stramma et al., 2016), which may explain the increased concentrations at 55 m. Profiles at station 7 and 18 reached down to the sediment but did not show increased concentrations towards the bottom. Increased sediment inputs, as reported, e.g., from estuarine regions (Zhang et al., 1998), apparently do not play a large role in the studied region, and fluxes to the atmosphere are not affected.

The study by Zhang et al. (1998) also raises the question of near-surface gradients, suggesting that our shallowest measurement depth of 5 m in both profile and underway sampling might underestimate the flux of OCS. On the other hand, strong near-surface stratification acts as a barrier for air–sea exchange (Fischer et al., 2019) and could lead to a bias of the OCS flux if the sampling depth is below the barrier. Since it is difficult to perform underway sampling at depths shallower than a few meters, we cannot fully resolve this issue. However, given the low a₃₅₀ compared to coastal and estuary regions as in Zhang et al. (1998), irradiation likely penetrates deeper into the water column in our study region than in the estuary in their study. Hence, photochemical production likely extended further down into the water column, which reduces the problem of underestimating the flux.

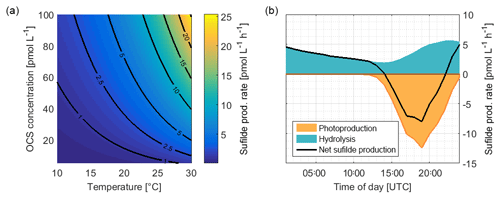
Figure 8 (a) Rate of sulfide production due to OCS hydrolysis as a function of temperature and OCS concentration, calculated with Eqs. (3) and (4). (b) Average consumption of S (organic or inorganic sulfide) by OCS photoproduction and the production of sulfide during hydrolysis from ASTRA-OMZ (average for 7–14 October).

Dark production rates of up to 1.81 pmol L⁻¹ h⁻¹ in our study were at the upper end of the range of previously reported rates in the open ocean (Von Hobe et al., 2001; Ulshöfer et al., 1996; Flöck and Andreae, 1996; Von Hobe et al., 1999) but similar to those from the Mauritanian upwelling region (Von Hobe et al., 1999). Only incubation experiments in the Sargasso Sea showed higher production rates than reported here, ranging between 4 and 7 pmol L⁻¹ h⁻¹ (Cutter et al., 2004). Cutter et al. (2004) concluded that particulate organic matter heavily influences dark production. Although no sample-to-sample comparison to particulate organic carbon (POC) is possible for our OCS data, the general range of POC during our cruise was 12.1±6.1 µmol L⁻¹ (145.2 µg L⁻¹), which is much higher than the POC (ca. 41 µg L⁻¹) reported from the Sargasso Sea (Cutter et al., 2004). We thus cannot confirm the influence of POC on dark production in the Peruvian upwelling and do not find a direct biotic influence.

Our results together with previous studies show that tropical upwelling areas are globally important regions for OCS dark production, likely due to the combination of high a₃₅₀ and moderate temperatures (15–18 ^∘C). The temperature dependency of dark production (Eqs. 7 and 8) is very similar to the one found by Von Hobe et al. (2001) in the North Atlantic, North Sea, and Mediterranean (Fig. 4). The similarity points towards a ubiquitous process across different biogeochemical regimes, as the dependence of the production rate on temperature and a₃₅₀ is very similar for an oligotrophic region like the Sargasso Sea (Von Hobe et al., 2001) or the Indian Ocean from the OASIS cruise (Lennartz et al., 2017) and a nutrient-rich and biologically very productive region such as the studied upwelling area. The fit in the Arrhenius dependency could not be improved by parameters other than a₃₅₀ and showed no influence on dissolved O₂. The characteristics that make a molecule part of the CDOM pool, i.e., unsaturated bonds and nonbonding orbitals, also favor radical formation. OCS dark production is thus best described using abiotic parameters such as a₃₅₀ and temperature rather than biologically sensitive parameters such as dissolved O₂ or apparent oxygen utilization as a proxy for remineralization. This independence from biotic parameters supports the radical production pathway. The results are in line with findings by Pos et al. (1998) showing that these molecules can form radicals in the absence of light, e.g., mediated by metal complexes, and by Kamyshny et al. (2003) showing a positive correlation of dark production rate and temperature. However, the profile at station 5 provides some evidence that an additional process occurs in the subsurface. The concentration peak was visible in the upcast and the downcast, but since we only observed it only once, we cannot conclusively rule out the possibility that the OCS peak at 136 m is an artifact. Still, similar subsurface peaks have been reported from stations in the North Atlantic by Cutter et al. (2004). They concluded that dark production is connected to remineralization.

Diapycnal fluxes at stations 2, 5, 7, and 18 indicate downward mixing from the surface to greater depths in all profiles. However, fluxes were several orders of magnitude smaller than emissions to the atmosphere, except for station 18. There, high diffusivities were observed using the microstructure probe, which most likely result from high internal wave activity as indicated by vertical water displacements of up to 30 m during four CTD cases. Diapycnal fluxes will change diurnally with the shape of the concentration profile and mixed layer variations; hence, the measurements here only represent a snapshot. Still, the difference in magnitude between air–sea exchange and diapycnal fluxes seems to be valid at varying times of the day and varying regions in the studied area. Hence, neglecting diapycnal fluxes when calculating OCS concentrations in mixed layer box models leads to only minor overestimations of the concentrations.

An interesting finding is the significant correlation of the photoproduction rate constant p with FDOM C2 (humic-like FDOM), but not with DOS_SPE, given a reported correlation of OCS and DOS in the Sargasso Sea where much higher DOS concentrations of ca. 0.4 µmol S L⁻¹ were present (Cutter et al., 2004). It should be noted that the method to extract DOS_SPE in our study does not recover all DOS compounds, and we cannot exclude the possibility that this influences the missing correlation between p and DOS. In the studied area, OCS photoproduction is apparently not limited by bulk organic sulfur but rather by humic substances. The humic-like FDOM component C2 is an abundant fluorophore in marine (Catalá et al., 2015; Jørgensen et al., 2011), coastal (Cawley et al., 2012), and freshwater (Osburn et al., 2011) environments. This FDOM component seems to be especially abundant in the deep ocean (Catalá et al., 2015), which might be the reason for higher C2 surface concentrations in regions of upwelling, as evident in our study (Fig. 2) and reported by Jørgensen et al. (2011). The significant correlation of p with humic-like fluorophores in our study highlights the importance of upwelling and coastal regions for OCS photoproduction.

A significant correlation (i.e., a limitation) of OCS photoproduction with humic-like substances, but not with bulk DOS_SPE, can be explained by two scenarios: under the assumption that only organic sulfur is used to form OCS, the limiting factor is contained in the humic-like C2 fraction of the FDOM pool. The sulfur demand (75.8 pmol L⁻¹; the orange area in Fig. 8) would need to be covered entirely by organic, sulfur-containing precursors. The limiting driver of this process is either organic molecules acting as photosensitizers or a sulfur-containing fraction of the DOM pool that correlates with FDOM C2 but not bulk DOS_SPE. In that scenario, FDOM C2 can be used as a proxy for the OCS photoproduction rate constant. More data from other regions would help to quantify such a relationship. In a second possible scenario under the assumption that both organic and inorganic sulfur can act as a precursor, the sulfur demand could theoretically be covered by the sulfur generated through the hydrolysis of OCS (i.e., 85.8 pmol L⁻¹; Fig. 8). In this case, FDOM C2 would only be limiting as long as enough organic or inorganic sulfur is present, for example when temperatures are high enough to recycle sulfur directly from OCS or when other inorganic sulfur sources are present.

Incubation experiments have shown that inorganic sulfur is a precursor for OCS (Pos et al., 1998). It is not clear whether the mechanism proposed in Pos et al. (1998) occurs under environmental conditions because sulfide concentrations were higher than in most marine areas, but also yielded much higher OCS production rates in the magnitude of nM h⁻¹ compared to the magnitude of pM h⁻¹ under natural conditions. Furthermore, the conversion of sulfide to sulfate, rather than to OCS, is thermodynamically favored. Based on our data, we cannot resolve the question about the role of inorganic sulfur in OCS photoproduction, but our results are consistent with the reaction mechanism suggested by Pos et al. (1998). Incubation experiments at environmentally relevant sulfide concentrations, as well as p–DOS relationships across different temperature and DOM regimes, will help to resolve this issue.

Our results show that FDOM C2 is a good candidate as a proxy for OCS photoproduction, but its sampling coverage is insufficient for global model approaches at the moment. On global scales, on which p varies on a broader range than within the area covered by this study, a₃₅₀ might still be an adequate but not perfect predictor for this variation (Lennartz et al., 2017). On local scales, the parameterization for p based on a₃₅₀ can be improved using FDOM C2.

In addition, we used parameterizations from previously reported 0-D box models and from this study to assess their applicability to biogeochemical models coupled to a 1-D physical host model. It should be noted, however, that the surface data shown here have been used, along with other data, to derive the parameterization for the photoproduction rate constant in Lennartz et al. (2017).

Photoproduction rates based on the wavelength-resolved simulation W95 underestimated observed concentrations in all cases. Other AQYs were not tested but can be interpreted in a relatively straightforward way, since the AQYs of a given spectral shape are proportional to the OCS production and concentration (in steady state). Higher wavelength-resolved AQY as reported by Zepp and Andreae (1994) from the North Sea and the Gulf of Mexico, as well as by Cutter et al. (2004), ranged from twofold to up to 2 orders of magnitude higher than the ones reported by Weiss et al. (1995). These differences in magnitude were attributed to the composition of the DOM pool. To reflect this influence of the DOM composition, Lennartz et al. (2017) parameterized the photoproduction rate constant (corresponding to an integrated AQY) to a₃₅₀, following the suggestion by von Hobe et al. (2003) that a₃₅₀ can be used as a proxy for OCS precursors on larger spatial scales. Using this parameterization for photochemical production in the 1-D water column model (simulation L19) yielded simulated concentrations closer to, but higher than, observations (Fig. 3). Although the absolute concentrations for the AQY W95 did not match observations for the reasons outlined above, the shape of the profile fits the observations well. The simulations thus support the experimental findings in most of the previously published AQY work, i.e., the highest OCS yield is at UV wavelengths for in situ conditions.

The simulation using the updated dark production rate and scaling p with FDOM C2 (this study, L19) led to simulated concentrations closest to observations. Remaining deviations between simulated and observed profiles occur, e.g., at station 5, possibly for the reasons discussed above for dark production rates. At station 18, vertical water displacements of up to 30 m during four subsequent CTD casts were observed, most likely due to internal waves. This displacement could violate assumptions inherent to the 1-D approach, i.e., the influence of horizontal water transport. In general, our results show that simulating OCS concentrations in the water column is possible by applying surface box model parameterizations as local source and sink terms to a physical host model in the upwelling area off Peru with its specific DOM conditions. The approach is similar to the 1-D model by von Hobe et al. (2003) for the Sargasso Sea, but the updated parameterizations yield a higher agreement in shape and actual concentrations between model simulations and observations.

4.2 Carbon disulfide

The CS₂ concentrations measured in this study were higher than those observed during an Atlantic transect (Kettle et al., 2001; average 10.9 pmol L⁻¹, n=744), in the North Atlantic (13.4 pmol L⁻¹), and the Pacific (14.6 pmol L⁻¹) (Xie and Moore, 1999) but lower than those reported in a more recent transect through the Atlantic (Lennartz et al., 2017). High concentrations of CS₂ coincided with elevated temperatures at the surface in our study and in previous studies. The significant relationship between surface temperature and CS₂ concentrations corroborates previous findings. Xie et al. (1999) found a positive correlation between CS₂ concentration and SST for the Pacific and the North Atlantic with a linear relationship of [CS₂] = 0.39 t+7.2 (t=temperature in ^∘C). Daily averages of our data close to the shelf (n=8, from 12 October onwards) between 15 and 20 ^∘C fall within this relationship. However, daily averaged concentrations were higher than predicted according to this relationship further away from the coast at the beginning of our cruise at temperatures between 20 and 30 ^∘C (n=4). Overall, we confirm that CS₂ concentrations increase with increasing temperatures, but the exact relationship varies spatially. The reasons for this relationship could result from, e.g., the temperature-driven decay of precursor molecules, but they remain speculative. The results are in line with findings by Gharehveran and Shah (2018), who found increased CS₂ formation with increasing temperatures in incubation experiments.

The surface box model to determine the photoproduction rate constants of CS₂ is set up as a very simple case, including only the processes of photoproduction and air–sea exchange. The rate constant p was only fitted for the increase in concentration during daylight, when photoproduction is expected to be much larger than potential other unknown, continuously acting sources or sinks. The photoproduction rate constant of CS₂ was highest when high DOS_SPE was present, indicating that the sulfur source might be limiting for this process. Organic sulfur is required to form CS₂ even if one S atom originates from an inorganic S source (like possibly for OCS). A potential mechanism could include a precursor with an existing C–S double or single bond that reacts with either another organic sulfur radical or sulfide. This mechanism would rationalize the correlation with DOS being present for CS₂ and not for OCS. Laboratory studies showed that the organic sulfur compounds cystine, cysteine, and (to a lesser extent) methionine are precursors for CS₂ photochemistry (Xie et al., 1998). Such organic sulfur-containing molecules are rare in the marine environment (Ksionzek et al., 2016), which can explain the overall lower photoproduction rate constant of CS₂ compared to OCS. We found higher DOS_SPE concentrations in the upwelling area off Peru compared to other regions, but they are similar to DOS_SPE concentrations in the Mauritanian upwelling reported by Ksionzek et al. (2016). There, elevated CS₂ concentrations were reported as well (Kettle et al., 2001). This spatial pattern suggests that upwelling regions might be hot spots for CS₂ photoproduction. It should be considered, however, that the extraction method used cannot recover all DOS compounds in seawater, so the correlation between CS₂ and DOS_SPE may be influenced by the DOM composition.

Our simulation X98 at stations 2, 5, 7, and 18 underestimates mixed layer CS₂ concentrations, indicating spatial variations of the AQY, most likely due to changes in the DOM composition, as previously found for other gases (OCS: see above; carbon monoxide, Stubbins et al., 2011; DMS, Galí et al., 2016). These results corroborate findings by Kettle (2000) and Kettle et al. (2001), who showed that the photoproduction of CS₂ was underestimated in some regions by the AQY from Xie et al. (1998). The scaling factor was on the order of 1–10 in Kettle's studies, which is in line with our results (factor of 2–4). In future model approaches, a photoproduction rate constant (expressing an integrated AQY) would need to be parameterized, and our results suggest that such parameterizations may rely on DOS or, on a global scale, DOC (since DOS covaries globally with DOC).

More detailed simulations were performed for station 5 because, at this station, the photic zone extended below the mixed layer. The wavelength dependence of photochemical production is assessed with a 1-D modeling approach, wherein the simulations X98x2 and pfit–psfit reproduce surface concentrations but differ in their wavelength dependence on photoproduction. In the simulation X98x2, the wavelength-dependent AQY was scaled to match surface concentrations but failed to reproduce the observed subsurface peak at station 5 because photoproduction at wavelengths ∼400 nm, which penetrate below the ML, was too low. In this scenario, another production process is needed to reproduce the observed profile. Similar conclusions were drawn by Xie et al. (1998). They suggested biological production, as the peaks coincided with the peak of chlorophyll a. However, we found no correlation with chlorophyll a or with marker pigments representing various phytoplankton functional types (data source described in Booge et al., 2018). Another potential dynamic process, e.g., downward mixing, that influences both gases cannot be ruled out, as concentrations for OCS were also higher than predicted around 50 m.

In our simulation pfit, a wavelength-integrated approach was adopted (Eq. 6). Photoproduction is calculated with the integrated irradiation (300–400 nm) and one rate constant, representing a wavelength-integrated AQY. In this simulation, photoproduction occurring at higher wavelengths, which penetrate deeper into the water column, is higher compared to the wavelength-resolved simulation (see also Fig. S3) and leads to the accumulation of CS₂ below the mixed layer.

The accumulation occurred because the production is detached from the air–sea exchange sink. In this simulation, a period of 6 d was needed to accumulate enough CS₂ below the mixed layer to reproduce the observed concentrations. This period highly depended on the actual production at wavelengths around 400 nm and can thus vary. By allowing for an additional sink process below the mixed layer (psfit) corresponding to an additional degree of freedom, observations can also be reproduced. Hence, it is possible to explain observed subsurface peaks by (1) photoproduction alone if higher production is assumed at a wavelength around 400 nm, which is the peak maximum depending on accumulation time and potential additional sink processes, (2) an additional production process only occurring shortly below the ML barrier, such as the biological production suggested by (Xie et al., 1999), or (3) physical downward transport processes related to mixed layer dynamics (given the long CS₂ lifetime, such processes could either be slow but continuous mixing processes or strong one-time events such as storms). Slow sinks below the ML would conserve potential higher concentrations advected from surface waters due to the absence of air–sea exchange in the subsurface. The process leading to the observed profiles thus remains inconclusive. Our results highlight the importance of Lagrangian experiments following the same water mass for compounds with a lifetime on the order of days. Information on the conditions prior to the profile measurements is needed to conclusively interpret the location and accumulation of subsurface peaks.

CS₂ was still detectable below 200 m at concentrations around 5–10 pmol L⁻¹ in shelf regions and around 20 pmol L⁻¹ in open-ocean regions (except station 1). This pattern reflects the spatial variation of surface concentrations, which were higher in the open ocean than at the shelf. The vertically relatively uniform concentration profiles suggest low degradation rates, and the travel distance of the water between the stations is too short to explain the concentration difference only by in situ degradation. A Lagrangian approach would be helpful to resolve this issue. Some profiles display small local maxima in the region of the oxycline (not shown), but due to unconstrained subsurface source and sink processes, no conclusion can be drawn on whether a chemical or physical process is responsible. The rather homogeneous concentrations below 200 m of depth suggest slow in situ degradation rates. As a result, physical processes resulting from currents, eddies, or shelf processes might gain higher importance for the distribution of CS₂ in the subsurface compared to the shorter-lived gas OCS. With sinks potentially acting on long timescales, CS₂ could possibly be transported from sources located further away, e.g., from contact to the sediment in shelf regions or subducted from the surface. Our results clearly show the limits of interpreting 1-D concentration profiles for long-lived compounds, with both subsurface sinks and sources unconstrained. Incubation experiments using isotopically labeled CS₂ would be helpful to constrain source and sink processes independently.

5 Summary and conclusion

We show concurrent measurements of the gases OCS and CS₂ together with sulfur-containing and optically active fractions of the DOM pool in the upwelling area off Peru. The results indicate how the quality and composition of DOM influence the production processes of both gases, with implications for predicting their concentrations on regional and, potentially, global scales.

A parameterization for the dark production of OCS is updated, resulting in a slight downward correction of the previously established parameterization. The photoproduction rate constant of OCS covaries regionally with humic-like FDOM, and more observations of OCS with humic-like DOM could help to improve parameterizations of OCS photoproduction. The absence of a correlation of the photoproduction rate constant with bulk DOS_SPE is not conclusively addressed. Possible scenarios involve either a sulfur-containing precursor in a constant-ratio FDOM C2 or surplus sulfur via allocation from OCS hydrolysis. In both cases, FDOM C2 is a promising proxy on regional scales and, in the case of scenario, 1 also on global scales. In contrast to OCS, the availability of organic sulfur might be a limiting factor for the photochemical production of CS₂.

These different limitations of photochemical production of both gases have implications for the expected spatial pattern of their marine surface concentrations. Both OCS dark production and photochemical production correlate with optically active parts of the DOM pool, which are abundant at high latitudes and in coastal and upwelling regions. Also, OCS is degraded by hydrolysis most efficiently in warm regions such as the tropics, resulting in longer lifetimes at high latitudes. The highest concentrations are thus expected in coastal regions of high latitudes, which is in line with observations. Increasing CS₂ photoproduction with increasing DOS_SPE concentrations suggests the highest surface concentrations in tropical and subtropical regions, where the highest DOC and DOS concentrations are expected. This spatial pattern is in line with the limited measurements available (Kettle et al., 2001). Regarding the tropical missing source of atmospheric OCS, the spatial pattern of oceanic emissions would then favor the oxidation of emitted CS₂ to OCS as a potential candidate to fill the gap in the atmospheric budget. Our measurements likely represent CS₂ concentrations from the upper end of the range of tropical concentrations, since they were performed in a region with high DOS abundance. As an upper limit, a sulfur flux calculated with average values from this cruise (T=20.2 ^∘C, S=35, u10 =7.3 m s⁻¹, CS₂=17.8 pmol L⁻¹) assumed for the whole tropical ocean (30^∘ N–30^∘ S, 1.95×10¹⁴ m²) results in annual emissions of 268 Gg S as OCS. This flux, which represents an additional 140 Gg S to the global sulfur flux of CS₂ reported by Lennartz et al. (2017), is still too low to sustain a missing source of an additional 400–600 Gg S yr⁻¹ (800–1000 Gg S⁻¹yr⁻¹ total oceanic OCS emissions).

Overall, we show that processes to model OCS distributions are well known and quantified and that the lifetime is sufficiently short to extend the parameterizations of the box model to a 1-D water column model. The OCS process understanding is better than for CS₂, for which a sufficient process understanding to conclusively model subsurface concentrations is still lacking. Our results emphasize the importance of vertical dynamics for longer-lived compounds such as CS₂ compared to the short-lived OCS.

This study highlights the need for more in situ measurements of OCS and CS₂ below the mixed layer in various biogeochemical regimes, together with fractions of the DOM pool, to improve the suggested quantitative relationships across larger DOM variations. Subsurface processes, especially for CS₂, remain elusive and require concerted experimental and field studies.