Circulation of the Turkish Straits System under interannual atmospheric forcing

A simulation of the Turkish Straits System (TSS) using a high-resolution, three-dimensional, unstructured mesh ocean circulation model with realistic atmospheric forcing for the 2008–2013 period is presented. The depth of the pycnocline between the upper and lower layers remains stationary after 6 years of integration, indicating that despite the limitations of the modelling system, the simulation maintains its realism. The solutions capture important responses to high-frequency atmospheric events such as the reversal of the upper layer flow in the Bosphorus due to southerly severe storms, i.e. blocking events, to the extent that such storms are present in the forcing dataset. The annual average circulations show two distinct patterns in the Sea of Marmara. When the wind stress maximum is localised in the central basin, the Bosphorus jet flows to the south and turns west after reaching the Bozburun Peninsula. In contrast, when the wind stress maximum increases and expands in the north–south direction, the jet deviates to the west before reaching the southern coast and forms a cyclonic gyre in the central basin. In certain years, the mean kinetic energy in the northern Sea of Marmara is found to be comparable to that of the Bosphorus inflow.

1 Introduction

The Turkish Straits System (TSS) connects the Marmara, Black and Mediterranean seas through the Bosphorus and Dardanelles straits. The near-surface layer of low salinity waters originating from the Black Sea enters from the Bosphorus, flowing west and exiting into the Aegean Sea at the Dardanelles. The deeper, more saline waters of Mediterranean origin enter from the Dardanelles in the lower layer and eventually reach the Black Sea through the undercurrent of the Bosphorus. The strongly stratified marine environment of the TSS is characterised by a sharp pycnocline positioned at a depth of 25 m (Ünlüata et al., 1990). The complex topography of the Sea of Marmara consists of a wide shelf in the south, a narrower one along the northern coast and three east–west deep basins separated by sills, connected to the two shallow, elongated narrow straits providing passage to the adjacent seas at the two ends, as shown in Fig. 1.

The TSS mass and property balances are mainly controlled by the Black Sea in the upstream. At the Bosphorus Black Sea entrance, the long-term salinity budget implies a ratio of about 2 between the upper and lower layer volume fluxes (Kara et al., 2008; Peneva et al., 2001). The net flux is estimated to be comparable to the Black Sea river runoff, as the annual average precipitation and evaporation over the sea surface are roughly of the same order (Özsoy and Ünlüata, 1997). Daily to seasonal variations in net fluxes through the TSS are driven by changes in Black Sea river runoff, barometric pressure and wind forcing.

Climatological means of water and tracer fluxes through the TSS were initially estimated from long-term observations of seawater properties at junctions of the straits and on surface water fluxes (Beşiktepe et al., 1994; Maderich et al., 2015; Tuğrul et al., 2002; Ünlüata et al., 1990), followed later by ship-borne and moored acoustic Doppler current profiler (ADCP) measurements at the straits (Altıok et al., 2012; Jarosz et al., 2011a, b, 2012, 2013; Özsoy et al., 1988, 1998). Updated reviews of TSS fluxes based on combined data have been provided by Schroeder et al. (2012), Özsoy and Altıok (2016), Sannino et al. (2017) and Jordá et al. (2017).

The hydrodynamic processes of the TSS extend over a wide range of interacting space scales and timescales. The complex topography of the straits and property distributions have resulted in hydraulic controls being anticipated in both straits (Özsoy et al., 1998, 2001), which can only partially be demonstrated by measurements at the northern sill of the Bosphorus (Dorrell et al., 2016; Gregg and Özsoy, 2002). Hydraulic controls have since been found by modelling at the southern contraction-sill complex and the northern sill, confirming a unique maximal exchange regime adjusted to the particular topography and stratification (Sannino et al., 2017; Sözer and Özsoy, 2017a). These findings support the notion that the Bosphorus is the more restrictive of the two straits in controlling the outflow from the Black Sea to the Mediterranean. The analysis of moored measurements by Book et al. (2014) demonstrated this and indicated a more restrained sea level response transmitted across the Bosphorus than in the Dardanelles.

Improvements in modelling have provided a better scientific understanding of the TSS circulation, and they can now address the complex processes characterising the system. The initial step in this formidable task is to construct separate models of the individual compartments of the system, which are the two straits and the Marmara basin. The first simplified models of the Bosphorus were by Johns and Oğuz (1989), who solved the turbulent transport equations in 2-D and found a two-layer stratification to develop. Simplified two-layer or laterally averaged models of the Dardanelles and Bosphorus were later developed by Oğuz and Sur (1989), Stashchuk and Hutter (2001) and Oğuz et al. (1990), respectively, while Hüsrevoğlu (1998) introduced a 2-D reduced gravity ocean model of the Dardanelles inflow into the Sea of Marmara. Similar 2-D laterally averaged models (Ilıcak et al., 2009; Maderich and Konstantinov, 2002; Maderich et al., 2015) and 3-D models (Kanarska and Maderich, 2008; Öztürk et al., 2012), which were of limited extent, have been used to construct simplified solutions for the Bosphorus exchange flows. Bosphorus hydrodynamics were extensively investigated by Sözer and Özsoy (2017a) using a 3-D model with turbulence parameterisation under idealised and realistic topography with stratified boundary conditions in adjacent basins, demonstrating the unique hydraulic controls in the maximal exchange regime that are to be established in the realistic case. The combined effects of the Bosphorus and the proposed parallel channel known as Kanal İstanbul have been investigated by Sözer and Özsoy (2017b), indicating weak coupling between the two channels, which have very different characteristics, but this has been found to be of climatic significance in modifying the fluxes across the TSS.

Very few studies have attempted to model the circulation in the Sea of Marmara, even as a stand-alone system excluding the dynamical influences of the straits and atmospheric forcing. Chiggiato et al. (2012) modelled the Sea of Marmara using realistic atmospheric forcing and open boundaries at the junctions of the straits with the sea, indicating surface circulation changes in response to changes in the strength and directional pattern of the wind force.

Similarly, the interannual variability of the Sea of Marmara has been examined by Demyshev et al. (2012) using open boundary conditions at the strait junctions in the absence of atmospheric forcing. They reproduced the S-shaped jet current traversing the basin under the isolated conditions of a net barotropic current, which with appropriate parameterisation successfully preserved the sharp interface between the upper and lower layers when the model steady state was reached after 18 years of simulation. The S-shaped upper layer circulation of the Sea of Marmara predicted by Demyshev et al. (2012) appears similar to what Beşiktepe et al. (1994) found in summer, when wind forcing is at its minimum or at least close to being in a steady state. An anticyclonic pattern has generally been identified in the central Sea of Marmara, like the cases reported by Beşiktepe et al. (1994).

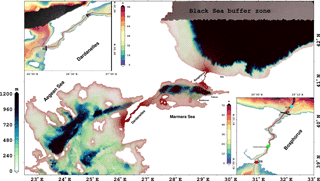
Figure 1 Bathymetry of the Turkish Straits System and the whole model domain. Bathymetry of the Bosphorus and Dardanelles straits is detailed in the small panels. The colours represent the depth. The colour bar scales are different for the straits and the whole domain. A triangular mesh is overlaid with red for the entire domain and with grey for the straits in small panels. The thalweg used to display the cross-section throughout the TSS is represented by the black line. The grey shaded area in the Black Sea functions as a buffer zone and is described in the text. Cross-sections at the boundaries of the straits are used for volume flux computations. NB, SB, ND and SD in the small panels are northern Bosphorus, southern Bosphorus, northern Dardanelles and southern Dardanelles, respectively. In the Bosphorus panel, the green and cyan squares show the locations of the contraction and northern sill, respectively. Finally, the red square B1 indicates the middle of the Sea of Marmara exit of the Bosphorus strait.

The challenges of modelling the entire TSS domain were recently undertaken by Gürses et al. (2016). The effects of atmospheric forcing were considered, excluding the effects of the net flux through the TSS. The study used an unstructured triangular mesh model, the Finite Element Sea-Ice Ocean Model (FESOM), with a high horizontal resolution reaching about 65 m in the straits in the horizontal. The water column is discretised by 110 vertical levels.

The study of Sannino et al. (2017) used curvilinear coordinate implementation of the MITgcm (Marshall et al., 1997) with a non-uniform grid in the horizontal, a minimum of 65 m resolution in the narrowest part of Bosphorus and 100 levels in the vertical. The model was used to investigate the circulation of the TSS under varying barotropic flow through the system in the absence of atmospheric forcing. The overall circulation in the Sea of Marmara was found to differ significantly in each of their experiments with variations in the net volume transport at the Bosphorus. The circulation changes from a large anticyclonic circulation at the centre of the basin at low flux values, to different gyres wrapped around an S-shaped jet as the net flux is increased. A cyclonic central gyre is eventually generated as the increased flux leads to the lower layer in the Bosphorus being blocked. The most significant finding was the non-linear sea level response, which deviated widely from the linear response predicted by the stand-alone Bosphorus model of Sözer and Özsoy (2017a).

Stanev et al. (2017) approached the challenge by using an unstructured mesh model. The model covers the entire Black Sea and is seamlessly linked to the TSS and the northern Aegean Sea with open boundaries in the south and uses realistic atmospheric forcing. The focus is on the transport at the straits and the resulting dynamics of the Black Sea. Regarding the TSS, the results support the notion of multiple controls of the barotropic flow. They were also able to simulate short-term events such as severe storm passages. However, in a high-resolution model of the TSS, the Courant–Friedrichs–Lewy (CFL) condition (Courant et al., 1967) restricts the time step to a few seconds with explicit schemes. As a solution, Stanev et al. (2017) used an implicit advection scheme for transport to handle a wide range of Courant numbers (Zhang et al., 2016) while satisfying the stability of the solution. However, the computational burden of using an implicit scheme imposed a coarser model resolution with 53 vertical levels at the deepest point of the Black Sea. We note that this limitation may, particularly in the Bosphorus, lead to excessive vertical mixing or a widened interface thickness, which are crucial for the intrusion of the Mediterranean origin water into the Black Sea. This can be seen in their Fig. 11c and d, for example.

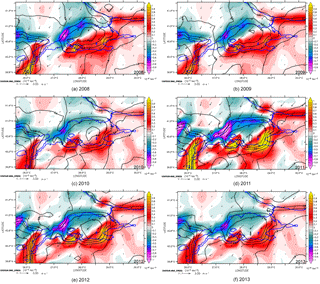
Figure 2 Annual mean of wind velocity (ms⁻¹, arrows), wind stress (10⁻² Nm⁻², black contours) and wind stress curl (10⁻⁶ Nm⁻³, shades) in the Sea of Marmara for each year from 2008 (a) to 2013 (f). The coastline is overlaid in blue.

Another recent study by Ferrarin et al. (2018) presents the tidal dynamics in the TSS which is seamlessly included in a model domain covering whole Black Sea – Mediterranean system. They use a barotropic version of SHYFEM (Umgiesser et al., 2004) to provide the hydrodynamical background to the tidal analysis.

In our work, we simulate the complete TSS with a high-vertical-resolution unstructured grid model forced by complete heat, water and momentum fluxes. A long-term 6-year simulation is used to analyse the combined response of the Sea of Marmara to atmospheric forcing and strait dynamics. The questions addressed in this paper are

• What is the mean Sea of Marmara circulation and its variability in a long-term simulation?

• What are the effects of the atmospheric forcing on the Sea of Marmara dynamics and circulation?

The paper is organised as follows. In the next section, we document the model setup and the details of the experiment. In Sect. 3, the validation of the water mass structure and sea level differences along the TSS are demonstrated. The resulting volume transport through the straits, and the kinetic energy and circulation in the Sea of Marmara, are presented. Finally, in Sect. 4, we summarise and discuss the results.

Table 1 Monthly Black Sea river discharge (R) and salinity relaxation values (S^*).

2 Model setup

Models for solving the dynamical equations for an unstructured mesh using finite element or finite volume methods have been implemented for many idealistic applications (Ford et al., 2004; White et al., 2008) and in realistic coastal ocean studies (Federico et al., 2017; Stanev et al., 2017; Zhang et al., 2016). An obvious advantage of using an unstructured mesh model is the varying resolution, which allows for a finer mesh resolution in coastal areas than in the open ocean. The general ocean circulation model used in this study is FESOM. FESOM is an unstructured mesh ocean model using finite element methods to solve hydrostatic primitive equations with the Boussinesq approximation (Danilov et al., 2004; Wang et al., 2008). We use the initial implementation of Gürses et al. (2016).

The model domain extends zonally from 22.5 to 33^∘ E and meridionally from 38.7 to 43^∘ N, covering a total surface area of 1.52×10¹¹ m² (Fig. 1). The mesh resolution is as fine as 65 m in the Bosphorus and 150 m in the Dardanelles. In the Sea of Marmara, the resolution is always finer than 1.6 km and is not coarser than 5 km in the Black Sea and the Aegean Sea. The water column is discretised by 110 vertical z levels. The vertical resolution is 1 m in the first 50 m depth and increases to 65 m at the bottom boundary layer in the deepest part of the model domain.

Model equations and parameters are documented in Appendix A. The current model implementation considers closed lateral boundaries. Therefore, volume and salinity conservations are imposed to prevent drifts in the tracer fields. Our approach for volume and salinity conservations is described in Appendix B.

The experiment detailed below was conducted over 6 years, commencing on 1 January 2008 and continuing until 31 December 2013. The initial fields were obtained after a 3-month integration of a lock-exchange case, which was initialised from different temperature and salinity profiles in the basins of the Black, Marmara and Aegean seas (Gürses et al., 2016; Sannino et al., 2017). Fine mesh resolution and energetic flow structures in the straits require small time steps so the CFL condition is not violated. The time step is thus set to 12 s throughout the integration. The simulation was forced by atmospheric fields provided by European Centre for Medium-Range Weather Forecasts (ECMWF) with $\mathrm{1}/\mathrm{8}{}^{\circ }$ resolution. The forcing data cover the whole experiment period with a time frequency of 6 h. Precipitation data are obtained from monthly CPC Merged Analysis of Precipitation (CMAP; Xie and Arkin, 1997) and interpolated to the ECMWF grid as daily climatology.

The annual means of wind, wind stress and wind stress curl for the simulation period are shown in Fig. 2. Wind stress, τ, is calculated as

$$\begin{array}{}\text{(1)}& \mathit{\tau }={\mathit{\rho }}_{\mathrm{0}}{C}_{\mathrm{d}}\left|{\mathit{u}}_{\mathrm{wind}}\right|{\mathit{u}}_{\mathrm{wind}},\end{array}$$

where C_d is the drag coefficient and u_wind is the wind velocity. The annual mean wind fields are northeasterlies which were strongest in 2011. τ was higher than 0.04 Nm⁻² in the central north Sea of Marmara in 2009. It then expands in a north–south direction, exceeding 0.05 Nm⁻² in the central basin, in 2011, and then weakens again in 2013. The wind stress curl is a dipole shaped by the northeasterlies and is negative in the north and west, and positive in the south and east of the Sea of Marmara. In 2011, the wind stress curl in the coastal zones was more intense than in the other years.

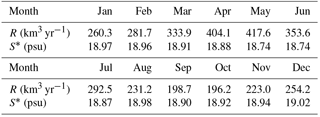
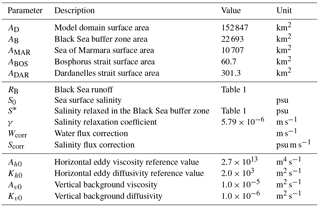
A surface area of 22 693 km² north of 42.5^∘ N in the Black Sea functions as a buffer zone (the grey shaded area in Fig. 1). This zone is utilised to provide required water fluxes for a realistic barotropic flow through the Bosphorus. The model is forced by climatological runoff in the Black Sea, which is essential to generate realistic sea level differences between the compartments of the system (Peneva et al., 2001). The monthly runoff climatology for water fluxes was obtained from Kara et al. (2008) and is the same for all the 6 years. The surface salinity at the buffer zone was relaxed to a monthly climatology, computed from a 15-year simulation by the Copernicus Marine Environment Monitoring Service Black Sea circulation model (Storto et al., 2016). The salinity relaxation time is approximately 2 days. Although this is a strong constraint, it is required to prevent the surface salinity from decreasing in the buffer zone due to the excessive amount of fresh water input. The climatological values used for runoff and salinity relaxation are shown in Table 1.

Here, we note again that the model having closed lateral boundaries requires a correction for the water and mass fluxes which we discuss in Appendices A and B. Very briefly, the access or deficit of the water fluxes is redistributed to the surface model nodes weighted by the corresponding element area. Since a runoff climatology is inserted in the Black Sea to maintain the sea level difference along the system, the correction will enforce the volume conservation. This method was also used by Gent et al. (1998) for a climate global model. Another method was explored by Gürses et al. (2016) where the correction was applied only in the Aegean area but salinities became too high and the salinity profile of the simulation became unrealistic.

3 Results

In this section, we present the results obtained from a simulation of the TSS between 2008 and 2013. The focus is on the Sea of Marmara and the straits, but we also consider the adjacent basins when necessary. We provide details of the main water mass characteristics of the system and our validation against the observations. The sea level differences and the volume transport through the Bosphorus and Dardanelles are analysed. Although we will include results demonstrating the response of the system to daily atmospheric events, we focus on the interannual changes in the TSS. Therefore, we consider only annual means in time averages. The computed time averages for the simulation are for the period 2009–2013, as the first months of 2008 are considered as an initial spin-up period.

3.1 Surface heat and water fluxes

The monthly averages of water fluxes and net heat flux are shown in Fig. 3a for the whole domain and Fig. 3b for the Sea of Marmara. The mean runoff, evaporation and precipitation in the whole domain are 278.1, −131.5 and 70.8 km³ yr⁻¹, respectively. The resulting net water flux into the ocean is therefore 226.4 km³ yr⁻¹ which is balanced by the correction term (see Appendix A) shown in red in Fig. 3a. As a result, the model volume is conserved.

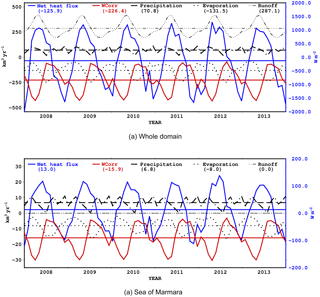
Figure 3 Monthly averaged net heat (blue) and water (black) fluxes in the Sea of Marmara, along with evaporation (dashed) and precipitation (dotted). Runoff is zero in the Sea of Marmara. The blue vertical axis (right) is for heat flux and the black vertical axis (left) for water fluxes. Water flux correction described in Appendix A is shown in red. The 6-year mean values of fluxes are marked on the figures and shown in legends.

In the Sea of Marmara, runoff is identically zero (Fig. 3b). Mean evaporation and precipitation are −8 and 6.8 km³ yr⁻¹, respectively. The water flux correction applied in the Sea of Marmara is −15.9 km³ yr⁻¹. This means there is a net surface flux loss in the Sea of Marmara of about −17.1 km³ yr⁻¹. The total water budget of the Sea of Marmara will be further discussed in Sect. 3.3.

The net heat flux in the Sea of Marmara is calculated in the range of −123.3 to 138.4 W m⁻² with minimums and maximums in December–January and May–June, respectively.

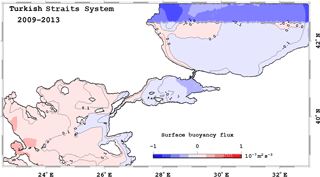
Figure 4 Mean of surface buoyancy fluxes for 2009–2013. A negative value is the buoyancy flux down into the ocean.

The daily buoyancy fluxes were averaged between 2009 and 2013, and are shown in Fig. 4. The buoyancy flux was computed using the following formula:

$$\begin{array}{}\text{(2)}& Q_b={\displaystyle \frac{g\mathit{\alpha }}{{\mathit{\rho }}_{\mathrm{0}}{C}_w}}{Q}_{\mathrm{H}}-\mathit{\beta }{S}_{\mathrm{0}}g{Q}_{\mathrm{w}},\end{array}$$

where α and β are thermal expansion and haline contraction coefficients (McDougall, 1987), Q_H is the heat flux (positive towards the ocean), C_w is the specific heat capacity, S₀ is the surface salinity, and Q_w is the water flux.

The Black Sea and the Sea of Marmara gain buoyancy except for a small area near their western coasts (Fig. 4), while the Aegean Sea has a buoyancy loss except near the Dardanelles exit and the Anatolian coast. The average buoyancy flux changes between $-\mathrm{7}\times {\mathrm{10}}^{-\mathrm{8}}$ and $\mathrm{3.4}\times {\mathrm{10}}^{-\mathrm{8}}$ m² s⁻³ over the domain. It does not show significant spatial differences interannually, but the gradient between the Aegean and Black seas was stronger in 2011 than in the other years (not shown).

3.2 Water mass structure and validation

Figure 5 The mean sea surface salinity for 2009–2013. Contours are overlaid with a 1 psu interval.

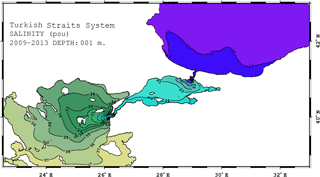
The surface salinity ranges from 16 to 38 psu over the whole domain (Fig. 5). The surface waters leave the Bosphorus and the Dardanelles with salinities of about 21 and 27 psu, respectively. The surface salinity in the northern Sea of Marmara is less than 23 psu and increases to 25 psu in the south. Long-term measurements from 1986 to 1992 in the Sea of Marmara (Beşiktepe et al., 1994) suggest a salinity range of 23±2 psu at the surface, which is satisfied by the simulation.

Figure 6 Annual mean of (a) salinity and (b) temperature for 2013 along the thalweg.

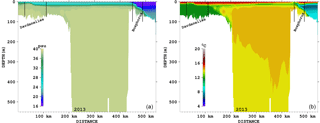
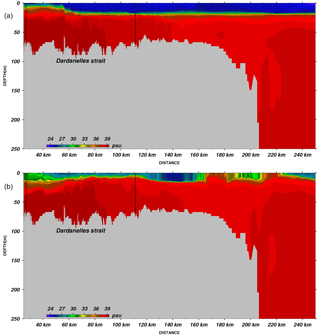
The vertical structure of the time mean salinity and temperature along the thalweg (see Fig. 1) is shown for the last year of the integration in Fig. 6. The depth of the interface between the upper and lower layers is stationary throughout the simulation and is located at a depth of around 20 m. The water column salinity is mixed below 25 m in the Sea of Marmara until approximately 200 m. However, the deeper layers are colder and continuously modified by the Dardanelles inflow after the initialisation, as can be seen in Fig. 7, in which the volume temperature has a negative trend and salinity a positive one. We argue that this is due to initialisation adjustment and the closed boundary conditions. Salinity is completely mixed in the Sea of Marmara below 100 m depth.

In the Bosphorus, Altıok et al. (2012) reported a cold tongue in June–July between 1996 and 2000, with a temperature of about 11–12 ^∘C, extending to the Sea of Marmara. This cold tongue is reproduced in the simulation (Fig. 6b) and emerges as a cold intermediate layer (CIL) at the position of the halocline.

The mean sea surface temperature in the Sea of Marmara fluctuates between 4.4 and 28.3 ^∘C (Fig. 7). Surface mean salinities are lower in the spring and early summer than at other times of the year. The volume mean temperature decreases from 11 to 9–10 ^∘C and varies seasonally.

Three datasets of in situ conductivity–temperature–depth (CTD) observations were collected by R/V Bilim-2 from the Institute of Marine Sciences (IMS/METU¹) on 4–11 April 2008, 1–4 October 2008 and 18–23 June 2013 are used to validate the simulation.

Figure 8 shows the spatial distribution of the salinity and temperature RMS errors in the first 50 m of the water column in October 2008. The error is higher in the eastern Sea of Marmara close to the Bosphorus. The mean RMS errors of temperature and salinity are listed in Table 2. The errors are similar in April and October 2008 but notably increase after 6 years of integration in June 2013, which can be expected after such a long integration and, spatially, the errors are this time higher on the Dardanelles side of the Sea of Marmara than on the Bosphorus side. The RMS error is larger than those found in operational models of the Mediterranean Sea (Oddo et al., 2009), but this is due to a thermocline and halocline vertical shift, as shown in Fig. 9a. The vertical mixing and the missing interannual variability of the Black Sea runoff probably account for this. The model performs substantially better at the surface and below 30 m in depth than it does at the depth of the interface between the upper and lower layers of around 20 m (Fig. 9b). Temperature RMS errors are highest around the seasonal thermocline in June 2013, while at the same level as the halocline in the other 2 months.

Table 2 Mean RMS of salinity and temperature error with respect to CTD measurements in April and October 2008 and June 2013.

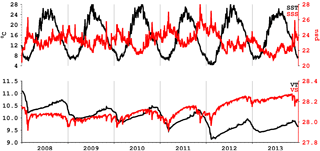
Figure 7 Daily time series of mean sea surface temperature (SST), mean sea surface salinity (SSS), volume mean temperature (VT) and volume mean salinity (VS) in the Sea of Marmara. Temperature and salinity are shown in black and red, respectively.

Figure 8 Spatial distribution of RMS of (a) salinity and (b) temperature error computed at the top 50 m of each CTD cast in October 2008.

Figure 9 (a) Mean temperature and salinity profiles of observations (dashed) and simulation (line) and (b) vertical distributions of RMS errors in April 2008 (blue), October 2008 (green) and June 2013 (red).

3.3 Sea level and volume fluxes through the straits

The time mean of the sea surface height across the system is shown in Fig. 10 for the 2009–2013 period. The SSH is approximately 0.12 m in the Black Sea and −0.12 m in the Aegean Sea. In the Sea of Marmara, SSH is higher in the western basin. The differences between the two ends of the Bosphorus are approximately 0.18 m and in the Dardanelles are about 0.11 m.

Figure 10 The mean sea surface height for 2009–2013. Contours are overlaid with 2 cm interval.

Table 3 Along-strait maximum velocity for the upper layer (UL) and lower layer (LL) and interface depth in each strait exit. Units are in m s⁻¹ and metres for the velocity and depth, respectively. A negative value indicates the flow in the direction from the Black Sea to the Aegean Sea.

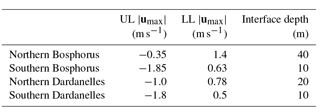
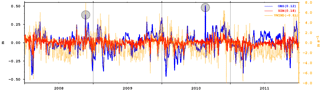
Figure 11 Sea level difference (SLD) between Yalova and Şile and daily averages of the meridional wind speed at B1 (see Fig. 1) between 2008 and 2011. The SLDs in the in situ observation (OBS) and the simulation (SIM) in metres are shown by the blue and red lines, respectively. The meridional wind speed is in orange in metres per second. The 4-year means, which are subtracted from the time series, are shown in the legend. A positive SLD means the sea level is higher in Yalova than in Şile. A positive wind speed means the wind direction is northward. The grey circles mark the Orkoz events on 22 November 2008 and 21 August 2010 as suggested by the observations.

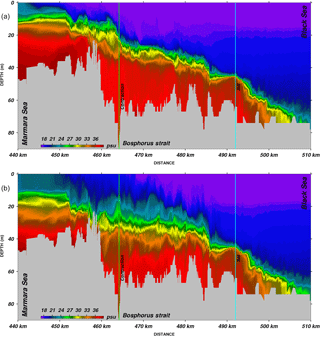
Figure 12 Cross-section of salinity in the Bosphorus strait on (a) 15 November and (b) 22 November 2008 along the thalweg between 440 and 510 km. Contraction and the northern sill locations are marked with green and cyan lines, respectively, as shown in Fig. 1.

Moller (1928) measured the sea level differences between the two ends of the Dardanelles and the Bosphorus as 7 and 6 cm, respectively. Gunnerson and Ozturgut (1974) and Büyükay (1989) found the sea level difference in the Bosphorus to be 35 cm for the 1966–1967 period and 28–29 cm for 1985–1986 period, respectively. Bogdanova (1969) gave a sea level difference of 42 cm between the northern Black Sea (Yalta) and southern coast of Turkey (Antalya) with high seasonal variability. Alpar et al. (2000) suggested a mean sea level difference of 55 cm between the Black Sea entrance of the Bosphorus and the Aegean entrance of the Dardanelles for the 1993–1994 period. We cannot assess the accuracy of our model against these values in the literature with such a wide range of variability.

As shown in Fig. 11, we compare the sea level difference between Yalova (Sea of Marmara; see Fig. 1) and Şile (Black Sea) with the time series of tide gauge measurements collected between 2008 and 2011 (Tutsak et al., 2016). The correlation between the observed and simulated sea level differences is 0.56. The response of the model is weaker during the arrival phase of severe storms, corresponding to southwesterly winds known as “lodos”, when the sea level difference becomes negative in the observations; i.e. the sea level in the Sea of Marmara is higher than in the southwestern Black Sea. The higher sea level in the Sea of Marmara often results in short-term blocking and reversal of the Bosphorus upper layer flow (called Orkoz). One such event was studied by Book et al. (2014) during the strong atmospheric cyclone passage of 22 November 2008 (Fig. 11). The signal of this event is captured in the sea level difference measurements (blue) and successfully reproduced by the model (red), though with a smaller amplitude. However, the event of 21 August 2010 is absent in the simulation as the atmospheric forcing (orange) shows no signal of a severe southerly storm. The accuracy of the atmospheric forcing is in this case limiting the correct oceanic response.

Figure 13 Same as Fig. 12 but for the Dardanelles strait and its Sea of Marmara extension.

The salinity structure on 15 November 2008 represented in Fig. 12 along the thalweg line of Fig. 1 corresponds to the situation typically observed in the Bosphorus with a normal range of net flow. The features of the salinity distribution shown in Fig. 12a are similar to those shown by the measurements of Özsoy et al. (2001) and Gregg and Özsoy (2002), and computed by Sözer and Özsoy (2017a) and Sannino et al. (2017), respectively, in stand-alone Bosphorus and integrated TSS models of exchange flows under a medium range of net flows excluding the effects of atmospheric forcing. The interface becomes thinner in the buoyant Bosphorus jet flowing into the Sea of Marmara and at the northern sill, where the lower layer reaches supercritical speeds through the hydraulic control, followed by a series of hydraulic jumps (Dorrell et al., 2016).

In comparison, the next section in Fig. 12b reflects the situation predicted in the Bosphorus on 22 November 2008. Under the conditions of an extreme Orkoz event, the upper layer flow of the Bosphorus becomes completely blocked. In rare instances, the entire Bosphorus has been observed to flow towards the Black Sea, as reported after 22 November 2008, which was covered by a period of extensive measurements. ADCP measurements in the middle of the Bosphorus indicated a flow towards the Black Sea over the entire depth of the Strait, with superposed minor oscillations (Tutsak et al., 2016) during the event (Book et al., 2014; Jarosz et al., 2011a). The increased flow of dense water of mixed Mediterranean and TSS origin was found to cascade over the Black Sea shelf and propagate over large distances across the interior of the sea at intermediate depths (Falina et al., 2017). The model results in Fig. 12 show increased vertical mixing in the upper layer up in the middle of the Bosphorus but not all the way to the northern end as indicated by the measurements. The upper layer has been pushed north of the southern contraction, suggesting that the hydraulic control there has been lost. However, the thin interface layer on top of the northern sill and the flow north of it continue to preserve its shape, suggesting continued hydraulic control at the northern sill.

All the above features are consistent with the findings obtained from idealised and realistic models of the Bosphorus provided in Sözer and Özsoy (2017a) and the TSS model experiments of Sannino et al. (2017).

In the Dardanelles, the two-layered water mass and flow structure can be seen in Fig. 13. The simulated layered-structure in the Dardanelles is similar to those of Sannino et al. (2017) under normal atmospheric conditions (Fig. 13a). The severe storm event on 22 November 2008 results in extensive mixing in the upper layer (Fig. 13b) where the salinity increases substantially. Furthermore, even the stratification is broken partially on the Sea of Marmara side of the strait.

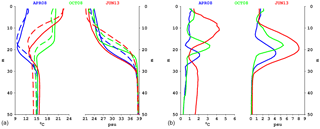
Upper layer velocity in the southern exits of both the Bosphorus and Dardanelles is generally higher than in their northern exits, due to the hydraulic controls exerted at the constrictions in the middle of both straits and the expansion area in the mouth (Sözer and Özsoy, 2017a). Conversely, the lower layer velocity has much higher maxima at the northern exits in both straits and is roughly 0.2 m s⁻¹ less than the measurements by Jarosz et al. (2011a, 2012). The upper layer maximum velocities are in accordance with most observations. The depths of the zero velocity level vary significantly in the exits of each strait and are listed in Table 3. These depths are consistent with the recent approximations reported in Jarosz et al. (2011a, 2012) for the northern Bosphorus, the southern Bosphorus, the northern Dardanelles and the southern Dardanelles, which are 39, 13.5, 22 and 13 m, respectively.

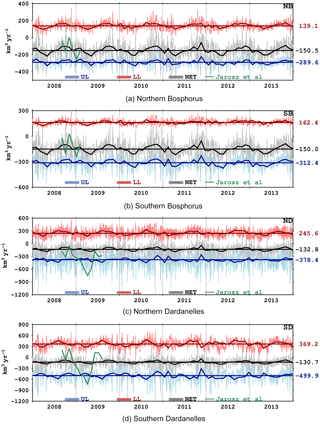
Figure 14 Daily upper layer (blue, UL), lower layer (red, LL) and net (grey, NET) volume fluxes through northern Bosphorus (NB), southern Bosphorus (SB), northern Dardanelles (ND) and southern Dardanelles (SD) in km³ yr⁻¹. Monthly and 6-year averages are overlaid with a darker tone of the same colour. The monthly averages of volume fluxes computed by Jarosz et al. (2011b, 2013) are shown in green for the period of observations.

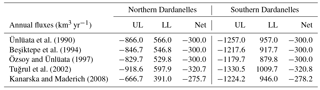
The net, annual mean upper layer and lower layer volume fluxes are given in Table 4, and the daily and monthly averages are shown in Fig. 14. The estimations from Jarosz et al. (2011b, 2013) from direct measurements are also indicated. The mean net volume fluxes through the straits compare well with the observations between 2 September 2008 and 5 February 2009 for the Bosphorus, and 1 September 2008 and 31 August 2009 for the southern Dardanelles. However, the variability in time is not as high as in the observations (Fig. 14). In the northern Dardanelles, there is a large discrepancy between the simulated net fluxes and the estimates from observations.

Sannino et al. (2017) and Özsoy and Altıok (2016) both have similar disagreements with the measurements of Jarosz et al. (2013) and have concluded that the discrepancies could be a result of measurement or computational inaccuracies at the wide northern section of the Dardanelles, where the instrument data were located.

The historical estimates of the Dardanelles layer volume fluxes show much higher values than our simulation (Table 5). The changes found in the layer flux from one end of the strait to the other have been attributed to turbulent entrainment processes, which transport water and properties across the hypothesised layer interface (Özsoy and Altıok, 2016; Özsoy et al., 2001; Ünlüata et al., 1990). The larger disagreement of baroclinic volume fluxes compared to the net fluxes, and the lower estimations of the model layer fluxes, suggest that bottom friction parameterisation is too strong and possibly a problem in the vertical mixing submodel chosen.

Table 4 Annual mean of net, upper layer and lower layer volume fluxes (km³ yr⁻¹) for the whole simulation period. A negative value indicates the flux is in the Black Sea – Aegean Sea direction.

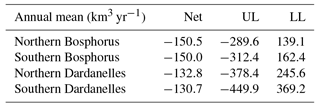
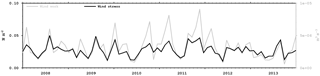
Figure 15 Monthly time series of the wind work (m³ s⁻³) and wind stress (Nm⁻²) in the Sea of Marmara. The wind work normalised by the density and surface area of the Sea of Marmara is shown in grey in the right vertical axis. The wind stress is the black curve and its values are shown on the left vertical axis.

Ünlüata et al. (1990)Beşiktepe et al. (1994)Özsoy and Ünlüata (1997)Tuğrul et al. (2002)Kanarska and Maderich (2008)

Table 5 Annual means of volume fluxes (km³ yr⁻¹) through the Dardanelles estimated by different studies. UL, LL and Net stand for upper layer, lower layer and net fluxes, respectively. A negative value indicates the volume flux is from the Sea of Marmara to the Aegean Sea.

The net volume transport in the model is approximately half of the historical estimations based on mass conservation laws assuming a net water flux into the Black Sea of about 300 km³ yr⁻¹. Our choice to conserve the model volume in a closed lateral boundary model by correcting the water flux every time step comes with the limitation of reducing the transport along its way from the Black Sea to the Aegean Sea. The total water flux over the Sea of Marmara is −17.1 km³ yr⁻¹ (Fig. 3b) which is balanced by the difference between the southern Bosphorus and northern Dardanelles (Table 4). Due to the surface flux correction, the net outflow in the Dardanelles is decreased by about 10 % with respect to what entered the Bosphorus. However, such correction allowed us to obtain realistic salinity profiles with respect to other correction methods such as that used by Gürses et al. (2016).

Finally, the differences in transport between the transects at the two ends of each strait are 0.5 and 2.1 km³ yr⁻¹ in the Bosphorus and Dardanelles, respectively. We attribute these differences partially again to the water flux correction at the surface. The rest is due to the numerical errors accumulating during the post-processing of the model outputs.

3.4 Dynamics and circulation in the Sea of Marmara

Using the 6-year simulation, it is now possible to estimate the kinetic energy input by the wind in the Sea of Marmara.

The time series of monthly mean wind stress is shown in Fig. 15. It exhibits interannual differences with a mean of about 0.03 Nm⁻² and a maximum of around 0.05 Nm⁻² in August 2008. The monthly mean is highly variable and there is not a well-defined seasonal cycle between 2008 and 2013. The wind work normalised by the density and surface area is computed as

$$\begin{array}{}\text{(3)}& {\displaystyle \frac{\mathrm{1}}{{\mathit{\rho }}_{\mathrm{0}}A}}\underset{A}{\int }\mathit{\tau }\cdot {\mathit{u}}_{\mathrm{s}}\mathrm{d}x\mathrm{d}y,\end{array}$$

where ρ₀ is the surface density, τ is the wind stress, u_s is the current velocity at the surface, and A is the surface area of the Sea of Marmara. The wind work is positively correlated with the wind stress. It is highest in 2011 and the maximum monthly mean wind work is $\mathrm{9.1}\times {\mathrm{10}}^{-\mathrm{6}}$ m³ s⁻³ in the autumn of 2011.

To compare with the other marginal seas described in Cessi et al. (2014), we normalise the integral in Eq. (3) by the volume of the Sea of Marmara. The 6-year mean of the wind work is computed as $\mathrm{1.09}\times {\mathrm{10}}^{-\mathrm{8}}$ m² s⁻³, 1 order of magnitude higher than in the Mediterranean Sea. The wind work in the Baltic Sea was computed to be $\mathrm{9.15}\times {\mathrm{10}}^{-\mathrm{9}}$ m² s⁻³, which is comparable to the Sea of Marmara but is still lower.

The volume-mean kinetic energy in the Sea of Marmara normalised by the unit mass is calculated as 0.006 m² s⁻² for 6 years. The daily mean kinetic energy time series reveals that severe atmospheric events are able to energise the basin up to 0.03 m² s⁻² (not shown). The monthly volume-mean kinetic energy averages fluctuate between 0.005 and 0.01 m² s⁻². It is higher in winter and early spring, whereas it is always below the mean in summer. The highest kinetic energy inputs are in October 2010, April 2011 and November 2011. The kinetic energy is higher in the upper layer of the water column. The time mean of surface kinetic energy is about 0.03 m² s⁻². Daily surface averages are capable of reaching 0.2 m² s⁻². The monthly mean increases to approximately 0.05 m² s⁻² in November 2011.

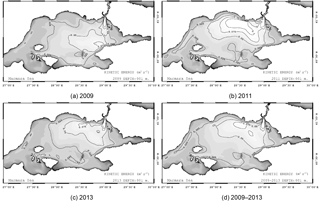
Figure 16 Annual mean of surface kinetic energy in the Sea of Marmara for (a) 2009, (b) 2011 and (c) 2013. (d) The time mean of the 2009–2013 period. Units are in m² s⁻² as kinetic energy is normalised by the unit mass.

In the Sea of Marmara, the buoyancy gain is mainly due to the Bosphorus inflow, and thus the latter competes with the wind work to change the kinetic energy of the basin, as explained by Cessi et al. (2014). However, at the surface, the kinetic energy shows that the Bosphorus surface jet energises the northeastern basin in addition to the wind (Fig. 16). The kinetic energy of the Bosphorus inflow is always greater than 0.075 m² s⁻². In 2009, a kinetic energy maximum appears in the north of the Bozburun Peninsula where the Bosphorus jet arrives. In the western basin, the kinetic energy is generally less than 0.025 m² s⁻². In 2011, the kinetic energy intensifies in the central north and exceeds 0.1 m² s⁻². Almost all of the basin, except near the coastal areas, has a kinetic energy higher than 0.025 m² s⁻². Energy is mostly confined to the northeast of the central basin in 2013. The time mean for 2009–2013 reflects the characteristics of 2011 but with less amplitude.

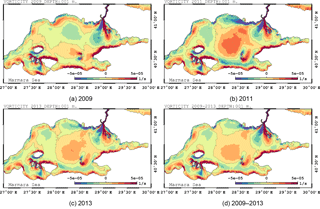
Figure 17 Annual mean of surface vorticity in the Sea of Marmara at the surface for (a) 2009, (b) 2011 and (c) 2013, and (d) the surface vorticity mean for the 2009–2013 period.

The energetic Bosphorus jet generates a dipole vorticity field, which is anticyclonic in the west and cyclonic in the east (Fig. 17). Northern and western coasts are dominated by anticyclonic vorticity. Conversely, cyclonic vorticity dominates the southern coast. Positive and negative vorticity in the northern and southern coasts of the islands and peninsulas, respectively, are other common structures for all the years. The mean vorticity fields are consistent with upwelling-favourable conditions on the southern coasts of the Sea of Marmara. Primarily, a cyclonic gyre located at 28^∘20^′ N–40^∘35^′ E forms in the central basin after 2011, showing that the circulation changed sign between 2008 and 2011.

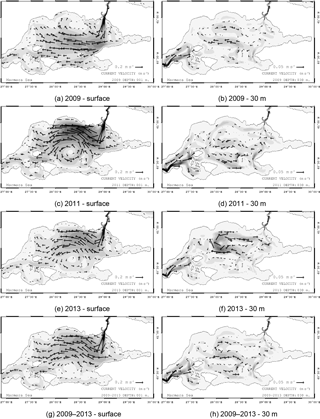
Figure 18 Annual mean of current velocity in the Sea of Marmara for (a) 2009 at the surface, (b) 2009 at 30 m, (c) 2011 at the surface, (d) 2011 at 30 m, (e) 2013 at the surface and (f) 2013 at 30 m. The means for the 2009–2013 period are shown in panel (g) at the surface and panel (h) at 30 m.

Figure 18 shows the annual mean of the current velocity at the surface and 30 m for 2009, 2011 and 2013, and the mean for the 2009–2013 period. The annual means of the surface circulation show two different circulation structures as was already evident from the vorticity structures. In 2009 (Fig. 18a), the Bosphorus plume reaches the Bozburun Peninsula and turns west towards the middle of the basin. One branch of the flow heads north and forms an anticyclone close to the Thracian coast. The southern branch instead splits into two when it reaches Marmara Island. The southwestward flow traverses the Sea of Marmara after turning south, merging with the flow circulating around the islands in the southwestern Sea of Marmara and eventually exiting from the Dardanelles. This circulation pattern in the western Sea of Marmara is persistent throughout the simulation but with different intensities. This type of circulation structure has been reported in other studies (Beşiktepe et al., 1994; Chiggiato et al., 2012). In 2011 (Fig. 18c), the circulation in the middle of the Sea of Marmara evolves into a single cyclonic structure. The shift in the circulation can be explained by the shift of the wind stress maximum towards the north (Fig. 2). Sannino et al. (2017) demonstrates a similar cyclonic pattern in the central Sea of Marmara due to the potential vorticity input by the Bosphorus. However, in our case, the main driver of the cyclone should be the wind, as the volume transport through the Bosphorus is much lower than that of Sannino et al. (2017) case. Thus, in certain conditions, both the wind and the Bosphorus can induce a cyclonic circulation in the Sea of Marmara. The cyclonic surface circulation dominates the mean between 2009–2013. The mean surface circulation in the sea can be sketched as in Fig. 19.

Below the pycnocline at 30 m, two main structures can be identified. An anticyclonic formation appears in the central basin intensifying in 2013. On the Dardanelles side, a flow enters the Sea of Marmara and partially heads southeast. Another structure recirculates after reaching Marmara Island and joins the southwestward flow exiting the Sea of Marmara. In 2011, a meander heading west is formed in the northern basin. This feature is not present in other years and results from the deepening of the upper layer (not shown) due to stronger wind stress.

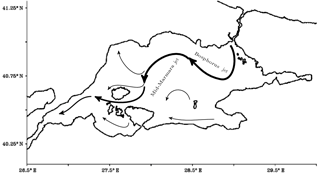
Figure 19 Schematic representation of the surface mean circulation in the Sea of Marmara for the 2009–2013 period. The thickness of curves shows the relative intensity of the associated current.

The mean circulation of the Sea of Marmara, schematically shown in Fig. 19, is dominated by the Bosphorus jet and the mid-Marmara jet meandering cyclonically. The mid-Marmara jet is divided into three before reaching Marmara Island, and one branch heads to the northwest and the other two reach the Dardanelles after circulating around the island. Finally, weak currents move in an east–west direction on the southern coast of the basin.

4 Summary and discussion

We present a 6-year simulation of the Turkish Straits System, with a highly resolved unstructured mesh model of the TSS using realistic atmospheric forcing to identify the circulation structure and the interplay between the atmospheric forcing and the Bosphorus input. The results demonstrate that a realistic representation of the pycnocline from the two straits to the Sea of Marmara is possible. The model is capable of reproducing the historically reported water mass structure of the Sea of Marmara. Model errors peak at the halocline and thermocline depths, where small changes in the interface depth induce greater error.

The strait volume transport has been compared with the observations. The net volume transport in the Bosphorus agrees with the estimates based on the observations. The model solution departs from the observations in the northern Dardanelles, but closer agreement is found elsewhere. The baroclinic transport shows larger discrepancies between the observations and the model, possibly because of uncertainties in the bottom boundary layer dissipation mechanisms and turbulence parameterisation. The model is capable of simulating blocking events in the straits during severe storm passages, to the extent that such storms are present in the atmospheric dataset, as shown for the 22 November 2008 case.

The circulation in the Sea of Marmara shows two patterns in the interannual timescales. The first is dominated by the buoyant plume of the Bosphorus to the south around an anticyclonic circulation structure in the eastern and northern parts of the basin. This type of circulation has been observed and modelled by several earlier studies (Beşiktepe et al., 1994; Chiggiato et al., 2012; Sannino et al., 2017). The other circulation structure includes a cyclone in the central basin because of intensifying and expanding wind stress over the Sea of Marmara. Small-scale vortices are also formed in various parts of the basin and a larger one appears in the northwest after 2011. The cyclonic gyre in the central Sea of Marmara is shown numerically only by Sannino et al. (2017), in the case of extreme net volume flux through the Bosphorus. However, here, we show that the wind can produce the cyclonic circulation in addition to the Bosphorus jet.

The long-term simulation with atmospheric forcing made it possible to evaluate the wind energy input and compute the kinetic energy in the Sea of Marmara. The wind work in the Sea of Marmara is shown to be even higher than the Baltic Sea. The high energy input from the wind significantly increases the kinetic energy in the Sea of Marmara. During severe storms, kinetic energy can increase by 10 times the time-averaged value. The annual mean of kinetic energy in the regions under the influence of the wind forcing can also exceed that from the Bosphorus jet, depending on the wind stress structure.

In our modelling approach, we focused our attention on the TSS proper, which is the central domain including the straits and the Sea of Marmara, while assigning a limited storage role to the truncated exterior domains of the Black and Aegean seas. This represents a trade-off between a truthful reproduction of the TSS circulation and the ability to impose far-field boundary conditions in artificial closed basins at the two ends, using a similar strategy to that of Sannino et al. (2017). In future studies, we expect to obtain improved results by incorporating lateral open ocean boundary conditions in the Aegean and Black seas. The skill of the model predictions also appeared sensitive to the accuracy of the atmospheric forcing used in the simulation. Within the relatively small domain of the TSS, an improved representation of the atmospheric forcing, particularly during the severe storms frequenting the region in winter, appears to be essential for improving its skill.

Overall, the results suggest further directions for long-term modelling in the TSS. We have demonstrated that wind forcing determines the surface circulation together with the Bosphorus inflow in the Sea of Marmara. A higher resolution atmospheric forcing and better representation of the Black Sea water budget, by using open lateral boundaries, would improve the model solution particularly for the volume flux and the salinity flux estimations. Data assimilation techniques, for which an example is recently given by Aydoğdu et al. (2018), should also be considered for a better state estimate.

Appendix A: Model equations

FESOM solves the standard set of hydrostatic primitive equations with the Boussinesq approximation (Wang et al., 2008).

The momentum equations are

$$\begin{array}{ll}{\displaystyle }{\partial }_t\mathit{u}& {\displaystyle }+\mathit{v}\cdot {\mathrm{\nabla }}_{\mathrm{3}}\mathit{u}+f\widehat{k}\times \mathit{u}=-{\displaystyle \frac{\mathrm{1}}{{\mathit{\rho }}_{\mathrm{0}}}}\mathrm{\nabla }p-g\mathrm{\nabla }\mathit{\eta }-\mathrm{\nabla }{A}_{\mathrm{h}}\mathrm{\nabla }\left({\mathrm{\nabla }}^{\mathrm{2}}\mathit{u}\right)\\ \text{(A1)}& {\displaystyle }& {\displaystyle }+{\partial }_z{A}_{\mathrm{v}}{\partial }_z\mathit{u},\end{array}$$

where $\mathit{u}=(u,v)$ and $\mathit{v}=(u,v,w)$ are 2-D and 3-D velocities, respectively, in the spherical coordinate system, ρ₀ is the mean density, g is the gravitational acceleration, η is the sea surface elevation, f is the Coriolis parameter, and $\widehat{k}$ is the vertical unit vector. ∇ and ∇₃ stand for 2-D and 3-D gradients or divergence operators, respectively. The horizontal and vertical viscosities are denoted by A_h and A_v. p is the hydrostatic pressure obtained integrating the hydrostatic relation (Eq. A3) from z=η. Atmospheric pressure is not considered in order to not excite basin modes in a closed lateral boundary model.

The Laplacian viscosity is known to be generally too damping and strongly reduces the eddy variances of all fields compared to observations when the model is run at eddy resolving resolutions (Wang et al., 2008). Therefore, biharmonic viscosity is used in the momentum equations. Here, A_h is scaled by the cube of the element size with a reference value A_h0 of 2.7×10¹³ m⁴ s⁻¹ (Table A1), which is set for the reference resolution of 1^∘.

The continuity equation is used to diagnose the vertical velocity w:

$$\begin{array}{}\text{(A2)}& {\partial }_{z}w=-\mathrm{\nabla }\cdot \mathit{u},\end{array}$$

and the hydrostatic equation is

$$\begin{array}{}\text{(A3)}& {\partial }_{z}p=-g\mathit{\rho },\end{array}$$

where ρ is the deviation from the mean density ρ₀.

Tracer Eqs. (A4) and (A5),

$$\begin{array}{}\text{(A4)}& {\displaystyle }& {\displaystyle }{\partial }_{t}T+\mathit{v}\cdot {\mathrm{\nabla }}_{\mathrm{3}}T-\mathrm{\nabla }\cdot K_{\mathrm{h}}\mathrm{\nabla }T-{\partial }_z{K}_{\mathrm{v}}{\partial }_{z}T=\mathrm{0}\text{(A5)}& {\displaystyle }& {\displaystyle }{\partial }_{t}S+\mathit{v}\cdot {\mathrm{\nabla }}_{\mathrm{3}}S-\mathrm{\nabla }\cdot K_{\mathrm{h}}\mathrm{\nabla }S-{\partial }_z{K}_{\mathrm{v}}{\partial }_{z}S=\mathrm{0},\end{array}$$

are solved for the potential temperature, T, and salinity, S, where K_h and K_v are the horizontal and vertical eddy diffusivities, respectively. Laplacian diffusivity is used for the tracer equations. K_h is again scaled as A_h but by the element size with a reference value of 2.0×10³ m² s⁻¹. These values are set following the convergence study of Wallcraft et al. (2005).

The Pacanowski and Philander (1981) (PP) parameterisation scheme is used for vertical mixing, with a background vertical viscosity of 10⁻⁵ m² s⁻¹ for momentum and diffusivity of 10⁻⁶ m² s⁻¹ for tracers. The maximum value is set to 0.005 m² s⁻¹.

The density anomaly ρ is computed by the full equation of state (Eq. A6).

$$\begin{array}{}\text{(A6)}& \mathit{\rho }=\mathit{\rho }(T,S,p)\end{array}$$

The surface and bottom momentum boundary conditions are, respectively,

$$\begin{array}{}\text{(A7)}& {\displaystyle }& {\displaystyle }{A}_{\mathrm{v}}{\partial }_z\mathit{u}=\mathit{\tau }\text{(A8)}& {\displaystyle }& {\displaystyle }{A}_{\mathrm{v}}{\partial }_z\mathit{u}+A_{\mathrm{h}}\mathrm{\nabla }H\cdot \mathrm{\nabla }\mathit{u}=C_{\mathrm{d}}\mathit{u}\mid \mathit{u}\mid ,\end{array}$$

where τ and C_d are the wind stress and the surface drag coefficient, respectively.

The surface kinematic boundary condition is

$$\begin{array}{}\text{(A9)}& w={\partial }_t\mathit{\eta }+\mathit{u}\cdot \mathrm{\nabla }\mathit{\eta }+(E-P-R)+W_{\mathrm{corr}},\end{array}$$

where E (m s⁻¹) and P (m s⁻¹) are evaporation and precipitation, respectively. R (km³ yr⁻¹) is runoff (see Table 1). It is converted to m³ s⁻¹ and normalised by the area of the buffer zone in the Black Sea (see Fig. 1) before entering to the equation. Finally, W_corr is a correction applied to conserve the volume of the model, as described later.

The sea surface height equation can now be derived from Eqs. (A2) and (A9) as

$$\begin{array}{}\text{(A10)}& {\partial }_t\mathit{\eta }+\mathrm{\nabla }\cdot \underset{z=-H}{\overset{z=\mathit{\eta }}{\int }}\mathit{u}\mathrm{d}z=-(E-P-R)-W_{\mathrm{corr}}.\end{array}$$

The upper limit of integration in Eq. (A10) is set to η in this version of FESOM and is different from Wang et al. (2008) to provide a non-linear free surface solution.

The bottom boundary conditions for the temperature and salinity are

$$\begin{array}{}\text{(A11)}& {\displaystyle }& {\displaystyle }(\mathrm{\nabla }T,{\partial }_{z}T)\cdot {\mathit{n}}_{\mathrm{3}}=\mathrm{0}\text{(A12)}& {\displaystyle }& {\displaystyle }(\mathrm{\nabla }S,{\partial }_{z}S)\cdot {\mathit{n}}_{\mathrm{3}}=\mathrm{0},\end{array}$$

where n₃ is the 3-D unit vector normal to the respective surface.

The surface boundary condition for temperature is

$$\begin{array}{}\text{(A13)}& K_{\mathrm{v}}{\partial }_{z}T{|}_{z=\mathit{\eta }}={\displaystyle \frac{Q}{{\mathit{\rho }}_{\mathrm{0}}{C}_p}},\end{array}$$

where C_p=4000 J kg⁻¹ K⁻¹ and Q (W m⁻²) is the surface net heat flux into the ocean.

In global applications, surface salinity is generally relaxed to a climatology to prevent a drift. In our regional application, the water flux term in the boundary condition (Eq. A14) is applied over the whole domain, whereas the relaxation term is prescribed only in the Black Sea buffer zone.

$$\begin{array}{}\text{(A14)}& K_{\mathrm{v}}{\partial }_{z}S{|}_{z=\mathit{\eta }}=S_{\mathrm{0}}(E-P-R)+\mathit{\gamma }(S^{*}-S_{\mathrm{0}})-S_{\mathrm{corr}}\end{array}$$

In Eq. (A14), S₀ and S^* are the surface salinity and the reference salinity, respectively, and γ is the relaxation coefficient (Table A1). Finally, S_corr is the counterpart of W_corr for salinity conservation corresponding to boundary conditions (Eq. A14), which will be defined in the following section.

Table A1 Parameters used in the model equations, surface boundary conditions and budget corrections.

Appendix B: Salt conservation properties

As our model domain is closed, we need to enforce salt conservation. Volume salinity conservation requires the time rate of the change in the volume salinity term in Eq. (B1) to be zero. A balance must be satisfied between the two integrals.

$$\begin{array}{}\text{(B1)}& {\displaystyle \frac{\partial }{\partial t}}\underset{V}{\iiint }S\mathrm{d}V=\underset{A_{\mathrm{D}}}{\iint }\left(K_{\mathrm{v}}{\partial }_{z}S{|}_{z=\mathit{\eta }}\right)d{A}_{\mathrm{D}}=\mathrm{0}\end{array}$$

In FESOM, this balance is achieved by applying a correction for each term separately. The amount of water flux by evaporation, precipitation and runoff is integrated over the surface with every time step (Eq. B2). After normalising by the domain area as in Eq. (B3), the surplus or deficit is added to or subtracted from the total water flux equally from each node of the mesh with the W_corr terms in Eqs. (A9) and (A10).

$$\begin{array}{}\text{(B2)}& {\displaystyle }& {\displaystyle }{\mathrm{\Delta }}_{(E-P-R)}=\underset{x,y}{\int }(E-P-R)\mathrm{d}x\mathrm{d}y\text{(B3)}& {\displaystyle }& {\displaystyle }{W}_{\mathrm{corr}}={\displaystyle \frac{{\mathrm{\Delta }}_{E-P-R}}{A_{\mathrm{D}}}}\end{array}$$

The salinity flux is corrected in a similar manner for the boundary condition:

$$\begin{array}{}\text{(B4)}& {\displaystyle }& {\displaystyle }\mathrm{\Delta }S=\underset{x,y}{\int }\left(S_{\mathrm{0}}\right(E-P-R)+\mathit{\gamma }(S^{*}-S_{\mathrm{0}}\left)\right)\mathrm{d}x\mathrm{d}y\text{(B5)}& {\displaystyle }& {\displaystyle }{S}_{\mathrm{corr}}={\displaystyle \frac{\mathrm{\Delta }S}{A_{\mathrm{D}}}}.\end{array}$$

After applying these corrections, we get a surplus of water corresponding to about 1 mm of sea surface height increase a year, which we believe is due to random numerical errors. Correspondingly, the volume-mean salinity decreases by an order of 10⁻⁵ psu a year. Although these errors may be significant in climate scales, they are acceptable for our 6-year long experiment.