Estimation of oceanic subsurface mixing under a severe cyclonic storm using a coupled atmosphere–ocean–wave model

A coupled atmosphere–ocean–wave model was used to examine mixing in the upper-oceanic layers under the influence of a very severe cyclonic storm Phailin over the Bay of Bengal (BoB) during 10–14 October 2013. The coupled model was found to improve the sea surface temperature over the uncoupled model. Model simulations highlight the prominent role of cyclone-induced near-inertial oscillations in subsurface mixing up to the thermocline depth. The inertial mixing introduced by the cyclone played a central role in the deepening of the thermocline and mixed layer depth by 40 and 15 m, respectively. For the first time over the BoB, a detailed analysis of inertial oscillation kinetic energy generation, propagation, and dissipation was carried out using an atmosphere–ocean–wave coupled model during a cyclone. A quantitative estimate of kinetic energy in the oceanic water column, its propagation, and its dissipation mechanisms were explained using the coupled atmosphere–ocean–wave model. The large shear generated by the inertial oscillations was found to overcome the stratification and initiate mixing at the base of the mixed layer. Greater mixing was found at the depths where the eddy kinetic diffusivity was large. The baroclinic current, holding a larger fraction of kinetic energy than the barotropic current, weakened rapidly after the passage of the cyclone. The shear induced by inertial oscillations was found to decrease rapidly with increasing depth below the thermocline. The dampening of the mixing process below the thermocline was explained through the enhanced dissipation rate of turbulent kinetic energy upon approaching the thermocline layer. The wave–current interaction and nonlinear wave–wave interaction were found to affect the process of downward mixing and cause the dissipation of inertial oscillations.

1 Introduction

The Bay of Bengal (BoB), a semi-enclosed basin in the northeastern Indian Ocean, consists of surplus near-surface fresh water due to large precipitation and runoff from the major river systems of the Indian subcontinent (Varkey et al., 1996; Rao and Sivakumar, 2003; Pant et al., 2015). The presence of fresh water leads to salt-stratified upper-ocean water column and the formation of a barrier layer (BL), a layer sandwiched between the bottom of the mixed layer (ML) and the top of the thermocline, in the BoB (Lukas and Lindstrom, 1991; Vinayachandran et al., 2002; Thadathil et al., 2007). The BL restricts the entrainment of colder waters from thermocline region into the mixed layer; it thereby maintains a warmer ML and sea surface temperature (SST). The warmer SST together with higher tropical cyclone heat potential (TCHP) makes the BoB one of the active regions for cyclogenesis (Suzana et al., 2007; Yanase et al., 2012; Vissa et al., 2013). The majority of tropical cyclones are generated during the pre-monsoon (April–May) and post-monsoon (October–November) seasons (Alam et al., 2003; Longshore, 2008). The number of cyclones and their intensity is highly variable on seasonal and interannual timescales. The oceanic response to the tropical cyclone depends on the stratification of the ocean. The BL formation in the BoB is associated with the strong stratification due to the peak discharge from rivers in the post-monsoon season. The intensity of the cyclone largely depends on the degree of stratification (Neetu et al., 2012; Li et al., 2013). The coupled atmosphere–ocean model was found to improve the intensity of cyclonic storms when compared to the uncoupled model over different oceanic regions (Warner et al., 2010; Zambon et al., 2014; Srinivas et al., 2016; Wu et al., 2016). Zambon et al. (2014) compared the simulations from the coupled atmosphere–ocean and uncoupled models and reported significant improvement in the intensity of storms in the coupled case as compared to the uncoupled case. The uncoupled atmospheric model produced large ocean–atmosphere enthalpy fluxes and stronger winds in the cyclone (Srinivas et al., 2016). When the atmospheric Weather Research and Forecasting (WRF) model interacted with the ocean model, the SST was found to be more realistic compared to the stand-alone WRF (Warner et al., 2010; Gröger et al., 2015; Jeworek et al., 2017; Ho-Hagemann et al., 2017). Wu et al. (2016) demonstrated the advantage of using a coupled model over the uncoupled model in a better simulation of typhoon Megi's intensity.

Mixing in the water column has an important role in energy and material transference. Mixing in the ocean can be introduced by the different agents such as wind, current, tide, eddy, and cyclone. Mixing due to tropical cyclones is mostly limited to the upper ocean, but the cyclone-induced internal waves can affect the subsurface mixing. Several studies have observed that the mixing in the upper-oceanic layer is introduced due to the generation of near-inertial oscillations (NIOs) during the passage of tropical cyclones (Gonella, 1971; Shay et al., 1989; Johanston et al., 2016). This mixing is responsible for the deepening of the ML and the shoaling of the thermocline (Gill, 1984). The vertical mixing caused by storm-induced NIO has a significant impact on upper-ocean variability (Price, 1981). The NIO are also found to be responsible for the decrease in SST along the cyclone track (Chang and Anthes, 1979; Leipper, 1967; Shay et al., 1992, 2000). This decrease in SST is caused by the entrainment of cool subsurface thermocline water from the mixed layer into the immediate overlying layer of water. This cooling of surface water is one of the reasons for the decay of cyclones (Cione and Uhlhorn, 2003). The magnitude of surface cooling differs largely depending on the degree of stratification on the right-hand side of the cyclone track (Jacob and Shay, 2003; Price, 1981).

The near-inertial process can be analyzed from the baroclinic component of currents. The vertical shear of horizontal baroclinic velocities that is interrelated with buoyancy oscillations of surface layers is utilized in various studies in order to gain an adequate understanding of the mixing associated with high-frequency oscillations, i.e., NIO (Zhang et al., 2014). The shear generated due to NIO is an important factor for the intrusion of the cold thermocline water into the ML during near-inertial scale mixing (Price et al., 1978; Shearman, 2005; Burchard and Rippeth, 2009). The alternative upwelling and downwelling features of the temperature profile are an indication of the inertial mixing. The kinetic energy bounded with these components of the current shows a rise in magnitude at the right side of a cyclone track (Price, 1981; Sanfoard et al., 1987; Jacob, 2003). This high magnitude of kinetic energy is linked to strong wind and the rotating wind vector conditions of the storm. The spatial distribution of near-inertial energy is primarily controlled by the boundary effect for inertial oscillations (Chen et al., 2017). The NIO is found to decline with decreasing depth and vanishes in the coastal regions (Schahinger, 1988; Chen et al., 2017).

The aim of this paper is to understand and quantify the near-inertial mixing due to the very severe cyclonic storm Phailin in the BoB. Phailin developed over the BoB in the northern Indian Ocean in October 2013. The landfall of Phailin occurred on 12 October 2013 around 17:00 GMT near the Gopalpur district of Odisha state on the east coast of India. After the 1999 super cyclonic event of the Odisha coast, Phailin was the second strongest cyclonic event that made landfall on the east coast of India (Sanil Kumar and Nair, 2015). The low-pressure system developed in the north of the Andaman Sea on 7 October 2013 and was transformed into a depression on 8 October at 12^∘ N, 96^∘ E. This depression was converted into a cyclonic disturbance on 9 October and further intensified while moving to the east-central BoB, showing a maximum wind speed of 200 km h⁻¹ at 03:00 GMT on 11 October. Finally, landfall occurred at 17:00 GMT on 12 October. More details on the development and propagation of Phailin can be found in the literature (IMD Report, 2013; Mandal et al., 2015). The performance of the coupled atmosphere–ocean model in simulating the oceanic parameters temperature, salinity, and currents during Phailin is discussed in Prakash and Pant (2017).

Most of the past studies on oceanic mixing under cyclonic conditions were carried out using in situ measurements, which are constrained by their spatial and temporal availability. To the best of our knowledge, the present study is the first of its kind to utilize a coupled atmosphere–ocean–wave model over the BoB to estimate cyclone-induced mixing, its associated energy propagation on the cyclone track, and the location of maximum surface wind stress during the period of the peak intensity of the cyclone. The study also focuses on analyzing the subsurface distribution of NIO with its vertical mixing potential. Further, the study quantifies the shear-generated mixing and the kinetic energy of the baroclinic mode of the horizontal current varying in the vertical section at a selected location during the active period of the cyclone. The dissipation rate of NIO and turbulent eddy diffusivity are quantified.

2 Data and methodology

2.1 Model details

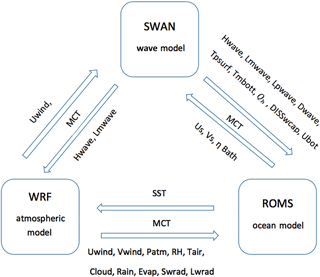
Numerical simulations during the period of Phailin were carried out using the Coupled Ocean–Atmosphere–Wave–Sediment Transport (COAWST) model, described in detail by Warner et al. (2010). The COAWST modeling system couples the three-dimensional oceanic Regional Ocean Modeling System (ROMS), the atmospheric WRF model, and the wind wave generation and propagation model Simulating Waves Nearshore (SWAN). The ROMS model used for the study is a free-surface, primitive-equation, sigma coordinate model. ROMS is a hydrostatic ocean model that solves finite difference approximations of the Reynolds averaged Navier–Stokes equations (Chassignet et al., 2000; Haidvogel et al., 2000, 2008; Shchepetkin and McWilliams, 2005). The atmospheric model component in the COAWST is a non-hydrostatic, compressible model Advanced Research Weather Research Forecast Model (WRF-ARW), described in Skamarock et al. (2005). It has different schemes for the representation of boundary layer physics and physical parameterizations of sub-grid-scale processes. In the COAWST modeling system, appropriate modifications were made in the code of the atmospheric model component to provide an improved bottom roughness from the calculation of the bottom stress over the ocean (Warner et al., 2010). Further, the momentum equation is modified to improve the representation of surface waves. The modified equation needs the additional information of wave energy dissipation, propagation direction, wave height, and wavelength that are obtained from wave components of the COAWST model. The spectral wave model SWAN, used in the COAWST modeling system, is designed for shallow water. The wave action balance equation is solved in the wave model for both spatial and spectral spaces (Booij et al., 1999). The SWAN model used in the COAWST system includes the wave wind generation, wave breaking, wave dissipation, and nonlinear wave–current–wind interaction. The Model Coupling Toolkit (MCT) is used as a coupler in the COAWST modeling system to couple different model components (Larson et al., 2004; Jacob et al., 2005). The coupler utilizes a parallel coupled approach to facilitate the transmission and transformation of various distributed parameters among component models. The MCT coupler exchanges prognostic variables from one model to another model component as shown in Fig. 1. The WRF model receives SST from the ROMS model and supplies the zonal (U_wind) and meridional (V_wind) components of 10 m wind, atmospheric pressure (P_atm), relative humidity (RH), cloud fraction (Cloud), precipitation (Rain), and shortwave (Sw_rad) and longwave (Lw_rad) radiation to the ROMS model. The SWAN model receives U_wind and V_wind from the WRF model and transfers significant wave height (H_wave) and mean wavelength (L_mwave) to the WRF model. A large number of variables are exchanged between ROMS and SWAN models. The ocean surface current components (U_s, V_s), free-surface elevations (η), and bathymetry (Bath) are provided for the SWAN model from the ROMS model. The wave parameters, i.e., H_wave, L_mwave, peak wavelength (L_pwave), wave direction (D_wave), surface wave period (T_psurf), bottom wave period (T_mbott), percentage wave breaking (Q_b), wave energy dissipation (DISS_wcap), and bottom orbit velocity (U_bot), are provided from the SWAN model to the ROMS model through the MCT coupler. Further details on the COAWST modeling system can be found in Warner et al. (2010).

Figure 1 The block diagram shows the component models WRF, ROMS, and SWAN of the COAWST modeling system together with the variables exchanged among the models. MCT, the model coupling toolkit, is a model coupler used in the COAWST system.

2.2 Model configuration and experiment design

The coupled model was configured over the BoB to study Phailin during the period of 00:00 GMT 10 October–00:00 GMT 15 October 2013. The setup of the COAWST modeling system used in this study included fully coupled atmosphere–ocean–wave (ROMS+WRF+SWAN) models, but sediment transport is not included. A non-hydrostatic, fully compressible atmospheric model with a terrain-following vertical coordinate system, WRF-ARW (version 3.7.1), was used in the COAWST configuration. The WRF model was used with 9 km horizontal grid resolution over the domain 65–105^∘ E, 1–34^∘ N and 30 sigma levels in the vertical. The WRF was initialized with National Centers for Environmental Prediction (NCEP) Final Analysis (FNL) data (NCEPFNL, 2000) at 00:00 GMT 10 October 2013. The lateral boundary conditions in WRF were provided at a 6 h interval from the FNL data. We used the parameterization schemes for calculating boundary layer processes, precipitation processes, and surface radiation fluxes. The Monin–Obukhov scheme of surface roughness layer parameterization (Monin and Obukhov, 1954) was activated in the model. The Rapid Radiation Transfer Model (RRTM) and cloud-interactive shortwave (SW) radiation scheme from Dudhia (1989) were used. The Yonsei University (YSU) planetary boundary layer (PBL) scheme (YSU-PBL), described by Noh et al. (2003), was used. At each time step, the calculated value of exchange coefficients and surface fluxes off the land or ocean surface by the atmospheric and land surface layer models (NOAH) was passed to the YSU-PBL. The grid-scale precipitation processes were represented by the WRF single-moment (WSM) six-class moisture microphysics scheme by Hong and Lim (2006). The sub-grid-scale convection and cloud detrainment were taken care of with the Kain (2004) cumulus scheme.

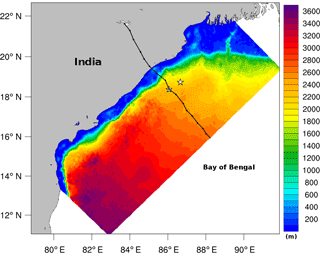
The terrain-following ocean model ROMS with 40 sigma levels in the vertical was used in this study. The ROMS model domain was used with zonal and meridional grid resolutions of 6 and 4 km, respectively. This high resolution in ROMS enables us to resolve mesoscale eddies in the ocean. The vertical stretching parameters, i.e., θ_s and θ_b were set to 7 and 2, respectively. The northern lateral boundary in ROMS was represented by the Indian subcontinent. The ROMS model observed open lateral boundaries in the west, east, and south in the present configuration. The initial and lateral open boundary conditions were derived from the Estimating the Circulation and Climate of the Ocean, Phase II (ECCO2) data (Menemenlis et al., 2005). The ocean bathymetry was provided by the 2 min gridded global relief (ETOPO2) data (National Geophysical Data Center, 2006). There was no relaxation provided for the model for any correction in the temperature, salinity, and current fields. The generic length scale (GLS) vertical mixing scheme parameterized as the K-ε model was used (Warner et al., 2005). Tidal boundary conditions were derived from the TPXO.7.2 (ftp://ftp.oce.orst.edu/dist/tides/Global) data, which include the phase and amplitude of the M2, S2, N2, K2, K1, O1, P1, MF, MM, M4, MS4, and MN4 tidal constituents along the east coast of India. The tidal input was interpolated from the TPXO.7.2 grid to the ROMS computational grid. The Shchepetkin boundary condition (Shchepetkin and McWilliams, 2005) for the barotropic current was used at open lateral boundaries of the domain, which allowed the free propagation of astronomical tide and wind-generated currents. The domains of the atmosphere and ocean models are shown in Fig. 2. ROMS and SWAN were configured over the common model domain shown with the shaded bathymetry data in Fig. 2. The two locations used for the time series analysis are marked with stars in Fig. 2. These two locations, one on-track and another off-track, were selected in the vicinity of the region of maximum surface cooling and wind stress during the passage of Phailin. The wave model SWAN was forced with the WRF-computed wind field. We used 24 frequency (0.04–1.0 Hz) and 36 directional bands in the SWAN model. The boundary conditions for SWAN were derived from the WaveWatch III model. In the COAWST system, the free-surface elevations (ELV) and current (CUR) simulated by the ocean model ROMS are provided for the wave model SWAN. The Kirby and Chen (1998) formulation was used for the computation of currents. The surface wind applied to the SWAN model (provided by WRF) was used in the Komen et al. (1984) closure model to transfer energy from the wind to the wave field. The baroclinic time step used in the ROMS model was 5 s. The SWAN and WRF models were used with time steps of 120 and 60 s, respectively. The coupled modeling system allows the exchange of prognostic variables among the atmosphere, ocean, and wave models at every 600 s. The SST simulation at high spatial and temporal resolutions enables accurate heat fluxes at the air–sea interface and the exchange of heat between the oceanic mixed layer and atmospheric boundary layer. The surface roughness parameter calculated in the WRF model is based on Taylor and Yelland (2001), which involved parameters from the wave model.

Figure 2 The COAWST model domain (65–105^∘ E, 1–34^∘ N) overlaid with ETOPO2 bathymetry (m). Locations used for time series analysis are marked with stars.

2.3 Methodology

The baroclinic current component was calculated by subtracting the barotropic component from the mean current with a resolution of 2 m in the vertical. The power spectrum analysis was performed on the zonal and meridional baroclinic currents along the depth section of the selected locations by using the periodogram method (Auger and Flandrin, 1995). The continuous wavelet transform using the Morlet wavelet method (Lilly and Olhede, 2012) was carried out to analyze the temporal variability in the baroclinic current at a particular level of 14 m. The near-inertial baroclinic velocities were filtered by the Butterworth second-order scheme for the cutoff frequency range of 0.028 to 0.038 cycle h⁻¹. The filtered zonal (u_f) and meridional (v_f) inertial baroclinic currents were used to calculate the inertial baroclinic kinetic energy (E_f) in m² s⁻² and inertial shear (S_f) following Zhang et al. (2014) and using Eq. (1).

$$\begin{array}{}\text{(1)}& S_{\mathrm{f}}^{\mathrm{2}}=({\displaystyle \frac{\partial u_{\mathrm{f}}}{\partial z}}{)}^{\mathrm{2}}+({\displaystyle \frac{\partial v_{\mathrm{f}}}{\partial z}}{)}^{\mathrm{2}}\end{array}$$

As the stratification is a measure of oceanic stability, the buoyancy frequency (N) was calculated using Eq. (2):

$$\begin{array}{}\text{(2)}& N^{\mathrm{2}}=-{\displaystyle \frac{g}{\mathit{\rho }}}{\displaystyle \frac{\partial \mathit{\rho }}{\partial z}},\end{array}$$

where ρ is the density of seawater and g is the acceleration due to gravity.

The analysis of the generation of the inertial oscillations and their dissipation was performed on the basis of turbulent dissipation rate (ϵ) and turbulent eddy diffusivity (k_ρ). These parameters were calculated by using the following formula (Mackinnon and Gregg, 2005; van der Lee and Umlauf, 2011; Palmer et al., 2008; Osborn, 1980):

$$\begin{array}{}\text{(3)}& {\displaystyle }& {\displaystyle }\mathit{\epsilon }={\mathit{\epsilon }}_{\mathrm{0}}\left({\displaystyle \frac{N}{N_{\mathrm{0}}}}\right)\left({\displaystyle \frac{S_{\mathrm{lf}}}{S_{\mathrm{0}}}}\right),\text{(4)}& {\displaystyle }& {\displaystyle }{k}_{\mathit{\rho }}=\mathrm{0.2}\times \left({\displaystyle \frac{\mathit{\epsilon }}{N^{\mathrm{2}}}}\right),\end{array}$$

where S_lf is the low shear background velocity and $N_{\mathrm{0}}=S_{\mathrm{0}}=\mathrm{3}$ cycle per hour and ${\mathit{\epsilon }}_{\mathrm{0}}={\mathrm{10}}^{-\mathrm{8}}$ W kg⁻¹.

Figure 3 Tracks of Phailin simulated by the coupled model (black) and IMD reported (red). The 3-hourly positions of the center of Phailin are marked with solid circles, and the daily position at 00:00 h is labeled with the dates. Location of buoy BD09 is marked with a blue circle.

3 Results and discussion

3.1 Validation of coupled model simulations

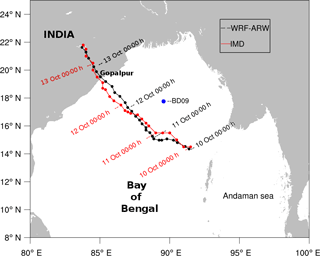
The WRF model-simulated track of Phailin was validated against the India Meteorological Department (IMD) reported best track of the cyclone. A comparison of the model-simulated track with the IMD track is shown in Fig. 3. Solid circles marked on both the tracks represent the 3-hourly positions of the cyclone's center, as identified by the minimum surface pressure. The daily positions of the center of Phailin are labeled with the date. The WRF model in the coupled configuration does a fairly good job of simulating the track, translational speed, and landfall location of Phailin. The positional track error was about 40 km when compared to the IMD track of Phailin. The stand-alone WRF model (not shown here) was found to simulate Phailin's track in an almost identical way to the WRF in the coupled configuration. However, the intensity (surface wind speed) in the WRF stand-alone model was higher compared to the coupled model. Figure 4 shows the comparison of stand-alone and coupled WRF model-simulated mean sea level pressure (MSLP), wind speed, and wind direction at a buoy (BD09) location (marked with a blue circle in Fig. 3). It can be inferred from the figure that stand-alone WRF simulated a larger pressure drop and higher wind speed compared to buoy measurements. In addition to the cyclone-induced pressure drop during 10–12 October, the semidiurnal variations in MSLP were observed in the buoy measurements. These semidiurnal variations in MSLP, primarily due to the radiational forcing (Pugh, 1987), were not captured by the model over the cyclone-influenced region. The WRF in coupled model configuration shows better performance in simulating the surface wind speed and pressure during Phailin. The exchange of wave parameters with the WRF model in the coupled configuration provides realistic sea surface roughness that resulted in the improvement of surface wind speed.

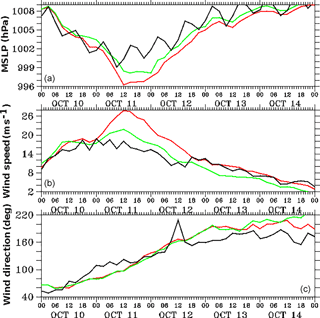
Figure 4 Comparison of coupled model (green), stand-alone WRF model (red), and observations from a buoy BD09 (black) for the (a) mean sea level pressure (hPa), (b) wind speed (m s⁻¹), and (c) wind direction (degree).

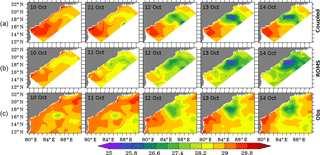
Figure 5 The daily averaged sea surface temperature (SST) in ^∘C simulated by the coupled model (a) and stand-alone ROMS model (b) and observed from AVHRR sensor on the satellite (c).

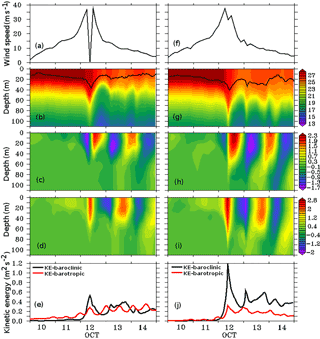
Figure 6 Coupled model-simulated and diagnosed variables at the on-track (left panel) and off-track (right panel) locations. (a, f) Surface wind speed (m s⁻¹); (b, g) temperature profile (^∘C) and mixed layer depth (black line); (c, h) u-component of current (m s⁻¹); (d, i) v-component of current (m s⁻¹); (e, j) kinetic energy of the baroclinic (m² s⁻²) and barotropic (× 10⁻² m² s⁻²) current.

The SST simulated by the ROMS model in coupled and stand-alone configurations was validated against the Advanced Very High Resolution Radiometer (AVHRR) satellite data on each day for the period of Phailin's passage over the BoB. The stand-alone WRF-simulated parameters were used to provide surface boundary conditions in the stand-alone ROMS model. Figure 5 shows that the coupled model captures the SST spatial pattern reasonably well with about −0.5 ^∘C bias in northwestern BoB on 13–14 October. This order of bias in SST could result from the errors in initial and boundary conditions provided for the model. The maximum cooling of the sea surface was observed on 13 October in the northwestern BoB in both the coupled model and observations. This post-cyclone cooling is primarily associated with the cyclone-induced upwelling resulting from the surface divergence driven by the Ekman transport. Thus, the coupled model reproduces dynamical processes and vertical velocities reasonably well. The stand-alone ROMS model overestimates the cyclone-induced cooling with a −2.2 ^∘C bias in SST on 13–14 October (Fig. 5). The stronger surface winds in the stand-alone WRF cause the larger cold bias in the stand-alone ROMS model.

3.2 Cyclone-induced mixing

The coupled atmosphere–ocean–wave simulation is an ideal tool to understand the air–sea exchange of fluxes and their effects on the oceanic water column. Surface wind sets up currents on the surface as well as initiating mixing in the interior of the upper ocean. In order to examine the strength of mixing due to Phailin, the model-simulated vertical temperature profile together with the surface wind speed, zonal and meridional components of the current, and kinetic energy at the on-track and off-track locations are plotted in Fig. 6. Comparatively stronger zonal and meridional currents were observed at the off-track location than the on-track location on 12 October. The larger kinetic energy available at the off-track location leads to greater mixing, resulting in a deeper mixed layer on 12 October compared to the on-track location. The surface wind speed at the on-track location shows typical temporal variation in a passing cyclone. The wind speed peaks, drops, and attains a second peak as the cyclone approaches, crosses over, and departs the location. The surface currents forced by these large variations in wind speed and direction at the on-track location result in a comparatively weaker magnitude than the off-track location.

The thermocline, defined as the depth of maximum temperature gradient, is usually given with reference to the location-dependent isotherm depth (Kessler, 1990; Wang et al., 2000). Over the BoB region, the depth of the 23 ^∘C isotherm (D23) was found to be an appropriate representative depth of the thermocline (Girishkumar et al., 2013). Based on the density criteria, we calculated the oceanic mixed layer depth (MLD) as the depth where density increased by 0.125 kg m⁻³ from its surface value. The inertial mixing introduced by the cyclone plays a central role in the deepening of D23 and MLD on 12 October 2013. The warmer near-surface waters mixed downward when the cyclone crossed over this location. After the passage of cyclone, shoaling of D23 and MLD has observed as a consequence of cyclone-induced upwelling that entrained colder waters from the thermocline into the mixed layer. The temperature of the upper surface water (25–30 m) decreased by 3.5 ^∘C from its maximum value of 28 ^∘C after the landfall of the cyclone on 12–13 October at the off-track location (Fig. 6g). In response to the strong cyclonic winds, the D23 deepening by 40 m (from 50 to 90 m) was observed during 04:00–12:00 GMT on 12 October. At the same time, the MLD, denoted by a thick black line in Fig. 6g, deepens by about 15 m. On the other hand, the on-track location showed cooling at the surface only for a short time on 13 October, and the deepening of D23 and MLD were 20 and 10 m, respectively. To examine the role of cyclone-induced mixing in modulating the thermohaline structure of the upper ocean, we carried out further analysis on the coupled model simulations as discussed in the following sections.

3.2.1 Kinetic energy distribution

During the initial phase of Phailin, the zonal and meridional currents were primarily westward and southward, respectively (Fig. 6c, d, h, and i). However, on and after 12 October when the cyclone attained peak intensity and crossed over the location, alternative temporal sequences running westward/eastward in the zonal current and southward/northward in the meridional current were noticed in current profiles (Fig. 6). The frequency of these reversals in zonal and meridional currents is recognized as a near-inertial frequency generated from the storm at these locations. The direction and magnitude of currents represent a variability that corresponds to the presence of near-inertial oscillations at the selected locations. The kinetic energy (KE) of currents at various depths is a proxy of energy available in the water column that becomes conducive to turbulent and inertial mixing. Time series of KE associated with the barotropic and depth-averaged baroclinic components of the current at the two point locations are illustrated in Fig. 6e (on-track) and 6j (off-track). The KE associated with the baroclinic component was found to be much higher than the barotropic component of current at both on-track and off-track locations. The depth-averaged baroclinic and barotropic current components' KE also depict the impinging oscillatory behavior. The peak magnitude of KE in baroclinic and barotropic currents at the off-track location was found to be 1.2 m² s⁻² and 0.3×10⁻² m² s⁻², respectively, on 12 October at 08:00 GMT, whereas the magnitude of KE in baroclinic and barotropic currents at the on-track location was smaller than the off-track location during the peak intensity of the cyclone. The peak magnitude of kinetic energy in the baroclinic current at the off-track location was more than double that of on-track location. The comparatively smaller magnitude of KE at the on-track location could be associated with the rapid variations in wind speed and direction leading to the complex interaction between subsurface currents in the central region of the cyclone. It is worth noting that the time of peak KE in baroclinic currents coincides with the deepening of MLD and D23. Therefore, the KE generated in NIO is responsible for subsurface mixing that acts to deepen the mixed layer. The analysis suggests that energy available for the mixing process in the water column was mostly confined to the baroclinic currents at various depths.

3.2.2 Primary frequency and depth of mixing

The power spectrum analysis was performed on the time series profiles at the two selected locations to get a distribution of all frequencies operating in the mixing process during the passage of Phailin. The power spectrum analysis was performed on the zonal and meridional components of the baroclinic current profile and shown in Fig. 7. It is clear from the figure that the tidal (M2, the semidiurnal component of tide) and near-inertial oscillations (f) are the two dominant frequencies on the surface during cyclone Phailin. Under the influence of cyclonic winds, the NIO signal was stronger (0.84 m² s⁻²) at the off-track than the on-track location. The depth penetration of NIO was up to 50 and 35 m at the off-track and on-track location, respectively. The tidal frequency (M2) and inertial frequency (f) bands shown in Fig. 7 implies that the inertial oscillations were dominant over the tidal constituent in zonal and meridional baroclinic currents. At the off-track location, the largest power of the NIO was noticed at 14 m depth, but the tidal oscillations were almost absent in the vertical section of baroclinic current (Fig. 7). This finding motivated us to analyze the significance and distribution of this subsurface variability that resulted in an anomalous deepening of MLD. The highest power of this signal at the off-track location was associated within 0–15 m, with a magnitude of 0.84 m² s⁻¹ in the zonal baroclinic current, and within 0–38 m, with a magnitude of 0.76 m² s⁻¹ in the meridional baroclinic current. These signals, however, weakened with increasing depth and almost disappeared around 120 m depth. Compared to any other process, these NIOs were the strongest signals at the 14 m depth in the presence of local wind stress that dominated the mixing. Other processes include the background flows, the presence of eddies, variations in sea surface height, and nonlinear wave–wave and wave–current interactions (Guan et al., 2014; Park and Watts, 2005).

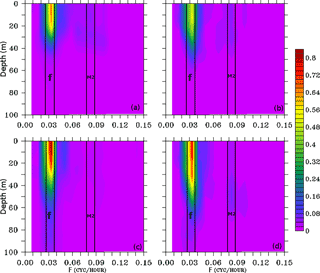
Figure 7 The power spectrum analysis (m² s⁻¹) performed on the simulation period at the on-track (upper panel) and off-track (lower panel) locations for (a, c) the baroclinic zonal current and (b, d) the baroclinic meridional current.

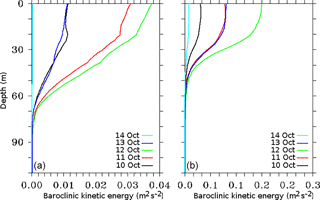
The second-order Butterworth filter was applied to the baroclinic current components to get the strength of NIO in the frequency range of 0.028 to 0.038 cycles h⁻¹ at the selected locations. The filtered baroclinic current was further utilized to calculate the filtered inertial baroclinic KE (E_f in m² s⁻²). The daily profiles of baroclinic KE were analyzed at the two selected locations and shown in Fig. 8. The peak baroclinic KE differs from 0.14 m² s⁻² at the on-track to 0.23 m² s⁻² at the off-track location on 12 October. As shown in Figs. 6 and 7, the filtered baroclinic KE profiles (Fig. 8) confirm the dominant presence of NIO at the off-track location compared to the on-track location. The decay of NIO with the increasing depth was noticed at both the locations. However, the NIO baroclinic KE penetrated up to 80 m in the case of an off-track location as compared to only 50 m at the on-track location. The analysis, therefore, suggests that the NIOs generated during Phailin were more energetic at the selected off-track location, which was also the location of maximum surface cooling as noted in Fig. 5. Therefore, the further analysis in the subsequent sections is limited to the off-track location only. To analyze the time distribution of the strong NIO, wavelet transform analysis was applied to the zonal and meridional baroclinic currents at 14 m depth. The scalogram, shown in Fig. 9, depicts the generation of NIO signal at the off-track location on 12 October that subsequently strengthened and attained its peak value in the middle of the day on 13 October. The energy percentage of the meridional component was always lower than the zonal component. The peak values of energy percentage were found in the time periods between 1 and 1.3 days.

Figure 8 Daily averaged baroclinic kinetic energy (m² s⁻²) profile at the on-track (a) and off-track (b) locations as marked with stars in Fig. 2.

3.2.3 Role of the downward propagation of energy

To investigate the energy propagation from the surface to the interior layers of the upper ocean, we derived the rotary spectra (Gonella, 1972; Hayashi, 1979) of near-inertial wave numbers shown in Fig. 10. The daily averaged vertical wave-number rotary spectra provide a clear picture of wind energy distribution in the subsurface water. The anticyclonic spectrum (A_m) dominates the cyclonic spectra (C_m) for the entire duration of the cyclone. This feature indicates that the energy generated by these inertial oscillations propagates downward. The magnitude of these oscillations increased from the initial stage up to 12 October and remained at a high energy density for the rest of the cyclone period. This downward-directed energy initiated a process of mixing between the mixed layer and the thermocline. This energy helps to deepen the mixed layer against oceanic stratification by introducing a strong shear. The buoyancy of the stratified ocean was overcome to some extent by the shear generated, which assisted in the mixing process during the very severe cyclone. Alford and Gregg (2001) highlighted that in most of the cases, the energy of inertial oscillations potentially penetrates the mixed layer but suddenly drops as it touches the thermocline. The energy dissipation mechanism has been studied in a few other studies (Chant, 2001; Jacob and Shay, 2003). The two-layer model described by Burchard and Rippeth (2009) illustrated the process of the generation of sufficient shear to start mixing near the thermocline. Their simple model ignored the effect of the lateral density gradient, mixing, and advection. Burchard et al. (2009) mentioned four important parameters for shear generation, i.e., surface wind stress (P_SS²), bed stress (−D_bS²), interfacial stress (−D_IS²), and barotropic flow (P_mS²). Utilizing simulations from our coupled atmosphere–ocean–wave model, we calculated individual terms as suggested by Burchard et al. (2009), and we present them in Fig. 11. Surface wind stress was found to be the most dominating term in modulating the magnitude of bulk shear during the stormy event. The rest of the terms were relatively weaker and, therefore, contributed only marginally to the variability in the bulk shear.

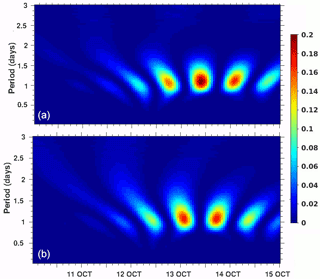
Figure 9 The scalogram by continuous wavelet transform (CWT) method in percentage at 14 m depth . Wavelet scalogram shown for the zonal baroclinic current (a) and for the meridional baroclinic current (b).

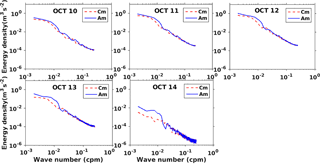
Figure 10 The daily averaged vertical wave-number rotary spectra of near-inertial oscillations. The anticyclonic and cyclonic spectra are represented by blue and dotted red lines, respectively.

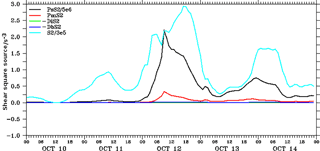
Figure 11 The model-simulated bulk properties at the selected point location. The vertical shear square axis is multiplied by a factor of 10⁻⁶. The magnitude of bulk shear squared S² (cyan color), surface wind stress P_sS² (black color), barotropic effect P_mS² (red color), bottom stress – D_bS² (blue color), and interfacial friction – D_iS² (green color) are shown for the duration of the cyclone.

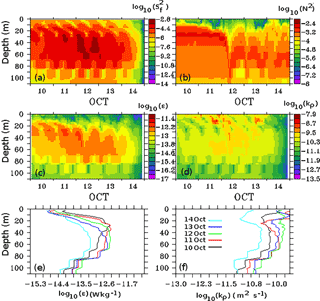
Figure 12 Profiles of (a) velocity shear log₁₀(S²), (b) buoyancy frequency log₁₀(N²), (c) turbulent kinetic energy dissipation rate log₁₀ (ε), and (d) turbulent eddy diffusivity log₁₀ (K_ρ); (e) and (f) are daily averaged turbulent kinetic energy dissipation rate and turbulent eddy diffusivity, respectively.

To examine the generation and dissipation of these inertial oscillations, the shear generated by the near-inertial baroclinic current ($S_{\mathrm{f}}^{\mathrm{2}})$ and turbulent kinetic energy dissipation rate (ε) was calculated and analyzed. The shear produced by inertial oscillations increased at 20–80 m depth, and a higher magnitude was associated with the peak wind speed of the cyclone (Fig. 12a). This shear overcame the stratification (Fig. 12b), represented by buoyancy frequency N², and played important role in the mixing and deepening of the thermocline and mixed layer on 12 October. The value of the kinetic energy dissipation rate (ε) increased from 4×10⁻¹⁴ to $\mathrm{2.5}\times {\mathrm{10}}^{-\mathrm{13}}$ W kg⁻¹ on approaching the thermocline (Fig. 12c). The increase in ε indicates the weakening of the shear generated by the inertial waves leading to the fast disappearance of these baroclinic instabilities from the region. The nonlinear interaction between the NIO and internal tides together with the prevailing background currents causes the rapid dissipation of kinetic energy in the thermocline. Guan et al. (2014) also reported an accelerated dampening of NIO associated with the wave–wave interactions between NIO and internal tides. The background currents were found to modify the propagation of NIO (Park and Watts, 2005). The magnitude of the turbulent eddy diffusivity (K_ρ), shown in Fig. 12d, implies that the greater mixing takes place within the mixed layer where K_ρ was high (6.3×10⁻¹¹ to 1.2×10⁻¹¹ m² s⁻¹). The daily averaged values of ε and K_ρ were 1.2×10⁻¹³ W kg⁻¹ and 1.5×10⁻¹⁰ m² s⁻¹, respectively, on 12 October, which were higher compared to the initial 2 days of the cyclonic event. Results from the present study, as well as conclusions from past studies, indicate that wave–current interaction, mesoscale processes, and wave–wave interaction can affect the process of downward mixing and cause the dissipation of inertial oscillations.

4 Conclusions

Processes controlling the subsurface mixing were evaluated under the high wind speed regime of the severe cyclonic storm Phailin over the BoB. A coupled atmosphere–ocean–wave (WRF+ROMS+SWAN) model as part of the COAWST modeling system was used to simulate atmospheric and oceanic conditions during the passage of the Phailin cyclone. A detailed analysis of model-simulated data revealed interesting features of generation, propagation, and dissipation of kinetic energy in the upper-oceanic water column. The deepening of the MLD and thermocline by 15 and 40 m, respectively, was explained through the strong shear generated by the inertial oscillations that helped to overcome the stratification and initiate mixing at the base of the mixed layer. However, there was a rapid dissipation of the shear with increasing depth below the thermocline. The peak magnitude of kinetic energy in baroclinic and barotropic currents was found to be 1.2 and 0.3×10⁻² m² s⁻², respectively. The power spectrum analysis suggested a dominant frequency operative in subsurface mixing that was associated with near-inertial oscillations. The peak strength of 0.84 m² s⁻¹ in the zonal baroclinic current was found at 14 m depth at a location in the northwestern BoB. The baroclinic kinetic energy remained higher (> 0.03 m² s⁻²) during 11–12 October and decreased rapidly after that. The wave-number rotary spectra identified the downward propagation, from the surface up to the thermocline, of energy generated by inertial oscillations. A quantitative analysis of shear generated by the near-inertial baroclinic current showed higher shear generation at 20–80 m depth during peak surface winds. Analysis highlights that greater mixing within the mixed layer takes place where the eddy kinetic diffusivity is high (> 6×10⁻¹¹ m² s⁻¹). The turbulent kinetic energy dissipation rate increased from 4 × 10⁻¹⁴ to 2.5 × 10⁻¹³ W kg⁻¹ on approaching the thermocline, which dampened the mixing process further down into the thermocline layer. The wave–current interaction, mesoscale processes, and wave–wave interaction increased the dissipation rate of shear and, thereby, limited the downward mixing up to the thermocline. The coupled model was found to be a useful tool to investigate air–sea interaction, kinetic energy propagation, and mixing in the upper ocean. The results from this study highlight the importance of atmosphere–ocean coupling for a better understanding of the oceanic response under strong wind conditions. The proper representation of kinetic energy propagation and oceanic mixing have applications in improving the intensity prediction of a cyclone, storm surge forecasting, and biological productivity.