Joint analysis of coastal altimetry and high-frequency (HF) radar data: observability of seasonal and mesoscale ocean dynamics in the Bay of Biscay

Land-based coastal high-frequency (HF) radar systems provide operational measurements of coastal surface currents (within 1–3 m depth) with high spatial (300 m–10 km) and temporal (≤1 h) sampling resolutions, while the near-continuous altimetry missions provide information, from 1993 until today, on geostrophic currents in the global ocean with typical along-track and temporal sampling resolutions of >7 km and >9 days, respectively. During the last years, the altimetry community has made a step forward in improving these data in the coastal area, where the data present lower quality than in the open ocean. The combination of HF radar and altimetry measurements arises as a promising strategy to improve the continuous monitoring of the coastal area (e.g. by expanding the measurements made by HF radars to adjacent areas covered by the altimetry or by validating/confirming improvements brought by specific coastal algorithms or new altimeter missions). A first step towards this combination is the comparison of both data sets in overlapping areas.

In this study, a HF radar system and two Jason-2 satellite altimetry products with different processing are compared over the period from 1 January 2009 to 24 July 2015. The results provide an evaluation of the performance of different coastal altimetry data sets within the study area and a better understanding of the ocean variability contained in the HF radar and altimetry data sets. Both observing systems detect the main mesoscale processes within the study area (the Iberian Poleward Current and mesoscale eddies), and the highest correlations between radar and altimetry (up to 0.64) occur in the slope where the Iberian Poleward Current represents a significant part of the variability in the circulation. Besides, the use of an Ekman model, to add the wind-induced current component to the altimetry-derived geostrophic currents, increases the agreement between both data sets (increasing the correlation by around 10 %).

1 Introduction

Ocean dynamics result from a combination of processes of different timescales and space scales. However, and mainly due to technical limitations, this complexity cannot be captured by the existing observational systems if each observing technique is analysed individually, since they are designed for resolving certain scales. Nowadays, there is a growing tendency to combine different observing systems for a more complete description and understanding of the ocean dynamics. Current observatories are designed to monitor, in an operational way, the ocean environment to support the human activities concentrated in the coast (Liu et al., 2015). In recent years, great effort has been focused on the development and improvement of these platforms. In the framework of European projects such as JERICO (2007–2013) and JERICO-NEXT (2014–ongoing, http://www.jerico-ri.eu, last access: 1 October 2018) progress has been made, on the one hand, regarding the improvement and creation of coastal observatory networks and, on the other hand, regarding the applications of these observatories for addressing European marine policies. As an example, the latter project aims to integrate emerging methodologies and technologies to proceed towards the automated monitoring at a high temporal and spatial resolution of wider areas in order to provide the best possible data and products necessary for the implementation of the European Marine Strategy Framework Directive. For this purpose, there is ongoing research on assessing the interconnection among physics, biogeochemistry, and biology at different spatial and temporal scales. In addition to the development of coastal observatories, there are global initiatives, such as the GLOBCURRENT project (2014–2017; http://www.globcurrent.org/, last access: 1 October 2018), aimed at advancing in the evaluation of the synergy of satellite sensors and in situ data for the quantitative estimation of ocean surface currents (e.g. Rio et al., 2014).

Among the different methodologies to retrieve surface currents, two are particularly interesting due to their high potential complementarity: satellite altimetry and land-based high-frequency (HF) radar (HFR) systems. The former technique consists in a constellation of altimeters onboard satellites measuring the global sea level, with a revisit period greater than a week and a track distance around tens of kilometres. These continuous sea level series are today close to completing 25 years of data, resolving the ocean dynamics from mesoscale to near-climate scale. HFRs are designed to measure the local ocean surface dynamics with a high time and space resolution. However, altimetry and HFR do not capture exactly the same dynamics. Altimetry detects surface currents that are in geostrophic equilibrium (by excluding the direct response of the surface layer to the wind and then part of the high-frequency variations), whereas HFRs measure surface total currents, i.e. the geostrophic and ageostrophic components (like wind-driven and inertial currents or the wave-induced Stokes drift; e.g. Graber et al., 1997; Law, 2001; Ardhuin et al., 2009).

Besides the effort made for collecting data from different platforms, methods for combining these data are under development. Recent studies focused on the evaluation of the performance of altimetry using HFRs, concluding that HFRs offer a way to improve the validation of altimetry products for coastal areas (Chavanne and Klein, 2010; Liu et al., 2012; Pascual et al., 2015; Troupin et al., 2015; Roesler et al., 2013). One of the most extended approaches found in the literature to study the synergy between altimetry and HFR data consists in the comparison of the total across-track currents in the along-track direction (e.g. Morrow et al., 2017; Troupin et al., 2015; Pascual et al., 2015). The combination of HFR and altimetry could help to potentiate their strengths by, for example, expanding the spatial and temporal coverage of the HFR systems or evaluating and correcting the altimetric signal near the coast.

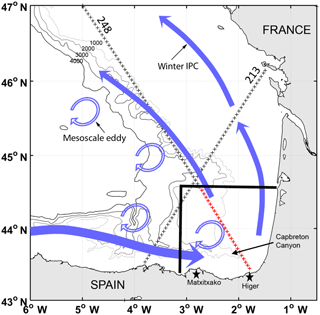
Figure 1 Study area, observational systems and main characteristics of the ocean circulation (figure modified from Rubio et al., 2018). The winter IPC is represented by blue solid arrows, whereas the blue hollow arrows show the mesoscale eddy regime (although only anticyclonic arrows are represented, eddies of anticyclonic and cyclonic polarity are observed in different locations along the slope). The bold black lines delimit the HFR total-current footprint. The black stars represent the HFR stations: Matxitxako (left) and Higer (right). Jason-2 tracks 213 and 248 are represented by black crosses and the part of the track used in this study is marked in red. Grey lines: 1000, 3000, and 4000 m isobaths.

In this study, we focus on the south-eastern Bay of Biscay (SE-BoB), which is characterized by the presence of canyons (e.g. Capbreton canyon), by an abrupt change in the orientation of the coast, and by a narrow shelf and slope. The winter surface circulation in the SE-BoB is mainly related to the Iberian Poleward Current (IPC), which affects the upper 300 m of the water column. In winter, the IPC flows over the slope, advecting warm surface waters (Le Cann and Serpette, 2009; Charria et al., 2013) eastwards along the Spanish coast and northwards along the French coast (Fig. 1). In summer, the flow is reversed, being 3 times weaker than in winter (Solabarrieta et al., 2014). Overlaid to the density-driven slope circulation, wind-induced currents are the main drivers of the surface circulation in the area (e.g. Lazure, 1997; Solabarrieta et al., 2015). During autumn and winter, south-westerly winds dominate and generate northward and eastward drift over the shelf. The wind regime changes to the NE during spring, when it causes sea currents to turn toward the W–SW along the Spanish coast. The summer situation is similar to that of spring, but the weakness of the winds and the greater variability in the direction of the general drift make currents more variable (González et al., 2004; Lazure, 1997; Solabarrieta et al., 2015). In addition to these processes, mesoscale eddies in the SE-BoB are generated, mainly during winter, by the interaction of the IPC with the abrupt bathymetry (Pingree and Le Cann, 1992) (Fig. 1). The combination of these processes makes the SE-BoB an area of interesting complexity.

The existence of a long historical time series of surface current fields from a long-range HFR system in the area provides an invaluable opportunity to explore the benefit of a combined analysis of satellite and land-based remote-sensing ocean currents. This HFR network (two sites; see Fig. 1) is part of the coastal observatory of the SE-BoB, also composed of a network of oceano-meteorological coastal stations and two slope buoys. The performance of this system and its potential for the study of ocean processes and of transport patterns in the area have already been demonstrated by previous work (e.g. Solabarrieta et al., 2015; Rubio et al., 2018). With regard to the usefulness of altimetry for describing ocean dynamics in the BoB, several studies have proven its suitability to study processes that go from mesoscale (Dussurget et al., 2011; Herbert et al., 2011; Caballero et al., 2008b, 2014, 2016) to climate scale (e.g. Pingree, 2005).

The main objectives of this study are first to obtain a diagnosis of the agreement of the surface currents measured by altimetry and HFR over the SE-BoB and, second, to evaluate the observability of certain mesoscale processes by both measuring systems.

2 Data and methods

2.1 Data

2.1.1 HFR data

HFRs are remote-sensing instruments that send radio waves to the ocean surface and use the signal backscattered by the waves to infer the radial velocity of the surface current (toward or away from each HFR antenna). They can measure surface currents over wide areas with high spatial (300 m–10 km) and temporal (≤1 h) resolution. In this study, surface currents were obtained by means of two long-range HFR antennae. These antennae emit at a central frequency of 4.5 MHz and with an operational 30 kHz bandwidth. They are located at Matxitxako and Higer capes (Fig. 1) and have provided operational data since 2009 (with some interruptions mostly due to maintenance stops or malfunctioning related to severe atmospheric conditions). The averaged Doppler backscatter spectrum obtained from the received signal (in a 3 h window) is processed to obtain hourly radial currents using the MUSIC algorithm (Schmidt, 1986). The coverage of radial data is up to 150 km, and the range cell and angular resolution are set to 5 km and 5^∘, respectively. Radial data are quality controlled using advanced procedures based on velocity and variance thresholds, signal-to-noise ratios, and radial total coverage. Since the deployment of the HFR system, the receiving antenna pattern of the two HFR sites has been calibrated at least every 2 years. A more detailed description of the system and of the HFR data validation exercises are provided by Solabarrieta et al. (2014, 2015, 2016) and Rubio et al. (2011, 2018).

To obtain total currents gridded onto a 5 km resolution regular orthogonal mesh, a least mean square algorithm (spatial interpolation radius of 10 km) was applied by using the HFR_Progs Matlab package (https://cencalarchive.org/~cocmpmb/COCMP-wiki/index.php/Main_Page#HFR_Progs_Documentation, last access: 1 October 2018), based on Gurgel (1994) and Lipa and Barrick (1983). Then, using the same grid, radial velocities were processed with HFR_Progs to generate spatially gap-filled open-mode analysis (OMA) total currents (Kaplan and Lekien, 2007). In order to generate hourly total fields, 85 OMA modes, built setting a minimum spatial scale of 20 km, were used. A first analysis of the comparisons between HFR and altimetry showed that the results obtained using total currents generated by least mean squares and OMA were very similar. Thus, only results using OMA currents are presented in this work.

The typical spatial scales resolved by the HFRs depend on the resolution of the data and thus mainly on the operation frequency of the systems (Rubio et al., 2017). For the SE-BoB, the spatial scales resolved are typically of O(15–20) km.

2.1.2 Altimetry data

The basic principle of the altimetry technology is to send a radar signal to the sea surface and then to measure the reflected return echo. The time needed for the signal to go and come back determines the distance between the altimeter and the sea surface (called the range). A physically based model (Brown, 1977) is adjusted to the resulting signal, called waveform, providing different parameters, including range. To reduce the measurement noise, the result is averaged and the final data rate is classically (and in our case) 1 Hz (i.e. one datum every ∼ 7 km along the satellite track). By subtracting the range to the satellite orbit altitude (with respect to the reference ellipsoid) and by applying several corrections (e.g. tropospheric and ionospheric effects on the radar wave, sea surface bias), the sea surface height (SSH) is obtained (SSH = orbit – range – corrections). To retrieve the total geostrophic currents, in balance with the SSH gradients, the surface height must be referenced to the geoid; this height is called dynamic topography (DT). However, since geoids are not known with enough accuracy, only geostrophic anomaly currents can be accurately derived from sea level anomaly (SLA). The SLA is referenced to a temporal average (Le Traon et al., 2003) by subtracting a mean profile to the SSH (SLA = SSH – 〈SSH〉). For more information about the SLA and the reference surfaces, the reader is referred to https://www.aviso.altimetry.fr/en/techniques/altimetry/principle/basic-principle.html (last access: 1 October 2018).

The two different along-track SLA time series used herein come from Jason-2's 248 and 213 tracks from cycle 18 to 259 and with a revisit period of ∼10 days. Track 248 covers the HFR footprint area, whereas track 213 only crosses a small area at the NW of the HFR total-current coverage (Fig. 1); therefore, track 213 is only useful for the comparison with HFR radial data.

One of the altimetry data sets used in this study is the CTOH (Center for Topographic studies of the Ocean and Hydrosphere)-XTRACK product (http://ctoh.legos.obs-mip.fr/products/coastal-products/coastal-products-1/sla-1hz, last access: 1 October 2018), which provides SLA data specifically processed for coastal areas. The filtered version of the product was used, meaning that a 40 km cut-off spatial Loess filter (Cleveland and Devlin, 1988) was also applied in order to reduce the remaining noise in the along-track SLA. For the same Jason-2 altimeter measurements, a differently processed data set was also used to assess possible discrepancies between the two altimetric products. This product is a preliminary version of the 2018 update of the reprocessed global ocean along-track level-3 data provided by the Copernicus Marine Environment Monitoring Service (CMEMS). As for the CTOH-XTRACK product, data filtered with a 65 km cut-off spatial Lanczos filter (Pujol et al., 2016) were used. Note that, on the one hand, the accuracy of altimetry data is lower in the 20–30 km coastal band, so it might be a source of differences between altimetry and HFR data, and that, on the other hand, the larger the oceanic signal (larger signal-to-noise ratio), the lower this effect will be observed to be. In the SE-BoB, part of the slope (characteristically narrow) is located within the 20–30 km coastal band; therefore, the altimetry data will be affected by this inaccuracy in this area.

2.1.3 Wind data and sea surface temperature images

Hourly wind data from the Weather Research and Forecasting model (WRF; http://mandeo.meteogalicia.es/thredds/catalogos/WRF_2D/catalog.html, last access: 1 October 2018) were provided by the meteorological agency of Galicia (MeteoGalicia). This model, with a native resolution of 12 km, reproduces the offshore wind fields of the SE-BoB (Ferrer et al., 2010) with reasonable accuracy. In this study, the WRF gridded fields were interpolated to the Jason-2 along-track points. Due to the cloudy weather in the SE-BoB, the most appropriate infrared sea surface temperature (SST) images were selected one by one from the AVHRR (Advanced Very High Resolution Radiometer) sensor series of 1 km resolution to process level-2 SST maps.

2.2 Methods

Since the time resolution of the altimetry (∼10 days) is lower than that of the HFR (hourly), the HFR current data were filtered using a low-pass filter, based on a 10-day running average. The objective was to remove the high-frequency (HF) signals contained in the data (see, for instance, Solabarrieta et al., 2014) and part of the ageostrophic signals to make the HFR data closer to the measurements from altimetry. Several tests were carried out to determine the sensibility of the results to the temporal window chosen for the filter. For that purpose, 2-, 5-, 10- and 15-day low-pass filter configurations were tested, and the resulting currents were compared to those derived from the SLA. The 10-day filtered HFR currents provided the highest correlation with the altimetry data. It is worth noting that the 10-day running average filtered out a significant part of the wind-induced currents, except for the low-frequency (LF) Ekman component.

Since from the altimetry data used here we can only obtain sea surface anomaly currents, as explained in Sect. 2.1.2, the comparisons with the radar data were carried out in terms of anomaly. In order to obtain the HFR anomaly currents (AC_HFR), the temporal average of the HFR currents for the study period was subtracted to the series of low-pass HFR currents (Eq. 1). Then, to obtain SLA relative to the same period, the average SLA for the study period was subtracted to the SLA series (Eq. 2).

$$\begin{array}{}\text{(1)}& {\displaystyle }& {\displaystyle }{\mathrm{AC}}_{\mathrm{HFR}}=V-\langle V{\rangle }_{t_{\mathrm{1}}-t_{\mathrm{2}}}\text{(2)}& {\displaystyle }& {\displaystyle }{\mathrm{SLA}}^{\prime }=\mathrm{SLA}-\langle \mathrm{SLA}{\rangle }_{t_{\mathrm{1}}-t_{\mathrm{2}}}\end{array}$$

Hence, the time referenced SLA^′ and AC_HFR were obtained as suggested in Pujol et al. (2016), where t₁=1 January 2009 and t₂=24 July 2015. Hereafter, when referring to AC_HFR computed using Eq. (1), we will use AC_HFR,R to refer to current anomalies computed directly from the radial HFR components and AC_HFR,T to refer to current anomalies computed from total OMA HFR currents.

For the altimetry velocity, across-track geostrophic anomaly currents (AC_G) were inferred by means of the finite-difference geostrophic velocity equation (Eq. 3):

$$\begin{array}{}\text{(3)}& {\displaystyle }{\displaystyle }{\mathrm{AC}}_{\mathrm{G}}=-{\displaystyle \frac{g}{f}}{\displaystyle \frac{\mathrm{\Delta }{\mathrm{SLA}}^{\prime }}{\mathrm{\Delta }x}},\end{array}$$

where g is the acceleration of gravity, f is the Coriolis parameter, x is the along-track distance, and SLA^′ is the time referenced SLA. AC_G was estimated along the altimeter track by a three-point central difference operator.

For the statistical comparison between AC_G and AC_HFR, two different strategies were used. The first and simplest approach is the comparison of HFR radial across-track currents with altimetry across-track currents at two given points (Sect. 2.2.1), which permits the direct use of radial HFR currents, that is, AC_HFR,R. The second approach is the along-track comparison (Sect. 2.2.2) of total OMA HFR and altimetry across-track currents, which provides additional information on the spatial variability of the agreement between both data sets. Finally, in order to take into account the LF Ekman component that remains in the low-pass-filtered HFR data, a model for the computation of this component was used (Sect. 2.2.3).

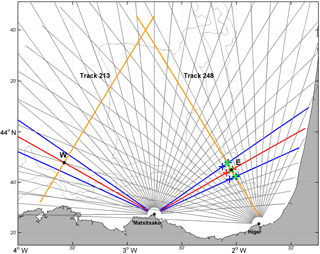
Figure 2 Schematic view of the pointwise comparison and of the data used for this approximation. Jason-2's 213 and 248 tracks are depicted by orange lines. The HFR radial directions from both sites are represented by grey lines and the selected radial directions (from the Matxitxako site) for the pointwise comparison are plotted in red (the central radial orthogonal to the track) and in blue (the adjacent radials). Points E and W are those along both tracks, where each of the HFR radial directions are orthogonal to the Jason-2's track directions. At point E, the blue and red crosses show the selected points of HFR radial directions where radial currents are averaged in a first step to obtain the corresponding values on the track (green crosses). Then, the along-track green crosses are averaged to obtain the corresponding HFR current values at the point at issue (the same process is carried out for point W, but it is not represented in the figure). Grey lines: 200, 1000, and 2000 m isobaths.

2.2.1 Pointwise comparison

This method, previously applied in Liu et al. (2012), consists in a direct comparison between HFR and altimetry data at a certain point, where one of the HFR radial directions (red lines in Fig. 2) crosses the altimeter track perpendicularly. This approximation allows us to directly use the radar radial currents, which are in the same direction as the across-track AC_G. This method was applied for Jason-2 altimeter tracks 213 and 248 shown in Fig. 1, by using the corresponding AC_HFR,R measured by the Matxitxako antenna at two points: point E on track 248 and point W on track 213 (Fig. 2). Note that the radials from Higer station were not used, since they did not provide any orthogonal radial direction for track 248 and were too gappy for track 213 due to the large distance between this track and the antenna. Point E is located near the Capbreton canyon at 43.75^∘ N, 2.05^∘ W, 46.86 km from the coast and at a depth of 500 m (on the slope), whereas point W is located at 43.80^∘ N, 3.58^∘ W, 40.73 km from the coast and at a depth of 3000 m (on the abyssal plain). It is worth noting that by using directly radial currents, additional errors that propagate in the combination of HFR radials into HFR OMA currents are avoided.

In order to make the computations more robust to the potential absence of HFR or altimetry data at points W and E, nearby points were considered to obtain the across-track currents (Fig. 2). With regard to AC_HFR,R, radial directions of ±5^∘, away from the orthogonal radial direction were also considered. For each of them, the points in a range of ±5 km from the track along the central and adjacent radials were selected. Then, the across-track AC_HFR,R in our point was obtained by firstly averaging the values for each radial, so that only three values along the track were obtained. Finally, the three values were again averaged to get the corresponding across-track AC_HFR,R.

On the other hand, the AC_G in the three along-track points considered for the HFR case were averaged to obtain the AC_G in the central point (E and W). This permitted us to ensure a similar spatial smoothing for both data sets. It must be mentioned that at point W and for the CTOH altimetry product, the points were located between the along-track HFR points, so instead of considering three along-track points, two points on each side of the central point (W) were selected.

2.2.2 Along-track current comparison

In order to assess the variability in the comparison between HFR and altimetry from the coast to the open ocean, the comparison between the across-track AC_HFR,T and AC_G along track 248 was performed. For that purpose, AC_HFR,T was interpolated into the along-track altimetry points, and it was rotated to the across-track direction. Then, for each along-track AC_G point, the average with its four adjacent points was calculated. As in the previous case, this permitted us to ensure a similar spatial smoothing for both data sets. The sensitivity to the number of adjacent points considered was tested, and this approach was the one that provided the best adjustment to the HFR data.

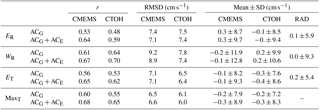
Table 1 Statistics of different points for the study period. r is the correlation parameter, and RMSD is the root mean square difference of the velocity anomalies between HFR and altimetry for different altimetry products (i.e. CMEMS and CTOH). The mean and the standard deviation (SD) are also estimated for each data set. E and W are the points where HFR radial velocities are orthogonal to tracks 248 and 213, respectively (see Fig. 1). E_T means that the parameters are estimated at point E but using the HFR current velocity anomaly fields rotated to across-track direction instead of using the HFR radial velocity anomalies. That HFR data have also been used for Max_T, which is the track point where the correlation r is maximal (point 2.10^∘ W, 43.82^∘ N for CTOH and point 2.09^∘ W, 43.80^∘ N for CMEMS). RAD refers to HFR data, which really means radial anomaly current for E_R and W_R and across-track rotated OMA anomaly currents for E_T and Max_T. There is no data in Max_T because they are different for each altimetry product.

2.2.3 Ekman currents

Ekman currents were estimated to evaluate what their contribution to LF currents in the area was, and how this component contributed to part of the differences observed between HFR and altimetry. Three different ways of calculating Ekman currents were tested to infer which one provided the best results in the comparisons: the rule of thumb that states that the surface currents are 3 % of the wind velocity; Ekman equations for the surface (Ekman, 1905); and the model M1 proposed in Rio and Hernandez (2003). Ultimately, the M1 model offered the best results:

$$\begin{array}{}\text{(4)}& {\displaystyle }{\displaystyle }{\mathit{u}}_{\mathrm{ek}}={\displaystyle \frac{b\mathit{\tau }}{\sqrt{f}}}{e}^{i\mathit{\theta }},\end{array}$$

where f is the Coriolis parameter, u_ek is the Ekman current vector (meridional and zonal components), b is the amplitude parameter, θ is the phase parameter, and τ is the wind stress vector (meridional and zonal components) that was obtained by means of the bulk–flux formula (Stewart, 2009):

$$\begin{array}{}\text{(5)}& {\displaystyle }{\displaystyle }\mathit{\tau }={\mathit{\rho }}_{\mathrm{air}}{C}_{\mathrm{d}}\left|\mathit{w}\right|\mathit{w},\end{array}$$

where ρ_air is the density of the air (1.22 kg m⁻³), w is the wind vector, and C_d is the drag coefficient proposed by Large and Pond (1981). b and θ were acquired by adjusting the model (by a least square fit) to the real data in the study area. These parameter values were taken from Caballero et al. (2008a), where from the fit of wind stress measurements and drifter-derived currents of the Bay of Biscay to Eq. (4), the following results were obtained: $b=\mathrm{4.45}\times {\mathrm{10}}^{-\mathrm{3}}$ m² kg⁻¹ s^1∕2 and $\mathit{\theta }=-\mathrm{23.68}$^∘. Once the parameters were obtained, u_ek was estimated using the wind data series described in Sect. 2.1.3.

Ekman currents initially computed in the locations of the WRF model nodes were interpolated and rotated (from zonal and meridional directions to along-track and across-track directions). For the pointwise comparison, they were interpolated in E, in W, and at their adjacent points and rotated to obtain the across-track component. Then, they were averaged to obtain the across-track Ekman current velocity at each point (E and W). In the along-track current comparison, they were interpolated to the altimetry along-track points and, then, rotated to get the across-track component. Ekman currents were also 10-day running averaged to remove the HF Ekman signal. For the comparisons with AC_HFR, Ekman anomaly currents (AC_E) were obtained by subtracting the average value of the study period like in Eqs. (1) and (2). Then, they were added to AC_G, and this is indicated as AC_G + AC_E in Table 1.

The results of all the comparisons described above are presented in terms of the correlation coefficient or correlation (r) (with a confidence level of 100 % and 90 % for the pointwise comparison and the along-track current comparison, respectively) and the root mean square difference (RMSD) between the across-track currents measured by each system. In addition, the mean and the standard deviation (SD) of such currents were also analysed. All these parameters were computed for the study period. Since the HFR radials are used at the pointwise comparison, the crossing points are called E_R and W_R. In the along-track comparison, the point E is precisely one of those along-track points. Therefore, considering that the rotated AC_HFR,T are used in this comparison, the point is named E_T. The points along the track where r is maximal (point 2.10^∘ W, 43.82^∘ N for CTOH and point 2.09^∘ W, 43.80^∘ N for CMEMS) are also called Max_T. All these points and their statistics are displayed in Table 1, as well as in Figs. 3–5, and they are also discussed in the next section. Moreover, in Fig. 5, apart from the results of E_T and Max_T, the results for all of track 248 are also shown.

Note that the HFR–altimetry comparisons were carried out for the CMEMS and CTOH data sets and that each comparison was also made with and without adding AC_E.

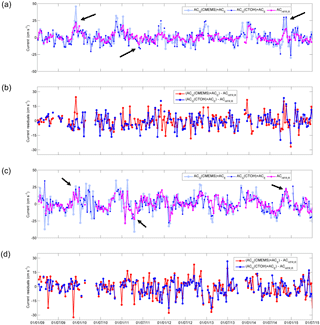
Figure 3 Across-track AC_G + AC_E and AC_HFR,R. (a) CTOH, CMEMS, and HFR data sets at point E_R. (b) CTOH-HFR and CMEMS-HFR residuals at point E_R. (c) CTOH, CMEMS, and HFR data sets at point W_R. (d) CTOH-HFR and CMEMS-HFR residuals at point W_R. Black arrows depict the slope current intensifications mentioned in the text.

3 Results and discussion

3.1 Statistical results

Table 1 provides an overview of the statistical results of the HFR and altimetry data set comparison at points E_R and W_R for the pointwise method and at points E_T and Max_T for the along-track method. Despite the differences between the two measuring systems, the comparison between AC_HFR and AC_G (AC_HFR and AC_G + AC_E) shows maximum correlations of 0.64 (0.70). Concerning the pointwise comparisons between AC_G and AC_HFR,R it can be observed that r depends on the location as well as on the altimetry product considered. In any case, the addition of AC_E increases r by 6 %–11 % for both altimetry products: from 0.53 and 0.48 to 0.64 and 0.59 in E_R and from 0.61 and 0.64 to 0.67 and 0.70 in W_R for CMEMS and CTOH, respectively. The RMSD also decreases between 0.1 and 0.4 cm s⁻¹. Therefore, in general terms, the addition of AC_E decreases the differences between AC_HFR,R and AC_G. However, it adds variability: the SD for AC_G + AC_E increases by 0.7–1.0 cm s⁻¹. It should be pointed out that the SD of AC_HFR,R is lower than the SD of AC_G (where CMEMS's variability is higher than CTOH's), probably due to the filtering of HF signals applied to the radar or because the finite-difference operator that estimates the geostrophic velocity from SLA^′ increases the variability. The same effect was observed in Liu et al. (2012) and in Verron et al. (2018). Nevertheless, although the addition of AC_E increases the variability even more, it improves the results in terms of correlation and RMSD.

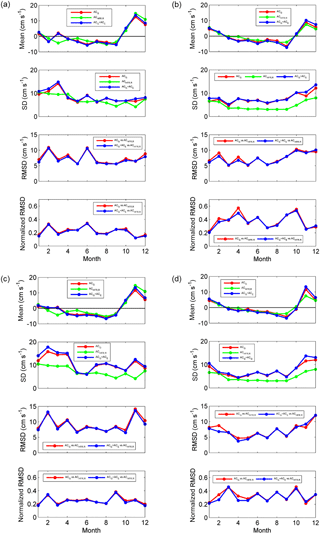
Figure 4 Monthly statistical parameters of the comparison between AC_G vs. AC_HFR,R and AC_G + AC_E vs. AC_HFR,R at points E_R and W_R for both altimetry products: (a) CTOH AC_G at point W_R, (b) CTOH AC_G at point E_R, (c) CMEMS AC_G at point W_R, and (d) CMEMS AC_G at point E_R. The normalized RMSD is the quotient between the RMSD and the values of the corresponding AC_HFR,R.

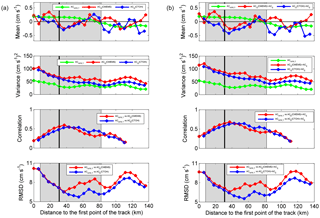
Figure 5 Mean and variance along track 248 of the different data sets – AC_HFR,T, AC_G (CTOH) and AC_G (CMEMS) – and correlation and RMSD between (a) AC_HFR,T and AC_G and (b) AC_HFR,T and AC_G + AC_E. The grey-coloured area corresponds to the slope between the 200 and 1000 m isobaths. The black line is the location of the point E, and the first point of the track is around 11 km away from the coast. Correlation values are not plotted for confidence levels under 90 % (i.e. at the points along the track with a distance from the first point beyond 120 km). Note that the first point is different for CTOH and CMEMS (which are around 10.5 and 13 km away from the coast, respectively) and that the spacing between the points is slightly different. Moreover, the first point in CTOH is removed because it is an outlier. The radar points are the same as CMEMS points.

Figure 3 displays the time series of AC_HFR,R and AC_G + AC_E at points E_R and W_R. In general, there is global agreement between the three series (AC_G (CTOH) + AC_E, AC_G (CMEMS) + AC_E, AC_HFR,R), and all the data sets observe the same variability. Although in Fig. 3 it is difficult to detect any differences between locations and data sets, the lowest RMSD is observed in E_R for CMEMS AC_G (RMSD =7.1 cm s⁻¹), while the RMSD rises up to 8.9 cm s⁻¹ in W_R for CTOH. A larger variability in W_R is shown in Table 1, which is also noticeable in Fig. 3a and c.

In terms of correlation, the results suggest greater agreement in W_R (0.67 and 0.70 for CMEMS and CTOH, respectively) than in E_R (0.64 and 0.59 for CMEMS and CTOH, respectively). This could be explained by the fact that point W_R is located in a deeper area and is more influenced by the IPC that flows over the slope. The IPC shows lower variability at point E_R than at point W_R, where the signal of the slope current is more persistent. These spatial differences agree with what was observed in the area by Rubio et al. (2009) from the analysis of the ADCP (Acoustic Doppler Current Profiler) time series of two buoys located over the slope in locations comparable to points E and W. These authors suggest that while there is a clear along-slope transport with intense mesoscale variability at Matxitxako buoy (slightly east from point W), at Donostia buoy (close to point E) the influence of the slope circulation was less significant. The lower current velocities and lower vertical coherence observed at Donostia buoy during winter could be linked to the complex bathymetry, which might force the IPC to flow over deeper grounds out of the point measured by the buoy. This could also explain why the addition of AC_E increases more r in E_R (by 11 %) than in W_R (by 6 %), where the circulation has a stronger geostrophic component.

With regard to the performances of the two altimetry products, it must be highlighted that CTOH shows higher (lower) r (RMSD) in W_R, while CMEMS shows higher (lower) r (RMSD) in E_R. However, the differences are small and do not permit us to draw conclusions on their relative accuracy.

In E_R (W_R) when r is higher for CMEMS (CTOH) than for CTOH (CMEMS), the RMSD is lower in the former. Therefore, the higher the correlation, the smaller the difference between AC_G and AC_HFR,R. However, the difference in the RMSD at each point (i.e. between the RMSD value of each altimetry product with the radar) is not related to the difference in r.

Figure 3b and d also show the residuals between AC_G and AC_HFR,R for each altimetry product. It can be observed that in W_R (Fig. 3d), the residuals' amplitudes are larger for CMEMS than for CTOH, agreeing with the higher RMSD value observed for CMEMS AC_G. In E_R the similar RMSD values observed for both altimetry products agree with the similar amplitudes of the residuals in Fig. 3b.

The IPC winter intensification is visible in all data sets, being stronger in AC_G for both altimetry products. There are some remarkable intensifications, for instance in November 2014, when a strong peak is shown in all the series and where the AC_HFR,R signal is higher in W_R than in E_R (see black arrows in Fig. 3a and c), approaching AC_G. There is another remarkable intensification in winter 2009, when the IPC shows a pronounced peak (see black arrows in Fig. 3a and c), especially in E_R, where CTOH is very similar to AC_HFR,R. This intensification is not so clear at point W_R, but it is still noticeable compared to the rest of the period. Equatorward slope current intensifications can be also observed through the whole period, as for instance in May 2011, where the peak is more prominent in W_R than in E_R (and even more for CMEMS) (see black arrows in Fig. 3a and c).

Since the presence of a stronger IPC signal is expected to improve the correlation between HFR and SLA data sets and the IPC shows marked seasonality, a monthly analysis has been carried out (Fig. 4). The monthly values of the statistical parameters shown in the figure, have been computed considering all the available data for that month during all the study period.

It can be observed that in terms of monthly mean currents, the three time series have the same tendency and that in general there is low discrepancy among them. No significant differences in terms of monthly patterns are observed among the two altimetry products. The winter poleward current intensification is evident from October to January with a maximum in November (ranging for all data sets from 7.5 to 13.4 cm s⁻¹ in E_R and from 11.7 to 14.8 cm s⁻¹ in W_R). In E_R, the current intensification is still perceptible in February, whereas in W_R there is a small increase in March in AC_G but not in AC_HFR,R. From March to September the mean is maintained around zero, with a slight decrease reaching the minimum in September (ranging from −7.3 to −3.9 cm s⁻¹ in E_R for all data sets and from −5.4 to −3.6 cm s⁻¹ in W_R) and showing an equator-ward weak mean slope current for that period. The addition of AC_E slightly strengthens the intensity of the slope currents for both poleward and equator-ward directions. This can be explained by the general wind patterns of the area, which are in agreement with the main local geostrophic regime, although winter south-westerlies are stronger than the summer north-easterlies (Herbert et al., 2011).

As has been mentioned previously, Figure 4 shows lower SD values for AC_HFR,R along all the period. These values are slightly increased by the addition of AC_E, especially in winter when winds are stronger. At point E_R, the tendency of the SD is similar to that of the mean, being slightly higher in January and then stable (with small oscillations) until September. In the last 3 months of the year, it is increased. Therefore, there is a higher variability in late autumn and winter, probably due to the slope current intensification and the stronger winds.

At point W_R, the highest variability takes place in the first 4 months of the year. This increase is coherent with the intensification of the slope current and the development of an anticyclonic structure in March and especially in April near Torrelavega canyon (Caballero et al., 2014). Afterwards, the variability is practically maintained, with small oscillations and an increase in CMEMS data.

Regarding the RMSD, the patterns are similar to those of the SD of AC_G, but with variability. In general, the addition of AC_E improves the results by a slight decrease in the RMSD. The major differences between AC_G and AC_G + AC_E time series are observed in February and April at point E_R. This can be clearly seen in the normalized RMSD, which measures the value of the RMSD with respect to the values of AC_HFR,R.

The same statistical parameters computed along track 248 are shown in Fig. 5 in addition to the correlation in order to study the spatial variability in the comparison between AC_HFR,T and AC_G. Temporal statistics considering all the study period for each point of the track are plotted as a function of the distance to the first point of the track.

AC_HFR,T show mean values close to zero along all the track, with low variability. Currents are oriented poleward over the shelf and upper slope over grounds shallower than 1000 m (i.e. until the point where the track leaves the slope current area). From there on, the mean is oriented equator-ward. The mean AC_G is also close to zero; however, it shows larger variability, changing between positive and negative values along the track, with a lack of agreement between both altimetry products at some points. Nevertheless, it should be pointed out that in any case the mean anomaly currents are very weak and that the high SD values compensate for changes in the mean values. The addition of AC_E does not cause any spatial variation, and it barely changes the values.

With regard to the variability, it is higher close to the coast. For AC_G, it slowly decreases as it gets away from the first point of the track, until the 1000 m isobath of the slope is reached (where the grey area ends in the figure). From there on, it is kept almost constant with a slight local maximum at around 120 km from the first point. For AC_HFR,T, the variability decreases until the point E_T is reached (where the Capbreton canyon area ends), and afterwards, it is also almost constant, with two maximums at around 60 and 105 km from the first point.

It can be once again observed that the addition of the AC_E slightly increases the variability (Fig. 5), that the variability in AC_HFR is lower than that of AC_G, and that CMEMS's variability is higher than CTOH's. Moreover, in Fig. 5, all these results are provided for all the track.

The highest r is observed between the 200 and 1000 m isobaths of the slope, where the IPC signal is the strongest, and thus the geostrophic component measured by the HFR is also stronger. At the points furthest from the coast, the r decreases. This can be linked to the absence of a strong and persistent geostrophic component and a higher signal-to-noise ratio for the HFR data (which increases as we get away from the antennae).

The maximum (minimum) values of r (RMSD) occur at around 37 and 45 km from the first point of the track for CMEMS and CTOH, respectively (Max_T points). These values could be explained by the fact that those points are located in the middle of the slope, where the slope current is stronger and where they are out of the Capbreton canyon area. At the same time, in that area, the slope current direction is nearly orthogonal to the track, so that the across-track component is stronger. For CTOH, the values around the maximum are relatively high, that is why the maximum is not a prominent peak. The same happens for CMEMS, but with a sharper peak and higher value (see Table 1). The addition of AC_E increases the r by 8 %–10 % as can be seen in the table (for E_T and Max_T points).

In general, the addition of AC_E slightly increases (decreases) the r (RMSD), along all the track. This fact is not perceptible in the figure, where it seems that the addition of AC_E does not make any difference, but it can be observed in the values of Table 1, except at point E_T for CMEMS data where it does not change.

3.2 Observability of mesoscale processes in HFR and altimetry data sets

In order to provide a complementary insight into the synergies and differences between HFR and altimeter data, in this section the observability of different processes detected by HFR and altimetry is qualitatively analysed. Since the data are spatially filtered (for AC_G) or time filtered (for AC_HFR and AC_E), the detectable processes are mesoscale, seasonal, and interannual processes, such as mesoscale eddies and the IPC. Only CMEMS data are used for this analysis, since the statistical results are very similar for both altimetry products and CMEMS data have less data gaps in the period and study area, which is more suitable for monitoring ocean processes.

3.2.1 Observability of the IPC

Along-track values of SLA^′, across-track AC_E and across-track AC_HFR,T for all the study period are shown in Fig. 6. The highest SLA^′ values are observed during late autumn and winter, whereas the lowest ones are observed in spring and summer, especially from March to July (Fig. 6a). This is coherent with the contribution of the main driving factor of the seasonal SLA variability in the area, the steric effect. It was observed in Caballero et al. (2008b) that the maximum amplitude of sea level in the BoB is reached in October, whilst the minimum takes place in April. AC_E shows a poleward seasonality with intensifications mainly in autumn and winter (usually from November to February) and weaker equator-ward currents in spring and summer (usually from March to October) (Fig. 6b). This fact agrees with the general wind pattern in the area. Along-track SLA^′ gradients indicate winter slope current intensifications (IPC events) mostly from November to January and from the coast to the 1000 m isobath, approximately. The poleward intensification in winter 2014/2015 is the most remarkable, as already described in Rubio et al. (2018). In spring and summer the gradients are weaker and even suggest equator-ward currents along all the track.

The IPC events are also detected by AC_HFR,T in late autumn and winter, mainly in the points nearest to the coast between the 200 and 1000 m isobaths (Fig. 6c). In spring and summer, although there are also several poleward current pulses, they are weaker. During this period, equator-ward current pulses are also observed. From the joint analysis of SLA^′ and AC_HFR,T data series, four main IPC events can be detected along the study period (Fig. 6a and c).

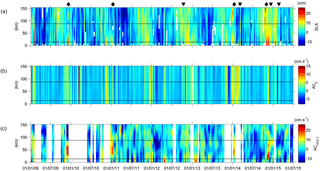
Figure 6 Time evolution from 1 January 2009 to 1 July 2015 along track 248 (y axis shows distance to the first point of the track in kilometres) of (a) CMEMS SLA^′ (cm), (b) AC_E (cm s⁻¹), and (c) AC_HFR (cm s⁻¹). The distance from the first point of the track to the coast is around 6 km. The horizontal black lines delimit the slope area between the 200 and 1000 m isobaths. The black diamonds depict the IPC intensification signals whereas the black inverted triangles show the eddy events, all mentioned in the text.

More details on these events are provided in Fig. 7, where four selected HFR total current field (obtained from OMA as explained in Sect. 2.1.1) snapshots are shown. Although each event is presented for a specific date, they last around 2–3 weeks (not shown), with the dates displayed in the figure being representative of all the period. Note that the SST maps do not show the same date as HFR snapshots and SLA^′ data, due to the limitations of this technique under cloudy conditions. For the four events, HFR total currents show a typical IPC spatial pattern, with poleward circulation along the slope intensifying between the 200 and 1000 m isobaths (Solabarrieta et al., 2015). The poleward patterns observed by the HFR agree with the AC_G observed along the altimetry track, which shows that poleward currents intensified over the slope. For the four events, the SST images show that the current intensifications along the slope are related to an increase of 0.5–1 ^∘C over time (not shown), which is the increase in temperature that is typically associated with the slope current intensification in the study area (Esnaola et al., 2013). The spatial extension of the warm water masses and the IPC along the French shelf/slope depends on the event, and it coincides with the area where the highest agreement between AC_G and HFR total currents is observed. During the IPC event of November 2009, the warm water tongue is closer to the coast. In this event, the strongest agreement between AC_G and HFR total currents is observed over the slope, while they disagree in the north-western area of the domain. Otherwise, during December 2010, the warm water extends over adjacent offshore areas, as well as the area presenting the strongest agreement between HFR and the altimeter. In three of the four events, AC_G and HFR total currents show a lower fit over the shelf. These observations corroborate the results obtained in Sect. 3.1, where the best statistical results are obtained for the data pairs inside the slope area (Fig. 5).

The relationship between the IPC and the NAO (North Atlantic Oscillation) in the study area was described in Garcia-Soto et al. (2002) and Garcia-Soto (2004). They concluded that for strong IPC years, January water warmings (as a signal of the IPC) were related to negative NAO index values in the previous months (November, December). On the other hand, the eastern Atlantic (EA) is also considered to be a possible factor of the IPC intensification, with positive EA values related to current intensifications. For the four events studied here, the relationship between the IPC intensification and those indexes is shown in Table 2. In general, the NAO (EA) indexes are negatively (positively) related to the IPC in strong intensification periods; however, this relationship does not always apply (see, for instance, the events of 2011 and 2014 where a negative EA index and a positive NAO index are observed, respectively). Moreover, the intensity of the currents is not related to the amplitude of the index, leading to the same conclusion as Le Cann and Serpette (2009) and Le Hènaff et al. (2011).

Table 2 NAO and EA indexes in the previous 2 months of the events. m−2 means 2 months before the event whereas m−1 means 1 month before.

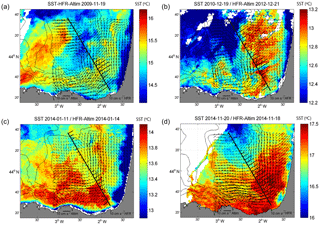
Figure 7 Snapshots showing four slope current intensification events observed by HFR, altimetry, and SST (see the dates of the events depicted in Fig. 6) in November 2009 (a), December 2010–January 2011 (b), January 2014 (c), and November 2014 (d). The small arrows depict the HFR current fields (not rotated) whereas the thick ones indicate the across-track AC_G. The black line shows the altimeter's track. The colormap depicts the sea surface temperature (^∘C) with values referenced in each colour scale. Note that the dates corresponding to the data are not the same for SST or for HFR and AC_G (specified in each panel's title).

3.2.2 Observability of mesoscale eddies

Figure 8 shows four examples of eddies detected by the HFR and the altimeter. Although the effect of the presence of mesoscale eddies has not been explored in terms of statistical results, there is a qualitative agreement between AC_G and HFR total currents when eddies are observed in the area covered by the two measuring systems (even if the eddy core is not crossed by the altimeter track). This happens when either the eddies cross the track of the altimeter or when the size of the eddies, whose centre is located off the track, is large enough to be observable by the altimetry. Across-track AC_G are generally in agreement with the HFR current fields, mainly in terms of current directions. For example, on 15 September 2012 the altimeter crosses a small anticyclone located to the north of the Capbreton canyon head. The maximum SLA^′ and minimum AC_G near the core of the eddy and the patterns of the SLA^′ and AC_G north and southwards of the core agree with the structure detected by the HFR. An eddy with a similar diameter and located near the same area, is observed on 15 February 2015. In this case the eddy is cyclonic, and though the HFR and altimetry currents in the area occupied by the structure agree with each other, this is not the case in the rest of the track. During winter, on 15 March 2014, a cyclone is detected by both data sets near the head of the Capbreton canyon, in addition to another cyclone in the north-western part of the domain. Finally, on 7 December 2014, an anticyclone, more energetic than all the former eddies, is observed over the Capbreton canyon. This anticyclone was analysed by Rubio et al. (2018), showing that it had an important role in the offshore transport of coastal waters. North of this eddy, the altimetry and the HFR detect a cyclonic circulation, but in this case, it is not clear from the HFR total current fields that the structure is an eddy.

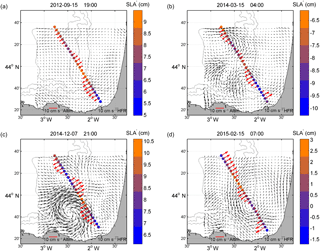
Figure 8 Four mesoscale eddies observed in the study area. The dots show the points of track 248 of the CMEMS database. SLA^′ (cm) values are indicated in the colour scale. Black arrows depict the HFR current fields. Red arrows correspond to across-track AC_G derived from the SLA^′ values in the dots. Grey lines: 200, 1000, and 2000 m isobaths. Note that the scale of each kind of arrow is not the same.

4 Summary and conclusions

In this study, we have investigated the synergies and differences between land-based HFR and satellite altimetry, two remote-sensing techniques that provide measurements of the ocean surface currents at different temporal and spatial scales. A general agreement between HFR and altimetry was observed in the study area, with correlations ranging up to 0.7. The comparisons were carried out in terms of time anomaly of currents, following different approaches with radial and total OMA HFR data. In all cases the addition of the LF Ekman component (AC_E) to the geostrophic component (AC_G) improved the results.

The best agreement between both data sets was observed in the slope area, mainly between 200 and 1000 m isobaths, where the surface circulation was dominated by a more energetic geostrophic component. In the coastal area, the agreement between both data sets was lower. AC_G have higher variability than AC_HFR, which could be explained by the error propagation in the finite-difference operator that estimates the geostrophic velocity from SLA^′ or by a more effective filtering of HF signals in the radar data (where HF signals can be efficiently removed using a running average temporal filter).

In terms of monthly mean currents, north-eastward currents were observed in all data sets in late autumn and in winter, while weaker north-eastward and south-westward currents were observed in spring and summer. In the winter period, higher variability was also observed at points E and W, possibly related to a more energetic slope current regime. Additionally, high variability was observed at point W in March–April, probably linked to an anticyclonic structure near Torrelavega canyon.

Four IPC events were isolated and described further by means of additional SST data. From this analysis we conclude that during the IPC intensifications the qualitative agreement between AC_G and HFR total currents is great and well related to the SST anomalies. In addition, a relationship between strong IPC events with negative (positive) NAO (EA) indexes in the previous months was detected for three of the four events. On the other hand, although the effect in terms of statistical results of the presence of mesoscale eddies was not explored, there is a qualitative agreement between AC_G and HFR total currents when eddies are observed in the area.

The low correlation between HFR and altimetry observed in some areas and periods can be due to several factors. It is worth noting that both technologies are based on different physical approaches to measure currents, at different spatial and temporal scales, and work under different physical assumptions. Besides, the quality of the radar data is expected to decrease in the furthest points from the antennae and varies as a function of the angle formed by the radial current components used for total current estimations (affecting the along-track comparison). Altimetry also has its own limitations and might have errors in the data editing procedure or in the corrections.

Future work should be oriented towards a better understanding of the relationship of the surface circulation and the dynamics of the subsurface layers by means of the combination of remote observations with data in the water column. Since the comparison near the shoreline is inconsistent, another future work line could be the investigation of the assumptions of geostrophic balance in the coastal area and the merging of altimetry and radar measurements to improve both products. In addition, further comparison with HFR data and higher-resolution coastal altimetry products would enable a better understanding of the differences between both observing systems.