Large-scale changes of the semidiurnal tide along North Atlantic coasts from 1846 to 2018

We investigated the long-term changes of the principal tidal component M₂ along North Atlantic coasts, from 1846 to 2018. We analysed 18 tide gauges with time series starting no later than 1940. The longest is Brest with 165 years of observations. We carefully processed the data, particularly to remove the 18.6-year nodal modulation. We found that M₂ variations are consistent at all the stations in the North-East Atlantic (Cuxhaven, Delfzijl, Hoek van Holland, Newlyn, Brest), whereas some discrepancies appear in the North-West Atlantic. The changes started long before the 20th century and are not linear. The secular trends in M₂ amplitude vary from one station to another; most of them are positive, up to 2.5 mm/yr at Wilmington since 1910. Since 1990, the trends switch from positive to negative values in the North-East Atlantic. Concerning the possible causes of the observed changes, the similarity between the North Atlantic Oscillation and M₂ variations in the North-East Atlantic suggests a possible influence of the large-scale atmospheric circulation on the tide. Our statistical analysis confirms large correlations at all the stations in the North-East Atlantic. We discuss a possible underlying mechanism. A different spatial distribution of mean sea level (corresponding to water depth) from one year to another, depending on the low-frequency sea-level pressure patterns, could impact the propagation of the tide in the North Atlantic basin. However, the hypothesis is at present unproven.

1 Introduction

Tides have been changing due to non-astronomical factors since the 19th century (Haigh et al., 2019; Talke and Jay, 2020). In the North Atlantic, secular variations have been observed at individual tide gauge stations, e.g. Brest (Cartwright, 1972; Wöppelmann et al., 2006; Pouvreau et al., 2006; Pouvreau, 2008), Newlyn (Araújo and Pugh, 2008; Bradshaw et al., 2016), New York (Talke et al., 2014), and Boston (Talke et al., 2018), but also at regional scale, e.g. Gulf of Maine (Doodson, 1924; Godin, 1995; Ray, 2006; Ray and Talke, 2019), at the North Atlantic basin scale (Müller, 2011), and at a quasi-global scale (Woodworth, 2010; Müller et al., 2011; Mawdsley et al., 2015). Long-term changes in tidal constituents are rather small at some coastal stations but tend to be statistically significant. The order of magnitude of these changes varies spatially and may reach a few centimetres per century for M₂ amplitude. For example, Ray and Talke (2019) found trends varying from −1 to 8 cm per century in the Gulf of Maine over the last century. Woodworth et al. (2010) and Müller et al. (2011) found trends of a few percent per century in the Atlantic. The changes can be larger in many estuaries and rivers (Talke and Jay, 2020).

The physical causes of these changes can be multiple and difficult to disentangle. In particular, the complexity comes from the possible interaction between local and large-scale causes. Changes may have a local-scale origin, such as changes in the nearby environment (e.g. harbour development, deepening of channels, dredging, siltation) or changes in the instrumentation (e.g. tide gauge technology, observatory location, instrumental errors). For example, Familkhalili and Talke (2016) show that mean tidal range at Wilmington has doubled since the 1880s, due to channel deepening in the Cape Fear River estuary. Changes may also have a large-scale origin, i.e. regional or global. Haigh et al. (2019) reported several possible large-scale mechanisms: (1) tectonics and continental drift, (2) water depth changes due to mean sea level rise or geological processes such as the Earth's surface glacial isostatic adjustment (Müller et al., 2011; Pickering et al., 2017; Schindelegger et al., 2018), (3) shoreline position, (4) extent of sea-ice cover (Müller et al., 2014), (5) sea-bed roughness, (6) ocean stratification which may modify the internal tides and bottom friction over continental shelves (Müller, 2012), (7) non-linear interactions, and (8) radiational forcing (Ray, 2009).

Several authors have explored mean sea level (MSL) rise as a potential mechanism to explain M₂ changes. For example, simulations by Pickering et al. (2012) show that a 2 m sea level rise could modify M₂ from −20 to 20 cm around the whole ocean. Idier et al. (2017) show that depending on the location, the changes can account for ±15 % of the regional sea level rise. Schindelegger et al. (2018) find changes of about 1 %–5 % of the sea level rise. Beyond MSL rise, other mechanisms have been explored to explain M₂ changes. For example, Colosi and Munk (2006) attribute the changes of M₂ amplitude at Honolulu, Hawaii, to a 28^∘ rotation of the internal tide vector in response to ocean warming. Ray and Talke (2019) suggest that long-term changes in stratification could play a role in the Gulf of Maine. Müller (2011) suggests a possible link between M₂ changes and atmospheric dynamics in the North Atlantic; he reported that the time series of the North Atlantic Oscillation (NAO) show similar characteristics to those of the tidal amplitudes and phases. In the Gulf of Maine, Pan et al. (2019) suggest that changes in the response of the nodal modulation of the M₂ tide from 1970s to 2013 may be linked with the NAO. In Southeast Asian waters, Devlin et al. (2018) show that the impact of atmospheric circulation (via the wind stress, through Ekman current) on the M₂ seasonal cycle may be significant and comparable to the effect of permanent (geostrophic) currents. In the North Sea, Huess and Andersen (2001) explain a large part of M₂ seasonal cycle by the role of atmospheric dynamics, whereas Müller et al. (2014) and Gräwe et al. (2014) suggest a major role of the thermal stratification. These examples show the diversity of mechanisms that play a role in tide changes. In the present paper, we focus on the role of MSL and atmospheric dynamics.

This paper has two main objectives. The first is to characterize the secular changes of the M₂ tide over the North Atlantic. We focus on the longest time series, i.e. starting no later than 1940. This approach is complementary to previous studies investigating M₂ changes focusing on smaller spatial scales, e.g. Brest (Pouvreau et al., 2006; Pouvreau, 2008), Gulf of Maine (Ray, 2006; Ray and Talke, 2019), or focusing on shorter temporal scales, i.e. recent decades (Woodworth, 2010; Müller, 2011). The second objective is to detect if there is any large-scale coherence in the observed changes in the North Atlantic and investigate the possible link with the atmospheric circulation, already mentioned by Müller et al. (2011), on the basis of qualitative criteria. Here, we further provide quantitative insights into the possible influence of the NAO and discuss a possible NAO-related climate mechanism that can partly explain the observed changes.

The paper is organized as follows. The first section below describes the data: the sea level data (i.e. tide gauges and their processing) and the atmospheric data (i.e. climate indices and sea level pressure data). The following section presents the results (i.e. M₂ variations and trends). We then discuss a possible link between the observed tidal changes and MSL, as well as climate indices.

2 Data

2.1 Sea level data

2.1.1 Tide gauge selection

The tide gauge data were retrieved from the University of Hawaii Sea Level Center (UHSLC, website accessed April 2020). The dataset consists of 249 stations in the Atlantic Ocean, with hourly sea level observations. Two additional long-term stations – Delfzijl and Hoek van Holland – were provided by Rijkswaterstaat (RWS) in the Netherlands.

We selected the stations following three criteria: time series (1) starting before 1940, (2) with at least 80 years of data, and (3) with tidal amplitude significant enough to detect trends, i.e. M₂ amplitude larger than 10 cm. Note that we selected only years with at least 75 % of data (see Sect. 2.1.2). Only 24 stations among the 249 from UHSLC fulfilled the two first criteria (Fig. 1). They are all located in the Northern Hemisphere. On the east side of the North Atlantic, Stockholm, Gedser, Hornbaek, Tregde and Marseille were discarded due to too small of an M₂ amplitude (i.e. lower than 10 cm). These stations are located in the Baltic Sea (Stockholm, Gedser), in the strait separating the Baltic and the North Sea (Hornbaek), in the North Sea (Tregde), and in the Mediterranean Sea (Marseille). On the west side of the North Atlantic, Galveston, Pensacola and Cristobal were also discarded due to too small of a tidal amplitude (i.e. lower than 10 cm). These stations are located in the Gulf of Mexico (Galveston, Pensacola) and the Caribbean Sea (Cristobal).

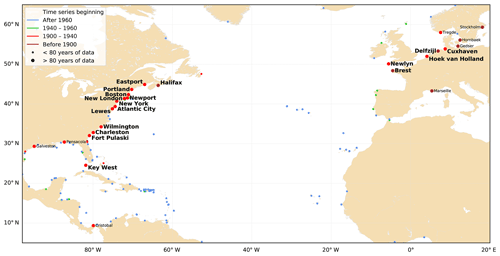
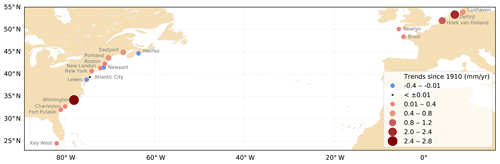
Figure 1 Tide gauges in the North Atlantic. Stations with time series starting before 1940 and longer than 80 years are labelled. Stations selected for this study are in bold.

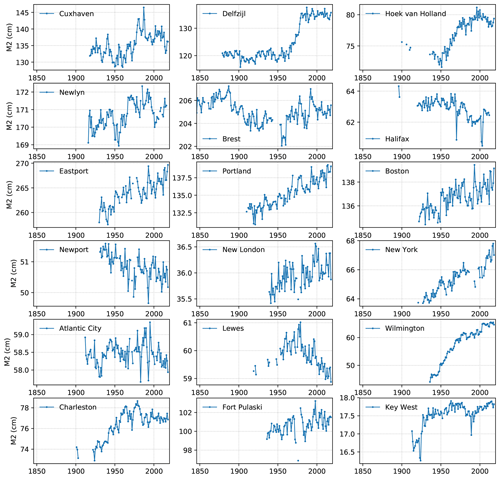
Finally, 18 stations followed the three criteria detailed above and were selected for this study (see stations in bold in Fig. 1, 16 stations are from UHSLC, and 2 from RWS). Among them, 5 are located on the North-East Atlantic coasts (Newlyn, Brest, Hoek van Holland, Delfzijl and Cuxhaven – note that Hoek van Holland, Delfzijl and Cuxhaven are located in the North Sea) and 13 are located on the North-West Atlantic coasts (Halifax, Eastport, Portland, Boston, Newport, New London, New York, Atlantic City, Lewes, Wilmington, Charleston, Fort Pulaski and Key West).

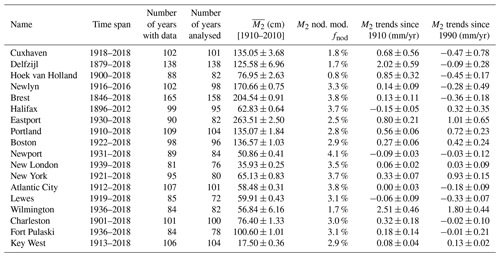
The main characteristics of the 18 selected stations are summarized in Table 1. Among them, only Brest, Hoek van Holland and Halifax started in the 19th century, in 1846, 1879 and 1896 respectively (Table 1, column 2). The number of years with data for each station varies between 81 and 165 years, Brest being the longest time series (Table 1, column 3).

Table 1 Main characteristics of tide gauge records selected for this study. Name of the station, time span, number of years with data, number of years analysed (i.e. with at least 75 % of data), M₂ average amplitude and standard deviation over the period 1910–2010, M₂ nodal modulation, estimated trends in M₂ amplitude since 1910 and since 1990 up to 2018 in each case (standard errors are 1σ, considering the noise content in the time series; see text).

2.1.2 Data processing

Harmonic analysis was performed in order to compute the M₂ amplitude. We used the MAS program (Simon, 2007, 2013), developed by the French Hydrographic Office (SHOM). This program gives results similar to the T_Tide harmonic analysis toolbox (Pawlowicz et al., 2002). For instance, Pouvreau et al. (2006) found no differences in the yearly amplitudes of M₂ at Brest over the period 1846 to 2005 using either T_Tide or MAS. Hourly time series were analysed yearly. Note that at Delfzijl and Hoek van Holland, data had to be interpolated every hour before 1970, as the temporal sampling was 3 h. (We checked with hourly time series from recent years (1971–2018) that 3-hourly sampling did not result in a significant reduction of M₂ amplitude in a tidal analysis compared to hourly sampling.) We processed only years with at least 75 % of data, to avoid seasonal modulation affecting the computed amplitudes. In the North Atlantic, M₂ is affected by a seasonal variation of a few percent (Pugh and Vassie, 1976; Huess and Andersen, 2001; Müller et al., 2014; Gräwe et al., 2014). Considering only years with at least 75 % of data resulted in excluding up to 15 years for a given station (Table 1, columns 3 and 4). We carefully removed the nodal modulation of M₂ amplitude (Simon, 2007, 2013), as described briefly in Appendix A. Finally, 3 station-years were discarded due to problems in the record (1953 and 1962 at Delfzijl, 1953 at Hoek van Holland), and 2 more station-years due to doubtful M₂ values (1972 at Eastport, 1978 at Newport).

At all the stations, we computed the normalized M₂ amplitude, removing the average and dividing by the standard deviation over the period 1910–2010:

$$\begin{array}{}\text{(1)}& \text{normalized}{M}_{\mathrm{2}}\left(t\right)={\displaystyle \frac{M_{\mathrm{2}}\left(t\right)-{\stackrel{\mathrm{‾}}{M_{\mathrm{2}}}}_{[\mathrm{1910},\mathrm{2010}]}}{{\mathit{\sigma }}_{M_{\mathrm{2}}[\mathrm{1910},\mathrm{2010}]}}}.\end{array}$$

The average $\stackrel{\mathrm{‾}}{M_{\mathrm{2}}}$ and standard deviation ${\mathit{\sigma }}_{M_{\mathrm{2}}}$ over the 1910–2010 period are given in Table 1 (column 5). The idea is to scale the data in order to compare all the stations together.

2.2 Atmospheric data

2.2.1 Climate indices

We investigated the correlation between secular changes in the tide and climate indices, such as the North Atlantic Oscillation (NAO) or the Arctic Oscillation (AO) – also called Northern Annular Mode (NAM) (Hurrell, 1995; Hurrell and Deser, 2009; Thompson and Wallace, 2000; Thompson et al., 2000). These climate indices are related to the distribution of atmospheric masses. They are based on the difference of average sea-level pressure between two centres of actions (i.e. stations) over long periods (e.g. monthly, seasonal, annual).

The NAO is the major pattern of weather and climate variability over the Northern Hemisphere (Hurrell, 1995; Hurrell and Deser, 2009). Variations of NAO drive the climate variability over Europe and North America (Hurrell et al., 2003). We used the wintertime (December to March) Hurrell station-based NAO Index (retrieved from https://climatedataguide.ucar.edu/climate-data/hurrell-north-atlantic-oscillation-nao-index-station-based, last access: April 2020). It is based on the difference of normalized average winter sea-level pressure between Lisbon (Portugal) and Stykkishólmur/Reykjavik (Iceland). The normalization involves removing the mean (1864–1983) and dividing by the long-term standard deviation. The NAO index covers the period 1864–2019.

The Arctic Oscillation (AO) is another index which resembles the NAO index. It is defined as the first EOF of Northern Hemisphere winter sea-level pressure data (Thompson and Wallace, 1998, 2000; Thompson et al., 2000). The AO index is highly correlated with the NAO. We used the wintertime Hurrell AO index (retrieved from https://climatedataguide.ucar.edu/climate-data/hurrell-wintertime-slp-based-northern-annular-mode-nam-index, last access: April 2020). The AO index covers the period 1899–2019.

To remove the interannual variability and estimate low-frequency variations, climate indices were low-pass filtered with a 9-year mean filter.

2.2.2 Sea level pressure

We employed the Twentieth Century Reanalysis (20CR version 3 dataset) (Compo et al., 2011; Slivinski et al., 2019), a historic weather reconstruction from 1836 to 2015, with a 1^∘ gridded global coverage. However, we made use only of data from 1850 to be more consistent with the temporal coverage of the tide gauge measurements. This will be discussed in Sect. 4.

3 Results

3.1 M₂ variations

For the North-East Atlantic, the variations of normalized M₂ amplitude are presented in Fig. 2a.

.

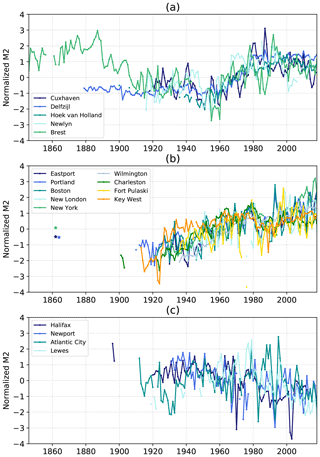
Figure 2 Normalized annual M₂ amplitude (a) in the North-East Atlantic (b) in the North-West Atlantic, stations with positive trends (c) in the North-West Atlantic, stations with negative or no trend. The stars in (b) in the 1860s correspond to M₂ amplitude at Eastport and Portland from Ray and Talke (2019), and New York from Talke et al. (2014), after normalization (Eq. 1).

The first result is that since 1910, the variations show similar patterns at all the stations; M₂ amplitude decreases up to the 1960s, then increases, and decreases again since the 1990s. This suggests that these changes are probably due to large-scale processes, rather than local effects due to changes in the environment (e.g. harbour development, dredging, siltation) or instrumentation errors. The similar patterns between Brest and Cuxhaven may be surprising, as Cuxhaven is located in the North Sea, and not in the open Atlantic Ocean, and far away from Brest, around 1300 km. This indicates that the spatial scale of the processes responsible for these changes must be at least as large as the North-East Atlantic. Different authors have noticed the increase of tidal range from 1960 to 1990 in the southern North Sea. Hollebrandse (2005) found a gradual increase during the period 1955–1980 at all the stations of the Dutch coast (five stations including Hoek van Holland) and the German coast (seven stations). Mudersbach et al. (2013) found a significant increase in M₂ amplitude at Cuxhaven since around the mid-1950s. Note that Cuxhaven is located in the German Bight; shallow depths and the shape of the coastline may induce some amplification. Variations in M₂ at Cuxhaven could therefore be sensitive to local effects, such as the migration of the underwater channels and the evolution of the tidal flats (Jacob et al., 2016). Moreover, Cuxhaven is located in the Elbe estuary, and some river engineering works, such as narrowing and deepening, may induce tidal amplification (Winterwerp and Wang, 2013; Winterwerp et al., 2013).

Before 1910, normalized M₂ values are higher at Brest than at Delfzijl. The construction of dykes that have gradually closed the harbour of Brest since the end of the 19th century may have altered the tide at Brest. The high values before 1910 may be due to local changes, in addition to large-scale changes. To go further, the potential role of these successive constructions needs to be investigated (Wikipedia contributors, 2020). Cartwright (1972) made a first attempt to evaluate the influence of reducing the width of access to the harbour but did not take into account a potential role of dredging, for which we have no information. This example underlines the complexity of interpretation of the variations when changes of local and large-scale origin occur at the same time. Note that in the following, we focus mainly on the 20th century, as most of the stations start after 1900 (15 out of 18 stations).

The second result is that there is no obvious linear trend in M₂ variations, but rather break or change points, M₂ increasing and then decreasing, depending on the periods considered. Overall, M₂ decreases from 1910 until 1960, increases again until 1980–1990, to finally decrease since 1990; note that the curve flattens between 1920 and 1940. Pouvreau et al. (2006) already noticed these variations at Brest and Newlyn and suggested a long-period oscillation of around 140 years, rather than a steady secular trend. A careful analysis of the harmonic development of the tidal potential showed that no tidal component could explain this oscillation. Similarly, no linear combination of tidal harmonic components could explain it (Pouvreau et al., 2006). This indicates that these variations are not due to an astronomical component. However, in contrast to Brest, M₂ at Delfzijl stays flat between 1880 and 1920. The decrease observed at Brest between 1880 and 1920 may be due to harbour development and/or dredging (see above). This underlines the importance of sea level data archaeology, for research studies related to long-term changes (Pouvreau, 2008; Woodworth et al., 2010; Marcos et al., 2011; Talke and Jay, 2013, 2017; Ray and Talke, 2019; Bradshaw et al., 2015, 2020).

The third result is that changes in M₂ have not the same order of magnitude at each station (see Fig. B1 in Appendix B for time series of M₂). Note that Fig. 2 represents normalized M₂, i.e. removing the average and dividing by the standard deviation. The order of magnitude of unnormalized M₂ changes is roughly the same at Brest and Newlyn (standard deviations of 0.9 and 0.8 cm respectively, Table 1, column 5), but more than three times larger at Cuxhaven (standard deviation of 3.7 cm), and even larger at Delfzijl (standard deviation of 7 cm). This suggests that the North Sea may be more sensitive to the processes responsible for these changes. Note also that the environmental setting of Cuxhaven and Delfzijl in the Elbe and Ems estuaries, respectively, could introduce some amplification (Winterwerp and Wang, 2013; Winterwerp et al., 2013).

For the North-West Atlantic, the variations of normalized M₂ amplitude are presented in Fig. 2b and c. The first feature is that M₂ amplitude varies differently in the North-West and in the North-East Atlantic. The second is that there are discrepancies between stations, even when close to each other (e.g. Atlantic City and Lewes). We split the stations into two groups, in order to facilitate the detection of patterns, each being consistent in terms of trends: one with positive trend (group 1 in Fig. 2b), the other one with negative or no trend (group 2 in Fig. 2c).

The first group (with positive trends) consists of nine stations (Fig. 2b). Three outcomes can be highlighted. The first is that M₂ amplitude has increased overall since 1900. However, between 1980 and 1990, all the stations slightly decrease, and since 1990 they have increased again. The second outcome is that the rate of increase is very different from one station to another (keeping in mind that M₂ is normalized by standard deviation in Fig. 2). Portland is increasing 1.4 times faster than Charleston (standard deviations being respectively of 1.82 and 1.33 cm) and 28 times faster than Key West (standard deviation being only 0.36 cm at Key West). The large increase in Portland may be explained by some amplification in the Gulf of Maine. In many semienclosed basins, resonance leads to tidal amplification (Talke and Jay, 2020; Haigh et al., 2019). In the Gulf of Maine, Ray and Talke (2019) reported that the tides in the Gulf are in resonance, with a natural resonance frequency close to the N₂ tide (Garrett, 1972; Godin, 1993). Tides may be then very sensitive to any changes in the environment (e.g. basin configuration – shape, depth – but also external forcing). The third outcome, and probably the most interesting one, is related to the values of M₂ at Eastport, Portland and New York in the 1860s, estimated from Ray and Talke (2019) and Talke et al. (2014), and represented (after normalization) as stars in Fig. 2b. These values are not consistent with the positive linear trends observed since 1900, which provides some consistency with the hypothesis formulated from the analyses of the data prior to the 20th century in Fig. 2a: long-term variations introduce some breaks or change points, M₂ increasing and then decreasing, depending on the periods considered. The decrease observed between the 1870s and 1920s at the four stations (Brest, Eastport, Portland, New York) suggests a possible large-scale signal, in addition to local processes.

The second group (with negative or no trend) consists of four stations (Fig. 2c). Two points can be highlighted. The first is that M₂ decreases overall for Halifax, Newport and Lewes. This is less clear for Atlantic City, which is quite noisy and shows no significant trend. The second point is that at Halifax, M₂ values in 1896–1897 are higher than those after 1920. This suggests that the decrease may have started before the 20th century. However note that at Halifax, there is a long gap in the data recording (1898–1919), which raises the possibility of an instrumentation origin in the observed decrease of the M₂ amplitude.

3.2 Estimated trends

We estimated the trends for M₂ amplitude at each station, using linear regression. We computed the trends over two periods: 1910–2018, which corresponds roughly to the whole period of data (only five stations start before 1910), and 1990–2018, which corresponds to recent decades. Some tests showed that the later results were not very sensitive to the start date (moving 1990 to 1985 or 1995). The trend uncertainties were estimated considering the noise content in the time series using SARI software (Santamaría-Gómez, 2019). The noise was modelled as a white plus power-law noise, whose spectral index was found to be close to −1 (flicker noise). The results are summarized in Table 1 (columns 7 and 8) and Figs. 3 and 4.

Figure 3 Estimated trends in M₂ amplitude over the period 1910–2018.

Figure 4 Estimated trends in M₂ amplitude over the period 1990–2018.

The trends estimated since 1910 vary significantly from one station to another (Fig. 3). They are positive overall (up to 2.5 mm/yr at Wilmington), which is consistent with previous findings (Araújo and Pugh, 2008; Ray, 2009; Woodworth, 2010; Müller et al., 2011; Ray and Talke, 2019). They are slightly negative at three stations (Halifax, Newport, Lewes), and one station shows no trend (Atlantic City). The estimates are statistically consistent with those found previously by different authors (e.g. 0.14 ± 0.09 mm/yr at Newlyn compared to 0.19 ± 0.03 mm/yr in Araújo and Pugh (2008), 0.56 ± 0.06 mm/yr in Portland, compared to 0.59 ± 0.04 mm/yr in Ray and Talke, 2019). Note that our error bars are larger, because we considered the noise content in the time series as a white noise plus power law noise (we obtained the same error bars considering white noise only). In the North-East Atlantic, the trends are consistent with each other (in terms of sign), which is not surprising as the stations vary similarly (Fig. 2a).

The largest trends since 1910 are mainly observed in semi-closed basins: Wilmington in the Cape Fear River estuary, Delfzijl in Ems estuary, Cuxhaven in Elbe estuary, and Eastport and Portland in the Gulf of Maine. This suggests a possible amplification due to resonance effects (e.g. Gulf of Maine) and/or propagation in shallow waters (e.g. Cuxhaven), in addition to local effects. The stations located in estuaries or in a harbour with a channel may have been subject to dredging. Channel deepening increases the water depths, which reduces the effective drag and leads to tidal range amplification. This effect may be particularly large in estuaries (Ralston et al., 2019; Talke and Jay, 2020) and may explain the larger trends at Wilmington (Familkhalili and Talke, 2016) and Delfzijl. Finally, the shifting locations of amphidromic points could also play a role (Haigh et al., 2019). In the North Sea, different authors show a possible migration of the present-day amphidromes, under a 2 m sea-level rise scenario (Pickering et al., 2012; Idier et al., 2017).

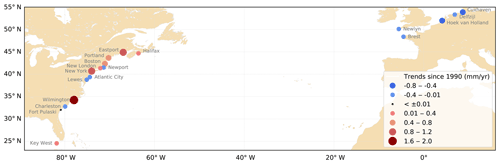
The trends estimated since 1990 are quite different from those estimated since 1910 (Figs. 3 and 4), with more stations with negative trends: 9 stations out of 18 have post-1990 negative trends, whereas only 3 stations out of 18 have post-1910 negative trends (Table 1, columns 7 and 8). In the North-East Atlantic, they all switch from positive to negative trends. This underlines (1) some spatially coherent changes in recent decades (Müller, 2011; Ray and Talke, 2019) and (2) the difficulty in estimating long-term trends from short records (i.e. less than 30 years), especially if the data are noisy (interannual variability) and the underlying processes non-linear (change points).

The trends have to be interpreted very carefully as the M₂ variations are not linear and may increase or decrease depending on the years; as a consequence, the estimated trends depend strongly on the period considered to estimate it. The interannual variability also plays an important role, and when substantial, trends can vary depending on the computational period. For example, at Cuxhaven, the large interannual variability leads to a large uncertainty on the trend computed since 1990 ($-\mathrm{0.47}\pm \mathrm{0.78}$ mm/yr).

4 Discussion

4.1 Possible link with mean sea level rise

The MSL rise could partly explain M₂ changes. Simulations show that MSL rise can result in an change of M₂ up to ±10 % of the rise (Pickering et al., 2017; Idier et al., 2017; Schindelegger et al., 2018). Schindelegger et al. (2018) show that the sign of the observed M₂ trend is correctly reproduced at 80 % of the tide gauges on a global scale, but their simulated trends tend to differ from observations by a factor of 3 to 5; i.e. their simulations underestimate the M₂ response to MSL rise in terms of magnitude. Schindelegger et al. (2018) conclude that “magnitudes of observed and modeled M₂ trends are within a factor of 4 (or less) from each other in nearly 50 % of the considered cases”. The large discrepancies between the simulations and the observations strongly suggest that MSL rise is not the only process that may explain M₂ changes – other large-scale processes, in addition to local processes, may also play a role.

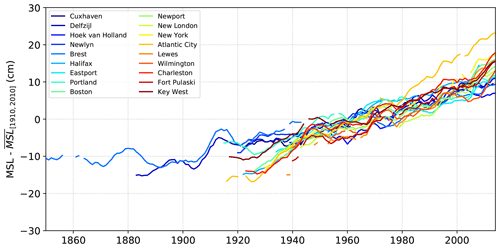
Figure 5 shows the annual MSL, after removing the average over the period 1910–2010 and filtering with 9-year time windows. The correlations between M₂ and MSL indicate that M₂ varies strongly with MSL (see Sect. 4.2). However, M₂ variations show some variability in the North-East Atlantic (Fig. 2a), which may not be explained with MSL rise alone.

Figure 5 Annual mean sea levels (MSLs), after removing the average over the period 1910–2010. MSL values are filtered using 9-year windows.

4.2 Possible link with MSL and climates indices

Processes other than MSL rise may impact the tide (see Sect. 1), such as the atmospheric circulation and the ocean stratification. Ocean and atmosphere are fully coupled, and air–sea fluxes are responsible for the exchange of momentum, water (evaporation and precipitation budget) and heat at their interface. Among the wide range of possible interactions, two mechanisms have been explored for their ability to modify the tide: (1) the momentum flux (wind stress) and the gradient of sea level pressure which act on the barotropic tide and (2) the water and heat fluxes which induce changes in both temperature and salinity distribution in the ocean. The latter effect acts on the stratification, which in turn could impact the tide in two different ways. The first way is the internal tide generation which transfers energy from barotropic and baroclinic motion and modifies surface tidal expression (Colosi and Munk, 2006). However, in the present study, most of the observations come from coastal stations sheltered by wide continental shelves which dampen internal waves. More important is the second way: the stratification acts on the eddy viscosity profile by modifying current profiles and bottom drag over continental shelves, which in turn modifies the M₂ surface expression (Kang et al., 2002; Müller, 2012; Katavouta et al., 2016).

Here, we focus on the effect of the atmospheric circulation on the tide. We used pressure indices (NAO and AO) that are relevant to represent atmospheric circulation. The NAO index represents the difference of normalized sea level pressure between the Azores high pressure system and the Iceland low pressure one (Hurrell, 1995). It indicates the redistribution of atmospheric masses between the subtropical Atlantic and the Arctic (Hurrell and Deser, 2009). In the North-East Atlantic, the similarity between the variations of the low-frequency winter NAO index and those of M₂ (Fig. 6) suggests a possible impact of large-scale atmospheric circulation on the tide. The NAO index varies from positive to negative phases. Filtering the interannual variability, the NAO index tends overall to decrease between 1910 and 1970, then increase until 1990, and once again decrease. In the same way, M₂ amplitude tends to decrease up to 1960, then increase until 1990, and once again decrease. These similar patterns raise a possible connection between NAO and M₂ variation, already mentioned by Müller (2011) on the basis of qualitative criteria. In the following, we provide quantitative insights into the possible influence of NAO.

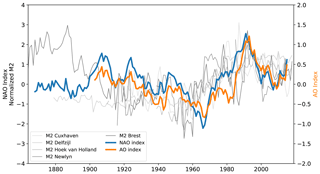
Figure 6 Low-frequency winter NAO and AO indices, obtained with a 9-year mean filter. Normalized annual M₂ amplitudes in the North-East Atlantic (from Fig. 2a) are also plotted in grey.

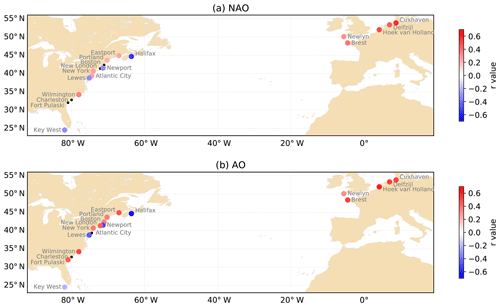
Figure 7 Correlation (r value) since 1910 between M₂ and (a) North Atlantic Oscillation and (b) Arctic Oscillation. Black dots are stations with no significant correlation. M₂, NAO and AO are filtered using the same time window (9 years).

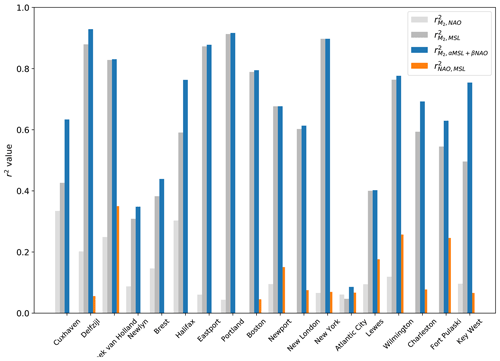
Figure 8 Variance explained (r² value) since 1910 between M₂ and NAO, M₂ and MSL, M₂ and fitted model αMSL+βNAO (model 2), NAO and MSL. M₂, NAO and MSL are filtered using the same time window (9 years). Note that there is no orange bar for NAO–MSL when the correlation is not significant (p>0.05).

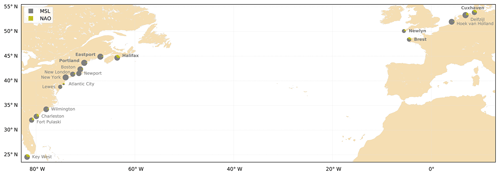
Figure 9 Relative contribution of α compared to β in the fitted model αMSL+βNAO. Black dots are stations with no significant M₂–NAO correlation. The size of each large dot is proportional to the correlation between M₂ and the fitted model. Stations with no MSL–NAO correlations are labelled in bold.

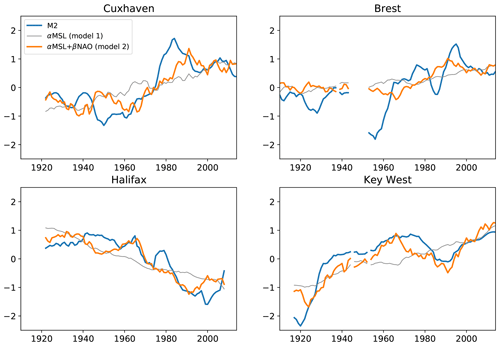
Figure 10 Variations since 1910 of M₂, αMSL (model 1), αMSL+ βNAO (model 2). M₂, NAO and MSL are filtered using the same time window (9 years).

We computed the correlations (r value) between normalized M₂ and climate indices, NAO and AO (Fig. 7). M₂, NAO and AO are filtered using the same time window (9 years). The correlations are computed since 1910, to have similar periods for all the stations. The correlations are considered as significant only if the p value is lower than 0.05 (95 % significance level). (Note that other statistics to measure the degree of association between the M₂ and NAO (AO) quantities would be worth exploring, for instance, nonlinear association using Spearman’s correlation coefficient. In this respect, our study should be regarded as a first step that identifies sites worth considering in future investigations, especially investigating causal relationships with physics-based modelling.) The results are the following: (1) for NAO, 14 stations out of 18 show significant correlation. Note that at Brest, the correlation is significant since 1910, but not since 1864 (the NAO index used in this study starts only in 1864). This can be explained by the M₂ larger amplitude over all the 19th century, which decreases between 1890 and 1910 (Fig. 2a), possibly due to harbour development and construction of dykes (see Sect. 3.1). (2) In the North-East Atlantic, all the stations are positively correlated with NAO. (3) The strongest correlations (i.e. greater than 0.5) are in the northern part of the North Atlantic, with strong positive correlations at Cuxhaven and Hoek van Holland and strong negative correlation at Halifax (−0.55). (4) For AO, we found similar, but overall larger, r values. This is not surprising as these two indices are closely related.

To go further in the relative contribution of MSL and NAO in M₂ variability, we fitted two linear regression models on M₂ variations. In the following, M₂, MSL and NAO are filtered over 9-year time windows and normalized. At all the stations, we fitted M₂ variations with a MSL linear regression model (model 1) and a MSL and NAO multiple linear regression model (model 2). Models 1 and 2 may be expressed as

$$\begin{array}{}\text{(2)}& {\displaystyle }\text{Model}\mathrm{1}={\mathit{\alpha }}_{\mathrm{1}}\mathrm{MSL}\text{(3)}& {\displaystyle }\text{Model}\mathrm{2}=\mathit{\alpha }\mathrm{MSL}+\mathit{\beta }\mathrm{NAO}.\end{array}$$

The correlations between M₂ and model 1 (MSL) and model 2 (NAO and MSL) are presented in Fig. 8. We checked if there was correlation between NAO and MSL at the stations: there is no correlation at six stations, and r value is between 0.2 and 0.6 at eight stations; see Fig. 8 and discussion below. The results are the following: (1) M₂ varies at first order with MSL (Fig. 8). (2) The introduction of the NAO (model 2) allows increasing the predictive performance of the model, beyond the inherent effect of adding an additional regression parameter. Indeed, on average, the Akaike information criterion (AIC) is 99.9 for model 2, instead of 112.7 for model 1. On average, the r² value is 0.67 for model 2 instead of 0.61 for model 1. At some stations, the increase is quite large. For example at Cuxhaven, the r² value jumps from 0.42 to 0.64 between model 1 and 2. (3) The ratio $\frac{\mathit{\beta }}{\mathit{\alpha }+\mathit{\beta }}$ represents roughly the relative contribution of the NAO compared to the total effect of MSL and NAO (Fig. 9), as MSL and NAO are normalized. We found a significant contribution at some stations (e.g. more than 30 % at Cuxhaven and Halifax), whereas it is negligible at others (e.g. only 5 % at Portland). A total of 8 stations out of 18 show large NAO contribution (>20 %). The North-East Atlantic seems to be more sensitive to the NAO. Note that the interpretation of the results is tricky when MSL–NAO correlation is significant (orange bars in Fig. 8). For example, at Hoek van Holland, the relative NAO contribution is very small, mainly because MSL and NAO are highly correlated (r=0.59). Figure 10 shows M₂ variations along with the predictions from the two models, at all four stations where the NAO contribution is significant ($\frac{\mathit{\beta }}{\mathit{\alpha }+\mathit{\beta }}>\mathrm{0.25}$), and the correlation between M₂ and model 2 is large enough (r>0.3). At Cuxhaven, Halifax and Key West, model 2 (MSL- and NAO-dependent) naturally captures the M₂ variations better than model 1 (MSL-dependent); at Brest, the improvement is less significant. The trend switch observed since 1990 in the North-East Atlantic could be partly explained by the influence of the NAO on the tide.

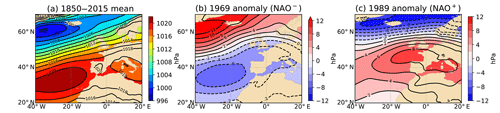
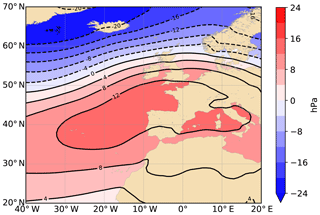
These results suggest that a NAO-related mechanism may explain part of the variability of M₂. As mentioned by Müller (2011), “it is shown that sea‐level, sea surface temperature and Arctic ice thickness are correlated with the NAO index. Thus, changes in the dynamics of the atmosphere could affect both M₂ and S₂ tides by processes discussed under (1), (2) and (3).” An underlying mechanism linked with (2) – sea surface temperature – could be changes in the ocean stratification. This is one of main possible hypotheses invoked in Ray and Talke (2019) to explain secular changes in M₂ amplitude in the Gulf of Maine; this is also the main hypothesis in Müller et al. (2014) and Gräwe et al. (2014) to explain seasonal modulation of M₂ in the North Sea. The relationship between the NAO index and stratification is complex and spatially variable across the North-East Atlantic (Fromentin and Planque, 1996). In the North Sea, the sea surface temperatures are positively correlated with NAO (Becker and Pauly, 1996), while subsurface temperatures show no significant correlation with NAO (Tian et al., 2016). Stratification could therefore be (positively) correlated with NAO, but a dedicated study, outside the scope of this paper, would be necessary. Another underlying mechanism linked this time with (1) – sea level – could be the difference of spatial distribution of water level, due to different sea-level pressure and wind stress patterns. This is the hypothesis invoked in Huess and Andersen (2011) to explain the seasonal modulation of M₂ in the North Sea. They ran a barotropic model, forced with tides only and with both tides and meteorological fields; their results show that the M₂ seasonal modulation is better captured when the model is forced with both tides and meteorological fields rather than with tides only. Figure 11a shows the average sea-level pressure during the period 1850–2015, derived from the Twentieth Century Reanalysis (20CR) (Compo et al., 2011; Slivinski et al., 2019). A positive NAO winter (e.g. 1989) corresponds to a situation with a stronger pressure gradient than average, between the two pressure systems of Azores and Iceland (Fig. 11c). By contrast, a negative NAO winter (e.g. 1969) corresponds to a weaker gradient pressure than usual (Fig. 11b). (We define winter here as December–February.) This way, from one year to another, the large-scale atmospheric masses are distributed differently, and as a consequence, the water volumes are also distributed differently in the North Atlantic. In a situation of NAO⁺, the surface waters are pushed onshore by westerly winds, moving from Iceland to the European coasts of France, Spain and Portugal. Figure 12 shows the redistribution of the sea-level pressure, between two years with high and low NAO indices (here 1989 and 1969). Note that this is an extreme situation, as these years have strong positive and negative indices. Assuming an inverse barometer response of sea level, the changes in terms of water level may vary from more than 24 cm in the northwestern part of the area to around −12 cm in the region that includes most of the North-East Atlantic tide gauges considered in this study. This variation of a few tens of centimetres is probably negligible offshore but may have some impact on tide propagation along the continental shelves and in shallow waters. It could also shift slightly the amphidromic points. Assuming that these changes have a similar impact (in terms of magnitude) on M₂ as MSL changes, that is, ±10 % in shallow waters according to recent simulations (Pickering et al., 2017; Idier et al., 2017), we find that they can yield centimetric changes in M₂ amplitude. In other words, their order of magnitude is roughly in agreement with the changes observed in M₂ (Table 1). However, it is difficult to disentangle the effects of stratification and meteorological forcing (sea-level pressure and wind stress) in M₂ changes, and possibly both mechanisms coexist. Dedicated simulations should be conducted to assess the effects of atmospheric forcing on M₂ variability.

Figure 11 Winter sea-level pressure over the North-East Atlantic (a) average over 1850–2015 (b) anomaly in 1969 (NAO⁻) (c) anomaly in 1989 (NAO⁺). Contour intervals are every 2 hPa.

Figure 12 Difference of winter sea-level pressure between 1989 (NAO⁺) and 1969 (NAO⁻) over the North-East Atlantic. Contour intervals are every 4 hPa.

5 Conclusions

We investigated the long-term changes of the principal tidal component M₂ over the North Atlantic coasts. We analysed 18 tide gauges with time series starting no later than 1940. The longest is Brest with 165 years of data. We carefully processed the data, particularly to remove the 18.6-year nodal modulation.

We found that M₂ variations were consistent at all the stations in the North-East Atlantic (Cuxhaven, Delfzijl, Hoek van Holland, Newlyn, Brest), whereas variations appear between stations in the North-West Atlantic. The changes started long before the 20th century and are not linear. The trends vary significantly from one station to another; they are overall positive, up to 2.5 mm/yr, or slightly negative. Since 1990, in many stations, the trends switch from positive to negative values. The significant differences between the trends since 1910 and 1990 indicate caution when interpreting trends based on short records, i.e. less than 30 years, especially if the data are noisy (interannual variability) and the underlying processes non-linear (change points).

Concerning the causes of the observed changes, M₂ varies primarily with the MSL, but MSL rise is not sufficient to explain the variations alone. The similarity between the North Atlantic Oscillation and M₂ variations in the North-East Atlantic suggests a possible influence of the large-scale atmospheric circulation on the tide. Our statistical analysis confirms large correlations at all the stations in the North-East Atlantic. The trend switch observed since 1990 could be the signature of the large-scale atmospheric circulation on the M₂ tide. The underlying mechanism would be a different spatial distribution of water level from one year to another, depending on the low-frequency sea-level pressure patterns, and impacting the propagation of the tide in the North Atlantic basin. In the future, dedicated modelling studies should be undertaken to confirm or discard this hypothesis. These simulations should also allow estimating the effect of the wind (through the Ekman current) and currents on M₂ changes (Devlin et al., 2018).

In this study, we focused only on M₂ amplitude. A similar analysis on the phase lag would draw a more complete picture of the M₂ variations (Müller, 2011; Woodworth, 2010; Ray and Talke, 2019). Other constituents are also affected. Results show that S₂ amplitude decreases at all the stations located in the North-West Atlantic and, in contrast, tends to increase in the North-East Atlantic (not shown). The large-scale decrease of S₂ observed in the North-West Atlantic is consistent with previous studies (e.g. Ray, 2006, in the Gulf of Maine). Further investigations should be definitely conducted to extend this work to more constituents.

The historic data show that the changes started long before the 20th century. This conclusion would not have been possible without the huge work of data rescue undertaken over the past decades (e.g. Pouvreau et al., 2006; Pouvreau, 2008; Bradshaw et al., 2016). This underlines the great importance of sea level data archaeology, which allows extending and improving historical datasets (Pouvreau, 2008; Woodworth et al., 2010; Marcos et al., 2011; Talke and Jay, 2013, 2017; Ray and Talke, 2019; Bradshaw et al., 2015, 2020; Haigh et al., 2019). This is essential for studies related to climate change.

Finally, we should mention several additional limitations and perspectives in this study. (1) We processed the time series considering that they were quality controlled. A fuller analysis of the data quality before processing would probably be valuable. (2) We did not investigate the history of each station. There are probably some local changes (e.g. environment or instrumentation) that may explain a part of the variability of M₂ amplitude and some discrepancies between stations. (3) The tide gauges are located mainly in harbours. They are affected at the same time by local- and regional/global-scale changes, which are difficult to separate. Moreover, they may not be representative of changes offshore. A similar study based on satellite altimetry data would probably be of great interest, even if temporal scale for satellite data is still rather short (i.e. <30 years) compared to climate-scale processes. (4) We focused mainly on the UHSLC dataset, which consists of 249 stations in the Atlantic Ocean. Other relevant stations (which are not in this dataset) may be considered in future studies. (5) We did not investigate the impact of storminess on the tide. Dedicated studies are necessary to estimate if changes in storminess could affect significantly tidal constituents. (6) We used only winter AO and NAO indices, which show more variability than annual indices. A similar analysis with annual indices shows similar results for the correlation with AO or NAO (positive correlation on the North-East Atlantic). With annual rather than monthly indices, the difference of pressure fields will decrease, and as a consequence, the magnitude of the sea-level response will also decrease. Further investigations should be conducted on this point.

Appendix A: Nodal modulation

The M₂ component is subject to a 18.6-year modulation, separated from a neighbouring line in the tidal potential (m₂) whose Doodson number differs in its fifth frequency (255 555 and 255 545 for M₂ and m₂, respectively) (Doodson and Warburg, 1941; Pugh and Woodworth, 2014). This fifth frequency corresponds to N^′, the negative of the mean longitude of the Moon ascending node – hence the “nodal” term – whose period is 18.6 years. Note that there is also another component close to M₂, whose Doodson number differs only from the fifth frequency (255 565), but it is negligible, its amplitude in the tidal potential being only 0.05 % of M₂, whereas m₂ amplitude is 3.7 % of M₂ (Simon, 2007, 2013). With one year of hourly data, the two components M₂ and m₂ cannot be separated by a yearly harmonic analysis (at least 18.6 years are necessary). As a consequence, M₂ amplitude is modulated by m₂. However, we can estimate this modulation and remove it. The harmonic formulation is expressed schematically as a sum of harmonic components:

$$\begin{array}{}\text{(A1)}& h\left(t\right)=\sum _i{a}_i\cos \left(V_i\right(t)-{\mathit{\kappa }}_i),\end{array}$$

where h(t) is the sea level height at time t, V_i(t) is the astronomical argument (computed from Doodson number) and a_i, κ_i the amplitude and phase lag of each component. Considering that M₂ and m₂ are very close in terms of frequency, we can assume that their phase lags are similar (${\mathit{\kappa }}_{M_{\mathrm{2}}}\simeq {\mathit{\kappa }}_{m_{\mathrm{2}}}$). As their difference of astronomical arguments is $V_{m_{\mathrm{2}}}-V_{M_{\mathrm{2}}}=N^{\prime }+\mathit{\pi }$, the M₂ and m₂ contributions to the total water level may be expressed as

$$\begin{array}{}\text{(A2)}& h_{M_{\mathrm{2}}}\left(t\right)+h_{m_{\mathrm{2}}}\left(t\right)=h_{M_{\mathrm{2}}}\left(t\right)[\mathrm{1}+f_{\mathrm{nod}}\cos (N^{\prime }+\mathit{\pi }\left)\right],\end{array}$$

where f_nod, the nodal modulation, is the ratio of the amplitude of m₂ and M₂. As M₂ and m₂ are very close in terms of frequency, f_nod is generally considered as close to the ratio of their amplitude in the tidal potential, $A_{m_{\mathrm{2}}}$ and $A_{M_{\mathrm{2}}}$:

$$\begin{array}{}\text{(A3)}& f_{\mathrm{nod}}={\displaystyle \frac{a_{m_{\mathrm{2}}}}{a_{M_{\mathrm{2}}}}}\simeq {\displaystyle \frac{A_{m_{\mathrm{2}}}}{A_{M_{\mathrm{2}}}}}\simeq \mathrm{0.037}.\end{array}$$

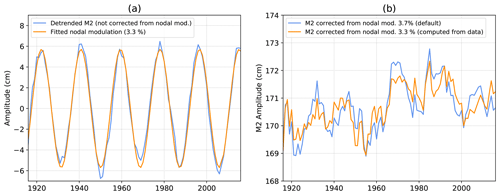
Figure A1 (a) Estimation of the nodal modulation of M₂ amplitude (mean removed) at Newlyn. (b) Impact on M₂ amplitude of the nodal modulation correction at Newlyn. M₂ is detrended in (a) to better fit the nodal modulation.

The negative of the mean longitude of the Moon ascending node is expressed simply as a function of time (p. 116 in Simon, 2007, p. 112 in Simon, 2013):

$$\begin{array}{}\text{(A4)}& N^{\prime }=-N=\mathrm{234.555}+\mathrm{1934.1363}T+\mathrm{0.0021}{T}^{\mathrm{2}},\end{array}$$

with N^′ in degrees, and T the time elapsed since 1 January 2000 at 12:00, expressed in Julian centuries (36 525 d).

The tidal program we used (MAS) corrected M₂ applying the usual 3.7 % nodal modulation (Eq. A3). However, this value may vary significantly from one station to another; Ray (2006) reported values ranging from 2.3 % to 3.6 % in the Gulf of Maine. Here, we computed directly f_nod from the observed data, proceeding as follows. (1) We added the default nodal correction $\mathrm{1}+\mathrm{0.037}\cos (N^{\prime }+\mathit{\pi })$ to the M₂ variations. (2) We detrended the obtained signal removing the last intrinsic mode function (IMF) of an empirical mode decomposition (EMD) (Huang et al., 1998); note that the EMD is an analysis tool which partitions a series into “modes” (i.e. IMFs), the last one being the trend of the signal. (3) We fitted a function $a_{m_{\mathrm{2}}}\cos (N^{\prime }+\mathit{\pi })$ to this detrended signal to estimate $a_{m_{\mathrm{2}}}$, N^′ being expressed as in Eq. (A4). (4) We finally computed f_nod as the ratio between m₂ and M₂ amplitudes (Eq. A3). Figure A1a shows an example of estimate of M₂ modulation at Newlyn: the fit leads to a nodal modulation of 3.3 %. Note that this value is consistent with Woodworth (2010) (3.2 %), whereas Woodworth et al. (1991) gave a slightly different value (2.8 %). Figure A1b shows the impact of this value rather than the default one: oscillations of 18.6 years are clearly reduced. Note that in this study, the m₂ amplitude – and then the nodal correction – could have been computed from the full time series harmonic analysis, as records are longer than 18.6 years. However, the method presented here to compute the nodal correction can be applied even for time series shorter than 18.6 years.

The computed nodal modulations are summarized in Table 1 (column 6). They vary from 0.8 % to 4.1 %. Note that these values are consistent with those obtained by previous authors (Ray, 2006; Müller, 2011; Woodworth, 2010; Ray and Talke, 2019). Only the value at Charleston differs significantly: 3.0 % in our study compared to 3.7 % in Müller (2011).

Appendix B: Time series of annual M₂ amplitude at all the stations

Figure B1 Annual M₂ amplitude at the 18 selected tide gauges.