Drifting dynamics of the bluebottle (Physalia physalis)

Physalia physalis, also called the bluebottle in Australia, is a colonial animal resembling a jellyfish that is well known to beachgoers for the painful stings delivered by its tentacles. Despite being a common occurrence, the origin of the bluebottle before reaching the coastline is not well understood, and neither is the way it drifts at the surface of the ocean. Previous studies used numerical models in combination with simple assumptions to calculate the drift of this species, excluding complex drifting dynamics. In this study, we provide a new parameterization for Lagrangian modelling of the bluebottle by considering the similarities between the bluebottle and a sailboat. This allows us to compute the hydrodynamic and aerodynamic forces acting on the bluebottle and use an equilibrium condition to create a generalized model for calculating the drifting speed and course of the bluebottle under any wind and ocean current conditions. The generalized model shows that the velocity of the bluebottle is a linear combination of the ocean current velocity and the wind velocity scaled by a coefficient (“shape parameter”) and multiplied by a rotation matrix. Adding assumptions to this generalized model allows us to retrieve models used in previous literature. We discuss the sensitivity of the model to different parameters (shape, angle of attack and sail camber) and explore different cases of wind and current conditions to provide new insights into the drifting dynamics of the bluebottle.

1 Introduction

Physalia physalis (Fig. 1), also called the Indo-Pacific Portuguese man o' war or the bluebottle (Physalia utriculus, a synonym), is well known on the east coast of Australia for stinging tens of thousands of beachgoers each year (Daw et al., 2020). The species is found throughout the world's oceans, in tropical, subtropical and (occasionally) temperate regions (Munro et al., 2019). The bluebottle resembles a jellyfish but is actually a siphonophore, a colonial organism composed of small individual animals called zooids (Totton and Mackie, 1960). There are four zooids depending on each other for survival and performing different functions, such as digestion (gastrozooids), reproduction (gonozooids) and hunting (dactylozooids). The last zooid, the pneumatophore, is a gas-filled float or sac that supports the other zooids and acts like a sail so the bluebottle is constrained to the ocean surface, moving at the mercy of the wind, waves and marine currents. The bluebottle's long tentacles hang below the float as they drift, fishing for prey to sting and drag up to their digestive zooids (Totton and Mackie, 1960).

Figure 1 Photograph of a bluebottle taken at Coogee Beach, Sydney. Courtesy of Lisa Clarke.

For each bluebottle, the float can be oriented towards the left or the right (dimorphism), believed to be an adaptation that prevents the entire population from being washed on shore to die (Totton and Mackie, 1956; Woodcock, 1944). The “left-handed” bluebottles sail to the right of the wind, while the “right-handed” bluebottles sail to the left. The wind will always push the two types of bluebottles in different directions, so at most half the population will be pushed towards the coast (Totton and Mackie, 1956; Woodcock, 1944). The Atlantic Portuguese man o' war (PMW) is considered the same species as the bluebottle, but with key differences in their size and the number of long tentacles used for hunting. The bluebottle's float rarely exceeds 10 cm and it has one long hunting tentacle that is less than 3 m in length (Fig. 1). In comparison, the PMW has floats of around 15 cm, reported up to 30 cm, and several hunting tentacles that can reach 30 m in mature colonies when fully extended (Munro et al., 2019).

Due to their inability to swim, the movement of the bluebottle can be modelled by calculating the forces acting on it, or by advecting virtual particles in ocean and atmospheric circulation models. Previous studies modelled the movement of the PMW with Lagrangian particle tracking to explain major beaching events. For example, Ferrer and Pastor (2017) were able to estimate the region of origin of a significant beaching event on the Basque coast in August 2010. They ran a Lagrangian model backwards in time, using wind velocity (V_A) and a wind drag coefficient (λ=4.5 %) as drivers of the PMW motion (V_bb=λV_A). They found that the region of origin was the North Atlantic subtropical gyre. Prieto et al. (2015) included both the effect of the surface currents (u) and wind (${\mathit{V}}_{\mathrm{bb}}=\mathit{u}+\mathit{\lambda }{\mathit{V}}_{\mathrm{A}}$) to predict initial colony position of major beaching events in the Mediterranean in 2010. This model assumed the PMW was advected by the surface currents, with the effect of the wind being added with a much higher wind drag coefficient of 10 %. Similarly, Headlam et al. (2020) used beaching and offshore observations to identify a region of origin, using the joint effects of surface currents and wind drag, for the largest mass PMW beaching on the Irish coastline in over 150 years.

These previous models made the key assumption that the PMW's sailing direction is the same as the wind direction. This may be based on the observation by Totton and Mackie (1960) that in winds stronger than force 4 (i.e. over 8 m s⁻¹), the PMW would sail straight downwind with its sail parallel to the wind direction. However, it should be noted that this was a second-hand visual observation of one instance by a single individual. In addition, Totton and Mackie (1960) performed their own experiments and observed that in light winds (about 4 m s⁻¹) the PMW balances itself at approximately 40^∘ to the wind (angle of attack), resulting in a completely different course of about 45^∘ relative to the wind. In another experiment, Shannon and Chapman (1983) found that left- and right-handed specimens would separate by about 40^∘ in force 7–8 winds (14–21 m s⁻¹). This suggests a course of about 20^∘ relative to the wind rather than both drifting downwind. More recently, Ferrer and González (2020) improved on the model from Ferrer and Pastor (2017) by analysing the same beaching event but incorporating dimorphism and different drift angles relative to the wind direction. They found different regions of origin depending on the drifting angle considered and concluded that the PMWs were likely right-handed.

Iosilevskii and Weihs (2009) took a different approach by expressing the forces acting on the PMW. By considering the equilibrium condition of the aerodynamic (above water) and hydrodynamic (below water) forces, when the velocity of the PMW is constant, they derive equations that can be solved for the PMW's speed and direction of motion relative to the wind. However, they consider a situation with no background ocean current, where the hydrodynamic force is only the drag, opposed to the PMW course. Here, we expand that model by adding the effect of the ocean current and simplifying the model down to an intuitive generalized vector form which could be implemented in Lagrangian models. We also analyse the impact of key variables such as angle of attack and sail camber (Sect. 4.3).

This paper is structured as follows. First, we explain the methods and key assumptions used for our theoretical model (Sect. 2), followed by the force balance acting on the bluebottle (Sect. 3). We then solve the equilibrium condition (Sect. 4.1), discuss the parameters in the model (Sect. 4.2 and 4.3) and apply the model to a few special cases that were chosen as instructive examples of the bluebottle's sailing dynamics (Sect. 5). Finally, we compare our results to previous studies and discuss some variables that were not included in the model (Sect. 6).

2 Methods

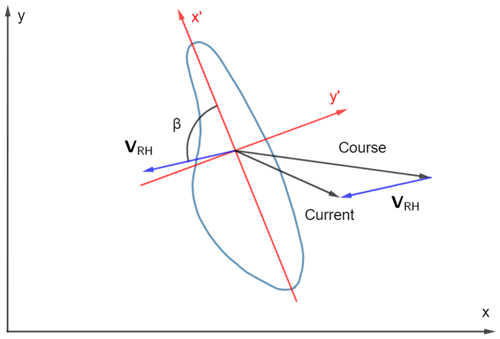
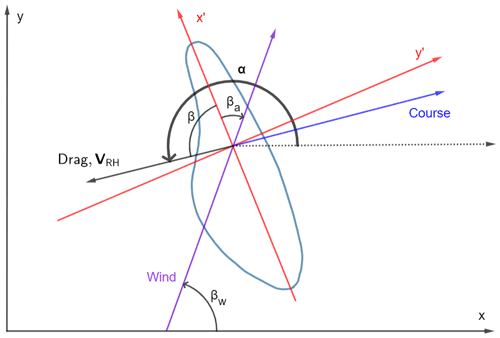
The bluebottle undergoes similar forces to those of a sailboat. Therefore, like Iosilevskii and Weihs (2009), we consider the aerodynamic and hydrodynamic forces acting on the bluebottle, as with a sailboat (Szelangiewicz and Żelazny, 2018). The aerodynamic force, generated by the wind blowing against the bluebottle's sail, is split into two components, $F_{\mathrm{A}{y}^{\prime }}$ (perpendicular to sail) and $F_{\mathrm{A}{x}^{\prime }}$ (parallel to sail), as shown in Fig. 2. The magnitude of the aerodynamic force is dependent on the wind speed, the area of the sail and the orientation of the bluebottle to the wind, which we call the angle of attack β_a (Fig. 2). We also refer to the angle between the x axis and the wind as β_w, using the standard x and y axes, which are east/west and north/south, respectively.

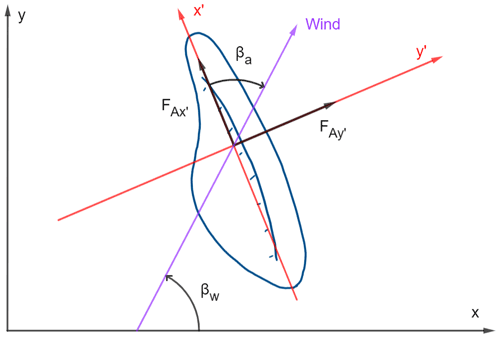
Figure 2 Top-down view of a left-handed (right-sailing) bluebottle. x^′, y^′, x and y axes are defined in Sect. 2. $F_{\mathrm{A}{x}^{\prime }}$ and $F_{\mathrm{A}{y}^{\prime }}$ are the components of the aerodynamic force on the x^′ and y^′ axes, respectively. β_a is the angle of attack. β_w is the angle of the wind.

The hydrodynamic force is caused by the interactions of the water with the submerged body of the bluebottle. The wind-driven motion of the bluebottle through the water creates a hydrodynamic drag opposite to the direction of motion. The sum of the wind-driven drag and the bluebottle motion due to the background ocean current results in a relative current, which determines the total hydrodynamic force acting on the bluebottle. Compared to Iosilevskii and Weihs (2009), here we add the effect of the ocean current but we do not consider the drag caused by the tentacles (see discussion in Sect. 6) and assume that the submerged part of the bluebottle is a cylinder. This is a reasonable assumption since the bluebottle has only one tentacle which is much shorter than the PMW's tentacles. The submerged body is important for drag but does not have a directional component to it because it is cylindrical. This differs from the submerged part of a sailboat, which has a long straight keel sticking down from the bottom of the boat. The keel minimizes sideways motion and rotation, allowing the boat to maximize forward motion. Since the bluebottle's body has no keel and is assumed to be perfectly symmetrical, it does not restrict rotation and the orientation of the bluebottle will be completely determined by the wind. Furthermore, the bluebottle's motion will not be restricted by a keel, so it can move forward, sideways or at any other angle with respect to its sail.

The forces acting on the bluebottle will be expressed as components on two axes where the force coefficients and affected surface areas are most easily calculated. We call these the x^′ and y^′ axes, and they are defined relative to the bluebottle's sail. The x^′ axis is along the chord of the sail. The y^′ axis is perpendicular to the x^′ axis and goes through the centre of the sail, which is also assumed to be symmetric (Fig. 2). We use the axes labels as subscripts for variables that are related to specific axes. Any vectors in this paper are labelled in bold text and their components are the standard x and y components. Angles that are measured anticlockwise are considered positive, while angles that are measured clockwise are considered negative. The only exception to this is β, which is always considered positive starting from the x^′ axis (Fig. 3).

3 Forces acting on the bluebottle

We now present the formulas that represent the aerodynamic and hydrodynamic forces acting on the bluebottle. Compared to Iosilevskii and Weihs (2009), we choose not to consider the moment force or the distances between the aerodynamic centre of effort and the hydrodynamic centre of effort, as these variables would require very rough estimates. Furthermore, Iosilevskii and Weihs (2009) do not use these variables in the final equations that describe the course and speed but rather use them to analyse the PMW's sail contraction and tilting of their tentacles – which we do not consider here. The moment force would result in a torque, and thus the orientation of the bluebottle would be influenced by a combination of the wind and current conditions. However, similarly to the leeway methodology (discussed further in Sect. 6), the orientation behaviour of the bluebottle (mainly represented by the angle of attack) can instead be determined by observations made in physical experiments.

3.1 Aerodynamic force

The aerodynamic force on the bluebottle F_A is expressed as components on the x^′ and y^′ axes. This can be represented by the standard aerodynamic force equation, often used for lift and drag force on an aeroplane wing, for instance.

$$\begin{array}{}\text{(1)}& {\displaystyle }\left\{\begin{array}{ll}{F}_{\mathrm{A}{x}^{\prime }}& =\frac{\mathrm{1}}{\mathrm{2}}{\mathit{\rho }}_{\mathrm{A}}{S}_{{\mathrm{x}}^{\prime }}{V}_{\mathrm{A}}^{\mathrm{2}}{C}_{\mathrm{A}{x}^{\prime }}\\ F_{\mathrm{A}{y}^{\prime }}& =\frac{\mathrm{1}}{\mathrm{2}}{\mathit{\rho }}_{\mathrm{A}}{S}_{{\mathrm{y}}^{\prime }}{V}_{\mathrm{A}}^{\mathrm{2}}{C}_{\mathrm{A}{y}^{\prime }},\end{array}\right.\end{array}$$

where ρ_A is the density of the air (taken as 1.225 kg m⁻³), $S_{{\mathrm{x}}^{\prime }}$ and $S_{{\mathrm{y}}^{\prime }}$ are the areas of the sail perpendicular to the respective axis, $C_{\mathrm{A}{x}^{\prime }}$ and $C_{\mathrm{A}{y}^{\prime }}$ are the respective force coefficients, and V_A is the wind speed. Wind speed is used rather than relative wind speed because the speed of the bluebottle is at least 1 order of magnitude smaller compared to the wind speed.

The areas $S_{x^{\prime }}$ and $S_{y^{\prime }}$ are fixed values for a particular bluebottle. On the other hand, the force coefficients $C_{\mathrm{A}{x}^{\prime }}$ and $C_{\mathrm{A}{y}^{\prime }}$ are functions of the angle of attack β_a. Note that here we separately calculate the components of the aerodynamic force on two different axes. This is because the values of the x^′ and y^′ force coefficients and areas will vary significantly.

Considering the order of magnitude of the parameters (discussed in Sect. 4.2), for wind speeds from 1 to 10 m s⁻¹, $F_{\mathrm{A}{x}^{\prime }}$ will range from $\mathrm{7}\times {\mathrm{10}}^{-\mathrm{6}}$ to $\mathrm{7}\times {\mathrm{10}}^{-\mathrm{4}}$ N, and $F_{\mathrm{A}{y}^{\prime }}$ will range from $\mathrm{1}\times {\mathrm{10}}^{-\mathrm{4}}$ to $\mathrm{1}\times {\mathrm{10}}^{-\mathrm{2}}$ N.

3.2 Hydrodynamic force

The hydrodynamic force on the bluebottle F_H is dependent on the relative current, which is the current felt by the bluebottle as it is in motion. The magnitude of the hydrodynamic force can be represented by an equation of the same form as the aerodynamic force.

$$\begin{array}{}\text{(2)}& {\displaystyle }{F}_{\mathrm{H}}={\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}{\mathit{\rho }}_{\mathrm{H}}{S}_{\mathrm{H}}{V}_{\mathrm{RH}}^{\mathrm{2}}{C}_{\mathrm{H}},\end{array}$$

where ρ_H is the density of the water (taken as 1025 kg m⁻³), S_H is the projected area of the submerged bluebottle surface onto the bluebottle's plane of symmetry, C_H is the force coefficient, and V_RH is the speed of the current relative to the bluebottle (Fig. 3). Considering the order of magnitude of the parameters, F_H will range from $\mathrm{1}\times {\mathrm{10}}^{-\mathrm{4}}$ to $\mathrm{1}\times {\mathrm{10}}^{-\mathrm{2}}$ N.

The hydrodynamic force F_H is calculated using a single equation, thus using just one value for both the area and the force coefficient. Unlike the aerodynamic force, we do not need to calculate two components of the force separately. This is because the submerged body of the bluebottle is close to cylindrical, so there is not much variance in the value of the area or force coefficient. The relative speed of the current can be represented by

$$\begin{array}{}\text{(3)}& {\displaystyle }{V}_{\mathrm{RH}}{\displaystyle }=\sqrt{V_{\mathrm{RH}x}^{\mathrm{2}}+V_{\mathrm{RH}y}^{\mathrm{2}}},\end{array}$$

with

$$\begin{array}{}\text{(4)}& {\displaystyle }\left\{\begin{array}{ll}{V}_{\mathrm{RH}x}& =u-V_{\mathrm{bb}x}\\ V_{\mathrm{RH}y}& =v-V_{\mathrm{bb}y},\end{array}\right.\end{array}$$

where V_RHx and V_RHy are the components of the relative velocity of the current in the respective axes, u and v are the x and y components of the ocean current velocity, and V_bbx and V_bby are the x and y components of the bluebottle velocity vector.

To later solve for the equilibrium condition (Sect. 4.1), when the velocity of the bluebottle is constant, we require the hydrodynamic force on the x^′ and y^′ axes. This is represented by

$$\begin{array}{}\text{(5)}& {\displaystyle }\left\{\begin{array}{ll}{F}_{\mathrm{H}{x}^{\prime }}& =F_{\mathrm{H}}\cos \mathit{\beta }\\ F_{\mathrm{H}{y}^{\prime }}& =F_{\mathrm{H}}\sin \mathit{\beta },\end{array}\right.\end{array}$$

where β is the angle between the x^′ axis and the relative velocity of the current (Fig. 3).

Figure 3 Relative current velocity V_RH is the difference between the ocean current velocity and the bluebottle's velocity (called course). β is the angle between the x^′ axis and the relative velocity of the current.

4 Solving bluebottle velocity

4.1 Equations

We now solve for the equilibrium condition, where the velocity of the bluebottle will be constant; hence, there is no acceleration since the bluebottle does not swim. Based on Newton's Second Law of Motion, this occurs when the net forces acting on the bluebottle are zero. Hence, the aerodynamic and hydrodynamic forces must be equal in magnitude on each axis. Expressing the equilibrium conditions,

$$\begin{array}{}\text{(6)}& {\displaystyle }\left\{\begin{array}{ll}{F}_{\mathrm{A}{x}^{\prime }}& =F_{\mathrm{H}{x}^{\prime }}\\ F_{\mathrm{A}{y}^{\prime }}& =F_{\mathrm{H}{y}^{\prime }},\end{array}\right.\end{array}$$

along the x^′ and y^′ axes yields the following equations:

$$\begin{array}{}\text{(7)}& {\displaystyle }\left\{\begin{array}{ll}{\mathit{\rho }}_{\mathrm{A}}{S}_{x^{\prime }}{V}_{\mathrm{A}}^{\mathrm{2}}{C}_{\mathrm{A}{x}^{\prime }}& ={\mathit{\rho }}_{\mathrm{H}}{S}_{\mathrm{H}}{V}_{\mathrm{RH}}^{\mathrm{2}}{C}_{\mathrm{H}}\cos \mathit{\beta }\\ {\mathit{\rho }}_{\mathrm{A}}{S}_{y^{\prime }}{V}_{\mathrm{A}}^{\mathrm{2}}{C}_{\mathrm{A}{y}^{\prime }}& ={\mathit{\rho }}_{\mathrm{H}}{S}_{\mathrm{H}}{V}_{\mathrm{RH}}^{\mathrm{2}}{C}_{\mathrm{H}}\sin \mathit{\beta }.\end{array}\right.\end{array}$$

Dividing the equations in Eq. (7) gives

$$\begin{array}{}\text{(8)}& {\displaystyle \frac{S_{y^{\prime }}}{S_{x^{\prime }}}}{\displaystyle \frac{C_{\mathrm{A}{y}^{\prime }}}{C_{\mathrm{A}{x}^{\prime }}}}=\tan \mathit{\beta },\end{array}$$

while taking the sum of squares of the equations in Eq. (7), then simplifying and taking the root gives

$$\begin{array}{}\text{(9)}& \begin{array}{rl}{V}_{\mathrm{RH}}^{\mathrm{2}}& ={\displaystyle \frac{{\mathit{\rho }}_{\mathrm{A}}{V}_{\mathrm{A}}^{\mathrm{2}}\sqrt{(S_{x^{\prime }}{C}_{\mathrm{A}{x}^{\prime }}{)}^{\mathrm{2}}+(S_{y^{\prime }}{C}_{\mathrm{A}{y}^{\prime }}{)}^{\mathrm{2}}}}{{\mathit{\rho }}_{\mathrm{H}}{S}_{\mathrm{H}}{C}_{\mathrm{H}}}}\\ V_{\mathrm{RH}}& =\mathit{\lambda }{V}_{\mathrm{A}},\end{array}\end{array}$$

where

$$\mathit{\lambda }=\sqrt{{\displaystyle \frac{{\mathit{\rho }}_{\mathrm{A}}\sqrt{(S_{{\mathrm{x}}^{\prime }}{C}_{\mathrm{A}{x}^{\prime }}{)}^{\mathrm{2}}+(S_{{\mathrm{y}}^{\prime }}{C}_{\mathrm{A}{y}^{\prime }}{)}^{\mathrm{2}}}}{{\mathit{\rho }}_{\mathrm{H}}{S}_{\mathrm{H}}{C}_{\mathrm{H}}}}}.$$

This equation gives an expression for the coefficient λ (shape parameter), where previous studies have used constant values. We see that λ is based on the ratio of densities, bluebottle areas and force coefficients. Note that λ is also dependent on the angle of attack β_a, since this affects the value of the force coefficients.

Once β and V_RH are known from Eqs. (8) and (9), we calculate the velocity and course of the bluebottle in terms of the x and y axes. The x and y components of V_RH, the relative velocity of the current, are

$$\begin{array}{}\text{(10)}& {\displaystyle }\left\{\begin{array}{ll}{V}_{\mathrm{RH}x}& =V_{\mathrm{RH}}\cos \mathit{\alpha }\\ V_{\mathrm{RH}y}& =V_{\mathrm{RH}}\sin \mathit{\alpha },\end{array}\right.\end{array}$$

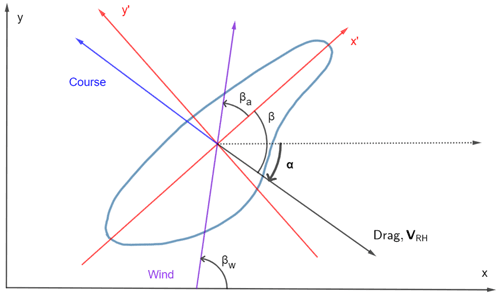
where α is the angle between the x axis and the relative current vector. Relating α to known angles (Fig. 2) gives

$$\begin{array}{}\text{(11)}& {\displaystyle }\mathit{\alpha }& {\displaystyle }=\mathit{\beta }-{\mathit{\beta }}_{\mathrm{a}}+{\mathit{\beta }}_{\mathrm{w}}\text{, for a left-handed bluebottle (Fig. 8)}\text{(12)}& {\displaystyle }\mathit{\alpha }& {\displaystyle }=-\mathit{\beta }-{\mathit{\beta }}_{\mathrm{a}}+{\mathit{\beta }}_{\mathrm{w}}\text{, for a right-handed bluebottle (Fig. A1)},\end{array}$$

where β_w is the angle of the wind (between the x axis and the wind), and β_a is the angle of attack (between the x^′ axis and the wind, Fig. 2) and β is the angle between the x^′ axis and the relative velocity of the current (Fig. 3). Note that β is always considered positive. To find α, we choose a constant value for β_a (see Sect. 5 and Fig. 8). The absolute direction of the wind β_w should also be known.

Once α is known, we find the velocity of the bluebottle relative to the x and y axes using Eqs. (4) and (10):

$$\begin{array}{}\text{(13)}& {\displaystyle }\left\{\begin{array}{ll}{V}_{\mathrm{bb}x}& =u-V_{\mathrm{RH}}\cos \mathit{\alpha }\\ V_{\mathrm{bb}y}& =v-V_{\mathrm{RH}}\sin \mathit{\alpha }.\end{array}\right.\end{array}$$

Finally, using Eq. (9),

$$\begin{array}{}\text{(14)}& {\displaystyle }\left\{\begin{array}{ll}{V}_{\mathrm{bb}x}& =u-\mathit{\lambda }{V}_{\mathrm{A}}\cos \mathit{\alpha }\\ V_{\mathrm{bb}y}& =v-\mathit{\lambda }{V}_{\mathrm{A}}\sin \mathit{\alpha }.\end{array}\right.\end{array}$$

Here, we can see the bluebottle velocity is a linear combination of the current velocity and wind velocity with some scaling and rotation. However, the velocity is non-linear with respect to the angle of attack, since both α and λ are dependent on β_a.

This solution for the bluebottle's velocity can be expressed in a generalized vector form. For a left-handed bluebottle, we have

$$\begin{array}{ll}{\displaystyle }{\mathit{V}}_{\mathrm{bb}}& {\displaystyle }=\mathit{u}-\mathit{\lambda }{V}_{\mathrm{A}}\left(\begin{array}{c}\cos \mathit{\alpha }\\ \sin \mathit{\alpha }\end{array}\right),\text{ with }\mathit{u}=(u,v)\\ {\displaystyle }& {\displaystyle }=\mathit{u}-\mathit{\lambda }{V}_{\mathrm{A}}\left(\begin{array}{c}\cos (\mathit{\beta }-{\mathit{\beta }}_{\mathrm{a}}+{\mathit{\beta }}_{\mathrm{w}})\\ \sin (\mathit{\beta }-{\mathit{\beta }}_{\mathrm{a}}+{\mathit{\beta }}_{\mathrm{w}})\end{array}\right)\\ {\displaystyle }& {\displaystyle }=\mathit{u}-\mathit{\lambda }{V}_{\mathrm{A}}\left(\begin{array}{c}\cos (\mathit{\beta }-{\mathit{\beta }}_{\mathrm{a}})\cos {\mathit{\beta }}_{\mathrm{w}}-\sin (\mathit{\beta }-{\mathit{\beta }}_{\mathrm{a}})\sin {\mathit{\beta }}_{\mathrm{w}}\\ \sin (\mathit{\beta }-{\mathit{\beta }}_{\mathrm{a}})\cos {\mathit{\beta }}_{\mathrm{w}}+\cos (\mathit{\beta }-{\mathit{\beta }}_{\mathrm{a}})\sin {\mathit{\beta }}_{\mathrm{w}}\end{array}\right).\end{array}$$

Now using the x and y components of the wind velocity, V_Ax=V_Acos β_w and V_Ay=V_Asin β_w, we have

$$\begin{array}{ll}{\displaystyle }{\mathit{V}}_{\mathrm{bb}}& {\displaystyle }=\mathit{u}-\mathit{\lambda }{V}_{\mathrm{A}x}\left(\begin{array}{c}\cos (\mathit{\beta }-{\mathit{\beta }}_{\mathrm{a}})\\ \sin (\mathit{\beta }-{\mathit{\beta }}_{\mathrm{a}})\end{array}\right)-\mathit{\lambda }{V}_{\mathrm{A}y}\left(\begin{array}{c}-\sin (\mathit{\beta }-{\mathit{\beta }}_{\mathrm{a}})\\ \cos (\mathit{\beta }-{\mathit{\beta }}_{\mathrm{a}})\end{array}\right)\\ {\displaystyle }& {\displaystyle }=\mathit{u}-\mathit{\lambda }\left(\begin{array}{cc}\cos (\mathit{\beta }-{\mathit{\beta }}_{\mathrm{a}})& -\sin (\mathit{\beta }-{\mathit{\beta }}_{\mathrm{a}})\\ \sin (\mathit{\beta }-{\mathit{\beta }}_{\mathrm{a}})& \cos (\mathit{\beta }-{\mathit{\beta }}_{\mathrm{a}})\end{array}\right)\left(\begin{array}{c}{V}_{\mathrm{A}x}\\ V_{\mathrm{A}y}\end{array}\right)\\ {\displaystyle }& {\displaystyle }=\mathit{u}-\mathit{\lambda }\left(\begin{array}{cc}\cos (\mathit{\beta }-{\mathit{\beta }}_{\mathrm{a}})& -\sin (\mathit{\beta }-{\mathit{\beta }}_{\mathrm{a}})\\ \sin (\mathit{\beta }-{\mathit{\beta }}_{\mathrm{a}})& \cos (\mathit{\beta }-{\mathit{\beta }}_{\mathrm{a}})\end{array}\right){\mathit{V}}_{\mathrm{A}}.\end{array}$$

Using the trigonometric identities $\cos \mathit{\theta }=-\cos (\mathrm{180}{}^{\circ }-\mathit{\theta })$ and $\sin \mathit{\theta }=\sin (\mathrm{180}{}^{\circ }-\mathit{\theta })$, we have

$${\displaystyle }{\mathit{V}}_{\mathrm{bb}}{\displaystyle }=\mathit{u}+\mathit{\lambda }\left(\begin{array}{cc}\cos (\mathrm{180}{}^{\circ }-\mathit{\beta }+{\mathit{\beta }}_{\mathrm{a}})& \sin (\mathrm{180}{}^{\circ }-\mathit{\beta }+{\mathit{\beta }}_{\mathrm{a}})\\ -\sin (\mathrm{180}{}^{\circ }-\mathit{\beta }+{\mathit{\beta }}_{\mathrm{a}})& \cos (\mathrm{180}{}^{\circ }-\mathit{\beta }+{\mathit{\beta }}_{\mathrm{a}})\end{array}\right){\mathit{V}}_{\mathrm{A}},$$

and finally

$$\begin{array}{}\text{(15)}& {\displaystyle }{\mathit{V}}_{\mathrm{bb}}{\displaystyle }=\mathit{u}+\mathit{\lambda }\mathbf{R}(\mathrm{180}{}^{\circ }-\mathit{\beta }+{\mathit{\beta }}_{\mathrm{a}}){\mathit{V}}_{\mathrm{A}},\end{array}$$

where R represents the rotation matrix. Similarly, for a right-handed bluebottle, we have

$$\begin{array}{}\text{(16)}& {\displaystyle }{\mathit{V}}_{\mathrm{bb}}{\displaystyle }=\mathit{u}+\mathit{\lambda }\mathbf{R}(\mathrm{180}{}^{\circ }+\mathit{\beta }+{\mathit{\beta }}_{\mathrm{a}}){\mathit{V}}_{\mathrm{A}}.\end{array}$$

These results show that the velocity of the bluebottle is a linear combination of the ocean current velocity vector u and the wind velocity vector scaled by the shape parameter λ and multiplied by a clockwise rotation matrix of $\mathrm{180}{}^{\circ }-\mathit{\beta }+{\mathit{\beta }}_{\mathrm{a}}$. This can be interpreted as the bluebottle simply drifting with the current, while the force imparted by the wind on the sail is a proportion (λ) of the wind velocity at an angle of $\mathrm{180}{}^{\circ }-\mathit{\beta }+{\mathit{\beta }}_{\mathrm{a}}$ clockwise from the wind direction.

We refer to Eqs. (15) and (16) as a generalized vector form. By adding assumptions, we can simplify our form to match Lagrangian models seen in previous literature. Hence, we can explain the assumptions required to use these previous models. This vector form is the link between the practical papers that used simple vector models (Ferrer and Pastor, 2017; Ferrer and González, 2020; Prieto et al., 2015) and the theoretical bottom-up approach used by Iosilevskii and Weihs (2009).

4.2 Determining parameters

The formulation shown in Eqs. (15) and (16) for the velocity of the bluebottle depends on several parameters. Firstly, we will consider the parameters required to find the shape parameter λ (see Eq. 9).

The areas required were measured from photographs taken at Coogee Beach, Sydney, on 23 January 2019. $S_{y^{\prime }}$ (area of the bluebottle's sail on the y^′ axis) was measured by estimating the area as a segment of a circle. This gave a value of $\mathrm{3}\mathit{\pi }-\frac{\mathrm{9}\sqrt{\mathrm{3}}}{\mathrm{4}}{\mathrm{cm}}^{\mathrm{2}}$ (approximately 5.5 cm²). $S_{x^{\prime }}$ (area of the bluebottle's sail on the x^′ axis) was measured by estimating the area as a triangle. This gave a value of 1.12 cm².

We assume the submerged body of the bluebottle is a cylinder, so S_H will be the rectangular cross section made by cutting through the cylinder's diameter. This is measured as 3.78 cm². Note that the tentacles are not taken into account since they can retract or vary their angle. C_H can be estimated as the drag coefficient of a cylinder, which is dependent on Reynolds number. The Reynolds number (for seawater) is defined as

$$\begin{array}{}\text{(17)}& \mathit{Re}={\displaystyle \frac{{\mathit{\rho }}_{\mathrm{H}}uL}{\mathit{\mu }}},\end{array}$$

where u is the current speed with respect to the bluebottle (order of 0.1–1 m s⁻¹), L is the characteristic length dimension (simply the diameter for a cylinder, which is 0.027 m), and μ is the dynamic viscosity of seawater (order of 10⁻³ Pa s, dependent on temperature). This gives a Reynolds number between 2781 and 27810 (turbulent flow). For these values, the drag coefficient of a cylinder is very close to 1, so we estimate C_H as 1.

The force coefficients $C_{\mathrm{A}{x}^{\prime }}$ and $C_{\mathrm{A}{y}^{\prime }}$ depend on the orientation of the bluebottle relative to the wind, which is measured by the angle of attack β_a. $C_{\mathrm{A}{x}^{\prime }}$ does not need to be estimated accurately because its value has little effect on the bluebottle's course and speed, since the product $S_{{\mathrm{x}}^{\prime }}{C}_{\mathrm{A}{x}^{\prime }}$ (used in Eqs. 8 and 9) is O(10⁻⁵) while $S_{{\mathrm{y}}^{\prime }}{C}_{\mathrm{A}{y}^{\prime }}$ is O(10⁻⁴). Hence, for $C_{\mathrm{A}{x}^{\prime }}$, we use the same constant value as Iosilevskii and Weihs (2009), which is 0.1.

Iosilevskii and Weihs (2009) derive the following expression for the force coefficient $C_{\mathrm{A}{y}^{\prime }}$ as a function of angle of attack by considering the aerodynamic forces acting on a wing surface (slender sail theory).

$$\begin{array}{ll}\text{(18)}& {\displaystyle }{C}_{\mathrm{A}{y}^{\prime }}& {\displaystyle }={\displaystyle \frac{\mathit{\pi }A}{\mathrm{2}}}{\mathit{\beta }}_{\mathrm{a}}+{\displaystyle \frac{\mathrm{4}\mathit{\pi }A}{\mathrm{3}}}{\displaystyle \frac{f_{\mathrm{0}}}{c}}{\displaystyle }A& {\displaystyle }={\displaystyle \frac{b^{\mathrm{2}}}{S_{{\mathrm{y}}^{\prime }}}},\end{array}$$

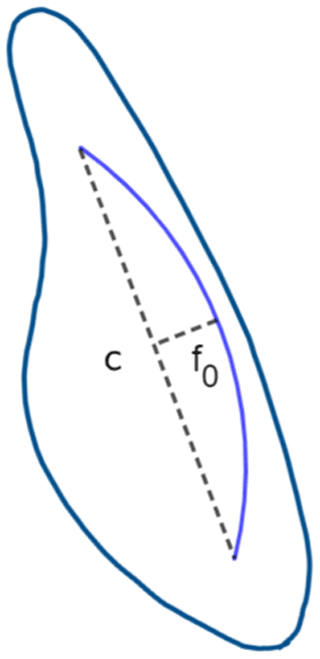
where A is the aspect ratio of the sail (calculated using b, the sail height, and $S_{{\mathrm{y}}^{\prime }}$, the sail area), β_a is the angle of attack (see Fig. 2), f₀ is the sail camber, and c is the sail chord (Fig. 4). f₀/c is referred to as the camber ratio.

Figure 4 Camber of a bluebottle sail. f₀ is the sail camber and c is the sail chord.

Using our bluebottle measurements, we have an aspect ratio of roughly 0.35 (half the value used by Iosilevskii and Weihs (2009), whose estimates were based on the PMW) and a sail chord of 5.2 cm.

It should be noted that in aerodynamic theory (for example, Abbott et al., 1945), it has been found that the lift coefficient of an airfoil increases roughly linearly with angle of attack until the lift coefficient approaches a maximum. This expression does not take this maximum into account.

4.3 Influence of angle of attack on bluebottle course

In this section, we discuss two key parameters: the angle of attack and the sail camber. These are related to the aerodynamic force, so we will assume there is no current and examine how changing the angle of attack varies the bluebottle's course relative to the wind. Firstly, a change in the angle of attack means the orientation of the bluebottle relative to the wind is changing. This results in a different course relative to the wind. Secondly, the force coefficient $C_{\mathrm{A}{y}^{\prime }}$ changes based on the angle of attack, which also varies the bluebottle's course (Eq. 8).

From the parameterization of $C_{\mathrm{A}{y}^{\prime }}$ (Eq. 18), the effect of the angle of attack on the bluebottle's course is dependent on the camber of the sail. Figure 5 illustrates such a link, showing that the camber is only relevant at low angles of attack (0 to 10^∘). At higher angles of attack the relationship between angle of attack and the bluebottle course relative to the wind becomes linear. This is because $C_{\mathrm{A}{y}^{\prime }}$ has become sufficiently large and hence the change in $C_{\mathrm{A}{y}^{\prime }}$ is insignificant. At this point, a 10^∘ change in the bluebottle's orientation simply results in a 10^∘ change in the bluebottle's course. As the camber becomes large, $C_{\mathrm{A}{y}^{\prime }}$ becomes sufficiently large even at zero angle of attack, and the relationship tends towards linearity.

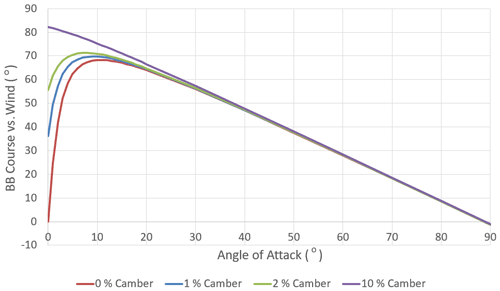
Figure 5 Bluebottle course relative to the wind (0^∘ means a downwind course) as a function of angle of attack (0^∘ means sail parallel to the wind) for different sail camber ratios.

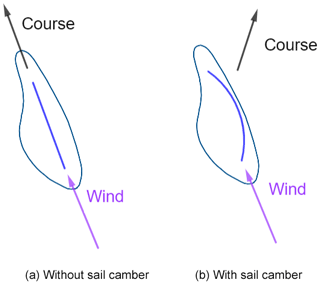
Figure 6 Bluebottle course at zero angle of attack is dependent on the sail camber. Panel (a) shows a bluebottle with no camber sailing straight downwind with sail parallel to the wind direction. Panel (b) shows a bluebottle with camber. Due to the curvature of the sail, even at zero angle of attack, the bluebottle course will diverge from the wind direction.

Previous modelling studies assumed a course straight downwind, which corresponds to a bluebottle course of 0^∘ relative to the wind. This behaviour has been described by Totton and Mackie (1960), who reported that in winds stronger than force 4 (i.e. over 8 m s⁻¹), the PMW would sail straight downwind with its sail parallel to the wind direction (Fig. 6a). This corresponds to an angle of attack of 0^∘, but, according to our model, this behaviour would only occur if the bluebottle sail has 0 % camber (Fig. 5). In this case, the wind will only hit the side of the bluebottle's sail and the bluebottle's course will also be parallel to the wind direction. However, if there is camber, the bluebottle will be pushed sideways (perpendicular to sail) even at zero angle of attack (Fig. 6b). Due to this, as the camber increases, the course tends towards being perpendicular to the wind at zero angle of attack (Fig. 5).

The bluebottle course straight downwind can also be explained by an angle of attack of 90^∘ (Fig. 5). At this angle of attack, the bluebottle's sail is perpendicular to the wind direction. We see that, at any camber, the bluebottle's course is parallel to the wind direction and perpendicular to its sail. However, to our knowledge, this situation has not been reported from observations, and it seems unlikely that the bluebottle balances itself perpendicular to the wind.

5 Special cases

5.1 Model and assumptions for downwind drift

We now discuss the assumptions required to reduce our generalized vector form to simpler models seen in some previous studies. Firstly, we must assume the bluebottle drifts straight downwind with its sail parallel to the wind direction under all conditions, despite the observation by Totton and Mackie (1960) that the PMW sails in this manner only in winds stronger than force 4 (i.e. over 8 m s⁻¹). Considering a downwind drift, the sail orientation corresponds to an angle of attack β_a of 0^∘ (Fig. 6). Substituting this into our vector form (Eq. 15) gives

$${\displaystyle }{\mathit{V}}_{\mathrm{bb}}{\displaystyle }=\mathit{u}+\mathit{\lambda }\mathbf{R}(\mathrm{180}{}^{\circ }-\mathit{\beta }){\mathit{V}}_{\mathrm{A}}.$$

Now, the bluebottle will only sail straight downwind if the force coefficient $C_{\mathrm{A}{y}^{\prime }}$ equals zero, resulting in no aerodynamic force perpendicular to the sail (Fig. 7). At an angle of attack of 0^∘, we expect $C_{\mathrm{A}{y}^{\prime }}$ to equal zero only if there is no camber (Fig. 6a). Hence we must also make this assumption that the sail camber is zero. Based on Eq. (8) and the fact that the relative current will always be opposite the wind (in order to have an equilibrium condition), we have β=180^∘ (Fig. 7), and R is the identity matrix. Using Eq. (16) also gives this result. This gives a form that we have seen in previous literature (discussed in Sect. 6):

$$\begin{array}{}\text{(19)}& {\displaystyle }{\mathit{V}}_{\mathrm{bb}}{\displaystyle }=\mathit{u}+\mathit{\lambda }{\mathit{V}}_{\mathrm{A}}.\end{array}$$

We can also exclude the current by assuming u=0 to reach another form seen in previous literature:

$$\begin{array}{}\text{(20)}& {\displaystyle }{\mathit{V}}_{\mathrm{bb}}{\displaystyle }=\mathit{\lambda }{\mathit{V}}_{\mathrm{A}}.\end{array}$$

Hence, we see that the models used in previous literature can be verified by our generalized form but require fairly strong assumptions of zero angle of attack in all conditions and no camber. In Sect. 5.2 and 5.3, we lift these assumptions to further explore the drifting dynamics of the bluebottle.

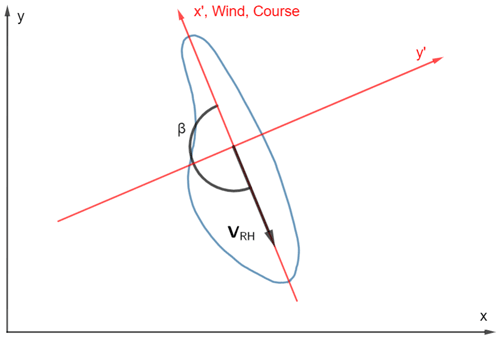
Figure 7 Case with no current for a left-handed (right-sailing) bluebottle sailing straight downwind with sail parallel to the wind direction (β_a=0^∘). Note that the wind direction and bluebottle course are on the x^′ axis. A right-handed (left-sailing) bluebottle would have the exact same course in this case.

5.2 Case with angle of attack of 40^∘ and no current

Totton and Mackie (1960) observed that in light winds the PMW balances itself at approximately 40^∘ to the wind. Hence, we now assume β_a has a value of 40 or −40^∘, depending on whether the bluebottle is right-handed (left-sailing) or left-handed (right-sailing), respectively. Since the orientation of the bluebottle is constant relative to the wind, the sail is always hit by the wind at the same angle and the force coefficients $C_{\mathrm{A}{x}^{\prime }}$ and $C_{\mathrm{A}{y}^{\prime }}$ can be considered as constants. For $C_{\mathrm{A}{x}^{\prime }}$, we will use a value of 0.1, as explained in Sect. 4.2. For $C_{\mathrm{A}{y}^{\prime }}$, we use Eq. (18), giving a value of 0.40. We assume a camber ratio of 1 %, the same as the value used in Iosilevskii and Weihs (2009). Recall that $C_{\mathrm{A}{y}^{\prime }}$ varies depending on the angle of attack. For example, it varies from 0.31 to 0.50, for an angle of attack of 30 to 50^∘. Assuming there is no current, our form (Eq. 15) simplifies to

$${\displaystyle }{\mathit{V}}_{\mathrm{bb}}{\displaystyle }=\mathit{\lambda }\mathbf{R}(\mathrm{180}{}^{\circ }-\mathit{\beta }+{\mathit{\beta }}_{\mathrm{a}}){\mathit{V}}_{\mathrm{A}}.$$

β can be calculated using Eq. (8) to be 87.1^∘ (varies from 86.2 to 87.7^∘ for an angle of attack of 30 to 50^∘), while λ is calculated using Eq. (9) to be 0.0266 (varies from 0.023 to 0.030 for an angle of attack of 30 to 50^∘). We will consider an example with a left-handed (right-sailing) bluebottle; thus, ${\mathit{\beta }}_{\mathrm{a}}=-\mathrm{40}$^∘. Substituting all these values gives

$${\displaystyle }{\mathit{V}}_{\mathrm{bb}}{\displaystyle }=\mathrm{0.0266}\mathbf{R}\left(\mathrm{52.9}{}^{\circ }\right){\mathit{V}}_{\mathrm{A}}.$$

We now have a clockwise rotation matrix. Hence, this means that the left-handed bluebottle will drift at an angle of 52.9^∘ clockwise (to the right) from the wind at 2.66 % of the wind speed. Similarly, a right-handed bluebottle will drift at an angle of 52.9^∘ anticlockwise (to the left) from the wind at 2.66 % of the wind speed. Note that since there is no current, the hydrodynamic force is only the drag from the submerged part of the bluebottle. Hence, the relative current vector V_RH is directly opposite the bluebottle's motion (Fig. 8).

Figure 8 Case with no current for a left-handed (right-sailing) bluebottle (${\mathit{\beta }}_{\mathrm{a}}=-\mathrm{40}$^∘). Note that β_a is negative because it is the angle between the x^′ axis and the wind, which is clockwise. The lengths of course and V_RH are to scale. Wind vector length has been scaled down by a factor of 8.

5.3 Case with angle of attack of 40^∘ with current

Including the current does not have any impact on the calculated values of β or λ. Hence, the effect of the wind on the bluebottle's speed and orientation will remain the same. By adding the current, we have

$${\displaystyle }{\mathit{V}}_{\mathrm{bb}}{\displaystyle }=\mathit{u}+\mathrm{0.0266}\mathbf{R}\left(\mathrm{52.9}{}^{\circ }\right){\mathit{V}}_{\mathrm{A}}.$$

Unlike Sect. 5.2, considering the effect of background ocean current means that the relative current velocity V_RH is no longer directly opposite the bluebottle's course (Fig. 9). However, since the wind conditions and other variables have not changed from Sect. 5.2, the aerodynamic force is identical. Hence, we also require the relative current vector to be identical since this determines the hydrodynamic force, which must balance out the aerodynamic force in order to have an equilibrium condition. This means that the course of the bluebottle must adjust such that V_RH is in the same position as Sect. 5.2 (β=87.1^∘). Figure 10 shows examples of different current conditions with a constant wind. In each example, V_RH is kept in the same position by adjusting the bluebottle's course.

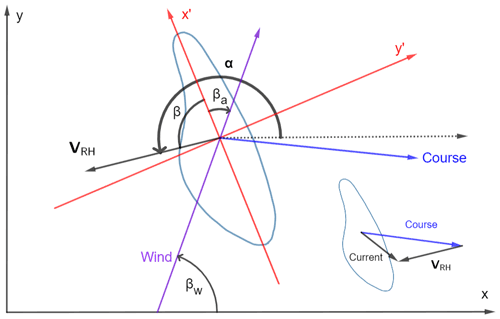
Figure 9 Case with current running southeast for a left-handed (right-sailing) bluebottle (${\mathit{\beta }}_{\mathrm{a}}=-\mathrm{40}$^∘). Diagram in the bottom right shows the vector addition between the bluebottle's course, the current and the relative current felt by the bluebottle. The lengths of the course, current and V_RH are to scale, based on a current speed that is 5 % of the wind speed. Wind vector length has been scaled down by a factor of 8.

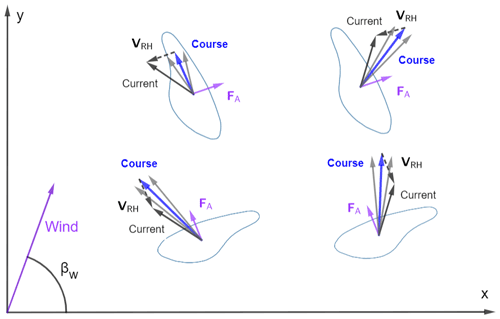
Figure 10 Examples of different ocean current directions for a constant wind. Top row depicts left-handed (right-sailing) bluebottles. Bottom row depicts right-handed (left-sailing) bluebottles for the same wind and current conditions. Grey vectors indicate confidence intervals for the bluebottle course if we consider that the angle of attack (β_a) could be 30 to 50^∘. Note that for each form, V_RH must always point in the same direction. The lengths of the course, current and V_RH are to scale, based on a current speed that is 5 % of the wind speed. Wind vector length has been scaled down by a factor of 8.

6 Discussion and conclusion

We have added the ocean background current to an existing theoretical model of aerodynamic and hydrodynamic forces acting on a bluebottle. We then solve for an equilibrium condition to create a generalized vector model for the speed and course of the bluebottle. Adding assumptions to our generalized model results in simplification to models that have been seen in previous literature. The generalized vector form is the link between the practical papers that used simple Lagrangian vector models and the theoretical papers that used a bottom-up approach. We also identify and discuss the key parameters: shape (λ), angle of attack and camber. Finally, we find that under typical sailing conditions reported in the literature (angle of attack of 40^∘), the bluebottle will drift at an angle of 52.9^∘ from the wind at 2.66 % of the wind speed, plus the velocity of the ocean background current.

It is worth noting that the form of Eqs. (15) and (16) is different from leeway methods, which consider the motion of the object as a wind vector plus leeway (divergence from the wind). The leeway is often estimated using physical experiments and statistics. This methodology has been used in many previous studies (Breivik et al., 2011; Hackett et al., 2006; Ni et al., 2010; Wang et al., 2015). Our theoretical bottom-up approach to calculate bluebottle drift using force balance in equilibrium is a completely different methodology, despite the similar-looking vector form that results from both techniques.

Our results compare well with previous Lagrangian model parameterizations. Ferrer and Pastor (2017) modelled the drift velocity of PMWs as wind velocity multiplied by a wind drag coefficient estimated from numerical simulations. The current was not used because wind was considered to be the main mechanism, based on Ferrer et al. (2014), who used symmetric fish tags for model calibration. The model calibration used in Ferrer et al. (2014) included a calculation of surface current as the combination of ROMS (Regional Ocean Modelling System) current and wind. They also assumed that the PMWs drift straight downwind. This matches our form in Eq. (20), where we assume the bluebottle has zero angle of attack and there is no current. The model used by Prieto et al. (2015) was advection by surface currents (computed by ROMS model) plus 10 % of wind velocity. This matches our form in Eq. (19), still assuming an angle of attack of 0^∘. In comparison, we have a generalized form for calculating the drift of a bluebottle for different angles of attack. We use a bottom-up approach for our wind velocity coefficient λ, which is determined by the specific areas and force coefficients of the bluebottle. We find that when the bluebottle has an angle of attack of 40^∘, as suggested by observations, λ=0.0266, and the wind pushes the bluebottle on a course of about 53^∘ to the wind. This value of λ falls within the range of 0.02–0.045 which was tested by Ferrer and Pastor (2017) but differs from the 10 % used by Prieto et al. (2015). The wind drift angle of 53^∘ is similar to the 45^∘ observed by Totton and Mackie (1960) and used amongst others in the model of Ferrer and González (2020). The α term in our model accounts for the angle of the current, the angle of the wind and the bluebottle's angle of attack. Our model also incorporates the current, which has a significant effect even at 10 m s⁻¹ winds. Indeed, at wind speeds of O(10), the speed imparted onto the bluebottle from the wind is about 0.266 m s⁻¹ (2.66 % of wind speed), which is the same order of magnitude as the speed of ocean currents. Hence based on our vector form, the current should not be ignored when predicting the drift of the bluebottle. Note that the current relevant for this study is the surface ocean current which would be felt by the bluebottle. Relatively good results from modelling studies which did not take into account that the ocean current can be explained by the great impact the wind has on the top few centimetres of the ocean.

It should be noted that the influence of waves is not taken into account in our model. The impact force of waves has an effect on drifters (Szelangiewicz and Żelazny, 2018), but several additional variables and functions are required to calculate this impact force. This will make our model significantly more complex and currently cannot realistically be added. The effect of Stokes drift, however, could be added into the ocean surface current vector, following Clarke and Vander (2018), for instance. Stokes drift is a phenomenon that occurs on the ocean surface where the surface waves affect the net particle movement in the top 1 or 2 m of the ocean, in the direction of the waves. Clarke and Vander (2018) found that Stokes drift is mostly in the direction of the wind, and thus it is mainly due to shorter waves generated by the local wind. It was also found that the magnitude of Stokes drift can be approximated by

$$\begin{array}{}\text{(21)}& u_{\mathrm{Stokes}}=\mathrm{4.4}{u}_{*}\ln \left({\displaystyle \frac{\mathrm{0.0074}{u}_{\mathrm{10}}}{u_{*}}}\right),\end{array}$$

where u₁₀ is the 10 m wind speed and u_* is a parameter calculated by

$$\begin{array}{}\text{(22)}& u_{*}=\sqrt{{\displaystyle \frac{\left|{\mathit{\tau }}_{\mathrm{0}}\right|}{{\mathit{\rho }}_{\mathrm{w}}}}},\end{array}$$

where $\left|{\mathit{\tau }}_{\mathrm{0}}\right|$ is the wind stress magnitude and ρ_w is the density of water. Assuming a constant drag coefficient, Clarke and Vander (2018) then show that u_Stokes can be estimated as 1 % of u₁₀. This Stokes drift estimate can be added as an additional term to Eq. (15), giving

$$\begin{array}{}\text{(23)}& {\displaystyle }{\mathit{V}}_{\mathrm{bb}}{\displaystyle }=\mathit{u}+\mathrm{0.01}{\mathit{V}}_{\mathrm{A}}+\mathit{\lambda }\mathbf{R}(\mathrm{180}{}^{\circ }-\mathit{\beta }+{\mathit{\beta }}_{\mathrm{a}}){\mathit{V}}_{\mathrm{A}}.\end{array}$$

However, another consideration is that large waves (at high wind speeds) may break on top of the bluebottle and result in the bluebottle becoming imbalanced or even toppling over. Our model cannot predict the behaviour of the bluebottle in this situation.

An assumption we used in Sect. 5 was a constant value for the angle of attack. In reality, the orientation of the bluebottle would be influenced by a combination of the wind and current conditions. In particular, observations suggest that the angle of attack decreases from about 40 to 0^∘ as wind speed increases (Totton and Mackie, 1960). More information from lab experiments and in situ surveys in the future is required to determine the value of this key parameter and its variability. Instead of using a constant value for the angle of attack, it could be implemented in the model as a function of wind speed, for example.

Another assumption in the model is that the body of the bluebottle is assumed to be a perfectly symmetrical cylinder with no tentacles. In reality, the submerged body is not perfectly symmetrical so the hydrodynamic force would also influence the orientation of the bluebottle's sail and body to some extent, like the keel of a sailboat. However, since the bluebottle can extend and retract the tentacle, changing its length and angle, it is hard to model. The drag force from the bluebottle's single tentacle (calculated using equations from Iosilevskii and Weihs (2009)) is O(10⁻⁴), which is insignificant compared to the overall hydrodynamic force of O(10⁻²) acting on the bluebottle.

This study is focused on the bluebottles found on the east coast of Australia. Different parameter values may be required for the larger PMW. For example, Iosilevskii and Weihs (2009) use an estimate of 0.7 for the aspect ratio of the PMW's sail, which affects the force coefficient $C_{\mathrm{A}{y}^{\prime }}$ (Sect. 4.2). This is much larger than our measured aspect ratio of 0.35 for the bluebottle's sail. In Sect. 5.2, we conclude that at an angle of attack of 40^∘ and no current, a left-handed bluebottle will drift at an angle of 52.9^∘ clockwise from the wind at 2.66 % of the wind speed. A PMW in the same conditions will drift at an angle of 51.5^∘ clockwise from the wind at 3.73 % of the wind speed. While the drift angle is almost the same, the velocity of the PMW is 40 % higher than the bluebottle due to the higher aspect ratio leading to a larger force coefficient $C_{\mathrm{A}{y}^{\prime }}$. It is worth noting that the drag caused by the PMW's many long tentacles may affect its velocity significantly more than for the bluebottle.

Further research that would supplement this study include

• physical experiments to observe bluebottle drifting and estimate the key parameter values (e.g. force coefficients, angle of attack, camber) of our model; and

• a detailed understanding of the specific habitat and life cycle of the bluebottle to determine the starting point for a drift model.

We hope our work, creating a generalized model for bluebottle drift, encourages new research in this area and helps in the development of accurate numerical tracking and, ultimately, a forecasting tool that can prevent tens of thousands of beachgoers from experiencing painful bluebottle stings.

Appendix A

Figure A1 Case with no current for a right-handed (left-sailing) bluebottle (β_a=40^∘). The lengths of course and V_RH are to scale. Wind vector length has been scaled down by a factor of 8.