the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
A monthly tidal envelope classification for semidiurnal regimes in terms of the relative proportions of the S2, N2, and M2 constituents
Do-Seong Byun
Deirdre E. Hart
Daily tidal water level variations are a key control on shore ecology, on access to marine environments via ports, jetties, and wharves, on drainage links between the ocean and coastal hydrosystems such as lagoons and estuaries, and on the duration and frequency of opportunities to access the intertidal zone for recreation and food harvesting purposes. Further, high perigean spring tides interact with extreme weather events to produce significant coastal inundations in low-lying coastal settlements such as on deltas. Thus an understanding of daily through monthly tidal envelope characteristics is fundamental for resilient coastal management and development practices. For decades, scientists have described and compared daily tidal forms around the world's coasts based on the four main tidal amplitudes. Our paper builds on this “daily” method by adjusting the constituent analysis to distinguish between the different monthly types of tidal envelopes occurring in the semidiurnal coastal waters around New Zealand. Analyses of tidal records from 27 stations are used alongside data from the FES2014 tide model in order to find the key characteristics and constituent ratios of tides that can be used to classify monthly tidal envelopes. The resulting monthly tidal envelope classification approach described (E) is simple, complementary to the successful and much used daily tidal form factor (F), and of use for coastal flooding and maritime operation management and planning applications in areas with semidiurnal regimes.
- Article
(7905 KB) - Full-text XML
- BibTeX
- EndNote
Successful human–coast interactions in the world's low-lying areas are predicated upon understanding the temporal and spatial variability of sea levels (Nicholls et al., 2007; Woodworth et al., 2019). This is particularly the case in island nations like New Zealand (NZ), where over 70 % of the population resides in coastal settlements (Stephens, 2015). An understanding of tidal water level variations is fundamental for resilient inundation management and coastal development practices in such places, as well as for accurately resolving non-tidal signals of global interest such as in studies of sea level change (Cartwright, 1999; Masselink et al., 2014; Olson, 2012; Pugh, 1996; Stammer et al., 2014).
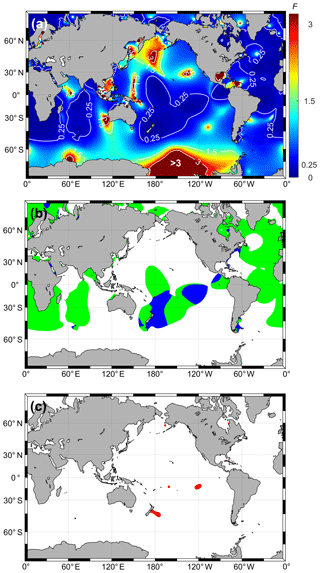
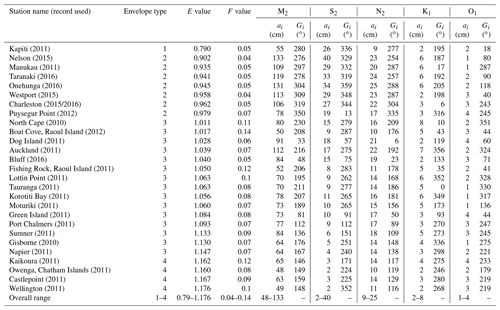
Figure 1(a) Global distribution of daily form factor (F) values indicating daily tidal regime types (F<0.25: semidiurnal; F>0.25 to F<1.5 mixed semidiurnal dominant; F>1.5 to F<3: mixed diurnal dominant; and F>3: diurnal; according to the classification of van der Stok, 1897, and Courtier, 1938); (b) the world's semidiurnal tidal areas (F<0.25) divided into those where spring–neap (green) versus perigean–apogean (blue) signals are the main influence on the monthly tidal envelope; and (c) semidiurnal tidal regimes (in red) in which the S2∕M2 constituent amplitude ratio is <0.04 and the spring–neap tidal signals are very weak as compared to perigean–apogean signals; derived from FES2014 tidal harmonic constants.
In terms of daily cycles, tidal form factors or form numbers (F) based on the amplitudes of the four main tidal constituents (K1, O1, M2, S2) have been successfully used to classify tidal observations from the world's coasts into four types of tidal regimes for nearly a century (Fig. 1a). Originally developed by van der Stok (1897) and based on three regime types, with a fourth type added by Courtier (1938), this simple and useful daily form factor comprises a ratio between diurnal and semidiurnal tide amplitudes via the equation
The results classify tides into those which roughly experience one high and one low tide per day (diurnal regimes), two approximately equivalent high and low tides per day (semidiurnal regimes), or two unequal high and low tides per day (mixed semidiurnal-dominant or mixed diurnal-dominant regimes) (e.g. Defant, 1958).
Albeit not part of their original design, some interpretation of the tidal envelope types observed at fortnightly and monthly timescales has accompanied the use of daily tidal form classifications (e.g. Pugh, 1996; Pugh and Woodworth, 2014). The daily tidal form factor identifies the typical number (1 or 2) and form (equal or unequal tidal ranges) of tidal cycles within a lunar day (i.e. 24 h and 48 min) at a particular site. In contrast, the term “tidal envelope” describes a smooth curve outlining the extremes (maxima and minima) of the oscillating daily tidal cycles occurring at a particular site through a specified time period. The envelope time period of interest in this paper is monthly.
Tidal envelopes at monthly scales depend on tidal regime. In general, semidiurnal tidal regimes often feature two spring–neap tidal cycles per synodic (lunar) month. These two spring–neap tidal cycles are usually of unequal magnitude due to the effect of the moon's perigee and apogee, which cycle over the period of the anomalistic month. In contrast, diurnal tidal regimes exhibit two pseudo-spring–neap tides per sidereal month. For semidiurnal regions where the N2 constituent contributes significantly to tidal ranges, tidal envelope classification should consider relationships between the M2, S2, and N2 amplitudes. The waters around NZ represent one such region; here the daily tidal form is consistently semidiurnal, but large differences occur between sites within this region in terms of their typical tidal envelope types over fortnightly to monthly timescales. More than 80 years after the development of the ever-useful daily tidal form factors, attention to the regional distinctions between different tidal envelope types within the semidiurnal category forms the motivation for this paper. In this first explicit attempt to classify monthly tidal envelope types, we examined the waters around NZ, a strong semidiurnal regime with relatively weak diurnal tides (daily form factor F<0.15) and little variation in the importance of the S2 and N2 amplitude ratios. The result is an approach for classifying monthly tidal envelope types that is transferable to any semidiurnal regime. As well as providing greater understanding of the tidal regimes of NZ, we hope that our paper opens the door for new international interest in classifying tidal envelope variability at multiple timescales, which is work that would have direct coastal and maritime management applications including contributing to explanations of the processes behind delta cities' coastal flooding hazards and their regional spatial variability.
2.1 Study area
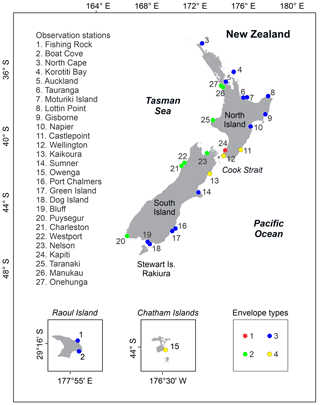
New Zealand (Fig. 2) is a long (1600 km), narrow (≤ 400 km) country situated in the south-western Pacific Ocean and straddling the boundary between the Indo-Australian and Pacific plates. Its three main islands, the North Island, the South Island, and Stewart Island/Rakiura, span a latitudinal range from about 34∘ to 47∘ S. The tidal regimes in the surrounding coastal waters are semidiurnal with variable diurnal inequalities, and they feature micro through macro tidal ranges. Classic spring–neap cycles are present in western areas of NZ, while eastern areas feature distinct perigean–apogean influences (Byun and Hart, 2015; Heath, 1977, 1985; LINZ, 2017b; Walters et al., 2001).
Highly complex tidal propagation patterns occur around NZ, including a complete semidiurnal tide rotation, with tides generally circulating around the country in an anticlockwise direction. This occurs due to the forcing of M2 and N2 tides by their respective amphidromes, situated north-west and south-east of the country respectively, producing trapped Kelvin waves (for a map of the K1 and M2 amphidromes, see Fig. 5.1 in Pugh and Woodworth, 2014). The S2 and K1 tides propagate north-east to south-west around NZ. This results in a southward travelling Kelvin wave along the west coast and small S2 and K1 amplitudes along the east coast, with amphidromes occurring south-east of NZ (Walters et al., 2001, 2010). Around Cook Strait, the waterway between the two main islands, tides travelling north along the east coast run parallel to tides travelling south along the west coast. The pronounced differences between these east–west tidal states, combined with their tidal range differences, together produce marked differences in amplitude and strong current flows through the strait (Heath, 1985; Walters et al., 2001, 2010).
2.2 Data analysis approach
Year-long sea level records were sourced from a total of 27 stations spread around NZ (Fig. 2): 18 records of 1 min intervals from Land Information New Zealand (LINZ, 2017a) and nine records of 1 h intervals from the National Institute of Water and Atmospheric Research (NIWA, 2017). For both the LINZ and NIWA data, an individual year of good-quality hourly data was selected for analysis per site from amongst the multi-year records. The 27 single-year sea level records were then harmonically analysed using T_Tide (Pawlowicz et al., 2002) with the nodal (satellite) modulation correction option to examine spatial variations in the main tidal constituents' amplitudes, phase lags, and amplitude ratios between regions (see Table A1 for raw results) and to compare them with values obtained from the tidal potential or equilibrium tide. An additional set of tidal constituent amplitudes was obtained from Tables 1 and 3 from Walters et al. (2010), which was derived from 33 records of between 14 and 1900 d in length from around the greater Cook Strait area, where spring–neap tides are the strongest in the country.
We then classified the monthly tidal envelope types found around NZ based on the examination of constituent ratios produced from the tidal harmonic analysis results, data from the FES2014 tide model (see Carrère et al., 2016, for a full description of this model), and examination of tidal envelope plots. Due to the strong semidiurnal tidal regimes in the study area, and in a similar way to the approach of Walters et al. (2010), we were able to ignore diurnal (K1, O1) effects and simply consider the effects of spring–neap (M2, S2) and perigean–apogean cycles (M2, N2) in our monthly tidal envelope type characterisation.
Figure 3Distribution of amplitudes for the (a) M2, (b) S2, (c) N2, (d) K1, and (e) O1 tides around NZ and (f) the resultant distribution of F, daily tidal form factor values, as calculated from the FES2014 tide model on a grid of 1∘ ∕ 16×1∘ ∕ 16. Note that the amplitude colour scales vary between panels (a) and (e).
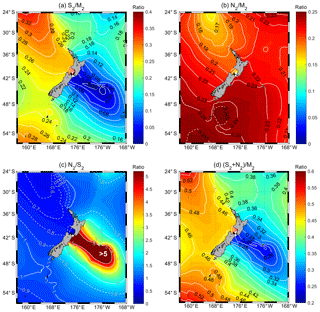
Figure 4Distributions of tidal constituent amplitude ratios around NZ for the following: (a) S2∕M2, (b) N2∕M2, (c) N2∕S2, and (d) , as calculated using the FES2014 tide model on a grid of 1∘ ∕ 16×1∘ ∕ 16. Note that the amplitude colour scales vary between panels (a) and (d).
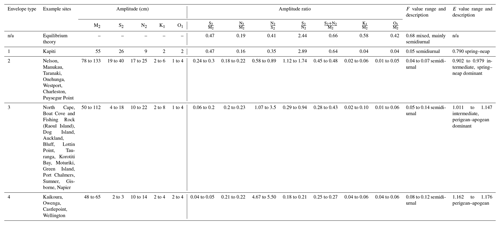
Table 1Comparison of tidal constituent amplitudes, amplitude ratios (including daily tidal form factor, F, and monthly tidal envelope factor, E), and ranges between the four distinct monthly tidal envelope types found in the 27 case study semidiurnal tide regimes of New Zealand and compared to equilibrium theory amplitude ratios. n/a: not applicable.
3.1 Key tidal constituent amplitudes and amplitude ratios
In order to better understand the key constituents responsible for shaping tidal height forms around NZ, we first mapped spatial variability in the amplitudes of the M2, S2, N2 K1, and O1 constituents and F (Fig. 3) and in the ratio values of the semidiurnal constituent amplitudes (Fig. 4). Table 1 summarises these data and contrasts them with those from equilibrium theory (values obtained from Defant, 1958), while Table A1 catalogues the detailed results.
Tidal amplitude ratio comparisons confirmed that the waters around NZ are dominated by the three astronomical semidiurnal tides: M2, S2, and N2 (Table 1), the combination of which can generate fortnightly spring–neap tides (M2 and S2) and monthly perigean–apogean tides (M2 and N2). Figure 3 shows the relatively minor magnitudes of diurnal constituent amplitudes (O1, K1), and it reveals the stronger west coast amplitudes of the spring–neap-cycle-generating constituents (M2 and S2), the relatively weak S2 amplitudes overall (half that of equilibrium theory), and the more concentric pattern around NZ of the perigean–apogean-cycle-generating N2 amplitude (Fig. 3c).
In terms of the semidiurnal constituent amplitude ratios, Fig. 4 and Table 1 show that S2∕M2 values cover a broad range around NZ (0.04 to 0.47), with most sites exhibiting smaller values (<0.3 at 26 out of 27 sites) than that of equilibrium theory (0.47). In contrast, N2∕M2 amplitude ratios were found to be more stable around NZ (values ranging from 0.16 to 0.23) and similar in magnitude to equilibrium theory (i.e. 0.19). By grouping the constituent amplitude and amplitude ratio results (Figs. 3–4), we were able to differentiate between four distinct monthly tidal envelope regimes around NZ (Table 1) with types 1 and 4 distinguished as follows.
-
Firstly, spring–neap type tidal regimes (Type 1) occur where the S2 tide amplitude is large compared to that of the N2 (Table 1; Fig. 3). In these areas, there are two spring–neap tides per month with similar ranges and negligible influence of perigean–apogean cycles. Type 1 regimes occur in the Kapiti and Cook Strait area (Fig. 2) where the N2 and M2 amplitudes reduce by 75 % to 90 % but the S2 amplitude reduces by only about 30 % compared to on the western coasts both north and south of this central NZ area.
-
In direct contrast, there are perigean–apogean type tidal regimes (Type 4) in areas where the N2 amplitude strongly dominates over the S2 (Table 1; Fig. 3). In Type 4 regimes, the M2 and the N2 tides combine to produce strong signals over monthly timeframes (27.6 d). Hence the highest tidal ranges in any given month occur in relation to the perigee, when the moon's orbit brings it close to Earth rather than in line with the moon's phase, as is typical in spring–neap regimes. Type 4 regimes occur, for example, around northern Chatham Rise near Kaikoura and as far north as Castlepoint on the east coast of the North Island.
The remaining coastal waters around NZ can be separated into two tidal subregions, one with strong spring–neap signals (Type 2) and the other with strong perigean–apogean signals (Type 3) but both with overall mixed or intermediate monthly tidal envelope types (Table 1). We distinguished between these two envelope types via the tides generated by variability in the amplitude ratios of S2∕M2 and N2∕M2 (i.e. the spring–neap cycle and perigean–apogean cycle forming tides respectively). In brief, the S2∕M2 amplitude ratio varies widely around NZ, with the highest values in the west, lowest values in the east, and intermediate values to the north and south, while variation in the N2∕S2 amplitude ratio exhibits an opposite pattern (compare Fig. 4a to 4c). By comparison, the N2∕M2 amplitude ratios are relatively stable and high except in the relatively small area of the Cook Strait to the Kapiti Coast, where this ratio drops and thus spring–neap cycles predominate (see spring–neap Type 1 regimes above). The variability in these two ratios means that, except where we find spring–neap or perigean–apogean monthly tidal envelope types, spring–neap tides do occur but the overall monthly envelope shape is fundamentally altered (asymmetrically) due to the perigean–apogean influence.
-
In the first of the intermediate subregions, tides exhibit two dominant but unequal spring–neap cycles per month due to subordinate perigean–apogean effects. We term this type of monthly tidal envelope an intermediate, predominantly spring–neap type regime (Type 2). Here values of the N2∕S2 amplitude ratio are <1, with S2 amplitudes being only around 24 % to 30 % of those of the M2 constituent (Figs. 3–4; Table 1). Also in these areas, values of the amplitude ratio are ≥0.45. Type 2 tides occur, for example, at Westport and Puysegur.
-
In the other intermediate subregion, tides exhibit a mainly perigean–apogean form with a weaker but noticeable spring–neap signal: we term this envelope type as intermediate, predominantly perigean–apogean (Type 3). Here values of the N2∕S2 amplitude ratio are between 1.07 and 3.5, while values of the amplitude ratio are between 0.28 and 0.43 (Figs. 3–4; Table 1). Type 3 tides occur, for example, at Auckland and Sumner.
Figure 5 illustrates the four types of monthly tidal envelopes found around NZ as idealised types, two with stronger spring–neap signals (types 1 and 2; see Fig. 5a–b) and two with stronger perigean–apogean signals (types 3 and 4; see Fig. 5c–d), while Fig. 2 includes a colour coded classification of the observation stations into the four tidal envelope types.
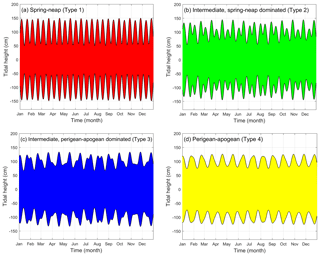
Figure 5Idealised examples of four different monthly tidal envelopes over 1 year, calculated using the amplitude value M2=100 cm and the amplitude ratio values of (a) , , and ; (b) , , and ; (c) , , and ; and (d) , , and . Note that the E values of these plots are (a) 0.71, (b) 0.93, (c) 1.09, and (d) 1.17.
3.2 A monthly tidal envelope factor (E) for semidiurnal regimes
The four types of monthly tidal envelopes found around NZ are essentially different combinations of spring–neap and perigean–apogean signals. Thus, in a similar manner to the method of Courtier (1938) for calculating daily tidal form factors, a monthly tidal envelope factor (E) may be calculated for semidiurnal tidal regions, including that of NZ, according to the following:
where M2, N2, and S2 refer to the constituent amplitudes. This equation can be further expressed as follows:
with , and
with .
E takes into account the roles of the S2 and N2 tides in spring–neap and perigean–apogean cycles while also factoring in the strong M2 tide influence in both types of cycles. E may be used to classify the monthly tidal envelope types of any semidiurnal region (i.e. where F<0.25) based on the analysis of constituent amplitudes and ratios from local data. The boundaries between our different NZ monthly tidal envelope types were as follows.
-
E<0.8 indicates a Type 1 spring–neap regime.
-
E between 0.8 and 1.0 indicates a Type 2 intermediate, predominantly spring–neap regime (with the upper bound also corresponding to an amplitude ratio of in semidiurnal regimes).
-
E between 1.0 and 1.15 indicates a Type 3 intermediate, predominantly perigean–apogean regime (with the lower bound also corresponding to an amplitude ratio of in semidiurnal regimes).
-
E>1.15 indicates a Type 4 perigean–apogean regime (with the lower bound also corresponding to an amplitude ratio of in our NZ regimes).
Here we explain how we set boundaries between the different envelope types around NZ using case study data and as summarised in Fig. 6. Firstly, in any semidiurnal tidal regime (F<0.25) anywhere in the world where the amplitude ratio , spring–neap cycles will feature clearly in the tidal height records. Thus, the boundary separating types 1 and 2 from types 3 and 4 occurs at , when also E=1. Type 1 and 2 areas of the NZ coast are characterised by relatively larger S2 amplitudes (19–40 cm) than areas with stronger perigean–apogean influences (2–18 cm) (Table 1). Secondly, tidal regimes with stronger spring–neap signals include places where spring–neap cycles occur as consecutive fortnightly cycles of similar magnitudes (Type 1 or spring–neap type regimes) and places where spring–neap signals dominate but with noticeable variability in the magnitudes of consecutive cycles due to subordinate perigean–apogean influences (Type 2 or intermediate spring–neap regimes). In NZ, the strongest spring–neap influence occurs in the Cook Strait to Kapiti area, where harmonic analysis revealed an amplitude ratio of and an E value of 0.79 (Table 1). Examining the shapes of tidal height plots showed that Kapiti had the only completely spring–neap-dominated tidal envelope amongst the case study sites. Hence the boundary between Type 1 versus Type 2 was set as E=0.790 for NZ, which is just greater than that of Kapiti and below the next strongest spring–neap-influenced site, Nelson, where E=0.902 (Fig. 6). Lastly, to set a boundary between perigean–apogean and intermediate perigean–apogean-dominant regimes (i.e. Type 3 versus Type 4), we again examined tidal height plots to determine a boundary value of E=1.15, which is between the intermediate perigean–apogean-dominated type regime of Napier (E=1.147) and the perigean–apogean type regime of Kaikoura (E=1.162) (Table A1; Fig. 6).
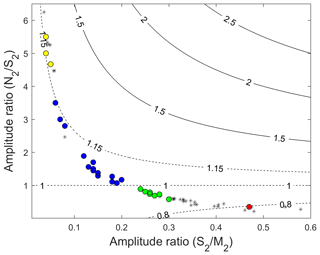
Figure 6Plot of the relationship between the N2∕S2 and S2∕M2 amplitude ratios (y and x axes respectively) and E values (shown as plot contours), with data points corresponding to New Zealand waters monthly tidal envelope Type 1 sites (red dots), Type 2 sites (green dots), Type 3 sites (blue dots), and Type 4 sites (yellow dots) (all from Table A1), as well as tidal data representative of the greater Cook Strait area (black stars) from Walters et al. (2010; Tables 1 and 3 therein).
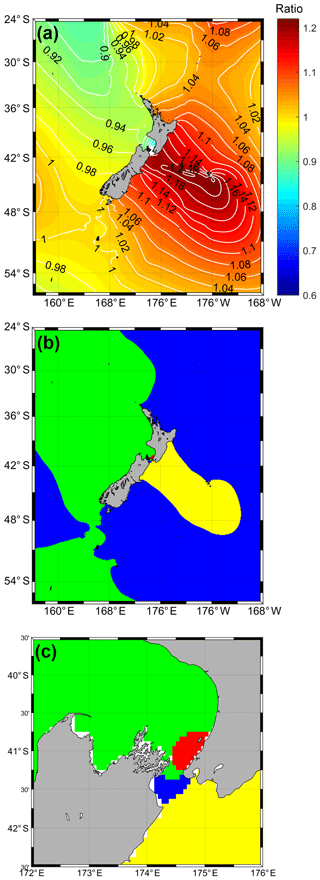
Figure 7(a) Distribution of monthly tidal envelope factor (E) values and (b) monthly tidal envelope types in the waters around New Zealand, including (c) in the Cook Strait area between the two main islands, all calculated using FES2014 data. In (b) and (c), envelope Type 1 areas are shown in red, Type 2 in blue, Type 3 in green, and Type 4 in yellow. See Fig. 5 for definitions and examples of monthly tidal envelope factor classes and patterns.
In summary, Fig. 7 illustrates the monthly tidal envelope values and types in the waters around NZ using E. The west coast is characterised by Type 2 monthly tidal envelopes with two unequal spring–neap cycles per month. As mentioned above, Type 1 monthly tidal envelopes, with their defined spring–neap tides, are only found in the western Cook Strait to Kapiti Coast area. The Cook Strait's tides were explored in detail by Walters et al. (2010); our Fig. 6 includes a re-analysis of their data using the E ratios. Note that the Cook Strait data include four sites in the Type 1 category, as well as a number of Type 2 and Type 4 sites and one Type 3 site, revealing this small strait to be a concentrated area of monthly tidal envelope diversity. Extensive areas of Type 3 intermediate perigean–apogean-dominated regimes are found along the north-east and south-east coasts of NZ, while the central eastern coasts show Type 4 perigean–apogean tidal envelopes. As shown in Fig. 1c, such regimes are unusual internationally, occurring also in limited areas of the Cook Islands, north-east of the Pitcairn Islands, in Canada's Hudson Bay, in Alaska's Bristol Bay, offshore of the North Carolinian to Virginian coast in the Unites States of America, on the north coast of the Bahamas, and in the Gulf of Ob in Russia.
The daily water level variations brought about by the tides are a key control on shore ecology and on the accessibility of marine environments via fixed port, jetty, and wharf infrastructure. These variations also moderate the functioning of drainage links between the ocean and coastal hydrosystems and determine the duration and frequency of opportunities to access the intertidal zone for recreation and food harvesting purposes. Fortnightly and monthly tidal envelope variations, such as those associated with spring–neap and perigean–apogean cycles, have similar moderating roles on human usage of intertidal and shoreline environments, and additionally these medium term variations in tide levels are important factors in coastal inundation risk (Menéndez and Woodworth, 2010; Stephens, 2015; Stephens et al., 2014; Wood, 1978, 1986). High perigean spring tides, for example, interact with extreme weather events (including low pressures, strong winds, and extreme rainfall) to produce significant coastal inundation in low-lying coastal settlements such as in the delta city of Christchurch (Hart et al., 2015).
In a world of rising sea levels and coastal inundation hazard cascades (Menéndez and Woodworth, 2010), having common ways of describing different types of tidal envelopes is helpful for living safely and productively in coastal cities. This paper has employed observations from NZ and FES2014 model data to demonstrate a simple approach to classifying different monthly tidal envelope types which is applicable to semidiurnal regions anywhere. The result is a widely applicable monthly tidal envelope factor, E, for classifying semidiurnal regimes based on the amplitudes and amplitude ratios of three key constituents: M2, S2, and N2.
At a very basic level, in any semidiurnal tidal regime anywhere in the world where the amplitude ratio of , spring–neap cycles will then be clearly visible in tidal height records either as consecutive fortnightly cycles of similar magnitude (Type 1) or as a dominant signal with noticeable variability in the magnitudes of consecutive fortnightly cycles due to a subordinate perigean–apogean influence (Type 2). Conversely, in semidiurnal areas of the world's oceans where the amplitude ratio of , perigean–apogean cycles will then be visible either as singularly evident monthly cycles (Type 4) or as a dominant influence with subordinate spring–neap signals (Type 3). Determining the actual boundaries between monthly tidal envelope Type 1 versus Type 2 and Type 3 versus Type 4 at a local scale involves the analysis of observational records, taking into account the important influence of the M2 amplitude compared to that of the S2 and N2 amplitudes.
Figure 1b illustrates the division of the semidiurnal areas of the world's oceans into those where spring–neap cycles are the main monthly tidal envelope influence versus those where the perigean–apogean signal is stronger, while Fig. 1c illustrates areas of the world's oceans where spring–neap signals are very weak compared to perigean–apogean influences in the monthly tidal envelope. The predictable tidal water level fluctuations such as those in our perigean–apogean monthly envelope classes are an important influence on coastal inundation hazards in different locations around the world (e.g. Wood, 1978, 1986; Stephens, 2015).
Our simple approach to classifying E, namely monthly tidal envelope types in semidiurnal regions, complements the existing, commonly used way of describing daily tidal forms, F, based on the amplitudes of the key diurnal (K1, O1) and semidiurnal (M2, S2) constituents. We hope that our work inspires other efforts to study tidal height variations at timescales greater than daily, which could draw renewed attention to the fundamental role of tidal water levels in shaping coastal environments, including in hazards such as coastal flooding.
The tidal data used in this paper are available from LINZ (2017a, https://www.linz.govt.nz/sea/tides/introduction-tides/tides-around-new-zealand, last access: 28 November 2019), LINZ (2017b, https://www.linz.govt.nz/sea/tides/introduction-tides/tides-around-new-zealand, last access: 28 November 2019), NIWA (2017, https://www.niwa.co.nz/our-services/online-services/sea-levels (last access: 28 November 2019), and Walters et al. (2010). Details of the FES2014 tide model database are found via https://www.aviso.altimetry.fr/en/data/products/auxiliary-products/global-tide-fes.html (last access: 28 November 2019) and in Carrère et al. (2016). Appendix A contains the data produced from the analysis of these primary resources in this paper.
Both authors conceived of the idea behind this paper. DEH produced the initial draft. DSB analysed the tidal data and wrote the results sections. Both authors worked on and finalised the full paper.
The authors declare that they have no conflict of interest.
This article is part of the special issue “Developments in the science and history of tides (OS/ACP/HGSS/NPG/SE inter-journal SI)”. It is not associated with a conference.
We are grateful to Land Information New Zealand (LINZ) and the National Institute of Water and Atmospheric Research (NIWA) for supplying the tidal data used in this research. We thank the University of Canterbury Erskine Programme for supporting Do-Seong Byun during his time in New Zealand, John Thyne for supplying the Fig. 2 outline map, and Derek Goring for interesting discussions regarding tidal data sources. We also thank Glen Rowe, Phillip Woodworth, and an anonymous reviewer for comments that helped us improve this paper.
This paper was edited by Mattias Green and reviewed by Philip Woodworth and one anonymous referee.
Byun, D.-S. and Hart, D. E.: Predicting tidal heights for new locations using 25h of in situ sea level observations plus reference site records: A complete tidal species modulation with tidal constant corrections, J. Atmos. Ocean. Tech., 32, 350–371, 2015.
Carrère L., Lyard, F., Cancet, M., Guillot, A., and Picot, N.: FES 2014, a new tidal model – validation results and perspectives for improvements, Presentation to ESA Living Planet Conference, Prague, 2016.
Cartwright, D. E.: Tides: A scientific history, Cambridge University Press, Cambridge, 1999.
Courtier, A.: Marées. Service Hydrographique de la Marine, Paris, available at: https://journals.lib.unb.ca/index.php/ihr/article/download/27428/1882520184 (last access: 28 November 2019), 1938.
Defant, A.: Ebb and flow: the tides of earth, air, and water, University of Michigan Press, Ann Arbor, 1958.
Hart, D. E., Byun, D.-S., Giovinazzi, S., Hughes, M. W., and Gomez, C.: Relative Sea Level Changes on a Seismically Active Urban Coast: Observations from Laboratory Christchurch, Auckland, New Zealand, Proceedings of the Australasian Coasts and Ports Conference 2015, 15–18 September 2015, 6 pp., 2015.
Heath, R. A.: Phase distribution of tidal constituents around New Zealand, New Zeal. J. Mar. Fresh., 11, 383–392, 1977.
Heath, R. A.: A review of the physical oceanography of the seas around New Zealand – 1982, New Zeal. J. Mar. Fresh., 19, 79–124, 1985.
LINZ (Land Information New Zealand): Sea level data downloads, available at: http://www.linz.govt.nz/sea/tides/sea-level-data/sea-level-data-downloads (last access: 28 November 2019), 2017a.
LINZ (Land Information New Zealand): Tides around New Zealand, available at: https://www.linz.govt.nz/sea/tides/introduction-tides/tides-around-new-zealand (last access: 28 November 2019), 2017b.
Masselink, G., Hughes, M., and Knight, J.: Introduction to Coastal Processes and Geomorphology, 2nd edn., Routeldge, 432 pp., 2014.
Menéndez, M. and Woodworth, P. L.: Changes in extreme high water levels based on a quasi-global tide-gauge data set, J. Geophys. Res., 115, C10011, https://doi.org/10.1029/2009JC005997, 2010.
Nicholls, R. J., Wong, P. P., Burkett, V. R., Codignotto, J., Hay, J., McLean, R., Ragoonaden, S., Woodroffe, C. D., Abuodha, P. A. O., Arblaster, J., and Brown, B.: Coastal systems and low-lying areas, in: Climate change 2007: impacts, adaptation and vulnerability, edited by: Parry, M. L., Canziani, O. F., Palutikof, J. P., van der Linden, P. J., and Hanson, C. E., Contribution of Working Group II to the fourth assessment report of the Intergovernmental Panel on Climate Change, Cambridge University Press, Cambridge, UK, 315–356, 2007.
NIWA (National Institute of Water and Atmospheric Research): Sea level gauge records (hourly interval), available at: https://www.niwa.co.nz/our-services/online-services/sea-levels (last access: 28 November 2019), 2017.
Olson, D.-W.: Perigean spring tides and apogean neap tides in history, American Astronomical Society Meeting Abstracts, 219, 115.03, 2012.
Pawlowicz, R., Beardsley, B., and Lentz, S.: Classical tidal harmonic analysis including error estimates in MATLAB using T_TIDE, Comput. Geosci., 28, 929–937, https://doi.org/10.1016/S0098-3004(02)00013-4, 2002.
Pugh, D. T.: Tides, surges and mean sea-level (reprinted with corrections), John Wiley & Sons Ltd, Chichester, UK, 486 pp., 1996.
Pugh, D. T. and Woodworth, P. L.: Sea-level science: Understanding tides, surges, tsunamis and mean sea-level changes, Cambridge University Press, Cambridge, ISBN 9781107028197, 408 pp., 2014.
Stammer, D., Ray, R. D., Andersen, O. B., Arbic, B. K., Bosch, W., Carrère, L., Cheng, Y., Chinn, D. S., Dushaw, B. D., Egbert, G. D., and Erofeeva, S. Y.: Accuracy assessment of global barotropic ocean tide models, Rev. Geophys., 52, 243–282, https://doi.org/10.1002/2014RG000450, 2014.
Stephens, S.: The effect of sea level rise on the frequency of extreme sea levels in New Zealand, NIWA Client Report No. HAM2015-090, prepared for the Parliamentary Commissioner for the Environment PCE15201, Hamilton, 52 pp., 2015.
Stephens, S. A., Bell, R. G., Ramsay, D., and Goodhue, N.: High-water alerts from coinciding high astronomical tide and high mean sea level anomaly in the Pacific islands region, J. Atmos. Ocean. Tech., 31, 2829–2843, 2014.
van der Stok, J. P.: Wind and water, currents, tides and tidal streams in the East Indian Archipelago, Batavia, 1897.
Walters, R. A., Goring, D. G., and Bell, R. G.: Ocean tides around New Zealand, New Zeal. J. Mar. Fresh., 35, 567–579, 2001.
Walters, R. A., Gillibrand, P. A., Bell, R. G., and Lane, E. M.: A study of tides and currents in Cook Strait, New Zealand, Ocean Dynam., 60, 1559–1580, https://doi.org/10.1007/s10236-010-0353-8, 2010.
Wood, F. J.: The strategic role of perigean spring tides in nautical history and North American coastal flooding, 1635–1976, Department of Commerce, University of Michigan Library, 1978.
Wood, F. J.: Tidal dynamics: Coastal flooding and cycles of gravitational force, M.A., USA, D. Reidel Publishing Co., Hingham, 1986.
Woodworth, P. L., Melet, A., Marcos, M., Ray, R. D., Wöppelmann, G., Sasak, I. Y. N., Cirano, M., Hibbert, A., Huthnance, J. M., Monserrat, S., and Merrifield, M. A.: Forcing factors affecting sea level changes at the coast, Surv. Geophys., 40, 1351–1397, 2019.