Internal tides in the Solomon Sea in contrasted ENSO conditions

Intense equatorward western boundary currents transit the Solomon Sea, where active mesoscale structures exist with energetic internal tides. In this marginal sea, the mixing induced by these features can play a role in the observed water mass transformation. The objective of this paper is to document the M2 internal tides in the Solomon Sea and their impacts on the circulation and water masses, based on two regional simulations with and without tides. Since the Solomon Sea is under the influence of ENSO, the characteristics of the internal tides are also analyzed for two contrasted conditions: the January–March 1998 El Niño and the April–June 1999 La Niña. The generation, propagation, and dissipation of the internal tides are sensitive to changes in stratification and mesoscale activity, and these differ between these contrasted El Niño and La Niña case studies. Mode 1 is the dominant vertical mode to propagate baroclinic tidal energy within the Solomon Sea, but mode 2 becomes more energetic during the El Niño period when the stratification is closer to the surface. The La Niña period with a higher level of mesoscale activity exhibits more incoherent internal tides. These results illustrate the complexity of predicting internal tides in marginal seas in order to clearly observe meso- and submesoscale signatures from altimetric missions, including the future Surface Water Ocean Topography (SWOT) mission. Diapycnal mixing induced by tides contributes to a stronger erosion of the salinity maximum of the upper thermocline water and to cooling of the surface temperature interacting with the atmosphere. Such effects are particularly visible in quieter regions, where particles may experience the tidal effects over a longer time. However, when averaged over the Solomon Sea, the tidal effect on water mass transformation is an order of magnitude less than that observed at the entrance and exits of the Solomon Sea. These localized sites appear crucial for diapycnal mixing, since most of the baroclinic tidal energy is generated and dissipated locally here, and the different currents entering/exiting the Solomon Sea merge and mix. Finally, the extreme ENSO condition case studies suggest the strong role of local circulation changes, as well as stratification changes, in modifying the internal tides.

1 Introduction

The Solomon Sea is a marginal sea that is the last passageway for the low-latitude western boundary currents (LLWBCs) of the southwest Pacific that connect the subtropics to the Equator and supply water of subtropical origin to the Equatorial Undercurrent (EUC), warm pool, and Indonesian Throughflow (Tsuchiya et al., 1989; Grenier et al., 2011). It is an important place for tropical circulation and climate that motivates the CLIVAR Southwest Pacific Ocean Circulation and Climate Experiment (SPICE) program (Ganachaud et al., 2014). Marginal seas have long been identified as regions that contribute significantly to kinetic energy dissipation and water mass modification (Munk and Wunsch, 1998; Price and Yang, 1998; Egbert and Ray, 2000). Their topographic properties make them unique regions where water properties are transformed by lateral stirring and vertical mixing due to the energetic eddy field and the tidal-driven internal wave field. Abundant literature exists on the South China Sea and the Indonesian seas, illustrating this distinctive feature of marginal seas but not in the Solomon Sea, even though the southwest Pacific and in particular the Solomon archipelago are recognized as generation areas of energetic internal tides (Niwa and Hibiwa, 2001). Internal tides with phase-locked solitary waves have been observed during the COARE experiment, and they appear to propagate northeastward from the Solomon Islands (Pinkel et al., 1997; Gourdeau, 1998).

The Solomon Sea is bordered by the main island of Papua New Guinea (PNG) to the west, the PNG islands of New Britain (NB) and New Ireland (NI) to the north, and the Solomon Islands to the east (Fig. 1). The circulation in this semi-enclosed basin is highly constrained by such bathymetric features and has been described in numerous recent studies, from observations (Cravatte et al., 2011; Hristova and Kessler, 2012; Kessler et al., 2019; Davis et al., 2012; Gasparin et al., 2012) and model outputs (Melet et al., 2010a; Djath et al., 2014). A strong Low-Latitude Boundary Current (LLWBC), the New Guinea Coastal Undercurrent (NGCU) fed by the Gulf of Papua Current (GPC) and the North Vanuatu Jet (NVJ), flows from the southern entrance of the Solomon Sea along the PNG coast. When approaching the New Britain coast, it separates into two branches that exit the Solomon Sea through Vitiaz and Solomon straits. The NGCU flows at the thermocline level below highly variable surface currents including the New Guinea Coastal Current (NGCC) and the Solomon Strait inflow (SSI), which is a branch of the South Equatorial Current (SEC) that enters the Solomon Sea through the Solomon Strait. Instabilities in these large-scale currents generate large mesoscale eddies that account for most of the surface eddy kinetic energy (EKE) (Gourdeau et al., 2014, 2017; Hristova et al., 2014), and interaction of the mesoscale flow with topographic features generates submesoscale eddies and fronts (Srinivasan et al., 2017).

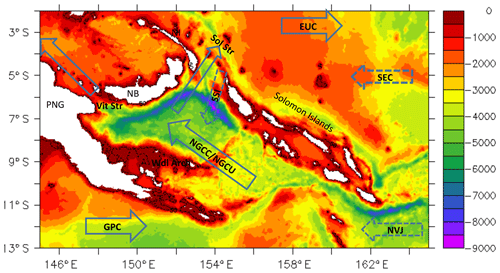
Figure 1 Bathymetry of the Solomon Sea over the domain of the regional simulation (in color; units: meters, m). The depth of 50 m has a black contour. PNG: Papua New Guinea; NB: New Britain; NI: New Ireland; Vit. Str.: Vitiaz Strait; Sol. Str.: Solomon Strait; Wdl arch.: Woodlark archipelago. The arrows illustrate the different currents mentioned in the text (dashed arrows are for surface currents, line arrows are for the thermocline currents). NGCC: New Guinea Coastal Current; NGCU: New Guinea Coastal Undercurrent; SSI: Solomon Strait inflow; EUC: Equatorial Undercurrent; SEC: South Equatorial Current; NVJ: North Vanuatu Jet; GPC: Gulf of Papua Current. The bathymetric file is the NOAA/ETOPO2v2 bathymetric file from the Smith & Sandwell database (https://doi.org/10.7289/V5J1012Q, National Geophysical Data Center, 2006).

Specific water masses entering the Solomon Sea are the South Pacific Tropical Water (SPTW; σθ∼24.5 kg m⁻³) in the upper thermocline level (UTW; $\mathrm{23.3}<\mathit{\sigma }\mathit{\theta }<\mathrm{25.7}$ kg m⁻³), referred to as the upper salinity maximum water and the Antarctic Intermediate Water (AAIW; σθ∼27.2 kg m⁻³) in the intermediate water range (IW; $\mathrm{26.7}<\mathit{\sigma }\mathit{\theta }<\mathrm{27.5}$) identified by a salinity minimum. These water masses undergo significant modification that erodes their extrema along their pathways through the Solomon Sea. This is characterized by a cooling and freshening of the SPTW and a warming and increased salinity of the AAIW, mainly due to diapycnal mixing (Fig. 3 in Germineaud et al., 2016; Melet et al., 2011). The modification of UTW affects the western Pacific with potential downstream effects on the eastern Pacific when the EUC upwells in the tropical eastern Pacific Ocean (Tsuchiya et al., 1989; Fine et al., 1994; Grenier et al., 2011; Qin et al., 2016).

In the Solomon Sea, Thorpe scales and fine-scale turbulence methods were applied to in situ observations to indirectly estimate the rate of dissipation of kinetic energy (Alberty et al., 2017). Depth-mean energy dissipation in the Solomon Sea is elevated by a factor of 8 relative to the rest of the equatorial Pacific, and energy dissipation is maximum in the surface and thermocline layers (4.1–$\mathrm{23}\times {\mathrm{10}}^{-\mathrm{8}}$ W kg⁻¹). To model this increased water mass mixing correctly in the Solomon Sea, tidal effects need to be included. Melet et al. (2011) used the tide-based vertical diffusivity parameterization proposed by Koch-Larrouy et al. (2007) for the Indonesian seas. This parameterization is based on the assumptions that all of the energy of the internal tides within a marginal sea is dissipated within that sea, and that energy dissipation is assumed to be maximum in the thermocline. Their modeled salinity without this tidal parameterization is biased high over the 24.5–27.5σθ range compared to observed properties, although it remains biased low with the parameterization, such that the erosion of SPTW is too strong.

This tidal parameterization is applied over the entire marginal sea and aims to take into account the general effects of internal tides in an ocean model. Yet internal tides are generated at a few specific locations where strong tidal currents encounter sharp topography in a stratified ocean. A global view of their generation, propagation, and dissipation has emerged from satellite altimetry observations (Ray and Mitchum, 1997; Ray and Zaron, 2016; Zhao et al., 2018) and global high-resolution numerical models (Arbic et al., 2010; Shriver et al., 2012; Simmons et al., 2004; Niwa and Hibiwa, 2014). Several studies have focused on the low vertical modes. M2 internal tides in the Pacific Ocean have been particularly investigated because of the numerous archipelagoes that are sources of internal tide generation. Regional studies based on in situ/satellite data and regional models have documented internal tides at the Hawaiian ridge (Merrifield and Holloway, 2002; Nash et al., 2006; Chavanne et al., 2010; Zhao et al., 2010) and at the Indonesian archipelago (Robertson and Ffield, 2008; Nagai and Hibiya, 2015; Nugroho et al., 2017). As far as we know, no dedicated studies have focused on internal tides in the southwest tropical Pacific, despite the high semidiurnal baroclinic tidal energy found here (Niwa and Hibiwa, 2011; Shriver et al., 2012). The main motivation of this paper is to document internal tides at the Solomon archipelago and their effects on the circulation and water masses in the Solomon Sea based on a regional model with and without tidal forcing.

Satellite altimeter maps show low-mode, phase-locked internal tides propagating across basins for thousands of kilometers (Shriver et al., 2012; Zhao et al., 2016; Ray and Zaron, 2016). This picture of coherent, phase-locked internal tides is somewhat partial as shown recently by several authors that point to the importance of nonstationary tides (Zaron, 2017; Shriver et al., 2014; Buijsman et al., 2017). In the world oceans, up to 44 % of the total semidiurnal internal tide signal is incoherent, and in the equatorial Pacific most of the tidal motions are incoherent (Buijsman et al., 2017). Several mechanisms contribute to the incoherence of internal tides. First, the internal tide generation may vary in time due to local changes in stratification (Colosi and Munk, 2006; Chavanne et al., 2010). Second, the propagation of the low-mode internal tides is modulated by spatial and temporal variability in stratification, currents, and vorticity with detectable changes in tidal sea surface height (SSH) (Zilberman et al., 2011; Ponte and Klein, 2015).

The southwest tropical Pacific is also marked by large interannual variability associated with the El Niño–Southern Oscillation (ENSO) with LLWBCs that vary to counterbalance interannual changes in the interior geostrophic flow (Melet et al., 2010b, 2013; Hristova and Kessler, 2012). The Solomon Sea experiences strong interannual variations in relation to ENSO. These include asymmetric circulation differences between El Niño and La Niña conditions that greatly impact the mesoscale activity and large temperature and salinity modifications particularly notable for the thermocline waters (Melet et al., 2013). So, it is suspected that internal tides in the Solomon Sea could be modulated by extreme ENSO conditions, with possible consequences for mixing of water masses flowing through to the Equator.

This particular study is a first attempt to investigate and describe internal tides over the complex Solomon Sea and their interaction with the mesoscale circulation, as well as to investigate their potential role in water mass transformation. We will address this issue using regional simulations at high resolution ($\mathrm{1}/\mathrm{36}{}^{\circ }$), with and without tidal forcing, that have been performed during a 3-year period. We will also consider case studies for two extreme periods: the January–March (JFM) 1998 El Niño and the April–June (AMJ) 1999 La Niña that exhibits different stratification and mesoscale activity.

The paper is organized as follows. Section 2 describes the regional model of the Solomon Sea with and without tides and the methodology used to analyze the tides. Section 3 describes the contrasting fields between the 1998 El Niño and the 1999 La Niña events for the different simulations. Section 4 describes the generation, propagation, and dissipation of the M2 baroclinic tide during the two ENSO conditions with a focus on their vertical signatures. Section 5 describes water mass transformation due to the tides over the longer 3-year period of the simulations. We illustrate some changes in the surface layer water mass properties due to tides for the contrasting ENSO conditions. Discussion and conclusion are given in Sect. 6.

2 Data and method

2.1 Model description: NEMO

The numerical model of the Solomon Sea used in this study is based on the Nucleus for European Modelling of the Ocean (NEMO) code (Madec, 2008) that resolved the standard primitive equations. It is a $\mathrm{1}/\mathrm{36}{}^{\circ }$ horizontal resolution model originally developed by Djath et al. (2014) that encompasses the Solomon Sea from 143 to 165.5^∘ E in longitude and from 13 to 2^∘ S in latitude. Atmospheric boundary conditions are diagnosed through classical bulk formulae (Large and Yeager, 2009), and wind, atmospheric temperature, and humidity are provided from the 3-hourly ERA-Interim reanalysis (Dee et al., 2011). This $\mathrm{1}/\mathrm{36}{}^{\circ }$ resolution model is embedded into a global NEMO $\mathrm{1}/\mathrm{12}{}^{\circ }$ ocean model forced with similar atmospheric boundary conditions and one-way controlled using an open boundary strategy (Treguier et al., 2001). The version used here is discretized on the vertical with 75 levels and includes the option of realistic tidal forcing. The simulation with tides is forced at the open boundary by prescribing the first nine main tidal harmonics (M2, S2, N2, K2, K1, O1, P1, Q1, M4) as defined from the global tidal atlas FES2014 (Carrere et al., 2015) through a forced gravity wave radiation condition. More technical details on this configuration may be found in Tchilibou et al. (2018).

Two simulations are performed as follows: one without tidal forcing (R36) and one with tidal forcing (R36T) over the 3-year 1997–1999 period. Daily mean model outputs are saved as R36(T)d. Instantaneous fields are saved hourly, R36(T)h, to document the baroclinic tides during the two contrasting 3-month periods: from January to March 1998 and from April to June 1999. The former period corresponds with summer austral conditions during an El Niño period and the latter with fall austral conditions during a La Niña period. For these two periods the interannual conditions dominate the effect of the mean seasonal cycle (not shown). These two periods in R36Th offer extremes in local stratification conditions, with a possible impact on the internal tides. The longer series of R36d and R36Td will be useful to investigate the effects of high-frequency baroclinic tides on the Solomon Sea water masses.

Very few in situ data exist to validate the high-frequency signal from the model. Some comparisons with coastal tide gauges and a mooring in Solomon Strait present satisfactory results at very localized positions (Tchilibou, 2018). The spatial patterns of phase-locked internal tide SSH patterns from 20 years of satellite altimetry will be compared with the R36Th 3-month model patterns under contrasting ENSO conditions in Sect. 4.2. Tchilibou et al. (2018) also used these simulations in the western Pacific, with and without tides, to illustrate how internal tides can explain the discrepancy in sea surface height wavenumber spectra, apparent in models (without tides) and altimetric data.

2.2 CARS climatology

CARS is a global ocean climatology on a $\mathrm{1}/\mathrm{2}{}^{\circ }$ grid of seasonal ocean water properties delivered by CSIRO (http://www.cmar.csiro.au/cars, last access: 30 April 2020). CARS differs from other climatologies as it employs extra in-house quality control of input data, and the mapping algorithm uses an adaptive-length-scale loess filter to maximize resolution in data-rich regions and takes into account topographic barriers. The result is an improved definition of oceanic structures and more accurate point values (Dunn and Ridgway, 2002). The CARS climatology will be used to provide some model validation, given the short period of the simulation including two extreme events.

2.3 Tidal decomposition and energetics

2.3.1 Barotropic/baroclinic tides decomposition

The central issue is to perform an accurate separation of the barotropic and baroclinic tide components, in terms of velocity and pressure as discussed in Nugroho et al. (2017). Although intuitive, this issue is not trivial, and we need to define precisely the meaning of “barotropic” and “baroclinic” dynamical terms. The method used to separate surface and internal tides ultimately defines properties such as internal tide generation and the depth structure of the internal tide energy flux (Kelly et al., 2010).

The most common definitions can be summarized as follows:

• 1.

  Barotropic tides are the ones that would be present in the absence of ocean stratification (uniform density ocean), and baroclinic tides are the departure from those barotropic tides when stratification is taken into account. This definition has been widely adopted by many authors. However, barotropic tides in a non-stratified ocean will differ significantly from barotropic tides in a stratified ocean. As a consequence, the “baroclinic” tides obtained by differencing non-stratified ocean tides and stratified ocean tides will contain parasite barotropic residuals.

• 2.

  Barotropic tides are the depth-averaged part of the tidal dynamics in a stratified ocean, baroclinic tides then being the residual between the full 3D tides and the barotropic tides. This definition is quite conventional and popular and mostly acceptable for first-order analysis. This reflects the idea that baroclinic quantities vanish when integrated with depth (also called the baroclinicity condition). This method has some consistency with model modes under a rigid lid assumption, but in the free surface case, it does not take account of the surface pressure, leading to an unsatisfactory tidal energy budget. The surface tide pressure can be expressed as the depth average of total pressure plus an additional depth-dependent profile of pressure, which is due to isopycnal heaving by free surface movements (Kelly et al., 2010).

• 3.

  Barotropic tides are the fast mode in a Sturm–Liouville vertical mode theoretical framework, and baroclinic tides are the slow modes. By using modal decomposition, this technique solves the inconsistencies that come from surface pressure variations due to isopycnal displacement. When this decomposition is applied to idealized cases, it also gives a barotropic energy flux that is consistent with energy conversion and has a good agreement with observations (Kelly et al., 2012). This definition has a much better physical meaning and has attracted much attention in the tidal community. It has been applied on models with realistic forcing and complex bottom topography such as in the Indonesian seas (e.g., Nugroho et al., 2017).

In this study, we will use the vertical mode decomposition (3) to define and separate the barotropic and baroclinic tides. In practice, the vertical mode computation and the decomposition of the simulation have been performed by solving the generalized Sturm-Liouville eigenvector/eigenvalue problem. Each successive mode decreases in group speed and increases in horizontal wavenumber. The lowest-mode tide (n=0) is the surface barotropic tide, and the higher-mode tides (n≥1) make up the internal tides with n zero crossings in the vertical for horizontal velocities.

2.3.2 Energy budget: generation, propagation, and dissipation

The generation, propagation, and dissipation of the barotropic and baroclinic tide is investigated with the time-averaged and depth-integrated barotropic and baroclinic energy equation (Niwa and Hibiya, 2004; Carter et al., 2008; Nagai and Hibiwa, 2015; Simmons et al., 2004; Buijsman et al., 2017). In each barotropic and baroclinic equation, the depth-integrated energy (E) is partitioned into tendency, flux divergence, nonlinear advection, barotropic to baroclinic conversion, and dissipation. We can ignore the rate of change term since the short averaging period (3 months and 3 years) makes this term orders of magnitude smaller than the other terms. Similarly, the nonlinear advection terms are assumed to be small in both the barotropic and baroclinic equations (Simmons et al., 2004; Buijsman et al., 2017). This means that little energy is transferred between tidal harmonics. The equations can then be written as

$$\begin{array}{}\text{(1)}& {\displaystyle }& {\displaystyle }\mathrm{\nabla }\cdot F_{\mathrm{bt}}+D_{\mathrm{bt}}+C=\mathrm{0},\text{(2)}& {\displaystyle }& {\displaystyle }\mathrm{\nabla }\cdot F_{\mathrm{bc}}+D_{\mathrm{bc}}-C=\mathrm{0},\end{array}$$

where bt indicates the barotropic term, and bc indicates the baroclinic terms; $F=\left(F_x;F_y\right)$ are the fluxes in the x and y directions. Dissipation (D) is computed as the residual of the flux divergence and conversion (C) terms. The conversion term is identical in the barotropic and baroclinic equations; it appears as a sink in the barotropic equation and a source in the baroclinic equation. It is defined as in Kelly and Nash (2010):

$$\begin{array}{}\text{(3)}& C={\mathrm{\nabla }}_{\mathrm{h}}H{\stackrel{\mathrm{‾}}{U_{\mathrm{bt}}{p}_{\mathrm{bc}}\mathrm{|}}}_{z=H+\mathit{\eta }}\left(\mathrm{W}{\mathrm{m}}^{-\mathrm{2}}\right),\end{array}$$

where U = (U, V) is the surface-tide velocity with components U and V along the x and y directions, p is the pressure, the overbar indicates a tidal average, z=H defines the bottom, and ∇_h is the horizontal gradient (∂x, ∂y) operator. (∇_h⋅) is the divergence operator, and η is the surface elevation.

The propagation of barotropic and baroclinic tides are examined through the divergences of the barotropic (F_bt) and baroclinic (F_bc) energy flux defined as in Nagai and Hibiya (2015):

$$\begin{array}{}\text{(4)}& {\displaystyle }& {\displaystyle }\mathrm{\nabla }\cdot F_{\mathrm{bt}}={\mathrm{\nabla }}_{\mathrm{h}}{\int }_H^{\mathit{\eta }}\stackrel{\mathrm{‾}}{U_{\mathrm{bt}}{p}_{\mathrm{bt}}}\mathrm{d}z\left(\mathrm{W}{\mathrm{m}}^{-\mathrm{2}}\right),\text{(5)}& {\displaystyle }& {\displaystyle }\mathrm{\nabla }\cdot F_{\mathrm{bc}}={\mathrm{\nabla }}_{\mathrm{h}}{\int }_H^{\mathit{\eta }}\stackrel{\mathrm{‾}}{U_{\mathrm{bc}}{p}_{\mathrm{bc}}}\mathrm{d}z\left(\mathrm{W}{\mathrm{m}}^{-\mathrm{2}}\right),\end{array}$$

where ∇_h is the horizontal divergence.

2.3.3 Calculating (non-)phase-locked internal tides

For each 3-month period of hourly time series corresponding to the January–March (JFM) 1998 El Niño and the April–June (AMJ) 1999 La Niña, the simulated time series are first harmonically analyzed to obtain the amplitude and phase of the main diurnal (K1, O1, P1) and semidiurnal (M2, K2, S2, N2) components. Then linear tidal frequency motions of vertical displacement and horizontal velocity are projected onto the barotropic mode (n=0) and the nine first orthogonal vertical modes ($n=\mathrm{1},\mathrm{2},\mathrm{\dots },\mathrm{9}$). This provides the description of the barotropic tide (mode 0) and the phase-locked baroclinic tide that can be analyzed for each mode or as the sum of the nine baroclinic modes. These harmonic analyses provide only the tidal signal that is coherent with the astronomical forcing over each 3-month period. But several mechanisms can contribute to incoherent tides such as changes in stratification, interactions with the mesoscale flows, and the internal wave field (Buijsman et al., 2017). A proxy for the incoherent part of the internal tide is to filter the signal for periods <24 h once the stationary, phase-locked tides have been subtracted. This incoherent or non-phase-locked component also includes the internal wave field and very rapid ocean circulation. However, the variance in the corresponding SSH field in the simulation without tides is quite small (Tchilibou et al., 2018; their Fig. 9), so in our region, the non-phase-locked component is mainly a tidal signal in the simulation with tides.

3 Contrasting El Niño and La Niña conditions

This section presents the Solomon Sea circulation, its variability, and its vertical stratification for the 3-year daily simulations and for the two extreme ENSO periods: the JFM 1998 El Niño and the AMJ 1999 La Niña. All of these dynamical elements may influence the internal tide fields from its generation to its propagation, and dissipation. In the western Pacific, El Niño and summer (JFM) conditions both raise the thermocline closer to the surface, La Niña and fall (AMJ) conditions have a deeper thermocline. Inspection of the model velocity and temperature showed that most of the circulation and stratification changes between these two periods are not due to the different phases of the mean seasonal cycle (not shown).

3.1 Circulation and EKE

The interannual variability in the surface circulation in R36Td is consistent with previous studies on ENSO cycles (Hristova and Kessler, 2012; Melet et al., 2013) (Fig. 2). At ENSO timescales, the LLWBCs transport tends to counterbalance the interior geostrophic transport. During the 1998 El Niño period, the NGCC/NGCU intensifies and increases the transport towards the Equator to counterbalance the equatorial discharge (Fig. 2a). During the 1999 La Niña period, the strengthening of the trade winds increases the SEC intensity in the equatorial band and the inflow transport at Solomon Strait. Some model experiments suggest that the induced circulation anomalies in the Solomon Sea are not symmetric between the two ENSO states. This may be due to the bathymetric control at the narrow Vitiaz Strait that limits the outflow of the stronger NGCC during El Niño, whereas the additional inflow through the wider Solomon Strait flows more freely during La Niña when the NGCC weakens (Melet et al., 2013).

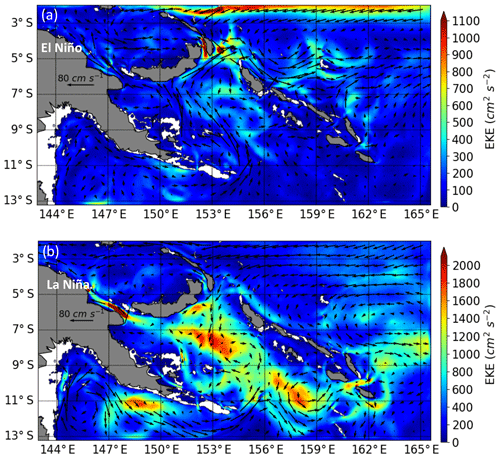
Figure 2 Mean surface EKE (shading; units: square centimeters per second squared) and mean surface circulation (arrows) from the 3-month TIDE simulations during (a) the El Niño state and (b) the La Niña state. Note the change of color bar between the two ENSO states. White color is for bathymetry of less than 50 m. Isobathymetric lines are from the NOAA/ETOPO2v2 bathymetric file from the Smith & Sandwell database (https://doi.org/10.7289/V5J1012Q, National Geophysical Data Center, 2006).

A consequence of this asymmetry is a level of surface Eddy Kinetic Energy (EKE) that varies strongly between the two ENSO states, as shown on the mean EKE maps representative of the different 3-month periods (Fig. 2). During the El Niño case, despite the increase in LLWBC transport, the level of EKE is relatively low. However, during the La Niña case, the strong shear between the NGCC and the SSI (Solomon Strait inflow) is at the origin of a high level of EKE as described in Gourdeau et al. (2014). Therefore, the mean circulation and the EKE level of these two contrasted periods provide different background conditions for the interactions between currents and internal tides.

3.2 SSH variability

SSH variability, as measured by altimetry, is a good proxy of energetic motions. In the tropics, the SSH wavenumber spectral signature of mesoscale variability is highly impacted by the signature of internal tides for scales up to 250–300 km (Tchilibou et al., 2018). This complicates the analysis of these spatial scales with a mix of mesoscale dynamics and internal tides, for all altimetric SSH observations and in the context of the future SWOT mission. This new swath-altimetry mission will be a great opportunity to study the 2D interactions between both dynamics in the tropics. The objective of this subsection is to give some insight on the SSH variability associated with mesoscale activity and internal tides in the Solomon Sea.

The largest SSH variability in the Solomon Sea is at seasonal and interannual timescales in response to large-scale and low-frequency atmospheric forcing and is responsible for up to 80 % of the gridded AVISO altimetric signal variance (Melet et al., 2010b; Gourdeau et al., 2014). These longer timescales have an EKE level reaching 2000 cm² s⁻² (Fig. 4 in Melet et al., 2010b) that is of same order as the intraseasonal EKE level during the La Niña period, as shown in Fig. 2b from the R36Th simulation.

The SSH variability associated with the intraseasonal EKE described above is a mix of mesoscale variability down to subinertial frequencies and internal waves at super-inertial frequencies (Savage et al., 2017). The super-inertial frequency range corresponds mostly to internal tides signatures as confirmed by the quasi-null SSH variability in the simulation without tides for such frequency range (not shown). Figure 3 shows how the SSH standard deviation of the R36Th outputs changes between the El Niño and La Niña periods for the full signal, the mesoscale component (>48 h), and the high-frequency component dominated by internal tides (<48 h). The variability in the incoherent part of the internal tides discussed in the next section is also plotted.

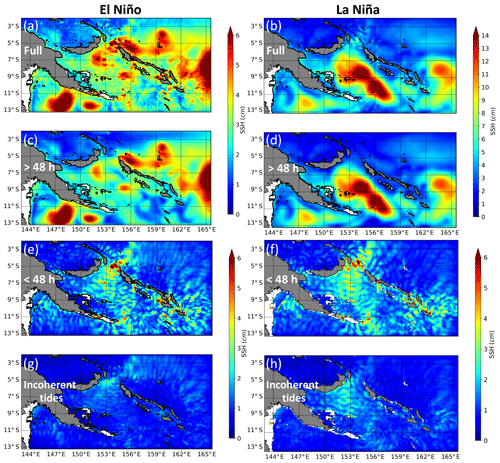
Figure 3 Root mean square of SSH variability for the 3-month periods of the (a, c, e, g) El Niño state and (b, d, f, h) La Niña state. Units are in centimeters. The top panel (a, b) is the full SSH variance, the second panel (c, d) is the mesoscale variability (periods >48 h), the third panel (e, f) is the high-frequency variability (periods <48 h), dominated by the internal tides (both coherent and incoherent components), and the bottom panel (g, h) is the incoherent internal tide variability. Note the change of color bar for the full and mesoscale variability in the La Niña period. Isobathymetric lines are from the NOAA/ETOPO2v2 bathymetric file from the Smith & Sandwell database (https://doi.org/10.7289/V5J1012Q, National Geophysical Data Center, 2006). White color is for bathymetry of less than 50 m.

Outside the Solomon Sea, the patterns of SSH variability are similar between the two ENSO states, although there is more mesoscale energy during El Niño (Fig. 3a, b). Increased variability is associated with instabilities in the GPC when it turns eastward at PNG coast near 12^∘ S, 148^∘ E and with instability from the South Equatorial Counter Current (SECC)–SEC current system east of the Solomon Islands near 8^∘ S, 164^∘ E (Qiu and Chen, 2004). Inside the Solomon Sea, the patterns of SSH variability differ greatly between the two ENSO states by a factor of 2–3. The El Niño period is marked by low variability with small-scale structures, compared to the La Niña period where high variability occupies the central Solomon Sea, in accordance with the EKE signal (Fig. 2). During the El Niño period, the level of mesoscale variability is of the same order of magnitude as the internal tides (Fig. 3c, e). This explains why the full signal is composed of small structures mixing both mesoscale activity and internal tides. The most energetic internal tides signal is concentrated in the Solomon Sea from the southern tip of PNG to Solomon Strait (described more in Sect. 4). Incoherent tides are ubiquitous, mainly in the northern Solomon Sea. During the La Niña period, the mesoscale variability is largely dominant compared to the internal tides signature (Fig. 3d, f). Note that the patterns of internal tides differ slightly between both ENSO states with a more continuous pattern crossing the Solomon Sea and a substantial signature of incoherent internal tides in the northern Solomon Sea during La Niña. This suggests potential interaction between mesoscale dynamics and internal tides, with a possible effect on changes in water mass stratification depending on the ENSO phase. This will be explored more in Sects. 4 and 5.

3.3 Water masses and stratification

Internal tides are sensitive to ocean stratification and such stratification is susceptible to be modified at ENSO timescales because of temperature and salinity anomalies of the different water masses entering the Solomon Sea (Melet et al., 2013). Because the internal tide propagates mainly in the meridional direction across the central Solomon Sea (e.g., Sect. 4), the section at 154^∘ E is used to investigate and validate the water mass characteristics and to illustrate the corresponding stratification changes in different ENSO conditions.

First, the averaged salinity section from the 3-year R36Td is compared with that of the long-term CARS climatology (Fig. 4a, b). Our model with tides shows a good positioning of the maximum salinity of the SPTW waters (σθ=24.5 kg m⁻³, z∼150 m) and the minimum of salt of the AAIW waters (z∼800 m) (e.g., Sect. 1).

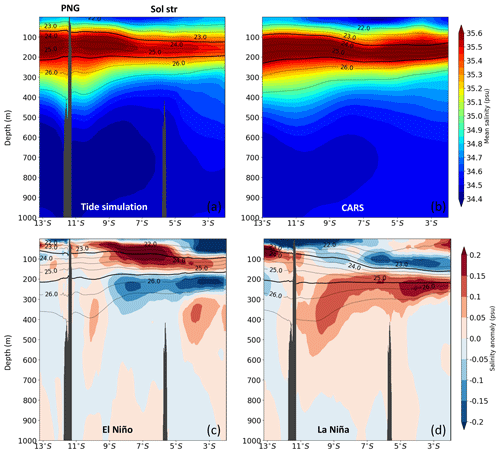
Figure 4 Latitude/depth section at 154^∘ E of mean salinity (a) from the R36Td simulation, (b) from CARS climatology, and of salinity anomalies for the 3-month (c) El Niño period and (d) La Niña period, relative to the full R36Td period. The Solomon Sea section is between the topographic features (vertical black lines) at 12 and 6^∘ S. The black contours highlight the upper thermocline layer (UTW).

To illustrate the role of the ENSO cycle in the vertical heaving of this mean structure, the salinity anomalies for El Niño and La Niña periods from R36Td are calculated with reference to the complete period (Fig. 4c, d). The main changes in salinity concern the first 500 m below the surface and particularly the upper thermocline waters ($\mathrm{23.3}<\mathit{\sigma }\mathit{\theta }<\mathrm{25.7}$ kg m⁻³). These interannual salinity anomalies are consistent with large-scale variability due to the effect of the anomalous wind stress curl that develops at ENSO timescales in the area by strongly pulling up (down) the thermocline during El Niño (La Niña) and from Rossby wave propagation forced by the anomalous Ekman pumping (Melet et al., 2013).

During El Niño conditions, the resulting thermocline shoaling brings fresher and colder water below the thermocline water compared to neutral conditions and saltier/warmer surface waters. The opposite situation prevails during La Niña conditions, with saltier and warmer lower thermocline water and fresher/colder upper thermocline water. During La Niña conditions, the saltier waters also intrude at the surface near 3^∘ S due to the advection of central Pacific salty water by the strong SSI (Gourdeau et al., 2017).

As a consequence of such ENSO variability, the density sections show a more pronounced thermocline shifted upward during El Niño in comparison with La Niña, particularly in the north of the section (Fig. 4c, d). These density profiles reflect changes in the vertical stratification represented by the Brünt Vaisala frequency (N). Figure 5 shows the mean N profiles averaged along the 154^∘ E section when averaged in latitude across the Solomon Sea. Figure 5 compares the long-term CARS climatology with the R36Td simulation characteristic of the mean 3-year state, as well as the two 3-month ENSO phases. First, the modeled mean N² profile with tides is in good agreement with the CARS climatology with maximum values in the 80–150 m depth range. The ENSO phases are clearly distinguishable from the mean. The La Niña period is marked by a deepening of the maximum N² frequency extending the thermocline down to a depth of 200 m. The situation during El Niño is very contrasting; N² is marked by significantly higher values and stronger thermocline gradients, especially in the surface layers with a maximum value at a depth of 50 m. Internal tides being very sensitive to these N² profiles, we can assume that different internal tide characteristics may occur between these two periods.

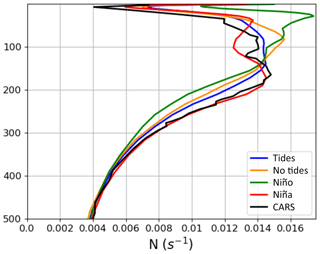
Figure 5 Mean N profile averaged for the Solomon Sea section at 154^∘ E from CARS climatology (black) and from the R36Td TIDES simulation averaged over the entire 3-year period (blue), the 3-month El Niño period (green), and the 3-month La Niña period (red). The yellow line is for the R36d NOTIDES simulation averaged over the entire 3-year period. Units are in per second (s⁻¹).

4 M2 tides

In this section, the tidal signal simulated by the regional model is described using the hourly outputs from R36Th. The daily averaged 3-year R36Td model runs allow us to investigate the net longer-term effects of the tides and internal tides on water mass properties but do not allow us to closely investigate the high-frequency tide signal. A first insight into the tides is through temporal spectra. SSH frequency spectral density averaged over the Solomon Sea is shown in Fig. 6a. Both models with and without tides agree well at low frequency (T>30 h). The simulation with tides shows large peaks at diurnal and semidiurnal frequencies and an energetic supertidal band (T<12 h). The tidal signal is a mixture of barotropic and baroclinic components, and the SSH variance is largely dominated by the former with K1 as the main barotropic component (Tchilibou, 2018).

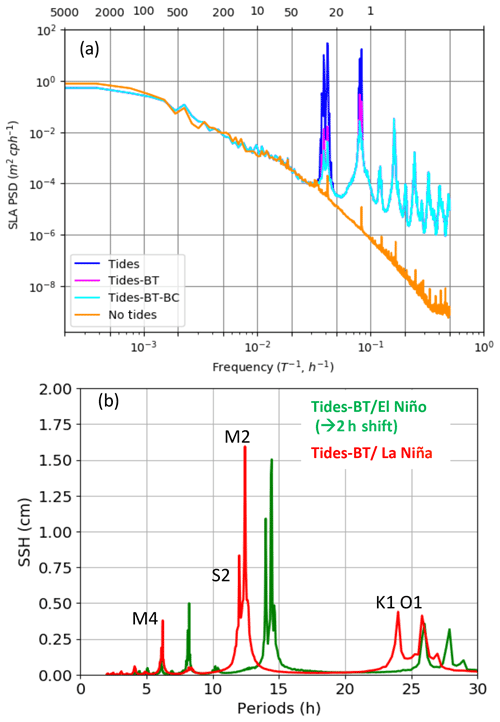
Figure 6 (a) SSH frequency spectra averaged over the Solomon Sea area based on the 3-month hourly outputs of the El Niño period for the R36h simulation (no tides, in yellow), for the R36Th simulation including barotropic and baroclinic tides (Tides, in blue), baroclinic tides only (Tides-BT, in pink), incoherent baroclinic tides only (Tides-BT-BC, in cyan). (b) Zoomed in on SSH frequency spectra showing the diurnal, semidiurnal, and quarter-diurnal signature of baroclinic tides calculated during the El Niño period (in green) and the La Niña period (in red). For clarity the green spectrum is shifted by 2 h.

The modal decomposition is done for each of the two ENSO phases using R36Th. To infer the baroclinic tidal signature (n≥1) the barotropic tide (n=0, BT) is removed (Tides-BT). The frequency spectra of the Tides-BT SSH signal, averaged over the Solomon Sea, shows that the main baroclinic tide is at the M2 period for both ENSO phases (Fig. 6b). Therefore in the following, our focus will be on the dominant M2 baroclinic component. There are small differences in the amplitudes of the components between the two ENSO phases, especially for semidiurnal frequencies (Fig. 6b; note that to clearly distinguish their peaks the El Niño spectrum is shifted in period by 2 h). The amplitude differences may be due to changes in circulation and mesoscale activity as well as in stratification. The first nine baroclinic modes that we compute from our model represent more than 90 % of the baroclinic energy for both ENSO phases. But before we analyze the baroclinic tidal components further for the two ENSO conditions, we will assess how well the barotropic component has been simulated.

4.1 M2 barotropic tide

The realism of the simulated barotropic tides is crucial for the ability of the model to generate realistic internal tides. The barotropic M2 tide simulated by our model is estimated for each of the 3-month ENSO periods, and both estimations provide similar results (not shown). The simulated barotropic M2 tide is forced at the open boundary by FES2014. Its free evolution within the Solomon Sea compares well with the FES2014 solution. The M2 barotropic tide is maximum outside the Solomon Sea and almost null within the Solomon Sea (Fig. 7). East of the Solomon Islands, the lines of constant M2 phase in Fig. 7 illustrate a southward propagation that turns westward at the southern tip of the Solomon Islands with a magnitude that decreases from 30 to 15 cm. The M2 barotropic tide interacts clearly with bathymetry at Solomon Strait (5–6^∘ S), at the southern extremity of the Solomon Islands, and at the southeastern tip of PNG (Fig. 7). The interaction of this barotropic tide with the topography enclosing the Solomon Sea is favorable for generating M2 internal tides.

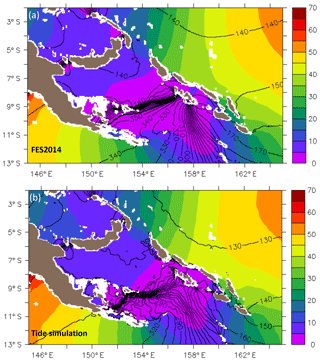
Figure 7 SSH M2 barotropic tide from (a) FES2014 and (b) the R36Th simulation. Amplitude is in color (unit: centimeters) and the contours are phase lines. Isobathymetric lines are from the NOAA/ETOPO bathymetric file from the Smith & Sandwell database (https://doi.org/10.7289/V5J1012Q, National Geophysical Data Center, 2006). White color is for bathymetry of less than 50 m.

4.2 M2 baroclinic tide

Following the method described in Sect. 2.2.3, we access only the coherent part of the internal tide that has the advantage to be predictable and can thus provide a SSH correction for altimetric measurements. Here we describe the dominant M2 phase-locked internal tide, in its depth-integrated form (combining the nine baroclinic modes).

4.2.1 SSH validation of the phase-locked component

An estimate of the SSH amplitude of the M2 stationary or phase-locked baroclinic tide based on more than 20 years of altimeter measurements is given in Ray and Zaron (2016). Their result is shown in Fig. 8a. The altimetric M2 baroclinic tide has a strong amplitude in the Solomon Sea, extending from the Solomon Strait in the north to the eastern tip of PNG. The amplitude of the baroclinic (coherent) tide is on the order of 3–5 cm in the Solomon Sea with an approximate wavelength of 150 km. The M2 internal tide estimated by the model during the 3-month La Niña period (Fig. 8c) is consistent with that estimated from the 20 years of altimetry but with higher amplitudes at Solomon Strait. The M2 internal tide estimated during the El Niño period has shorter wavelengths and more dispersion over the entire domain of the Solomon Sea. Both patterns of the M2 coherent baroclinic tide resemble the full signal of internal tides calculated over these 3-month periods (Fig. 3), illustrating that M2 is the main contributor to the internal tide variability. Indeed, the M2 tide semidiurnal tide corresponds to more than 70 % of the full internal tide variance within the Solomon Sea.

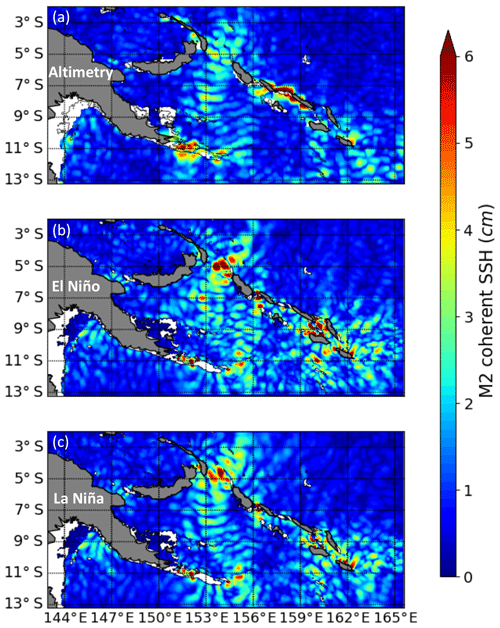
Figure 8 SSH amplitude of the stationary M2 baroclinic tide as estimated from (a) altimetry by Ray and Zaron (2016), the R36Th simulations during the 3-months of (b) the El Niño period, and (c) the La Niña period. Units in centimeters. Isobathymetric lines are from the NOAA/ETOPO2v2 bathymetric file from the Smith & Sandwell database (https://doi.org/10.7289/V5J1012Q, National Geophysical Data Center, 2006). White color is for bathymetry of less than 50 m.

The large internal tide differences between the two ENSO states raise the question of the predictability of the stationary internal tide when the level of mesoscale activity and the stratification change at interannual timescales. Note that it is during the La Niña condition when the mesoscale activity is high (e.g., Fig. 3) that the M2 internal tide appears well organized in accordance with the altimetric estimation. One explanation is that the deeper stratification during La Niña is closer to the long-term mean stratification, compared to El Niño (e.g., Fig. 5). The M2 baroclinic tide is dominated by mode 1 during La Niña, whereas the higher modes have increased energy during El Niño. This could also explain why the spatial pattern of the long-term coherent baroclinic M2 tide of Ray and Zaron (2016) looks like the modeled results for the La Niña period.

Mesoscale activity also influences the characteristics of baroclinic tides. Indeed, the part of coherent baroclinic tides versus the incoherent part varies substantially between the two ENSO states. During El Niño, when the LLWBCs are strong and stable and dominate the circulation, the coherent baroclinic tides explains 67 % of the variance in the full internal tides. Whereas during La Niña, when the mesoscale activity is stronger because of the interactions between the LLWBCs and the SSI (Solomon Strait inflow), only 50 % of the baroclinic tide is coherent. This is clearly shown in the maps of incoherent baroclinic tides (Fig. 3) where stronger incoherent baroclinic tides are present in the northern Solomon Sea basin during the La Niña period.

4.2.2 Generation, propagation, and dissipation

The distribution of the baroclinic energy flux, the energy conversion rate, the divergence of the baroclinic energy flux, and the baroclinic energy dissipation are all shown in Fig. 9 for the M2 harmonic, for both the La Niña and El Niño periods. Table 1 also provides the area integrals of the different terms of the energy equation at the different generation sites as defined by the boxes on Fig. 9f for the two ENSO phases.

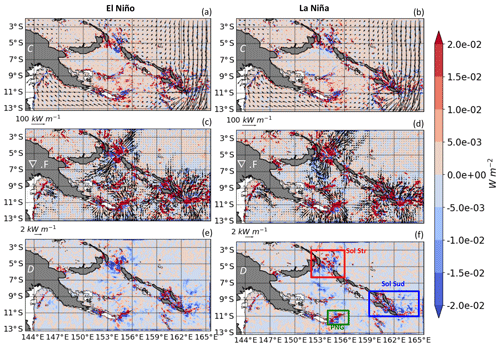
Figure 9 (a, b) Conversion rate (C), (c, d) the baroclinic flux divergence (∇F), and (e, f) the dissipation rate (D) for the M2 harmonic (negative values shaded in blue; positive values in red; unit: watts per square meter). The corresponding barotropic and baroclinic energy flux are superimposed with arrows in (a)–(d), with a scaling of 100 and 2 kW m⁻¹, respectively. Panels (a), (c), and (e) correspond to the El Niño period and panels (b), (d), and (f) to the La Niña period. The boxes define the different generation areas where energetics are quantified in Table 1. Isobathymetric lines are from the NOAA/ETOPO2v2 bathymetric file from the Smith & Sandwell database (https://doi.org/10.7289/V5J1012Q, National Geophysical Data Center, 2006). White color is for bathymetry of less than 50 m.

Table 1 ∇F_bt (∇F_bc) is the divergence of the barotropic (baroclinic) flux, D_bt (D_bc) is the dissipation of the barotropic (baroclinic) flux, and C is the conversion rate from barotropic to baroclinic energy. Units are in gigawatts. P1 is the percentage of the barotropic energy converted into baroclinic energy, and P2 is the percentage of the baroclinic energy dissipated within the box.

For both ENSO phases, the M2 barotropic energy flux comes from the Equatorial Pacific and flows southward in the southwestern pacific, east of the Solomon Islands and then turns westward south of the Solomon Sea. There are two main pathways for the M2 tide to enter the Solomon Sea, either by the Solomon Strait or by the southern portal. On its way it encounters three main complex bathymetric features that generate intense internal tides: the Solomon Strait (5–6^∘ S), the southern extremity of the Solomon Islands, and the southeastern tip of PNG. They are the three main areas of baroclinic tide generation as shown by the negative values of the energy conversion rate (the sign is consistent with it being a sink term in the barotropic equation) (Fig. 9a, b). Weaker internal tides are also found within the Solomon Sea over the seamounts extending eastward from the Woodlark archipelago (∼9^∘ S–155^∘ E).

Strong baroclinic energy fluxes originate in regions where significant energy conversion is occurring (Fig. 9c, d). The excited baroclinic energy radiates away from the generation zones, and the largest fluxes are contained within two beams: one propagating inside the Solomon Sea and the other one propagating outward into the open ocean. The main baroclinic energy flow entering the Solomon Sea comes from the southeastern tip of PNG where it propagates to the northwest and from the Solomon Strait where it propagates to the southwest. Both fluxes cross the Solomon Sea between 153 and 156^∘ E. This description is in accordance with the SSH signature of the M2 baroclinic tide (Fig. 8).

Estimates for the dissipation of internal tides (Fig. 9e, f) in the model are made as a residual between the divergence of the baroclinic flux (Fig. 9c, d) and the conversion rate (Fig. 9a, b) following Eq. (2). This equation does not take into account the nonlinear advection (Buijsman et al., 2017) that might be contained in the dissipation estimate. This might overemphasize the energy of the dissipation estimate. It is interesting to note that most of the dissipation occurs locally near the generation sites (Table 1), although some energy is dissipated along the main propagation pathway between 152 and 156^∘ E, especially in the northern Solomon Sea.

Some modulations are noted between the El Niño and La Niña periods, with a slightly stronger conversion rate, stronger local dissipation, and stronger energy flux during the El Niño period. The dissipation is also quite significant during La Niña in the northern Solomon Sea, away from the generation site (Fig. 9, Table 1).

4.2.3 Quantification of the tidal energy budget for the two ENSO states

For the Solomon Strait box (Fig. 9f, red), the divergence of the barotropic flux energy is around 3 GW (Table 1). The majority of this flux divergence is converted into baroclinic tides (∼70 %, ∼2.10 GW) with the bottom friction (barotropic dissipation) accounting for ∼0.85 GW. The majority of the energy converted from barotropic to baroclinic energy is dissipated within the box, but there is stronger local dissipation during El Niño (75 %) than during La Niña (66 %). So we observe a stronger baroclinic energy flux radiating out of the box during the La Niña period that may dissipate in the far field. Overall, 0.7 GW radiates out of the box as a baroclinic flux during the La Niña period compared to 0.55 GW during El Niño. More than half of this energy propagates into the Solomon Sea.

For the box representative of the southern extremity of the Solomon archipelago (Fig. 9f, blue), the divergence of the barotropic flux energy is around 6 GW, twice that of the Solomon Strait box. The majority (∼60 %) of this flux divergence is converted into baroclinic tides (4 GW) with the bottom friction (barotropic dissipation) accounting for 2 GW. The majority of the energy converted from barotropic to baroclinic energy is dissipated within the box, and the dissipation rate varies from 70 % to 80 % between El Niño and La Niña, respectively. During the El Niño event, the barotropic flux divergence is larger than during the La Niña event (6.83 vs. 5.89 GW). As a consequence, the conversion rate is stronger in the same proportion (Table 1), but the dissipation is identical between the two ENSO events (∼3 GW). The baroclinic flux radiating out of the box increases during El Niño (1.27 GW compared to 0.75 GW during La Niña) meaning that more dissipation must occur in the far field during El Niño. Most of this baroclinic energy radiates out of the Solomon Sea, and only 0.24∕0.17 GW radiates into the Solomon Sea during the El Niño/La Niña periods.

The PNG box (Fig. 9f, green) is smaller than the other boxes, and the divergence of the barotropic flux energy is around 1.8 GW. More than 75 % of this flux divergence is converted into baroclinic tides (1.36 GW). The majority of the energy converted from barotropic to baroclinic energy radiates out of the box (0.75 GW), and 0.22 GW radiates into the Solomon Sea. No contrasting situations are observed between the two ENSO phases.

In summary, there are three areas where a large part of the barotropic flux energy is converted into baroclinic energy (63 % to 79 %). Most of the excited baroclinic energy is dissipated locally (46 % to 80 %), and only two generation sites at Solomon Strait and at the southeast extremity of PNG radiate significant baroclinic tidal energy into the Solomon Sea. The Solomon Strait radiates most of the baroclinic energy into the Solomon Sea, especially during the La Niña state with a 27 % increase in the energy flux compared to El Niño. Most of this baroclinic energy is dissipated in the northern Solomon Sea as illustrated by Fig. 9f, with higher dissipation here during La Niña compared to El Niño. This is likely to be impacted by the contrasting circulation and mesoscale activity in this area between the El Niño and La Niña periods. The strong northward LLWBC current exiting the Solomon Sea during El Niño is replaced by the southward SSI current during the La Niña period (see Fig. 2), which favors the advection of the tidal baroclinic energy inside the Solomon Sea. Also, the higher EKE level during La Niña than during El Niño (Fig. 2) favors stronger interactions between eddies and internal tides. This appears to render the internal tide more incoherent (e.g., Fig. 3g, h) and to increase the tidal dissipation (Fig. 9f). At the southeast extremity of PNG (Fig. 9f, blue) crossed by the strong NGCU, the tidal baroclinic energy exhibits no contrasting situations between the two ENSO phases.

4.2.4 Vertical signature

In the previous sections, baroclinic tides were investigated by considering their depth-integrated form. For a more quantitative discussion on the vertical structure of the propagating M2 baroclinic tide, we perform modal decomposition of the model-predicted baroclinic energy fluxes. Figure 10 shows the spatial distribution of the M2 modes 1 and 2 for the El Niño and La Niña states. These two modes account for almost the entire variance in the full baroclinic M2 energy flux. Mode 1 is the dominant mode (note the different scales between mode 1 and 2). However, mode 2 is particularly present within the Solomon Sea during the El Niño period, compared to the La Niña period where mode 2 energy is locally dissipated at the generation sites. An explanation for such a difference is the change in stratification between the two ENSO states, with stratification being closer to the surface during El Niño, which favors the excitation of higher-order modes (Fig. 5).

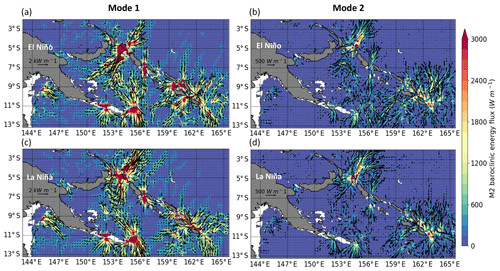
Figure 10 Modal decomposition of the M2 energy flux during the 3-month (a, b) El Niño and (c, d) La Niña periods, corresponding to (a, c) mode 1 and (b, d) mode 2. Mode 1 flux is scaled with arrows of 2 kW m⁻¹ and mode 2 flux with arrows of 500 W m⁻¹. The shading is the amplitude (units: watts per meter). Isobathymetric lines are from the NOAA/ETOPO2v2 bathymetric file from the Smith & Sandwell database (https://doi.org/10.7289/V5J1012Q, National Geophysical Data Center, 2006). White color is for bathymetry of less than 50 m.

Whatever the ENSO state, mode 1 energy flux propagates into the Solomon Sea, from Solomon Strait and from the southeastern tip of PNG. The PNG flux is relatively stable (see Table 1) and follows the NGCU pathway until the Woodlark archipelago (9^∘ S). Whereas the Solomon Strait flux exhibits strong changes in propagation between the two ENSO states that appear related to the background circulation. During El Niño, this mode 1 flux is directed to the southwest in the lee of the LLWBC exiting at Solomon Strait. It breaks into two branches when encountering the northward NGCC to the west. During La Niña, the flux is southward in the wake of the Solomon Strait inflow. This suggests the constraint of the propagation of the baroclinic tidal energy by the background circulation. The mode 1 baroclinic flux emanating from the south Solomon Sea is less intense during La Niña (Table 1), and this flux exits the Solomon Sea to the south.

To illustrate the changes brought by the stratification and the circulation on the vertical structure of the M2 baroclinic flux, we show a vertical section along 154^∘ E of the meridional baroclinic energy fluxes for the two ENSO phases (Fig. 11). This section transects the prominent baroclinic energy flux in the Solomon Sea. The highest energy fluxes are located in the upper 300 m, but they extend deeper during the La Niña period than during El Niño in accordance with changes in stratification (Fig. 5). During El Niño, when the NGCC/NGCU are strong, the northward baroclinic energy flux from the southern tip of PNG crossed practically all of the Solomon Sea up to 6.5^∘ S. During La Niña, when the SSI is strong, the baroclinic energy flux from the Solomon Strait extends to the south and the southward and northward fluxes meet in the central Solomon Sea (8^∘ S).

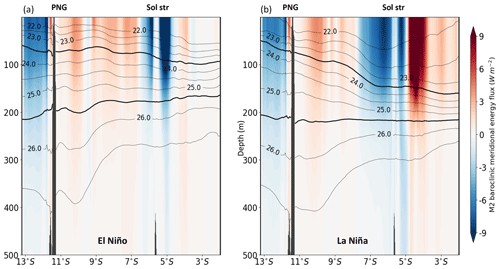
Figure 11 Vertical section at 154^∘ E of the mean meridional energy flux estimated during (a) El Niño state and (b) La Niña state (units: watts per square meter). The corresponding isopycnals are in contours, with σ=23.5 and σ=24.5 kg m⁻³ in bold.

In summary, the M2 baroclinic energy flux is concentrated in the upper 200–300 m. Propagation and depth penetration of this energy vary between the two ENSO states depending on the background circulation and stratification. Mode 1 accounts for most of the propagation of the energy flux but mode 2 is also significant, particularly during the JFM El Niño period characterized by a stratification close to the surface.

5 Tidal effect on water mass transformation

Here, we take advantage of our 3-year R36d twin simulations, forced with tides (TIDE) and without tides (NOTIDE), to analyze the net impact of internal tides on the water mass modification of the Solomon Sea. Most of the transformation occurs in the SW (σθ<23.3 kg m⁻³), UTW ($\mathrm{23.3}<\mathit{\sigma }\mathit{\theta }<\mathrm{25.7}$ kg m⁻³), and IW ($\mathrm{26.7}<\mathit{\sigma }\mathit{\theta }<\mathrm{27.5}$ kg m⁻³) water masses. We recall that the salinity maximum of the SPTW waters in the UTW is the key variable that impacts the T–S modifications on the EUC. Whereas the SWs, which feed into the west Pacific warm pool, can modulate the critical air–sea interactions there. At depth, the IW influences the water mass properties of the cross-equatorial intrusion, in turn impacting on the overturning circulation of the North and equatorial Pacific (Qu and Lindstrom, 2004).

This section will firstly address the long-term impacts of internal tides on the SW, UTW and IW, based on the daily outputs from the 3-year simulations. Secondly, the transit time for the SW waters are short enough (e.g., Melet et al., 2013) to allow us to investigate any sensitivity of the internal tide to the SW properties during our contrasting ENSO conditions.

5.1 Long-term changes between TIDE and NOTIDE simulations

Salinity is a key parameter defining the water mass extrema. The mean salinity distribution of UTW waters shows the intrusion of the high-salinity SPTW water in the Solomon Sea on Fig. 12 for the 3-year NOTIDE and TIDE simulations compared to the CARS climatology. This high-salinity tongue is firstly advected westward by the NVJ at 11^∘ S before joining the NGCU around 155^∘ E. As it continues to be carried northward into the Solomon Seas, it is eroded along its route. Interactions between the NGCU and the bathymetry, as well as the merging of the different currents, and the effects of tides are components that can erode the salinity maximum. The models with and without tides and the CARS data all show a strong erosion at the entrance of the Solomon Sea with a 0.06 psu freshening between the southeastern extremity of PNG and the Woodlark archipelago at 9^∘ S. The salinity erosion is enhanced in the TIDE simulation compared to the NOTIDE simulation, and erosion is also visible in the northern Solomon Sea along the NGCU pathway. We note that the mean N² profile along the axis of this high-salinity tongue at 154^∘ E (Fig. 5) had already highlighted the closer resemblance of the UTW in the CARS and TIDES simulations compared to the NOTIDES simulation.

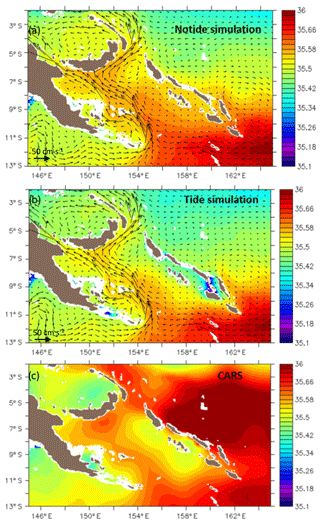
Figure 12 Mean salinity distribution (in color) and mean circulation (arrows) of the UTW waters from the 3-year (a) NOTIDE simulation, (b) TIDE simulation, and (c) the multidecadal CARS climatology. Isobathymetric lines are from the NOAA/ETOPO2v2 bathymetric file from the Smith & Sandwell database (https://doi.org/10.7289/V5J1012Q, National Geophysical Data Center, 2006). White color is for bathymetry of less than 50 m.

Another difference between the TIDE and NOTIDE simulations concerns the zonal salinity gradient between the high-salinity tongue carried by the LLWBCs and the lower UTW salinity along the Solomon Islands. This zonal salinity gradient within this isopycnal UTW layer is enhanced in the TIDE simulation, suggesting that tides induce diapycnal mixing that is particularly efficient in the eastern and northern parts of the Solomon Sea. These regions where mean currents and EKE are relatively low (eastern Solomon Sea) and where strong recirculation exists (northern Solomon Sea) could be favorable to tidal mixing because of longer transit time for particles here.

The strong zonal salinity gradient in the TIDE simulation is also visible in the CARS climatology, although a fresh bias of about 0.02 psu may be noted in the TIDE simulation compared to CARS. This comparison with the long-term CARS climatology has some limitations with regard to the particular conditions of our 3-year simulation including strong El Niño and La Niña events. We note that CARS shows a strong salinity maximum around 5^∘ S outside and to the east of the Solomon Sea that does not match our 3-year period simulations, where this salinity maximum in the open ocean has a bias and is shifted to the south around 11^∘ S. We have verified that the UTW salinity averaged over the same period as our simulations based on a monthly gridded T–S data (CORA05; Cabanes et al., 2013) also exhibits such a southward shift (not shown). Unfortunately, CORA05 has few observations available inside the Solomon Sea, since it is based mainly on ARGO data. So we can perform interannual validations outside the Solomon Sea, but inside the sea only long-term comparisons are possible.

Temperature and salinity changes between the NOTIDE and TIDE simulations are presented in Fig. 13 for the different water masses. The difference between these 3-year simulations shows that tidal mixing reduces the T∕S extrema and induces cooler and saltier SW, cooler and fresher UTW, and warmer and saltier IW. It means that the corresponding salt flux is transferred downward to IW and upward to SW. In the same way, the diapycnal mixing from tides at the thermocline level induces a heat flux that cools the UTW and SW and warms the IW. This results in a weaker stratification at the thermocline level in the TIDE simulation compared to the NOTIDE simulation (e.g., Fig. 5).

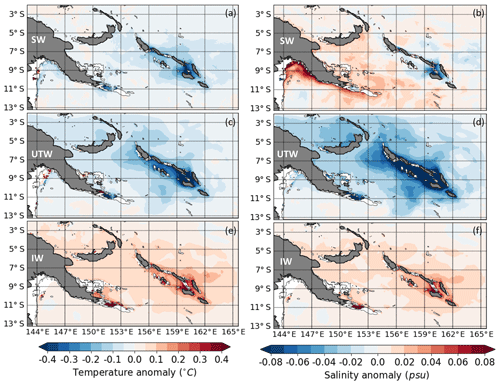
Figure 13 Mean difference in (a, c, e) temperature (units: degrees Celsius) and (b, d, f) salinity between the simulation with tides and the simulation without tides (TIDES-NOTIDES) for (a, b) the surface waters (SW), (c, d) the upper thermocline waters (UTW), and (e, f) the intermediate waters (IW). The density range for these water masses are defined in the text. Isobathymetric lines are from the NOAA/ETOPO2v2 bathymetric file from the Smith & Sandwell database (https://doi.org/10.7289/V5J1012Q, National Geophysical Data Center, 2006). White color is for bathymetry of less than 50 m.

The largest impact of the tides is on the UTW layer, and the tide effect is strongest along the Solomon Islands with fresher salinity up to −0.08 psu and colder temperatures up to −0.3 ^∘C for the TIDE simulation. But when averaged over the Solomon Sea, the rectified anomalies due to the tides are only −0.04 for salinity and −0.1 ^∘C for temperature. The salt and heat fluxes in the TIDE simulation impact the SW and IW waters to a lesser effect, again with the highest differences along the Solomon Islands. Once again, when averaged over the Solomon Sea, the rectified anomalies due to the tides are only −0.06 ^∘C (0.08 ^∘C) for temperature and ≈0.01 psu for salinity for SW and IW, respectively, although locally the differences may reach 0.9 ^∘C and 0.15 psu (Fig. 13).

At the surface, the cooling of SW by the tides could affect the SST field that in turn affects the latent heat flux and the corresponding net heat flux (Q_net). This corresponds to a positive Q_net anomaly between the simulation with and without tides that matches the pattern of SW temperature difference in Fig. 13 and represents a 15 % increase in Q_net when tides are included. This Q_net increase acts to reduce the SST cooling induced by internal tides. Averaged over the Solomon Sea, the SST cooling due to the tides is −0.06 ^∘C for SW and only −0.04 ^∘C at the surface. This is an order of magnitude less that the SST cooling in the Indonesian seas that drastically affects the overlying deep atmospheric convection when modeled in a coupled ocean–atmosphere model including a tidal parameterization (Koch-Larrouy et al., 2010).

5.2 Sensitivity to extremes conditions

The mean tidal effect on water mass transformation is rather modest, but we can ask if extreme conditions like ENSO events impact the role of tides in water mass transformation because internal tides are sensitive to contrasting ENSO periods (e.g., Sect. 4). To illustrate this point, we focus on the 3-month periods of El Niño and La Niña, and we concentrate on SW waters since the transit time of SW waters is short enough to be influenced by these extreme conditions (Melet et al., 2011). Figure 14 shows the temperature differences of SW between the TIDE-NOTIDE simulations for the two ENSO periods, calculated relative to their 3-year mean. The tidal impact on SWs during the ENSO period is quite small, with maximum differences in the Solomon Sea reaching ±0.15 ^∘C between the TIDE and NOTIDE simulations. The tide-induced temperature differences are weaker in the La Niña case with a temperature difference of 0.018 ^∘C compared to 0.05 ^∘C for the El Niño case when averaged over the Solomon Sea. These values are of the same order as the mean tidal effect (e.g., Fig. 13a), but they are an order of magnitude smaller than the temperature changes introduced by the circulation and stratification changes between the El Niño and La Niña cases (≈0.8 ^∘C).

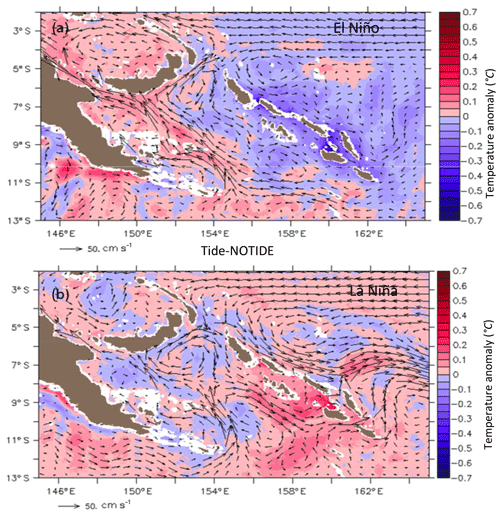
Figure 14 TIDE–NOTIDE Temperature anomalies (in color, ^∘C) and mean circulation (arrows) for the SW waters during (a) the El Niño period and (b) the La Niña period. Isobathymetric lines are from the NOAA/ETOPO2v2 bathymetric file from the Smith & Sandwell database (https://doi.org/10.7289/V5J1012Q, National Geophysical Data Center, 2006). White color is for bathymetry of less than 50 m.

Indeed, the differences between the two ENSO states are strongly related to the circulation anomalies. During El Niño, the LLWBC strongly increases in both simulations, and we observe maximum positive temperature differences due to the tides along its pathway (Fig. 14a). In the same way, during La Niña maximum positive differences are present along the Solomon Islands where the SSI (Solomon Strait inflow) turns and flows strongly southward (Fig. 14b). Since these positive temperature anomalies are relative to the 3-year mean cooling of SWs (Fig. 13) by the tides, they highlight that the intense circulation changes during the ENSO periods lead to a reduced effect of the tides on the SW waters. In other words, the tidal effect will be more efficient when the circulation has lower energy.

6 Discussion/conclusion

We have analyzed here the role of internal tides in the Solomon Sea and their impact on the circulation and the surface and subsurface water masses, based on two regional simulations with and without tides. Since the interaction of the internal tide with the background circulation has strong nonlinear interactions, and the energy cascade between them can cover similar scales of space and time, it is not easy to cleanly separate the two signals from a single model. In our model setup, having two distinct models with and without tides but with the same resolution and surface forcing has allowed us to more easily explore the impacts of introducing the barotropic and baroclinic tides into a regional circulation model, for both the phase-locked and non-phase-locked components.

Since the Solomon Sea is influenced by ENSO, the characteristics of the internal tides were analyzed for two contrasted ENSO conditions: the JFM 1998 El Niño and the AMJ 1999 La Niña. These are two extreme events with strong stratification changes in the western Pacific and Solomon Seas, and provide good case studies for investigating the impact of the internal tides on the regional circulation and water mass transformation. We are conscious though that we have only analyzed one El Niño and one La Niña event, each over a limited 3-month period of hourly averages, which is insufficient to draw concludes about the influence of ENSO on the internal tides. Indeed, 3-months is roughly twice the mesoscale eddy decorrelation time in the tropics, but it is also the local residence time for surface waters flowing through the Solomon Sea (Melet et al., 2011). A longer simulation, including more contrasted El Niño/La Niña events, would be needed to better characterize the response of the tides to the ENSO variability. Nevertheless, these two contrasted events are sufficiently different to qualitatively describe the changes induced in the internal tide field.

Within the Solomon Sea, the M2 barotropic tide is rather weak, but its interaction with the strong topographic features (islands, shelves, deep ocean ridges) generates the strongest component of the internal tide. Although the M2 mode 1 is the dominant mode to propagate baroclinic tidal energy within the Solomon Sea, during the JFM El Niño period, when the peak in N² stratification is close to the surface, more energy becomes partitioned into mode 2. This is important since studies that aim to predict and remove the internal tide from altimetric SSH observations, before calculating geostrophic currents, may use an empirical “all mode” fitting of the M2 internal tide (e.g., Ray and Zaron, 2016) or concentrate only on mode 1 (Zhao et al., 2016). In this Solomon Sea region, with strong stratification changes, we need at least modes 1 and 2.

We have concentrated on this M2 component for our study, to simplify the presentation, but other modes are also energetic (S2, M4, K1, O1; Fig. 6). The second highest baroclinic tide mode is S2, which is well observed by the current TOPEX/Jason altimeter orbits and will also be observed in the future SWOT mission, whose orbit is designed to characterize the 2D structure of the tides and internal tides (Morrow et al., 2019). Other altimeters in a sun-synchronous orbit (Envisat, Saral-AltiKa, Sentinel-3, planned future wide-swath missions) will not be able to observe this S2 12 h cycle, which poses a problem for the understanding of the S2 internal tide, its interaction with the changing ocean circulation, and the validation of models with tides in the future (post SWOT). Future studies are needed to investigate the impacts of the S2 internal tide in the Solomon Sea and in the tropics.

We find that the generation, propagation, and dissipation of the internal tides are sensitive to changes in stratification and to the circulation changes and mesoscale activity that occurs between these two El Niño and La Niña cases. Our AMJ La Niña case study with its high level of mesoscale activity and deeper stratification favors the appearance of more non-phase-locked internal tides. So it appears that the strong mesoscales are refracting, scattering, and eventually dissipating the internal tide field that propagated away from its generation sites, contributing to the increase in the non-phase-locked component.

Where and how the 1 TW of global internal tide energy is dissipated in the open ocean has also been a long-standing question (Egbert and Ray, 2000). The dissipation of internal tides may occur right after generation or after radiation away from the generation sites. Our analysis showed that most of the dissipation in the Solomon Seas occurs locally (from 60 % to 80 %), but the proportion of local to far-field dissipation varies during these particular El Niño or La Niña periods. For example, during the la Niña period, there is a lower baroclinic tide generation in the Solomon Strait box, thus less local dissipation, but an increase in the far field dissipation between 7 and 8^∘ S that is quite significant. This may be influenced by the interaction of the EKE with the southward propagative internal tides generated in the Solomon Strait but highlights the variability in the dynamical interactions and the complications this introduces in the energy budget estimations (see Table 1).

The description of the TIDE and NOTIDE simulations shows a rather modest effect of the tides on water mass transformation inside the Solomon Sea compared to the observations in Germineaud et al. (2016) that show large variations of thermocline water properties (up to 0.2 psu for the SPTW waters) between the different entrances and exits of the Solomon Sea. It is worth noting that the property differences between entrance and exits could be due to the merging and presumably mixing of the different flows with different characteristics transiting at these places. These specific places correspond with the areas of internal tide generation, and most of the internal tide energy is dissipated locally and could contribute to the water mixing at the entrance and exits of the Solomon Sea (Fig. 12).

Water mass transformation inside the Solomon Sea had already been investigated with the use of a 1∕10^∘ regional model including a tidal parameterization and Lagrangian diagnostics during neutral and ENSO conditions (Melet et al., 2011, 2013). These authors indicate that their tidal parametrization might overestimate the erosion of the SPTW salinity maximum. Along the main pathways of UTW waters the erosion of the salinity maximum varies from 0.07 to 0.11 psu as the consequence of mixing by tides and also many other processes. Such values are higher than the ones due only to the tides as discussed in this paper.

Our modeling results show that the diapycnal mixing induced by the tides acts to erode the salinity maximum of the upper thermocline water and to cool the surface temperature interacting with the atmosphere. The effect of tides on water mass mixing is modest but is stronger closer to the generation sites where most of this tidal energy is dissipated locally and where different water masses merge. Tidal effects are also visible away from the strong currents, where particles may experience the effect of tide during a longer time. Indeed, the impacts are quite different when considering particular ENSO conditions over the shorter 3-month period. For example, the stronger surface mesoscale circulation in different regions during the El Niño or La Niña periods, tends to reduce the mean SST cooling by the tides, with possible effects on regional air sea interactions. But the global impact of such tidal effects for this marginal sea, given its key position upstream of the equatorial Pacific circulation, needs to be evaluated.

Finally, we note some caveats. Our 3-month hourly simulations in contrasting ENSO conditions represent examples of particular ENSO events, over one season in each case and including a slowly varying mesoscale field. Longer simulations covering more interannual events are needed to better understand how the internal tides may be modified under varying ENSO cases and to better separate the role of mesoscale variability interacting with the internal tides. We have thus not attempted to quantify the energetics of these tide–circulation interactions with such short time series. These short model simulations are also difficult to validate, since in situ data are scarce, and longer time series are needed to build up robust internal tidal signals from 10 or 35 d altimetric sampling. Future work using longer model simulations, compared to swath observations of the 2D internal tide structure from the future SWOT mission in 2022–2025, should give us a more quantitative picture of the interaction of the ocean circulation and internal tides in the Solomon Sea.