Seasonal variation of the principal tidal constituents in the Bohai Sea

The seasonal variation of tides plays a significant role in water level changes in coastal regions. In this study, seasonal variations of four principal tidal constituents, M₂, S₂, K₁, and O₁, in the Bohai Sea, China, were studied by applying an enhanced harmonic analysis method to two time series: 1-year sea level observations at a mooring station (named E2) located in the western Bohai Sea and 17-year sea level observations at Dalian. At E2, the M₂ amplitude and phase lag have annual frequencies, with large values in summer and small values in winter, while the frequencies of S₂ and K₁ amplitudes are also nearly annual. In contrast, the O₁ amplitude increases constantly from winter to autumn. The maxima of phase lags appear twice in 1 year for S₂, K₁, and O₁, taking place near winter and summer. The seasonal variation trends estimated by the enhanced harmonic analysis at Dalian are different from those at E2, except for the M₂ phase lag. The M₂ and S₂ amplitudes show semi-annual and annual cycles, respectively, which are relatively significant at Dalian. The results of numerical experiments indicate that the seasonality of vertical eddy viscosity induces seasonal variations of the principal tidal constituents at E2. However, the tested mechanisms, including seasonally varying stratification, vertical eddy viscosity, and mean sea level, do not adequately explain the observed seasonal variations of tidal constituents at Dalian.

1 Introduction

Tidal motion is one of the major dynamical processes in the Bohai Sea and has been widely studied (Fang et al., 2004). Although there is no primary seasonal cycle in the moon's orbit, a significant seasonal variation in the principal lunar tidal constituent has been observed and is dominant in coastal and polar regions (Müller et al., 2014). The seasonal variations of several semi-diurnal tides are also found to be significant in the Bohai Sea (Fang et al., 1986), but the corresponding comprehensive investigations are sparse, which means that the seasonal variation characteristics and mechanisms need to be further studied.

The seasonal variation in the major tidal constituent M₂ has received considerable attention (Gräwe et al., 2014). Corkan (1934) inferred a seasonal modulation of the M₂ tide by analysing several sea level records near the coast of Britain. Foreman et al. (1995) observed a seasonal cycle of the M₂ amplitude at Victoria, which is on the southern tip of Vancouver Island off Canada's Pacific coast. Kang et al. (1995) revealed the seasonal variability of the M₂ harmonic constants in the seas adjacent to the Korean peninsula. Huess and Andersen (2001) found a seasonal variation in the M₂ constituent in the northwest European shelf. Kang et al. (2002) investigated the seasonal variability of the M₂ tide in the Yellow Sea and East China Sea. Georgas (2012) observed seasonal episodes of significant tidal damping and modulation in the Hudson River estuary. Müller et al. (2014) studied the global seasonal cycle of the M₂ tide and found significant seasonal variations in several coastal areas, including the North Sea; East China Sea; Yellow Sea; Sea of Okhotsk; and regions of the Banda, Timor, and Arafura seas north of Australia. Tazkia et al. (2017) found that the M₂ amplitude changed markedly between winter and summer in the northern Bay of Bengal. Several other studies have analysed the seasonal variability of the M₂ tide in polar regions. Mofjeld (1986) observed seasonal fluctuations of the tidal harmonic parameters on the northeastern Bering Sea shelf. Kagan and Sofina (2010) showed that the seasonal variability of tidal constituents was widespread in the Arctic Ocean. Further, Müller et al. (2014) studied the global seasonal cycle of the M₂ tide and also identified significant seasonal variations in the Arctic regions.

Most previous studies primarily focus on the seasonal variation in the M₂ amplitude without considering the seasonality of other tidal constituents and their phase lags (Gräwe et al., 2014). However, several studies have investigated the seasonality of multiple constituents. For example, Fang and Wang (1986) studied the seasonal variations of M₂, N₂, O₁, and M₄ in the Bohai Sea by introducing astro-meteorological constituents; Devlin et al. (2018) found that the diurnal (K₁ and O₁) and semi-diurnal (M₂ and S₂) amplitudes and phase lags exhibited strong seasonal variability in the seas of Southeast Asia.

In this study, sea level observations at one mooring station (E2) and one tidal gauge station (Dalian) in the Bohai Sea were used to investigate the seasonal variability of the principal tidal constituents M₂, S₂, K₁, and O₁ with the enhanced harmonic analysis (EHA). The rest of the paper is organized as follows. In Sect. 2, the sea level observations in the Bohai Sea are reported and the analysis methods are described. In Sect. 3, the seasonal variability of the principal tidal constituents is estimated by analysing observations. The mechanisms underlying the seasonal variability are discussed by using numerical experiments in Sect. 4. Further discussions and conclusions occupy Sects. 5 and 6, respectively.

Figure 1 (a) General location of the Bohai Sea (rectangle with dashed lines); (b) locations of the observation stations (red stars), E2 and Dalian, in the Bohai Sea, and bathymetry of the Bohai Sea (colours).

2 Observations and methods

2.1 Observations

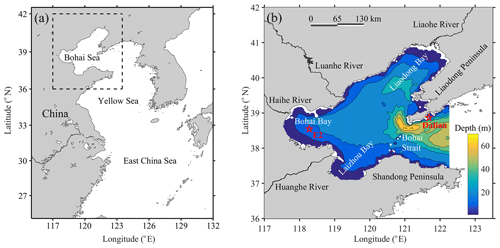
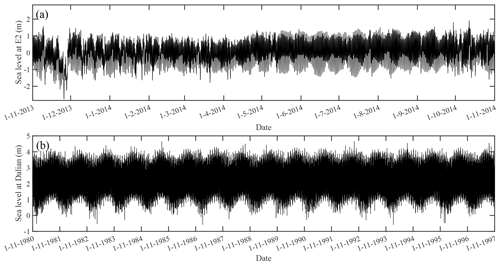
From 00:00 UTC 1 November 2013 to 00:00 UTC 1 November 2014, total sea levels were observed hourly using a moored pressure gauge accurate to within 5 cm (Lv et al., 2019) at E2 station (38.65^∘ N, 118.28^∘ E) in the Bohai Bay, China (Fig. 1). The time series of the total sea levels at E2 is shown in Fig. 2a, demonstrating the continuous coverage of the observations. The obvious sea level drops in November 2013 at E2 are mainly caused by the winter storms.

Figure 2 Time series of the observed sea level at (a) E2 and (b) Dalian.

Hourly sea level data at the Dalian tidal gauge station used in this study were obtained from the University of Hawaii Sea Level Center. As indicated in Feng et al. (2015), the stations at Dalian and Laohutan (7 km away) have data for the period 1975–1990 and 1991–1997, respectively; in addition, the Dalian station was relocated in 1976 and again in 1979, after which Dalian station shared the same position as Laohutan. Therefore, following Feng et al. (2015), the tidal gauge station data at Dalian used in this study were comprised of data from Dalian from 1980 to 1990 and from Laohutan from 1991 to 1997, as shown in Fig. 2b.

2.2 Classical harmonic analysis

A sea level is composed of components from different sources (Godin, 1972; Foreman, 1977; Foreman et al., 2009; Fang et al., 1986; Pawlowicz et al., 2002):

$$\begin{array}{}\text{(1)}& \begin{array}{rl}\mathit{\zeta }& \left(t\right)={\mathit{\zeta }}_{\mathrm{0}}+\sum _{k=\mathrm{1}}^K\left\{f_k\left(t\right)A_k\cos \left[V_k\left(t\right)+u_k\left(t\right)-g_k\right]\right\}\\ & +R\left(t\right)={\mathit{\zeta }}_{\mathrm{0}}+\sum _{i=\mathrm{1}}^{N_{\mathrm{NR}}}\left\{f_i\left(t\right)A_i\cos \left[V_i\left(t\right)+u_i\left(t\right)-g_i\right]\right\}\\ & +R\left(t\right)+\sum _{j=\mathrm{1}}^{N_{\mathrm{R}}}\mathit{\left\{}{f}_j\right(t)A_j\cos \left[V_j\left(t\right)+u_j\left(t\right)-g_j\right]\\ & +\sum _{n=\mathrm{1}}^{N_{\mathrm{I}}}{f}_n\left(t\right)A_n\cos \left[V_n\left(t\right)+u_n\left(t\right)-g_n\right]\mathit{\}},\end{array}\end{array}$$

where ζ(t) is the total sea level; ζ₀ is the mean sea level; A and g are the amplitude and phase lag (UTC time, the same below), respectively; f and u are the nodal corrections to amplitude and phase lag, respectively; V is the astronomical argument; R is the non-tidal component; K is the number of tidal constituents; N_NR is the number of non-reference constituents; N_R is the number of reference constituents; and N_I is the number of constituents to be inferred from the jth reference constituent.

The mean sea level, amplitude, and phase lag of each constituent can be solved by analysing a time series of sea level observations at a specific point using classical harmonic analysis (CHA). With different assumptions and conditions, CHA can be performed using the T_TIDE (Pawlowicz et al., 2002), U_TIDE (Codiga, 2011), or Institute of Ocean Sciences Tidal Package (Foreman et al., 2009). In this study, T_TIDE, in which the astronomical argument varies linearly and the nodal correction is performed after least squares fit, is used to realize CHA.

2.3 Segmented harmonic analysis

Following Foreman et al. (1995), Kang et al. (1995), Müller et al. (2014), and Devlin et al. (2018), sea level observations are divided into monthly segments by calendar month and CHA with nodal and inference corrections is applied to each monthly segment to obtain the discrete tidal harmonic parameters (i.e. amplitude and phase lag). Then the discrete amplitude and phase lag for each month are interpolated using cubic spline interpolation to obtain the temporally varying amplitudes and phase lags. This methodology is termed segmented harmonic analysis (SHA). Following Kang et al. (1995), one monthly segment is analysed only when the duration of the observations is longer than 26 d.

2.4 Enhanced harmonic analysis

By combining CHA with independent point scheme and cubic spline interpolation, Jin et al. (2018) developed EHA to directly obtain temporally varying mean sea level and tidal harmonic parameters. In contrast, the harmonic parameters are assumed to be constant in CHA and constant within each month in SHA. A MATLAB toolkit, S_TIDE, was released to realize EHA by Pan et al. (2018b). In this study, nodal and astronomical argument corrections are embedded into the least square fit, following Foreman et al. (2009); in addition, the harmonic parameters of the minor tidal constituents are assumed to be constant and calculated together with the temporally varying harmonic parameters of the principal tidal constituents to resolve more constituents and retain computational stability. The sea level in EHA is as follows:

$$\begin{array}{}\text{(2)}& \begin{array}{rl}\mathit{\zeta }\left(t\right)& ={\mathit{\zeta }}_{\mathrm{0}}\left(t\right)+\sum _{i=\mathrm{1}}^I\left\{f_i\left(t\right)A_i\left(t\right)\cos \left[V_i\left(t\right)+u_i\left(t\right)-g_i\left(t\right)\right]\right\}\\ & +\sum _{j=\mathrm{1}}^J\left\{f_j\left(t\right)A_j\cos \left[V_j\left(t\right)+u_j\left(t\right)-g_j\right]\right\},\end{array}\end{array}$$

where I is the number of principal tidal constituents with temporally varying harmonic parameters; J is the number of minor tidal constituents with constant harmonic parameters; and the mean sea level and non-tidal component are included in ζ₀(t).

Similar to Jin et al. (2018) and Pan et al. (2018b), the independent point scheme and cubic spline interpolation are used to jointly solve the temporally varying and constant harmonic parameters, which are not shown here for brevity. As mentioned in Pan et al. (2018b), the temporally varying harmonic parameters obtained using EHA with different numbers of independent points represent fluctuations on different timescales. In this study, six independent points are used to obtain the seasonal variability of the principal tidal constituents.

3 Results

One-year sea level observations at E2 were analysed using CHA with the automated constituent selection algorithm (Pawlowicz et al., 2002). According to the signal-to-noise ratio (Pawlowicz et al., 2002; Matte et al., 2013), M₂, K₁, S₂, and O₁ were selected as the principal tidal constituents to be investigated in this study.

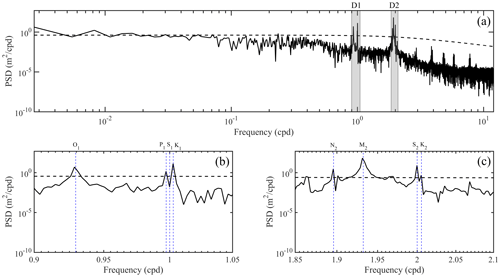
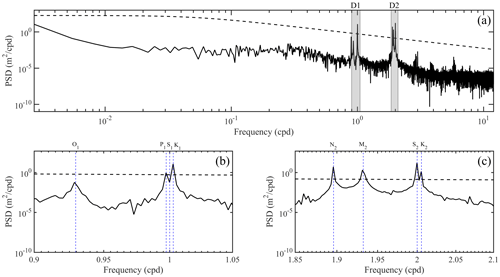
Figure 3 Power spectral densities of the observed sea level at E2 (black line) in (a) all frequency bands, (b) the diurnal frequency band, and (c) the semi-diurnal frequency band. In all panels, black dashed lines denote the corresponding 5 % significance level against red noise.

3.1 Seasonal variability at E2

As shown in Fig. 3, the significant constituent near K₁ was P₁, which was unable to be resolved when analysing 1-month observations (Fang and Wang, 1986), while that for S₂ was K₂ in the semi-diurnal frequency band. Therefore, when the monthly analysis was performed in SHA, the automated constituent selection algorithm in T_TIDE was used to determine the analysed constituents; in addition, the unresolved constituents P₁ and K₂ were inferred from K₁ and S₂, respectively, with the inference parameters taken from a yearly harmonic analysis of the 1-year sea level observations at E2 (Kang et al., 1995; Foreman et al., 2009). When EHA was used to directly analyse the sea level observations at E2, the harmonic parameters of M₂, K₁, S₂, O₁, P₁, and K₂ were estimated together, among which the harmonic parameters of M₂, K₁, S₂, and O₁ were assumed to be temporally varying and those of P₁ and K₂ were assumed to be constant.

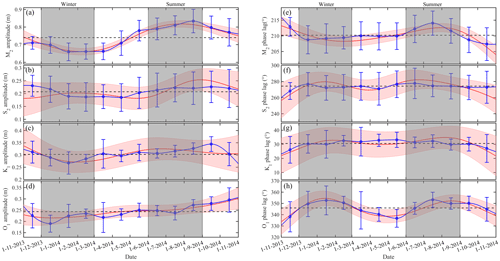
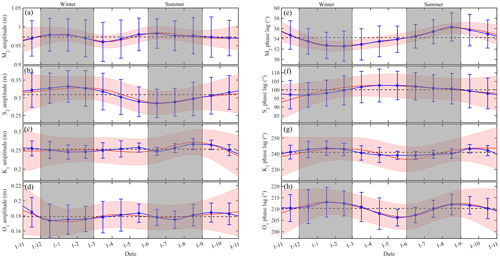
Figure 4 Time series of the temporally varying tidal amplitudes of principal tidal constituents (a) M₂, (b) S₂, (c) K₁, and (d) O₁ at E2 estimated with CHA (black dashed lines), SHA (blue lines), and EHA (red lines). Panels (e)–(h) similar to (a)–(d) but for the estimated temporally varying tidal phase lags. Blue vertical bars and pink shading indicate the corresponding 95 % confidence intervals.

As shown in Fig. 4, the estimated harmonic parameters obtained with SHA and EHA, including the temporally varying amplitudes and phase lags, were nearly equal and the averaged values were near to that estimated using CHA, indicating that the temporal variations in the harmonic parameters of the principal tidal constituents at E2 can be reasonably estimated using both SHA and EHA. Based on Wei and Wang (2012) and Zhang et al. (2017), spring, summer, autumn, and winter were defined as March to May, June to August, September to November, and December to February of the following year, respectively. The temporally varying harmonic parameters of the principal tidal constituents showed seasonal variations (Fig. 4). For M₂, the seasonal variations were significant: both amplitude and phase lag reached maximum in summer and minimum in winter, as in Müller et al. (2014). The seasonality of the S₂ amplitude was not significant, but the estimated results using EHA increased significantly in summer. The temporal variation of the K₁ amplitude spanned 1 year, with maxima and minima in summer and winter, respectively. In stark contrast, the O₁ amplitude increased from winter to autumn. The phase lags of the S₂, K₁, and O₁ components showed semi-annual cycles: larger in summer and winter and smaller in spring and winter, respectively. Among the four principal tidal constituents, only the M₂ amplitude had the similar variation trend as the phase lag.

Table 1 Averaged amplitudes (cm) and phase lag (^∘) of the principal tidal constituents obtained using EHA at E2.

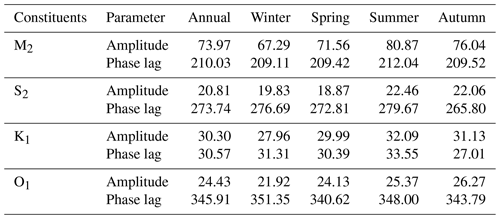
The seasonally averaged amplitudes and phase lags of the principal tidal constituents are listed in Table 1. The variation trends of the averaged harmonic parameters of these constituents were the same as those in Fig. 4. Compared to the annual averages, the seasonal mean M₂ amplitude increased by 6.90 cm (approximately 9.33 %) in the summer and decreased by 6.68 cm (approximately 9.03 %) in the winter, close to the estimated values in Foreman et al. (1995) (6 %), Huess and Andersen (2001) (6 %), and Müller et al. (2014) (5 %–10 %). For S₂ (K₁), the seasonally averaged amplitudes decreased by 4.71 % (7.72 %) in the winter and increased by 7.93 % (5.91 %) in the summer, indicating a nearly annual cycle as shown in Fig. 4. The seasonal mean O₁ amplitude in the summer increased by 3.45 cm compared to that in the winter. The M₂ phase lag in winter was smaller than its annual average, and the other three principal tidal constituents shared a different pattern: values in both winter and summer were larger than the corresponding annual average.

Figure 5 Similar to Fig. 3 but for those at Dalian.

3.2 Seasonal variability at Dalian

The multi-year data at Dalian shown in Fig. 2b were analysed year by year. In each year, 1-year sea level observations were analysed using CHA, SHA, and EHA with similar settings to E2. As shown in Fig. 5, P₁ and K₂ were the significant constituents unresolved in the monthly analysis, just like at E2. Therefore, P₁ and K₂ were inferred from K₁ and S₂ in SHA and taken as minor constituents with constant harmonic parameters in EHA. The estimated harmonic parameters from various years were then averaged (Fang and Wang, 1986) and are shown in Fig. 6. The averaged harmonic parameters estimated using both the SHA and EHA were near to those obtained using CHA, showing that the estimated results were reasonable. In addition, the estimated harmonic parameters obtained using EHA were much closer to those obtained using SHA for data at Dalian than those at E2.

The variation trends of the harmonic parameters estimated using EHA at Dalian were different from those at E2, except for the M₂ phase lag (Fig. 6). The M₂ amplitude at Dalian showed a semi-annual cycle, with large values in summer and winter and small values in spring and autumn, respectively. The S₂ amplitude had significant annual cycle, with maximum in winter and minimum in summer, which is opposite of the variation trend of S₂ amplitude at E2. The K₁ amplitude was nearly constant from winter to spring and increased during the summer. The O₁ amplitude reached the minimum in the winter and summer, while increasing slightly in the spring and autumn. The estimated S₂ phase lag reached the maximum in the spring with small variation. The K₁ and O₁ phase lags had the same trend, increasing in the winter and summer, while decreasing in the spring and early autumn.

Figure 6 Similar to Fig. 4 but for multi-yearly averaged values at Dalian.

Table 2 Averaged amplitudes (cm) and phase lag (^∘) of the principal tidal constituents obtained using EHA at Dalian.

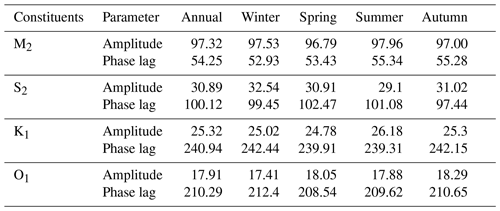
The averaged amplitudes and phase lags of the principal tidal constituents at Dalian, as listed in Table 2, showed a seasonal variation that was generally smaller than that at E2. All of the seasonal changes of the principal tidal constituents were less than 1.80 cm, which is the case only for S₂ amplitude at E2. In addition, all of the seasonal changes of the phase lags were less than 2.20^∘, while the S₂ and K₁ phase lags at E2 changed by at least 5.00^∘ in the summer and winter, respectively. The relative change of the M₂ amplitude at Dalian was less than 1 %, which was significantly less than that at E2. The relative changes of all phase lags were less than 1 % except for the M₂ tide, which was larger than 2 % in both summer and winter compared to the annual averages and larger than those at E2. An increase in the S₂ amplitude of 5.34 % occurred in the winter, larger than its decrease in the winter at E2.

In summary, the harmonic parameters of the principal tidal constituents at E2 and Dalian varied seasonally but with different patterns. The amplitude of the principal tidal constituent M₂ at E2 showed an annual cycle, while that at Dalian had a semi-annual cycle. The M₂ phase lags at E2 and Dalian had a similar variation trend, with larger values in summer and small values in winter. The S₂ amplitude in winter at E2 was less than that in summer, which was opposite to that at Dalian. The K₁ amplitude at E2 had an annual frequency, with large values in summer and small values in winter, while the O₁ amplitude increased steadily. In contrast, the variations of the K₁ and O₁ amplitudes at Dalian were small. The maxima of the S₂, K₁, and O₁ phase lags at E2 appeared twice a year, like those of K₁ and O₁ and different from that of S₂ at Dalian.

4 Mechanisms for the seasonal variability

Several previous studies have investigated the seasonal variability of the M₂ amplitude. Three main mechanisms have been proposed:

1. Seasonal variations of the mean sea level. Corkan (1934) related the seasonal modulation of the M₂ tide near the coast of Britain to seasonal variations of sea level and atmospheric pressure. Tazkia et al. (2017) pointed out that the seasonal variability of the sea level generated by many processes can induce a seasonal variation of the M₂ tide, as tidal wave propagation was controlled by water depth on the first order.

2. Seasonally varying stratification. Foreman et al. (1995) presumed that the seasonal variability of the M₂ amplitude at Victoria, Canada, was induced by the changes in stratification due to seasonal variability in estuarine flow. Kang et al. (2002) used a two-layer numerical model to investigate the baroclinic response of the tide and tidal currents in the Yellow Sea and East China Sea, and they found that seasonal stratification had several noticeable effects on the tides, including varying degrees of current shear, frictional dissipation, and barotropic energy flux. Müller (2012) indicated that in shallow seas, seasonal variations in stratification were a major factor for the observed seasonal modulation in tides. Müller et al. (2014) pointed out that the seasonal changes in stratification on the continental shelf affected the vertical profile of the eddy viscosity to further cause the seasonal variability of the M₂ tide.

3. Seasonally varying ice coverage. St-Laurent et al. (2008) proposed that the significant seasonal variations of the M₂ surface elevation in all regions of the Hudson Bay system were essentially caused by under-ice friction. Georgas (2012) pointed out that the seasonal episodes of significant tidal damping (reductions in tidal amplitudes by as much as 50 %) observed in the Hudson River estuary were primarily caused by the under-ice friction as well. Müller et al. (2014) found that the frictional effect between the sea ice and ocean surface layer led to the seasonal variability of the M₂ tide. The Bohai Sea in north China freezes to varying degrees every winter for approximately 3–4 months (Su and Wang, 2012). According to the back-effect connection of the coastal shelf and open ocean via resonance mechanisms (Arbic et al., 2009; Arbic and Garrett, 2010), sea ice may be important to the seasonality of principal tidal constituents. However, Zhang et al. (2019) performed numerical experiments with a three-dimensional ice–ocean coupled model and found that the damping effect of sea ice on the astronomical tides was almost negligible in the Bohai Sea. Therefore, ice coverage was not considered in this study.

Other mechanisms – including long-term changes in the tidal potential (Molinas and Yang, 1986), monsoon (Devlin et al., 2018), interactions with other physical phenomena (Huess and Andersen, 2001; Pan et al., 2018a), changes in the internal tide with corresponding small changes in its surface expression (Ray and Mitchum, 1997; Colosi and Munk, 2006), and a number of technical reasons – may also change the M₂ amplitude on various timescales. The above reasons have been presented or discussed in Woodworth (2010), Müller (2012), Müller et al. (2014), Tazkia et al. (2017), and Talke and Jay (2020).

4.1 Design of numerical experiments

Several numerical experiments (Exp1–Exp4) were carried out to simulate the four principal tidal constituents in the Bohai Sea under different conditions using MITgcm (Marshall et al., 1997), testing the influence of seasonal variations of mean sea level and stratification on the seasonal variability of the principal tidal constituents.

Identical model settings used in all of the numerical experiments were described as follows. The simulation area of the Bohai Sea is shown in Fig. 1b. The horizontal resolution was ${\mathrm{2}}^{\prime }\times {\mathrm{2}}^{\prime }$ and there were 16 layers in the vertical direction with thicknesses ranging from 2–5 m. The four principal tidal constituents M₂, S₂, K₁, and O₁ were implemented as tidal forcing at the east open boundary, whose data were predicted using the constant harmonic parameters extracted from the TPXO model (Egbert and Erofeeva, 2002). Sea surface boundary conditions were not considered. The horizontal eddy viscosity coefficient was set to 1.0×10³ m² s⁻¹, and the quadratic bottom drag coefficient was set to $\mathrm{1.3}\times {\mathrm{10}}^{-\mathrm{3}}$ (Wang et al., 2014). The integral time step was 60 s, and the total simulation time was 60 d. The results of the final 30 d were used to calculate the harmonic parameters using CHA with the automated constituent selection algorithm.

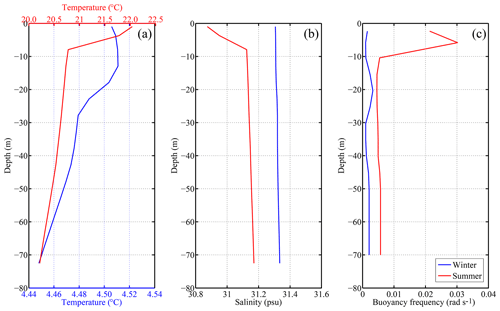
Figure 7 Horizontally homogeneous profiles of the initial (a) temperature, (b) salinity, and (c) buoyancy frequency used in the numerical experiments, in winter (blue solid lines) and in summer (red solid lines).

Details of the model settings for numerical experiments Exp1–Exp4 are listed in Table 3. In Exp1, the simulation started from 00:00 UTC 1 January 2014, while the simulation started from 00:00 UTC 1 July 2014 in Exp2–Exp4. In Exp1, horizontally homogeneous profiles of the initial temperature and salinity (Fig. 7) were extracted from the HYbrid Coordinate Ocean Model (HYCOM) global analysis results in winter, while those in summer were used in Exp2–Exp4. The vertical eddy viscosity coefficient was specified directly and no turbulence closure schemes were used. In Exp1, the vertical eddy viscosity coefficient was set to $\mathrm{2.0}\times {\mathrm{10}}^{-\mathrm{3}}$ m² s⁻¹ through a trial-and-error procedure. According to Müller et al. (2014), the eddy viscosity in summer was reduced by orders of magnitude compared to well-mixed conditions in winter, as the stratification stabilized the water column. Therefore, the vertical eddy viscosity coefficient was decreased by one-half in Exp3 to test the influence of the vertical eddy viscosity caused by the stratification. As shown in Fig. 8, monthly means of the low-pass sea levels, filtered using a cosine-Lanczos filter with a high-frequency cut-off of 0.8 cpd (cycles per day), were nearly equal to the estimated mean sea level using SHA. They exhibited the same variation trend as those obtained using EHA, with large values in summer and small values in winter. As the difference between the averaged mean sea level in summer and that in winter was about 0.2 m, Exp4 included 0.2 m increase of water depth to test the influence of mean sea level.

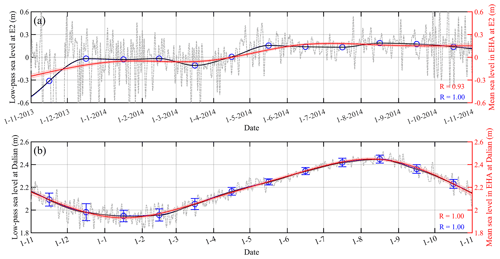
Figure 8 Time series of the original low-pass sea level (grey line), their monthly averages (blue circles), the interpolated values of the monthly averages using the cubic spline interpolation (blue line), and the estimated mean sea level using SHA (black line) and EHA (red line) at (a) E2 and (b) Dalian. Only the original low-pass sea levels with absolute values less than 0.6 m are shown in panel (a). Pink shading indicates the corresponding 95 % confidence intervals, while blue vertical bars designate the standard deviation in multi-yearly averaging.

Table 3 Model settings for the numerical experiments.

^* Vertical eddy viscosity coefficient.

4.2 Modelling results

The simulated harmonic parameters of the four principal tidal constituents in the numerical experiments and those obtained from observations at E2 and Dalian are shown in Fig. 9. The simulated harmonic parameters were a little far from the observed results, except the M₂ amplitude at E2 simulated in Exp1 and that simulated in Exp2, possibly because the constant bottom drag coefficient was used (Wang et al., 2014) and the ocean circulation and other important factors were not considered. However, the differences between the simulated results in the different numerical experiments can be used to display the influence of potential factors on the seasonal variability of the principal tidal constituents.

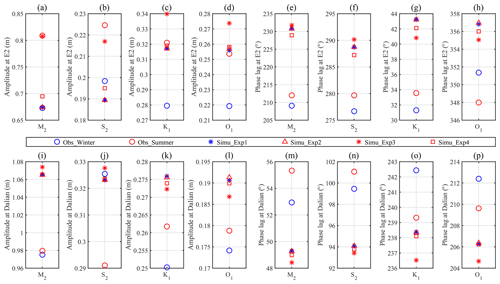
Figure 9 (a) Averaged M₂ amplitude in winter (blue circle) and summer (red circle) by analysing observations at E2 using EHA and those obtained by analysing the simulated results in Exp1 (blue asterisk), Exp2 (red triangle), Exp3 (red asterisk), and Exp4 (red square). Panels (b)–(d) similar to (a) but for S₂, K₁, and O₁ at E2, respectively. Panels (e)–(h) similar to (a)–(d) but for the phase lags at E2. Panels (i)–(p) similar to (a)–(h) but for those at Dalian.

The observed amplitudes at E2 in summer were larger than those in winter for all four principal tidal constituents, as shown in Fig. 9. However, the simulated amplitudes in Exp2 were nearly equal to those in Exp1. In contrast, both the decreased vertical eddy viscosity coefficient in Exp3 and the increased mean sea level in Exp4 increased the amplitudes for all principal tidal constituents. The increases of the observed M₂ and S₂ amplitudes at E2 from winter to summer were 13.58 and 2.62 cm, respectively, while they were 13.34 (2.08 cm) and 2.75 cm (0.56 cm) for simulated results in Exp3 (Exp4) compared to those in Exp1. In addition, the increases of the observed K₁ and O₁ amplitudes were also captured better by the simulated results in Exp3 than those in Exp4, as shown in Fig. 9. Therefore, the seasonally varying amplitudes of all principal tidal constituents were primarily caused by the seasonal variation of vertical eddy viscosity. For M₂, S₂, and O₁ tides, the variation trend of simulated phase lags between Exp3 and Exp1 shared the same pattern with the observed variations between summer and winter, indicating the effects of the seasonally varying vertical eddy viscosity. In contrast, Exp2 with the changes in stratification and Exp4 with changes in mean sea level only reproduced the variation trend of the S₂ and O₁ phase lags, respectively. The aforementioned results demonstrated that seasonal variation in the vertical eddy viscosity was the most important mechanism influencing the seasonal variability of principal tidal constituents at E2.

The observed S₂ amplitude at Dalian was larger in winter than in summer. The simulated result in Exp2 (summer) showed a decrease from Exp1 (winter), while those in Exp3 and Exp4 were larger than that in Exp1, indicating the seasonality of stratification as a possible reason. However, the simulated seasonal variation between Exp2 and Exp1 was too weak, which was less than 1 cm, possibly because the simple horizontally homogeneous temperature and salinity profiles could not reflect reality. The water depth is large in the eastern part of Bohai Sea (Fig. 1b), so the stratification and ocean circulation were noteworthy and had significant effects on the tides. The increases of the M₂ and O₁ amplitudes were only captured by Exp3 with changes in the vertical eddy viscosity coefficient and Exp2 with changes in stratification, respectively. The variation trends of the M₂ and S₂ phase lags were not reproduced well in any experiments, among which Exp2 performed the best, while those of K₁ and O₁ were best captured by Exp3, where the simulated results were smaller than those in Exp1. On the whole, the seasonal variations of the principal tidal constituents at Dalian were not adequately reproduced by the numerical experiments, indicating that all the tested mechanisms were not the possible mechanism.

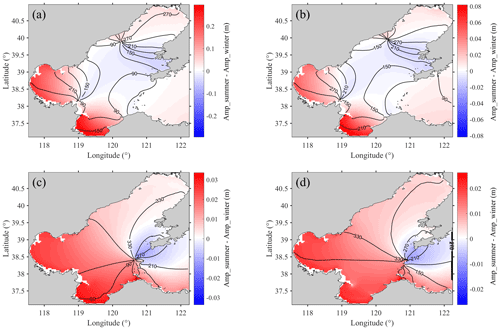
Figure 10 (a) Difference between the simulated M₂ amplitudes in summer (Exp3) and those in winter (Exp1) (colours) and the co-phase lines of the M₂ tide in winter (Exp1) (black lines). Panels (b)–(d) similar to (a) but for S₂, K₁ and O₁, respectively.

The variations of the simulated amplitudes from winter (Exp1) to summer (Exp3) in the entire Bohai Sea are shown in Fig. 10. The spatial distribution of the variations in M₂ amplitude had a strong positive correlation (R=0.98) with that in the S₂ amplitude, similar to that for the diurnal tides (R=0.98). Furthermore, the distributions were possibly related to tidal wave propagation as their patterns were similar to the co-phase lines, as shown in Fig. 10. For the semi-diurnal tides M₂ and S₂, the simulated amplitudes in summer were larger than those in winter in Bohai Bay, Laizhou Bay, and Liaodong Bay, which was the same as that obtained by analysing the sea level data at several tidal gauge stations in the Bohai Sea in Fang and Wang (1986) and that simulated by numerical model in Kang et al. (2002), while the simulated results in summer were smaller than those in winter in the middle of the Bohai Sea. The spatial distribution of the absolute differences between the M₂ amplitude in summer and that in winter was similar to that in Müller et al. (2014). For the diurnal tides K₁ and O₁, the simulated amplitudes in summer were larger than those in winter in Bohai Bay, Laizhou Bay, Liaodong Bay, and the middle areas, while smaller in the northeast part of the Bohai Strait.

5 Discussions

In this study, the EHA developed in Jin et al. (2018) and Pan et al. (2018b) was further improved in order to resolve more tidal constituents by adding the minor constituents whose harmonic parameters were assumed to be constant and calculated together with the temporally varying harmonic parameters of the principal tidal constituents. The nodal and astronomical argument corrections were embedded into the least square fit to eliminate the influences of nodal cycle and linearly varying astronomical argument. In fact, there have been multiple improvements to T_TIDE in the past decades, such as R_T_TIDE (Leffler and Jay, 2009), versatile tidal analysis (Foreman et al., 2009), U_TIDE (Codiga, 2011), and NS_TIDE (Matte et al., 2013). In R_T_TIDE, versatile tidal analysis and U_TIDE, the harmonic parameters (i.e. amplitude and phase lag) are assumed to be constant. However, harmonic parameters are not constant and have multiscale temporal variations, as shown in research by Corkan (1934), Kang et al. (1995), Müller et al. (2014), Devlin et al. (2018), and Talke and Jay (2020). Neglecting seasonal variation of tides will introduce significant error in sea level prediction (Fang and Wang, 1986). EHA assumes the harmonic parameters of the principal tidal constituents are temporally varying and incorporate their calculation into the least squares fit, which is an important improvement to T_TIDE. In NS_TIDE, the harmonic parameters are also assumed to be temporally varying. However, the harmonic parameters are taken as functions of river flow and greater diurnal tidal range at the reference station. Therefore NS_TIDE can only be applied to river tides, while EHA can be applied in analysing any time series. On the whole, EHA used in this study is indeed superior to other methods.

It is noted that the duration of sea level observations at E2 is from 2013 to 2014 and that for Dalian is from 1980 to 1997, which are from different eras and may defy comparison because the 1997–1998 El Niño is one of the strongest in the 20th century (Chavez et al., 1999) and changes many of the physical oceanic properties (Nezlin and Mcwilliams, 2003; Shang et al., 2005; Liu et al., 2010). In addition, the duration of hourly sea level observations at E2 used in this study is only 1 year, which is also a limitation. Although the different time eras and the rare event might slightly skew the seasonal pattern of tides, the seasonal variations of the principal tidal constituents M₂, S₂, K₁, and O₁ obtained using EHA are the same as those using traditional SHA, indicating that the results are not unreasonable and can reflect the seasonal variations of tides in the analysis period. It is a limitation that only the sea level observations at E2 and Dalian are analysed, so studies using much more non-publicly available data to further investigate the seasonality of tides in the Bohai Sea are encouraged. The strong seasonal variation trends of the principal tidal constituents at E2 can be captured by the results of numerical experiments. The multi-annually averaged results at Dalian also showed the seasonal variations of the principal tidal constituents, but the results of numerical experiments were not in good accordance with the observed results, which may be because horizontally homogeneous profiles of the initial temperature and salinity were used and the temporally varying ocean circulation was not considered. In addition, the constant harmonic parameters were used to predict the sea level at the eastern open boundary that near the Dalian, which may be another reason for the disagreement between the observed and simulated seasonal variations of the tidal constituents.

The seasonality of the principal tidal constituents has been investigated widely. As shown in Müller et al. (2014), there were significant seasonal variations in M₂ tide in several coastal regions and the maximum annual tide was in July (±1 month) in most of the ocean. However, spatial and temporal inhomogeneities also existed and the summer amplitudes of M₂ tide were less than those in winter in several areas, as shown in Kang et al. (1995), Müller et al. (2014), Devlin et al. (2018), and Fig. 10 in this study. In general, the M₂ tidal amplitude in summer was larger than that in winter in many areas, such as the Bohai Sea (Fang and Wang, 1986), the North Sea (Huess and Andersen, 2001; Gräwe et al., 2014; Müller et al., 2014), most of the Ganges-Brahmaputra-Meghna delta (Tazkia et al., 2017), the seas of Southeast Asia (Devlin et al., 2018), Liverpool (Corkan, 1934), Victoria (Foreman et al., 1995), the western part of the Yellow Sea and East China Sea (Kang et al., 2002), the Hudson Bay, and Foxe Basin (St-Laurent et al., 2008), which was the same as that obtained by analysing the observations at E2 and Dalian in this study. Devlin et al. (2018) found that the diurnal and semi-diurnal tidal amplitudes and phases exhibited a high degree of seasonality in the seas of Southeast Asia, and Fang and Wang (1986) indicated that the O₁ amplitude in summer was also larger than that in winter in the Bohai Sea, which were similar to those concluded in this study. The seasonality of the principal tidal constituents obtained in the study was mainly similar to those in previous studies, but the novel EHA was firstly used to estimate the seasonal variations of the principal tidal constituents and the numerical experiments using the three-dimensional MITgcm were performed to explore the physical mechanisms.

The seasonal variations of stratification and vertical eddy viscosity and their influences on the tidal amplitudes may be as follows. In winter, the strong northwest Asia monsoon develops a vertically well-mixed condition (Yanagi et al., 2001; Jeon et al., 2014). The vertically well-mixed condition will not stabilize the tidal currents and loses more energy, leading to smaller tidal amplitudes. As the surface heating rate and freshwater discharge increase in summer, the mixing is insufficient to homogenize the input potential energy and cause stratified conditions (Huang et al., 1999; van Haren, 2000). Hence, the reduced vertical eddy viscosity will increase the tidal amplitudes. However, the S₂ amplitude at Dalian was larger in winter and smaller in summer, which is inconsistent with the other principal tidal constituents. It may be related to the atmospheric variations and should be further investigated in future studies.

6 Conclusions

In this study, based on 1-year sea level observations at E2 and 17-year sea level observations in the Bohai Sea, the seasonal variability of the principal tidal constituents was investigated using different methods. In analysis of sea level observations at E2 and Dalian, the seasonal variations of all principal tidal constituents obtained using EHA were nearly equal to those obtained using SHA (Figs. 4 and 6), indicating that the seasonal variations were not related to the applied methods. At both E2 and Dalian, the principal tidal constituents M₂, S₂, K₁, and O₁ exhibited seasonal variations (Figs. 4 and 6). The M₂ amplitude at E2 had an annual cycle, while that at Dalian showed a semi-annual cycle. The M₂ phase lags at E2 and Dalian had a similar variation trend, with large values in summer and small values in winter. The S₂ amplitude in winter at E2 was less than that in summer, which was opposite to that at Dalian. The K₁ amplitude at E2 had an annual cycle, with large values in summer and small values in winter, while the O₁ amplitude increased steadily. On the contrary, the variations of the K₁ and O₁ amplitudes at Dalian were small. The maxima of the S₂, K₁, and O₁ phase lags at E2 appeared twice a year, which was the same as those of K₁ and O₁ and different from that of S₂ at Dalian.

Through several numerical experiments, the mechanisms of the seasonal variability of the principal tidal constituents were investigated. Although the simulated harmonic parameters of four principal tidal constituents were not consistent well with the observations in most cases, the differences between the simulated results in summer and winter indicated that the seasonal variations of the principal tidal constituents at E2 were caused by the seasonality of the vertical eddy viscosity, while the seasonal variations at Dalian were not reproduced by the test mechanisms, including seasonally varying stratification, vertical eddy viscosity, and mean sea level. Therefore, taking into consideration the temporally varying harmonic parameters, the synchronous simulation of circulation and tides and a reasonable parameterization scheme to convert the variations in stratification to those in vertical eddy viscosity were needed for precise simulation of the tides.