Submesoscale dispersion of surface drifters in a coastal sea near offshore wind farms

We analysed relative dispersion of surface drifters released as pairs (six instances) or triplets (two instances) during three field experiments conducted in the German Bight in close proximity to wind farms. There is some tentative evidence that nearly exponential growth of relative dispersion (non-local dispersion) preferably occurs for drifter pairs that are most exposed to the influence of a wind farm. Kinetic energy spectra and velocity structure functions are analysed with regard to the assumption that turbulent energy could be injected by tides, possibly also via an interaction between tidal currents and wind turbine towers. Applicability of inertial range turbulence theory, however, can be doubted given distinct peaks of overtides observed in velocity power spectra. More comprehensive studies would be needed to better separate submesoscale effects of wind farms, tides and possibly baroclinic instabilities on observed drifter behaviour in a complex coastal environment.

1 Introduction

Observing the spreading of drifters deployed pairwise is a powerful tool for analysing submesoscale flow structures. Submesoscale features are of interest for different reasons. From a theoretical point of view, studying mesoscale turbulent features helps understand the mechanisms of how energy in a 2-D quasi-geostrophic regime cascading towards larger scales (inverse energy cascade, see Charney, 1971) can nevertheless lose geostrophic balance and be injected to the microscale, where it is dissipated (McWilliams, 2008). Another reason is a more practical one. Knowing about the efficiency of relative dispersion at the submesoscale is important for proper simulation of early-phase spreading of pollutant patches. It is crucial to know whether spreading will be driven by mesoscale structures resolved in numerical models (non-local dispersion) or if submesoscale turbulence on the scale matching the size of a pollutant patch is energetically relevant (local dispersion). In the latter case growth of a small-size oil slick, for instance, will exceed the rate predicted by traditional parameterisations in terms of hydrodynamic currents resolved in a model (Özgökmen et al., 2012).

Table 1 Drifters considered in this study.

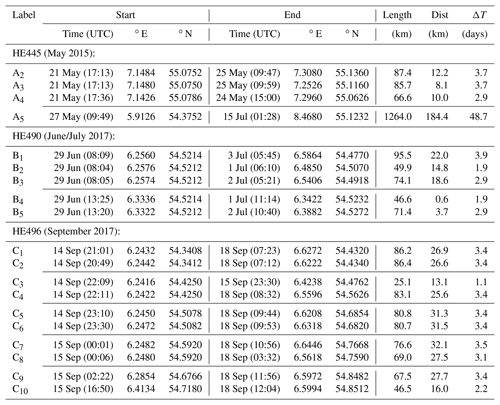
Drifters released as pairs or triplets during three different field experiments in the German Bight. Initial and final locations were defined according to the list of locations communicated via the satellite communication network. Length: sum of the lengths of linear segments connecting observed drifter locations. Dist: linear distance between the first and the last drifter location observed. ΔT: days between the first and the last observation. Single drifter A₅ is not a subject of the present study but due to its long-lasting journey used as a reference in Fig. 10a.

In this study we analyse drift trajectories in the German Bight (North Sea) that cover just short periods (maximum 3.9 d, see Table 1). The German Bight (Fig. 1) is characterised by frequent eddies and meanders on different scales. Nearshore gyres may occur or be absent depending on prevailing wind conditions or baroclinic instabilities in connection with fronts (Becker et al., 1992), for instance. The submesoscale we focus on has also been addressed by numerous other studies (e.g. Berta et al., 2016; Ohlmann et al., 2017; Poje et al., 2014). A key observation is that spreading rates may be much higher than those observed on the large scale (e.g. Corrado et al., 2017). Initial separations of drifter pairs we analyse (see Table 2) are much below the local internal radius of deformation, which in the German Bight is in the range of approximately 2–20 km (Becker et al., 1983, 1999; Badin et al., 2009). Therefore our experiments explore the submesoscale regime in which geostrophic horizontal turbulence interacts with vertical mixing (e.g. McWilliams, 2008), possibly triggered by the presence of wind farms (Floeter et al., 2017). Departure from geostrophic dynamics in submesoscale eddies can be quite substantial (Ohlmann et al., 2017). A recent experiment in the Gulf of Mexico with hundreds of drifters released (D'Asaro et al., 2018) revealed a quite complex behaviour: local clustering of drifters due to submesoscale convergences was observed to coexist with spreading of such clusters.

A recent summary of relative dispersion in the ocean was given by Corrado et al. (2017). Analysing data from the Global Drifter Program, these authors found consistent behaviours in different ocean sub-basins. Conditions in coastal regions, however, are generally less homogeneous than in the open sea and may give rise to flow features that vary substantially on a scale of only a few kilometres (Ohlmann et al., 2012). In the German Bight, strong tidal waves (M₂) become distorted and shallow-water overtides (M₄ and M₆) are generated via reflection and non-linear transformation processes (Stanev et al., 2014, 2016). The German sector of the German Bight is also an area in which a large number of offshore wind farms (OWFs) are planned, built or already operated. Although generation of turbulent wakes by OWF structures is a known effect (e.g. Li et al., 2014), the number of targeted studies of the impacts of OWFs on hydrodynamic conditions is very limited. Seasonal variation in stratification is a crucial factor influencing the North Sea food web (e.g. Ruardij et al., 1997). While Carpenter et al. (2016) estimated little impact of OWFs on mean stratification in the German Bight, Floeter et al. (2017) found some observational evidence that stirring effects might increase vertical mixing and create upwelling cells near the OWFs. Impacts on hydrodynamic conditions could occur via changes in the atmospheric wind field from which energy is extracted, including additional atmospheric turbulence. An alternative process is tidally induced mixing in an array of OWF foundations. In this case turbulent wakes and vertical mixing generated by tide-driven oscillatory currents may also depend on the type of foundation structures used.

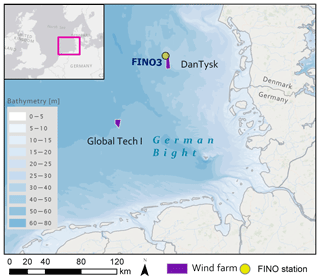
Figure 1 The study area German Bight. Drifter experiments were conducted in close vicinity to the two wind farms indicated in the plot. Research station FINO3 provides hydrodynamic currents on a 10 min basis.

Based on data from experiments in the Mediterranean Sea, Schroeder et al. (2011) raised doubts that submesoscale turbulent eddies are pervasive phenomena underlying turbulent transports. Alternatively, turbulent transports may be governed by larger mesoscale flow features. Such non-local transports (or drifter dispersion) are expected to occur in combination with Eulerian energy wave number spectra proportional to k⁻³ or steeper (Bennett, 1984). Kraichnan (1967) predicted this for the enstrophy-cascading inertial range of 2-D turbulence, for instance. Indicative of a non-local regime driven by flow features larger than drifter separation is exponential growth of relative drifter dispersion (LaCasce, 2008). By contrast, local dispersion with power law dependence on time should coincide with a shallower slope of the energy spectrum, indicating the presence of energetic small-scale eddies. Özgökmen et al. (2012) compiled relevant analyses available at that time (LaCasce and Ohlmann, 2003; Koszalka et al., 2009; Lumpkin and Elipot, 2010; Berti et al., 2011; Schroeder et al., 2011), and more recent studies were reported by Beron-Vera and LaCasce (2016), Corrado et al. (2017), Poje et al. (2017) or Sansón et al. (2017). An assessment of the influence of the different flow regimes on turbulent transport is complicated by the fact that exponential increase in tracer separation in time is also characteristic of so-called Lagrangian chaos dealt with in dynamical systems theory. This occurs when passive objects show chaotic movements sensitive to initial conditions although they are embedded in laminar Eulerian currents (Boffetta et al., 2000; Tsinober, 2001, Sect. 4.2, 4.3). Wiggins (2005) reviews applications of the dynamical systems approach in the context of oceanography.

The issue of either local or non-local dispersion at submesoscale seems to not yet have been solved. Berti et al. (2011) found early-phase exponential separation at scales of the order of 1 km. By contrast, Corrado et al. (2017) observed rates of dispersion at the submesoscale being about 1 order of magnitude higher than at the mesoscale or large scale and took this as an indication that dispersion was increased by the action of local eddies similar in size to drifter separation. In an experiment specifically targeted to a persistent coastal buoyant front possibly containing submesoscale mixed layer instabilities, Schroeder et al. (2012) also found indications of relative dispersion enhanced by local dynamics.

The data studied here represent quite a complex situation in which effects of tides modified by travelling under shallow sea conditions, baroclinic instabilities on the scale of the Rossby deformation radius and anthropogenic effects of OWFs may possibly combine. Section 2 describes the data available, the method of spectral analysis we applied to drifter velocities and summarises basic concepts of two-particle statistics. In addition, it describes how simulated counterparts of observed trajectories were produced. The results section starts with a detailed analysis of observed drifter trajectories and drifter pair separations being influenced by changing weather conditions (Sect. 3.1). Observed trajectories are supplemented with corresponding simulations. Section 3.2 presents spectral analyses of both Eulerian and Lagrangian current velocities. Section 3.3 deals with two-particle statistics like separation velocities and velocity structure functions. Finally, Sect. 3.4 presents examples of simulated drifter dispersion based on two different stochastic parameterisations. After a discussion of our findings in Sect. 4, conclusions are summarised in Sect. 5.

2 Material and methods

2.1 Observational data

Surface drifter data were collected during three research cruises with RV Heincke (HE445, HE490, HE496) in the German Bight in the years 2015 and 2017. Table 1 summarises for all drifters positions and times of their deployment. In addition, the table provides lengths of drifter tracks together with the linear distances between initial and final locations. We used drifters of type MD03i from Albatros Marine Technologies, shaped as cylinders with 0.1 m diameter and 0.32 m length. About 0.08 m protrude from the water surface, the ratio of drag area inside to drag area outside the water is 33.2. Drogues of 0.5 m both length and diameter are attached 0.5 m below the sea surface so that drifters are supposed to reliably represent currents in a surface layer of about 1 m depth. No drogue presence sensors were mounted for checking the conditions of the devices.

Table 2 Initial distances between drifter pairs.

Distances “Dist” refer to the time of the first synchronous GP-based localisation (recordings every 20 min). See Sect. 2.1 for a discussion of uncertainties.

Although Albatros MD03 drifters have been widely used during the last years (e.g. Lana et al., 2016; Callies et al., 2017; Sentchev et al., 2017; Onken et al., 2018), to our knowledge slippage of this drifter type has never been quantified. However, considering the drag ratio of 33.2, the parameterisation given in Niiler et al. (1995) would predict a slippage of 1.1 to 1.6 cm s⁻¹ for a 10 m s⁻¹ wind speed and a velocity difference across the vertical extent of the drogue of roughly 0.1 cm s⁻¹. Quantification of a drifter's slip is not trivial due to an influence of sea state. For another type of drifter, the CODE drifter, Poulain et al. (2009) estimated slippage to be 1 % of wind speed. By contrast, according to Poulain and Gerin (2019), slippage was estimated to be 0.1 % of wind speed. Fortunately, specification of slippage effects is of minor importance for the present study. First, it can be expected that slippage effects affecting two drifters of the same type will not dominate separation of these drifters. Second, when comparing observations with corresponding simulations, the additional wind drag tuned for successful simulations will also cover slippage effects. Therefore, for the present study slippage effects were neglected.

Drifter positions were obtained from the Global Positioning System (GPS) and transmitted to the lab via the satellite communication system Iridium. A lab test was set up to evaluate accuracies of GPS devices. Four drifters were deployed in a small water tank at fixed positions so that changes in their distances relative to each other (recorded for each of six pairs yielded from the four drifters) could directly be attributed to errors of GPS-based localisation. Based on 48 h of observations, the 50th, 90th and 95th percentiles of relative distance errors were 12.4, 33 and 42 m, respectively. Note that initial recordings of distances between drifter pairs (Table 2) are often within this estimated range of uncertainty. Real errors could be slightly larger because our test could not take into account possible effects of orbital motions due to waves. Haza et al. (2014) provide an extensive study on the extent to which position errors can corrupt scale-dependent two-point dispersion rates estimated from Lagrangian data.

In all field experiments sampling rates were about once every 20 min. For being able to calculate time-dependent separations between drifters, all drifter locations were linearly interpolated to regular 20 min time intervals. Drifter velocities were derived from these interpolated regular data.

Drifter set A

On 21 May 2015, three drifters (A₂–A₄) were deployed as a triplet near the OWF DanTysk (Fig. 2a). DanTysk covering an area of roughly 19 km×5 km is located about 70 km to the west of the coastal islands near the Danish and German border (Fig. 1). The three drifters crossing the area of the OWF were tracked for a maximum time of 3.7 d (see Table 1).

The three drifters are a subset of nine drifters released in May 2015 during a longer cruise (HE445) of RV Heincke. The other six drifters, released individually and monitored between 9 and 54 d while they were drifting across the German Bight, were analysed by Callies et al. (2017). Here, just drifter A₅ will be referred to by analysing its Lagrangian velocity power spectrum (see Sect. 3.2). Data from all nine drifters are freely accessible from a data repository (Carrasco and Horstmann, 2017).

Drifter set B

On 29 June 2017, one drifter triplet (B₁, B₂ and B₃) was deployed to the west of OWF Global Tech I (Fig. 4a). The OWF (Fig. 1) comprises 80 turbines with tripod foundations. It covers an area of about 41 km² and is located more than 90 km to the north-west of the German island Juist. Water depth in the region is about 40 m. Drifter data taken on cruise HE490 of RV Heincke are freely accessible from Carrasco et al. (2017a).

Drifters were tracked for 1.9, 2.9 and 3.9 d, respectively. Another pair of drifters (B₄ and B₅) was deployed within the OWF about 5 h later. These drifters were tracked for 1.9 and 2.9 d, respectively (see Fig. 4d).

Drifter set C

On 14/15 September 2017, five drifter pairs were deployed with spatial spacing of 5 nautical miles along a north–south transect to the west of OWF Global Tech I (Fig. 6a). Drifter tracks were recorded for up to 3.5 d. For drifters C₉ and C₁₀ some technical problems encountered after drifter deployment endured for nearly 1 d. Figure 6 shows only data after these problems had been settled and the signals were obtained on a regular basis. All data taken on cruise HE496 are freely accessible from Carrasco et al. (2017b).

All launch locations and times listed in Table 1 refer to the first signal received from the positioning system. As a result, the initial distances listed in Table 2 seem larger than they actually were at the time of drifter deployment, which may have taken place about 30 min earlier. In particular the large “initial” distances indicated for drifters C₉ and C₁₀ result from the technical problems already mentioned above.

Eulerian surface currents observed at 2 m depth were available from research station FINO3 (https://www.fino3.de), located approximately 80 km off the German coast in the immediate vicinity of the OWF DanTysk where experiment A took place (Fig. 1). Time resolution of these measurements taken with an acoustic wave and current profiler (AWAC) is 10 min. For technical reasons each hour one of these measurements is usually skipped. A special period without such data gaps (April–May 2010), needed for spectral analysis, unfortunately did not overlap with the time periods of our drifter experiments.

2.2 Spectral analyses

Power spectra of both Eulerian and Lagrangian drifter velocities have been calculated using the maximum entropy method (MEM) based on algorithms presented in Marple (1987) and Press et al. (2002). This method has been chosen since it is very efficient in detecting narrow spectral features or sharp peaks even if the underlying data series have a quite low number of sample points (N). The behaviour of the spectral estimate using MEM depends on the appropriate choice of the order of the autoregressive model (M). The number of peaks typically increases with M. If the order is chosen too high, spurious peaks may occur in the spectra. Therefore, several spectra for each case with different model orders have been calculated. The model order suggested by the Akaike information criterion (Akaike, 1974) has been found to be too low, and known peaks were not resolved. Here an order selection of N=4 to N=3 produced satisfactory results in accordance with Weedom (2003). For some cases (longer data series) MEM spectra have been compared to fast Fourier transform-based power spectra to verify main peaks and spectral slopes as they are discussed here.

Besides all mentioned advantages, a drawback of the MEM method is that the statistical significance of the spectral peaks is difficult to assess. Nevertheless, to estimate the statistical significance of spectral peaks, a permutation test (Good, 2000) as proposed and exemplified by Pardo-Igúzquiza and Rodríguez-Tovar (2005, 2006) has been followed. Identified spectral peaks referred to in the discussion section show high statistical confidence levels with values between 95 % and 99 % based on the permutation test (10 000 spectra) using an underlying red noise spectrum.

2.3 Velocity increments and structure functions

Let D_ij(t) denote separation between two drifters i and j at time t being located at x⁽ⁱ⁾(t) and x^(j)(t), respectively:

$$\begin{array}{}\text{(1)}& D_{ij}\left(t\right)=\mid {\mathit{x}}^{\left(i\right)}\left(t\right)-{\mathit{x}}^{\left(j\right)}\left(t\right)\mid .\end{array}$$

Given a cloud of drifters, the mean squared separation of N pairs of drifters provides a measure of relative two-particle dispersion

$$\begin{array}{}\text{(2)}& D^{\mathrm{2}}\left(t\right)=\langle D_{ij}^{\mathrm{2}}\left(t\right)\rangle ={\displaystyle \frac{\mathrm{1}}{N}}\sum _{i\ne j}{D}_{ij}^{\mathrm{2}}\left(t\right),\end{array}$$

where brackets denote averaging over all particle pairs. In the present study, however, we will analyse each drifter pair separately so that squared separation $D_{ij}^{\mathrm{2}}\left(t\right)$ will be our key parameter. Of course such detailed analysis would not be feasible if the number of drifter pairs studied were larger.

Relative dispersion is to be distinguished from absolute dispersion, a parameter from single-particle statistics that describes a particle cloud's spread around its centre of mass in combination with its drift from its release point. Differences between absolute and relative dispersion are relevant at medium timescales when two-particle velocity cross correlation depends on the character of Eulerian flows (LaCasce, 2008). Being the second moment of the distribution of relative particle displacements, relative dispersion is informative when this distribution is nearly Gaussian. Otherwise studying full distributions of relative drifter separations may be preferable (LaCasce, 2010).

In his seminal paper, Richardson (1926) assumed that separation of particle pairs will hardly be affected by eddies larger in diameter than the distance between the two tracer particles. Similarly, turbulent structures much smaller than drifter separation will not contribute much to further spreading. A disadvantage of relative dispersion D²(t) is that its value at given time t does not necessarily relate to a specific spatial scale. Drifter pairs contributing to the average may travel under different flow regimes and thereby give rise to scale interference (Corrado et al., 2017). Considering Eulerian velocity differences $\mathit{\delta }{\mathit{v}}^{\left(\mathrm{E}\right)}(\mathit{r},t)=\mathit{v}(\mathit{x}+\mathit{r},t)-\mathit{v}(\mathit{x},t)$ between two locations separated by distance r helps address the role of spatial scales. If possible implications of non-uniform sampling due to specific flow structures are neglected (Poje et al., 2017), Eulerian velocities can be identified with Lagrangian drifter velocities. As a convenient scalar parameter the following Eulerian longitudinal velocity difference (Poje et al., 2014, 2017) can be used,

$$\begin{array}{}\text{(3)}& \mathit{\delta }{v}_{\parallel }^{\left(\mathrm{E}\right)}(r,t)=\mathit{\delta }{\mathit{v}}^{\left(\mathrm{E}\right)}(\mathit{r},t)\cdot \widehat{\mathit{r}}\left(t\right),\end{array}$$

with $r=\parallel \mathit{r}\parallel$ and $\widehat{\mathit{r}}=\mathit{r}/r$. In 3-D turbulence, the corresponding transverse velocity difference, $\mathit{\delta }{\mathit{u}}_{⟂}^{\left(\mathrm{E}\right)}$, could have any direction within a plane perpendicular to $\widehat{\mathit{r}}$ (e.g. Lévêque and Naso, 2014). In 2-D, however, its orientation is well defined and the component can be obtained as

$$\begin{array}{}\text{(4)}& \mathit{\delta }{v}_{⟂}^{\left(\mathrm{E}\right)}(r,t)=\mathit{\delta }{\mathit{v}}^{\left(\mathrm{E}\right)}(\mathit{r},t)\times \widehat{\mathit{r}},\end{array}$$

where the convenient 2-D analogue $\mathit{a}\times \mathit{b}=a_x{b}_y-a_y{b}_x$ of the 3-D vector product was used. The second-order structure function is defined as the second moment of velocity differences between two neighbouring points (e.g. Kolmogorov, 1941; Pope, 2000). Based on Eqs. (3) and (4) it can again be decomposed into longitudinal and transverse components (Poje et al., 2017):

$$\begin{array}{}\text{(5)}& S_{\mathrm{2},\parallel }^{\left(\mathrm{E}\right)}\left(r\right)=\langle \mathit{\left\{}\mathit{\delta }{v}_{\parallel }\right(r,t){\mathit{\}}}^{\mathrm{2}}\rangle ;S_{\mathrm{2},⟂}^{\left(\mathrm{E}\right)}(r)=\langle \mathit{\{}\mathit{\delta }{v}_{⟂}(r,t){\mathit{\}}}^{\mathrm{2}}\rangle .\end{array}$$

In Eq. (5) we assumed isotropic conditions so that vector r can be replaced by its scalar length r. Angular brackets denote averaging over each subset of paired locations after the full data were binned with regard to distance r (regardless of time t).

Both time evolution of relative dispersion D²(t) and spatial scale dependence of velocity structure functions like $S_{\mathrm{2},\parallel }^{\left(\mathrm{E}\right)}\left(r\right)$ can be theoretically linked to wave number power laws that hold for turbulent kinetic energy. In two dimensions the spectrum of turbulent energy E as a function of wave number k may combine an inverse energy cascade at large scale with a direct enstrophy cascade at smaller scale, separated by a frequency where energy is injected (Kraichnan, 1967; Lesieur, 1997; LaCasce, 2008; Boffetta and Ecke, 2012):

$$\begin{array}{}\text{(6)}& E\left(k\right)\propto \left\{\begin{array}{ll}{\mathit{\epsilon }}^{\mathrm{2}/\mathrm{3}}{k}^{-\mathrm{5}/\mathrm{3}}& \text{inverse energy cascade},\\ {\mathit{\eta }}^{\mathrm{2}/\mathrm{3}}{k}^{-\mathrm{3}}& \text{direct enstrophy cascade}.\end{array}\right.\end{array}$$

Here, energy dissipation ε assumes the meaning of an energy flux to larger scales and η denotes an enstrophy dissipation or transfer rate. The spectrum for the 2-D inverse energy cascade is identical with that for the direct cascade towards smaller scales that Richardson (1926) derived for 3-D turbulence. From Eq. (6) the following explicit time dependences of squared drifter separation can be derived (Babiano et al., 1990; Ollitrault et al., 2005),

$$\begin{array}{}\text{(7)}& D^{\mathrm{2}}\left(t\right)\propto \left\{\begin{array}{ll}\mathit{\epsilon }{t}^{\mathrm{3}}& \text{inverse energy cascade},\\ \exp \left(c{\mathit{\eta }}^{\mathrm{1}/\mathrm{3}}t\right)& \text{direct enstrophy cascade},\end{array}\right.\end{array}$$

with some positive constant c. It is known, however, that observing scaling laws (Eq. 7) does not necessarily prove the existence of an inertial energy cascade and the corresponding spectral power law (e.g. Zouari and Babiano, 1994; Tsinober, 2001).

After a sufficiently long time, particle motions will become decorrelated and the power law behaviour of squared drifter separation will settle into normal diffusion (Kraichnan, 1966) for which relative diffusivity is expected to be constant (LaCasce and Bower, 2000) and twice the value of absolute diffusivity considered by Taylor (1921).

Following K41 scaling (Kolmogorov, 1941), in the inertial range of two-dimensional turbulence one has (Babiano et al., 1985; Boffetta and Ecke, 2012):

$$\begin{array}{}\text{(8)}& S_{\mathrm{2},\parallel }^{\left(\mathrm{E}\right)}\left(r\right),S_{\mathrm{2},⟂}^{\left(\mathrm{E}\right)}\left(r\right)\propto {\mathit{\epsilon }}^{\mathrm{2}/\mathrm{3}}\left\{\begin{array}{ll}{r}^{\mathrm{2}/\mathrm{3}}& \text{inverse energy cascade},\\ {\mathit{\eta }}^{\mathrm{2}/\mathrm{3}}{r}^{\mathrm{2}}& \text{direct enstrophy cascade.}\end{array}\right.\end{array}$$

Equations (6) and (8) are special instances of a more general phenomenological correspondence between $E\propto k^{-\mathit{\alpha }}$ and $S_{\mathrm{2}}^{\left(\mathrm{E}\right)}\left(r\right)\propto r^{\mathit{\alpha }-\mathrm{1}}$ for different values of α. However, for steep spectra with α>3 this relationship does no longer hold and the velocity structure function saturates at r² (Babiano et al., 1985). Boffetta and Ecke (2012) state that velocity structure functions may provide less information about small-scale turbulent components than vorticity structure functions. The latter, however, are not available from the drifter data analysed in this study.

2.4 Drifter simulations

For drifter simulations we employed the 2-D Lagrangian transport module PELETS (Callies et al., 2011), based on surface currents archived from the hydrodynamic model BSHcmod (Dick et al., 2001). BSHcmod is run operationally by the Federal Maritime and Hydrographic Agency (BSH). PELETS, developed at Helmholtz-Zentrum Geesthacht (HZG), is designed for particle tracking on unstructured triangular grids. If hydrodynamic fields are provided on a structured grid, as in the case at hand, introducing diagonals splits each rectangular grid cell into two triangles. Using a simple Euler forward method, particle velocities are updated each time a particle passes from one to another triangular grid cell. As a result of this concept, time step is not a constant; it has, however, an upper limit. If no edge is reached within 15 min, an additional update of drift velocity will be triggered.

BSHcmod is run on a two-way nested grid covering both the North Sea and the Baltic Sea. In the German Bight its horizontal resolution is 900 m. Although the vertical coordinate in BSHcmod is dynamical (Dick et al., 2008), regridded archived output represents surface currents in terms of the mean in an upper 5 m water column. In a model validation study, Callies et al. (2017) found that an additional wind drag in terms of 0.6 % of the 10 m wind velocity u_10 m is appropriate to compensate for the lack of vertical grid resolution in archived model output. Therefore, for simulating drifter location x as a function of time t, the following equation is used:

$$\begin{array}{}\text{(9)}& {\displaystyle \frac{\mathrm{d}\mathit{x}}{\mathrm{d}t}}={\widehat{\mathit{v}}}_{\mathrm{E}}={\mathit{v}}_{\mathrm{E}}+\mathit{\beta }{\mathit{u}}_{\mathrm{10}\mathrm{m}}.\end{array}$$

Here v_E denotes Eulerian marine surface currents from BSHcmod, archived on a 15 min basis, and u_10 m corresponding atmospheric forcing from the regional model COSMO-EU (Consortium for Small-Scale Modelling; Schulz and Schättler, 2014) run by the German Meteorological Service (Deutscher Wetterdienst – DWD) with spatial resolution of 7 km. The value 0.006 is assigned to weighting factor β. This value, estimated by Callies et al. (2017) for the same drifter type, seems largely consistent with findings of a more recent experimental study by Meyerjürgens et al. (2019). From seven drifters tracked in the German Bight they estimated a wind slip of 0.27 % and a total wind-induced drifter motion of 1 % of 10 m winds.

Grid resolution limits the scale of flow features that can be resolved. Drifter separations of less than 1 km are clearly beyond the resolution of BSHcmod. The general approach to overcome such a problem is to include sub-grid-scale turbulent processes via a scale-dependent random diffusion term. With such an approach being implemented, even particles released at the same initial location will start separating. Assuming that movements in the two dimensions are decoupled, in PELETS updates of a particle's position vector x(t) after time dt are described by the following discretised version of the corresponding stochastic Langevin equation for each vector component x_i:

$$\begin{array}{}\text{(10)}& \begin{array}{rl}{\displaystyle }\mathrm{d}{x}_i\left(t\right)& {\displaystyle }=x_i(t+\mathrm{d}t)-x_i\left(t\right)=\left[{\widehat{v}}_{\mathrm{E},i}\left(t\right)+v_i^{\prime }\left(t\right)\right]\mathrm{d}t\\ {\displaystyle }& {\displaystyle }={\widehat{v}}_{\mathrm{E},i}\left(t\right)\mathrm{d}t+\sqrt{\mathrm{2}K}\mathrm{d}W\left(t\right).\end{array}\end{array}$$

The right-hand side of this equation combines a deterministic Eulerian velocity component ${\widehat{v}}_{\mathrm{E},i}\left(t\right)$ with a white-noise-driven diffusion term $v_i^{\prime }\left(t\right)$. K denotes horizontal eddy diffusivity and W is a Wiener process, independent increments of which have a zero mean and a second-order moment 〈dW²〉=dt. Equation (10) is appropriate for time increments that exceed the time particles need to lose memory of turbulent momentum (Heemink, 1990; Zambianchi and Griffa, 1994). The assumption of a clear gap between scales of mean and turbulent motions also underlies the common eddy-diffusion parameterisation as the Eulerian analogue of the Lagrangian model Eq. (10).

Following Schönfeld (1995), diffusivity K is assumed to depend on a characteristic length scale l according to a 4∕3 power law (Stommel, 1949):

$$\begin{array}{}\text{(11)}& K\left(l\right)=K\left(l_{\mathrm{0}}\right){\left({\displaystyle \frac{l}{l_{\mathrm{0}}}}\right)}^{\frac{\mathrm{4}}{\mathrm{3}}}.\end{array}$$

For a reference length scale l₀=1 km we chose K(l₀)=1  m² s⁻¹. This value roughly agrees with the value of 2.5 m² s⁻¹ for a reference length scale of 1 nautical mile chosen by Schönfeld (1995). The length scale l in Eq. (11) was chosen to equal spacing of the numerical grid.

To improve performance at early times after drifter deployment, Eq. (10) may be replaced by a random flight model that assigns a finite memory to turbulent drifter velocity (Durbin, 1980; Heemink, 1990; Griffa et al., 1995; LaCasce, 2008):

$$\begin{array}{}\text{(12)}& v_i^{\prime }\left(t\right)=\left(\mathrm{1}-{\displaystyle \frac{\mathrm{d}t}{T_{\mathrm{L}}}}\right)v_i^{\prime }(t-\mathrm{d}t)+{\displaystyle \frac{\sqrt{\mathrm{2}K}}{T_{\mathrm{L}}}}\mathrm{d}W\left(t\right).\end{array}$$

Here T_L denotes the Lagrangian decorrelation time. For dt=T_L, Eq. (12) coincides with the turbulent component in Eq. (10). For drift times t−t₀ much exceeding T_L, the diffusivity K equals the product σ²T_L (Falco et al., 2000), where σ² denotes the turbulent velocity variance. With this substitution the random component of the turbulent velocity component $v_i^{\prime }$ assumes the form $\sqrt{\mathrm{2}{\mathit{\sigma }}^{\mathrm{2}}/T_{\mathrm{L}}}\mathrm{d}W\left(t\right)$, which is more common (e.g. Griffa et al., 1995; Falco et al., 2000; Ohlmann et al., 2012). The advantage of Eq. (12) is that it directly refers to the scale dependent model parameter K in Eq. (11).

3 Results

The objective of this study is to examine whether drifter separations observed during three different experiments reflect the presence of wind-farm-related turbulence. It is reasonable to assume that wind farm effects would increase with decreasing distance between drifter and wind farm. However, due to the large wind farm area this distance is not well defined. Table 3 lists for each drifter its distance from the wind farm at the time of its first GPS-based localisation. The table provides two different measures, referring to either the centre of the wind farm or the location of the nearest wind turbine. The two distances may differ by a factor exceeding four (see experiment A), becoming similar only when drifters are already far from the wind farm (see experiment C). Comparing experiments A and B, for instance, a clear ranking with regard to distance to the nearest wind turbine is not reproduced when referring to wind farm centres. Considering experiment C, distances of drifters C₅ and C₆ seem generally comparable with those of drifters B₁ and B₃, while for all other drifters C_i distances increase substantially.

Table 3 Distances between drifters and wind farm

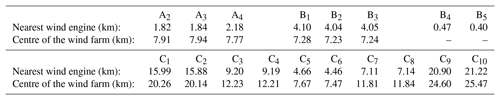
For drifters from set A, distances are evaluated relative to wind farm DanTysk; for drifters from sets B and C they refer to wind farm Global Tech I. For drifters B₄ and B₅ distances to the centre of the wind farm are not given as these drifters were released from inside the wind farm (see Fig. 4d).

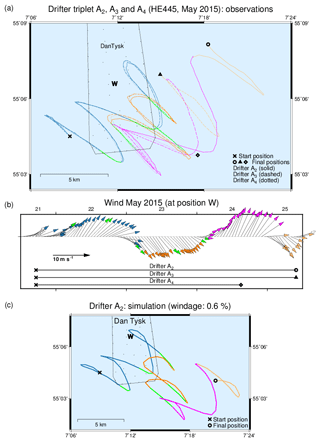
Figure 2 (a) Observed trajectories of drifters A₂, A₃ and A₄. (b) Wind conditions during the experiment. The panel also indicates travel times of all trajectories. (c) Simulated trajectory A₂. Different colours partitioning the observational period are used consistently across all panels.

It must also be noted that all experiments were conducted in different years and therefore under completely independent weather conditions. Unfortunately, experiments can therefore not be interpreted as a set of realisations within a fixed experimental set-up. Section 3.1 presents details of all drift trajectories showing how drifters were located relative to wind farms and which winds they were exposed to. In Sect. 3.3, looking for indications that drifter separation might be influenced by wind-farm-related turbulence, separation velocities and velocity structure functions are shown for different groups of drifters, separating in particular those drifters that are far enough to presumably not experience wind farm effects (C₁–C₄, C₇–C₁₀; see Table 3).

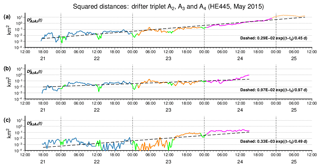
Figure 3 Time evolutions of pairwise squared distances between members of drifter triplet A₂, A₃ and A₄. Segmentation using different colours is consistent with Fig. 2. Dashed lines represent the fitted exponential growth models annotated in each graph.

3.1 Drifter trajectories and separations

3.1.1 Drifter set A

Trajectories of drifters A₂, A₃ and A₄ are shown in Fig. 2a. Different colours are used to distinguish between periods with different wind conditions (Fig. 2b) or to highlight periods of special interest. Superimposed to tidal oscillations roughly oriented between south-east and the north-west, the drifter triplet first moves from the location of its deployment in the south-west of DanTysk towards the north-east, roughly in parallel with prevailing winds. Within about 1 d the drifters cross the OWF area. After winds veered to blow from the north-west, residual transports reverse their direction and the tide-induced pattern of oscillatory drifter movements is shifted back towards the OWF area. This reversal does not depend on the choice of wind drag parameter β in Eq. (9) but is already represented by the Eulerian surface currents v_E. The third day is again characterised by winds from the south-west, giving rise to another reversal of the residual transport direction. Now separation between drifters becomes clearly noticeable on the scale of the plot. At the end of the observation period, winds change again and blow from the north-west. The reaction to this last change in wind direction, however, differs between drifters A₂ and A₃ (drifter A₄ has already been recovered at that time), reflecting gradients in residual current fields on a scale of a few kilometres (the final distance between A₂ and A₃ is approximately 4 km).

Figure 2c displays the simulated counterpart of trajectory A₂ without random diffusion. In the model any information about the presence of a wind farm is lacking. Simulations well reflect the general patterns observed, which in particular confirms the reliability of winds underlying the simulations. On the mean, however, simulated transports are more southward resulting in an error of about 8 km in the final locations predicted for drifter A₂ or A₃ (as initial location practically coincide, simulations without diffusion would differ just slightly in drift time). Simulation errors seem substantial relative to observed overall drifter displacements (A₂: 12.2 km; A₃: 8.1 km) but are very moderate in the light of the lengths of undulating drift paths (A₂: 87.4 km; A₃: 85.7 km; see Table 1).

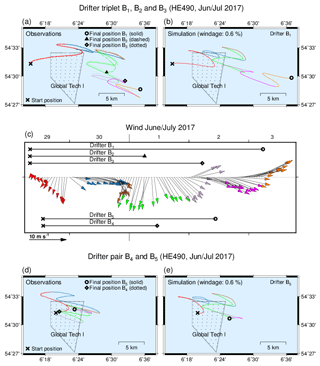
Figure 4 (a) Observed trajectories B₁, B₂ and B₃. (b) Simulated trajectory B₁. (c) Wind conditions during the observational period. Travel times of all trajectories are indicated. (d) Observed trajectories B₄ and B₅. (e) Simulated trajectory B₅. Different colours are used for a consistent segmentation of the observational period.

For all three pairs yielded from the drifter triplet, semi-log plots in Fig. 3 show how squared drifter separations develop with time. Techniques for the evaluation of three-particle dispersion (LaCasce and Ohlmann, 2003; Berta et al., 2016) were not applied. Colours used for time segmentation are consistent with those in Fig. 2. For each drifter pair, a model of exponential growth, as expected for a non-local regime, was fitted. For the two pairs A₂, A₃ and A₃, A₄ very similar e-folding times (about half a day) were obtained, corresponding with a bit less than 1 d for non-squared separation. For drifters A₂–A₄ the estimated e-folding time is approximately twice as large. It should be noted, however, that the fit in Fig. 3c is quite uncertain and mainly based on the behaviour at larger distances. The more random behaviour observed at smaller distances might already reflect an uncertainty in measurements (a squared distance of 10⁻³ km² corresponds with the 90th percentile of errors measured in the lab, see Sect. 2.1). However, it is hard to tell why this uncertainty does not show up for the two other drifter pairs.

3.1.2 Drifter set B

This experiment comprised two drifter releases at slightly different locations. One triplet (B₁, B₂ and B₃) was released west of OWF Global Tech I (see Fig. 1) and drifters were tracked for between 1.9 and 3.9 d (see Table 1). Observations are shown in Fig. 4a, and a corresponding simulation without random diffusion in Fig. 4b. With a delay of a bit more than 5 h, another two drifters (B₄ and B₅) were deployed inside the OWF and tracked for 1.9 and 2.9 d, respectively. Observations and a corresponding simulation are shown in Figs. 4d and e.

Time evolutions of squared drifter separations are presented in Fig. 5. For all drifter pairs an exponential model fitted to the data revealed approximately the same e-folding time of half a day. However, again these fits must not be overrated as observations show large variability at small drifter distances. Spatial scales at which such variability occurs seem comparable to those in experiment A (compare Figs. 5d and 3c) and again fluctuations might be attributable to uncertainties in GPS-based drifter localisation. On the other hand, variations show a certain coherence in time and sometimes include distances (up to 300 m, see Fig. 5a) that clearly exceed the limits of uncertainty.

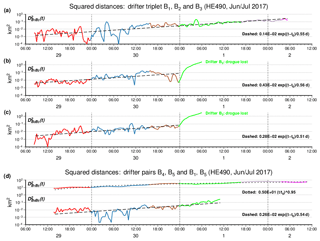
Figure 5 (a–c) Time evolutions of pairwise squared distances between members of the drifter triplet B₁, B₂ and B₃. Dashed lines indicate the fitted exponential growth models annotated in each graph. In the two cases with drifter B₂ involved, data in July are ignored in the fit as at that time the drifter presumably lost its drogue. (d) Distance between drifter pair B₄ and B₅. For comparison, the panel also contains the distance between the two drifters B₁ and B₅ that belong to different clusters. Colours used for segmentation of the observational period agree with those used in Fig. 4.

Figure 5d also includes the evolution of the squared distance between drifters B₁ and B₅ that belong to different clusters but nevertheless have overlapping periods of travel time. The fitted power law with an exponent close to 1 indicates a diffusive regime with linear growth of squared separation. This would be expected for separation distances larger than the typical size of relevant eddies, when uncorrelated velocities imply a constant relative diffusivity (e.g. LaCasce, 2008). According to Fig. 4d the two drifters stay always within or at least in the immediate vicinity of OWF Global Tech I so that OWF-related turbulence could possibly explain diffusive behaviour at drifter separations between roughly 3 and 8 km observed in this case.

3.1.3 Drifter set C

In experiment C, five drifter pairs were deployed at different locations along a south–north transect west of OWF Global Tech I (Fig. 6). Unlike the other two experiments, experiment C included periods of rather weak wind conditions (see Fig. 6c). All drift trajectories are characterised by persistent transports to the north-east. Generally, simulations tend to underestimate the eastward transport components but successfully represent a south–north gradient of the northward drift velocity component.

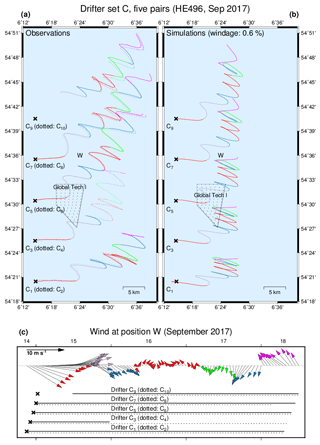
Figure 6 (a) Trajectories of five drifter pairs. (b) Corresponding simulations. (c) Wind conditions during the observational period. Horizontal lines indicate drifter travel times. Different colours are used for a consistent segmentation of the observational period.

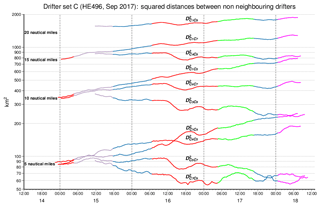
Squared separations reveal large differences between the five drifter pairs (Fig. 7). Only for one pair (C₅ and C₆) relative dispersion growing exponentially seems a reasonable assumption (Fig. 7c); for all other pairs a less systematic non-monotonic behaviour is observed (the time series for drifter C₃ is too short for an assessment). Fitting the exponential growth model for squared distances between drifters C₅ and C₆ depends on times when drifters have already left the OWF but may still feel OWF-related turbulent wakes. The origin of short-term decreases of distance during the first day of the drifter journey remains unclear.

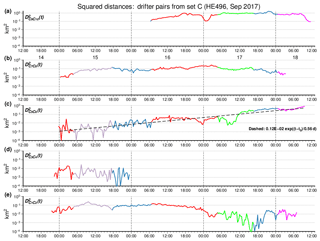
Figure 7 Panels show for each drifter pair the time dependent squared distance between them. For drifter pair C₅ and C₆ an exponential growth model was fitted with an e-folding time as indicated in the graph. Colours used for segmentation of the observational period agree with those used in Fig. 6.

Figure 8 shows the time evolutions of squared distances between drifters selected from different pairs released at different locations. Due to the fact that initial distances between drifters released together (Table 2) are negligible relative to distances between different drifter pairs, we involved just one drifter from each pair (we chose C₄ over C₃ as the latter drifter's trajectory ended early and had little temporal overlap with other drifters, see Fig. 6c). Due to the regular spacing of drifter pair release points (see Fig. 6a), the regrouped drifter pairs fall into classes with initial distances of approximately 5, 10, 15 or 20 nautical miles. Even for the same initial separation drifters are found to disperse very differently, and trends even differ in sign. It is quite obvious that averaging such observations would not provide meaningful insights.

Figure 8 Time evolutions of squared distances between drifters not released together (members of different drifter pairs). Colours used for segmentation of the observational period agree with those used in Figs. 6 and 7.

3.2 Kinetic energy spectra

Figure 9 shows a power spectrum of Eulerian velocities observed at research platform FINO3 (see Fig.1) during a 2-month period. The station is located next to where drifters from drifter set A were deployed. Although the time period underlying Fig. 9 does not overlap with our field experiment, the spectrum nevertheless summarises the general characteristics of kinetic energy at that location.

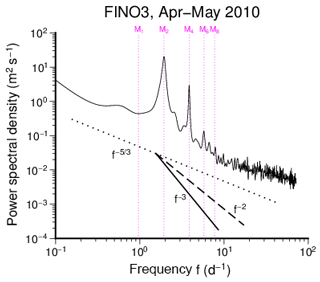
Figure 9 Power spectrum of Eulerian velocities observed at research platform FINO3 (see Fig. 1). Magenta coloured lines indicate frequencies of tidal constituents. Auxiliary black lines indicate reference spectral slopes.

The spectrum shows a broadened peak around the frequency of the lunar semidiurnal tide M₂, which is the principal tidal constituent in European continental shelves. In addition, a clear signal of overtide M₄ occurs, while higher harmonics are only weakly recognisable. Overtides play a major role for shallow sea tidal variability and are also relevant in the German Bight region (e.g. Stanev et al., 2014). They are generated by tidal distortion due to non-linear mechanisms of either advection, causing all even harmonics such as M₄, or friction, causing odd harmonics such as M₆ (Andersen, 1999).

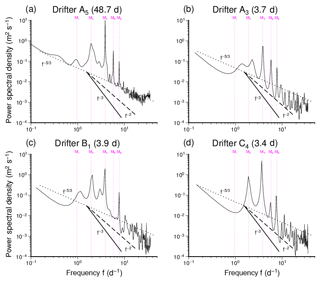
According to Callies and Ferrari (2013) it is important for better understanding of the role of submesoscale turbulence to know how motions represented in the Eulerian spectrum project onto spatial scales. In a first step we compare the Eulerian energy spectrum (Fig. 9) with its Lagrangian counterparts. Figure 10 shows Lagrangian velocity spectra analysed from four different drifters. Figure 10a refers to drifter A₅ that is not subject of our study on drifter pairs. Drifter A₅ travelled, however, for nearly 49 d (see Callies et al., 2017) so that the length of data recorded compares to the time span underlying the Eulerian spectrum in Fig. 9. In the low-frequency range spectral slopes (approximately $-\mathrm{5}/\mathrm{3}$) seem similar in the Eulerian and Lagrangian framework. Note, however, that these low-frequency estimates are not very robust considering the limited lengths of time series. In the high-frequency range a theoretical spectrum with slope −2 (Landau and Lifshitz, 1987) approximates the Lagrangian data reasonably well. The Eulerian spectrum (Fig. 9) flattens out at its high-frequency end beyond the tidal modes, reaching a slope of slightly less than $-\mathrm{5}/\mathrm{3}$, which would be expected for an inertial energy cascade.

Fig. 10b–d refer to three drifters from our present study. Although these drifters travelled for much shorter times, the spectra found are again at least not in obvious contradiction with an assumed theoretical f⁻² spectrum. It must be noted, however, that uncertainties are high and that the spectrum for drifter A₂ (not shown), for instance, could also be approximated by $f^{-\mathrm{5}/\mathrm{3}}$. A finding consistent among all drifters including reference drifter A₅ is that the M₂ peak in the Eulerian spectrum (Fig. 9) is less dominant or smoother in the Lagrangian spectra (Fig. 10). Instead, sharp peaks of overtides up to even M₈ are much more pronounced in Lagrangian than in Eulerian spectra.

Figure 10 Power spectra of Lagrangian velocities observed for four selected drifters. Auxiliary black lines indicate reference spectral slopes. Vertical magenta lines indicate frequencies of tidal constituents.

3.3 Velocity increments and structure functions

While single-point velocity fluctuations are often close to a Gaussian distribution (e.g. LaCasce, 2005), this is often not true for two-point statistics (e.g. Tsinober, 2001, his Fig. 7.3). Figure 11 shows the distributions of both longitudinal and transverse components of Eulerian separation velocity (see Eqs. 3 and 4). The analysis refers to a subset of data conditioned by drifter separations below 2500 m, which is roughly the maximum distance drifters released as pairs reach within the few days considered. It excludes, however, combinations of drifters deployed at different locations (as occurs in drifter sets B and C).

According to Fig. 11 probability distribution functions of longitudinal and transverse Eulerian separation velocities are both nearly Gaussian and not very different from each other. Both graphs in Fig. 11 also distinguish between drifter pairs getting in direct contact with OWFs in the sense that they enter the OWF area and others that travel more distant from the wind farm (drifter set C). Results for these two groups turn out to be very similar, slight differences can possibly be attributed to different weather conditions under which observations were taken. Longer tails of distributions indicate probabilities of fast divergence or convergence being slightly higher than expected for strictly Gaussian distributions. However, distributions in Fig. 11 do not show the pronounced exponential tails Poje et al. (2017) analysed from Grand LAgrangian Deployment (GLAD) data in the northern Gulf of Mexico in particular at small separation scales.

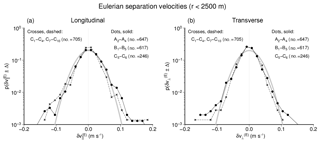
Figure 11 Probability distribution functions of (a) longitudinal and (b) transversal components of Eulerian separation velocities. Velocities grouped in bins of 2Δ=0.016 m s⁻¹ width were evaluated for drifter separations r<2500 m. Solid lines (dots) refer to drifters that were particularly close to and even entered OWFs (all drifters from sets A and B plus drifters C₅ and C₆), and dashed lines (crosses) to those that presumably did not experience direct OWF effects (all remaining drifters from set C). For each group of drifters the number of pairwise samples it contributed is indicated. A reference normal distribution (indicated in grey) was fitted to the longitudinal component (panel a) and then just copied to panel (b) as a reference that facilitates a comparison of longitudinal and transverse velocity components.

The limited number of drifters travelling pairwise motivates a consideration of Lagrangian velocity increments δv^(L) along single trajectories instead of Eulerian velocity increments δv^(E) between trajectory pairs. Increments δv^(L)(t) were obtained as differences between velocities of the same drifter at times t and t+τ, where τ=20 min corresponds with the time resolution of drifter observations. Distributions of the two components $\mathit{\delta }{v}_{\parallel }^{\left(\mathrm{L}\right)}$ and $\mathit{\delta }{v}_{⟂}^{\left(\mathrm{L}\right)}$ are shown in Fig. 12. Note that sample sizes annotated in Fig. 12 are larger than those in Fig. 11 because, in the Lagrangian framework, data from just one drifter must be available as opposed to two in the Eulerian framework.

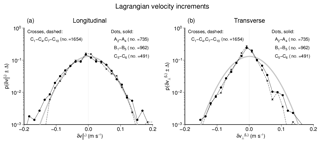
Figure 12 Distributions of (a) longitudinal and (b) transversal components of Lagrangian separation velocities, calculated from binned velocities (bin width 2Δ=0.016 m s⁻¹) based on 20 min time resolution. Solid lines (dots) refer to drifters that were particularly close to and even entered OWFs (all drifters from sets A and B plus drifters C₅ and C₆), and dashed lines (crosses) to those that presumably did not experience direct OWF effects (all remaining drifters from set C). A normal distribution fitted to the longitudinal data (indicated in grey) was just copied from panel (a) to panel (b) as a reference that facilitates a comparison of distributions of the two velocity components.

Like in the Eulerian framework, distributions of Lagrangian longitudinal separation velocities look smooth and nearly normal with, however, slightly enhanced probabilities of large positive or negative values. Distributions obtained from different sets of drifters are again very similar. By contrast, distributions of transverse velocity components (Fig. 12b) do not just replicate the corresponding longitudinal distribution as they did in the Eulerian framework (Fig. 11b). Instead, the distributions of transverse Lagrangian velocity increments look more triangular (with more exponential wings) than their longitudinal counterparts (Fig. 12a). They also show a preference of negative values indicating anticlockwise rotation. The latter possibly arises from M₂ tidal ellipses, which in the German Bight preferably rotate anticlockwise (Stanev et al., 2014).

Returning to the Eulerian framework, Fig. 13 analyses expected drifter separation velocity as a function of spatial distance r, considering the second-order structure functions $S_{\mathrm{2},\parallel }^{\left(\mathrm{E}\right)}\left(r\right)$ and $S_{\mathrm{2},⟂}^{\left(\mathrm{E}\right)}\left(r\right)$ (see Eq. 5). Like in Figs. 11 and 12 the analysis again distinguishes between two groups of drifters classified in terms of their possible contact with OWFs. Auxiliary dashed lines indicate the 2∕3 slope expected from standard K41 scaling of inertial range turbulence within an either forward (3-D) or inverse (2-D) energy cascade. An alternative model (∼r², dotted lines) is associated with the assumption of a direct enstrophy cascade in two-dimensional turbulence (see Eq. 8).

The most striking feature that occurs for both $S_{\mathrm{2},\parallel }^{\left(\mathrm{E}\right)}$ and $S_{\mathrm{2},⟂}^{\left(\mathrm{E}\right)}$ is a plateau-like structure in the range of roughly r=50–1000 m. This range falls within the distance between individual turbines of the OWF. The structure seems most pronounced for the transverse structure function analysed for drifters that were in contact with OWFs (Fig. 13b). Although some data points suggest a steeper slope for very small distances r, the hypothesis of a two-dimensional enstrophy cascade (scaling ∼r²) cannot be substantiated based on Fig. 13.

For data from experiment C, values of the longitudinal structure function $S_{\mathrm{2},\parallel }^{\left(\mathrm{E}\right)}\left(r\right)$ are too scattered to support the assumption of a plateau (Fig. 13c). On the other hand, for the transverse component $S_{\mathrm{2},⟂}^{\left(\mathrm{E}\right)}\left(r\right)$ even all values in the range of up to 1000 m could be assumed to be on a similar level given the degree of uncertainty indicated in the plot (Fig. 13d). As experiment C includes releases from different locations, Figs. 13c and d cover a larger range of values of r than Figs. 13a and b. For large values of r, the transverse structure function $S_{\mathrm{2},⟂}^{\left(\mathrm{E}\right)}\left(r\right)$ in Fig. 13d seems to increase approximately as r^2∕3, as expected for an inverse 2-D energy cascade, for instance. Surprisingly, for the longitudinal component (Fig. 13c) this r dependence is missing, values of $S_{\mathrm{2},\parallel }^{\left(\mathrm{E}\right)}\left(r\right)$ tend to remain on a similar level as for smaller distances.

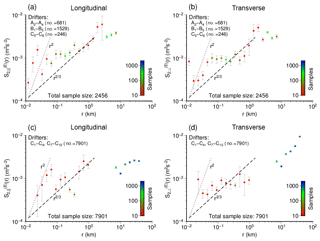
Figure 13 Second-order velocity structure functions depending on drifter separation r. The range of distance r was subdivided into 25 bins with constant width on a logarithmic scale. Bins populated with less than 10 data points were ignored in the plots. Values are given for longitudinal (left) and transverse (right) components separately. Panels at the top or bottom combine drifters in contact with OWFs (a, b) and those travelling more distantly (c, d), respectively. Error bars represent standard deviations estimated by bootstrapping with sample size 1000.

We did not consider the Lagrangian counterparts of the Eulerian structure functions shown in Fig. 13. So far a general consensus about possible scaling laws of Lagrangian velocity structure function seems to be lacking (e.g. Biferale et al., 2008; Falkovich et al., 2012). Another reason is that with increasing values of travel time increment τ the contributions from tidal currents will start to dominate Lagrangian single-particle velocity differences.

3.4 Simulated drifter dispersion

Taking drifter A₂ as an example, Fig. 14 shows the evolution of simulation error in terms of squared separation. Surprisingly, again an exponential model fits quite well, even e-folding time 0.64 d resembles those between different drifters. For comparison, Fig. 14 shows also the simulated spread of a particle cloud, obtained by using a random walk stochastic model superimposed to simulated mean Eulerian currents (Eq. 10). After a short phase of very quick spreading from a common source point, for a period of approximately 1 d, relative dispersion D² (Eq. 3) of the particle cloud develops in a way similar to simulation error. Later on, however, a simulated linear growth of D² clearly underestimates the increase in simulation error.

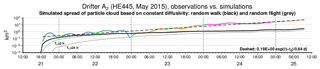
Figure 14 Time evolution of squared separation between observed and simulated trajectories of drifter A₂. Segmentation using different colours is consistent with that in Fig. 3. The dashed line indicates the fitted exponential growth model annotated in the graph. The solid black line represents relative dispersion D² obtained from 100 trajectories initialised at the same location and simulated with random walk model Eq. (10). Grey lines show results when using random flight model Eq. (12) with T_L=3 h and T_L=24 h, respectively.

Replacing the random walk by a random flight stochastic model (Eq. 12), the period with reasonable rates of spreading can be adjusted by changing the values of Lagrangian decorrelation time T_L. Figure 14 shows example simulations obtained with Lagrangian decorrelation times T_L=3 h (analysed by Ohlmann et al., 2012, for instance) or T_L=24 h. For larger values of T_L it takes longer until drifters lose memory of their initial turbulent velocities (zero in our example). Therefore initial turbulent velocities are another tuning parameter of the random flight model (together with diffusivity K). In the long term, however, simulated drifter separation will always increase less quickly than exponentially.

4 Discussion

4.1 Drifter separations

Coastal currents can be complex and corresponding drifter experiments more site specific than open-ocean experiments evaluated by Corrado et al. (2017), for instance. The identification of relevant scales may be affected by regional bathymetry. Diverging time evolutions within the same bundle in Fig. 8 convincingly illustrate how averaging dispersions of drifter pairs with same initial separation can sometimes be non-informative. Lumpkin and Elipot (2010) discuss some examples of “atypical” drift trajectories influenced by mesoscale flow features in the North Atlantic and state that at larger scales separation is often non-monotonic.

In our analyses, noisy scatter of relative dispersion occurred at times when drifter separation was still below approximately 100 m. At this spatial scale, averaging over larger ensembles seems indispensable to achieve a stable statistical characterisation, and errors in drifter localisation may be relevant for the analysis. In the longer term, however, all drifter pairs we studied could clearly be classified into those with separation growing monotonically and others that did not show such regular behaviour. The latter group of drifters was found to combine those with the largest distances to the wind farm.

For 8 out of 12 individual drifter pairs, assuming that relative dispersion grows exponentially was found to be in reasonable agreement with observations. Except for one instance (e-folding time 0.97 d), all e-folding times fell into the narrow range between 0.45 and 0.56 d, suggesting a common physical background that distinguishes these cases from those that exhibit a long-term non-monotonic behaviour. On the other hand, it must also be acknowledged that among the pairs with monotonic growth of separation, a clear distinction between exponential (non-local dispersion) or power law (local dispersion) dependence on time is impossible on a purely statistical basis, given the number of data we have available. To exemplify this problem, Fig. 15 redisplays time evolutions of squared distances between four drifter pairs from experiment B (Fig. 5), now using a logarithmic timescale. The graph highlights the longest time series (B₁ and B₂), including the corresponding exponential fit. In addition, it also indicates the slope expected if Richardson's power law corresponding with local dispersion (Eq. 7) would be satisfied. It is quite obvious that fitting the power law model is sensitive to the lower bound of the time interval taken into consideration. For the exponential growth model, distinction between assumed curvature and the influence of not precisely known accuracy of GPS-based localisation is difficult. A tentative indicator in favour of the exponential model is that estimated e-folding times seemed more stable than estimated exponents in assumed power laws (not shown). However, given the low number of observations available, prior knowledge about what could be expected remains an essential ingredient of the overall analysis.

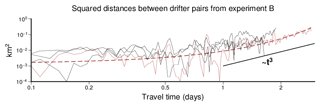
Figure 15 Squared distances from all pairs of experiment B are combined using a logarithmic time axis. Time series replicate the data already shown in Fig. 5, excluding just the very distant pair B₁ and B₅. The brown time series highlights the pair B₁ and B₃ (Fig. 5a); the dashed line represents the corresponding exponential fit. The bold black line represents the slope that would be expected according to Richardson's law for local dispersion in, for instance, the inertial range of turbulent energy (see Eq. 7).

Pooling roughly 75 drifter pairs deployed with 5–10 m spacing in the Santa Barbara Channel, Ohlmann et al. (2012) observed circulation to change substantially on a scale of a few kilometres. They found exponential growth of mean square pair separation until separation reached a value of approximately 100 m after just 5 h time. Thereafter alternative models of D² growing either quadratically or exponentially (e-folding time 0.38 d) both fitted the data reasonably well for the period 12 to 30 h. Regarding scales in space and time, our data correspond with this latter period. However, in our case exponential models (Figs. 3 and 5) seem acceptable for 3 d and more, possibly because drifters in experiments A and B stayed within areas smaller than relevant mesoscale hydrodynamic structures.

Many studies find the Rossby radius of deformation to separate exponential growth of pair separation from a Richardson growth regime. Data from the Gulf of Mexico Surface Current Lagrangian Program (SCULP), for instance, provided a large set of 140 drifter pairs (the majority of them being chance pairs) with initial separation below 1 km (LaCasce and Ohlmann, 2003; LaCasce, 2008). Given clear evidence of D² growing exponentially for about 10 d (e-folding time roughly 2 d), LaCasce and Ohlmann (2003) suggest injection of enstrophy at the spatial scale of 40–50 km (deformation radius in the gulf) which then cascades down to smaller scales in agreement with the assumption of non-divergent 2-D turbulence.

Koszalka et al. (2009) analysed exponential growth with an e-folding time of 0.5 d (like in our study) from drifter pairs and triplets deployed within the POLEWARD experiment (2007–2008) conducted in the Nordic Seas. Starting from initial distances <2 km, the phase of exponential separation lasted for just 2 d up to a final distance of approximately 10 km, in agreement with the size of the local deformation radius. Also Schroeder et al. (2011) analysed e-folding times of 0.5–1 d from drifter clusters deployed in the Liguro-Provençal basin (Mediterranean Sea). These authors found exponential growth lasting for 4–7 d until drifter separation reached a value comparable with the scale of mesoscale circulation patterns (10–20 km in that region).

Also for drifters released near the Brazil Current, Berti et al. (2011) found exponential growth of relative dispersion (e-folding time ∼3 d) at scales comparable to the Rossby radius of deformation (∼30 km). They also identified, however, a second exponential growth regime (e-folding time ∼1 d) on a much smaller scale of 𝒪(1) km, assumed to be related to submesoscale flow structures. Studying surface drifter pairs released during the CLIMODE experiment in the Gulf Stream region, Lumpkin and Elipot (2010) found weak evidence for such exponential relative dispersion at scales < 2 km (e-folding time roughly 1 d). On larger scales up to the Rossby deformation radius (∼30 km) drifter separation clearly did not grow exponentially. Lumpkin and Elipot (2010) discuss possible reasons for this discrepancy with other studies, including the use of chance pairs or insufficient temporal spacing of data.

Taken altogether, results on relative dispersion at submesoscale are still inconclusive. Uncertainties are high and results from different studies may be conflicting. According to Haza et al. (2008), whether or not an exponential regime can be identified may also depend on the sampling strategy underlying the analysis. Recent comprehensive analyses by Poje et al. (2014, 2017) or Corrado et al. (2017) illustrate the present state of knowledge.

Rich data from the GLAD experiment conducted in the Gulf of Mexico from July to October 2012 provides 300 CODE drifters positions and two-point Lagrangian velocities with high resolution in both space (<10 m) and time (15 min) (Özgökmen and CARTHE, 2012). From an analysis of these data, Poje et al. (2014) reported evidence that at scales <10 km surface drifter dispersion was driven locally by the effects of eddies comparable in size with drifter separation. In agreement with Richardson's law this implies a shallower spectrum of Eulerian kinetic energy than would be expected for non-local exponential drifter dispersion. Poje et al. (2017) further elaborate on this idea, emphasising the relevance of ageostrophic submesoscale motions for bypassing the quasi-geostrophic inverse energy cascade.

By contrast, conducting a comprehensive analysis of surface drifter data from the NOAA Global Drifter Program (GDP), Corrado et al. (2017), employing finite-scale Lyapunov exponents (Aurell et al., 1997) to resolve spatial scale dependence, came to the conclusion that exponential growth of drifter pair separation can be found in all parts of the global ocean on spatial scales below the Rossby deformation radius. However, at the submesoscale they found dispersion rates 1 order of magnitude larger, corresponding with an e-folding time of roughly 0.5 d for D²(t). Corrado et al. (2017) suggest the presence of structures in the Eulerian current field that are similar in size to trajectory separation. Existence of two distinct exponential growth regimes could reflect the presence of a spectral gap between mesoscale and submesoscale transport regimes (Özgökmen et al., 2012, their Fig. 2).

Oscillatory tidal currents are dominant components of drifter transport in the German Bight (see Fig. 2a, for instance), similar to wind driven inertial oscillations in the GLAD data (Poje et al., 2014, 2017) which in that region may be difficult to separate from diurnal tidal motions (Gough et al., 2016). However, we found direct manifestation of oscillatory tides being restricted to small short-term dips, colour coded (green) in Fig. 3, for instance. According to Fig. 2a these short-term drifter convergences all occurred during periods when tidal currents were oriented towards the south-east, possibly pointing towards bathymetry-related effects. The observation is not indicative of convergences being related to any frontal structures or cyclonic vortices as reported by D'Asaro et al. (2018), for instance. Stirring by evenly distributed OWF turbines may be relevant for an injection of tidal energy into the turbulent system. It can plausibly be assumed that via straining such a regular stirring process would generate filaments of vorticity that are expected to be seen in the presence of a 2-D enstrophy cascade (Piretto et al., 2016).

Ridderinkhof and Zimmerman (1992) showed that Lagrangian chaos can be the principal mixing process in shallow tidal seas where tides interact with bottom topography (“tidal random walk”). Although the hypothesis of similar chaotic stirring cannot be substantiated based on our data, it is at least consistent with the observation that monotonic (possibly exponential) growth was absent only for those drifters from experiment C that did not travel in close proximity to the OWFs (see Figs. 6a and 7). Experiments A and B were all conducted in the immediate vicinity of OWFs (see Figs. 2 and 4) and drifters even entered the wind farm area. It should be noted, however, that also wind speeds (and therefore impacts of OWFs on turbulence) were generally lower in experiment C than in experiments A and B (compare Fig. 6c with Figs. 2b and 4c).

For OWF forcing being non-local (relative dispersion growing exponentially), turbulent energy should be injected at a spatial scale larger than drifter separation. In fact drifter separations stayed below the distance of individual wind turbines (approximately 800 m) for most of the time drifters were tracked. Also the OWF as a whole might generate relevant hydrodynamic features at a larger scale. An interesting event at the end of the journey of drifters A₂ and A₃ (Fig. 3a) hints at the potential influence of a flow feature at a scale comparable to the already larger drifter separation at that time (∼2 km). For a couple of hours beginning at the end of 24 May the distance between the two drifters increased substantially (Fig. 3a, keep in mind the logarithmic scale of the graph). According to Fig. 2a this occurred because for some hours drifter A₃ did not share a north-east drift component with drifter A₂. An interesting question is whether this reflects a flow feature generated by the presence of the OWF. It is to be kept in mind, however, that a drifter distance of a few kilometres is also near the lower bound of possible values of the baroclinic Rossby radius of deformation reported for the North Sea (Becker et al., 1983, 1999; Badin et al., 2009).

Finally, it is interesting to see also that the discrepancy between the observed trajectory A₂ and corresponding simulations (Fig. 14) develops exponentially. The same holds for A₃ and A₄ (not shown). Also a comparison of Figs. 2a and c reveals that the distance between observed and simulated trajectories of drifter A₂ grows at a rate comparable with the growth of distance between drifters A₂ and A₃. In the case at hand, there is probably little scope left for further improvement of simulations.

4.2 Kinetic energy spectra

Some aspects of the Lagrangian velocity spectra in Fig. 10 resemble results that Lin et al. (2017) obtained in their analysis of data from the GLAD experiment in the Gulf of Mexico (Özgökmen and CARTHE, 2012; Poje et al., 2014, 2017). Lin et al. (2017) identified two spectral ranges with different spectral slopes separated by a (in that case diurnal) tidal peak. A $f^{-\mathrm{5}/\mathrm{3}}$ model approximated the data in the low-frequency range, which parallels our finding. For the high-frequency range, Lin et al. (2017) identified a spectrum with an exponent of about −2.75.

In the Gulf of Mexico study the two spectral ranges were sharply separated at the frequency of a diurnal oscillation. Lin et al. (2017) speculate that tidal oscillations inject energy which then may cascade towards both smaller and larger scales. In our study we were in the favourable position to have direct measurements of Eulerian spectra (Fig. 9) that could be indicative of such cascade dynamics. On the other hand, the German Bight coastal tidal regime may be more complex than that in the Gulf of Mexico. According to Fig. 9 it seems that three rather than just two spectral ranges should be distinguished. In an intermediate frequency range between about 2 and 8 d⁻¹ a spectral slope of approximately f⁻² occurs with sharp peaks related to the principal tidal constituent M₂ and at least overtide M₄. A spectral slope of −3 would be in agreement (using Taylor's frozen turbulence transformation $k\sim f/u$, where u denotes mean velocity) with the assumption of a direct enstrophy cascade in 2-D turbulence (see Eq. 6). Here, however, tidal energy input can obviously not be described as local in the frequency domain; overtides injecting energy at frequencies higher than M₂ could possibly reduce the spectral slope. Based on numerical simulations for a 2-month period without extreme atmospheric conditions, Stanev et al. (2014) found that an area of major M₄ amplitudes off the North Frisian Wadden Sea originated from reflection and refraction of the Kelvin wave that underlies the North Sea M₂ tide. Large M₆ velocity components were found to occur in estuaries and tidal channels with strong velocities and high friction. Such energy transfers between tidal constituents are clearly not a matter of pure turbulence expected to follow classical scaling laws.

For high frequencies beyond the range of tidal signals a Eulerian power spectrum of even less than $-\mathrm{5}/\mathrm{3}$ is observed in Fig. 9. With Taylor's frozen turbulence assumption, a $-\mathrm{5}/\mathrm{3}$ slope would reproduce Kolmogorov's law (Eq. 6). Although this law can be found for very different systems (Tsinober, 2001, Sect. 7.3.4), it is also theoretically consistent with either a direct energy cascade in fully developed 3-D turbulence or an inverse energy cascade in 2-D turbulence. A $-\mathrm{5}/\mathrm{3}$ slope in Eulerian spectra would also be consistent with the fact that slopes in the Lagrangian spectra (Fig. 10) seem to be close to −2, predicted by the Kolmogorov–Landau theory (Landau and Lifshitz, 1987) and confirmed experimentally for fully developed 3-D turbulence (e.g. Mordant et al., 2001, 2003).

The low-frequency part of the Eulerian spectrum in Fig. 9 is poorly underpinned by data and must be interpreted with due care. However, surprisingly, the Lagrangian spectrum (Fig. 10a) seems to replicate a $-\mathrm{5}/\mathrm{3}$ slope of the Eulerian spectrum. A −2 slope expected theoretically in a Lagrangian framework derives from dimensional arguments, and exponents in the Eulerian and Lagrangian framework differ because only in the Eulerian context the spectrum is assumed to depend on a mean velocity (Landau and Lifshitz, 1987, p. 135). However, a $-\mathrm{5}/\mathrm{3}$ Lagrangian spectrum at low frequencies was also found by Lin et al. (2017) in their Gulf of Mexico study. As a possible problem these authors mention the presence of tidal movements which according to Beron-Vera and LaCasce (2016) can cause conflicting results between different types of analyses.

Middleton (1985) addresses the general question of how Eulerian spectra translate into their Lagrangian counterparts. Elaborating on an original idea of Corrsin (1959), Middleton (1985) found that spectra observed in an Eulerian and Lagrangian framework should agree when velocity changes depend more on local variations than on advective processes (see also LaCasce, 2008, for a summary of the concept). This situation might prevail with the scales involved in tidal movements. Off the coast, spatial scales over which tidal currents change are larger than the tidal excursions of individual water bodies, which implies a minor role of advective processes.

4.3 Velocity increments and structure functions

According to Fig. 13, velocity structure functions do not show the scaling with r² that would be expected for non-local (i.e. exponential) relative dispersion (see Eqs. 7 and 8). Figure 13 suggests a fast increase in $S_{\mathrm{2}}^{\left(\mathrm{E}\right)}$ only for very small distances before the structure function levels off towards a plateau-like behaviour. Although our data are insufficient for fitting statistical models, for parts of the spectra shallower slopes proportional to r^2∕3 seem more consistent with observations. A similar situation has also been reported in other studies based on larger sets of data (Beron-Vera and LaCasce, 2016), even when more sophisticated distance-based measures like the finite-scale Lyapunov exponent (FSLE, see Aurell et al., 1997) were employed (Sansón et al., 2017). Beron-Vera and LaCasce (2016) understand their study as a warning not to deduce kinetic energy spectra from measurements of relative dispersion. To explain the seeming discrepancy, they proposed two different effects. First, values of distance r between drifters deployed pairwise often do not cover the whole range up to the mesoscale structure where energy for non-local forcing is injected. In our case one might argue that this range is covered by combinations of drifters from different pairs in experiment C, which provide the instances of large r values in Fig. 13c and d. However, these values are not indicative of structure functions growing faster than r^2∕3.

A second explanation Beron-Vera and LaCasce (2016) propose is that $S_{\mathrm{2}}^{\left(\mathrm{E}\right)}\left(r\right)$ values for small values of r are larger due to the effects of (in their experiment) regular inertial oscillations. The mechanism proposed is that for constant angular velocity the size of an inertial loop should correlate with drifter velocity, which may give rise to a correlation between drifter separation and separation velocity while mean dispersion after closed cycles remains unaffected. However, the strong externally forced tidal oscillations in our experiments vary smoothly in space and neighbouring drifters are supposed to experience similar movements. Also the spatial scale of tidal waves seems clearly larger than the separations of mostly less than 1 km reached by most of our drifter pairs within the drift period of 3–4 d. Given the large tidal excursions (see Fig. 2a, for instance) in our case tidal movements cannot be seen as small-scale disturbances overlaid large-scale movements. The situation seems different in experiment C (see Fig. 6a). However, for analysing such large-scale homogeneous movements our time series of 3–4 d are too short.

For isotropic turbulence the following relationship should relate the longitudinal and transverse second-order structure functions to each other (Kraichnan, 1966; Monin and Yaglom, 1975):

$$\begin{array}{}\text{(13)}& S_{\mathrm{2},⟂}^{\left(\mathrm{E}\right)}\left(r\right)=\left(\mathrm{1}+{\displaystyle \frac{r}{\mathrm{2}}}{\displaystyle \frac{d}{\mathrm{d}r}}\right)S_{\mathrm{2},\parallel }^{\left(\mathrm{E}\right)}\left(r\right).\end{array}$$

Kramer et al. (2011) propose verifying Eq. (13) for checking the assumption of homogeneity and isotropy. However, our data are too noisy for following this approach, which according to Babiano et al. (1985) would not be fully conclusive anyway. It must also be noticed that for large drifter separations (up to 40 km in experiment C), systematic spatial patterns of the tidal regime may dominate the analysis in Fig. 13. It can reasonably be assumed that rotational components of tidal currents preferably impact the transverse components of velocity increments (Lévêque and Naso, 2014). Resulting dependences might happen to resemble what one would expect from statistical analyses.

4.4 Simulated drifter dispersion

Figure 14 exemplifies simulation error growth for drifter A₂. Interestingly, also simulation errors for drifters C grow exponentially with similar e-folding times (not shown), notwithstanding the irregular behaviour of observed relative dispersion (Fig. 7). Comparing Fig. 6a and b reveals a (possibly location-dependent) lack of eastward transport in simulations, which means that observed and simulated drifters persistently experience different large-scale background currents. This is reminiscent of exponential growth rates that occur when distances between drifters are stretched by eddies much larger in size than the distance between two drifters considered.

Simulation errors exceed simulated random spread of drifters. Simulations that employ an either zeroth-order (Eq. 10) or first-order (Eq. 12) stochastic model both underestimate drifter separation after more than about 2 d while overestimating drifter separation in the very first hours after drifter deployment (Fig. 14). A clear distinction between processes resolved by the hydrodynamic model and sub-grid-scale processes to be parameterised may be missing. Instead of assuming constant diffusivity, Ohlmann et al. (2012) used turbulent velocity standard deviations, σ, ranging between 0.7 and 5.1 cm s⁻¹ depending on separation scales between 5 m and 2 km. With T_L=3 h, this corresponds with values of diffusivity K=σ²T_L approximately ranging between 0.5 and 28 m² s⁻¹. The lower bound of these values corresponds with the magnitude of the value obtained from Eq. (11) with a grid resolution of 900 m used in our simulations.

5 Conclusions

By analysing 11 trajectory pairs released in the German Bight, trajectories could clearly be grouped into eight pairs that showed a long-term monotonic increase in drifter separation (for distances exceeding estimated uncertainty of GPS-based drifter localisation) and three pairs' distances of which changed in an irregular non-monotonic way (one pair travelled too short for a clear assessment). In all cases with monotonic behaviour, exponential growth of squared pair distance seemed a reasonable assumption, supported also by the fact that for seven pairs the fitted e-folding time was consistently about half a day (for one pair it was twice as large). Pair separations growing exponentially would indicate the action of eddies that are much larger than distances between the drifters. Unfortunately, due to the brevity of time series and the low number of drifters, it was impossible to statistically distinguish such non-local dispersion from local dispersion with power law dependence on time. Reasons for the differences we found can only be speculated. One hypothesis attributes observed dispersion rates to the effects of OWFs. Although this hypothesis cannot really be substantiated based on our limited data, it is nevertheless consistent with the observation that the three pairs with non-monotonic growth were exactly those that did not travel within a OWF or in the close neighbourhood on its lee side.

Shelf sea conditions with irregular coastal geometry and bathymetry manifest themselves in characteristic hydrodynamic structures at specific spatial scales. Non-monotonic drifter separation could possibly be indicative of drifters getting trapped by coherent structures. Indeed, already at distances >5 nautical miles we found drifter behaviour to depend on location (see Fig. 8) which makes statistical analysis of evolving drifter separation a questionable enterprise. A threshold of scale separation can possibly be derived from a plateau-like structure only hinted at; however, in the Eulerian second-order structure function (Fig. 13), the estimated separation at a scale of 𝒪(1) km would overlap with distances between individual turbines in OWFs but is also not far from the magnitude of the internal radius of deformation, which in the German Bight is estimated to be a few kilometres. Important flow characteristics in the German Bight also include strong tidal currents. In the Eulerian kinetic energy spectrum we found peaks of tidal constituents embedded in a spectral range with an approximately −2 slope. In the Lagrangian spectra derived from drifter movements, even peaks related to higher-order overtides M₆ and M₈ were well defined. Energy injected at different frequencies and non-linear transformation of energy between different tidal constituents, however, obviously goes beyond the classic concept of turbulent energy cascading across an inertial spectral range.

A dedicated and more comprehensive field study would be needed to really pin down possible effects of OWFs on turbulent mixing in the German Bight. Longer drift times could reveal transitions between different regimes like non-local or local dispersion. Reference drifter pairs travelling windward of the wind farm would enable a better distinction between wind-farm-related and other turbulent effects in the complex coastal environment. The present study combined data from three independent experiments that were conducted under different weather conditions. With a sufficiently large number of drifters being deployed, conditioning on atmospheric forcing could further support the analysis.