The land–sea coastal border: a quantitative definition by considering the wind and wave conditions in a wave-dominated, micro-tidal environment

A quantitative definition for the land–sea (coastal) transitional area is proposed here for wave-driven areas, based on the variability and isotropy of met-ocean processes. Wind velocity and significant wave height fields are examined for geostatistical anisotropy along four cross-shore transects on the Catalan coast (north-western Mediterranean), illustrating a case of significant changes along the shelf. The variation in the geostatistical anisotropy as a function of distance from the coast and water depth has been analysed through heat maps and scatter plots. The results show how the anisotropy of wind velocity and significant wave height decrease towards the offshore region, suggesting an objective definition for the coastal fringe width. The more viable estimator turns out to be the distance at which the significant wave height anisotropy is equal to the 90th percentile of variance in the anisotropies within a 100 km distance from the coast. Such a definition, when applied to the Spanish Mediterranean coast, determines a fringe width of 2–4 km. Regarding the probabilistic characterization, the inverse of wind velocity anisotropy can be fitted to a log-normal distribution function, while the significant wave height anisotropy can be fitted to a log-logistic distribution function. The joint probability structure of the two anisotropies can be best described by a Gaussian copula, where the dependence parameter denotes a mild to moderate dependence between both anisotropies, reflecting a certain decoupling between wind velocity and significant wave height near the coast. This wind–wave dependence remains stronger in the central bay-like part of the study area, where the wave field is being more actively generated by the overlaying wind. Such a pattern controls the spatial variation in the coastal fringe width.

1 Introduction

Land–sea border areas are narrow strips of water that display unique met-ocean dynamics due to (a) non-linearity and sea bottom interactions (including bathymetric control) for the ocean (Shaw et al., 2008) and (b) differential land–sea heat and a topographic control on winds (e.g. channelled winds and coastal jets) (Miller et al., 2003; Estournel et al., 2003). This results in enhanced gradients that interact with very productive ecosystems and a large number of infrastructures and socio-economic uses related to tourism, fisheries and aquaculture, or maritime transport (Halpern et al., 2008; Bulleri and Chapman, 2010; Barbier et al., 2011; Sánchez-Arcilla et al., 2016). However, the limits of this land–sea transition remain fuzzy and even somewhat subjective, depending on the type of process or application considered and with technical, economic and legal implications.

There is, thus, a need for a systematic and objective definition of the coastal fringe that considers underlying processes and that has general applicability allowing for the time/space dynamics of this fringe. This type of approach has been explored in the literature; for instance, Sánchez-Arcilla and Simpson (2002) reviewed a number of possibilities based on a dynamic balance of competing processes (i.e. drivers) such as inertial effects, geostrophic steering, sea bed friction or water column stratification. Another suitable option is to focus on the consequences of such processes, such as the nearshore morphodynamic features (Geleynse et al., 2012; i.e. deltas, sand spits, overwash fans, beach berms). Both complementary classifications require spatial data that need to be accordingly updated within timescales that may range from years (i.e. long-term erosion due to sea level rise) to days (i.e. storm-scale).

In the last decades, the advent of remote sensing has led to environmental monitoring at spatio-temporal scales that were previously hard to achieve with just in situ measurements. Hence, such high spatial resolution and short revisit time offer an alternative source of information for such a coastal zone definition, although with some limitations since the data may start degrading at a few kilometres (approximately 10 km) offshore (Cavaleri and Sclavo, 2006; Wiese et al., 2018; Cavaleri et al., 2018). The land boundaries induce errors in the satellite observations. Hence, it is useful to use high-resolution numerical simulations supported by in situ data so that land–sea boundary effects are properly captured for the subsequent coastal definition that will be based on the heterogeneity introduced by the presence of the land boundary.

The geostatistical anisotropy in wind and wave fields (Swail et al., 1999) can be a useful indicator of spatial structure, affected by topo-bathymetric constraints that generate substantial wave-driven gradients under strong met-ocean conditions. In this text, the term “anisotropy” refers only to the geostatistical anisotropy, not the geophysical one. A wind or wave field that has a high anisotropy can present a predominant wind or wave direction, respectively. It is well known that the geostatistical anisotropy can be a measure to define directional variation, e.g. for mineral configuration in rocks (Amadei, 1996), for propagation velocity in heterogeneous media (Crampin, 1984) or for seismic waves (Verdon et al., 2008). Similarly, topographically induced geostatistical anisotropy affects coastal wind patterns that force wave and current fields (Soomere, 2003).

The aim of this paper is to analyse the geostatistical anisotropy of nearshore wind and waves for wave-driven coasts. From that, what follows is to propose a new quantitative and objective definition for the land–sea border that benefits from these high-resolution (spatial and temporal) fields and from the underlying process-based knowledge. This definition can be useful to determine a set of criteria for numerical purposes (e.g. nesting coastal domains) but also for more practically oriented applications (e.g. offshore limit for outfall dispersion). The analysis is based on a set of high-resolution wind and wave fields in the latter case using a well-tested code such as SWAN (Simulating Waves Nearshore; Booij et al., 1999; van der Westhuysen et al., 2007; WISE Group, 2007; Zijlema, 2010). The numerical results, pertaining to a micro-tidal environment to avoid any distortion of spatial patterns by tides, will be subject to computationally inexpensive statistical methods to characterize spatial structures. Following this approach, the paper is structured as follows. Section 2 introduces the theoretical background. Section 3 describes the study area, and the methodology is presented in Sect. 4. Section 5 lists the main results, which are discussed in Sect. 6, followed by some conclusions in Sect. 7.

2 Theoretical background

Given a spatio-temporal field X(s, t), where s stands for a 2-D vector (zonal and meridional components) and t is time, it is assumed that the iso-level contours of the correlation functions are invariant, i.e. ellipses in two dimensions. The main axes of these ellipses are termed u and v (see Fig. 1). The metric of the geometric anisotropy then becomes their ratio $R=\frac{u}{v}$ (R∈[0, ∞); Chorti and Hristopulos, 2008; Petrakis and Hristopulos, 2017). An R value close to unity means that u and v are isotropic, i.e. homogeneous across the different directional sectors. As R increases, the difference between the main axes increases, showing higher anisotropy at certain directional sectors.

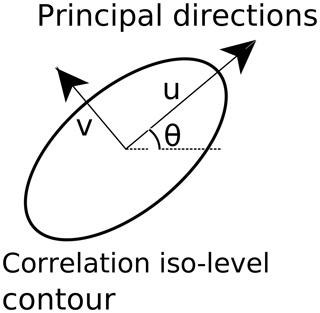
Figure 1 Representation of a generic ellipse that represents the geostatistical geometric anisotropy of a wind or wave field. Supposing u and v are the two principal directions of anisotropy, the anisotropy ratio is $R=\frac{u}{v}>\mathrm{1}$; symbol θ is the rotation angle of the field.

Considering the ratio R as a 1-D random variable, it can be fitted to a probability distribution function. Such a fitting depends on theoretical and practical considerations. The preferred shape is determined by looking at statistical characteristics such as mean, variance, skewness and kurtosis, or by examining the similarity between quantiles (dataset versus theoretical probability distribution) using a quantile–quantile plot. The more direct candidates to fit variable R are (a) the log-normal function, where the probability distribution of its log-transform is Gaussian (Aitchison and Brown, 1958), and (b) the log-logistic function, with a logistic probability distribution for the log-transformed variable. A logistic distribution has a probability density function of the following form:

$$\begin{array}{}\text{(1)}& {\displaystyle }{\displaystyle }f\left(x\right)={\displaystyle \frac{\mathrm{1}}{s}}\exp \left(\right(x-m)/s){\left(\mathrm{1}+\exp \left(\right(x-m)/s)\right)}^{-\mathrm{2}},\end{array}$$

where m is its location parameter and s is its scale parameter.

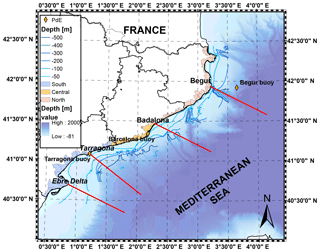
Figure 2 Study area showing the gradients in topo-bathymetry that exert a strong control over the resulting met-ocean conditions. The four transects (red lines) used to estimate the limit of the coastal fringe are depicted, located in (from south to north) (a) Ebro Delta, (b) Tarragona, (c) Badalona and (d) Begur. The map also shows the Puertos del Estado (PdE) buoys and the division of the Catalan coast into the northern, central and southern sections (different colours on the land).

Sklar's theorem (Sklar, 1959) expresses the multivariate joint probability structure of two variables x and y as the product of their cumulative probability distributions F(x) and G(y), and a 2-D copula. The interval of variation in F(x), G(y) is [0, 1] and a 2-D Gaussian copula has the following form:

$$\begin{array}{ll}{\displaystyle }{C}_{\mathit{\rho }}\left(F\right(x),G(y\left)\right)=& {\displaystyle }\underset{-\mathrm{\infty }}{\overset{{\mathrm{\Phi }}^{-\mathrm{1}}\left(F\right(x\left)\right)}{\int }}\underset{-\mathrm{\infty }}{\overset{{\mathrm{\Phi }}^{-\mathrm{1}}\left(G\right(y\left)\right)}{\int }}{\displaystyle \frac{\mathrm{1}}{\mathrm{2}\mathit{\pi }\sqrt{\mathrm{1}-{\mathit{\rho }}_{\mathrm{12}}^{\mathrm{2}}}}}\\ \text{(2)}& {\displaystyle }& {\displaystyle }\exp \left\{-{\displaystyle \frac{s^{\mathrm{2}}-\mathrm{2}{\mathit{\rho }}_{\mathrm{12}}st+t^{\mathrm{2}}}{\mathrm{2}\left(\mathrm{1}-{\mathit{\rho }}_{\mathrm{12}}^{\mathrm{2}}\right)}}\right\}\mathrm{d}s\mathrm{d}t,\end{array}$$

where the correlation parameter $-\mathrm{1}<{\mathit{\rho }}_{\mathrm{12}}<\mathrm{1}$ is used as the dependence parameter and Φ is the univariate standard normal distribution function (Embrechts et al., 2001). ρ₁₂=0 means total independence between the variables, whereas $\left|{\mathit{\rho }}_{\mathrm{12}}\right|=\mathrm{1}$ means total dependence. Whenever a joint probability structure has the form of a Gaussian copula, this structure can be applied without excessive computational cost (Li et al., 2014; Rueda et al., 2016) compared, for instance, to an Archimedean copula approach (Wahl et al., 2011; Lin-Ye et al., 2016; Okhrin et al., 2013).

3 Study area

The selected pilot site is the wave-driven and micro-tidal environment of the western Mediterranean Sea (Fig. 2), where enough validated met-ocean simulations exist and where the spatial wind/wave structure will not be distorted by tidal forcing. Current fields, slower to respond to the overlying meteorological driving, have not been considered in this initial analysis. The focus is on the Spanish north-eastern Mediterranean coast, where we have in situ and altimeter supporting data. Moreover, the continental shelf varies from 10 km to more than 100 km in an alongshore distance of less than 500 km. The wind fields are affected (most frequent wind direction is from land, approximately corresponding to the north-west) by the presence of a mountain chain roughly parallel to the coastline and featuring several openings corresponding to river valleys. The geometrical anisotropy analysis was performed at four transects, characteristic of their common topo-bathymetric features. They correspond to the following locations (from south-west to north-east): Ebro (40.7^∘ N, 0.87^∘ E), Tarragona (41.12^∘ N, 1.25^∘ E), Mataró (41.53^∘ N, 2.45^∘ E) and Begur (42.28^∘ N, 3.02^∘ E) (Fig. 2).

The north-western Mediterranean presents a particularly intense wind forcing, which is shaped by local orography (Jordi et al., 2011; Lebeaupin Brossier et al., 2012). The Pyrenees mountain chain across the strip of land connecting the Iberian Peninsula to the European continent forces a strong northern wind flux following the French–Spanish Mediterranean coast (Nicolle et al., 2009; Schaeffer et al., 2011; Obermann-Hellhund et al., 2017). This same wind pattern is channelled by the river valleys resulting in a north-western orientation for winds blowing from land to sea further down along the coast (Cerralbo et al., 2015) for latitudes southward of 41^∘ N. The most frequently observed patterns are thus from the north in the coastal sector closer to the Pyrenees barrier and from the north-west further south, conditioned by the river valleys and gaps in the coastal parallel mountains (Obermann et al., 2016; Lin-Ye et al., 2016). The second most frequent pattern corresponds to western winds, associated with atmospheric depressions in northern Europe (Barnston and Livezey, 1987; Trigo et al., 2002; Lin-Ye et al., 2017). Easterly winds are frequent during the summer, triggered by an intense high-pressure area over the British Isles.

The most common wave fields in the northwestern Mediterranean Sea correspond to the wind-sea spectral band driven by easterly, northerly and north-westerly winds (Lionello and Sanna, 2005; Bolaños et al., 2009). Because of the semi-enclosed character of the basin, the waves are fetch-limited, with maximum trajectory lengths around 600 km, one-sixth of the average distance that a wave train travels across the Atlantic (García et al., 1993). The average wave climate in the north-western Mediterranean Sea presents a mean significant wave height (H_s) of 0.78 m at the southern part of the Catalan coast, near the Ebro Delta and slightly lower values (around 0.72 m) further north and close to the French border. The spatial distribution of wave storms presents an opposite trend, with maximum H_s between 5.48 m in the southern sector and 5.85 m at the northern coastal stretch (Bolaños et al., 2009). Future projections (Casas-Prat and Sierra, 2013) indicate, for the interval 2071–2100 and the A1B scenario (IPCC, 2000), a variation in the significant wave height around ±10%, whereas the same variable for a 50-year return period exhibits rates of change around ±20 %. Additionally, the variability in large-scale indices (i.e. North Atlantic Oscillation, NAO; East Atlantic Oscillation, EA; or Scandinavian Oscillation) may drive significant changes in wave-storm components (Lin-Ye et al., 2017).

4 Methods

The approach suggested for assessing the geostatistical anisotropy of wind and wave fields is schematized in Fig. 3. It requires high-resolution met-ocean fields to determine how the covariance of the geostatistical anisotropies of wind and wave fields evolve with distance to the land–sea border. The starting point is wind and associated wave fields, as the suggested candidates for reflecting the heterogeneity induced by coastal topo-bathymetry. Although other definitions of the coastal boundary can be based on river plumes or biogeochemical processes, it has been intended to focus on a more hydro-dynamical expression of such a boundary for wave-driven coasts. It is intended to show that, as one approaches the coast, the wind and the wave fields should present a greater geostatistical anisotropy, i.e. they should display predominant wind and wave directions. Furthermore, there should be a geostatistical boundary to the value of this anisotropy that could help define a coastal boundary.

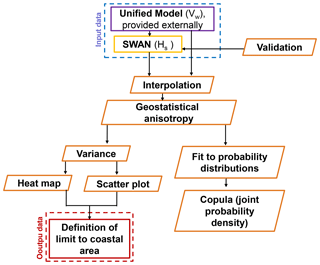
Figure 3 Flow chart summarizing the methodology used in this paper. The dashed blue rectangle represents the input data, and the dashed red rectangle indicates the output data. The wind velocity is obtained from an external source, and it was validated in Martin et al. (2006). The rest of the steps have been carried out for this analysis. Rectangles indicate data generation (input/output), and rhombuses indicate the subsequent analyses of the proposed methodology.

The wind fields have been provided by the UK Met Office from their Unified Model (Cullen, 1993) for weather and climate applications. This code solves the compressible, non-hydrostatic equations of motion with semi-Lagrangian advection and semi-implicit time stepping, including suitable parameterizations for sub-grid scale processes such as convection, boundary layer turbulence, radiation, cloud microphysics and orographic drag (Brown et al., 2012). There are two atmospheric prognostics: the dry one (three-dimensional wind components, potential temperature, Exner pressure and density) and the moist one (specific humidity and prognostic cloud fields (Walters et al., 2011). Both long- and short-wave radiation (from the Sun and the Earth itself) are included, and the effect of aerosols reflecting radiation is taken into consideration. These wind data have been validated in previous works, such as in Martin et al. (2006).

The computational domain of the wind field spans the whole Mediterranean Sea using a regular grid with spacing of 17 km and a time step of 1 h. The wave fields have been calculated with the SWAN code, covering the same geographical domain and with an equal time step of 1 h. SWAN is a spectral wave model based on the wave action balance equation (Booij et al., 1999; Zijlema, 2010) that includes non-linear interactions at various depths and dissipation processes (i.e. whitecapping, bottom friction, wave breaking). It applies a fully implicit numerical scheme for propagation in geographical and spectral spaces that is unconditionally stable.

SWAN employs an unstructured grid with spatial resolutions of 600 m–40 km, denser near the land–sea boundary. Mesh sizes are proportional to bathymetry gradients and distance to the coastline, following the same criteria than in Pallarés et al. (2017). Such a non-structured-grid approach avoids nesting and internal boundary conditions, while maintaining a good spatial resolution to capture bottom and coastline irregularity (submarine canyons and capes or pro-deltas that are found in the Catalan continental shelf). Furthermore, unstructured meshes are well suited to tackle non-linear effects (Qi et al., 2009; Roland et al., 2012; Roland and Ardhuin, 2014). The resulting wave fields have been validated with two directional wave buoys at the northern (Begur, deployed at 1200 m) and southern (Tarragona coastal buoy, deployed at 15 m) ends of the domain, managed by Puertos del Estado (Fig. 2). Altimeter data from three satellites (CryoSat, Jason-2 and Jason-3) are also used as a complementary observational source. The simulation period ranges from October 2016 to March 2017.

Once obtained the wave outputs, the empirical semi-variograms for the significant wave height and the wind velocity at 10 m are estimated. In order to have enough data, the spatial radius of influence is assumed to be 5 km, plus time blocks of 24 h. From these semi-variograms, the anisotropy for the wave height ($R_{H_{\mathrm{s}}}$) and the wind velocity ($R_{V_{\mathrm{w}}}$) is estimated along the four transects in Fig. 2.

Distance to the coast (x) and water depth (h) are selected as independent variables for analysing the anisotropy spatial patterns. $R_{V_{\mathrm{w}}}$ and $R_{H_{\mathrm{s}}}$ are taken to represent the behaviour of met-ocean conditions under the effect of the land–sea boundary (in this initial analysis height/depth gradients in topo-bathymetry). Hence, $R_{V_{\mathrm{w}}}$ and $R_{H_{\mathrm{s}}}$ have been interpolated (1 km spacing) along a 100 km transect perpendicular to the coast (see Fig. 2), considering periods of 24 h, long enough for the waves to respond to the acting wind forcing.

The geostatistical anisotropy needs to be computed on a regular grid and therefore both wind velocity (V_w) and significant wave height (H_s) have been interpolated on a rectangular mesh, first on a grid of 1 km then to a finer mesh of 10 m.

The interpolation method used in this case is the inverse distance weighted (IDW) interpolation, which estimates the value at an interpolated location (x) as the weighted average of neighbouring points with weights w(x) given by

$$\begin{array}{}\text{(3)}& {\displaystyle }{\displaystyle }w\left(x\right)={\displaystyle \frac{\mathrm{1}}{d{\left(x,x_i\right)}^p}}.\end{array}$$

Here, x_i is a neighbouring point, d is the Euclidean distance and p is the inverse distance weighting power. The IDW power chosen is 1 for $R_{V_{\mathrm{w}}}$ and 3 for $R_{H_{\mathrm{s}}}$ and h, based on a sensitivity analysis for this area and consistent with the physical relation between wind velocity and generated wave height.

Heat maps are used to represent the spatial distribution of the geostatistical anisotropy, showing how the density of R behaves as a function of distance to the coast and time (see Figs. 6 and 7). These maps are scatter plots that act as a 2-D histogram, in which two variables (in this case R and distance to the coast) are grouped in pre-defined intervals. The elements selected to aggregate samples for the heat map are hexagons with 5 km side and a scale for anisotropy of 20 units for both $R_{V_{\mathrm{w}}}$ and $R_{H_{\mathrm{s}}}$. Both R and its variance are calculated on a discrete number of distances to the coastline, assuming that the width of the fringe affected by boundary effects is below 100 km for this coastal sector (Sánchez-Arcilla and Simpson, 2002). From here, as is with significant wave height to determine the presence of wave storms (Eastoe et al., 2013; Bernardara et al., 2014), the proposed coastal zone limit is the cutting point where the variance in R is equal to the 90th percentile of the total R variance spanning a fringe between 0 and 100 km:

$$\begin{array}{}\text{(4)}& {\displaystyle }{\displaystyle }l=\mathrm{90}\mathrm{th}\mathrm{percentile}\mathrm{of}\mathrm{var}\left(R_{H_{\mathrm{s}}}\left(\mathrm{0}\mathrm{km}\le x\le \mathrm{100}\mathrm{km}\right)\right).\end{array}$$

This cutting point has shown, as expected, larger stability for the wave field than for the forcing wind patterns. The variation in $R_{H_{\mathrm{s}}}$ with coastal distance x (Fig. 7) indicates for reference the 20 km distance where satellite data offer enough robustness (Cavaleri and Sclavo, 2006; Janssen et al., 2007; Durrant et al., 2009). The plot also displays depth against x. The obtained $R_{V_{\mathrm{w}}}$ and $R_{H_{\mathrm{s}}}$ values were fitted to a probability distribution, empirically selecting the log-normal function for the inverse of $R_{V_{\mathrm{w}}}$ and the log-logistic function for $R_{H_{\mathrm{s}}}$. Once the marginal distributions are estimated, the dependence structure of the joint probability is adjusted to a Gaussian copula (see Sect. 2).

5 Results

The modelled wave heights (H_s) have been validated with buoys from the Puertos del Estado monitoring network and available altimeter data (Jason-2, CryoSat and Jason-3). Two locations have been selected, located at the southern (Tarragona) and northern (Begur) coastal sectors (Figs. 4 and 5). The H_s buoy data show good agreement with the simulated H_s, quantified in Table 1 and in Figs. 4 and 5.

In general, the wave model performs better for deep waters than for coastal waters. The standard deviation is higher in the model than in the observations. At Begur, the bias and the scatter index are lower, whereas the RMSE is higher (Table 1). At the same buoy, the correlation coefficient is near 95 % and the difference between standard deviations is lower (0.2 m vs. 0.4 m). Note that the northern part of the Catalan coast is more energetic than the southern one (see Fig. 5). For instance, in Begur the storm peaks can reach about 7 m, whereas at Tarragona the highest recordings are 3.5 m.

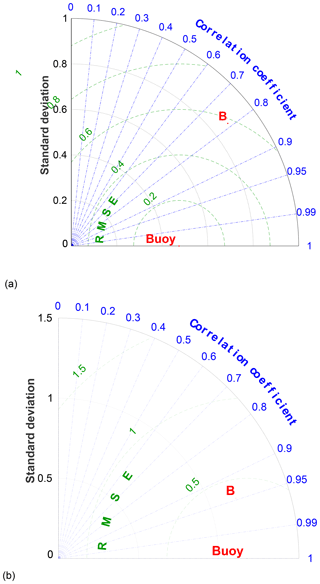
Figure 4 Taylor diagram for the significant wave height (H_s) showing correlation, standard deviation and root mean square error (RMSE) between numerical and observed data for (a) south sector (Tarragona location) and (b) north sector (Begur location). The time period ranges from November 2016 to March 2017.

The collocated altimeter data have a positive bias in the coastal zone, and the opposite (i.e. negative bias) in deep waters. Nevertheless, there exists qualitative consistency between the in situ and remote-sensing sources. Additionally, SWAN has been able to capture the regime switching and the proper timing of the storms, despite that it tends to underestimate the magnitude of the storm peaks.

$R_{V_{\mathrm{w}}}$ and $R_{H_{\mathrm{s}}}$ have been analysed with heat maps (Figs. 6 and 7) and scatter plots (Figs. 8 and 9). $R_{V_{\mathrm{w}}}$ presents values that span from 1 to 250 and display a dependence on coastal distance (Fig. 6), featuring a combination of anisotropy close to the land boundary (0 to 20 km) and then a more isotropic behaviour towards the offshore region (up to 100 km), although with a rich variability. The wind fields present, in summary, a decreasing variance from 0 to 100 km with a pronounced slope from 0 to about 40 km (southern sector) or even further offshore (northern sector) and then an almost asymptotical trend. $R_{H_{\mathrm{s}}}$ behaves similarly to $R_{V_{\mathrm{w}}}$, but with a turning point at about 40 km in all transects (Figs. 8 and 9) and, thus, a higher level of consistency. From December to January, there are some winds and waves registered within 20 km of the coast that present higher $R_{V_{\mathrm{w}}}$ and $R_{H_{\mathrm{s}}}$; however, they are so few that the variances in $R_{V_{\mathrm{w}}}$ and $R_{H_{\mathrm{s}}}$ in this area do not differ from warmer seasons. Therefore, there is not a clear seasonality to the $R_{V_{\mathrm{w}}}$ or the $R_{H_{\mathrm{s}}}$. The coastal zone limit l, corresponding to the 90th percentile of the total variance (fringe between 0 and 100 km), is calculated from Eq. (4) (Figs. 8 and 9) and is 3 km. It is consistent with the time interval (month of study) and location (sector).

Table 1 Statistics of the agreement between numerical significant wave height fields (SWAN model) and observations in terms of root mean square error (RMSE), bias and scatter index (SI) for the control points at the southern and northern coastal sectors.

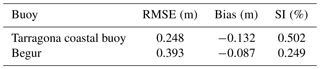
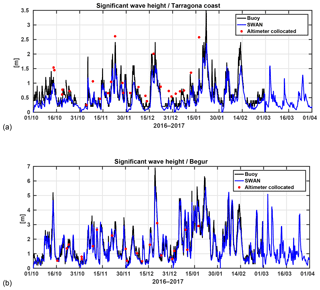
Figure 5 Comparison of numerically simulated significant wave height (SWAN model) with observations for (a) south sector (Tarragona location) and (b) north sector (Begur location) for the period October 2016 to March 2017. The red dots are altimeter data (Jason-2, Jason-3 and CryoSat).

In order to find a copula structure, marginal probability distributions for the two anisotropies are needed. Skewness and kurtosis from the analysed data show that the inverse anisotropy of V_w follows a log-normal distribution, while the anisotropy of H_s follows a log-logistic distribution. Quantile–quantile plots were used to assess the fit of each probability function (not shown here) to its target dataset, verifying that the selected samples can be adjusted to the corresponding probability distributions. The joint probability structure of the two anisotropies does not present any marked dependence for the upper-tail percentiles, suggesting the use of a Gaussian copula, whose dependence parameter ρ is shown in Fig. 10. The so obtained dependence ranges from total independence (0) to a mild ($\left|{\mathit{\rho }}_{\mathrm{12}}\right|=\mathrm{0.1}$) dependence between $R_{V_{\mathrm{w}}}$ and $R_{H_{\mathrm{s}}}$.

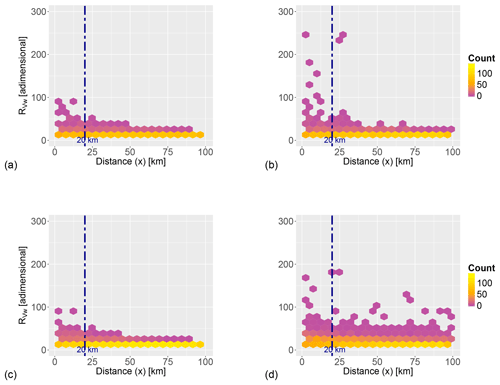
Figure 6 Heat map of the geostatistical anisotropy ratio of the wind velocity ($R_{V_{\mathrm{w}}}$) against distance to the coast for (a) south control transect (near the Ebro Delta), (b) central-south transect (near Tarragona harbour), (c) central-north transect (near Mataró harbour) and (d) north control transect (near Begur cape). The elements selected to aggregate samples for the heat map are hexagons with 5 km side and a scale for anisotropy of 20 units. The counts are the number of elements within a hexagon. A rough limit of the order of magnitude for the direct applicability of remote-sensing data (20 km) is also shown (dashed blue line). All plots correspond to February 2017.

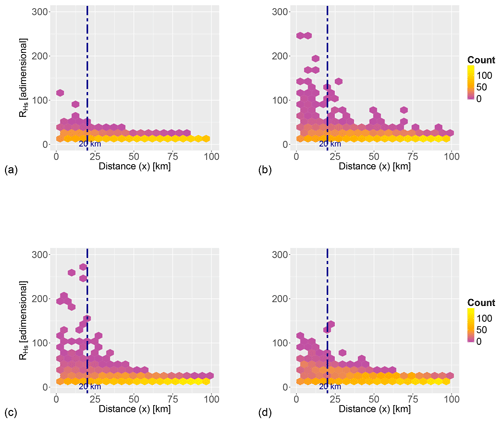
Figure 7 Heat map of the geostatistical anisotropy ratio of significant wave height ($R_{H_{\mathrm{s}}}$) against distance to the coast for (a) south control transect (near the Ebro Delta), (b) central-south transect (near Tarragona harbour), (c) central-north transect (near Mataró harbour) and (d) north control transect (near Begur cape). The elements selected to aggregate samples for the heat map are hexagons with 5 km side and a scale for anisotropy of 20 units. The counts are the number of elements within a hexagon. A rough limit of the order of magnitude for the direct applicability of remote-sensing data (20 km) is also shown (dashed blue line). All plots correspond to February 2017.

6 Discussion

The calculated anisotropies should be as robust as the starting wave or wind fields that are employed in the analysis. Because of that, the SWAN code has been calibrated with local atmospheric and hydrodynamic conditions (Pallarés et al., 2017). Special emphasis has been put on using high-quality wind fields, both for the direct assessment linked to meteorological fields and for the indirect effect they exert on the behaviour of the forced hydrodynamics. The results show, as expected, a higher level of robustness for the wave-based geostatistical anisotropy, where the calculations used an unstructured grid and a locally adjusted whitecapping term calibration (Pallarés et al., 2014). The cell size has been determined as a function of depth and distance to the coast, consistently with the transect analyses performed in the paper. The application of an unstructured grid allows for reducing computational costs (by about 50 %) and the troublesome imposition of internal boundaries.

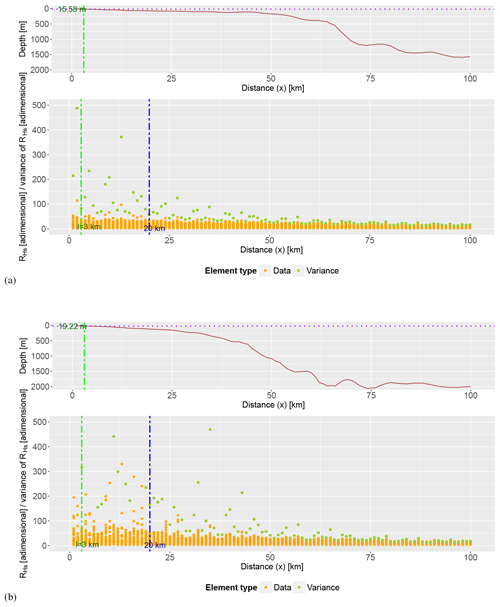
Figure 8 Relation for winter conditions (February 2017) between distance to the coast x, depth and anisotropy ratio of significant wave height ($R_{H_{\mathrm{s}}}$) from shore to 100 km offshore. Locations are (a) south control transect (near the Ebro Delta) and (b) central-north transect (near Mataró harbour). The distance of 20 km, which has been suggested as an approximate order of magnitude limit for direct applicability of remote-sensing data, is also shown (dashed blue line) together with the variance in $R_{H_{\mathrm{s}}}$ across the transect. From here, the coastal zone anisotropy-based boundary has been calculated and is also depicted. A dash-dotted green line delimits its horizontal distance from the coast, whereas a dotted purple line denotes its elevation.

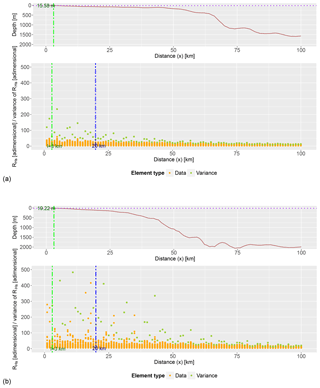
Figure 9 Relation for autumn conditions (November 2016) between distance to the coast x, depth (a) and geostatistical anisotropy ratio of significant wave height ($R_{H_{\mathrm{s}}}$) from shore to 100 km offshore. Locations are (a) south control transect (near the Ebro Delta) and (b) central-north transect (near Mataró harbour). The distance of 20 km, which has been suggested as a rough order of magnitude limit for direct applicability of remote-sensing data, is also shown (dashed blue line) together with the variance in $R_{H_{\mathrm{s}}}$ across the transect. From here, the coastal zone anisotropy-based boundary has been calculated and is also depicted. A dash-dotted green line delimits its horizontal distance from the coast, whereas a dotted purple line denotes its elevation.

This leads to an efficient determination of the coastal water boundary that contains some of its common geometric settings (e.g. bathymetric gradients affecting wave fields). Other processes, such as the continental discharge are of course not captured by the present analysis and would require a similar approach based on the resulting circulation fields, which would certainly capture the regions of fresh-water influence and wave–current interactions (Staneva et al., 2016). However, the performance of the wave model has shown commonalities with previous studies. For instance, the good performance of spectral models at the Begur buoy can be found in multi-model comparisons (see Bertotti et al., 2012), and also the consistent underestimation under storm peaks (Cavaleri, 2009).

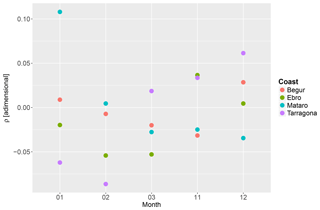
Figure 10 Copula parameters ρ of the proposed Gaussian copulas for all considered profiles: (a) south control transect (near the Ebro Delta), (b) central-south transect (near Tarragona harbour), (c) central-north transect (near Mataró harbour) and (d) north control transect (near Begur cape). The plot shows the variation with time (horizontal axis) between November 2016 and March 2017. The parameters are placed in a manner such that they start from January.

The anisotropy-based approach will lead to different results depending on met-ocean conditions (wave conditions in our case), requiring a reliable simulation of both average and extreme patterns, as shown by the validation process (e.g. see Figs. 4 and 5). The transfer of energy from the coastal to the offshore domain and vice versa may condition the results of the analysis for areas near the transition, which is where the boundary will be likely located. This suggests a combined approach using numerical fields and satellite data supplemented by along-track in situ observations, all suitably interpolated in space and time to provide a picture that is as consistent as possible.

The values of V_w, H_s and h obtained through the IDW interpolation, using an IDW weighting from 1 to 3, are similar and reasonable. For marine variables the weight of 3 has been selected to account for the influence of the closest neighbours based on the water inertia (which is 3 orders of magnitude larger than for air). The proposed IDW power for V_w is smaller because gas is more turbulent than water and thus should have a smaller spatial dependence. The obtained pattern for $R_{V_{\mathrm{w}}}$ is consistent for the four selected transects in the study area, showing a mostly isotropic behaviour for coastal distances from 0 to 100 km. Higher values of $R_{V_{\mathrm{w}}}$ at distances from the coast below 20 km (see Fig. 6) indicate a clear directional spread of winds within the coastal fringe, linked to orographic control such as channelling by local mountains and river valleys.

Despite the fact that the results are based on November 2016 and February 2017, the spatial trends of the anisotropy were coherent throughout the simulation period, thus exhibiting the robustness of the methodology.

The numerical wind fields present errors below 2 m s⁻¹ (Martin et al., 2006), which means that the V_w calculated can well represent actual wind conditions. The $R_{V_{\mathrm{w}}}$ is lower in the Ebro Delta (Fig. 6a) than at Tarragona (Fig. 6b) due to the fact that the orography at the Ebro Delta is flat, and wind blows from a wide range of directions; whereas Tarragona features mountain chains that channel the winds into a more limited directional subset. The anisotropy pattern at Begur (Fig. 6d) may be explained by the strong mistral and eastern winds (Obermann et al., 2016; Obermann-Hellhund et al., 2017) that both affect nearshore and deep waters.

Hence, the behaviour of $R_{V_{\mathrm{w}}}$ near the coast can show sharp local variations due to the joint effect of orography, mesoscale circulation and large-scale circulation, all affecting wind strength and directionality. However, the seasonality does not affect $R_{V_{\mathrm{w}}}$ as much. In all cases, V_w becomes more isotropic towards the offshore, denoting a decreasing control by the land–water boundary.

The $R_{H_{\mathrm{s}}}$ pattern is similar, with wave fields showing boundary effects (mainly in directional properties) for coastal distances below 50 km, which has also been considered an order of magnitude estimate for land wind effects. Farther from the coast there is a clear trend to isotropy, more pronounced for transects with more stable atmospheric conditions. The link between $R_{H_{\mathrm{s}}}$ and land-originated winds can be appreciated by the shift from a homogeneous to anisotropic behaviour in the northern- most transect (Begur) where the effect of V_w on H_s is only evident up to 38 km from the coast. Note that the Ebro Delta shows a more isotropic value at the coastal zone. This area presents a wider continental shelf than the other profiles, where wave dissipation and refraction tend to be more homogeneous. Henceforth, more anisotropic winds plus a steeper profile may be considered as the main reasons for the discrepancies among the beach profiles.

Such behaviour of $R_{H_{\mathrm{s}}}$ with coastal distance parallels that of particulate matter diffusivity, which tends to become isotropic at around 10 km (Romero et al., 2013) from the land–water boundary. The degree of geostatistical anisotropy in diffusivity is physically related to eddy kinetic energy, which varies as x^5∕4 (x being separation distance) for depths below 20 m (Gràcia et al., 1999). A steep bottom slope will favour deep-water wave behaviour at relatively short distances from the coast, as shown by the distinctive behaviour of $R_{H_{\mathrm{s}}}$ for coasts of different slope. However, although $R_{H_{\mathrm{s}}}$ presents greater variance (more outliers) for steep slopes (e.g. due to the combination of deep- and shallow-water wave regimes as in the central-north transect near Mataró harbour), the gradient of $R_{H_{\mathrm{s}}}$ with distance to the coast is similar for all types of bathymetry considered, suggesting a generic value of the proposed approach. This is also true for any time of the year.

The coastal boundaries suggested by Sánchez-Arcilla and Simpson (2002) for the Catalan Coast can be 0.1–0.6 km (frictional coupling of fluids between shelf and nearshore), 10 km (non-linear coupling between shelf and slope) and 1 km (non-linear coupling between shelf and nearshore), among other suggested values of the same order of magnitude. The l provided in our analysis is slightly larger than the value given for the frictional coupling of fluids between shelf and nearshore, whereas it is similar or smaller than in the non-linear couplings. Nevertheless, the orders of magnitude are similar.

The ρ parameter of the Gaussian copula, characterizing the dependence structure among $R_{V_{\mathrm{w}}}$ and $R_{H_{\mathrm{s}}}$, reflects a certain similarity to the spatial behaviour for both variables (see Figs. 6 and 7). The overall mutual dependence of $R_{V_{\mathrm{w}}}$ and $R_{H_{\mathrm{s}}}$ is strongest for the northern-most transect (Begur), where the topo-bathymetric control of the Pyrenees and their submerged signature becomes better defined. Such mutual dependence gets weaker for the central and southern coastal transects (see Fig. 10). There seems to be a strong wind channelling aligned with the main river valleys (Sánchez-Arcilla et al., 2014; Rafols et al., 2017) in February and March, dominating the local wave fields. The ρ parameter should reflect this spatial and temporal variation, resulting in a coastal zone width that will be a function of the prevailing met-ocean drivers and should thus be considered a dynamic concept.

The resulting coastal definition can be data (numerical or observed) driven, being directly applicable to any region with a forecasting system or with enough coverage of in situ plus satellite data. The proposed criteria appear to work well for wave-dominated and micro-tidal environments; and although suitable for any combination of factors, their application to macro-tidal regimes or river-discharge-dominated areas should account for the corresponding signature in the hydrodynamic fields. Under these conditions, the preferred variable could change to current velocity or to temperature, considering in all cases the effect of spatial resolution in the results.

7 Conclusions

The proposed coastal fringe (water sub-domain) definition is based on an objective estimation of the geostatistical anisotropy as a proxy for the influence of the land border. The suggested statistical assessment can be applied to any variable that reflects such an influence (here it has been illustrated with wind velocity and significant wave height) and can be easily automated for any field, numerical or observational, that presents enough resolution.

The methodology has been tested with numerically generated fields and validated with datasets from Puertos del Estado buoys and altimeter. Anisotropies of wind velocity and significant wave height have been extracted along a set of characteristic profiles spanning widths of up to 100 km (see Fig. 2), considered sufficient for the relatively narrow shelves in the Spanish Mediterranean coast. The performed analysis has shown how wind and wave fields are influenced by the land–sea border, demonstrating the topo-bathymetric control on met-ocean factors. This control depends on topographic (mountain chains and river valleys) and bathymetric (bottom slope, submarine canyons or pro-deltas) features but also on the energetic level of the prevailing weather, leading to a dynamic definition of the coastal water domain. The resulting widths, based on variance variation, span distances in the kilometre range, depending on bottom slope and coastal plan-shape geometry. The correlation between the wind- and wave-based definitions (i.e. the mutual dependence among $R_{V_{\mathrm{w}}}$ and $R_{H_{\mathrm{s}}}$) seems to be stronger in the northern-most parts of the study area, where the topo-bathymetric control is most prominent.

This new definition of the coastal zone can be useful for setting up standards to delimit this transitional fringe, facilitating the selection of processes and boundary conditions for modelling and providing an objective coastal zone limit for impact assessments. Such an approach can also support directional and asymmetric measures of error and the underlying metrics (between model and data), leading to improved products and standards in the coastal zone.