Assimilating high-resolution sea surface temperature data improves the ocean forecast potential in the Baltic Sea

We assess the impact of assimilating the satellite sea surface temperature (SST) data on the Baltic forecast, particularly on the forecast of ocean variables related to SST. For this purpose, a multivariable data assimilation (DA) system has been developed based on a Nordic version of the Nucleus for European Modelling of the Ocean (NEMO-Nordic). We use Kalman-type filtering to assimilate the observations in the coastal regions. Further, a low-rank approximation of the stationary background error covariance metrics is used at the analysis steps. High-resolution SST from the Ocean and Sea Ice Satellite Application Facility (OSISAF) is assimilated to verify the performance of the DA system. The assimilation run shows very stable improvements of the model simulation as compared with both independent and dependent observations. The SST prediction of NEMO-Nordic is significantly enhanced by the DA forecast. Temperatures are also closer to observations in the DA forecast than the model results in the water above 100 m in the Baltic Sea. In the deeper layers, salinity is also slightly improved. In addition, we find that sea level anomaly (SLA) is improved with the SST assimilation. Comparisons with independent tide gauge data show that the overall root mean square error (RMSE) is reduced by 1.8 % and the overall correlation coefficient is slightly increased. Moreover, the sea-ice concentration forecast is improved considerably in the Baltic Proper, the Gulf of Finland and the Bothnian Sea during the sea-ice formation period, respectively.

1 Introduction

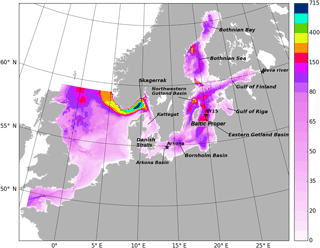
Monitoring the marine status of the Baltic Sea with relevant resolution and accuracy is a key requirement to serve the marine policy for detecting the influence of human activities on the environment and better understanding the response of ocean to accelerating global climate change. The Baltic Sea is one of the largest brackish seas in the world. It is a semi-enclosed basin, whose hydrography is highly variable and influenced by large-scale atmospheric processes and significant influx of freshwater from river runoff and precipitation (Leppäranta and Myrberg, 2009). In addition, the water exchange between the North Sea and Baltic Sea through the Danish Straits is hindered by shallow topographic restrictions in the transition zone (Fig. 1).

A characteristic feature of numerical forecast in the Baltic Sea is in itself a major challenge because of complex topography and rich dynamics. A number of ocean forecasting systems for the Baltic Sea have been developed using hydrological models by operational agencies around this region. Traditionally, these models have a horizontal resolution of 1–5 km and approximately 20–100 layers in vertical structure (Omstedt et al., 2014). Due to the geographic location and conditions of the Baltic Sea, even higher resolutions are often needed to better understand the circulation dynamics. However, even ocean circulation models with a particularly high spatial resolution (e.g., 1 km) cannot resolve all dynamically important physical processes in the ocean (Malanotte-Rizzoli and Tziperman, 1996). In general, the forecast quality for a numerical model depends on initial conditions, boundary conditions (lateral, open boundaries as well as meteorological forcing and bathymetry) and a robust numerical model itself. As an operational forecasting agency, the Swedish Meteorological and Hydrological Institute's (SMHI) needs to issue well-informed forecasts and warnings for decision making by other authorities during, e.g., severe weather events, but also to the public. To improve the forecast quality, the core three-dimensional dynamic model of the SMHI operational forecast system has recently migrated to the Nordic version of the Nucleus for European Modelling of the Ocean (NEMO-Nordic).

Figure 1 Geographical domain and bathymetry (in meters) of the NEMO-Nordic configuration.

In additional to model development, an extended observational network has been established by the joint efforts of the countries surrounding the Baltic Sea. The observation platforms include vessels, buoys, coastal stations, satellites, etc. Specially, the observations from satellites have dominated the coverage of sea surface temperature (SST) observational networks in the Baltic Sea (She et al., 2007). Among satellite products, the SST is most popularly and widely used for the operational forecast, reanalysis or validation of the model because of both its coverage and properties. SST acts as a medium between atmospheric and oceanic variations through activation of coupling mechanisms. SST is also a key ocean variable to link many processes that occur in the upper ocean, for example, air–sea exchange of energy, primary productivity and formation of water masses.

A realistic forecast of SST is essential to an ocean forecasting system. SST is especially important for the Baltic Sea because the average water depth is only 56 m and its surface water is directly related to the bottom water by the mixing in the shallow sub-basins. Recently, the applications of SST for forecasting and analyzing the status of the North Sea and Baltic Sea have received particular attention. In the short-term forecast, Losa et al. (2012, 2014) investigated the systematic model uncertainties for forecasting in the North Sea and Baltic Sea by assimilating the Advanced Very High Resolution Radiometer (AVHRR) SST data. Nowicki et al. (2015) applied SST observed from the Moderate Resolution Imaging Spectroradiometer (MODIS) aboard the Aqua satellite into 3-D coupled ecosystem model of the Baltic Sea with the Cressman analysis scheme. O'Dea et al. (2012) enhanced the SST prediction skill of the operational system by assimilating both in situ data and level 2 SST data provided by the Global Ocean Data Assimilation Experiment High-Resolution SST (GHRSST) into a European northwest shelf operational model. Moreover, SST has been used in the long-term analysis in this region. For instance, Stramska and Bialogrodzka (2015) analyzed spatial and temporal variability of SST in the Baltic Sea based on 32 years of satellite data, which indicate that there is a statistically significant trend of increasing SST in the entire Baltic Sea. However, these long-term SST data have not been used to verify the application of sophisticated data assimilation (DA) methods for hydrography model in the Baltic profiles' simulation, especially at the Baltic deep water regions. Another important question is what amount of satellite SST can improve long-term forecast of ocean variables related to SST in the Baltic Sea.

The objective of this study is to address the impact of assimilating a high-resolution SST product on the forecast of the Baltic Sea, particularly the forecast of SST-related variables like sea level and sea ice. It is also the first time that satellite SST from the Ocean and Sea Ice Satellite Application Facility (OSISAF) was assimilated into NEMO-Nordic model (NEMO variant for the North Sea and Baltic Sea). For operational forecast, the SST from OSISAF is the most important dataset in the Baltic Sea because it differs from hindcast-analyzed products like OSTIA (Operational SST and Sea Ice Analysis) data. As a level 2 product, the OSISAF SST has both good temporal and spatial coverage in the Baltic Sea. As there is no hindcast information included in the OSISAF SST, we are able to assess direct impacts of assimilating SST observations. Therefore, exploring the potential of this product is critically important to further improving the new operational forecast system. In addition, our study will enrich the reanalysis database of the Baltic Sea. In this study, we use the local singular evolutive interpolated Kalman (LSEIK) filter (Pham, 2001) to account for the model uncertainties arising from a wide range of spatial and temporal scales (Haines, 2010). One of our focuses is the impact of assimilating SST on the modeled sea level and the sea ice in the Baltic Sea. For the whole Baltic Sea, how the SST assimilation influences the temperature and salinity (T/S) at different depths is another focus of this study.

The outline of the paper is as follows: the model configuration and LSEIK scheme are described in Sect. 2. An overview of the observations used in this study is presented in Sect. 3. The implementation of the DA experiment is given in Sect. 4 together with the sampling of ensemble and localization. Results are compared with observations for temperature, salinity, sea level anomaly and sea ice in Sect. 5. In this section, the impact of data assimilation on the forecasts is also investigated. Conclusions and discussions are given in Sect. 6.

2 Methodology

2.1 NEMO-Nordic

NEMO-Nordic has been set up at SMHI for the North Sea and the Baltic Sea (Hordoir et al., 2015) (Fig. 1). Open boundaries are implemented in the northern North Sea between Scotland and Norway, and in the English Channel between Brittany and Cornwall, respectively (Hordoir et al., 2013). In this study, NEMO-Nordic employs a horizontal resolution of 2 nautical miles (3.7 km) and 56 vertical levels, and with a vertical resolution of 3 m close to the surface, decreasing to 22 m at the bottom of the deepest part of the Norwegian trench. NEMO-Nordic uses a fully nonlinear, explicit free surface (Adcroft and Campin, 2004). A bulk formulation is used for the surface boundary condition (Large and Yeager, 2004). The ocean model is coupled to the Louvain-la-Neuve (LIM3) sea-ice model (Vancoppenolle et al., 2008) with a constant value of 10⁻³ psu for the sea-ice salinity. A time-splitting approach is used to compute a barotropic and a baroclinic mode, as well as the interaction between them. A tidal inversion model is used to define the barotropic mode at the open boundary conditions (Egbert and Erofeeva, 2002). A total of 11 tidal harmonics are defined for sea level and barotropic tidal velocities. In addition, a coarse-resolution barotropic storm surge model covering a large area of the northern Atlantic Basin provides wind-driven sea level that is added to the tidal contribution. The T/S data at the open boundary are provided by the Levitus climatology (Levitus and Boyer, 1994). Radiation conditions are applied to calculate baroclinic velocities at these boundaries. A quadratic friction is applied with a constant bottom roughness of 3 cm, and the drag coefficient is computed for each bottom grid cell. NEMO-Nordic uses a total variation diminishing (TVD) advection scheme with a modified leapfrog approach that ensures a very high degree of tracer conservation (Leclair and Madec, 2009). Unresolved vertical turbulence is parameterized with κ−ε scheme (Umlauf and Burchard, 2003). In addition, Galperin parameterization is used to obtain a stable long-term stratification for the Baltic Sea (Galperin et al., 1988).

A Laplacian isopycnal diffusion is used for both momentum and tracers with a diffusion parameter that is constant in time but varies in space. Additional strong isopycnal diffusion is used close to the Neva River inflow (Gulf of St. Petersburg) in order to avoid negative salinities. The bottom boundary layer is parameterized to ease the propagation of saltwater inflows between the Danish Straits and the deepest layers of the Baltic Sea (Beckmann and Döscher, 1997). A free-slip option is used for lateral boundaries.

The model is forced by meteorological forcing derived from a downscaled run of Euro4M reanalysis (Dahlgren et al., 2014). The downscaling is based on the regional atmospheric model RCA4 (Samuelsson et al., 2011) which uses the reanalysis data as boundary conditions. A runoff database provides the river flow to NEMO-Nordic (Donnelly et al., 2016); it includes interannual variability for the Baltic Sea basin and is based on climatological values for the North Sea basin. The salinity of the river runoff is set to a constant value of 10⁻³ psu, which is the same value used for the sea ice to avoid any negative salinity.

2.2 Local singular evolutive interpolated Kalman (LSEIK) filter

The method used to assimilate SST into NEMO-Nordic is the local singular evolutive interpolated Kalman (LSEIK) filter (Pham, 2001; Nerger et al., 2006). This is a sequential data assimilation scheme, which is an error subspace extended Kalman filter that uses a minimum number of ensemble members to reduce the prohibitive computation burden (Pham, 2001). The LSEIK filter produces the correction for the model state by weighting the difference between the observations and the model state estimation. The weight coefficients are constructed by the model error covariance matrix and observation error covariance matrix. Similar to other ensemble-based data assimilation methods, the LSEIK filter uses the spread of the sample ensemble to estimate the uncertainties of the model state. Further, a forgetting factor ρ is introduced to parameterize the imperfect model by amplifying the already existing modes of the background error (Pham et al., 1998; Pham, 2001). Furthermore, the LSEIK filter is based on an explicit low-rank approximation of the model error covariance matrix. A second-order exact sampling method is used to initialize the LSEIK filter (Pham, 2001). Localization was also used to remove the unrealistic long-range correlation with a quasi-Gaussian function and a uniform horizontal correlation scale (Liu et al., 2013). It was performed by neglecting observations that were beyond correlation distance from an analyzed grid point. In other words, only data located in the “neighborhood” of an analyzed grid point should contribute to the analysis at this point (Liu et al., 2009; Janjić et al., 2011).

3 Observations

3.1 Satellite observations

The satellite SST used in DA was provided by OSISAF (http://www.osi-saf.org/?q=content/high-latitude-sea-and-ice-surface-temperature, last access: 10 June 2018). OSISAF's aim is to produce, control and distribute operationally near-real-time products using available satellite data. The satellite dataset products used here include the observations from polar-orbiting satellites (the EUMETSAT MetOp-A and NOAA-18, -19) with the AVHRR instrument. The SST product has a resolution of 5 km and is produced twice daily at 00:00 and 12:00 UTC. It covers the Atlantic Ocean from 50 to 90^∘ N. The SST observations are thermal infrared observations from the AVHRR instrument and are therefore limited by cloud cover (Kilpatrick et al., 2001). The cloud mask in use is based on a multispectral thresholding algorithm by SMHI. The products were retrieved using a nonlinear split window algorithm (Walton et al., 1998). The coefficients in the retrieval algorithm are determined through regression toward in situ observations, and the dataset thus represents the sub-skin temperature of the oceans. Further, sub-skin observations are subject to diurnal warming effects, which can be significant in the Baltic Sea. Here, only the sub-skin SST at night (00:00 UTC), which is comparable to in situ (buoy) measurement, is used to minimize this effect. The SST is controlled with the climatology check. A quality level from 0 to 5 is associated with every pixel. The higher the level value, the better the quality of the observations (Brisson et al., 2002). Observations with quality level 4 (good) or 5 (excellent) are collected for the analysis, and low-quality observations were removed. By applying the above quality control processes, only a subset of the original OSISAF products is kept in this study. Based on the former validation, a bias value of 0.5 ^∘C is given for this product.

Further, the IceMap from a sea-ice concentration dataset with a high spatial resolution of 5 km (https://www.smhi.se/klimatdata/oceanografi/havsis, 8 February 2018) is used to validate the DA results. It is produced by SMHI and originates from digitized ice charts. An advantage of these data is that the ice charts are quality checked manually. However, the drawback is that they include some subjective steps. The temporal resolution of the IceMap SST is twice a week in the experimental period. Sea ice occurs most frequently in the Bay of Bothnia, with up to 100 ice-covered days per year. However, sea ice can occur in all parts of the Baltic Sea and Danish Straits, demonstrating the need for careful treatment of sea ice in the SST analysis.

3.2 In situ data

The observations from the German Maritime and Hydrographic Agency (BSH) moored buoy stations were collected as an independent dataset to validate the assimilation results. The observations have high temporal resolution and a long continuous record. The second dataset was downloaded from the Swedish Oceanographic Data Centre SHARK database (http://sharkweb.smhi.se, 8 February 2018). SHARK mainly contains low-resolution conductivity–temperature–depth (CTD) data from a list of predefined standard stations in the Baltic Sea, as well as in Kattegat and Skagerrak. Only observations that have passed gross quality control procedures are collected into the SHARK database. This procedure includes, for example, location checks and local stability checks. In addition, validated data records from tide gauges are also used. The sea level anomaly measurements from tide gauges (sea level stations) are measured in a local height system, and values are presented relative to theoretical mean sea level, a level calculated from many years of annual means, which takes into account the effect of land uplift and sea level rise. The values are averaged over a 1 h period.

Not all the available observations from satellites, moored buoys, CTDs and tide gauges were included in this study. To obtain the high assimilation quality results, another quality control was applied for these data before they were used in assimilation and validation. These controls include examination of forecast observation differences by excluding those observations for which the difference between the forecast and the measurement exceeded given standard maximum deviations. The criteria were set up empirically based on past validation results of the model (Liu et al., 2013). Furthermore, stations located on land, according to the NEMO-Nordic grid, were excluded. We also removed the duplicate records of these data.

The accuracy of observation error is difficult to be defined for all water points. The observation is commonly assumed to be spatially irrelevant, which results in an error covariance matrix that is time-invariant diagonal and its diagonal elements equal the variance of observation error. The error for an observation used in data assimilation mainly includes the representation error and the measurement error. The measurement error arises primarily from the measurement device alone, the temporary reading error and imperfect retrieval algorithm. According to Janjić et al. (2017), the representation error in data assimilation comprises the error due to unsolved scales or processes, the preprocessing error and the observation-operator error. In this study, the observation error was estimated to one value as the sum of all observation uncertainties used in the analysis. In addition, the uncertainties of satellite SST vary from the coast to the open sea, i.e., higher uncertainties in the coastal region relative to the open sea. We used a constant standard deviation value of 0.4 ^∘C based on the standard deviation of satellite SST, which ranged from the ∼ 0.1 to ∼ 0.5 ^∘C in the Baltic Sea (She et al., 2007; Høyer et al., 2016).

4 Configuration of LSEIK in the experiment

As above mentioned, the initialization of the filter requires an initial analyzed state and a low-rank approximation of the corresponding estimation of error covariance matrix. The data assimilation process was initialized by a free model simulation. First, the model was spinning up 20 years to reach a statistically steady state. Then, a further (free-run) integration that covered the period 2006–2009 was carried out to generate a historical sequence of model state. To reduce the calculation cost, we took a snapshot every 6 days and saved 183 state vectors, which includes sea level, temperature and salinity, in total to describe the model variability because successive states are quite similar. The initial ensemble provided an estimate of the initial model state and its uncertainty before the assimilation of SST observations. The quantity of the model variability was expected to be reasonably comparable with the forecast error, which was dominated by misplacement of mesoscale features and varied in location and intensity seasonally. Further, the very high frequencies of model variability were also unfavorable in an ensemble of state vectors for SST data assimilation (Oke et al., 2005). Therefore, a band-pass filter was used to remove the unwanted frequency of model variability. To initial the low-rank error covariance matrix, a multivariable empirical orthogonal function (EOF) analysis was applied on the 183 state vectors of model variables (sea level, temperature and salinity). In the North Sea and Baltic Sea, error covariances of different variables are not uniform and strongly dependent on whether the variable resides in the open sea or coastal zone. Each state variable was then normalized by the inverse of its spatially averaged variance at every model level. At last, 34 leading EOF modes were kept and they explained 85 % overall variability. Then, the initial error covariance matrix was estimated by ${\mathbf{P}}^a\left(t_{\mathrm{0}}\right)\approx {\mathbf{L}}_{\mathrm{0}}{\mathbf{U}}_{\mathrm{0}}{\mathbf{L}}_{\mathrm{0}}^T$, where the L₀ is composited by the leading EOF modes and U₀ is diagonal matrix with the corresponding eigenvalues on its diagonal. We used a time-invariant sample ensemble to approximate the background error covariance during the experimental period (Korres et al., 2012; Liu et al., 2017). This stationary ensemble affords a good approximation of the ocean's background error covariance. Meanwhile, it is computationally efficient for our objective.

The localization scale is another import factor to the assimilation system, especially at the coastal region. Large correlation scale may transfer artificial increments to the positions far away from the analysis observation during the DA process. However, the small correlation scale is prone to cause the singularity of ocean state around analyzed observation and break the continuity of the ocean state. Hence, an unreasonable scale causes the instability of the model integration or degrades the assimilation quality. Unfortunately, the accuracy length for the correlation is unknown for the North Sea and Baltic Sea. The correlation length scale is to some extent dependent on the Rossby radius of deformation (Losa et al., 2012), which varies from ∼ 200 km in the barotropic mode to ∼ 10 km or even less in the baroclinic mode (Fennel et al., 1991; Alenius et al., 2003). According to the former research like Liu et al. (2013, 2017), a length scale of 70 km was specified for both the North Sea and Baltic Sea in this study. Note that this value may be not perfect and more accurate correlation length needs to be tested for LSEIK. For example, spatially variable length scales are the next step for the regional DA simulations.

To define the forgetting factor, a 1-month simulation experiment with varying the factor ρ was done in January 2010. At last, a factor ρ=0.3 resulted in the best assimilation performance. Further, we define a 2-day assimilation window in assimilation experiment. As a result, the observations in the 2 days before the assimilation time were used to calculate the innovation with observation operator. When we calculated the innovation, we also changed the observation error according to the observation time by $\mathit{\epsilon }=\mathrm{0.4}\times \exp (-\mathrm{0.15}\mathrm{\Delta }t)$; here, Δt is the absolute time difference between observation time and DA time.

5 Results

In the following subsections, we conducted two runs with and without assimilation of the SST observations from the OSISAF database, both runs with the above setup of the analysis system. Accordingly, the runs with and without assimilation are called ASSIM and FREE, respectively. We considered the evolution of SST based on 48-hourly local analysis from 1 January to 31 December 2010. The 48-hourly forecast SST from two runs was assessed with observations from different datasets. Then, we analyzed the impact of the data assimilation on the profile simulation of T/S. At last, we evaluated the system performance with respect to sea surface anomaly and sea ice, respectively.

5.1 Comparison with satellite data

First, we presented two cases to show the ocean state before and after the assimilation of the OSISAF SST data in Fig. 2. The first case was given at 11 January 2010, a date with clear weather and many observations available. The model has obvious difficulties in reproducing the observed SST. The cold biases in the forecast were found in the Skagerrak, west coast of the Baltic Proper and the Bothnian Bay, respectively. However, the warm biases appeared in the interior of the Baltic Sea and the Kattegat. The largest deviation in FREE reached 2.2 ^∘C at the Skagerrak. Apparently, temperature by assimilation analysis agreed with the satellite-derived data much better. This correction at the analysis step has allowed us to reduce the deviation of the SST forecast from the observations. The DA system simulation was also verified on 2 June 2010, which has also many available OSISAF observations. The biases on 2 June 2010 were obviously different from those on 11 January 2010. Moreover, it was found they had a roughly opposite bias signal. For example, relative to the OSISAF SST at the Baltic Proper, Bothnian Sea and Bothnian Bay, FREE produced relatively warmer water on 11 January and colder water on 2 June (Fig. 2), respectively. After data assimilation, the analysis increments were appropriately added to the model field. In general, the SST DA has improved the simulated SST in both cases (Fig. 2).

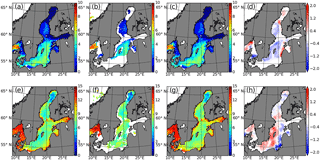
Figure 2 Map of SST from FREE (a, e), OSISAF (b, f), ASSIM (c, g) and the assimilation increments (d, h) on 11 January 2010 (a–d) and 2 June 2010 (e–h), respectively.

Maps of annual averaged root mean square error (RMSE) of SST from two runs relative to the IceMap observation are shown in Fig. 3. Obviously, the RMSE in FREE and ASSIM had different distributions in the Baltic Sea. In general, FREE had smaller error in the Skagerrak, the eastern Kattegat and the interior of the Bothnian Sea relative to other subbasin of the Baltic Sea. The largest RMSE was found at the connection region between the Baltic Proper and the Bothnian Sea. This could be caused by the shallow water, complicated bathymetry and large observation biases in this area. It was also noted that the RMSE was larger in the coastal region compared to its interior in the Baltic Proper and Bothnian Sea. After the assimilation, the SST was significantly improved. The RMSE of SST from ASSIM was generally smaller than 1.0 ^∘C. However, there were still some regions where the improvements were relatively small and the RMSE of SST was greater than 1.0 ^∘C. These large errors were predominantly located at the edge of the Baltic Sea and the Danish Straits. For instance, the RMSE of SST was greater than 1.2 ^∘C at both the entrance of the Gulf of Finland and the west coast of the Bothnian Sea. The relatively small improvements were regularly caused by the rare observations or the less accurate observations near the coastal water.

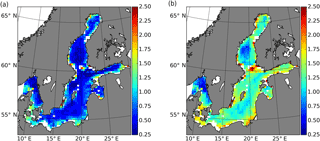
Figure 3 Map of the RMSE of SST from ASSIM (a) and FREE (b) calculated against IceMap SST in 2010, respectively.

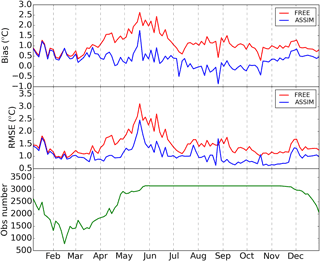
The overall daily averaged SST errors against the IceMap observations have been estimated (Fig. 4). The observations had better coverage in summer and autumn than in winter and spring. The variability of the number of observations directly affected the assessment of DA results. The model biases had pronounced seasonal variability, which had small values in spring and winter. In general, the assimilation provided better SST estimations. The free run had a RMSE of 1.47 ^∘C. After the assimilation, the RMSE was reduced to 1.03 ^∘C, whereas the bias was reduced by 0.73 ^∘C. An interesting feature was that the SST error reduction due to the assimilation was almost consistent with the variability of the number of IceMap observations. For example, the improvement became larger with the increasing number of IceMap observations from March to June 2010. However, the number of observations was kept constant during the period June–November 2010 and the improvement shown in both the bias and RMSE of SST did not exhibit large variability, which meant reliable performance of the DA system.

Figure 4 The evolution of basin-averaged bias and RMSE of SST from FREE and ASSIM relative to IceMap SST and the number of IceMap observations in 2010.

5.2 Comparison with independent in situ data

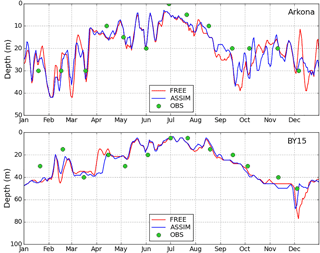
The time series of T/S were compared with independent observations located at the Arkona station (54.88^∘ N, 13.87^∘ E) in the Arkona Basin and at BY15 (57.33^∘ N, 20.05^∘ E) in the Eastern Gotland Basin, respectively. These two stations were selected to verify the experiment results because of their relatively completed observation records for the experimental period. In the Arkona Basin, the water depth was shallow and the water column can be well mixed between the surface and bottom water. Thus, the bottom T/S was largely affected by the surface dynamic (Liu et al., 2014). Relative to observations, the model had warm biases at this station (Fig. 5). At a depth of 25 m, the observed temperature showed the largest variability, which was a good representation of the bottom characteristics of the mixed layer. In mid-August, the temperature was abruptly increased by 10 ^∘C at a depth of 25 m and slightly decreased at the surface, respectively. The reason is that the surface water suddenly sinks to deeper layers, which warm the deep water. However, this dynamic process has not reached to Arkona bottom and it did not cause the obvious bottom temperature variability (Fig. 9). Both FREE and ASSIM had reproduced this process, whereas FREE showed larger temperature biases. To the salinity at the Arkona station, the surface observations were missing; the comparison at 7 m depth verified the subsurface simulations. The observations showed larger salinity variability in winter relative to summer. This pronounced seasonal variation is associated with the variation of fresh river runoff and net E–P (evaporation–precipitation) flux (Fu et al., 2012). At a depth of 7 m, salinity was obviously underestimated from April to September and overestimated after November, although ASSIM had slightly better results compared to FREE. The DA also provided better simulation of salinity at 25 m depth. For example, the salinity bias in the October was reduced by 3 psu by DA. At a depth of 40 m, the saltwater inflows were observed, resulting in sudden increases of salinity. For instance, the salinity was increased by 3.5 psu in February followed by a decreasing trend. The variations were reproduced in both FREE and ASSIM, whereas the intensity of the decreased process is weakly simulated with a difference of 3 psu, and the inflow in March was not strong enough relative to the observed one. Observations also showed that a large salinity variability amounts to 4–8 psu in the autumn. Although FREE and ASSIM had shown these changes, their magnitude was obviously weaker than observations. The possible reason was that the model's resolution was inadequate to well resolve the topography and eddies in this area. Both the large runoff and the complicated bathymetry posed challenges for the model to tackle the small-scale dynamic process in such a shallow basin. A higher-resolution model perhaps was more preferable to study this dynamic process.

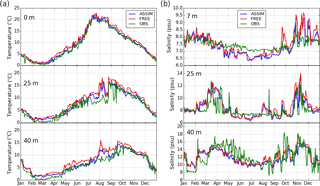
Figure 5 The time series of temperature (a) at depths of 0, 25 and 40 m and salinity (b) at depths of 7, 25 and 40 m at the Arkona station (54.88^∘ N, 13.87^∘ E), respectively.

The Eastern Gotland Basin has deeper water depth compared to the Arkona Basin, in which the water column is permanently stratified and the halocline lies at about 60–80 m (Fu et al., 2012). The mixing and sinking of T/S are hindered by the strong stratification. Unlike observations in the Arkona Basin (Fig. 5), the CTD observations at BY15 had lower temporal resolution with almost one observation per month. In the mixing layer, it can be seen model had overestimated the temperature (Fig. 6). At a depth of 10 m, ASSIM has remarkably improved the simulation of temperature relative to FREE. The bias has been reduced by 3 ^∘C in the spring of 2010. At 175 m depth, observed temperature showed very small variation. The reason was that the main source for deep water ventilation is the saltwater inflows which are suppressed by runoff within a depth range of 75–135 m in the Eastern Gotland Basin (Väli et al., 2013). As a result, updating the bottom water is very slow. Both FREE and ASSIM overestimated the temperature in the spring and the beginning of summer of 2010. Further, ASSIM has increased the temperature bias after midsummer relative to FREE. This result might be explained by the fact that the strong correlation is not expected between surface and layers below the halocline because of the strong stratification in this basin, which perhaps yield the artificial correction. Therefore, the improvement of the surface temperature cannot guarantee its positive influence on the bottom temperature. To the salinity, the model had less accurate simulation with generally low salinity biases at 10 m depth. ASSIM provided better salinity simulation compared to FREE. At 70 m depth, the small variation of salinity was found after DA. Moreover, at 175 m depth, the observation had very small variability (about 0.1 psu). In general, both experiments have reproduced these variations. However, FREE increased salinity by 0.2 psu from March to April relative to the observation, which caused the overall salinity overestimated amount to 0.2 psu. This increasing process was not shown in observations and the reason remained unclear. The DA has shown slight improvement, but it is still saltier than the observations.

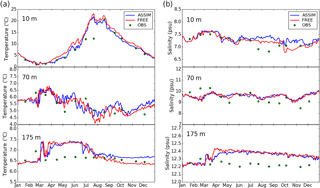
Figure 6 The time series of temperature (a) and salinity (b) at the BY15 station (57.33^∘ N, 20.05^∘ E) at depths of 10, 70 and 175 m, respectively.

The mixed layer depth (MLD) was calculated at the Arkona and BY15 stations and compared with the SHARK observations in Fig. 7. We used the temperature criterion to define the MLD, i.e., the depth at which the temperature deviated from the surface value by 0.5 ^∘C (Fu et al., 2012). Figure 7 shows that the MLD at the Arkona station had larger variability relative to the MLD at BY15. The reason for this feature is that the deeper water at Arkona is easily affected by wind forcing because of the shallow bathymetry and well mixing, whereas the temperature variation in the upper water at BY15 has difficulty influencing the deeper water because of the strong stratification. Both runs had reproduced the MLD variability feature similarly to the observations. For example, the minimum MLD appeared in summer, which was about several meters. The assimilation of satellite SST caused strong changes in the MLD at both stations, especially in winter. One explanation was that the Baltic Sea was largely affected by wind forcing and the winter wind was much stronger than the summer wind. Further, strong heating in summer promoted stratification in summer and shoaled the MLD.

Further, the temporal and spatial distribution of the SHARK observations is shown in Fig. 8a. These observations were unevenly distributed in the Baltic Sea. In the Skagerrak, the observations appeared at the Danish and Swedish coast. However, in the Bornholm Basin, Kattegat and Baltic Proper, the observations mainly were found in the central and the Swedish coast sides. There were also many observations in the Bothnian Sea and rare observations in the central part of the Bothnian Bay. It must be noticed that there are no SHARK observations in both the Gulf of Finland and Gulf of Riga during the experimental period. Moreover, these SHARK profiles in the first 4 months were mainly located in the Skagerrak to the Baltic Proper, which are relatively rare in the northern Baltic Sea. In the Bothnian Bay, the observations are mainly in the winter period.

Figure 7 The time series of mixed layer depth at the Arkona and BY15 stations.

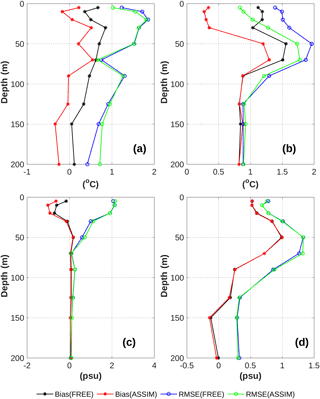
Figure 9 shows the change of overall bias and RMSE of T/S with depth against the SHARK dataset. In the Baltic Sea, DA had a large impact on the temperature forecast in the water above 100 m. The RMSE showed that the forecast of temperature was obviously improved from surface to thermocline in ASSIM and the improvements generally decreased with depth. Above 100 m, the overall RMSE of temperature in ASSIM was decreased by 21.38 % (from 1.59 to 1.25 ^∘C). It was also found the temperature error had similar variability to the warm biases in the two runs. In the transition zone, the RMSE in ASSIM was reduced by 5.59 and −20.31 % above and below 100 m relative to FREE, respectively. Below 90 m, the temperature was also overadjusted, which changed the warm bias to cold bias. It is worth noting that the number of the deeper water observations in the transition zone is substantially less than that in the Baltic Sea. For the salinity, both RMSE and bias of ASSIM showed very minor changes relative to FREE inside the Baltic Sea. For the water above 100 m, the total RMSE of salinity was increased by 3.48 % (from 1.15 psu in FREE to 1.19 psu in ASSIM) in the transition zone and 1.04 % (from 0.96 psu in FREE to 0.97 psu in ASSIM) in the Baltic Sea.

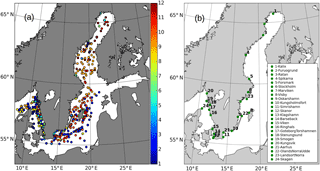
Figure 8 (a) Map of the temperature and salinity profiles from the SHARK database in 2010. The colors show the observation months. (b) The tide gauge stations along the Swedish coast.

Figure 9 The overall RMSE and bias of temperature (a, b) and salinity (c, d) from FREE and ASSIM relative to observations as a function of water depth inside (b, d) and outside (a, c) of the Baltic Sea.

5.3 Sea level anomaly

SLA represents a vertically integrated effect of the T/S variations over the whole water column. The accurate simulation of SLA is thus a good indicator of the model performance. Therefore, validating the impact of SST assimilation on the simulation of SLA is very important to the Baltic Sea forecast. The observations from the 24 tide gauge stations were used. These gauge stations are mainly located on the Swedish coast (see Fig. 8b). Since only the SST is assimilated in this study, the SLA observations are completely independent.

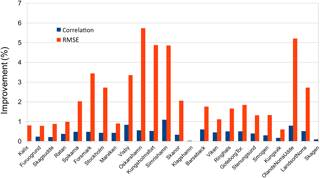
We calculated the RMSE and correlation coefficients for both FREE and ASSIM against the observations from tide gauges (Fig. 10). The overall RMSE was reduced by 1.8 % and the correlation coefficients were slightly increased. Among these stations, RMSE at Oskarshamn was decreased by 5.6 %, which is larger than that at other stations. The minimum RMSE change of SLA was seen at Klagshamn. For the correlation coefficient, improvement in the SLA by the DA is very small. The Simrishamn station showed the biggest change of correlation coefficient, which is 1.1 %. The RMSE and correlation comparison demonstrated that the SST DA has generally positive effects on the forecast of the SLA.

In addition, the time series of the SLA error discrepancy (ASSIM minus FREE) in two runs at four stations were selected to evaluate the simulation results (Fig. 11). These four stations were selected to represent the model performance at different positions on the Swedish coast. Two runs showed evidently different performance at these four stations. The variability of the SLA difference between two experiments at the Smogen station had higher frequency compared to other stations. The reason was that the Smogen station was located at the transition zone where the water had higher frequency variations caused by the brackish Baltic in-/outflowing water relative to other three stations. At these four stations, the improvements were mainly in late spring and summer, whilst the degraded simulations were mostly after mid-September, respectively. The SST assimilation had less impact in late winter and early spring compared to other seasons. In addition, the impact of SST assimilation on SLA simulation was not the same at the four positions. For instance, during the period from mid-November to mid-December, the SLA in ASSIM was improved at Simrishamn and degraded at both the Ratan and Landsort Norra stations, respectively. This phenomenon was possibly caused by the imperfect correlation between SST and SLA in the stationary samples. Further, these steric small changes of SLA by DA were what we expected because only SST was assimilated into NEMO-Nordic.

Figure 10 The improvement (%) of correlation and RMSE for the SLA at the tide gauge stations. The station positions are shown in Fig. 8b.

5.4 Sea ice

Sea ice in the Baltic Sea occurs primarily in its north region and influences the Baltic climate. Accurately detecting the sea ice is very useful to the northern Baltic population because too much or too little sea ice can be a problem for wildlife and people. Sea-ice concentration (SIC) and sea-ice extent (SIE) are two important and common indicators for modeling sea-ice environment. We assessed the SIC and SIE from simulations against the IceMap observations in Figs. 12–13. In contrast to the daily evaluation in Losa et al. (2014), the monthly mean SIC was used to represent the general status of sea ice in the Baltic Sea. In addition, SIC in January, February and December showed the variation of the sea ice in winter.

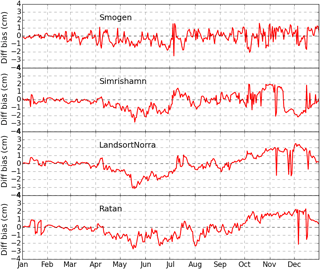
Figure 11 The variation of SLA biases in ASSIM relative to FREE against observations as a function of time. The station positions are shown in Fig. 8b.

In January 2010, the observations showed large ice coverage in the Bothnian Bay and the Gulf of Finland, and small SIC in the Gulf of Riga, respectively. Models generally reproduced this distribution of sea ice. However, FREE simulated too much sea ice in the Gulf of Finland and the eastern coast of the Baltic Proper relative to the observations. For example, SIC from FREE was almost 30 % higher than observations along the Estonian coastline. It could be seen that the SST DA reduced these biases. The reason is the SST DA modified the thermal expansion by providing the well temperature fields above the thermocline. The temperature in February became colder relative to January in the Baltic Sea. As a result, the sea ice in February extended to the Bothnian Sea and the whole Gulf of Riga. Observations also showed small SIC in Kattegat and Skagerrak. The model simulated higher SIC in the Bothnian Sea with largest biases along the Swedish and Finnish coasts. As an example, the observed ice in the Bothnian Sea was characterized by concentrations mainly smaller than 0.5, whereas modeled ice in FREE had concentrations greater than 0.9 in the shallow region of the Bothnian Sea. FREE also had smaller ice coverage with lower SIC in the transition zone between the North Sea and the Baltic Sea relative to IceMap. After the SST assimilation, ASSIM reduced SIC in the Bothnian Bay and the west coast of the Baltic Sea, which was closer to the observations. The ice in ASSIM did not have obvious variations in Kattegat and Skagerrak yet. ASSIM also reduced too much ice at the southern end of the Bornholm Basin. The reason is that the satellite SST observations had limited accuracy near the coast and could bring artificial information into the modeling. In March, compared to observations, FREE produced low SIC at the western coast of the Bothnian Sea, Gulf of Finland, Gulf of Riga and the connecting zone between the Bothnian Sea and Gulf of Finland. However, the model SIC in FREE was higher than IceMap in the interior the Bothnian Bay. For instance, the SIC from FREE in the western Bothnian Sea was 40 % higher than the observation. On the south coast of the Arkona Basin and Baltic Proper, FREE failed to reproduce the sea ice as in the observation. After the DA, the high SIC was decreased in the western Bothnian Sea and closer to that in IceMap in Bothnian Sea. In the Gulf of Finland and Gulf of Riga, the SIC error was increased in ASSIM. In April, the large SIC error in FREE was shown in the Bothnian Sea, Bothnian Bay, Gulf of Riga and Gulf of Finland, where no clear improvements were seen in ASSIM. In December, sea-ice coverage was smaller because of relatively warm temperature compared to that in other winter months. Most of the sea ice with high concentration was observed at the edge of the Bothnian Bay. Nevertheless, high concentration ice in FREE also formed at the transition zone between the Bothnian Sea and Bothnian Bay. Relatively, ASSIM reduced the high concentration biases of sea ice. By contrast, both ASSIM and FREE had lower concentration ice than observations on the eastern coast of the Bothnian Sea. The SIC from ASSIM was relatively lower than that from FREE in the northern Finish coast, whereas the observations had high concentration ice there.

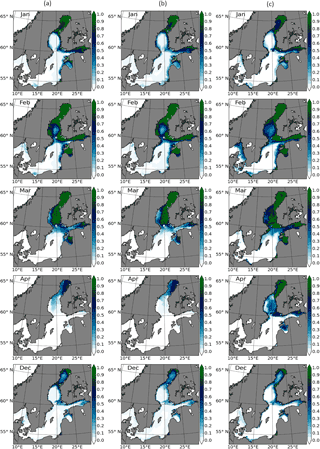
Figure 12 The monthly mean sea-ice concentrations in FREE (a), ASSIM (b) and IceMap (c), respectively.

The daily SIE from FREE and ASSIM was compared with observations in Fig. 13. The observed SIE was generally increased from January to February and reached the maximum in mid-February. During the period of March–May, SIE was decreased as temperature was increasing. SIEs in both FREE and ASSIM experiments were generally underestimated by comparison with the observations in 2010, especially in the period from mid-March to early April. The SIE bias in both runs was roughly increased from January to early April. In early April, the maximum negative bias of SIE was found to be 105 000 km² for ASSIM and 10 000 km² for FREE. The impact of SST assimilation on the SIE was positive during the phase of sea-ice formation. For example, the SIE bias was reduced by 25 000 km² at the end of February and in mid-December. However, during the phase of sea-ice melting (March to April), the SIE error was increased in ASSIM even with the decreased error of SST. For example, the SIE bias in ASSIM was increased by 42 000 km² relative to FREE in the early March. These increased SIE error in March mainly happened in the Gulf of Riga and Gulf of Finland.

6 Conclusion and discussions

A DA system based on a LSEIK filter has been coupled to the NEMO circulation model of the North Sea and Baltic Sea. The method was successfully applied for assimilating high-resolution satellite SST data. We demonstrated that, over the period of 2010, the agreement of the SST forecast with the independent satellite observation was improved by ∼ 29.93 % in comparison with the regular forecast without DA. The assimilation quality is directly related to the number of observations.

Compared with independent in situ data from SHARK, the RMSE of temperature was reduced by 21.38 and 5.59 % for the water above 100 m inside and outside of the Baltic Sea, respectively. However, in the deeper layers, the temperature was slightly degraded in the Baltic Sea. This is partially caused by the artificial correlation between surface layer and deeper layers. The improvement of temperature by SST DA cannot guarantee corresponding improvement of the salinity. The statistics show that the salinity RMSE was increased by 1.04 and 3.48 % in the transition zone and the Baltic Sea, respectively. Both ASSIM and FREE have captured the main dynamic process in the Baltic Sea, for example, the inflow and the sink. However, ASSIM is closer to the observed one relative to FREE.

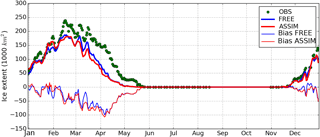
Figure 13 The daily sea-ice extent from FREE, ASSIM and IceMap, and the sea-ice extent bias (modeled minus observed field), respectively.

The forecast results were further validated with the independent SLA observations. The result shows that all RMSEs and correlations for all 21 stations are smaller than 0.12 m and greater than 0.86, respectively. After DA, the SLAs at these stations have been slightly improved. In general, the RMSE was reduced by 1.8 % and correlation coefficients were slightly increased, respectively. Further, the model–observation comparison at the selected four stations indicates that these improvements are mainly in late spring and summer. The comparisons also denote the SST assimilation has less impact in the late winter and early spring relative to other seasons.

When compared with monthly mean observations of SIC, both the assimilation run and free run reproduced the main spatial distributions of sea ice in the Baltic Sea. During the sea-ice formation period, the SST assimilation has improved the results of SIC from FREE in the Gulf of Finland, the Bothnian Sea and eastern coast of the Baltic Proper. However, minor improvements were found in Kattegat and Skagerrak. In addition, over the sea-ice melting period, the SIE comparison showed the SST assimilation increased the SIE error, especially in the Gulf of Finland and Gulf of Riga.

The daily MLD from two runs has been compared with the observations at the Arkona and BY15 stations. The model could capture the variability features of the MLD. Similar to Fu et al. (2012), it was found that SST assimilation had less impact on the MLD in summer than in winter. In general, the SST DA produced less influence on the MLD in the deeper region (BY15) relative to that in the shallow region (Arkona).

Further, the reliability of the DA system is worthy of assessment. In Rodwell et al. (2016), a perfectly reliable system error variance for ensemble assimilation was calculated by the sum of the variance of the sample ensemble, the square of innovation (misfit between observation and model) and the variance of observation at assimilation time. In this study, we used a constant observation error similar to Rodwell et al. (2016) because our DA design is different from that paper. The major difference between these two studies is that we estimate the background error covariance from a stationary ensemble and avoid the perturbation of observation error. Therefore, the variance of the sample ensemble and observation is univariate and the diagnostic of the assimilation stability can be directly obtained from the forecast error like the RMSE in Fig. 4.

The results of the SST assimilation are encouraging and the assimilation helps to ameliorate some model deficiencies such as the simulation of sea ice in the Gulf of Finland. However, some problems need to be further addressed in the SST DA in the future. Firstly, the SST assimilation has a worse influence on the simulation of salinity in the upper layers and temperature in the deeper layers. Losa et al. (2012) denoted that the salinity simulation quality crucially depends on the assumptions about the model and data error statistics. Here, a stationary ensemble sample was used to represent the correlation between T/S and between surface and deep water. These relationships could be changed with the varying dynamics and forcing conditions. More sophisticated assumptions should be used in the DA of the Baltic Sea. Secondly, the SHARK observations in this study are absent in the Gulf of Finland and Gulf of Riga. This denotes the validation results with SHARK observations did not include the evaluation of the simulation of T/S in the deep water of these two basins. Thirdly, the univariate localization scale used in this study could be another problem. The spreading of observation information strongly depended on the correlation scale. The large localization scale can introduce the artificial information, which could degrade the assimilation quality. A flow-dependent background error covariance with varying correlation scale may be more appropriate for the Baltic Sea with complex bathymetry and rich dynamics. Fourthly, the remote sensing observations near the coast could have a large bias because of the limit of the instrument itself. More strict quality controlling methods needed to be used for the satellite coastal observations before their assimilation.

Appendix A

Here, we describe the details of the mathematical formulation used in the forecast and correction (analysis) steps of the LSEIK filter:

1. Forecast: the analysis state X^a at time t_i−1 is integrated forward to the time of the next available observations t_i to compute the forecast state X^f,

   $$\begin{array}{}\text{(A1)}& {\mathbf{X}}^{\mathrm{f}}\left(t_i\right)=\mathbf{M}\left(t_{i-\mathrm{1}},t_i\right){\mathbf{X}}^{\mathrm{a}}\left(t_{i-\mathrm{1}}\right),\end{array}$$

   where M denotes the nonlinear dynamic model operator that integrates a model state from time t_i−1 to time t_i. The superscripts “f” and “a” denote the forecast and analysis. The corresponding error covariance matrix can be expressed as

   $$\begin{array}{}\text{(A2)}& {\displaystyle }& {\displaystyle }{\mathbf{P}}^{\mathrm{f}}\left(t_i\right)={\mathbf{L}}_i{\left[\left(r+\mathrm{1}\right){\mathbf{T}}^{\mathrm{T}}\mathbf{T}\right]}^{-\mathrm{1}}{\mathbf{L}}_i^{\mathrm{T}}+{\mathbf{Q}}_i,\text{(A3)}& {\displaystyle }& {\displaystyle }{\mathbf{L}}_i={\mathbf{X}}^{\mathrm{f}}\left(t_i\right)\mathbf{T},\end{array}$$

   with Q_i being the covariance matrix of model uncertainties and r+1 is the minimum number of sample ensemble members for error covariance matrix. The superscript “T” denotes the transpose of matrix. The full-rank matrix T has a dimension of $\left(r+\mathrm{1}\right)\times r$ with zero column sums, and L is a full-rank $\left(r+\mathrm{1}\right)\times r$ matrix which implicitly represents the model variability.

2. Correction: when the observation is available at time t_i, the LSEIK filter merged the information from model and observations to produce the analysis state with the formula:

   $$\begin{array}{}\text{(A4)}& {\mathbf{X}}^{\mathrm{a}}\left(t_i\right)={\mathbf{X}}^{\mathrm{f}}\left(t_i\right)+{\mathbf{K}}_i\left[{\mathit{Y}}^o\left(t_i\right)-{\mathbf{H}}_i{\mathbf{X}}^{\mathrm{f}}\left(t_i\right)\right].\end{array}$$

   Here, Y^o is a vector of observations. The gain matrix K, which linearly interpolates between the observations and the forecast, is given by

   $$\begin{array}{ll}{\displaystyle }{\mathbf{K}}_i& {\displaystyle }={\mathbf{P}}_i^{\mathrm{f}}{\mathbf{H}}_i^{\mathrm{T}}{\left({\mathbf{H}}_i{\mathbf{P}}_i^{\mathrm{f}}{\mathbf{H}}_i^{\mathrm{T}}+{\mathbf{R}}_i\right)}^{-\mathrm{1}}\\ \text{(A5)}& {\displaystyle }& {\displaystyle }={\mathbf{L}}_i{\mathbf{U}}_i{\left({\mathbf{H}}_i{\mathbf{L}}_i\right)}^{\mathrm{T}}{\mathbf{R}}_i^{-\mathrm{1}},\end{array}$$

   where H_i denotes the linearization of observation operator, which maps the model space to the observation space. R is the observation error covariance matrix. The matrix U_i is updated according to

   $$\begin{array}{}\text{(A6)}& {\mathbf{U}}_i^{-\mathrm{1}}=\mathit{\rho }\left(r+\mathrm{1}\right){\mathbf{T}}^{\mathrm{T}}\mathbf{T}+{\mathbf{L}}_i^{\mathrm{T}}{\mathbf{H}}_i^{\mathrm{T}}{\mathbf{R}}_i^{-\mathrm{1}}{\mathbf{H}}_i{\mathbf{L}}_i.\end{array}$$

   Here, ρ is a forgetting factor.

   A second-order exact sampling is used to initialize the LSEIK filter. At time t_i−1, a analysis state X^a(t_i−1) and its corresponding error covariance matrix P^a(t_i−1), in the factorized form ${\mathbf{L}}_{i-\mathrm{1}}{\mathbf{U}}_{i-\mathrm{1}}{\mathbf{L}}_{i-\mathrm{1}}^{\mathrm{T}}$, are available. The samples can be given by the following formula:

   $$\begin{array}{ll}{\displaystyle }{\mathbf{X}}_k^{\mathrm{a}}\left(t_{i-\mathrm{1}}\right)& {\displaystyle }=\stackrel{\mathrm{‾}}{{\mathbf{X}}^{\mathrm{a}}}\left(t_{i-\mathrm{1}}\right)+\sqrt{r+\mathrm{1}}{\mathbf{L}}_{i-\mathrm{1}}\\ \text{(A7)}& {\displaystyle }& {\displaystyle }{\left({\mathbf{\Omega }}_{k,i-\mathrm{1}}{\mathbf{C}}_{i-\mathrm{1}}\right)}^{\mathrm{T}}.\end{array}$$

For $\mathrm{1}\le k\le r+\mathrm{1}$, the C_i−1 is the Cholesky decomposition of ${\mathbf{U}}_{i-\mathrm{1}}^{-\mathrm{1}}$ and Ω_i−1 is a $\left(r+\mathrm{1}\right)\times r$ matrix with orthonormal columns and zero column sums, where ${\mathbf{\Omega }}_{k,i-\mathrm{1}}$ denotes the kth row of Ω_i−1. $\stackrel{\mathrm{‾}}{{\mathbf{X}}^{\mathrm{a}}}$ is the average of the analysis state.