Note on the directional properties of meter-scale gravity waves

The directional distribution of the energy of young waves is bimodal for frequencies above twice the peak frequency; i.e., their directional distribution exhibits two peaks in different directions and a minimum between. Here we analyze in detail a typical case measured with a peak frequency f_p=0.18 Hz and a wind speed of 10.7 m s⁻¹ using a stereo-video system. This technique allows for the separation of free waves from the spectrum of the sea-surface elevation. The latter indeed tend to reduce the contrast between the two peaks and the background. The directional distribution for a given wavenumber is nearly symmetric, with the angle distance between the two peaks growing with frequency, reaching 150^∘ at 35 times the peak wavenumber k_p and increasing up to 45 k_p. When considering only free waves, the lobe ratio, the ratio of oblique peak energy density over energy in the wind direction, increases linearly with the non-dimensional wavenumber k∕k_p, up to a value of 6 at $k/k_{\mathrm{p}}\simeq \mathrm{22}$, and possibly more for shorter components. These observations extend to shorter components' previous measurements, and have important consequences for wave properties sensitive to the directional distribution, such as surface slopes, Stokes drift or microseism sources.

1 Introduction

Directional properties of waves shorter than the dominant scale play a very important role in many aspects that range from air–sea momentum fluxes (Plant, 1982) to remote sensing, surface drift (Ardhuin et al., 2009) and underwater acoustics (Duennebier et al., 2012). In a landmark paper, Munk (2009) analyzed the linear trends of down-wind and cross-wind mean square slopes of the sea surface, as measured by satellites Bréon and Henriot (2006). These trends cannot be explained by today's understanding of ocean wave spectra, and he proposed that there may be localized sources that could generate oblique propagating waves looking like ship wakes. However, as he put it, the dataset “says nothing about time and space scales” because the reflectance measurements that they present are integrated across all wave scales. Munk further challenged us all: “I look forward to intensive sea-going experiments over the next few years demolishing the proposed interpretations”. We thus went out to sea with the objective of resolving space scales and timescales, and providing further constraints on the wave properties.

Previous time-resolved measurements of ocean waves have clearly established a prevalence of directional bimodality at frequencies above twice the peak frequency f_p, using in situ array (Long and Resio, 2007; Young et al., 1995) and buoy data (Ewans, 1998; Wang and Hwang, 2001). These were confirmed by airborne remote sensing techniques used by Hwang et al. (2000) and Romero and Melville (2010). All the resolved wavenumber spectra have been limited to $f/f_{\mathrm{p}}<\mathrm{4}$. Numerical modeling by Banner and Young (1994) suggests that the bimodality is caused by the nonlinear cascade of free wave energy from dominant to high frequencies. Bimodality is also found after having solved for the nonlinear evolution equation of the surface elevation field, whether computing it for Gaussian wave packets according to a nonlinear Schrödinger equation (Dysthe et al., 2013) or for unimodal wave spectra from the Euler equations (Toffoli et al., 2010). Alves and Banner (2003) demonstrate the importance of the parametrizations of wave generation and dissipation in the setting of bimodality. The model results of Gagnaire-Renou et al. (2010) show that bimodality is followed at smaller scales by a return to a unimodal directional distribution, somewhere above $f/f_{\mathrm{p}}=\mathrm{10}$, depending on the parametrizations of wave generation and dissipation.

The distribution of radar backscatter as a function of azimuth clearly shows that the directional wave spectrum is unimodal above 6 cm wavelength in the gravity-capillary range (Elfouhaily et al., 1997). Recent backscatter data in L-band presented by Yueh et al. (2013) show a larger cross-wind than down-wind backscatter, consistent with a bimodal distribution at scales around 1 m wavelength, at least for wind speeds around 5 m s⁻¹.

As shown by Leckler et al. (2015), stereo-video imagery is capable of resolving these waves and providing information on the timescales and space scales needed to interpret integrated wave parameters such as down-wind and cross-wind mean square slopes. In that earlier paper, a record with young wind waves was analyzed (U₂₃=13.2 m s⁻¹, f_p=0.33 Hz). That record revealed the presence of second-order harmonics and a strong bimodality of the directional distribution. Here we use the same measurement method and analyze the directional properties of the free waves in more detail. In particular, we analyze new data that provide a wider range of frequencies and quantitatively characterize the bimodality characteristics together with its impacts on several physical variables.

The data and analysis methods are presented in Sect. 2. Directional distributions and bimodality are described in Sect. 3. Discussions and conclusions follow in Sect. 4.

2 Wave measurements and spectral analysis

2.1 Stereo processing

We have chosen one typical stereo record with dominant waves longer than those described in Leckler et al. (2015). It was acquired on 10 March 2014, starting at 09:40 UTC, from the Acqua Alta oceanographic research platform, 15 km offshore of Venice, Italy, in the northern Adriatic Sea. The mean water depth there is approximately d=17 m. The experimental setup has been described in detail in Benetazzo et al. (2015). It is made up of two digital cameras mounted on a horizontal bar, properly synchronized and calibrated. The cameras are located d=12.5 m above the mean sea level. The stereo device points in a direction oriented 46^∘ clockwise from geographical north, i.e., looking to the northeast. The cameras' elevation angle is 50^∘. This record is 30 min long and uses a 15 Hz sampling rate.

In the following all variables use the meteorological convention; that is, the directions are directions from which wave, wind and current come. Provenance directions, unless otherwise specified, are measured anticlockwise from the direction along the bar, i.e., 136^∘ clockwise from geographical north.

The mean wind speed measured at 10 m above sea level is 10.7 m s⁻¹, with mean direction θ_U=77^∘ (northeasterly). The significant wave height estimated from the stereo system is H_m0=1.33 m, with peak frequency f_p=0.185 Hz, corresponding to a dominant wavelength on the order of 45 m. We note that wave gauges on the platform give independent measurements of H_m0=1.36 m and f_p=0.189 Hz. Dominant waves and shorter components of the wave spectrum can be considered deep water waves. An acoustic Doppler current profiler (ADCP) deployed at the sea floor provides measurements of the horizontal current vector with a vertical resolution of 1 m.

The raw video images are processed into a three-dimensional surface elevation matrix $\mathit{\zeta }(x,y,t)$ following the method of Benetazzo et al. (2015). A local Cartesian reference frame is defined, in which the surface elevation is reconstructed, with horizontal axes x and y. By convention, the cameras' look direction is the y axis, increasing away from the cameras, and the x axis is perpendicular, increasing towards the right of the cameras. The sea surface is discretized with a pixel size $\mathrm{\Delta }x=\mathrm{\Delta }y=\mathrm{20}$ cm. A snapshot of the reconstructed sea-surface elevation map is presented in Fig. 1. We have selected a 25.6 m by 25.6 m area for Fourier analysis, delimited by a black square. Its location, close to the cameras, is chosen to minimize errors in the estimate of the surface elevation. These errors increase with increasing distance from the cameras, and are dominated by the quantization error (Benetazzo, 2006). Wavelengths longer than 25 m can be resolved using standard slope array techniques (Graber et al., 2000) as done by Leckler et al. (2015). These longer components are not the focus of the present paper.

All of our analysis is based on a three-dimensional power spectral density of these data (Figs. 2 and 3). This is obtained by applying a Hann spatiotemporal window with 50 % overlap in time, and averaging the spectra in time following Welch (1967). The frequency resolution is Δf=0.015 Hz. The double-sided Cartesian spectrum $E(k_x,k_y,f)$ is normalized so that

$$\begin{array}{}\text{(1)}& E=\iiint d{k}_{x}d{k}_{y}dfE(k_x,k_y,f)\end{array}$$

is the variance of the surface elevation.

The polar spectrum is more convenient for the study of directional distributions and for working at a given wavenumber. The single-sided polar spectrum is

$$\begin{array}{}\text{(2)}& E(k,\mathit{\theta },f)=\mathrm{2}kE(k_x,k_y,f),\end{array}$$

where $k=(k_x^{\mathrm{2}}+k_y^{\mathrm{2}}{)}^{\mathrm{1}/\mathrm{2}}$ and $\mathit{\theta }=\arctan (k_y,k_x)+\mathit{\pi }$ is the wave provenance direction. For convenience, we use a regular polar grid whose resolution is set to Δk=0.17 rad m⁻¹ and Δθ=1^∘.

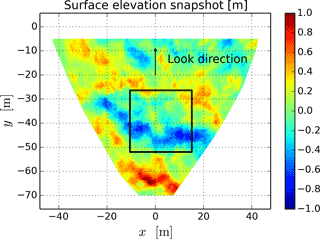
Figure 1 Stereo-video reconstructed sea-surface elevation matrix snapshot and sea-surface area used for spectrum calculations (black square).

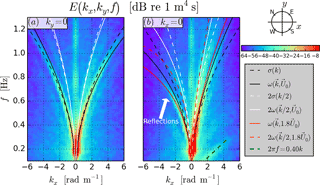
Figure 2 Frequency–wavenumber surface elevation spectrum at Acqua Alta on 10 March 2014 in dB and various dispersion lines. Spectrum along the cross-look (a) and look direction (b). The current used here, U₀, is evaluated in the Appendix.

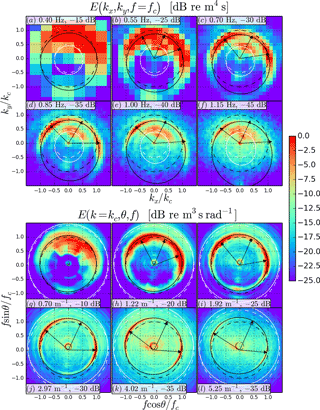
Figure 3 Surface elevation spectrum at Acqua Alta (continued). (a) to (f): Cartesian spectrum at constant frequencies f_c. (g) to (l): Cartesian spectrum interpolated into polar coordinates at constant wavenumbers $k_{\mathrm{c}}=\mathit{\kappa }(f_{\mathrm{c}},\mathrm{0})$. The reference levels are indicated in the text boxes. The arrows point to the directions of the two peaks of the bimodal distributions (outer arrows) and to the central minimum (inner arrow). See legend in Fig. 2 for the various meanings of the lines.

2.2 General properties of the three-dimensional spectrum

The surface elevation spectrum can be interpreted as the distribution of wave energy, which can generally be divided into free and bound waves,

$$\begin{array}{}\text{(3)}& E\left(\mathit{k},f\right)=E_{\mathrm{free}}\left(\mathit{k},f\right)+E_{\mathrm{bound}}\left(\mathit{k},f\right).\end{array}$$

Free waves have a relation between wavenumber and frequency that closely follows the linear dispersion relation. In the presence of a horizontally homogeneous and stationary current vertical profile u(z), and in the limit of small wave steepness, this dispersion relation is given by Stewart and Joy (1974):

$$\begin{array}{}\text{(4)}& \mathit{\omega }(\mathit{k},\mathit{U})=\mathit{\sigma }\left(k\right)+kU\left(k\right)\cos (\mathit{\theta }-\mathit{\alpha }),\end{array}$$

where

$$\begin{array}{}\text{(5)}& \mathit{\sigma }\left(k\right)=\sqrt{gk\tanh \left(kd\right)}\end{array}$$

and the effective current U(k) is approximated by a weighted integral of the Eulerian current u(z) over the water column:

$$\begin{array}{}\text{(6)}& U\left(k\right)=\mathrm{2}k\underset{-\mathrm{\infty }}{\overset{\mathrm{0}}{\int }}u\left(z\right)e^{\mathrm{2}kz}\mathrm{d}z.\end{array}$$

Here we have assumed that the current has a constant direction α at all depths. Moreover, Eq. (6) holds only for linear waves, i.e., waves for which hydrodynamic nonlinearities have been neglected, although free waves may encompass some weakly nonlinear contributions – see Leckler et al. (2015) and Janssen (2009). The depth weighting in the integral of Eq. (6) gives a stronger influence of surface currents on shorter wave components. In practice, waves with wavenumber k feel the integrated current over a depth $\sim \mathrm{1}/k$. For convenience, the inverse function providing the wavenumber as a function of frequency and direction will be denoted κ in the following, namely by definition: if

$$\begin{array}{}\text{(7)}& k=\mathit{\kappa }(\mathit{f},\mathit{U}),\end{array}$$

then

$$\begin{array}{}\text{(8)}& \mathrm{2}\mathit{\pi }f=\mathit{\omega }(\mathit{k},\mathit{U}),\end{array}$$

where $\mathit{f}=\left[f\cos \right(\mathit{\theta }),f\sin (\mathit{\theta }\left)\right]$.

Once the effective current (Eq. 6) is known, the location of free waves in the (k,f) plane can be deduced from Eq. (4), which relates the radian frequency 2πf to the wave vector k. It is represented in Figs. 2 and 3 by a black solid line. The addition of a current is necessary to fit the observations of energy distribution. The free modes' bimodality is clearly visible, i.e., the fact that two energy patches detach progressively from a main direction as the wave scale decreases.

Bound waves are dominated by the second-order interaction of free components with wavenumbers k₁ and k₂. The sum interaction gives waves of wavenumber $\mathit{k}={\mathit{k}}_{\mathrm{1}}+{\mathit{k}}_{\mathrm{2}}$, and frequency $\mathit{\omega }=\mathit{\omega }\left({\mathit{k}}_{\mathrm{1}}\right)+\mathit{\omega }\left({\mathit{k}}_{\mathrm{2}}\right)$, with an energy E_sum. The difference interaction gives $\mathit{k}={\mathit{k}}_{\mathrm{1}}-{\mathit{k}}_{\mathrm{2}}$ and $\mathit{\omega }=\left|\mathit{\omega }\left({\mathit{k}}_{\mathrm{1}}\right)-\mathit{\omega }\left({\mathit{k}}_{\mathrm{2}}\right)\right|$ , E_diff. These two kinds of interactions have themselves distinct signatures in the surface elevation spectrum, namely

$$\begin{array}{}\text{(9)}& E_{\mathrm{bound}}\left(\mathit{k},f\right)=E_{\mathrm{sum}}\left(\mathit{k},f\right)+E_{\mathrm{diff}}\left(\mathit{k},f\right).\end{array}$$

At a given propagation direction, the sum interaction is found at frequencies higher than the dispersion surface, while the difference interaction components are found at lower frequencies (Krogstad and Trulsen, 2010; Leckler et al., 2015). E_bound can be deduced from E_free (Hasselmann, 1962). More specifically, for a narrow spectrum, the sum interaction component is characterized by a signature in the (k,f) plane (Senet et al., 2001)

$$\begin{array}{}\text{(10)}& \mathrm{2}\mathit{\pi }f=\mathrm{2}\mathit{\omega }(\mathit{k}/\mathrm{2},\mathit{U}),\end{array}$$

also referred to as the first harmonic. The latter corresponds to sum interactions of free waves traveling in the same direction, with the same frequency and propagation direction, for which the interaction cross section is highest (Aubourg and Mordant, 2015). This curve is represented in Figs. 2 and 3 by a white solid line. Its equivalent without a current is also plotted as a white dashed line. Nonlinear components do not exhibit the same directionality as linear waves in general, especially from snapshots at constant frequency. In this case, the harmonic peaks in the dominant wave direction (see Fig. 3b–f), although this is not the only possible behavior.

We also note that waves that are probably reflected by the platform legs are present, as shown by a white arrow in Fig. 2b, and their energy decreases with increasing distance. When interpreted as plane waves, the reflected components appear slightly off the dispersion relation of the incident waves. Fitting the current for the incident waves gives U≃0.22 m s⁻¹, whereas a fit for the reflected components only would give a current velocity of 0.4 m s⁻¹.

Finally, there are other spectral features that do not correspond to surface waves, which we shall call noise. We distinguish four kinds of noise. Firstly, a background noise is present below −50 dB, particularly visible in Fig. 3d–f and j–l. This noise practically limits the use of stereo video to k<8 rad m⁻¹. Secondly, some energy propagates at a speed of 0.4 m s⁻¹ along the look direction and at slower speeds for other directions (green dashed lines in Figs. 2b and 3i–n). For k=2 rad m⁻¹ this noise amplitude is comparable in magnitude to the free wave signature and is distributed around a surface of the type 2πf=0.4sin²(θ)k, for $\mathit{\theta }\in [\mathrm{0};\mathit{\pi }[$ only. It could be associated with the difference interaction between incident and reflected wavenumbers.

Besides these noises, uncertainties in the spectral densities are caused by the poor spectral resolution close to k=0, and quantization error noise, mostly for k>7.5 rad m⁻¹ and in the look direction (Benetazzo, 2006). We thus exclude from our analysis the spectral components for which any of the following conditions is met

$$\begin{array}{}\text{(11)}& {\displaystyle }& {\displaystyle }f\le \mathrm{\Delta }f,\text{(12)}& {\displaystyle }& {\displaystyle }f>\mathrm{1.4}\mathrm{Hz},\text{(13)}& {\displaystyle }& {\displaystyle }k\le \mathrm{\Delta }k,\text{(14)}& {\displaystyle }& {\displaystyle }k>\mathrm{7.5}\mathrm{rad}{\mathrm{m}}^{-\mathrm{1}},\text{(15)}& {\displaystyle }& {\displaystyle }\mathrm{2}\mathit{\pi }f\left[\mathrm{Hz}\right]<\mathrm{1.1}\times \mathrm{0.4}\times {\sin }^{\mathrm{2}}\left(\mathit{\theta }\right)k\left[\mathrm{rad}{\mathrm{m}}^{-\mathrm{1}}\right].\end{array}$$

Outside of these components the spectrum is separated into free and bound components. This uses a determination of the effective current that is discussed in the Appendix. Identifying the free wave energy as that close to the linear dispersion relation, the bound components are defined as the rest,

$$\begin{array}{}\text{(16)}& E_{\mathrm{bound}}(k,\mathit{\theta })=E(k,\mathit{\theta })-E_{\mathrm{free}}(k,\mathit{\theta }),\end{array}$$

and the same is done for the frequency–direction spectrum.

3 Directional properties of free waves

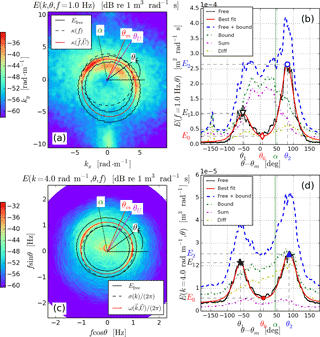
Figure 4 Free wave extraction (a, c) and corresponding directional distributions (b, d). Left panels: semi-automatic extraction of free waves, with α the current direction, θ_m the spectral mean direction of wave propagation and θ_U the wind direction. Right panels: directional distributions of free waves (solid line), with fits and the various nonlinear contributions.

The spectrum of free waves E_free(k,θ) is clearly bimodal for k>4k_p. Bimodal energy distributions can be characterized from the knowledge of the position and height of the energy peaks. The processing starts from the radially integrated directional distributions, both at a given frequency $E_{\mathrm{free}}\left(\mathit{\theta }\right)=\int dk{E}_{\mathrm{free}}\left(k,\mathit{\theta }\right)$ and wavenumber $E_{\mathrm{free}}\left(\mathit{\theta }\right)=\int df{E}_{\mathrm{free}}\left(f,\mathit{\theta }\right)$ (see Fig. 4). The same processing is performed on bound waves, obtained from Eq. (16). Bound waves are found to stand for a significant proportion of the overall energy at given slices (62 and 64 % on panels b and d, respectively), but only the free waves are bimodal. The energy level of bound waves at these small scales is dominated by the contribution of the more energetic longer waves. The contributions of the sum and difference interactions are also indicated. Directional distributions are centered on the spectral mean direction of wave propagation θ_m=68^∘ from Benetazzo et al. (2015).

As the directional distributions are noisy, they need to be fitted by an appropriate shape function. Inspired by Ewans (1998), the double pseudo-Voigt function with a positive floor has been chosen. The fit is performed using the Python lmfit package (Newville et al., 2014). The double pseudo-Voigt function allows for more various curve shapes than only two Gaussian beams, with its 9 degrees of freedom, when the Lorentzian fraction x is nonzero,

$$\begin{array}{ll}{\displaystyle }{E}_{\mathrm{fit}}\left(\mathit{\theta }\right)=& {\displaystyle }{C}^{\mathrm{st}}+f(\mathit{\theta };A_{\mathrm{1}},{\mathit{\mu }}_{\mathrm{1}},{\mathit{\sigma }}_{\mathrm{1}},x_{\mathrm{1}})\\ \text{(17)}& {\displaystyle }& {\displaystyle }+f(\mathit{\theta };A_{\mathrm{2}},{\mathit{\mu }}_{\mathrm{2}},{\mathit{\sigma }}_{\mathrm{2}},x_{\mathrm{2}}),\end{array}$$

where

$$\begin{array}{ll}{\displaystyle }f(\mathit{\theta };A,\mathit{\mu },\mathit{\sigma },x)=& {\displaystyle \frac{(\mathrm{1}-x)A}{{\mathit{\sigma }}_g\sqrt{\mathrm{2}\mathit{\pi }}}}{e}^{-(\mathit{\theta }-\mathit{\mu }{)}^{\mathrm{2}}/\mathrm{2}{\mathit{\sigma }}_g^{\mathrm{2}}}\\ \text{(18)}& {\displaystyle }& {\displaystyle }+{\displaystyle \frac{xA}{\mathit{\pi }}}{\displaystyle \frac{\mathit{\sigma }}{(\mathit{\theta }-\mathit{\mu }{)}^{\mathrm{2}}+{\mathit{\sigma }}^{\mathrm{2}}}},\end{array}$$

with ${\mathit{\sigma }}_g=\mathit{\sigma }/\sqrt{\mathrm{2}\ln \mathrm{2}}$. The use of a double Voigt profile does not strictly ensure a smooth periodic distribution (around $\mathit{\theta }={\mathit{\theta }}_{\mathrm{m}}\pm \mathit{\pi }$). However, in practice, due to the relative directional narrowness of the bimodal profiles, the constant energy floor is quickly reached away from the mean wave propagation direction. Bimodality can then be characterized using a set of three remarkable points in the double Voigt profile (see Fig. 4b, d) (Wang and Hwang, 2001), i.e., the central minimum (θ₀,E₀) and the two peaks (θ₁,E₁) and (θ₂,E₂), with θ₁<θ₂.

4 Results

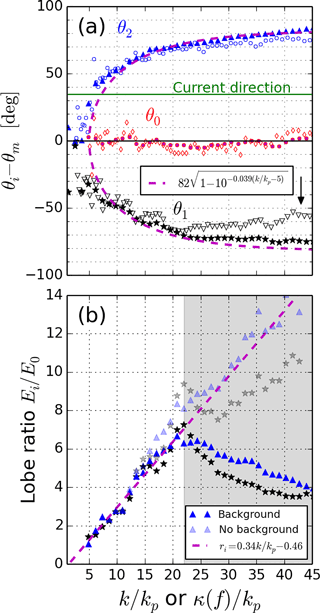
Figure 5 Bimodal directional distribution characteristics from stereo video as a function of normalized wavenumber. (a) Peak positions. (b) Lobe ratios. Empty markers correspond to constant frequency estimates and full markers to constant wavenumber estimates (see Fig. 4 for definitions).

The present-case bimodality is characterized by plotting the positions of the two peaks and the so-called lobe ratios as a function of normalized wavenumber k∕k_p (see Fig. 5). Full markers (triangles, disks and stars) correspond to estimates from constant wavenumber snapshots, while empty markers (circles, diamonds and upside down triangles) correspond to estimates from constant frequency snapshots. For the latter, the x-axis is κ(f)∕k_p – see Eq. (7). Bimodal profiles are first detected at f=0.43 Hz and k=0.7 rad m⁻¹, corresponding approximately to $k/k_{\mathrm{p}}=\mathrm{5}$. The previously mentioned direction θ_m is the best compromise for centering the bimodality. An empirical parametrization is found for the constant wavenumber estimates of the directional distributions, that is,

$$\begin{array}{}\text{(19)}& (\mathit{\theta }-{\mathit{\theta }}_{\mathrm{m}})\left[{}^{\circ }\right]=\mathrm{82}\sqrt{\mathrm{1}-{\mathrm{10}}^{-a\left(k/k_{\mathrm{p}}-\mathrm{5}\right)}},\end{array}$$

where the value a=0.039 was found after a least squares fit of constant wavenumber data points in the range $\mathrm{5}<k/k_{\mathrm{p}}<\mathrm{45}$. This parametrization fits most of the measurements, except the position of the peak furthest from the current direction (θ₁), particularly for the estimates from constant frequency snapshots above $k/k_{\mathrm{p}}=\mathrm{22}$ (see the black arrow in Fig. 5). At this location, the peak is progressively moved towards the center of the directional distribution.

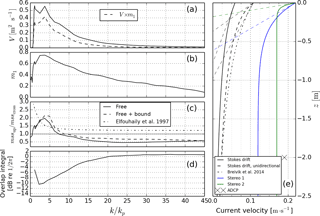
Figure 6 Short wave contribution to various sea state variables. (a) Spectrum of non-directional Stokes drift, Eq. (24). (b) Stokes drift directional correction, Eq. (23). (c) Mean square slope up-wind over cross-wind ratio, Eqs. (30) and (31). (d) Overlap integral, Eq. (34). (e) Near-surface current profiles (see Appendix), with the two-parameter exponential integral profile of Breivik et al. (2014).

The lobe ratios r_i are conventionally defined as the ratios of the energy of each peak of the bimodal directional distribution to the one of the central minimum (Wang and Hwang, 2001), namely

$$\begin{array}{}\text{(20)}& r_i={\displaystyle \frac{E_i}{E_{\mathrm{0}}}},i=\mathrm{1},\mathrm{2}.\end{array}$$

We can note that they are particularly sensitive to the background energy level. This level is given by the constant term C^st of the fitting function (17), without knowing whether this level is an actual surface wave signal or noise. The lobe ratios of the current record are plotted in Fig. 5b, from estimates at constant wavenumber only, with and without this background term. The overall tendency consists in their linear and symmetric increase at intermediate wave scales, until $k/k_{\mathrm{p}}\simeq \mathrm{22}$. As for peak positions in Fig. 5a, the lobe ratios from constant frequency estimates exhibit a more pronounced asymmetry. A fit is performed over constant wavenumber lobe ratios (full markers) for which $\mathrm{4}<k/k_{\mathrm{p}}<\mathrm{22}$, providing the parametrization

$$\begin{array}{}\text{(21)}& r_i=\mathrm{0.34}k/k_{\mathrm{p}}-\mathrm{0.45}.\end{array}$$

Above $k/k_{\mathrm{p}}\simeq \mathrm{22}$, the lobe ratios progressively decrease, except if the background term C^st>0 is removed (transparent markers in Fig. 5). The lobe ratio decrease is natural since the lobe ratios without background are

$$\begin{array}{}\text{(22)}& r_i^{\prime }={\displaystyle \frac{E_i-C^{\mathrm{st}}}{E_{\mathrm{0}}-C^{\mathrm{st}}}}>r_i\end{array}$$

as long as r_i>1 and the proportion of background noise increases towards shorter scales. We cannot however formally associate this noise with an actual surface wave signal.

The Stokes drift current for linear waves in deep water is (Kenyon, 1969)

$$\begin{array}{}\text{(23)}& u_{\mathrm{s}}\left(z\right)=\underset{\mathrm{0}}{\overset{\mathrm{\infty }}{\int }}dkV\left(k\right)m_{\mathrm{1}}\left(k\right)e^{\mathrm{2}kz},\end{array}$$

where

$$\begin{array}{}\text{(24)}& V\left(k\right)=\mathrm{2}\mathit{\sigma }\left(k\right)k{E}_{\mathrm{free}}\left(k\right)\end{array}$$

is plotted in Fig. 6a, and where the impact of the wave field directionality is included in the factor

$$\begin{array}{}\text{(25)}& m_{\mathrm{1}}\left(k\right)=\sqrt{a_{\mathrm{1}}^{\mathrm{2}}+b_{\mathrm{1}}^{\mathrm{2}}},\end{array}$$

plotted in Fig. 6b with

$$\begin{array}{}\text{(26)}& a_{\mathrm{1}}\left(k\right)=\underset{\mathrm{0}}{\overset{\mathrm{2}\mathit{\pi }}{\int }}d\mathit{\theta }{M}_{\mathrm{free}}\left(k,\mathit{\theta }\right)\cos \left(\mathit{\theta }-\overline{\mathit{\theta }}\right)\end{array}$$

and

$$\begin{array}{}\text{(27)}& b_{\mathrm{1}}\left(k\right)=\underset{\mathrm{0}}{\overset{\mathrm{2}\mathit{\pi }}{\int }}d\mathit{\theta }{M}_{\mathrm{free}}\left(k,\mathit{\theta }\right)\sin \left(\mathit{\theta }-\overline{\mathit{\theta }}\right)\end{array}$$

the Longuet-Higgins coefficients with respect to the mean wave propagation direction, where

$$\begin{array}{}\text{(28)}& E\left(k,\mathit{\theta }\right)=M\left(k,\mathit{\theta }\right)E\left(k\right)\end{array}$$

and

$$\begin{array}{}\text{(29)}& \underset{\mathrm{0}}{\overset{\mathrm{2}\mathit{\pi }}{\int }}M\left(k,\mathit{\theta }\right)d\mathit{\theta }=\mathrm{1}.\end{array}$$

The resulting Stokes drift vertical profile has been plotted in Fig. 6e, together with two profiles compatible with the effective current measured from stereo video (see Appendix). Waves slightly shorter than peak waves are the main contributors to the Stokes drift (Fig. 6a). Half of the Stokes drift is carried by waves with frequencies greater than 0.4 Hz approximately (wavelength 10 m). In order to correct for the stereo device field of view limitation (long waves are indeed not spatially resolved), the wavenumber spectrum for k<Δk has been evaluated from their frequency spectrum using the Jacobian transform. In particular, the short wave bimodality substantially reduces the contribution of those waves to the Stokes drift. At a given wave scale, contributions symmetric with respect to the mean wave propagation direction cancel out laterally, resulting in a decrease in the Stokes drift at those scales (Fig. 6b). In particular, the Stokes drift at z=0 is reduced by 44 % (from 0.11 to 0.06 m s⁻¹), which is greater than the approximately 20 % reduction reported in Ardhuin et al. (2009) and Breivik et al. (2014). Mean square slopes in the up-wind and cross-wind direction are defined by

$$\begin{array}{}\text{(30)}& {\mathrm{mss}}_{\mathrm{up}}\left(k\right)=\underset{\mathrm{0}}{\overset{\mathrm{2}\mathit{\pi }}{\int }}d\mathit{\theta }{k}^{\mathrm{2}}E\left(k,\mathit{\theta }\right){\cos }^{\mathrm{2}}\left(\mathit{\theta }-\overline{\mathit{\theta }}\right)\end{array}$$

and

$$\begin{array}{}\text{(31)}& {\mathrm{mss}}_{\mathrm{cross}}\left(k\right)=\underset{\mathrm{0}}{\overset{\mathrm{2}\mathit{\pi }}{\int }}d\mathit{\theta }{k}^{\mathrm{2}}E\left(k,\mathit{\theta }\right){\sin }^{\mathrm{2}}\left(\mathit{\theta }-\overline{\mathit{\theta }}\right),\end{array}$$

and are of particular interest for ocean remote sensing (Munk, 2009). Due to the wave field bimodality, the mean square slope is rather carried by cross-wind propagating waves than up-wind ones (Fig. 6c) at short scales, as was qualitatively described in Elfouhaily's delta ratio (Elfouhaily et al., 1997). Bound waves cause a slight increase in the mean square slopes in the up-wind direction. Finally, short wave directional distributions are critical in understanding the source of seismo-acoustic noise (Farrell and Munk, 2010), caused by quasi-stationary pressure oscillations at the sea surface (Longuet-Higgins, 1950). The spectrum of stationary pressure waves can be written as

$$\begin{array}{}\text{(32)}& F_{\mathrm{p}}=F_{\mathrm{p},\mathrm{free}}+F_{\mathrm{p},\mathrm{bound}},\end{array}$$

where the free wave contribution is proportional to the overlap integral I (Wilson et al., 2003),

$$\begin{array}{}\text{(33)}& F_{\mathrm{p},\mathrm{free}}\propto E_{\mathrm{free}}^{\mathrm{2}}\left(k\right)I\left(k\right),\end{array}$$

given by

$$\begin{array}{}\text{(34)}& I\left(k\right)={\displaystyle \frac{\mathrm{2}{\int }_{\mathrm{0}}^{\mathit{\pi }}d\mathit{\theta }{E}_{\mathrm{free}}\left(k,\mathit{\theta }\right)E_{\mathrm{free}}\left(k,\mathit{\theta }+\mathit{\pi }\right)}{E_{\mathrm{free}}^{\mathrm{2}}\left(k\right)}}.\end{array}$$

The correction arising from bound harmonics F_p,bound has never been rigorously considered in past studies, but should remain weak. The overlap integral (Eq. 34) has been plotted in Fig. 6d. For the same energy level at a given wave scale, the overlap integral is increased from a unimodal to a bimodal directional distribution. In particular, at short enough scales, more energy should be radiated by a bimodal surface wave field than by an equivalent isotropic wave field (for which the value 1∕(2π) is reached). The parametrization of Duennebier et al. (2012) is also superimposed.

5 Discussion and summary

The characteristics of a bimodal short surface wave energy distribution are extracted from the spectrum of a single stereo-video reconstruction of the sea surface at the Acqua Alta platform. Peak positions and lobe ratios are computed which can quantitatively summarize the observations, with associated parametrizations.

The domain of surface waves which can be measured with this system depends on the configuration of the device. Stereo video has a wide scale coverage and an upper bound that is not limited by the Nyquist frequency and wavelength (here $f_{\mathrm{s}}/\mathrm{2}=\mathrm{7.5}$ Hz and $\mathrm{1}/\left(\mathrm{2}\mathrm{\Delta }x\right)=\mathrm{15.7}$ rad m⁻¹), but rather by the accuracy of reconstruction of short waves of small amplitudes. The effective directional resolution can be computed using

$$\begin{array}{}\text{(35)}& \mathrm{\Delta }\mathit{\theta }\sim \arctan \left[{\displaystyle \frac{max\left(\mathrm{\Delta }{k}_x,\mathrm{\Delta }{k}_y\right)}{\mathit{\kappa }\left(f,U\left(f\right)\right)}}\right].\end{array}$$

In our case, for 1 Hz waves, Δθ∼5^∘, and for 0.5 Hz waves, it reaches 15^∘.

Bimodality has been characterized by extracting the positions of the two bimodal peaks and the central minimum from directional distributions of the free waves, either at constant frequency or constant wavenumber (see Fig. 4). Free waves only are affected by bimodality at both a given wavenumber and frequency. Moreover, bound waves' distribution can be deduced from one of the free waves (Leckler et al., 2015). The short waves' field bimodality starts growing between $k/k_{\mathrm{p}}=\mathrm{3.6}$ and $k/k_{\mathrm{p}}=\mathrm{4.3}$ from constant wavenumber snapshots, or between $k/k_{\mathrm{p}}=\mathrm{4.8}$ ($f/f_{\mathrm{p}}=\mathrm{2.16}$) and $k/k_{\mathrm{p}}=\mathrm{5.2}$ ($f/f_{\mathrm{p}}=\mathrm{2.23}$) from constant frequency snapshots. Bimodality may be initiated at even larger scales and not detected, due to a directional resolution at those scales which is smaller than the peak distance – Eq. (35). The two peaks then detach from the main direction θ_m. Apart from the asymmetry introduced by the current, the three points characterizing bimodality sensibly fluctuate around their positions, reaching a distance of ∼160^∘ towards $k/k_{\mathrm{p}}=\mathrm{45}$, the latter being the accepted limit for stereo-video measurement validity. The real bimodal directional distribution differs from its parametrizations mainly at wave scales smaller than $k/k_{\mathrm{p}}=\mathrm{22}$. This is particularly the case for the peak furthest from the current direction at a given frequency (see the arrow in Fig. 5a) which gets away from the parametrization by slowly moving closer to the center of the directional distribution, while the constant wavenumber estimates remain close to the parametrization, with an almost perfectly symmetric distribution. This difference might come from the effect of the current. Indeed, the two peaks at a given wavenumber do not appear at the same frequency because of the presence of the current. For example, in Fig. 4d, the waves at k=4.0 rad m⁻¹ exhibit a bimodal behavior which is symmetric with respect to the main wave propagation direction θ_m. In the absence of a current, the two peaks would appear at the same frequency: f=1.0 Hz. In this snapshot, the peak furthest from the current, i.e., θ₁, is located at a frequency f=0.95 Hz, while the other peak is located at a frequency f=1.022 Hz. The shift is larger for the former, θ₁, than for θ₂; hence, the current is a cause of asymmetry in bimodality characteristics. As a consequence, the wavenumber parametrization is more robust against currents than is the frequency one, as was already observed by Wyatt (2012). This is the one chosen throughout this paper. This asymmetry is also visible in Fig. 5b.

We have reported on new stereo-video recordings of ocean waves that offer a wider range of resolved scales than previous datasets, up to $k/k_{\mathrm{p}}=\mathrm{45}$. Looking at free waves, the bimodal nature of their directional distribution is more pronounced at the shorter scales, with a separation of the two peaks that exceeds 160^∘. This distribution was found to reduce the Stokes drift by over 40 % compared to a unidirectional wave field, with a significant source of acoustic noise due to waves in opposing directions, typically larger than an isotropic spectrum for $k/k_{\mathrm{p}}>\mathrm{20}$. These effects are partly compensated for by the importance of bound harmonics which have directions closer to the mean wave direction. The analysis of the contribution of these nonlinear components to the Stokes drift and acoustic noise is beyond the scope of the present paper.

Appendix A: Free wave extraction and current vector estimation

The extraction of free wave components from the surface elevation spectrum is detailed here. Looking at snapshots of Figs. 2 and 3, there is no ambiguity in the distinction between free (along the dispersion line, black) and bound (white line) waves, except if the spatial resolution is limiting. From Eqs. (4) to (6), their location in the (k,f) space is determined by the value of the effective current U, Eq. (6), at each wave scale. It depends on the true near-surface current vertical profile u(z).

A1 Effective current measurement

Starting from a snapshot of the surface elevation spectrum at a given frequency or wavenumber (see Fig. 4 for example), the estimate of the effective current which minimizes the cost function

$$\begin{array}{ll}{\displaystyle }g\left(U_x,U_y\right)=& {\displaystyle }\sum _{j=\mathrm{1}}^N{\displaystyle \frac{w_j}{{\mathit{\chi }}^{\mathrm{2}}}}\left[\mathrm{2}\mathit{\pi }{f}_j-\sqrt{g{k}_j}\right.\\ \text{(A1)}& {\displaystyle }& {\displaystyle }{\left.-k_j\left(U_x\cos {\mathit{\theta }}_j+U_y\sin {\mathit{\theta }}_j\right)\right]}^{\mathrm{2}}\end{array}$$

is retained, where (U_x,U_y) are the coordinates of the effective current vector in the local frame and w_j are empirical weights, normalized so that ${\sum }_{j=\mathrm{1}}^N{w}_j=N$, and where χ is the expected standard deviation of model and data, adapted from Senet et al. (2001):

$$\begin{array}{}\text{(A2)}& {\mathit{\chi }}^{\mathrm{2}}={\displaystyle \frac{\mathrm{1}}{N-\mathrm{2}}}\sum _{j=\mathrm{1}}^N{w}_j{\left[\mathrm{2}\mathit{\pi }{f}_j-k_j\left(U_x\cos {\mathit{\theta }}_j+U_y\sin {\mathit{\theta }}_j\right)\right]}^{\mathrm{2}}.\end{array}$$

The flexibility of this method relies upon a careful choice of data points and weights.

This choice is exposed here for the case of a constant frequency snapshot. First, a rough estimate of the current is required in order to approximately locate the dispersion relation. For this experiment, the current vector does not vary much with wave scales. This estimate is obtained by manually selecting data points on the dispersion relation of ∼1 Hz waves (10 are enough) and by minimizing the cost function with equal weights. The index 0 is put on the current value obtained (U₀=0.22 m s⁻¹ and α₀=102^∘). A second cost function is computed by keeping only data points for which

$$\begin{array}{}\text{(A3)}& \mathit{\kappa }({\mathit{f}}_j,{\mathit{U}}_{\mathrm{0}})-\mathrm{0.1}\mathit{\kappa }\left({\mathit{f}}_j\right)<k_j<\mathit{\kappa }({\mathit{f}}_j,{\mathit{U}}_{\mathrm{0}})+\mathrm{0.1}\mathit{\kappa }\left({\mathit{f}}_j\right).\end{array}$$

Then, among the rest, the ones with the lowest signal-to-noise ratio are removed:

$$\begin{array}{}\text{(A4)}& {\displaystyle \frac{E_j}{\underset{j}{max}\left(E_j\right)}}<\mathrm{0.01}.\end{array}$$

The weights are

$$\begin{array}{}\text{(A5)}& w_j\propto {\displaystyle \frac{E_j-\underset{j}{min}\left(E_j\right)}{\underset{j}{max}\left(E_j\right)}}d{S}_j\end{array}$$

and then normalized, where the index j runs over remaining data points, and dS_j stands for the elementary surface around data point j. The minimization algorithm is initiated with values U₀ and α₀, and run until convergence at each frequency, providing a more accurate result than the rough estimate. Finally, free waves are isolated using this more accurate estimate. Only the points with coordinates (k_j,θ_j) are kept if they fall in the interval

$$\begin{array}{}\text{(A6)}& \mathit{\kappa }({\mathit{f}}_j,\mathit{U})/\mathrm{1.15}<k_j<\mathrm{1.15}\mathit{\kappa }({\mathit{f}}_j,\mathit{U}).\end{array}$$

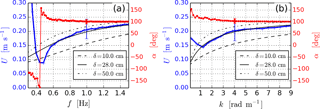
Figure A1 Effective current magnitude (blue) and direction (red) as a function of frequency (a) and wavenumber (b), after smoothing over five adjacent points. Superimposed are the analytical profiles corresponding to a typical wind drift current when u_b=0.1 m s⁻¹ with various values of δ (see text for explanations).

The same procedure can be applied to constant wavenumber snapshots. It is the same as the one of the previous paragraph, after having exchanged k with f and κ with ω∕(2π).

A2 Current profile

The effective current values at all wave scales from the extraction of free waves are plotted in Fig. A1. Either as a function of frequency or wavenumber, both estimates show a gradual increase in the effective current magnitude towards U₀=0.22 m s⁻¹ and α₀=102^∘. These values are in agreement with ADCP measurements indicating a current of 0.19 m s⁻¹ flowing from the direction 110^∘ at 2 m below the surface, which is already too deep to significantly influence the effective current. Effective currents for typical wind drift profiles $u\left(z\right)=u_a+u_b{e}^{z/\mathit{\delta }}$ are plotted in Fig. A1 for various values of δ. We assume that u_b=0.1 m s⁻¹, i.e., 1 % of the surface wind speed, and $u_a=U_{\mathrm{0}}-u_b=\mathrm{0.12}$ m s⁻¹, yielding a surface vertical shear $u_b/\mathit{\delta }=\mathrm{0.36}{\mathrm{s}}^{-\mathrm{1}}$. Two plausible profiles have been plotted in Fig. 6e, for which

$$\begin{array}{}\text{(A7)}& u\left(z\right)\left[\mathrm{m}{\mathrm{s}}^{-\mathrm{1}}\right]=\mathrm{0.12}+\mathrm{0.1}{e}^{z/\mathrm{0.28}\left[\mathrm{m}\right]},\end{array}$$

denoted Stereo 1, and

$$\begin{array}{}\text{(A8)}& u\left(z\right)\left[\mathrm{m}{\mathrm{s}}^{-\mathrm{1}}\right]=\mathrm{0.17}+\mathrm{0.05}{e}^{z/\mathrm{0.04}\left[\mathrm{m}\right]},\end{array}$$

Stereo 2.