Mean circulation and EKE distribution in the Labrador Sea Water level of the subpolar North Atlantic

A long-term mean flow field for the subpolar North Atlantic region with a horizontal resolution of approximately 25 km is created by gridding Argo-derived velocity vectors using two different topography-following interpolation schemes. The 10-day float displacements in the typical drift depths of 1000 to 1500 m represent the flow in the Labrador Sea Water density range. Both mapping algorithms separate the flow field into potential vorticity (PV) conserving, i.e., topography-following contribution and a deviating part, which we define as the eddy contribution. To verify the significance of the separation, we compare the mean flow and the eddy kinetic energy (EKE), derived from both mapping algorithms, with those obtained from multiyear mooring observations.

The PV-conserving mean flow is characterized by stable boundary currents along all major topographic features including shelf breaks and basin-interior topographic ridges such as the Reykjanes Ridge or the Rockall Plateau. Mid-basin northward advection pathways from the northeastern Labrador Sea into the Irminger Sea and from the Mid-Atlantic Ridge region into the Iceland Basin are well-resolved. An eastward flow is present across the southern boundary of the subpolar gyre near 52^∘ N, the latitude of the Charlie Gibbs Fracture Zone (CGFZ).

The mid-depth EKE field resembles most of the satellite-derived surface EKE field. However, noticeable differences exist along the northward advection pathways in the Irminger Sea and the Iceland Basin, where the deep EKE exceeds the surface EKE field. Further, the ratio between mean flow and the square root of the EKE, the Peclet number, reveals distinct advection-dominated regions as well as basin-interior regimes in which mixing is prevailing.

1 Introduction

The subpolar North Atlantic (SPNA) has been in the focus of both observational and modeling efforts with regard to circulation- and water mass changes as part of the climate relevant Atlantic Meridional Overturning Circulation (AMOC; e.g., reviewed by Daniault, et al., 2016). In this context the intermediate depth circulation, which also determines the spreading pathways of newly ventilated Labrador Sea Water (LSW) through the SPNA, is of specific importance and has been investigated from observations and models for several decades. A better understanding of the mechanisms that control the transport properties at mid-ocean depth through the interplay of advection and diffusion is fundamental to our understanding of subpolar LSW circulation and export, and thus potentially subpolar AMOC contributions. Unlike the surface circulation, which can be analyzed for example from satellite and drifter data, the intermediate depth circulation and energetics is known to a much lesser extent. Studies that map energetics at the intermediate depth from observational data and at gyre scales are rare but identified, for example, as important evaluation metrics for basic verification of ocean model simulations, including the Coupled Model Intercomparison Project (CMIP) models (Griffies et al., 2016).

In the late 1990s, the technology of profiling floats advanced such that investigations of the intermediate deep circulation could be undertaken. Two experiments were carried out in the western SPNA (mainly in the Labrador and Irminger seas) using Profiling ALACE (PALACE, where ALACE is the Autonomous Lagrangian Circulation Explorer) floats and are of special interest to the investigation carried out herein. The first was by Lavender et al. (2000, 2005) with a large fleet of floats drifting through the Labrador and Irminger seas at 700 m of depth (the approximate depth level of upper LSW in the SPNA). A major result of the study was that the intermediate depth circulation could well be described as a cyclonic boundary current system along the topography and a series of anticyclonic recirculation cells adjacent to the Deep Western Boundary Current (DWBC). The second experiment was dedicated to the boundary current off Labrador, and conducted in summers 1997 and 1999 with 15 PALACE floats seeded into the DWBC off Labrador to drift at 1500 m, the core depth of classical LSW (Fischer and Schott, 2002). The main finding of this study, and contrary to the expectations, was that none of the floats were able to exit the subpolar gyre via the boundary current route. Instead, some of the floats confirmed the existence of a recirculation cell off Labrador and others indicated an eastward route following the North Atlantic Current (NAC) at its northeastern pathway. This result stimulated a series of Lagrangian experiments (Bower et al., 2009) using RAFOS (where ROFAS is SOFAR spelled backwards with SOFAR meaning SOund Fixing And Ranging) drifters but also model studies (e.g., Spall and Pickart, 2003).

With the deployment of the global array of Argo profiling floats at the end of the 1990s the number and spatial homogeneity of displacement vectors at the floats parking depth of typically 1000 or 1500 m increased significantly. The data set is assembled in the YoMaHa'07 data base (Lebedev et al., 2007). Based on this much larger database it is of interest to revisit the earlier results. One of the immediate questions is how robust the earlier findings are; and moreover, whether the present-day Argo data coverage would be sufficient to prove and possibly refine the earlier results. There are two approaches to these objectives: one is to investigate temporal changes in the deep circulation on interannual timescales but with a drawback on spatial resolution. Palter et al. (2016) followed that approach and found a slowdown in boundary current flow in the Labrador Sea but no significant changes in the large-scale subpolar gyre circulation. Another approach, and this is taken here, is to neglect temporal variability and use all available displacement data for determining a mean flow field on a finer spatial resolution that resembles narrow circulation elements in a higher resolution compared to what has been discussed in the past.

Several attempts have been undertaken to estimate advective (long-term mean) and diffusive contributions in the displacement vectors on the basis of statistical and physical constraints. While the displacements of the profiling floats may be well suited to determine the long-term mean of the flow field, this is not straight forward for the eddy component of the flow field (Davis, 2005; Davis et al., 2001). The author suggested calculating the diffusivity from displacement anomalies u^′ calculated from the difference of the mean flow <U> and the measured displacement vector U_m. Here, we loosely follow the method proposed by Davis (1998), in which the mean flow is controlled by topography (f∕H, where H is the water depth), an assumption that should hold true in the SPNA regime where weak stratification and small vertical current shear is encountered. Thus, we will estimate the advective part of the flow that is related to the concept of potential vorticity (PV) conservation (LaCasce, 2000), and the residual flow contribution that is attributed to the diffusive part of the flow. Validation of this principle has been performed in the past (see Fischer and Schott, 2002; Fischer et al., 2004) through a comparison of deep displacements along curved topography in relation to moored (Eulerian) records.

We focus here on the SPNA north of 45^∘ N and make use of the extended set of Eulerian (current meter moorings) and Lagrangian (floats) observations available in the region. Over the previous two decades (regionally even longer) an impressive observing effort has been undertaken north of 45^∘ N on the (intermediate) deep flow. Boundary currents are, thanks to their strength, the prominent circulation features in the SPNA and found all along the shelf edges in particular on the western side of the gyre. However, there are also interior circulation features of both advective- and eddy-dominated patterns, and the primary research objective of this effort is to discriminate the mean flow <U> from the turbulent (eddy) component u^′ of the flow field from which the deep EKE field could be determined.

The paper is structured as follows. First, we briefly describe the methods to separate <U> and an accompanying u^′, obtained for each displacement vector from the difference between the observed displacement and the displacement projected to a PV contour. The fields obtained by two different gridding methods are verified for internal consistency, and in comparison to independent measurements from mooring records. Next, a gridded velocity and an eddy kinetic energy (EKE) field of relatively high spatial resolution (on the order of 25 km grid size) for the SPNA is created by both gridding procedures. We discuss the fields for internal consistency based on major flow features. Furthermore, the ratio of advective flow and diffusion (Peclet number) is estimated. The EKE field at depth is then compared with the EKE field at the surface, based on satellite data. The gridded data sets are provided for download and further use, e.g., for model and data comparison; so far we are not aware of an intermediate depth EKE map.

Figure 1 Data density in $\mathrm{1}{}^{\circ }\times \mathrm{1}{}^{\circ }$ fields; the number of 10-day displacement vectors per cell.

2 Material and methods

Two quality controlled Argo displacement (deep and surface) sets exist, but cover somewhat different time spans. Here, we use the YoMaHa'07 Argo data set (Lebedev et al., 2007), which contains estimates of velocities of deep and surface currents using data of the trajectories from displacements between consecutive dives of Argo floats. The YoMaHa'07 data set is frequently updated on a monthly basis.

This technical paper contains most of the necessary processing stages for both the deep and the surface velocity. There is also some discussion regarding the error sources arising as a consequence of the 3-dimensional measurements; in this report there is a discussion on the error assessment of deep velocity due to vertical shear of horizontal flow. While the floats are ascending from their drift, they will be subject to the flow field in the water column. In a weakly sheared environment like the SPNA this effect is considered to be small. However, there is a much larger error source that is due to calculating straight-line displacement vectors, which in the presence of curved bathymetry is large and has a bias. This is illustrated by the following example of the DWBC surrounding Hamilton Bank near 55^∘ N off Labrador. A float that travels in this area at a mean speed of 15 cm s⁻¹ will pass around Hamilton Bank within one or two dive cycles of the float. The difference between a straight-line displacement and the displacement estimated from the length of, for example, the 1500 m isobath can be different by about 30 %; thus, the straight-line displacement is biased low especially in areas of high velocities and curved topography, e.g., the DWBC.

2.1 Temporal and spatial distribution of the Argo float array

By March 2017 (this is the latest date considered for this analysis) the displacement data set includes data from 4284 floats stored in nine data assembly centers worldwide and about 297 000 values of velocity. We define a velocity vector as the displacement between an Argo float descent (last surface position) and the consecutive ascent (first surfacing position) divided by the corresponding time difference. Some inhomogeneity in position and time accuracy based on the communication and positioning technology (Argos, Iridium) is discussed in Lebedev et al. (2007). The nominal position of the velocity vector is the mean position between the descent and ascent position pair.

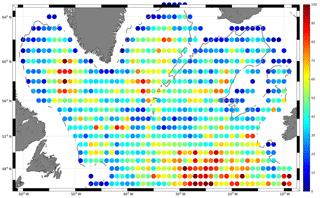
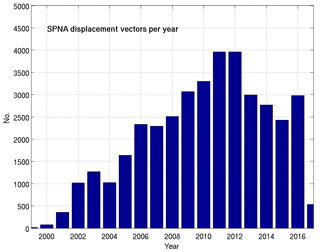
The area under investigation ranges from 45^∘ N, the latitude just south of the Flemish Cap, to 65^∘ N, which is just south of the Denmark Strait (Fig. 1). The westernmost longitude is 62^∘ W, i.e., the Labrador shelf break, and to the east the area is bounded at 7^∘ W west of the British Isles. The evolution of the Argo data in this domain shows a rapid increase in data density in the first 5 years of the program (Fig. 2), and from 2006 onwards the data density is adding around 2500 to 3000 displacement vectors per year; this is roughly equivalent to the number of temperature and salinity profiles gained through Argo per year. Maximum annual data increase is reached in 2011/2012 with 4000 additional current vectors each year. Thereafter, the yearly data gain stabilizes at 2500 to 3000 current vectors.

The regional data density ranges from approximately 10 to more than 100 per bin (2^∘ longitude × 1^∘ latitude; Fig. 1); the bin size corresponds with the typical area in which data will be used for the interpolation to a certain grid point. Given the barotropic nature of the flow field in the SPNA, we merged the displacement vectors from the two drift depths (1000 and 1500 m depths). Considering the temperature and salinity data recorded by the floats, the mean potential density field at 1500 m varies between σ_θ=27.72 and 27.92 kg m⁻³ with an average density of σ_θ=27.77 kg m⁻³. This density is slightly lower than the commonly used lower boundary of classical LSW at σ_θ=27.80 kg m⁻³, and thus the resulting circulation pattern represents the core depth of the LSW.

Figure 2 Temporal evolution of the Argo data density in the subpolar domain independent of the parking depths (1000 and 1500 m), and from year 2000 to March 2017.

2.2 Auxiliary data

To estimate contours of constant PV defined as the Coriolis parameter divided by water depth (f∕H), we used the high-resolution topographic data 2-minute Gridded Global Relief Data (ETOPO2; National Geophysical Data Center, 2006). This topography is based on a combination of depth soundings and depth estimates from multiple sources and gridded to a 2 min special resolution. Only in one case we use the higher resolved ETOPO1 version, but this did not change the results.

Furthermore, we used altimetry-based absolute dynamic topography from which the surface geostrophic flow and EKE were derived (Le Traon et al., 1998). The altimeter products were produced by Ssalto/Duacs and distributed by Aviso with support from CNES (http://www.aviso.altimetry.fr/duacs/). We used the gridded product with a 0.25^∘ horizontal resolution, similar to the resolution of the deep velocity field. We note, however, that the surface EKE, derived from this product, will be biased low as subgrid-scale variability is smoothed out.

Lastly, Eulerian time series data from moored instrumentation that recorded in the depth interval considered in the analysis here (1000–1500 m) were used to locally evaluate the results of the gridded data product (see Table 1 for an overview). Given the floats inherent sampling at 10 days, the moored records were smoothed accordingly.

Table 1 Eulerian EKE: statistics in the subpolar North Atlantic SPNA. BODC: British Oceanographic Data Centre (https://www.bodc.ac.uk/, last access: March 2018).

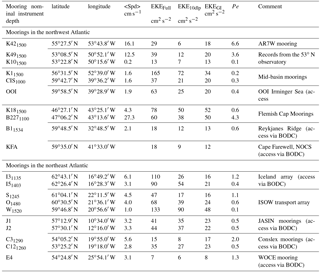
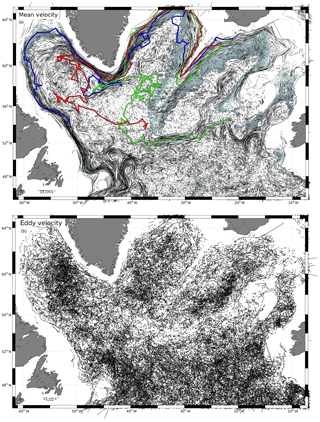
Figure 3 Mid-depth circulation (a) in the western SPNA from ∼38 500 Argo deep drifts (1000 or 1500 m parking depth) derived from the YoMaHa'07 data. This is an attempt to present the advective contribution of the flow field at each measurement location; i.e., for each measured 10-day drift vector (for details of the processing see text). Colored lines for selected float trajectories (deployed in the Iceland Basin); blue shaded area is for the topographic depth range (1500 to 2500 m). The residual (b) is thought to be u^′, the eddy velocity contribution to the flow field.

2.3 Separating mean flow and its fluctuation and interpolation of the results

Two interpolation methods were used to map the displacement vector data: the first is a weighted Gaussian interpolation (GI) and the second is an optimum interpolation (OI) procedure. Both methods use the same physical constraints, and both operate on an identical grid of 0.5^∘ longitudinal range and 0.25^∘ latitudinal range.

2.3.1 Gaussian interpolation method

The strategy of the GI method was to include two constraints in the interpolation procedure, namely a weighted distance between target (grid) point and data point, and the second is to reduce the influence of data points located in regions with very different water depths. The latter is a manifestation of our assumption that flow in the region follows PV contours. Thus, data points across the boundary current at steep topography would only weakly be influenced from nearby but much deeper or shallower locations outside the boundary current (a topography-following mapping).

The weights used have a Gaussian shape described by two parameters for each dimension: for the distance weighting we chose 40 km for the half width of the Gaussian and 80 km for the cut-off – such that points outside a radius of ∼80 km around a selected grid point will not be used. For the other dimension (water depth difference between data location and target location as a measure of PV difference), we chose 200 m half width and 600 m cut-off range. The choice of these values was guided by the dimensions of the boundary current along steep topography (e.g., the Labrador shelf break), with the width of the DWBC (Zantopp et al., 2017) between 100 and 150 km, and a change of water depth across the DWBC from about 1000 to 3000 m. Through this procedure, boundary currents would be conserved and not smeared out, while in the basin interior with a flat bottom the weighting is more toward distance – with little influence of the underlying bathymetry.

We analyzed the impact of different weights over a wide range of scales, but the selection applied here appears to generate the most robust result with a clear definition of the circulation elements described hereafter. Using a higher resolved grid (smaller scales) results in a noisier flow field with larger overall variance, while a coarser grid (together with larger interpolation scales) results in a smoother field and certain details of the flow field are suppressed. The procedure could be applied to both irregular target locations and regular grid locations.

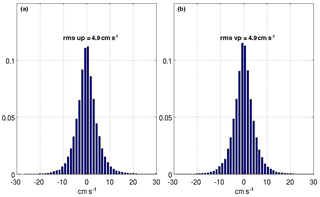
Figure 4 Normalized distribution of the mid-depth eddy velocity components; (a) is u^′ (east–west component) and (b) is v^′ (north–south component) – Gaussian distribution with equal rms of 4.9 cm s⁻¹.

In a first processing step we separate the measurements into a mean flow contribution <U> and a fluctuating part u^′ that will be used later to determine the EKE field. Around each measurement location we selected all data within the cut-off radius and by using the selected weights (see above) we estimate a mean flow vector at the measurement location by applying the above-described algorithm. Thus, we generate a velocity field that has the dimension of the original data set, and it contains only the weighted, PV-related ensemble-mean contribution (Fig. 3a). As an illustration, we show three floats that were deployed at roughly the same location in the northern Iceland Basin at water depths of around 1800 to 2500 m. The length of the trajectories correspond to more than 2 years elapsed since deployment. The floats stayed within that depth range for a significant fraction of that time, and the close correspondence of the float trajectories and the shaded area is an indication of the PV-following nature of the deep flow field.

Subsequently we applied the mapping procedure to the measured velocity field (U_m) to obtain a field on a regular 0.5^∘ longitude × 0.25^∘ latitudinal grid and the result is <U> on a regular grid, which is considered as one of our final data products.

After estimating the mean velocity from the displacement vectors, we calculated the residual flow components (u^′ and v^′) by subtracting the mean component from the original data (Fig. 3b). The EKE is estimated independently for each of the two interpolation methods (GI and OI). Assuming that the separation of the measured displacement vectors into <U> (advective) and a fluctuating (eddy) component is successfully performed by the above methods, it allows one to calculate u^′ and v^′, the fluctuating (eddy) velocity contribution of each displacement vector (Fig. 3b). Both eddy components show similar overall (basin wide) statistics of a Gaussian shape and equal rms values of 4.9 cm s⁻¹ (Fig. 4). The second final data product is the gridded EKE produced from the u^′ and v^′ fields derived through the first interpolation step.

2.3.2 Optimum interpolation method

The second procedure uses the method of optimum interpolation (OI method), similar to the one described in detail in Schmidtko et al. (2013). Data were only mapped if the grid points have a water depth deeper than 1200 m according to the topographic data set. All data within a radius of 110 km and at locations with similar water depths – less than 1000 m difference – were used in the OI. Linear gradients in latitudinal direction, longitudinal direction, and water depth were fitted to the data. For the covariance matrix a diagonal value of 1.5 was used as an estimate for the signal-to-noise ratio (see Schmidtko et al., 2013 for details). The background field used in the OI was taken from a least squares linear and quadratic fit of the data using depth, longitude, and latitude.

The field, resulting from the OI was used as the mean flow field <U>, which was then used to compute the residual flow (u^′) from each displacement vector (U_m) by linear four-point interpolation. An individual EKE value was computed for each displacement. To exclude extreme outliers, an interquartile range filter was applied, rejecting data points 2.2 times the interquartile range above the third quartile or that range below the first quartile. This is similar to a 99.98 % standard deviation filter in the case of normal distributed data. The EKE data were then mapped in an identical procedure as the mean field.

3 Results

3.1 The intermediate depth large-scale circulation from a displacement vector point of view

First we inspected the GI-based interpolation of <U> on the original displacement vector positions, which represents individual mean flow realizations and added a number of selected float trajectories (Fig. 3a). The flow realizations nicely sample the different flow regimes in the SPNA and cover the boundary currents; flow associated with topographic features, such as the Mid-Atlantic Ridge; and prominent flow features, such as the deep extension of the NAC in the NWC. Selected areas are discussed in the following sections.

3.1.1 Boundary currents

Individual mean flow realizations sample the boundary currents and indicate the coherence of the flow along the topography. This is also confirmed by individual float trajectories. Individual floats that were released in the northern Iceland Basin, near the northernmost part of the Reykjanes Ridge (RR), follow the deep boundary current along the topographic slope of the RR southwestward. The displacement vectors indicate swift speeds of approximately 6 to 7 cm s⁻¹. For the selected floats, it takes about 3 months to reach the first gaps in the RR and thus to enter the Irminger Basin. However, different gaps exist and influence the exchange with the Irminger Basin. After crossing the RR, the floats take a northward drift on the western side of RR in the boundary current that surrounds the northern Irminger Sea and downstream merge into the deep East Greenland Current (dEGC). The selected floats stayed for almost 2 years in the deep boundary current inshore of the 1800 m isobaths before they reached Cape Farewell, the southern tip of Greenland and which is about 2500 km downstream (comparable with a mean drift speed of about 4 cm s⁻¹). At about the latitude of Cape Farewell, the northward flow along the western flank of the RR is on the order of 5 cm s⁻¹, while the southward flow along the east Greenland shelf break regionally exceeds 10 cm s⁻¹. The trajectories clearly show that the PV (depth) constraint on the flow is very strong and as such our gridding procedure appropriate.

3.1.2 Labrador Sea

The intermediate circulation in the Labrador See shows narrow cyclonic boundary circulation where the topography is steep, i.e., along the East Greenland and Labrador shelf breaks (Fig. 3a), while in regions with a gentler slope (e.g., northern part of the Labrador Sea) the boundary current widens considerably. From the boundary current to the interior Labrador Sea the flow reveals stable but weak recirculation cells with cyclonic rotation, and the interior of these elongated cells is almost stagnant, as is also seen in time series measurements (Fischer et al., 2010) of the 53^∘ moored array at location K10, where the mean 1500 m flow is 0.8 cm s⁻¹ northwestward, and at K9 where the mean flow is 12.5 cm s⁻¹ but southeastward (Fig. 5b; Table 1).

The nearly stagnant, weakly anticyclonic circulation is observed for the area where deep convection takes place. Here the water is trapped within the closed circulation in the region of strong wintertime buoyancy loss. Both the cyclonic recirculation cells along the Labrador shelf break and the anticyclonic interior are thus favorable for deep convection. At 1500 m depth, the lightest water is found in the central Labrador Sea and is surrounded by extremely weak (on the order of 1 cm s⁻¹) anticyclonic flow. Eventually the water in the central Labrador Sea feeds the advective path around Cape Farewell thereby exporting light and weakly stratified water into the Irminger Sea. Further south, at the exit of the Labrador Sea, the flow enters a very active eddy regime in a region with very variable topography – the Orphan Knoll region near 47^∘ W, 51^∘ N. Here the northwest corner of the NAC and the outflow of the Labrador Sea merge and interact.

3.1.3 Irminger Sea

The Irminger Sea has several characteristic flow patterns at intermediate depth (Fig. 3a). The most pronounced feature is the dEGC that exists over the whole western part of the basin. On the opposite side the Irminger Sea is bounded by the RR that is a barrier for most of the flow beneath 1000 m depth. Further south, several gaps in the ridge allow the water from the eastern basin to spill over the ridge and a northward deep boundary current forms along the western flank of the ridge. This is one source of the dEGC. A second source of the intermediate dEGC is the mid-basin current band that is fed from the Labrador Sea and extends up to 64^∘ N where it enters the dEGC; the cyclonic circulation that this mid-basin vein forms is sometimes called the Irminger Gyre. Within the Irminger Gyre, a number of long-term moorings have been maintained for more than a decade to record the thermohaline evolution of the gyre center and possibly deep convection underneath the Greenland tip jet (e.g., Pickart et al., 2003); the moorings are nowadays incorporated into the international OSNAP (Overturning in the Subpolar North Atlantic Program) program (Lozier et al., 2016) and the OOI (Ocean Observatories Initiative, http://ooinet.oceanobservatories.org, last access: March 2018). The mid-basin current band appears to have a number of meanders that are also visible in the 1500 m geopotential derived from the Argo profile data.

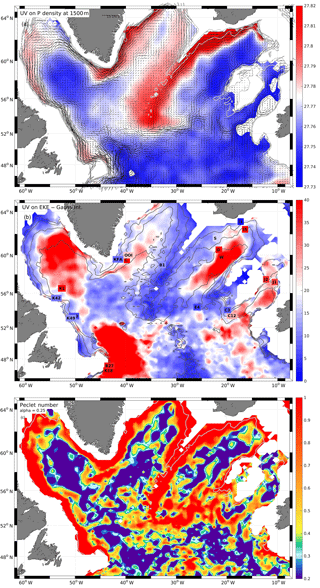
Figure 5 (a) Gridded velocity field from the GI method overlaid on potential density distribution from 1500 m depth. (b) Gridded EKE (in cm² s⁻²) map from the GI method with selected EKE values from moored observations (numbers in boxes). Mooring fluctuations are low-pass filtered at 10 days cut-off for better comparability of mooring time series with 10-day displacement velocity from Argo data. Mooring location markers are colored with respect to the EKE from the moored record; color map is identical to that of the background field. (c) The ratio of mean speed to the square root of the EKE scaled by a factor alpha = 0.25, i.e., a measure of the Peclet number Pe.

3.1.4 Iceland Basin

The Iceland Basin, which is less well investigated, has two major topographic features that influence the circulation strongly. The western limit of the Iceland Basin is the RR that shows the already discussed boundary current. At the location of the CGFZ, which is at about 52^∘ N, dynamically forms the southern boundary of the basin and where the circulation at the LSW depth is eastward in connection to the NAC supplying water towards the eastern SPNA.

Two branches of the NAC are evident (Fig. 3a): the majority of the floats drift far eastward in a strongly meandering current band (300–350 km wavelength) until arriving at the topography (still at the latitude of the CGFZ, i.e., 52^∘ N). Thereafter, the flow follows the topography northward into the Rockall Trough west of Ireland. On the western flank of the Rockall Plateau, a narrow eastern boundary current forms and flows northward until it reaches the Iceland–Scotland Ridge, where it feeds the southwestward boundary current (discussed above) that eventually becomes a “western” boundary current along the RR. However, the broadest inflow comes from the mid-basin flow regime that extends from the NAC northward from about 27^∘ W, and follows the deep trench northward to 62^∘ N. This mid-basin flow is characterized by stable advection and several large wave number meanders.

3.1.5 The North Atlantic Current regime

The southern exit of the Labrador Sea is the region where the NAC meets the DWBC (Fig. 5a); and while the LSW follows the topography inside a topographic feature called “Orphan Knoll” (50^∘ N, 46^∘ W), the NAC is located seaward of the Orphan Knoll and is retroflected toward the east in a feature known as the NWC. The latitude of the NWC is also at 52^∘ N, and from there the NAC meanders eastward through the CGFZ. The zonal flow field and the associated southern signature of the polar front can be interpreted as the southern limit of the SPNA and it forms the zonal component of the large-scale cyclonic circulation. In the LSW depth range the Polar-Front separates the lighter water to the south from the denser subpolar gyre.

3.2 Gridded mean flow

By application of the GI method, the velocity field was interpolated to a regular grid of 0.25^∘ latitude and 0.5^∘ longitude (Fig. 5a). As for the raw data maps (Fig. 3a) the gridded data reflect all the major circulation elements. The interpolation method keeps the deep boundary currents as narrow and stable jets that are resolved by five or more grid points. Mid-basin jets in the Irminger Sea and the Iceland Basin appear as continuous but meandering pathways of the intermediate deep circulation. The correspondence of the current field and the potential density at 1500 m depth is evident. The strongest density gradients are associated with the western boundary current elements along the eastern RR, associated with the East Greenland Current (EGC), and to a lesser extent with the Deep Labrador Current. In combination with the deep density, the major export routes for newly ventilated LSW are also visible in the potential density pool of the central Labrador Sea draining into the Irminger Sea. There is also a connection between the NWC and the convection area by a low density anomaly that is not associated with the DWBC, but with the reverse circulation into the Labrador Sea.

Although, we only show the mean gridded flow field from the GI method we do obtain the same results from the OI method. The differences in the two estimations mainly contain small-scale elements that reflect the scales of the influencing radii by either method.

3.3 Gridded eddy kinetic energy

From the individual u^′ and v^′ fields we generated a smoothed and gridded version of the EKE (Fig. 5b) using the same interpolation parameters as for the mean field – i.e., both fields have the same length scales in consideration, and the grid is identical. “Smoothed” also means that some de-spiking and noise reduction during the gridding operation was applied, as there were a few individual spikes along the edges of the mapping environment, i.e., in regions where the mapping area intersects the 1500 m topography and where floats might have become bottom-stuck. These spikes could be easily detected and accounted to less than 2 % of the data contributing to an individual grid point. As a result the cleaned EKE distribution is smoother and more reliable.

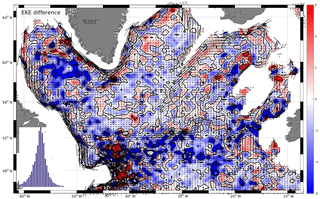
Figure 6 EKE map difference between optimum interpolation (OI) and Gaussian interpolation methods. Inset at lower left: histogram of difference reveals Gaussian shape and a weak bias of $\mathit{<}\mathrm{dEKE}\mathit{>}=-\mathrm{1}$ cm² s⁻².

We note several intense EKE hot spots in the Labrador Sea, in the NWC of the NAC, and in the eastern SPNA located east and west of the Rockall Plateau. While it is not surprising that the retroflection of the NAC (i.e., the NWC) shows large EKE values exceeding 250 cm² s⁻², it is surprising that the zonal basin-crossing of the NAC has relatively weak EKE at LSW levels. The second strongest EKE is located in the northeastern Labrador Sea and is generated by instabilities and eddy shedding of the West Greenland Current (WGC), known to occur from surface flow observations. This EKE maximum shows relatively large values around 60 cm² s⁻² and covers a large fraction of the interior Labrador Sea. Then there are mid-basin EKE maxima in both the Irminger Sea and even stronger in the Iceland Basin, extending along the whole lengths of the basins. Interestingly, there are EKE minima along both sides of the RR and zonally all across the basin just north of the NAC. Comparably weak EKE is located directly at the topography off Labrador and off East Greenland where the DWBC is stabilized by the steep topography.

The EKE maximum in the central Labrador Sea has been linked in the past to the WGC (e.g., Brandt et al., 2004; Eden and Böning, 2002). For example Eden and Böning (2002) attributed the EKE maximum to barotropic instability of the WGC with a seasonal peak at the time of maximum surface forcing (winter wind-stress maximum). It appears that there is a significant difference in the EKE intensity on both sides of the Labrador Sea; while the northward flowing WGC is subject to intense eddy formation and hence high EKE, the southward flowing Deep Labrador Current is much more stable with remarkably low EKE levels. A possible reason is the PV conservation that stabilizes the flow when progressing southward (towards lower f) and consequently the flow is driven toward the stabilizing topography, while for northward flow there is a tendency to move into deeper water with smaller topographic beta or less cross-flow topographic slope. This is further supported by the weak EKE in the southward flowing East Greenland Current.

3.4 Advection versus diffusion – Peclet number

The western subpolar basin has very different regimes regarding mean flow and EKE pattern. Even at greater depths, there are narrow boundary currents along the topography, interior persistent current bands, and regimes of almost stagnant mean flow with intense eddy motion, but it is a priori not clear which of the processes – advection or diffusion – dominates in either of the circulation regimes. This objective is investigated through the calculation of a local dimensionless number, the Peclet Number (Pe), which is the ratio of advection to diffusion. Here, we calculate a simplistic Pe version that allows one to regionally compare the relative importance of advection versus diffusion:

$$\begin{array}{ll}\text{(1)}& {\displaystyle }& {\displaystyle }Pe=L_d\cdot \mathit{<}\mathit{U}\mathit{>}/\mathcal{K},\text{with}\mathcal{K}=\mathit{\alpha }\surd \mathrm{EKE}\cdot L_d;{\displaystyle }& {\displaystyle }\mathrm{\text{for EKE see Figs. 3b, 6a;}}\end{array}$$

α is an empirical (non physical) scaling factor; here we chose α=0.25, such that the resulting Pe field varies between 0 and 1; L_d is the Lagrangian length scale chosen to be related to the first baroclinic Rossby radius (on the order of 1 to 2×10⁴ m) (see Chelton et al., 1998); <U> is the mean current speed taken from the gridded velocity fields.

The resulting Pe distribution (Fig. 5c) basically shows two regimes; one with very small Pe (i.e., Pe<0.2), these are the regions where the deep eddy motion is a strong component of the current field, such as the central basins of the SPNA with the central Labrador Sea being the largest area with low Pe. Similarly, the southern Irminger Sea shows low values of Pe; and in addition to these, the transatlantic zone south of the CGFZ is also subject to intense eddy motion.

The contrasting regimes with strong mean flow and relatively high Pe are the boundary currents along the east and west Greenland shelves and all along the Labrador coastline. There are also deep western and eastern boundary currents along the RR and along the Rockall Plateau. In these areas, the advection is relatively strong compared to the eddy motion. Finally, there are mid-basin regions with stable advection and relatively weak eddy motions away from the topography and associated with the cyclonic recirculation cells. One such regime is south of Cape Farewell and it extends far into the Irminger Sea; this band connects the “convection regime” of the central Labrador Sea with the central Irminger Sea (CIS). A similar mid-basin advection regime is found in the Iceland Basin where it connects the high Pe band associated with the zonally oriented polar front at 52^∘ N with the meridional current band directed along the deep Maury Channel, i.e., the central axis of the Iceland Basin. Finally, the recirculation regime off the Labrador shelf break is associated with relatively high Pe, as the eddy motion is relatively weak.

4 Verifications of the results

We verified our results in three different ways. First the results from GI and OI were compared in order to identify a superior interpolation method. Then we compared the mean flow and mean EKE fields with similar quantities derived from Eulerian time series data from moored stations (EKE_moor) in the region; and the third way of verification was a comparison between the deep EKE and the EKE_surf from satellite sea-level anomaly (SLA) data.

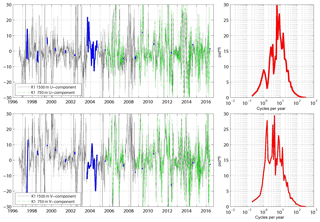
Figure 7 Example of a current time series from the central Labrador Sea at mooring K1. Two depth levels were occupied regularly (750 m since 2006, green curve; 1500 m since 1996). Gaps (blue lines) are filled by interpolation based on empirical orthogonal functions (Zantopp et al., 2017). High-frequency spectra from 1500 m records (right column).

4.1 Consistency of interpolation techniques

The mean flow fields from the two gridding methods are surprisingly similar and there are no significant differences between the velocity and speed fields. The overall speed-difference is −0.16 cm s⁻¹, which illustrates that there are no systematic differences (biases) between the two speed estimates as a result of the gridding technique. The difference field is patchy in structure with patch scales on the order of the interpolation radii. Thus, by choosing the GI method, the current map (Fig. 5a) is considered to be representative and independent of the two mapping procedures applied.

Likewise, the difference in GI and OI EKE fields (Fig. 6) agreed well. Most of the EKE differences occurred in the range ±5 cm² s⁻² with the strongest deviations around the NAC path across the SPNA; here, the GI method produces somewhat larger values. In contrast, the NWC reveals larger EKE values for the OI method. A patchy structure is observed with scales associated to the influencing radii of the gridding methods (roughly 100 km). The difference has an overall Gaussian distribution but with a slight bias of 1 cm² s⁻² toward larger EKE in the OI method map. We note that each of the mapping procedures requires de-spiking of the velocities (e.g., see spikes in the eddy field near the boundary, Fig. 3), which is treated differently in the two methods. The strongest impact on the EKE field is due to the removal of individual large velocity spikes in the GI method, which leads to a regional reduction of the corresponding EKE field. In this procedure we sorted the selected eddy velocity data (typically within the cut-off scales, on the order of 100 km, about 100–200 data points) with respect to their magnitude, and removed the largest of the data. Removing only the largest 1 % of eddy velocities results in a positive bias of 4 cm² s⁻². When using additional statistical criteria, e.g., removal of data only if exceeding a threshold based on statistics (like 2 times the standard deviation), then the bias would be in the range 1 to 2 cm² s⁻². This might be taken as a cautionary hint for interpreting the EKE map as a quantitative measure for the small-scale details of the eddy field. No explicit de-spiking has to be used in the OI method, as it is inherent in the method itself (see Schmidtko et al., 2013).

4.2 Comparison with local Eulerian measurements

The second method for verification was a comparison between the derived mean fields (<U> and EKE) and selected locations where time series data from moored instrumentation was available (Fig. 5b; Table 1).

4.2.1 Labrador and Irminger seas

In the convection area of the Labrador Sea, a time series of currents is available at the K1 site since 1996 (the site is close to where the Ocean Weather Ship Bravo; 56^∘30^′ N, 51^∘00^′ W; was operated; Fig. 7). In general the mean flow at the location of K1 is very weak (on the order of 1 cm s⁻¹) with a northwestward direction into the Labrador Sea and, given the mooring position, consistent with the anticyclonic circulation around the basin center (Fig. 5a). Short timescales dominate the variability in the flow (Fig. 7), and the spectra indicate that the bulk of the energy is on intra-seasonal periods with strong decay toward longer timescales. The strongest variations occur in late spring and are associated with eddies shed by the WGC near the location of Cape Desolation (Avsic et al., 2006; Funk et al., 2009). These eddies are only weakly sheared in the LSW depth range which is an important aspect as it supports combining 1000 and 1500 m parking depths for Argo float displacements. The EKE from 180-day high-pass filtered time series is around 170 cm² s⁻² in both levels (750 and 1500 m; Table 1). These values are larger than what is derived from the Argo data set and we interpret this to be a result of the inherent low-pass filter in the float processing. With respect to the Pe (Fig. 5c), the area is characterized as an eddy-dominated regime.

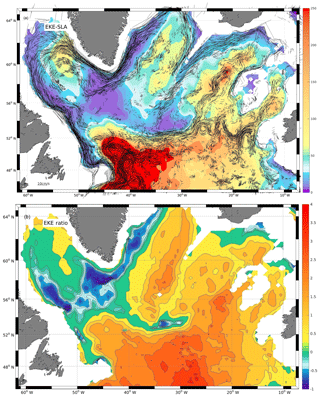
Figure 8 (a) Surface EKE derived from the AVISO geostrophic surface flow that is high-pass filtered at 180-day cut-off (in cm² s⁻²) as an estimate of the geostrophic turbulence. Overlaid is the Argo-derived mean (PV-related) flow at 1000–1500 m depth, with flow speeds below 1.5 cm s⁻¹ omitted; this better reveals the major advective pathways. (b) The logarithmic ratio of surface EKE to deep EKE; green and blue colors show areas in which the deep EKE dominates.

In the CIS a current time series is available at about 1000 m depth. As for K1, the site is characterized by a weak mean flow (around 1 cm s⁻¹), while the EKE (based on intra-seasonal velocity fluctuations) is around 80 cm² s⁻² (Fan et al., 2013). The location of CIS is at the edge of the mid-basin velocity band connecting the Labrador Sea around the tip of Greenland, and into the Irminger Sea.

In the boundary current system of the Labrador Sea a number of records could be analyzed. In general, the flow is rather stable and strong (Lazier and Wright, 1993; Fischer et al., 2004; see also Table 1). Representative for the DWBC at 53^∘ N (K9, Zantopp et al., 2017), the long-term mean flow along the topography is 12.5 cm s⁻¹ and the EKE (again for periods less than 180 days) is 62 cm² s⁻². Farther toward the topography, the mean speed is even larger and the EKE smaller, as the DWBC appears to be more focused by the steep topography at 53^∘ N. In any of the boundary current records a large energy contribution is on timescales less than 10 to 20 days (Fischer et al., 2015), which are not captured by the Argo displacement vectors and different from the basin interior were the flow variability is on timescales longer than a month and thus better resolved by 10-day displacement vectors from Argo (Fig. 8).

In the records in the center of the DWBC at Hamilton Bank, the total EKE of the moored record is larger than that from the float displacement but similar to K9 (Table 1). For a better comparison we calculated the EKE fraction that Argo would represent in their 10-day displacement vectors by low-pass filtering the mooring data (10 days cut-off period of the filter). Then, the EKE values coincide much better as is demonstrated by the colored mooring numbers in Fig. 5b.

Near the offshore edge of the DWBC, at mooring K10 of the 53^∘ N array, the flow speed is rather low, as the mooring lies in the transition regime between the DWBC and the recirculation pathway in the upper 2000 m; while at deeper depths it is still part of the DWBC (Zantopp et al., 2017). At 1500 m the flow is mainly the reverse of the DWBC direction and the EKE is rather small, but in good agreement with the EKE from Argo.

Associated with weak mean speeds (only 10 % of the DWBC speed is found at locations offshore of K10) and moderate EKE_moor, values coincide when the resulting Peclet numbers (Fig. 5c; Table 1) are low and indicate sufficient diffusion in the presence of weak advection. This structure is reflected in the Argo flow pattern, which shows an increasing advective contribution further toward the basin interior, and from the mean current map and the density field it is tempting to assume this route as one of the supply routes for the deep central Labrador Sea.

4.2.2 Subpolar locations

Moored observations in the Iceland Scotland Overflow Water were available at four positions (Named I, S, O, and W; see Kanzow and Zenk, 2014). Only three (S, O, W) moorings delivered data in the appropriate depth range for this study. While S was located in the area of low deep EKE, the fluctuations increase toward east with mooring W located in the EKE max along the northward flow (Fig. 5a).

North of the I S O W array the Iceland array is located at the shelf break south of Iceland, and the northern mooring direct at the topography reflects the low EKE_moor typical for topographically guided currents, while the one further offshore is located in the northern extension of the EKE maximum of the Iceland Basin.

During the JASIN program in the late 1970s a number of moorings were deployed in the northern Rockall Trough (Gould et al., 1982) and these moorings reflect the intermediate intensity of the deep EKE_moor that is also present in the Argo-derived values (Table 1).

The EKE from the moorings represent mean regional variations. In order to compare the high-resolution time series with the Argo data, a 10-day low-pass filter is applied. There is a remaining discrepancy between EKE from Argo and from moorings with a tendency that in regions with low EKE (taking now the Argo-derived map as a reference) the Argo estimates are larger than the 10-day low-pass filtered mooring estimates, while in regions of high EKE the situation is reversed. We interpret this discrepancy by the inherent (nonlinear) temporal filtering in the EKE derived from Argo that tend to low-pass filter the field with unpredictable filter characteristics (depending at which times the floats enter the corresponding interpolation radius).

4.3 Surface EKE versus intermediate depth EKE

In addition to the deep EKE we estimated the surface EKE (EKE_surf) field calculated from remote sensing-based absolute dynamic topography observations. The geostrophic surface flow from SLA contains variability over a wide range of frequencies, and some of the long-term components are not generally thought to be part of the turbulent eddy field. Thus, we extracted the intra-seasonal variability by applying a high-pass filter (Hanning window) with a cut-off period at 180 days. The result is a field of geostrophic fluctuations from which we calculate EKE_surf (Fig. 8a). This field is independently derived, and thus allows for an independent comparison of the Argo-derived fields (here, the deep circulation and EKE).

The EKE_surf also resembles major (deep) circulation elements, such that the zonal flow in the CGFZ region located underneath the zone of maximum EKE_surf gradient at the surface. (Note in Fig. 8 only currents larger than 1.5 cm s⁻¹ are shown, and thus only vector magnitudes that would be sufficient to travel one Rossby radius within the 10-day schedule of the floats are included). A similar surface versus deep EKE and flow pattern is seen for the northeastern flow from the Labrador Sea into the Irminger Sea. Within the Iceland Basin the deep flow is associated with the surface EKE_surf maximum, suggesting the mid-basin path is present from surface to LSW depth range. Interestingly, the surface EKE shows a clear EKE minimum all along the DWBC in the western SPNA, and this is due to the slanting shape of the boundary circulation and the slope of the western shelves. In a region with less slope, i.e., the northern Labrador Sea we observe strong EKE at all levels (surface and LSW depth range). This is the area where the deep WGC turns away from the steep Greenlandic shelf and intense eddies are formed and shed from the DWBC (Eden and Böning, 2002).

Following Ollitraut and de Verdiere (2013) we calculated the logarithmic ratio of surface EKE to the deep EKE; i.e., ln(EKE_surf∕EKE), such that the ratio becomes negative when the deep EKE is larger than that at the surface. Generally, in a baroclinic ocean one would expect positive ratios, with the EKE_surf sufficiently larger than the EKE at depth, as is the case for the region south of the North Atlantic Drift, i.e., south of 52^∘ N. A global much coarser map of such a ratio reveals that this is the case for almost the whole Atlantic Ocean (Ollitraut and de Verdiere, 2013). In their paper, the SPNA appears as broad negative area in which the deep EKE exceeds the upper layer or is of similar magnitude. The much higher resolution of the field generated herein (Fig. 8b) allows for a more detailed view, which reveals two centers of deep EKE dominance. The first is associated with the DWBC all along the Labrador shelf break and the strongest signal around Hamilton Bank. The second center is associated with the deep action center south of Cape Farewell that shows both stable advection and EKE at depth, while at the surface these components are rather weak. This zone extends far north into the Irminger Sea where it appears to be related to the deep EGC and its variability. This behavior indicates that for the inter-basin spreading and mixing of newly formed water masses the deep EKE field contains important information , which is not easily available elsewhere; at least not from the surface variability alone.

Besides the boundary-current-related anomalies there is one additional zone in which the deep EKE is close to the surface EKE, and that is along the CGFZ at the northern flank of the NAC. In this area the flow is guided by the deep topography and advection appears to be dominating the zonal flow (relatively large Pe).

5 Summary and conclusion

The results of the investigation can be summarized as follows:

1. Based on nearly 17 years of quality controlled Argo displacement vectors, a high-resolution (∼25 km grid) map of mean flow in the depth layer of the LSW was constructed for the subpolar North Atlantic (SPNA). Robust circulation elements were identified consisting of boundary currents along topographic slopes, mid-basin advective pathways, and stagnation regimes with very low mean speeds.

2. The mapping procedures were twofold: Gaussian interpolation (GI) and optimum interpolation (OI), both methods were applied using potential vorticity (PV) constraints, and the resulting mean flow fields were very similar – almost identical.

3. The second product was the fluctuating (eddy – u^′, v^′) velocity component, which was determined as the residual after subtracting the average and PV-conserving contribution from the individual measurements (displacement vectors). The u^′, v^′ fields were used to map the mean EKE distribution, to our knowledge for the first time.

4. The ratio of mapped mean flow to the square root of the EKE, the Peclet number (Pe), was estimated and showed regions that are advection dominated (boundary currents and internal LSW routes), and regions with low PE, in which eddy diffusion prevails.

5. The mapped fields were analyzed for consistency between the OI and GI methods. In addition velocity time series from moored sensors were used to estimate mean flow and EKE in an attempt to verify the mapped fields locally with independent data. While the general pattern of high and low EKE regimes are consistent, the mooring EKE appears to be larger than EKE from Argo, but the differences become smaller when the Eulerian measurements are low-pass filtered with a cut-off at the Argo sampling timescale (10 days).

6. Comparing the mid-depth EKE with the independently derived surface EKE from Aviso SLA data, we found qualitative agreement of the two fields in many regions, with the surface EKE larger than the mid-depth EKE. However, other regions showed the local EKE maxima were horizontally displaced between surface and the deep EKE, thus there are areas with larger EKE at mid-depth. This seems to be a special (robust) feature of the SPNA.

The gridded velocity field can be used for a variety of follow-up investigations, e.g., estimating water mass spreading via artificial tracer release experiments or using the gridded flow field as a reference level velocity for geostrophic calculations (e.g., based on Argo-derived geostrophic shear).

By focusing on the Labrador Sea, the “surprisingly rapid spreading” of LSW throughout the SPNA (Sy et al., 1997) is well supported by our gridded mean flow field: newly formed LSW is exported by the mid-basin advective pathway into the Irminger Sea (Figs. 3a and 5a) and eastward through the pathway that connects the western SPNA with the northern Iceland Basin through the NAC and its northern pathway. Individual floats released in the DWBC off Labrador used that path to drift within a few (3–4) years far north into the Iceland Basin.

More regional aspects were discussed in the float release experiments performed in the late 1990, i.e., before Argo started officially. On the basis of these investigations, export pathways for LSW out of the Labrador Sea were discussed (e.g., Straneo et al., 2003) in which the export of LSW into the Irminger Sea, and the boundary current export around the Flemish Cap were identified as major export routes. While the Irminger Sea route appears strong and robust, the flow along the topography (Flemish Cap) is relatively narrow and the EKE maximum in this region is due to the NAC interaction with the upper part of the DWBC near the steep topographic slope. Another major export route is into the eastern SPNA via the NAC path along 52^∘ N.

Traditionally the upper ocean eddy variability represented by the EKE distribution has been investigated from SLA data (Brandt et al., 2004; Funk et al., 2009). Just recently (Zhang and Yan, 2018), the Labrador Sea surface EKE based on altimeter data has been investigated with regard to interannual to decadal variability in the time period 1993 to 2012. They find strong interannual variability in the EKE field near the WGC, but no trend over the observational period.

Generally, mid-depth EKE maps based on observational data are rare but important for the deep ocean water mass and tracer spreading. Thus, both the mean current field and the EKE at the transition between the deep water masses LSW to LNADW should be useful metrics for ocean model evaluations.