An estimate of the eddy diffusivity tensor from observed and simulated Lagrangian trajectories in the Benguela Upwelling System

Lateral mixing of unresolved processes in ocean models is usually parameterized with a scalar diffusivity, although the observed mixing can be highly anisotropic. Estimating the full diffusivity tensor from Lagrangian dispersion observations is challenging because shear dispersion from background currents can prevent the diffusive limit from being reached. This study investigates the diffusivity tensor with Lagrangian single- and pair-particle statistics in the Benguela upwelling region, using (1) a set of Lagrangian trajectories derived from a recent drifter dataset with an hourly resolution and background currents from the Ocean Surface Current Analysis Real-time (OSCAR) and (2) another trajectory set from simulations using the $\mathrm{1}/\mathrm{10}\mathrm{°}$ Parallel Ocean Program (POP) simulation. Theory predicts that pair-particle diffusivities, which are expected to be independent of background mean flows, are twice the single-particle diffusivities if the pair velocities are uncorrelated. In this study, it is found that, although pair-particle diffusivities are much less influenced by mean flow, they are generally significantly smaller than twice the single-particle diffusivities. Subtracting the mean flow reduces this discrepancy and improves convergence in both methods, although single-particle diffusivities remain higher. Velocity autocorrelations decay faster than pair correlations, with mean flow subtraction accelerating decorrelation, especially in the zonal direction. The pair correlation term in the diffusivity equation contributes significantly to the differences between single-particle and pair-particle diffusivities, explaining why pair-particle diffusivities are generally smaller, making them a less accurate estimate in diffusive parameterizations. In both the POP simulation and the observations, convergence properties improve significantly after mean flow subtraction. Mean flow removal plays a critical role in achieving convergence in the components of the diffusivity tensor and in the major-axis component after diagonalization. The significant anisotropy in the diffusivity tensor is mainly explained by the anisotropy in the Lagrangian integral timescales, while the major-axis component of the velocity variance tensor is only about 1.2 times the minor-axis component. The motions that are not resolved by the OSCAR surface current product but are captured by the surface drifters contribute significantly to the diffusivities, accounting for 8 % and 42 % of the contributions to the zonal and meridional components, respectively, after mean flow subtraction. This study highlights the importance of including the full diffusivity tensor in the Benguela upwelling region in lateral mixing parameterizations.

1 Introduction

Upwelling systems, found in equatorial and coastal regions, are areas where cold, nutrient-rich water from the deep ocean rises to the surface. This phenomenon is primarily driven by subtropical basin-scale circulations that create a slow, Equator-ward gyre flow near the shore (Capet et al., 2008). All eastern boundary upwelling systems share specific features, such as wind-driven flows, alongshore currents, shallow thermoclines, and significant vertical and offshore nutrient transport (Large and Danabasoglu, 2006). However, each system exhibits unique characteristics in terms of circulation, primary productivity, and phytoplankton biomass, influenced by their specific geographic settings (Berger and Wefer, 2002).

The focus of this study is the Benguela Upwelling System, characterized by a frontal system of strong sea surface temperature (SST) gradients. This frontal system is frequently interrupted by finger-like structures of lower SST, known as filaments, resulting from meso- and submesoscale dynamics (Hösen et al., 2016). These filaments are influenced by eddies from two distinct origins: warm-core eddies, known as Agulhas rings, produced by the interaction between the Agulhas Current and the Antarctic Circumpolar Current (Agulhas Retroflection) after passing the Agulhas Bank at the southern tip of Africa (Lutjeharms, 2006), and cold-core eddies generated from boundary current instabilities near the coast of Namibia.

The dynamics in coastal upwelling systems like the Benguela Upwelling System range from well-understood processes to complex meso- and submesoscale flow instabilities (Capet et al., 2008). Due to the intricacies of these processes, climate simulations frequently face significant challenges, resulting in notable SST biases, although an adequate resolution of atmospheric processes is important as well (Small et al., 2015). This underscores the crucial need for ongoing research to enhance the accuracy of climate models and better understand the complexities of upwelling systems.

In coupled climate models with a resolution of 0.5° (∼50 km) or lower, meso- and submesoscale eddies at their smallest spatial scales are likely to remain unresolved (Richter, 2015). Eddies contribute significantly to the transport of momentum and tracers (e.g., salinity and temperature) due to the comparatively weak mean ocean currents in upwelling systems, and they play a crucial role in the oceanic transport of colder water from the coast to the interior. In most climate models, the effects of eddies on a tracer T are parameterized using the tracer conservation equation:

$$\begin{array}{}\text{(1)}& {\displaystyle }{\displaystyle \frac{\partial \stackrel{\mathrm{‾}}{T}}{\partial t}}+\stackrel{\mathrm{‾}}{\mathit{u}}\cdot \mathrm{\nabla }\stackrel{\mathrm{‾}}{T}=\mathrm{\nabla }\cdot \stackrel{\mathrm{‾}}{{\mathit{u}}^{\prime }{T}^{\prime }}+\stackrel{\mathrm{‾}}{Q},\end{array}$$

where the overline denotes an average over intervals in time and space, ^′ denotes the deviation from that aforementioned average, and $\stackrel{\mathrm{‾}}{Q}$ describes the sources and sinks of the tracer T. Using the Transformed Eulerian Mean framework, the eddy flux can be decomposed into components across and along isolines of the mean tracer, e.g., diffusive and skew-diffusive fluxes (e.g., Griesel et al., 2019). Using $\stackrel{\mathrm{‾}}{{\mathit{u}}^{\prime }{T}^{\prime }}=-\mathbf{K}\mathrm{\nabla }\stackrel{\mathrm{‾}}{T}+\mathit{B}\times \mathrm{\nabla }\stackrel{\mathrm{‾}}{T}$, we receive the following expression:

$$\begin{array}{}\text{(2)}& {\displaystyle }{\displaystyle \frac{\partial \stackrel{\mathrm{‾}}{T}}{\partial t}}+(\stackrel{\mathrm{‾}}{\mathit{u}}+\mathrm{\nabla }\times \mathit{B})\cdot \mathrm{\nabla }\stackrel{\mathrm{‾}}{T}=\mathrm{\nabla }\cdot \mathbf{K}\mathrm{\nabla }\stackrel{\mathrm{‾}}{T}+\stackrel{\mathrm{‾}}{Q},\end{array}$$

where B is the vector stream function defining the eddy-driven advection velocity ∇×B depending on the tracer T, and K is a 3×3 diffusivity tensor denoting irreversible mixing of the tracer T. This diffusivity tensor K contains both lateral and vertical mixing components and has to be estimated for parameterizing eddies in climate models. Thus, an accurate representation of eddies in climate models is crucial to improve the general understanding of involved oceanic processes and their impact on future climate predictions (e.g., Ernst et al., 2023; Huot et al., 2022; Hewitt et al., 2020). This study focuses on the lateral components of the diffusivity tensor.

Diffusivities can be quantified using both Eulerian and Lagrangian methods (Griesel et al., 2014, 2019; Klocker and Abernathey, 2014). The Lagrangian approach is based on the spreading of floats or tracers as they follow the flow (Taylor, 1953, 1921; Nakamura, 1996), whereas Eulerian diffusivities can be quantified relative to a fixed geographical location, e.g., from Eulerian eddy tracer fluxes (e.g., Eden, 2006; Griesel et al., 2014). The traditional way to estimate eddy diffusivities originates from the dispersion of Lagrangian particles (Taylor, 1921, 1953), which provides the means to test the applicability of the eddy-diffusion model, where particles are expected to spread in a diffusive manner only after some time period determined by the temporal and spatial scales of the largest eddies (e.g., LaCasce et al., 2008). There are two possible statistical methods to estimate diffusivities, referred to as single- and pair-particle statistics. Single-particle statistics measure the spreading of particles from their origin and depend strongly on the background mean flow. Pair-particle statistics measure how two particles spread apart and would not depend on the background mean flow if both particles experienced the same mean flow during their spreading (Dräger-Dietel et al., 2018; Sansòn et al., 2017). In a flow with homogeneous statistics, the pair-particle diffusivity is expected to be twice the single-particle diffusivity.

In climate models, lateral eddy diffusion is typically represented by a single scalar, κ_i, aligned along isopycnal surfaces below the mixed layer. This approach is suitable when eddy diffusion is isotropic in the horizontal or along-isopycnal directions. In the presence of strong background flows, eddy diffusion is suppressed in the cross-stream component (Ferrari and Nikurashin, 2010; Klocker et al., 2012b, a; Klocker and Abernathey, 2014; Griesel et al., 2014) and eddy mixing becomes anisotropic (Bachman et al., 2020). Shear dispersion increases the effective diffusivity in the along-stream component (Taylor, 1953; Oh et al., 2000). This shear dispersion in the real ocean results from large-scale background mean flow, but it also occurs due to the eddies themselves, as large velocity shears exist at the eddy rims. The prevailing premise is that it is the mesoscale eddy motions with timescales of weeks and spatial scales corresponding to the first Rossby radius of deformation that contribute to eddy mixing (e.g., Ni et al., 2020; Stammer, 1998). Mixing is likely to be most efficient at the edge of the eddies, where large temperature gradients and large horizontal velocity shears occur. However, we further hypothesize that submesoscale motions with spatial scales below the first internal Rossby radius of deformation and associated with timescales shorter than a few days may contribute substantially. Recently, Peng et al. (2015) and Peng et al. (2020) reported that symmetric and shear instability occurs at the southern boundary of a filament in the Benguela Upwelling System, the same one that is investigated in this study. Diffusion might become more isotropic once the effect of the shear dispersion associated with the local shear from the mesoscale eddies is subtracted.

Dispersion processes are particularly important in the Benguela Upwelling System, where filaments are elongated in an east–west direction by the action of the velocities at the eddy rims, leading to increased mixing in this direction. This effect should be captured in ocean models. However, a question remains as to whether mixing in the along-stream component can be adequately described with a diffusivity. Oh et al. (2000) illustrated how the along-stream component of the diffusivity tensor is influenced by mean flow shear and does not always converge to a constant value. Oh et al. (2000) further advised using the minor-axis component of the diffusivity tensor, which is oriented across the background mean flow, as the diffusivity estimate. The minor-axis component of the diffusivity tensor can be estimated from drifter data (Zhurbas et al., 2014; Rühs et al., 2018). Davis (1987) and Davis (1991) devised the underlying theory regarding the computation of the diffusivity tensor in principle in the presence of an inhomogeneous background mean flow where, instead of diagnosing the statistics from the absolute Lagrangian velocities and displacements, diffusivities are computed from residual velocities and displacements after the Eulerian mean has been subtracted.

While most observational studies have focused on the minor axis of the diffusivity tensor, only a few, such as Rypina et al. (2012) in the North Atlantic and Peng et al. (2015) in the Indian Ocean, have considered all components of the diffusivity tensor from observational drifter data. Griesel et al. (2010, 2014) and Chen et al. (2014, 2015) demonstrated that, in many cases, the along-stream component of the diffusivity tensor can also be determined once the Eulerian mean is subtracted at each float point. However, they used trajectories from eddying ocean models where the background mean flow is known at each grid point.

In this study, for the first time, all components of the diffusivity tensor are estimated from the Lagrangian single- and pair-particle statistics (Taylor, 1921; Davis, 1987, 1991; LaCasce et al., 2008) in the Benguela upwelling region. Additionally, for the first time, our study compares the effect of the mean flow on both single- and pair-particle diffusivities simultaneously. Furthermore, we specifically quantify the contribution not resolved by the altimeter product to the diffusivity. An observed set of drifters (Dräger-Dietel et al., 2018) and simulated trajectories from drifters deployed in a high-resolution state-of-the-art eddy-permitting global ocean model (the $\mathrm{1}/\mathrm{10}\mathrm{°}$ Parallel Ocean Program, hereinafter referred to as the POP simulation) are analyzed in detail. Similarly to Rypina et al. (2012), the background flows from the Ocean Surface Current Analyses Real-time (OSCAR) (Bonjean and Lagerloef, 2002) are considered in the analysis of the surface drifter dataset. This study aims to address the following questions:

• What is the dependence of the components of the diffusivity tensor on time lag, and can a diffusive limit be reached for all components?

• How do the diffusivities depend on eddy-mean flow decompositions considering both single- and pair-particle statistics, and can the pair-particle diffusivity emerge as an alternative to the single-particle diffusivity, as it should be independent of the mean flow, which does not resolve the motions induced by the eddies?

• What is the role of smaller-scale motions that are captured by the drifters but not by current altimeter products and that have timescales shorter than a few days for the diffusivities and anisotropy?

The study is organized as follows: Sect. 2 presents the datasets used for this study, including the observed and simulated drifter trajectories. Section 3 describes the theory and methods used to estimate all components of the diffusivity tensor and the mean flow decomposition. Section 4 examines the prevailing background mean flow and eddy kinetic energy in the Benguela Upwelling System. Section 5 evaluates all components of the diffusivity tensor for single- and pair-particle statistics and highlights the impact of the background mean flow decomposition on the eddy diffusivities. Autocorrelations and pair correlations are examined in detail, and the impact of motions not resolved by satellite altimetry and their contributions to the diffusivities are investigated. Section 7 focuses on the evaluation of anisotropy by decomposing the diffusivity tensor in major- and minor-axis components in the Benguela Upwelling System. Section 8 presents the main conclusions and suggestions for future work.

2 Data

The observational dataset includes 35 surface drifters. The drifters of the type SVP-I-XDGS from MetOcean, consist of a surface buoy and a subsurface drogue, mounted in a 16 in. (40.6 cm) hull and equipped with Iridium telemetry and an SST sensor (Dräger-Dietel et al., 2018). With the drogue at 15 m depth, they provide the ability to monitor currents from this depth with less influence from surface winds.

The drifters were deployed in the eastern South Atlantic in November–December 2016 by the R/V Meteor during cruise M132 from Walvis Bay (Namibia) to Cape Town (South Africa) (Dräger-Dietel et al., 2018). The drifters were deployed at the northern boundary (at 26.0° S, 12.58° E) and the southern boundary (26.4° S, 12.0° E) of a filament identified by satellite altimetry (Fig. 1a). The drifters were released as triplets in a triangular shape with initial separations of 100–200 m. In total, there were four drifter release sites, with the first and third groups released at the southern boundary and the second and fourth groups released at the northern boundary of the filament. After approximately 150 d, the drifters were transferred to the Global Drifter Program (GDP), where the temporal resolution was increased from 30 to 60 min. For this study, the drifter dataset with the lower resolution, as in Elipot et al. (2016), is used for a period of 250 d.

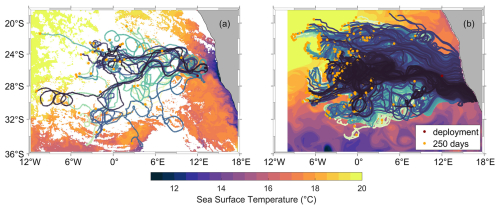
Figure 1 The drifter trajectories are shown for (a) surface drifter observations and (b) particles advected with the velocities from the POP simulation from the deployment date (red dots) to 120 d after deployment (orange dots). The background colors display the snapshots of SST for the observations and the POP simulation. For the observations, the SST data are shown for the day of 28 November 2016 and represent measurements from the Moderate Resolution Imaging Spectroradiometer (MODIS) provided by the Earth Observing System (EOS) (dataset accessed in November 2020). For the POP simulation, the SST is shown for the day of 28 November 1996.

The set of simulated drifter trajectories consists of 948 drifters released at 10 m depth in the $\mathrm{1}/\mathrm{10}\mathrm{°}$ global Parallel Ocean Program (POP) simulation. The run was initialized from the ocean state by Maltrud et al. (2010), which was integrated for 120 years using the annually repeating normal year Coordinated Ocean-ice Reference Experiments (COREs) surface forcing (Large and Yeager, 2004). In 1983, the COREs forcing was switched to vary interannually (Large and Yeager, 2009) and the model was integrated for an additional 27 years (Chouksey et al., 2022). The simulated drifters were released on 2 November 1996 with a spacing of $\mathrm{1}/\mathrm{5}\mathrm{°}$ in both latitude and longitude between 24 and 30° S and between 10 and 18° E, covering a filament in the Benguela Upwelling System (Fig. 1b). The drifters are advected online for each model time step by the three-dimensional velocity field with a fourth-order Runge–Kutta scheme (Griesel et al., 2010). We note that the particles do not move vertically in our analysis period of 250 d; rather, they remain in the 5–15 m depth range.

Moreover, in the analysis of the observational drifter dataset, the OSCAR product is used to investigate the surface conditions with respect to the background mean flow and the eddy kinetic energy. The OSCAR product is provided by Earth Space Research (ESR, 2009, dataset accessed in November 2020). The dataset is on a $\mathrm{1}/\mathrm{3}\mathrm{°}$ grid with a 5 d temporal resolution. The OSCAR product offers near-surface ocean current estimates that are derived using quasi-linear and steady-flow momentum equations. The spatial velocities in this dataset are directly estimated from sea surface height (SSH), surface winds, and sea surface temperature (SST) measurements taken by various altimetric satellites and in situ instruments.

3 Theory and methods

This section outlines the theoretical framework and methodologies used to investigate all components of the diffusivity tensor through both single- and pair-particle statistics, focusing on diffusive behavior, mean flow dependence, and smaller-scale motions.

3.1 Single-particle diffusivities

In a one-dimensional, stationary flow with zero mean, the mean square displacement r² of particles satisfies the following:

$$\begin{array}{}\text{(3)}& {\displaystyle \frac{\mathrm{d}〈r^{\mathrm{2}}\left(t\right)〉}{\mathrm{d}t}}& {\displaystyle }=〈\mathrm{2}{\displaystyle \frac{\mathrm{d}r\left(t\right)}{\mathrm{d}t}}r\left(t\right)〉\text{(4)}& {\displaystyle }& {\displaystyle }=〈\mathrm{2}u\left(t\right)\underset{\mathrm{0}}{\overset{t}{\int }}u\left(t^{\prime }\right)\mathrm{d}{t}^{\prime }〉\text{(5)}& {\displaystyle }& {\displaystyle }=\mathrm{2}\underset{\mathrm{0}}{\overset{t}{\int }}〈u\left(t\right)u\left(t^{\prime }\right)〉\mathrm{d}{t}^{\prime }\text{(6)}& {\displaystyle }& {\displaystyle }=\mathrm{2}\underset{\mathrm{0}}{\overset{t}{\int }}R\left(t^{\prime }\right)\mathrm{d}{t}^{\prime },\end{array}$$

where r(t) is the displacement of the particles at time t from their position at time t=0; angle brackets (〈〉) denote an average over all particles considered; and R(t) is the Lagrangian velocity autocovariance, which is characterized by its value at the origin R(0)=〈u(0)²〉 and the Lagrangian integral timescale

$$\begin{array}{}\text{(7)}& {\displaystyle }{\displaystyle }{T}_{\text{int}}={\displaystyle \frac{\mathrm{1}}{R\left(\mathrm{0}\right)}}\underset{\mathrm{0}}{\overset{\mathrm{\infty }}{\int }}R\left(t^{\prime }\right)\mathrm{d}{t}^{\prime }.\end{array}$$

For times much longer than the integral timescale, it follows that

$$\begin{array}{}\text{(8)}& {\displaystyle }{\displaystyle }\langle r^{\mathrm{2}}\left(t\right)\rangle =\mathrm{2}Kt\text{with}K=\langle u^{\mathrm{2}}\rangle T_{\text{int}};\end{array}$$

i.e., in analogy to molecular diffusion, the mean square displacement grows linearly with time with constant turbulent diffusivity K (Taylor, 1921; LaCasce et al., 2008). In reality, with finite times and spatially varying background flows, the integral may not necessarily converge, and the diffusivity and timescale do not converge to a constant.

In a two-dimensional flow field that includes a spatially varying background current, the diffusivity is a 2×2 symmetric tensor and the equations generalize to

$$\begin{array}{}\text{(9)}& {\displaystyle }{\mathit{\kappa }}_{ij}& {\displaystyle }={\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}{\displaystyle \frac{\mathrm{d}}{\mathrm{d}t}}〈r_i^{\prime }\left(t\right)r_j^{\prime }\left(t\right)〉\text{(10)}& {\displaystyle }& {\displaystyle }=\underset{\mathrm{0}}{\overset{t}{\int }}〈u_i^{\prime }\left(t\right)u_j^{\prime }\left(t^{\prime }\right)〉\mathrm{d}{t}^{\prime }\text{(11)}& {\displaystyle }& {\displaystyle }\underset{t\gg T_{\text{int}}}{=}{\displaystyle \frac{〈r_i^{\prime }\left(t\right)r_j^{\prime }\left(t\right)〉}{\mathrm{2}t}},\end{array}$$

with indices i and j both run over the zonal (1) and meridional (2) velocity and displacement directions. If the velocity statistics are homogeneous and stationary, Eqs. (9)–(11) lead to the same diffusivity – for real oceanic flows, the methods can lead to different results, as the averaging 〈〉 is applied at different stages (LaCasce et al., 2014). In this study, the integral of the velocity autocovariance (Eq. 10) is used to calculate the single-particle diffusivities.

3.2 Flow decompositions

Following Davis (1987, 1991), in Eqs. (9)–(11), u^′(t) represents the drifter velocities at time t with the spatially varying Eulerian background flow removed and r^′(t) denotes the displacements with displacement due to the background flow removed. In that sense, the diffusivity introduced by Davis (1987) is a mixed Eulerian–Lagrangian quantity that can directly be related to the eddy tracer fluxes in a diffusive parameterization. Hence, the diffusivity reflects the turbulent mixing due to the residual components of the flow field and depends on the flow decomposition. In this study, two different flow decompositions are tested to estimate the contribution of different flow components to the magnitude and orientation of the diffusivity tensor:

$$\begin{array}{}\text{(12)}& {\displaystyle }\begin{array}{rl}{\displaystyle }& {\displaystyle }{\mathit{u}}^{\prime }\left(t\right)=\mathit{u}\left(t\right)-\stackrel{\mathrm{‾}}{\mathit{U}}(x,y){|}_{\mathit{r}\left(t\right)},\\ {\displaystyle }& {\displaystyle }{\mathit{u}}^{\prime \prime }\left(t\right)=\mathit{u}\left(t\right)-\mathit{U}(x,y,t_{\mathrm{E}}){|}_{\mathit{r}\left(t\right)}.\end{array}\end{array}$$

Here, x is the zonal direction, y is the meridional direction, the subscript |r(τ) indicates that the Eulerian velocities U are evaluated at the float positions and times, and t_E is the time at which the Eulerian currents are available.

In the first decomposition, the temporal mean but spatially varying Eulerian background flow $\stackrel{\mathrm{‾}}{U}$ is interpolated to each drifter location and subsequently removed from the drifter velocities. In the observational drifter dataset, $\stackrel{\mathrm{‾}}{U}$ is the temporal mean velocity of the $\mathrm{1}/\mathrm{3}\mathrm{°}$ OSCAR surface currents interpolated to the drifter locations, whereas in the POP simulation, $\stackrel{\mathrm{‾}}{U}$ is the temporal mean of the $\mathrm{1}/\mathrm{10}\mathrm{°}$ Eulerian currents interpolated to the numerical drifter locations (Table 1). Note that the current altimeter-derived products, such as the OSCAR product, could have effective resolutions in space and time closer to about 100 km and 30 d (Ballarotta et al., 2019), respectively, and should, in those instances, be regarded as a coarse-grained velocity.

Table 1 Summary of different flow components used for diffusivity calculations.

In the second decomposition, which is only applied to the observed drifter data that capture motions with an hourly temporal resolution, the time-dependent background velocities $U(x,y,t)$ from the OSCAR surface current product are interpolated spatially and temporarily to match each drifter location and time and are subsequently removed from the drifter velocities. The $U(x,y,t)$ is the spatially varying OSCAR surface current available at 5 d intervals, and it allows for the estimation of the contribution of velocity variations to the diffusivity tensor that are not captured by OSCAR. These contributions can be associated with unresolved mesoscale motions as well as submesoscale motions that contain significant ageostrophic components (e.g., North et al., 2024). In addition, we can use the velocities from the OSCAR surface current product only to estimate diffusivities from u and u^′ (Table 1).

To visualize the displacements due to different flow components, similarly to Rypina et al. (2012) and Griesel et al. (2010), trajectories are calculated using the following residual velocities:

$$\begin{array}{}\text{(13)}& {\displaystyle }{\displaystyle }{r}^{\prime }\left(t\right)=\underset{\mathrm{0}}{\overset{t}{\int }}{u}^{\prime }\left(t^{\prime }\right)\mathrm{d}{t}^{\prime },r^{\prime \prime }\left(t\right)=\underset{\mathrm{0}}{\overset{t}{\int }}{u}^{\prime \prime }\left(t^{\prime }\right)\mathrm{d}{t}^{\prime }.\end{array}$$

These trajectories are referred to as pseudo-trajectories, as (in contrast to the trajectories obtained from advection with the Eulerian flow fields) they are artificial trajectories obtained from integration with residual velocities.

3.3 Pair-particle diffusivities

As an alternative to the single-particle diffusivities, pair-particle diffusivity is calculated considering two particles (m and n), their separation (s), and their separation velocity ($\mathit{\nu }=u^m-u^n$):

$$\begin{array}{}\text{(14)}& {\displaystyle }{\mathit{\kappa }}^{\text{rel}}\left(t\right)& {\displaystyle }={\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}{\displaystyle \frac{\mathrm{d}〈s^{\mathrm{2}}\left(t\right)〉}{\mathrm{d}t}}\text{(15)}& {\displaystyle }& {\displaystyle }=〈s\left(t\right)\mathit{\nu }\left(t\right)〉=\underset{\mathrm{0}}{\overset{t}{\int }}〈\mathit{\nu }\left(t\right)\mathit{\nu }\left(t^{\prime }\right)〉\mathrm{d}{t}^{\prime }\text{(16)}& {\displaystyle }& {\displaystyle }=\mathrm{2}\underset{\mathrm{0}}{\overset{t}{\int }}〈u^m\left(t\right)u^m\left(t^{\prime }\right)〉\mathrm{d}{t}^{\prime }-\mathrm{2}\underset{\mathrm{0}}{\overset{t}{\int }}〈u^m\left(t\right)u^n\left(t^{\prime }\right)〉\mathrm{d}{t}^{\prime }\text{(17)}& {\displaystyle }& {\displaystyle }=\mathrm{2}\mathit{\kappa }-\mathrm{2}\underset{\mathrm{0}}{\overset{t}{\int }}〈u^m\left(t\right)u^n\left(t^{\prime }\right)〉\mathrm{d}{t}^{\prime }.\end{array}$$

From Eqs. (16) and (17), it is seen that the pair-particle diffusivity κ^rel is twice the single-particle diffusivity κ if the individual velocities are uncorrelated. For turbulent diffusion, the average correlation is positive for pair distances smaller than the correlation length (Koszalka et al., 2009) and leads to a reduced κ_rel(t), where the reduction depends on the average initial pair separation. The pair-particle diffusivity is expected to be less dependent on the background mean flow, as any influence from the same background flow experienced by both particles is automatically subtracted in their relative dispersion. However, if the particles move apart into regions with different background flows, the relative diffusivity will include contributions from the background shear. As for the single-particle diffusivity, all tensor components of the pair-particle diffusivity are considered using the zonal and meridional particle separations $s_i=x^m-x^n,s_j=y^m-y^n$ and the zonal and meridional separation velocity ${\mathit{\nu }}_i=u_i^m-u_i^n,{\mathit{\nu }}_j=v_i^m-v_j^n$:

$$\begin{array}{}\text{(18)}& {\displaystyle }{\displaystyle }{\mathit{\kappa }}_{ij}^{\text{rel}}\left(t\right)={\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}{\displaystyle \frac{\mathrm{d}〈s_i\left(t\right)s_j\left(t\right)〉}{\mathrm{d}t}}\underset{t\gg T_{\text{int}}}{=}{\displaystyle \frac{〈s_i\left(t\right)s_j\left(t\right)〉}{\mathrm{2}t}}.\end{array}$$

Furthermore, pair-particle diffusivities are calculated with the background flows removed, similar to the single-particle diagnostics. However, for the pair-particle diagnostics, s^′(t) is derived from the pseudo-trajectories (Eq. 13).

3.4 Anisotropy

The diffusivity tensor K, which is symmetric by construction, can be diagonalized $\mathbf{K}=R\left(\mathit{\alpha }\right)\left(\begin{array}{cc}{\mathit{\lambda }}_{\mathrm{1}}& \mathrm{0}\\ \mathrm{0}& {\mathit{\lambda }}_{\mathrm{2}}\end{array}\right)R(\mathit{\alpha }{)}^{\mathrm{T}}$, where $R\left(\mathit{\alpha }\right)=\left(\begin{array}{cc}\cos \left(\mathit{\alpha }\right)& -\sin \left(\mathit{\alpha }\right)\\ \sin \left(\mathit{\alpha }\right)& \cos \left(\mathit{\alpha }\right)\end{array}\right)$ is a rotation matrix characterizing the orientation of the principal axes of the diffusivity components. The eigenvalues of the symmetric Lagrangian eddy diffusivity tensor are given by

$$\begin{array}{}\text{(19)}& {\displaystyle }{\displaystyle }{\mathit{\lambda }}_{\mathrm{1},\mathrm{2}}={\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}\left({\mathit{\kappa }}_{xx}+{\mathit{\kappa }}_{yy}\pm \sqrt{{\left({\mathit{\kappa }}_{xx}-{\mathit{\kappa }}_{yy}\right)}^{\mathrm{2}}+\mathrm{4}{\mathit{\kappa }}_{xy}^{\mathrm{2}}}\right),\end{array}$$

where the angle is given by

$$\begin{array}{}\text{(20)}& {\displaystyle }{\displaystyle }\tan \mathrm{2}\mathit{\alpha }=\mathrm{2}{\mathit{\kappa }}_{xy}/({\mathit{\kappa }}_{xx}-{\mathit{\kappa }}_{yy})\end{array}$$

(Haigh et al., 2020), and λ₁ is the diffusivity along the major axis of diffusion and corresponds to the eigenvector ${\mathit{e}}_{\mathbf{1}}=\left(\cos \left(\mathit{\alpha }\right),\sin \left(\mathit{\alpha }\right)\right)$. As described by Oh et al. (2000), it is the along-stream component that is amplified by the shear dispersion of the background mean flow and does not converge to a constant value. However, when the background mean flow is subtracted from each drifter velocity, the shear dispersion effect should be minimized even in the along-stream direction.

3.5 Bootstrapping and diffusive limit

Finally, the important concept of this study is the investigation with regards to the saturated behavior of the diffusivities (the convergence to a constant value κ^∞) and how this behavior is affected by the subtraction of the background mean flow. A convergence criterion is established, requiring the standard deviation to be less than 15 % of the average eddy diffusivity from 100 to 250 d. This criterion ensures consistent comparison of convergence properties and diffusivities.

Given the limited sample size, an error estimation is derived through bootstrapping. This involves subsampling 35 bootstrap samples from the original datasets and conducting the analysis for single and pair particles with 100 repetitions. From these values, the mean and standard deviation from the mean are calculated. This approach yields a more accurate standard deviation than a simple calculation of the standard deviation from the original datasets.

4 Background mean flow, eddy kinetic energy, and pseudo-trajectories

The annual mean surface currents in the POP simulation (Fig. 2a, b) closely resemble those in the OSCAR surface current product, with both showing a predominantly northwestward Benguela Current near Africa's western coast between 6 and 18° E. In both datasets, the mean surface currents are primarily westward across the region. Generally, the zonal mean flow at the drifter locations is stronger in the POP simulation than in the OSCAR product, particularly near the coast, while the flows are similar in magnitude further offshore. Snapshots of surface currents from both datasets, taken 200 d after drifter release (5 d interpolation for OSCAR and daily for the POP simulation; Fig. 2c, d), reveal extensive eddy activity of similar magnitudes, filling the upwelling region. These eddies, with many originating from the Agulhas Retroflection site, appear in both datasets, although the POP simulation benefits from higher spatial and temporal resolution. The eddy kinetic energy (EKE) calculated from the annual means of both products (Fig. 2e, f) shows higher EKE magnitudes along the drifter trajectories in the POP simulation compared with the OSCAR product.

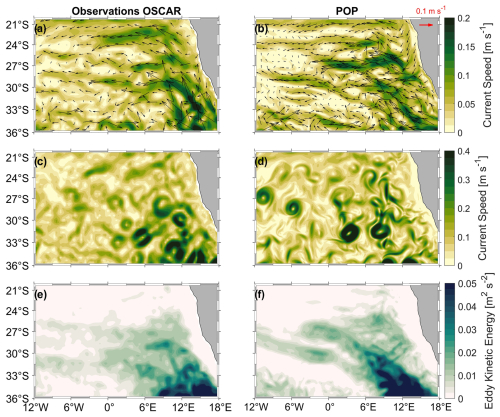
Figure 2 The annual means of surface current speeds are calculated for (a) observations (OSCAR product, 2016–2017) and (b) the POP simulation (1996–1997, 15 m depth). The annual mean current speeds are superimposed with velocity vectors (black arrows) for each respective dataset. The reference vector is given in red. The 5 d interpolation (OSCAR) and daily (POP simulation) snapshots of current speeds (c, d) 200 d after the drifter release are presented to emphasize the strong daily variations in current speeds. The eddy kinetic energy (e, f), calculated from the annual means, highlights the effects of eddies on the background mean flow after the drifter deployments. Blue markers are as in Fig. 1.

The POP simulation with numerical trajectories is only available for 1996–1997, while the observational dataset was obtained in 2016–2017. Regardless, as Fig. 2e and f illustrate, the horizontal distributions of kinetic energies are similar. There is visible interannual variability for the region (Fig. 3a) that is largely driven by the variability in the Agulhas rings. While there are discrepancies between OSCAR and POP, particularly around 2004, the area-averaged energy levels in 1996 in POP (red solid and dashed lines in Fig. 3a) and in 2016 for the OSCAR product (black solid and dashed lines in Fig. 3a) are similar, and so are the total kinetic energies of POP and OSCAR averaged along the drifter locations (red and cyan diamonds in Fig. 3a). However, the total kinetic energy of the surface drifter dataset at an hourly resolution averaged over the surface drifter locations in the observations is substantially higher (black diamond in Fig. 3a). This is largely due to inertial oscillations, visible as semidiurnal oscillations in the time series of the observational drifter velocities (black lines in Fig. 3b and c) as compared to the velocities obtained from POP and OSCAR that are similar in magnitude (red and cyan lines in Fig. 3b and c) but do not capture motions on these timescales.

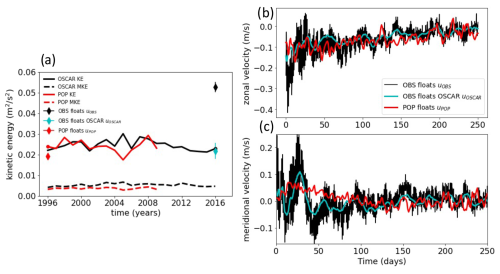
Figure 3 The time series of annual mean kinetic energies for POP (red) compared with the OSCAR product (black) averaged over the Benguela upwelling region (as shown in Fig. 1) are shown in panel (a), where the total kinetic energies (solid lines) and the annual mean background flows (dashed lines) are displayed. Additionally, the total kinetic energies averaged over all float locations for POP, the observations, and the OSCAR velocities interpolated to drifter locations (red, black, and cyan diamonds, respectively) are shown. The time series of zonal and meridional velocities averaged over all drifters are displayed in panels (b) and (c) for POP (red), the observations (black), and OSCAR velocities interpolated to drifter locations (cyan).

The pseudo-trajectories (Fig. 4) reveal various motions occurring at different scales and due to different processes. Both the observations and the POP simulation exhibit a dominant westward mean flow. This is evident from the zonal extent of the pseudo-trajectories with the mean flow subtracted (Fig. 4a, d), which is reduced by up to 1000 km in both datasets. The total motion of particles (black trajectories in Fig. 4a and c) in both datasets consists of two components: the northwestward motion driven by the mean Benguela Current, which shows a stronger zonal flow in the POP simulation and a stronger northward component in the observations (gray trajectories in Fig. 4b and d), and the motion caused by eddies, which includes a net westward component as the eddies entrain filaments of cold water offshore (red trajectories in Fig. 4b and d) as also described in Dräger-Dietel et al. (2018).

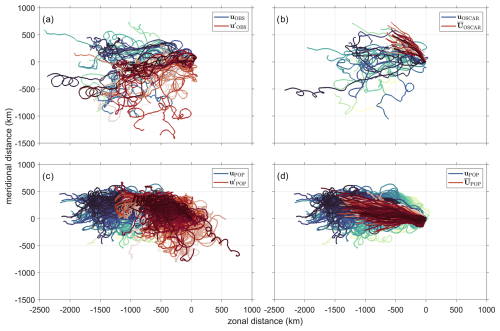
Figure 4 The pseudo-trajectories (Eq. 13) for the observations (a, b) and the POP simulation (c, d). Note that all trajectory components are shown using the Cartesian coordinate system. For the POP simulation, every fifth trajectory is shown to improve the visibility of underlying patterns. The original trajectories are marked in shades of blue (a, c), whereas the pseudo-trajectories from the integration with u^′ (Eq. 12) are marked in shades of red (a, c). The pseudo-trajectories from the integration with the OSCAR surface currents u_OSCAR and the POP simulation daily mean velocities u_POP are highlighted in shades of blue (b, d) and those with the annual mean velocities interpolated to the drifter locations $\stackrel{\mathrm{‾}}{\mathit{U}}{|}_{r\left(t\right)}$ are shown in shades of red (b, d). All pseudo-trajectories have been constructed such that (0,0) is the origin. Note that the coloring of trajectories was chosen such that every trajectory has a slightly different color in the range of blue or red so that patterns of individual trajectories are highlighted.

5 The effect of the mean flow on eddy diffusivities

5.1 Diffusivities

As introduced in Sect. 3, the diffusivity reflects the turbulent mixing according to residual components of the flow field and, thus, depends on the flow decomposition. In this section, the eddy diffusivities calculated from the drifter velocities before and after subtraction of the annually averaged and spatially varying mean flow are compared for the observations and the POP simulation and for the single- and pair-particle approaches. This allows for investigation of the contribution of each mean flow decomposition on the diffusivity tensor and also enables a comparison of the mean flow contributions within each of the datasets and methods, for example, the comparison of single- and pair-particle-derived diffusivities. Note that, from this point onward, the diffusivities derived from pair-particle statistics are defined as ${\mathit{\kappa }}_{xx,xy,yx,yy}^{\text{rel}*}=\mathrm{0.5}{\mathit{\kappa }}_{xx,xy,yx,yy}^{\text{rel}}$ (Eq. 14) to allow for a direct comparison between pair- and single-particle diffusivities. Before the effect of the mean flow on single-particle diffusivities is discussed, we note that the eddy diffusivities from the POP simulation and observations are comparable to each other, as discussed in Sect. 4.

For single-particle diffusivities without mean flow subtraction (Fig. 5, red), the κ_xx component is smaller in the POP simulation $\left(\right(\mathrm{50.98}\pm \mathrm{10.28})\times {\mathrm{10}}^{\mathrm{3}}{\mathrm{m}}^{\mathrm{2}}{\mathrm{s}}^{-\mathrm{1}})$ compared with the observations $\left(\right(\mathrm{60.14}\pm \mathrm{10.15})\times {\mathrm{10}}^{\mathrm{3}}{\mathrm{m}}^{\mathrm{2}}{\mathrm{s}}^{-\mathrm{1}})$. Similarly, the κ_yy component is also smaller in the POP simulation $\left(\right(\mathrm{1.56}\pm \mathrm{0.39})\times {\mathrm{10}}^{\mathrm{3}}{\mathrm{m}}^{\mathrm{2}}{\mathrm{s}}^{-\mathrm{1}})$ compared with the observations $\left(\right(\mathrm{4.59}\pm \mathrm{0.55})\times {\mathrm{10}}^{\mathrm{3}}{\mathrm{m}}^{\mathrm{2}}{\mathrm{s}}^{-\mathrm{1}})$. In contrast, the off-diagonal component κ_xy=κ_yx shows larger diffusivities in the POP simulation $\left(\right(\mathrm{3.84}\pm \mathrm{1.54})\times {\mathrm{10}}^{\mathrm{3}}{\mathrm{m}}^{\mathrm{2}}{\mathrm{s}}^{-\mathrm{1}})$ than in the observations, with the latter exhibiting negative eddy diffusivities $\left(\right(-\mathrm{3.80}\pm \mathrm{4.95})\times {\mathrm{10}}^{\mathrm{3}}{\mathrm{m}}^{\mathrm{2}}{\mathrm{s}}^{-\mathrm{1}})$.

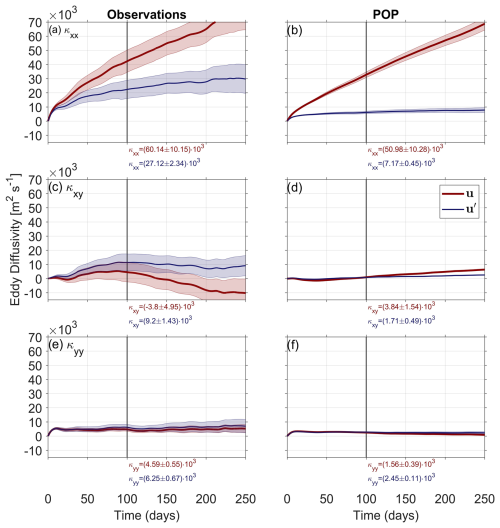
Figure 5 Single-particle eddy diffusivities are shown without subtraction of the mean flow (red) and with subtraction of the annually averaged mean flow (blue), as shown in Fig. 2a and b. The eddy diffusivities are given for all components of the diffusivity tensor κ for the observations (a, c, e) and the POP simulation (b, d, f) (in m² s⁻¹). The vertical black line in each panel marks the 100th day after drifter deployment, after which the eddy diffusivities are temporarily averaged. The temporarily averaged eddy diffusivities are shown with their standard deviations below each panel in the respective colors with and without mean flow subtraction (blue and red). The shaded areas in each panel indicate the uncertainties in eddy diffusivity calculations from bootstrapping (35 subsampled drifters with 100 repetitions).

The mean flow subtraction from absolute drifter velocities (blue in Fig. 5) affects the component of the diffusivity tensor that is most strongly impacted by the mean flow. κ_xx represents the zonal component of the diffusivity tensor and demonstrates the strongest reduction in diffusivities after subtraction of the mean flow across both datasets. This is to be expected, as the mean flow in the Benguela Upwelling System is predominantly zonal, as discussed in Sect. 4. The reductions in κ_xx are about 55 % for the observations and 86 % for the POP simulation. Thus, the zonal mean flow contribution is largest for the diffusivities of the POP simulation. After the mean flow subtraction, κ_xx fulfills the convergence criterion (Sect. 3) for the POP simulation and the observations.

The κ_xy components are reduced by 55 % in the POP simulation, while they show an increase of 342 % in the observations (from negative diffusivities to positive diffusivities). It follows that largest reductions in κ_xy are again found for the POP simulation, but the reductions are smaller (with respect to the percentage) compared with the κ_xx component for the POP simulation. Additionally, with respect to the κ_xy component, the POP simulation does not fulfill the convergence criterion and, thus, does not show saturated behavior after the subtraction of the mean flow. In contrast, κ_xy shows convergence towards a constant value after the subtraction of the mean flow.

Finally, for the meridional component κ_yy, the diffusivities show an increase after the subtraction of the mean flow, where the diffusivities of the observations increase by 36 % and the diffusivities for the POP simulation increase by 57 %. This demonstrates that the subtraction of the mean flow does not necessarily lead to a reduction in diffusivities for all tensor components as the meridional component κ_yy increases for both datasets. After the subtraction of the mean flow, the convergence criterion is fulfilled for both datasets and saturates towards a constant value.

For the pair-particle diffusivities derived from the relative drifter velocities (Fig. 6), the ${\mathit{\kappa }}_{xx}^{\text{rel}*}$ component for the observations $\left(\right(\mathrm{3.38}\pm \mathrm{1.83})\times {\mathrm{10}}^{\mathrm{3}}{\mathrm{m}}^{\mathrm{2}}{\mathrm{s}}^{-\mathrm{1}})$ is about 55 % larger than for the POP simulation $\left(\right(\mathrm{1.41}\pm \mathrm{0.26})\times {\mathrm{10}}^{\mathrm{3}}{\mathrm{m}}^{\mathrm{2}}{\mathrm{s}}^{-\mathrm{1}})$, but it still remains the component with the largest eddy diffusivities. The ${\mathit{\kappa }}_{yy}^{\text{rel}*}$ component also demonstrates almost 78 % smaller eddy diffusivities for the POP simulation $\left(\right(\mathrm{0.92}\pm \mathrm{0.11})\times {\mathrm{10}}^{\mathrm{3}}{\mathrm{m}}^{\mathrm{2}}{\mathrm{s}}^{-\mathrm{1}})$ compared with the observations $\left(\right(\mathrm{4.31}\pm \mathrm{0.47})\times {\mathrm{10}}^{\mathrm{3}}{\mathrm{m}}^{\mathrm{2}}{\mathrm{s}}^{-\mathrm{1}})$. The ${\mathit{\kappa }}_{xy}^{\text{rel}*}$ components for the POP simulation $\left(\right(\mathrm{0.73}\pm \mathrm{0.05})\times {\mathrm{10}}^{\mathrm{3}}{\mathrm{m}}^{\mathrm{2}}{\mathrm{s}}^{-\mathrm{1}})$ are also about 70 % smaller than the components from the observations $\left(\right(\mathrm{2.5}\pm \mathrm{0.91})\times {\mathrm{10}}^{\mathrm{3}}{\mathrm{m}}^{\mathrm{2}}{\mathrm{s}}^{-\mathrm{1}})$.

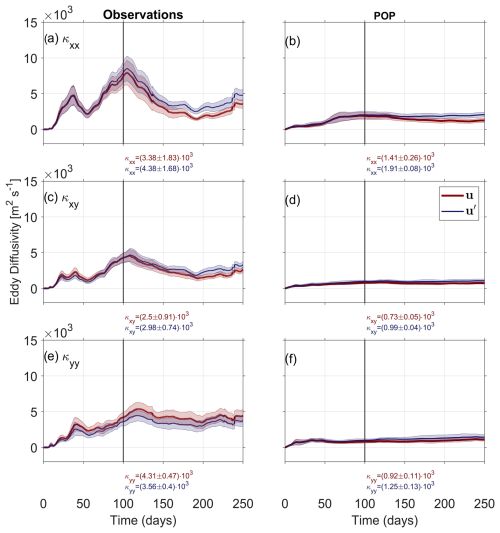
Figure 6 Pair-particle eddy diffusivities are shown without subtraction of the mean flow (red) and with subtraction of the annually averaged mean flow (blue), as shown in Fig. 2a and b. The eddy diffusivities are given for all components of the diffusivity tensor κ for the observations (a, c, e) and the POP simulation (b, d, f) (in m² s⁻¹). The vertical black line and shaded areas mark properties of the plot, as in Fig. 5.

In contrast to single-particle diffusivities, the pair-particle diffusivities show significantly smaller effects on eddy diffusivities after the subtraction of the mean flow. This is to be expected, as the relative drifter velocities are, in theory, less affected by the mean flow because they are derived from the velocity difference in the pairs, from which a common mean flow is then automatically subtracted (Sect. 3). ${\mathit{\kappa }}_{xx}^{\text{rel}*}$ shows that, also for pair-particle statistics, the subtraction of the mean flow does not necessarily lead to a reduction in eddy diffusivities.

The mean flow subtraction demonstrates eddy diffusivities with an increase of 30 % for the observations and an increase of 35 % for the POP simulation. This indicates that, in contrast to single-particle diffusivities, which mostly decrease after the mean flow subtraction, ${\mathit{\kappa }}_{xx}^{\text{rel}*}$ increases for the observations and the POP simulation. After the mean flow subtraction, ${\mathit{\kappa }}_{xx}^{\text{rel}*}$ fulfills the convergence criterion for the POP simulation but not for the observations. For ${\mathit{\kappa }}_{xy}^{\text{rel}*}$, there is a similar increasing behavior for both datasets after the mean flow subtraction. The eddy diffusivities change with an increase of 19 % for the observations and 36 % for the POP simulation. The convergence criterion is fulfilled for the POP simulation but not for the observations. ${\mathit{\kappa }}_{yy}^{\text{rel}*}$ shows opposite signs and presents decreasing behavior of the diffusivities after the subtraction of the mean flow with respect to the other tensor components. The diffusivities after the mean flow subtraction for ${\mathit{\kappa }}_{yy}^{\text{rel}*}$ show a reduction of 17 % for the observations and an increase of 36 % for the POP simulation. The convergence criterion after the mean flow subtraction is fulfilled for both datasets. It is important to note that the impact of the mean flow on pair-particle diffusivities is smaller compared with single-particle diffusivities across all tensor components.

The comparison of single- and pair-particle diffusivities clearly highlights that, specifically for the zonal component, κ_xx components are significantly larger for the single-particle approach than for the pair-particle approach. This is mostly the case before and after the subtraction of the mean flow. Before the mean flow subtraction, the κ_xx components with the single-particle approach are significantly larger, by 94 % for the observations and 97 % for the POP simulation. After the mean flow subtraction, κ_xx components (compared with ${\mathit{\kappa }}_{xx}^{\text{rel}*}$ components) are larger, by about 84 % for the observations and 73 % for the POP simulation. Although, κ_xx and ${\mathit{\kappa }}_{xx}^{\text{rel}*}$ do not show the same overall behavior before or after the subtraction of the mean flow, it is of note that smaller differences between κ_xx and ${\mathit{\kappa }}_{xx}^{\text{rel}*}$ improve comparability in all datasets. The κ_xy components compared with the ${\mathit{\kappa }}_{xy}^{\text{rel}*}$ components are larger, by 166 % for the observations and 189 % for the POP simulation, before the mean flow subtraction. After the mean flow subtraction, the κ_xy components (compared with ${\mathit{\kappa }}_{xy}^{\text{rel}*}$) are 68 % larger for the observations and 42 % larger for the POP simulation. The meridional components κ_yy compared with ${\mathit{\kappa }}_{yy}^{\text{rel}*}$ before the mean flow subtraction show that κ_yy is 6 % larger for the observation and 41 % larger for the POP simulation. After the subtraction of the mean flow, the κ_yy components are larger than the ${\mathit{\kappa }}_{yy}^{\text{rel}*}$ components across both datasets, with percentages of 43 % for the observations and 48 % for the POP simulation.

This study further reveals that the convergence criterion is predominantly satisfied for the pair-particle approach, where 8 out of 12 tensor components across all datasets before and after subtraction of the mean flow showed saturated behavior. For the single-particle approach, 6 out of 12 tensor components demonstrated saturated behavior, where the subtraction of the mean flow had a positive effect on the convergent behavior for 4 out of 12 tensor components. The slightly stronger convergent properties for the pair-particle approach are to be expected, as relative drifter velocities are less affected by the mean flow. However, the results indicate that the single-particle approach generally provides larger diffusivities before and after the mean flow removal, which might indicate that some components of the mean flow may still be affecting the data, not only across the zonal component but also across the other tensor components. In most cases, the diffusivities from the observations and the POP simulation demonstrate similar values, although the values from the POP simulation are slightly smaller before and after the mean flow subtraction.

In summary, our results show that the impact of the mean flow is smaller on pair-particle diffusivities than on single-particle diffusivities, whereas the subtraction of the mean flow improved comparability between single- and pair-particle diffusivities for all tensor components and across different datasets. In some cases, the subtraction of the mean flow improved the convergent properties specifically for the single-particle approach. However, even after the subtraction of the mean flow, single-particle diffusivities tend to be larger than pair-particle diffusivities and are not equal (as one might expect). This indicates that there might be an effect of the mean flow varying on scales smaller than the separation distance of the pair (which should be notable especially for longer time lags) or a contribution of the correlation term (Eq. 17).

5.2 Velocity correlation term analysis

To analyze the effect of the correlation term, the velocity autocorrelations (Fig. 7a, b) and the velocity pair correlations (Fig. 7c, d) are compared in detail. The correlations are normalized by their values at zero time lag. In particular, the comparison focuses on the xx and yy correlations after the mean flow is subtracted. Furthermore, the integral timescales from the autocorrelations and pair correlations are calculated as a measure of the decorrelation timescales (Eq. 7). It should be noted that if significant negative lobes and oscillations appear in the velocity correlations after the first zero crossing, the integral timescale will be considerably smaller than the time required for the diffusivities to converge.

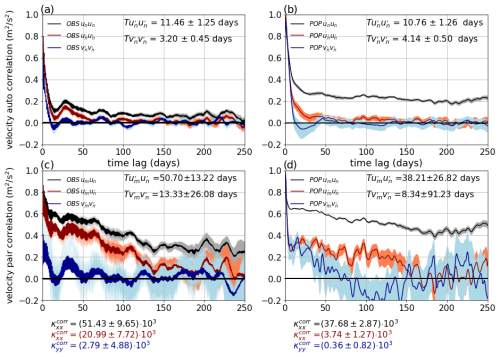
Figure 7 Panels (a) and (b) show the velocity autocorrelations normalized by their value at zero time lag 〈u(t)u(t^′)〉 (black), $\langle u^{\prime }\left(t\right)u^{\prime }\left(t^{\prime }\right)\rangle$ (red), and $\langle v^{\prime }\left(t\right)v^{\prime }\left(t^{\prime }\right)\rangle$ (blue), where the angle brackets (〈〉) represent an average over all particles, as a function of time lag. Panels (c) and (d) display the corresponding normalized velocity pair correlations $\langle u_i^m\left(t\right)u_j^n\left(t^{\prime }\right)\rangle$, where the angle brackets (〈〉) represent an average over all particle pairs. Also given are the integral timescales $T_{u^{\prime }{u}^{\prime }}$ and $T_{v^{\prime }{v}^{\prime }}$, averaged over 100–250 d (Eq. 7), when the mean flow is subtracted. Panels (a) and (c) show the results for observations, whereas panels (b) and (d) show the results for the POP simulation. The temporarily averaged (100–250 d) eddy diffusivities associated with the pair correlation terms ${\int }_{\mathrm{0}}^t\langle u_i^m\left(t\right)u_j^n\left(t^{\prime }\right)\rangle \mathrm{d}{t}^{\prime }$ (last term on the right-hand side of Eq. 17) are shown with their standard deviations below the lower panels for κ_xx with and without mean flow subtraction (black and red) and for κ_yy with mean flow subtraction (blue) (in m² s⁻¹).

First, it is noted that the kinetic energy averaged along the drifter trajectories (i.e., the non-normalized velocity autocorrelation at zero time lag) is higher for the observations than for the POP simulation (cf. black and red diamonds in Fig. 3). The total zonal and meridional kinetic energy is approximately 2.5 and 3.2 times greater in the observations compared with the POP simulation. When the mean flows are subtracted, the total zonal and meridional kinetic energy are approximately 3.6 and 3.3 times larger, respectively. The increase in the ratio with mean flow subtraction, particularly for the zonal component, is consistent with the stronger mean flow observed in the POP simulation, especially in the zonal direction (Fig. 4), leaving a smaller residual in the POP simulation.

The tails of the normalized correlations (Fig. 7) reveal that both the velocity autocorrelations and pair correlations for the xx component do not approach zero when the mean flow is not subtracted. This behavior aligns with the observation that single-particle diffusivities continue to increase with time lag (Fig. 5a, b). When the mean flow is subtracted (red lines in Fig. 7a and b), the autocorrelations for the xx components first cross zero at 83 d for the observations and at 182 d for the POP simulation. The yy components (blue lines in Fig. 7a and b) decay to zero much faster, occurring after 10 d in the observations and after 12 d for the POP simulation, followed by a significant negative lobe within the first 40 d and subsequent oscillations around zero. The meridional components exhibit similar behavior to the autocorrelations with mean flow subtraction (not shown), with the primary difference being reduced values at zero time lag. The times to the first zero crossing are longer for the pair correlation terms. For the xx component, the first zero crossing occurs at 236 d for the observations and at 167 d for the POP simulation when the mean flow is subtracted. In contrast, the yy components reach their first zero crossing much earlier, at 10 d for the observations and at 67 d for the POP simulation.

The autocorrelation integral timescales (Fig. 7a, b) are slightly longer for the POP simulation compared with the observations and are larger in the zonal direction than in the meridional direction. In contrast, the pair correlation integral timescales (Fig. 7c, d) are significantly larger, ranging from 2 to 5 times those of the autocorrelations.

The diffusivity values (Fig. 7) indicate that the correlation term in Eq. (17) is substantial and plays a key role in explaining the differences between single- and pair-particle diffusivities. This term is predominantly positive, contributing to the generally smaller pair-particle diffusivities. For instance, the correlation term for the xx component, without mean flow subtraction, is $(\mathrm{51.43}\pm \mathrm{9.65})\times {\mathrm{10}}^{\mathrm{3}}{\mathrm{m}}^{\mathrm{2}}{\mathrm{s}}^{-\mathrm{1}}$ for both the observations and the POP simulation, accounting for the over 90 % higher single-particle diffusivities. When the mean flow is subtracted, this correlation contribution decreases significantly, leading to better convergence between single- and pair-particle diffusivities, although the pair-particle diffusivities themselves remain relatively unaffected by the mean flow. Even after mean flow subtraction, the contribution of the pair correlation term for the xx component remains $(\mathrm{3.75}\pm \mathrm{1.27})\times {\mathrm{10}}^{\mathrm{3}}{\mathrm{m}}^{\mathrm{2}}{\mathrm{s}}^{-\mathrm{1}}$. Notably, there are instances where the correlation contribution is negative; for example, in the xy component of the observations without mean flow subtraction, there is a negative contribution of $(-\mathrm{2.38}\pm \mathrm{8.25})\times {\mathrm{10}}^{\mathrm{3}}{\mathrm{m}}^{\mathrm{2}}{\mathrm{s}}^{-\mathrm{1}}$, which corresponds to cases in which pair-particle diffusivity exceeds single-particle diffusivity (not shown). It is important to note that these values are sensitive to the chosen averaging interval with large error bars.

In summary, the analysis of the correlation terms reveals that pair diffusivities are not a reliable measure of lateral mixing, primarily because pair velocities remain correlated, especially in the zonal direction, where the first zero crossings occur only after more than 150 d following mean flow subtraction. The velocity autocorrelations decay to zero more rapidly than the pair correlations after mean flow subtraction.

Given that autocorrelation integral timescales are similar in both the observations and the POP simulation, the generally larger single-particle diffusivities observed in the observations compared with the POP simulation can be attributed to the higher kinetic energies (see Eq. 7). Furthermore, oscillations in the velocity autocorrelation reflect particle motions with timescales of a few days associated with mesoscale eddies (Griesel et al., 2010). Additionally, inertial oscillations with periods of about half a day, which are only present in the observational data, appear as oscillations in Fig. 7a and c, although they are not identifiable in the figure (due to the small periods) but, rather, appear as thickened lines. As inertial oscillations are associated with circular motions, they are hypothesized to not contribute much to net mean square displacement and, thus, should not impact the diffusivities. However, the energy contained in the inertial oscillations may contribute to the larger diffusivities in the observations compared with POP, which is further discussed in Sects. 6 and 7.

6 Effect of motions not resolved by satellite data

This section examines the contribution of unresolved motion in the OSCAR product to diffusivities from the observations by subtracting OSCAR-derived velocities from the total observed velocities, thereby isolating the impact of these unresolved motions on diffusivity estimates. The corresponding pseudo-trajectories (Fig. 8) display inertial oscillations as well as other motions that are not resolved by the OSCAR product. The net displacements are found to be about a quarter of the total displacements in the pseudo-trajectories (Fig. 4a).

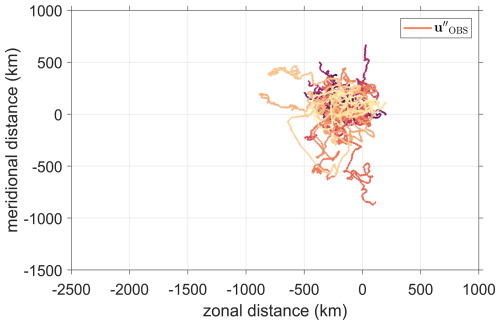
Figure 8 The pseudo-trajectories from the integration with the residual velocity u^′′ from the observations. All pseudo-trajectories have been constructed such that (0,0) is the origin.

Figure 9 Single-particle (black) and pair-particle (red) eddy diffusivities using ${{\mathit{u}}^{\prime \prime }}_{\text{OBS}}$ (Eq. 11). The eddy diffusivities are given for all components of the diffusivity tensor for the observations in panels (a)–(c). The vertical black line and shaded areas mark the properties of the panels, as in Fig. 5.

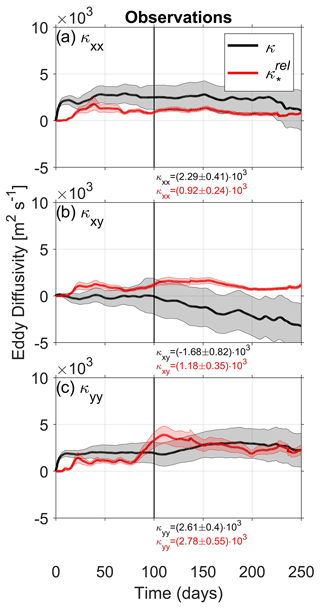
The diffusivity tensor components for both single and pair particles (Fig. 9a–c) indicate contributions in the range of (1.00–$\mathrm{2.50})\times {\mathrm{10}}^{\mathrm{3}}{\mathrm{m}}^{\mathrm{2}}{\mathrm{s}}^{-\mathrm{1}}$. For single-particle diffusivities, the xx and yy components are found to be similar within the error bars, while the xy component becomes negative and does not converge, continuously decreasing with time lag, which suggests the presence of substantial nonzero autocorrelations for this component. Significant differences are observed between single- and pair-particle diffusivities for the xx and xy components, highlighting persistent pair correlations, whereas the yy components remain consistent within the error bars.

Overall, the contribution to the xx component is approximately 8 % of that with the mean flow subtracted, while the contribution to the yy component is around 42 % of the value with the mean flow subtracted. This indicates that diffusivities calculated from trajectories that are advected with altimeter-derived velocities in the Benguela upwelling region are likely to be significantly underestimated, especially in the zonal component.

7 Anisotropy

The diffusivity tensors are characterized in terms of their major- and minor-axis components as well as the angle that defines the orientation of the principal axes of the diffusivity components (Eq. 19). In the following, the anisotropy of the diffusivity tensor is measured by the ratio of the major- to minor-axis components.

In both the POP simulation and the observations, the major-axis components do not converge but, rather, increase continuously, as expected (Fig. 10). However, convergence is observed when the mean flow is removed, with the satisfaction of the convergence criterion, although this is only the case for the diffusivity plateaus for large time lags. For the POP simulation, mean flow subtraction results in a decrease in anisotropy, with the ratio of major- to minor-axis diffusivities dropping from about 44 to 4. Averaged over time lags of 100–250 d, the major-axis component drastically decreases from $(\mathrm{50.77}\pm \mathrm{10.24})\times {\mathrm{10}}^{\mathrm{3}}{\mathrm{m}}^{\mathrm{2}}{\mathrm{s}}^{-\mathrm{1}}$ to $(\mathrm{7.77}\pm \mathrm{0.71})\times {\mathrm{10}}^{\mathrm{3}}{\mathrm{m}}^{\mathrm{2}}{\mathrm{s}}^{-\mathrm{1}}$, whereas the minor-axis component actually increases from $(\mathrm{1.18}\pm \mathrm{0.57})\times {\mathrm{10}}^{\mathrm{3}}{\mathrm{m}}^{\mathrm{2}}{\mathrm{s}}^{-\mathrm{1}}$ to $(\mathrm{1.81}\pm \mathrm{0.33})\times {\mathrm{10}}^{\mathrm{3}}{\mathrm{m}}^{\mathrm{2}}{\mathrm{s}}^{-\mathrm{1}}$, consistent with the increase in the yy component (Sect. 5). In contrast, the observations show an increase in anisotropy that becomes negative, due to the minor-axis component being predominantly negative for time lags greater than about 70 d, although the error bars from the bootstrapping samples are large. The absolute value of the minor-axis component, averaged over time lags from 100 to 250 d, is less than $(\mathrm{0.4}\pm \mathrm{1.0})\times {\mathrm{10}}^{\mathrm{3}}{\mathrm{m}}^{\mathrm{2}}{\mathrm{s}}^{-\mathrm{1}}$. The negative minor-axis component would indicate a decrease in mean square displacement with time along the minor-axis component due to convergence of particles, although the error bars from the standard deviation are large.

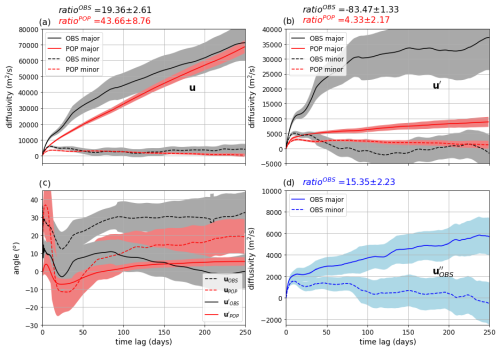
Figure 10 (a) Major- and minor-axis diffusivities (Eq. 19) for the POP simulation and the observations without mean flow subtraction. (b) Major- and minor-axis diffusivities for the POP simulation and the observations with mean flow subtraction. (c) Angle (Eq. 20) for the observations and the POP simulation with and without mean flow subtraction. (d) Major- and minor-axis diffusivities for subtraction with daily mean for the observations. Shown are the means of the diagonalization of the bootstrapping samples and their standard deviations (shading). The numbers in black, red, and blue are the ratios of the major- to minor-axis diffusivities, where the diffusivities were averaged over time lags of 100–250 d.

The diffusivities can be written as the product of major- and minor-axis kinetic energies and integral timescales, as in Eq. (7) (Table 2). It is found that after mean flow subtraction, the ratio of major- to minor-axis kinetic energies is 1.24 and 1.25 for the observations and the POP simulation, respectively. It is mainly the integral timescales that explain the large anisotropy in diffusivities. After mean flow subtraction, the major-axis timescales are about 14 d for the observations and 12 d for the POP simulation, while the minor-axis timescales are −0.21 and 3 d for the observations and the POP simulation, respectively. It should be noted that, while the small anisotropy in the kinetic energy components is similar in the POP simulation and the observations and the major integral timescales are similar, the kinetic energies are larger in the observations (Table 2), explaining the larger major-axis diffusivities compared with the POP simulation. The R(0) values are significantly larger in the observations compared with the POP simulation, even after subtraction of the OSCAR velocities (third row in Table 2). This implies that the kinetic energy associated with inertial oscillations might contribute to the diffusivities in Sect. 6, even though the integral timescales for u^′′ are small. Using the pseudo-trajectories derived from the contributions u^′′ not captured by OSCAR, the analysis shows that convergence is not achieved and the major-axis diffusivity continuously increases with time lag, while the minor-axis diffusivity decreases progressively and becomes negative after time lags exceeding approximately 220 d. The anisotropy remains significant, with a ratio of major- to minor-axis diffusivities of around 15.

Table 2 Velocity autocorrelation at zero time lag for major- and minor-axis components and integral Lagrangian timescales T^int (in days) for different flow velocities (rows). The products of the timescales and velocity autocorrelations are the diffusivities, as given in Fig. 10, averaged over time lags of 100–250 d. A black asterisk indicates that the integral timescales and, therefore, that the diffusivities do not converge for that component.

The results show that the angle of the diffusivity ellipse is close to approximately 30° in the observations when the mean flow is subtracted, while it converges to nearly zero without mean flow subtraction (Fig. 10c). Note that the angle is less steep for the POP simulation compared with the observations after mean flow subtraction. When the daily mean is subtracted, the average angle is −30°, although with large error bars (not shown). The angle is expected to be correlated with the mean flow direction, as the maximum diffusion is anticipated to be oriented in the direction of the mean flow. The mean flow has a stronger meridional component in the observations compared with the POP simulation (Fig. 2a, b), especially for longitudes east of 6° E. Further offshore, the mean flow is zonally oriented and perpendicular to the coast for the observations as well as the POP simulation.

In summary, this study highlights that the minor-axis diffusivity can become negative and that anisotropy occurs for all flow components. The net westward displacements of the drifters and the anisotropy is not only caused by the action of the mean flow but also by the action of the mesoscale eddies that entrain the cold, upwelled water westward. Thus, the mixing is suppressed across both strong mean flow and mesoscale motions.

8 Discussion and conclusions

In this study, two sets of drifter trajectories were analyzed: one derived from observational drifter data and another from trajectories simulated using the POP (Parallel Ocean Program) simulation. The model simulation served as a test bed with about 30 times more drifter trajectories than available in the observations. One challenge in diffusivity estimates is that the influence of shear dispersion by background currents often inhibits the attainment of a diffusive limit, which is why many studies focus on the minor-axis or cross-stream components of the diffusivity tensor. Here, the first goal was to investigate all components of the diffusivity tensor, study their dependence on mean flow subtraction using available background currents, and assess whether diffusive limits were reached. In the observations, the $\mathrm{1}/\mathrm{3}\mathrm{°}$ OSCAR surface current product was used, while the $\mathrm{1}/\mathrm{10}\mathrm{°}$ Eulerian background mean flow was readily available in the model. The single-particle diffusivities were also compared with pair-particle diffusivities, which are hypothesized to be less influenced by background mean flows, making them a potential alternative for single-particle diffusivity estimates where high-quality mean flows are not available.

The results show, as expected, that single-particle diffusivities are much more sensitive to mean flow subtraction than pair-particle diffusivities. In both the POP simulation and the observations, convergence properties significantly improve after mean flow subtraction. Mean flow removal plays a critical role in achieving convergence in the xx and xy tensor components for the single-particle diffusivities. Pair-particle diffusivities, on the other hand, demonstrate more consistent convergence and are less impacted by the mean flow, likely due to the inherent subtraction of common flow components between particle pairs.

However, pair-particle diffusivities are predicted by theory to be twice the single-particle diffusivity if the pair velocities are uncorrelated, and our study demonstrates that pair-particle diffusivities are considerably smaller than that (even after mean flow subtraction). We find that velocity autocorrelations decay more rapidly than the pair correlations, with the subtraction of mean flow leading to even faster decorrelation, particularly in the zonal direction. The integration of the pair correlation term in the equation for pair-particle diffusivity significantly contributes to the observed differences between single- and pair-particle diffusivities and explains why pair-particle diffusivities are generally smaller. As demonstrated by Davis (1987, 1991), the single-particle diffusivity after mean flow subtraction appears in diffusive parameterizations, so our pair-particle estimates would likely underestimate mixing in diffusive parameterizations. Pair-particle diffusivities can be an alternative to the single-particle estimates with mean flow subtraction if the deployment locations are such that the pair velocities are uncorrelated from the beginning or quickly decorrelate.

The diffusivity can be written as the product of kinetic energy, i.e., the velocity autocorrelation at zero time lag, and the integral timescale, and we summarize the results for all flow components in Table 3. The results show that, after mean flow subtraction, the kinetic energies for the zonal and meridional directions become more similar to each other with ratios of 1.1–1.2 for the observations, the POP simulation, and the OSCAR product. However, the zonal integral timescales are 3.6 (observations), 2.6 (POP), and 1.5 (OSCAR) times larger than the meridional ones. The reduction in timescale for the meridional direction can be related to mixing suppression by a zonal mean flow, as discussed in Klocker et al. (2012a), Klocker and Abernathey (2014), and Griesel et al. (2015). The degree of mixing suppression can be based on mixing-length theory, although eddy propagation relative to the mean flow must also be taken into account. In the presence of a zonal background flow, the meridional diffusivity can then be written as follows:

$$\begin{array}{}\text{(21)}& {\displaystyle }{\displaystyle }{\mathit{\kappa }}_{yy}=\mathit{\alpha }R\left(\mathrm{0}\right){\displaystyle \frac{\mathit{\gamma }}{{\mathit{\gamma }}^{\mathrm{2}}+k^{\mathrm{2}}(\stackrel{\mathrm{‾}}{U}-c{)}^{\mathrm{2}}}},\end{array}$$

where γ is a typical Lagrangian decorrelation timescale and is equal to the growth rate of unstable waves in linear instability theory (Griesel et al., 2015), k is related to a typical eddy size and can be regarded as the wavenumber of maximum growth in linear instability theory (although both might differ in the presence of an inverse energy cascade), U is the zonal background mean flow, c is a typical phase speed of the eddies, and α=0.35 as diagnosed by Klocker and Abernathey (2014). It is the difference in U and c that leads to the mixing suppression effect; otherwise, the diffusivity is equal to the velocity autocorrelation at zero lag times the Lagrangian decay scale γ. For the POP simulation, we use the eddy sizes and translational speeds as diagnosed from an eddy-tracking algorithm (Griesel et al., 2015), which amount to 90 km for the average eddy radius and −0.033 m s⁻¹ for the zonal translational speed. We note that the translational speeds are close to, but not necessarily equal to, the phase speed in Eq. (21) (Griesel et al., 2015). With γ as the decay scale (time to first zero crossing) for the meridional direction of about $\mathrm{1}/\left(\mathrm{12}\mathrm{d}\right)$ and using our mean flow values averaged over the drifter trajectories, the timescale is about 3 d, which is close to the Lagrangian integral timescale obtained for POP for yy (Table 3). On the other hand, if we apply Eq. (21) to the suppression by the mean meridional flow, using the region-averaged meridional translational eddy speeds of 0.003 m s⁻¹ and $\mathit{\gamma }=\mathrm{1}/$(182 d), we arrive at a timescale of 14 d, which is indeed close to T_xx from Table 3. These timescales are also consistent with those obtained by Klocker and Abernathey (2014) and Rühs et al. (2018). We note that mixing suppression in the zonal direction due to the mainly zonally oriented topographic background potential vorticity gradient might also be relevant here, a mechanisms that was recently discussed by Sterl et al. (2024).

Table 3 Velocity autocorrelation at zero time lag and integral Lagrangian timescales T^int (in days) (compare Eq. 7) for different tensor components (columns) and flow velocities (rows). The products of timescales and velocity autocorrelations are the diffusivities, as given in Figs. 5 and 9. A black asterisk indicates that the integral timescales and, therefore, that the diffusivities do not converge for that component.

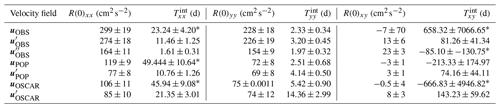
We find that the diffusivities in the observed drifter dataset are larger than those inferred from the POP trajectories, particularly after mean flow subtraction. After mean flow subtraction, the integral timescales are slightly larger in the POP simulation compared with the observations, although they are similar overall (second and fifth rows of Table 3). However, the velocity autocorrelation at zero lag after mean flow subtraction is 2–3 times larger in the observations than in the POP simulation and, thus, explains the larger eddy diffusivities in the observations. This is partly due to the fact that the background flow is larger and more highly resolved in the POP simulation than in the OSCAR surface current product, hence leaving a smaller EKE residual, and illustrates the importance of using high-resolution background flow components. However, the total kinetic energy (R(0) for u_OBS in Table 3) is also larger in the observations than in the POP simulation, while the R(0) values, when considering the contribution from the OSCAR velocities alone (last two rows in Table 3), are more comparable to the POP simulation.

This relates to the research question that addresses the role of smaller-scale motions which are detected by drifters but not by current altimeter products in influencing diffusivities and anisotropy. The study highlights the significant contribution of these unresolved motions. We found that these motions contribute 8 % to the xx component and 42 % to the yy component of diffusivities after mean flow subtraction. The observed differences between single- and pair-particle diffusivities, particularly in the xx and xy components, emphasize the influence of ongoing pair correlations within the unresolved small-scale dynamics. These small-scale motions include inertial oscillations, which are hypothesized to not contribute much to the net diffusion, as they may only lead to oscillations in the velocity autocorrelation, which average out in the integral over the time lag. Indeed, as Table 3 shows, the integral timescales for $u_{\text{OBS}}^{\prime \prime }$ are only about 1 d for the xx and yy components. However, the velocity autocorrelation at zero lag is significant and is largely due to the kinetic energy in the inertial motions. Further studies with more trajectories are needed to clarify the role of inertial motions for mixing. The underestimation of diffusivities when using altimeter-derived velocities indicates that small-scale motions substantially influence diffusivity values and anisotropy, with the potential for large discrepancies when these motions are not accounted for. Promising improvements are anticipated from the recent SWOT (Surface Water and Ocean Topography) satellite mission, which will provide a much higher resolution in geostrophic surface velocity measurements. However, as highlighted by North et al. (2024), velocities in the Benguela upwelling filament contain significant ageostrophic components at scales smaller than about 15 km, which will not be captured by geostrophic velocities derived from sea surface height data. A promising approach was recently suggested by Zhang and Wolfe (2024), who showed that eddy diffusivity can be inferred from the eddy tracks without the need for drifter deployments or altimetry-derived geostrophic velocity measurements.

Finally, the study finds significant anisotropy (measured by the ratio of major- to minor-axis components) in the diffusivities with all flow components. Similarly to the difference between the xx and yy components of the diffusivity tensor, the anisotropy of the diffusivity tensor is mainly explained by the difference in major- and minor-axis timescales, as the anisotropy in the velocity variance ellipses is small and similar in both the observations and the POP simulation (Table 2). The major-axis components of the diffusivity tensor increase with time when no mean flow is subtracted, while the major-axis components converge in the POP simulation and the observations after the mean flow subtraction. The minor-axis component in the observations becomes negative for time lags greater than about 70 d after mean flow subtraction. This highlights the complex nature of diffusivity behavior, where the Lagrangian diffusivity tensor is not necessarily positive definite, as mean square displacement can decrease over time. This might be due to the presence of convergent velocities associated with the filament. Negative minor-axis components were also recently found by Haigh et al. (2020), who diagnosed Eulerian eddy diffusivities from tracer flux–gradient relations in an eddying North Atlantic model simulation, and by Chen et al. (2014), who also diagnosed a significant number of negative Lagrangian cross-stream eddy diffusivities in the Kuroshio Extension. Negative Lagrangian diffusivities are, in principle, consistent with mean square displacements decreasing over time and net up-gradient eddy tracer fluxes.

Subtracting the mean flow reduces the anisotropy in the POP simulation but increases it in the observations due to the near-zero (negative) minor-axis component (division by a very small number). Mean flow subtraction aligns the diffusivity ellipse more closely with the mean flow direction (orientation northwestward). Hence, there is a difference between the yy component of the diffusivity tensor and the minor-axis component. This finding is different from what was found for the Indian Ocean from Global Drifter Program data in Peng et al. (2015), where the mean flow was predominantly meridional; the zonal diffusivity, in most cases, aligned with the minor-axis component; and the meridional diffusivity aligned with the major-axis component. The anisotropy illustrates the role of mesoscale eddies in contributing to westward displacements and anisotropy while suppressing mixing across strong mean and mesoscale flows.

Overall, the minor-axis components before mean flow subtraction are of the order of 3000 m² s⁻¹ for the observations and 1000 m² s⁻¹ for the POP simulation, which is similar to what has been found previously for this component from Lagrangian observations (Zhurbas et al., 2014; Rühs et al., 2018; Peng et al., 2015). However we find that the minor-axis component is also influenced by the mean flow subtraction, with a 1.5-fold increase for the POP simulation but a drastic decrease for the observations to a small, negative value. This may depend on the temporal averaging interval used for the mean flow, which is 1 year in our case. The values of major- and minor-axis components might change if a longer averaging interval is used.

Overall, our findings emphasize the necessity of using the full 2×2 diffusivity tensor to represent lateral mixing in climate models, rather than simplified isotropic representations. We speculate that the current warm SST bias in climate models in the eastern boundary upwelling regions may be reduced if the offshore, predominantly zonally oriented mixing of cold upwelled water by the action of eddies entraining the cold water of the filaments is represented properly.