Non-negligible impact of Stokes drift and wave-driven Eulerian currents on simulated surface particle dispersal in the Mediterranean Sea

Numerical simulations of marine surface particle dispersal are a crucial tool for addressing many outstanding issues in physical oceanography of societal relevance, such as marine plastic pollution. However, the quality of these Lagrangian simulations depends on the ability of the underlying numerical model to represent prevailing ocean circulation features. Here, we investigate how simulated marine surface particle dispersal changes if the – often omitted or only approximated – impact of wind-generated surface waves on upper-ocean circulation is considered. We use velocity fields from a high-resolution coupled ocean–wave model simulation and a complementary stand-alone ocean model simulation for the Mediterranean Sea to answer the following questions: (1) how does the explicit representation of waves impact simulated surface particle dispersal, and what is the relative impact of Stokes drift and wave-driven Eulerian currents? (2) How accurately can the wave impact be approximated by the commonly applied approach of advecting particles with non-wave-driven Eulerian currents and Stokes drift from stand-alone ocean and wave models? We find that the representation of surface waves tends to increase the simulated mean Lagrangian surface drift speed in winter through the dominant impact of Stokes drift and tends to decrease the mean Lagrangian surface drift speed in summer through the dominant impact of wave-driven Eulerian currents. Furthermore, simulations that approximate the surface wave impact by including Stokes drift (but ignoring wave-driven Eulerian currents) do not necessarily yield better estimates of surface particle dispersal patterns with explicit wave impact representation than simulations that do not include any surface wave impact. Our results imply that – whenever possible – velocity fields from a coupled ocean–wave model should be used for surface particle dispersal simulations.

1 Introduction

Understanding how seawater moves around in the global ocean and transports heat, dissolved substances, and particulates is crucial for solving many outstanding issues in physical oceanography and climate science. Due to limited available observations, seawater pathways are often estimated by making use of 3D and time-varying oceanic velocity fields computed with numerical models. With so-called Lagrangian ocean analysis methods, large sets of virtual fluid particle trajectories are simulated and statistically evaluated, whereby the quality of the analyses strongly depends on how well the underlying numerical model represents the oceanic velocity fields (van Sebille et al., 2018).

Surface particle dispersal simulations that estimate how floating, i.e., surface-bound, particles are transported by horizontal ocean surface velocities are of particular importance for addressing a range of societally relevant issues, such as marine plastic pollution (van Sebille et al., 2020; Sutherland et al., 2023), oil spills (Spaulding, 2017), larval dispersal, and biological connectivity (Christensen et al., 2018; Swearer et al., 2019), as well as search and recovery missions (Breivik et al., 2013).

Here, we investigate how the simulated dispersal of surface-bound particles changes if the – often omitted or only approximated – impact of wind-generated surface waves on upper-ocean current dynamics is considered. Under the influence of surface waves, a particle not only moves according to the horizontal Eulerian current velocity, u_E= (u_E,v_E) (with velocity vectors representing 2D horizontal velocities in the following, unless otherwise noted), but additionally experiences a net drift in the direction of wave propagation, known as Stokes drift (u_S) (van den Bremer and Breivik, 2018; Stokes, 1847). Moreover, the presence of surface waves alters the Eulerian current field itself via various (partially non-linear and interacting) processes. By pragmatically defining wave-driven Eulerian currents as the residual of the circulation with and without wave forcing, the Eulerian velocity can be decomposed into a wave-driven component (u_Ew) and a non-wave-driven component (u_Enw) (e.g., Cunningham et al., 2022). Notably, at least part of the wave-driven Eulerian currents tend to act in the opposing direction of Stokes drift (see Higgins et al., 2020, and references therein for a review of this “anti-Stokes” effect). Combining these individual terms, the Lagrangian surface drift velocity of the particle (u_L) can be expressed as

$$\begin{array}{}\text{(1)}& {\mathit{u}}_{\mathrm{L}}={\mathit{u}}_{\mathrm{Enw}}+{\mathit{u}}_{\mathrm{Ew}}+{\mathit{u}}_{\mathrm{S}}.\end{array}$$

The determination of u_L requires a detailed knowledge of the temporally and spatially varying oceanic current and wave fields, as well as their interactions. However, large-scale Lagrangian dispersal simulations nearly always rely on velocity outputs from ocean-only models without the representation of surface wave effects, which implies that the wave impact is either not included or only approximated in the particle tracking. In particular, an increasing number of Lagrangian studies have used a simple superposition of u_Enw from an ocean model and u_S from a stand-alone wave model for their Lagrangian trajectory calculations, neglecting u_Ew (see Tamtare et al., 2022, and references therein). However, due to the lack of direct observations and large-scale coupled ocean–wave models, this approximation is poorly validated. Specifically, the following questions arise:

1. How does the representation of surface waves impact simulated surface particle dispersal? What is the relative impact of wave-driven Eulerian currents compared to that of Stokes drift?

2. How accurately can the wave impact be approximated by the superposition of non-wave-driven Eulerian currents and Stokes drift obtained from stand-alone ocean and wave models?

We address these questions in a case study for the Mediterranean Sea. While previous studies have already highlighted the overall importance of wave-driven processes for upper-ocean dynamics and transport in this region (Morales-Márquez et al., 2021, 2023), we here specifically evaluate the relative roles of Stokes drift and wave-driven Eulerian currents in surface dispersal. We do so by comparing Lagrangian surface dispersal simulations with different representations of waves, which were performed using the velocity output from a newly developed, realistic, high-resolution coupled ocean–wave model configuration and a complementary stand-alone ocean model configuration.

2 Theoretical background and state of the art

2.1 Impact of waves on Lagrangian surface drift velocities

Surface waves can impact Lagrangian surface drift velocities, as expressed by Eq. (1), in two ways – by giving rise to Stokes drift and by altering the Eulerian current field itself via wave-driven Eulerian currents (Fig. 1).

Stokes drift was first described by George G. Stokes, who noted that in the presence of surface waves, a particle experiences a net horizontal drift in the direction of wave propagation (Stokes, 1847). This drift can be explained by (linear) wave kinematics. A particle which oscillates forwards and backwards due to surface waves travels faster, undergoes larger displacements, and stays longer in the crest phase (where horizontal velocities are directed in the direction of wave propagation) than in the trough phase (where horizontal velocities are directed against the direction of wave propagation) (van den Bremer and Breivik, 2018; Guha and Gupta, 2024). As the oscillatory motion related to surface waves decays rapidly with depth, so does the Stokes drift. However, the overall magnitude and vertical shear of Stokes drift depend on the sea state (Breivik and Christensen, 2020; Röhrs et al., 2012). Under wind–sea conditions, where young, locally generated waves with short wave periods dominate, the magnitude of Stokes drift at the surface is high, and its vertical shear is strong. If long-period swell dominates, Stokes drift is less surface-intensified.

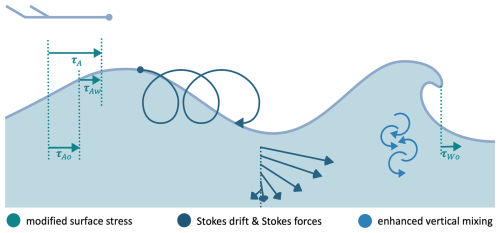
Figure 1 A sketch of how wind-generated surface waves impact Lagrangian surface drift velocities by giving rise to Stokes drift and altering the Eulerian current field. Wave-driven alterations in the Eulerian current field arise from modifications to surface stress, enhanced vertical mixing, and wave-driven Eulerian currents due to Stokes forces. The Stokes forces include the Stokes–Coriolis force, which alters upper-ocean Ekman currents. Vertical mixing is enhanced, for example, through wave breaking and Langmuir turbulence. Changes in the surface stress forcing ocean currents (τ_O) result from (i) a wave-induced increase in surface roughness and hence a decrease in the incoming atmospheric surface stress (τ_A), as well as from (ii) growing waves that absorb momentum from the wind (wave-supported stress, τ_Aw) and dissipating waves that feed momentum back to ocean currents (wave-to-ocean stress, τ_Wo): ${\mathit{\tau }}_{\mathrm{O}}={\mathit{\tau }}_{\mathrm{A}}-{\mathit{\tau }}_{\mathrm{Aw}}+{\mathit{\tau }}_{\mathrm{Wo}}$. The employed coupled ocean–wave model configuration features a representation of all these impacts, with the exception of the regional redistribution of momentum via τ_Aw and τ_Wo (see Sect. 3.1.1). Figure adapted from Janssen et al. (2013).

Wave-driven Eulerian current velocities arise from a combination of different processes related to interactions between Eulerian currents and Stokes drift, acting on a fluid particle through so-called Stokes forces (see, e.g., van den Bremer and Breivik, 2018, for a review), as well as wave-induced changes in air–sea momentum and turbulent energy fluxes (see, e.g., Breivik et al., 2015; Couvelard et al., 2020; and references therein).

The different effects of (non-breaking) surface waves on the Eulerian mean flow in the form of Stokes forces are described by wave-averaged momentum equations (e.g., Craik and Leibovich, 1976; Suzuki and Fox-Kemper, 2016). These equations can be represented in different (mathematically equivalent) forms, resulting in different Stokes terms and, ultimately, different corresponding interpretations of the wave impact. They always include the Stokes–Coriolis force (Hasselmann, 1970, 1971), which, however, appears either together with the vortex force and a wave-induced modification of the pressure (e.g., Craik and Leibovich, 1976) or together with Stokes advection and Stokes shear forces (e.g., Suzuki and Fox-Kemper, 2016). We focus here on the former formulation with the following corresponding interpretation: the Stokes–Coriolis force results from interactions between Stokes drift and the Coriolis force and modifies the turning of upper-ocean Ekman currents (e.g., McWilliams and Restrepo, 1999; Song, 2009; Lewis and Belcher, 2004), while the vortex force arises from interactions between Stokes drift and the mean-flow vorticity and introduces an overturning circulation that explains open-ocean Langmuir cells (Craik and Leibovich, 1976).

The momentum flux from the atmosphere to the ocean is impacted by surface waves in two ways. Firstly, waves modify the sea surface roughness and, consequently, the regional atmospheric momentum flux (e.g., Charnock, 1955; Li et al., 2020). Secondly, waves alter when, where, and how much of this momentum flux is available to drive ocean currents: as waves grow, they absorb momentum from the wind (also referred to as wave-supported stress) that otherwise would have contributed to driving ocean currents, whereas as waves dissipate, they transfer momentum to ocean currents (also referred to as wave-to-ocean stress) (see Breivik et al., 2015; Couvelard et al., 2020). In other words, in the absence of coastlines onto which momentum can be transferred, waves act as a net-zero source and sink of momentum.

As waves break, they inject turbulent kinetic energy into the surface layer, and vertical mixing is enhanced over a depth on the order of the significant wave height (Craig and Banner, 1994; Drennan et al., 1992). Moreover, the wave-averaged flow generates Langmuir turbulence, resulting in vertical mixing over even greater depths (McWilliams et al., 1997), and significantly deepens the mixed layer in large areas of the world ocean (Couvelard et al., 2020). The related hydrographic changes can, in turn, introduce changes in horizontal Eulerian currents. These changes in horizontal Eulerian surface currents due to wave-induced mixing could be as important as the impact of Stokes drift (Rascle et al., 2006; Rascle and Ardhuin, 2009).

2.2 Representation of wave impact in large-scale Lagrangian simulations

So far, in the absence of large-scale operational coupled ocean–wave models, three main approaches have been used to deal with the potential impact of waves on surface particle dispersal simulations – to which we refer as the “old standard”, the “basic approximation”, and the “advanced approximation”.

When following the old standard, no approximation for wave impact is applied. Particles are advected solely with u_Enw from a stand-alone ocean model. The underlying (implicit) assumption is that impacts of wave-driven Eulerian currents and Stokes drift either are completely negligible or offset one another. In early large-scale dispersal studies, adopting this approach was most likely a pragmatic choice since the impact of waves has been difficult to measure and to model due to the complex processes that couple the fast, small-scale wave dynamics with the slower, larger-scale motion of ocean currents (see Suzuki and Fox-Kemper, 2016).

For the basic approximation, the wave impact is included via a Stokes drift term. Particles are advected with u_Enw+ u_S from independently run ocean and wave models (or with u_Enw and a parameterization of Stokes drift based on wind speed; see Tamtare et al., 2022). Here, the (implicit) assumption is that – at the ocean surface – the impact of wave-driven Eulerian currents is negligible or at least less important than Stokes drift (see Clarke and van Gorder, 2018). This approach has been extensively used in a wide range of Lagrangian applications (see Tamtare et al., 2022, and references therein). Several studies have attempted to validate this approach by comparing simulated and observed surface drifter trajectories. While in some studies the inclusion of Stokes drift led to better agreement between observed and simulated surface drifter trajectories (e.g., Tamtare et al., 2022), other studies remained inconclusive (e.g., van Sebille et al., 2021a). Moreover, Wagner et al. (2023) recently advocated that transport studies that make use of ocean models that do not resolve surface waves should not include a Stokes drift term to estimate the Lagrangian surface drift velocity. Based on a scaling analysis of the wave-averaged momentum equations, they conclude that such wave-agnostic models do not simulate the Eulerian mean velocity but rather provide fields that are representative of the Lagrangian mean velocity. This suggests that the old standard may indeed be the most appropriate approach for surface particle dispersal simulations.

For the advanced approximation, recently proposed by Higgins et al. (2020), the wave impact is represented via Stokes drift and an approximation of the wave-driven Eulerian currents. Following this approach, particles are advected with u_Enw from a stand-alone ocean model; u_S from a stand-alone wave model; and an offline-computed wave-driven Eulerian current, largely arising from the Stokes–Coriolis force. This approach assumes that the impacts of wave-driven Eulerian currents and Stokes drift are not negligible and do not offset one another, as suggested by, e.g., Röhrs et al. (2012). Applying the advanced approximation instead of the basic approximation has been shown to improve the agreement between simulated and observed global marine plastic distributions (Cunningham et al., 2022).

3 Materials and methods

To answer the research questions formulated in Sect. 1 and to yield further insights into which of the approaches introduced in Sect. 2.2 is best suited for surface particle dispersal simulations, we performed and compared different types of surface particle dispersal simulations based on velocity output from hindcast experiments with a high-resolution coupled ocean–wave model and a complementary non-coupled stand-alone ocean model configuration. The employed model configurations and corresponding experiments are introduced in Sect. 3.1, and the different types of Lagrangian surface particle dispersal simulations are described in Sect. 3.2.

3.1 Hindcast experiments with a high-resolution coupled ocean–wave model and a complementary stand-alone ocean model

We used the outputs from a regional high-resolution coupled ocean–wave model configuration (ca. 4 km horizontal grid spacing) and a complementary stand-alone ocean model configuration for the Mediterranean Sea. The coupled configuration is based on the Mediterranean Sea Physics Analysis and Forecast system, developed within the framework of the Copernicus Marine Service (MedFS, version EAS6; Clementi et al., 2021), which was rerun for the IMMERSE (Improving Models for Marine EnviRonment SErvices) Horizon 2020 project (https://immerse-ocean.eu/, last access: 15 November 2024), with updated model code including advanced representations of wave–current interactions but without data assimilation and tides in hindcast mode. The Nucleus for European Modelling of the Ocean (NEMO, version 4.2; Madec and the NEMO System team, 2022) served as the ocean component, and the third-generation spectral wave model WAVEWATCH III (WW3, version 6.07; The WAVEWATCH III Development Group, 2019) provided the wave component. The ocean and wave model components were coupled with the OASIS Model Coupling Toolkit (OASIS3-MCT, version 4.0; Craig et al., 2017). The stand-alone ocean model configuration is identical to the ocean component of the coupled ocean–wave model configuration, except for adjustments due to wave coupling. Hindcast simulations were forced using atmospheric fields from the high-resolution European Centre for Medium-Range Weather Forecasts (ECMWF HRES). A detailed description and validation of the model simulations can be found in Moulin and Clementi (2024b). Below, we highlight the aspects most relevant to this study.

3.1.1 The NEMO ocean model

For the coupled and stand-alone regional model configurations, the NEMO hydrodynamic model code is implemented on a horizontal Arakawa C-grid with a $\mathrm{1}/\mathrm{24}$° resolution and 141 unevenly distributed, time-varying vertical levels (z^* coordinates). The bottom cells are partially filled to better represent the model topography. Recent updates to the NEMO code allow for an improved representation of the impact of waves via modifications to the surface stress driving the ocean currents; the inclusion of Stokes drift terms in the horizontal momentum, continuity, and tracer advection equations; and altered parameterizations of the subgrid-scale physics (Couvelard et al., 2020). The employed coupled model configuration makes use of nearly all features described in Couvelard et al. (2020) but uses an alternative formulation for the wave-induced modification of the surface stress, as summarized below.

In the stand-alone model configuration, the surface wind stress forcing the ocean model (τ_O) is calculated via the MedFS bulk formulae using relative wind – the difference between the atmospheric wind at 10 m (u_A10) and the oceanic surface current velocity (u_E(0)) – and a parameterization for the drag coefficient (c_d), following the formulation of Hellerman and Rosenstein (1983):

$$\begin{array}{}\text{(2)}& {\mathit{\tau }}_{\mathrm{O}}={\mathit{\rho }}_{\mathrm{A}}{c}_{\mathrm{d}}∥{\mathit{u}}_{\mathrm{A}\mathrm{10}}-{\mathit{u}}_{\mathrm{E}}\left(\mathrm{0}\right)∥\left({\mathit{u}}_{\mathrm{A}\mathrm{10}}-{\mathit{u}}_{\mathrm{E}}\left(\mathrm{0}\right)\right),\end{array}$$

where ρ_A is the atmospheric density.

For the coupled model configuration, the surface wind stress calculation is adjusted to account for wave processes, as detailed in Clementi et al. (2017): by making use of the neutral coefficient from the wave model, the drag coefficient is computed according to the stable/unstable conditions of the air–sea interface, following Large and Yeager (2004). The wave-supported stress and wave-to-ocean stress (see Sect. 2.1 and Fig. 1) are not included. Their current implementation breaks the momentum conservation and hence is not fully satisfactory (Couvelard et al., 2020).

The discretized vertical profile for the horizontal Stokes drift velocity (u_S(z)) is calculated based on a Phillips spectrum, which provides a good representation of the Stokes drift velocity near the surface (Breivik et al., 2016). It is derived from the surface Stokes drift (u_S(0)) and the Euclidean norm of the total (depth-integrated) Stokes transport (∥T_s∥) from the wave model:

$$\begin{array}{}\text{(3)}& {\displaystyle }{\mathit{u}}_{\mathrm{S}}\left(z\right)={\mathit{u}}_{\mathrm{S}}\left(\mathrm{0}\right)\left[e^{\mathrm{2}{k}_{\mathrm{p}}z}-\mathit{\beta }\sqrt{-\mathrm{2}{k}_{\mathrm{p}}\mathit{\pi }z}\mathrm{erfc}\left(\sqrt{-\mathrm{2}{k}_{\mathrm{p}}z}\right)\right],\text{(4)}& {\displaystyle }{k}_{\mathrm{p}}={\displaystyle \frac{∥{\mathit{u}}_{\mathrm{S}}\left(\mathrm{0}\right)∥}{\mathrm{2}∥{\mathbf{T}}_{\mathrm{s}}∥}}\left[\mathrm{1}-{\displaystyle \frac{\mathrm{2}\mathit{\beta }}{\mathrm{3}}}\right],\end{array}$$

where k_p represents the peak wave number and β=1 (assuming a Phillips spectrum); “erfc” refers to the complementary error function. Due to the C-grid implementation, the horizontal velocity components of Stokes drift are evaluated at the horizontal grid cell interfaces. Divergence of the horizontal Stokes drift velocities induces an additional vertical velocity component (w_S), which can be derived from the continuity equation (see Eq. 8).

The wave-averaged momentum equations for the temporal evolution of the horizontal Eulerian mean velocity (u_E) are formulated in a vector-invariant form and – in addition to the usual non-wave-driven terms in the stand-alone ocean model configuration – include the wave-induced Stokes–Coriolis force (W_St-Cor), vortex force (W_VF), and pressure (W_Prs). The implementation of the first two makes use of the discretized Stokes drift velocity components, and the implementation of the latter uses depth-uniform wave-induced kinematic pressure, also referred to as the Bernoulli head term (J), directly provided by the wave model:

$$\begin{array}{}\text{(5)}& {\displaystyle }{\mathit{W}}_{\text{St-Cor}}=\left(f{v}_{\mathrm{S}},-f{u}_{\mathrm{S}}\right),\text{(6)}& {\displaystyle }{\mathit{W}}_{\mathrm{VF}}=(\mathit{\zeta }{v}_{\mathrm{S}}-w_{\mathrm{S}}{\displaystyle \frac{\partial u}{\partial z}},-\mathit{\zeta }{u}_{\mathrm{S}}-w_{\mathrm{S}}{\displaystyle \frac{\partial v}{\partial z}}),\text{(7)}& {\displaystyle }{\mathit{W}}_{\mathrm{Prs}}=-{\displaystyle \frac{\mathrm{1}}{{\mathit{\rho }}_{\mathrm{0}}}}\left({\displaystyle \frac{\partial J}{\partial x}},{\displaystyle \frac{\partial J}{\partial y}}\right),\end{array}$$

where f is the Coriolis parameter, ζ is the relative vorticity, and ρ₀ is a reference density.

Stokes drift also enters the continuity and 3D tracer advection equations, which take on the following form:

$$\begin{array}{}\text{(8)}& {\displaystyle }\mathbf{\nabla }\cdot \left({\mathit{u}}_{\mathrm{E}}+w_E\mathit{k}+{\mathit{u}}_{\mathrm{S}}+w_{\mathrm{S}}\mathit{k}\right)=\mathrm{0},\text{(9)}& {\displaystyle \frac{\partial C}{\partial t}}=-\mathbf{\nabla }\cdot \left[C\left({\mathit{u}}_{\mathrm{E}}+w_{\mathrm{E}}\mathit{k}+{\mathit{u}}_{\mathrm{S}}+w_{\mathrm{S}}\mathit{k}\right)\right]+D^C+F^C,\end{array}$$

where u_E and u_S are the horizontal Eulerian current and Stokes drift velocity vectors over the (i,j) plane, respectively; w_E and w_S are the vertical Eulerian current and Stokes drift components, respectively, with k as the local upward vector; C is the tracer of interest (i.e., temperature (T) or salinity (S)); ∇ is the derivative vector operator over the ($\mathit{i}\mathbf{,}\mathit{j}\mathbf{,}\mathit{k}$) plane; D^C represents parameterizations of small-scale physics; and F^C represents surface forcing terms (i.e., sources and sinks).

The subgrid-scale physics are modified through adjustments to the turbulent-kinetic-energy (TKE) closure scheme to better account for wave-driven mixing, including changes to the Langmuir turbulence parameterization. In the employed closure scheme, the vertical eddy viscosity and diffusivity coefficients are derived from a prognostic equation for TKE and a closure assumption for turbulent length scales, as described by Madec and the NEMO System team (2022). The temporal evolution of TKE is computed based on its production through vertical current shear and Langmuir turbulence, its destruction due to stratification, its vertical diffusion, and its dissipation. In the coupled simulation, the TKE equation includes an extra term for the production of TKE via Stokes drift shear. In addition, in the coupled simulation, the TKE surface boundary conditions, the mixing length scale, and the dissipation length scale are modified to incorporate wave-induced changes in surface roughness and wave breaking. The Langmuir turbulence parameterization, already employed in the stand-alone ocean model simulation, is expected to be more realistic in the coupled simulation by incorporating the sea-state-dependent Stokes drift obtained from the wave model instead of an approximation of Stokes drift based on the surface wind stress.

The inclusion of wave coupling has been shown to improve simulated upper-ocean circulation patterns and thermohaline properties, as evidenced, for example, by reduced root mean square errors for temperature and salinity in the upper 150 m when compared with ARGO observations (see Moulin and Clementi, 2024b, for a detailed model validation).

3.1.2 The WW3 wave model

The spectral wave model WW3 is implemented using the same domain and horizontal discretization as the hydrodynamic model. It uses 24 equally distributed directional bins with a 15° resolution and 30 frequency bins ranging from 0.0573 to 1.1 Hz to represent the wave spectral distribution. The western boundary is closed, preventing swells from entering from the Atlantic.

WW3 solves the wave-action balance equation, which describes the evolution of a 2D wave spectrum in the presence of slowly varying currents, with individual spectral components following linear wave theory. In the employed coupled ocean–wave model configuration, the WW3 implementation is based on the third-order “Ultimate Quickest” propagation scheme, including the “Garden Sprinkler” correction (Tolman, 2002). Wind input and dissipation terms are derived from the semi-empirical source terms for wind–wave interaction (ST4; Ardhuin et al., 2010). Non-linear wave–wave interactions are accounted for by making use of the discrete interaction approximation (DIA; Hasselmann and Hasselmann, 1985). Furthermore, the model incorporates wave–bottom interactions, depth-induced wave breaking (Battjes and Janssen, 1978), and the reflection of waves at the shoreline.

The wave characteristics in the coupled ocean–wave model simulations align well with observations, as illustrated, for example, by a very high correlation between the significant wave heights obtained from the simulations and those inferred from satellite observations (with a correlation coefficient of 0.956; see Moulin and Clementi, 2024b, for a detailed model validation).

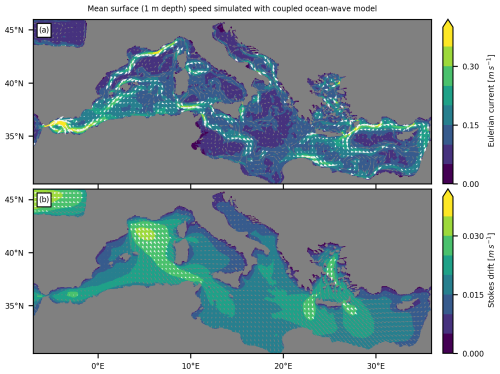
Figure 2 Lagrangian surface velocity components in the 2-year hindcast with the coupled ocean–wave model. The mean speed (color shading) and direction of the mean velocities (arrows displayed at every 10th grid point in the latitude and longitude directions) in the uppermost ocean grid cell (1 m depth) are shown for (a) Eulerian currents (arrows indicating velocities with a mean speed greater than 0.15 m s⁻¹ are rescaled and displayed in white) and (b) Stokes drift (arrows indicating velocities with a mean speed greater than 0.025 m s⁻¹ are rescaled and displayed in white).

3.1.3 Coupled and non-coupled hindcast experiments

Two hindcast experiments were performed: one with the coupled ocean–wave model configuration (hereafter sometimes referred to by the superscript “c”) and one with a complementary non-coupled stand-alone ocean model configuration (superscript “nc”). Both hindcasts used an identical setup, except for the wave coupling (see Table 1 for a summary of the major differences between the two experiments). The non-coupled experiment was performed first, covering a 3-year period from 2018–2020, with the first year considered a spin-up year. The coupled experiment was then initialized with the oceanic fields from the non-coupled experiment on 1 January 2019 and covered a 2-year period from 2019–2020.

Table 1 Important specifications for the experiments using the employed coupled ocean–wave model and complementary stand-alone ocean model. Listed are changes affecting the ocean model component NEMO, grouped according to the parts of the model code they concern – i.e., modifications to surface stress, additional Stokes terms in the primitive equations, and changes in the subgrid-scale parameterizations.

Both hindcast experiments were atmospherically forced by 6-hourly operational analysis and forecast fields from the ECMWF at a $\mathrm{1}/\mathrm{10}$° horizontal resolution. The forcing fields were interpolated over time to provide hourly updates. Atmospheric momentum and heat fluxes were computed using bulk formulae based on the ECMWF atmospheric fields and the model-predicted sea surface temperatures, as described in Pettenuzzo et al. (2010) and Tonani et al. (2015). The water balance was computed as the evaporation minus the precipitation and runoff. While evaporation was indirectly derived from the latent heat flux, precipitation was directly provided as daily averages by the ECMWF, and the runoff from the 39 main rivers entering the Mediterranean Sea was obtained in the form of monthly climatological averages from a combination of several data products, as detailed in Clementi et al. (2021).

For the coupled experiment, a one-way hourly exchange of variables (i.e., the neutral drag coefficient, the sea surface Stokes drift, the total Stokes drift transport, the wave-induced Bernoulli head pressure, the wave-to-ocean energy flux term, and the significant wave height) from the wave model to the ocean model was realized with the OASIS3-MCT coupler. The deviation from the two-way coupling approach described in Couvelard et al. (2020) is justified here since past studies have shown that the impact of ocean current variability on wave dynamics is most important for extreme events (Clementi et al., 2017), which are not the focus of the present study.

For our analyses, we make use of the daily mean outputs from the non-coupled and coupled experiments for the 2-year period from 2019–2020. Specifically, the horizontal Eulerian current and Stokes drift surface velocities of the uppermost cell at approximately 1 m depth are used (Fig. 2).

Table 2 Types of Lagrangian surface dispersal simulations performed. For each simulation type, we employed a different combination of velocity fields from the non-coupled (superscript “nc”) and coupled (superscript “c”) model experiments, representing different combinations of theoretical non-wave-driven and wave-driven velocity components.

3.2 Lagrangian surface dispersal simulations

We employed the “Parcels” particle-tracking package (version 2.4.0; Lange and van Sebille, 2017; Delandmeter and van Sebille, 2019) to calculate the dispersal of idealized surface-bound Lagrangian particles for different representations of the wave impact. The particles were assumed to be positively buoyant, passive, and dimensionless, meaning their movement was completely governed by the horizontal surface velocities. This implies that no vertical motion within the water column, direct drag with the wind, or additional behavior patterns were considered. The particles were released uniformly every 0.05° (approximately one particle per model grid cell) at 5 d intervals over 1 year (2019) in the uppermost model grid cell (approximately 1 m depth) for three subregions located in different near-coastal regions of the Mediterranean Sea. The regions were chosen so that they feature different patterns of the impact of waves on Lagrangian surface speed, as detailed in Sect. 4.1. Overall, 94 243 particles were released in the Gulf of Lion; 98 550 in the Gulf of Antalya; and 109 427 in the Ionian Sea, east of Sicily. Subsequently, the trajectory calculations were performed forward in time using pure horizontal advection with a fourth-order Runge–Kutta scheme and an integration time step of 25 min for a total integration time of 30 d. Particle position and speed (time, latitude, longitude, and ∥u_L∥) were stored daily. We did not add a diffusion term since we aimed to infer the impact of those processes that are resolved by the coupled versus non-coupled model experiments, and diffusion would have added additional noise to this analysis.

We performed four complementary types of Lagrangian simulations per release area, all of which follow the general integration scheme outlined above but differ in the surface velocities employed for particle advection. For each simulation type, we made use of a different combination of fields from the non-coupled and coupled ocean model experiments (Table 2). The simulation with only (non-wave-driven) Eulerian currents from the non-coupled model represents the old standard for Lagrangian simulations that do not consider any wave effect. The simulation with (non-wave-driven) Eulerian currents from the non-coupled model and additional Stokes drift from the coupled model is representative of dispersal simulations that employ the basic approximation of the wave effect. It should be noted, however, that Stokes drift was obtained from the ocean model component on the same horizontal and vertical grid as the Eulerian currents and not directly from the wave model (see Sect. 3.1.1 for a description of the employed vertical Stokes drift profile). The simulation with (non-wave-driven and wave-driven) Eulerian currents and Stokes drift from the coupled model represents our best guess, with the most realistic representation of the impact of waves on particle dispersal. Additionally, we performed a sensitivity simulation using only the (non-wave-driven and wave-driven) Eulerian currents from the coupled model. This simulation type does not follow any conventional approach for surface particle dispersal simulations but is included here to better quantify the impact of waves on surface particle dispersal via Stokes drift versus changes in the Eulerian current velocity. We do not include particle dispersal simulations using the advanced approximation as this approach is (so far) not widely used and represents an intermediate step between simulations with the basic approximation and our best guess, with presumed limited additional value for answering the research questions outlined in Sect. 1.

Note that, in contrast to what has been reported in various previous studies (e.g., Bosi et al., 2021; Delandmeter and van Sebille, 2019), no significant beaching occurred in any of our Lagrangian simulations. This is related to the fact that all employed velocity fields (Eulerian currents and Stokes drift) were provided on the same ocean model C-grid, with zero velocities from ocean to land grid cells, and that these boundary conditions were preserved during particle tracking with Parcels (Delandmeter and van Sebille, 2019).

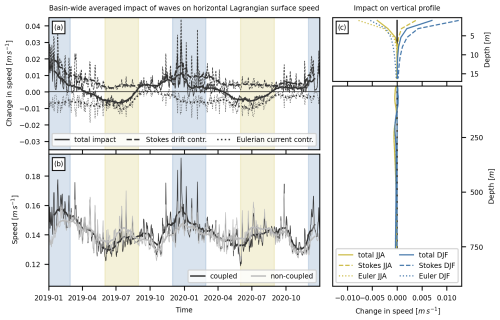
Figure 3 Impact of surface waves on simulated horizontal Lagrangian speed averaged over the entire Mediterranean Sea. (a) Temporal variability in the impact of waves on surface speed. Shown are daily filtered (thin line) and monthly filtered (thick line; 30 d running mean) time series of the total wave impact (solid line) and the corresponding contributions from Stokes drift (dashed line) and Eulerian currents (dotted line). Note that “contr.” stands for contribution. (b) Full time series of the simulated Lagrangian surface speed for the coupled and non-coupled simulations. (c) Vertical profile of the impact of waves during winter (December–February, DJF; blue) and summer (June–August, JJA; yellow). Note that the vertical axis is split and that the Stokes drift component is zero for all depths displayed in the lower part of the profile (i.e., the curves for the total impact and Eulerian current contribution overlap).

4 Results

To obtain an initial estimate of the potential impact of the representation of waves on Lagrangian surface dispersal simulations, we evaluate the changes in the Eulerian averages (i.e., grid-based as opposed to particle-based averages) of the resolved Lagrangian surface drift speed from the coupled simulation compared to the non-coupled simulation (Sect. 4.1). This analysis enables us to define three types of regions with distinctively different impacts of waves on Lagrangian surface drift speed. We then examine exemplary Lagrangian dispersal simulations for each of these region types and perform a more detailed analysis of the impact of waves on general Lagrangian dispersal statistics, such as the along-track distance traveled by a particle, the magnitude and direction of the net particle displacement, and spatial patterns of particle distributions (Sect. 4.2).

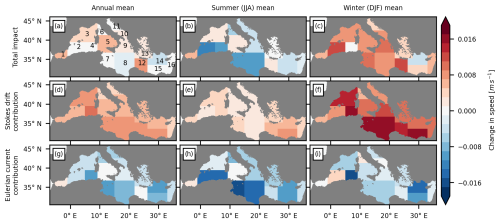
Figure 4 Regionally averaged impact of the representation of surface waves on simulated horizontal Lagrangian surface speed. (a–c) Total impact of the representation of waves. (d–f) The Stokes drift contribution. (g–h) The Eulerian current contribution. Spatial averages were calculated individually for annual, summer (JJA), and winter (DJF) mean speeds over the following regions: (1) the Alboran Sea, (2) the southwestern Mediterranean Sea 1 (western part), (3) the northwestern Mediterranean Sea, (4) the southwestern Mediterranean Sea 2 (eastern part), (5) the Tyrrhenian Sea 2 (southern part), (6) the Tyrrhenian Sea (northern part), (7) the Ionian Sea 1 (western part), (8) the Ionian Sea 2 (southeastern part), (9) the Ionian Sea 3 (northeastern part), (10) the Adriatic Sea 2 (southern part), (11) the Adriatic Sea 1 (northern part), (12) the Levantine Sea 1 (western part), (13) the Aegean Sea, (14) the Levantine Sea 2 (central-northern part), (15) the Levantine Sea 3 (central-southern part), and (16) the Levantine Sea 4 (eastern part).

4.1 Impact of waves on Lagrangian surface drift speed

Figures 3 and 4 illustrate the changes in the Eulerian averages of the gridded horizontal Lagrangian surface drift speed from the coupled simulation compared to the non-coupled simulation. The gridded horizontal Lagrangian velocity was defined as ${\mathit{u}}_{\mathrm{L}}^{\mathrm{nc}}={\mathit{u}}_{\mathrm{E}}^{\mathrm{nc}}$ for the non-coupled experiment and ${\mathit{u}}_{\mathrm{L}}^{\mathrm{c}}={\mathit{u}}_{\mathrm{E}}^{\mathrm{c}}+{\mathit{u}}_{\mathrm{S}}^{\mathrm{c}}$ for the coupled experiment, corresponding to the particle-based Lagrangian velocity definitions of the old standard and the best guess (see Table 2), respectively. The total change in the Lagrangian surface drift speed, along with the contributions of the Stokes drift and Eulerian currents, was then derived as follows: for each model grid point and time step, we calculated the surface speed from the zonal and meridional Lagrangian velocity components. In addition, for the coupled simulation, we computed the scalar projections of both Stokes drift and Eulerian current velocity onto the total horizontal Lagrangian velocity vector, representing their respective contributions to the total Lagrangian speed (see Appendix A). Subsequently, we derived the total impact of waves and the impact of changes in the Eulerian current component by subtracting the respective values of the non-coupled simulation from those of the coupled simulation.

The time series of the impact of waves on Lagrangian surface drift speed, averaged over the entire Mediterranean Sea, reveals distinct and opposing effects of Stokes drift and wave-driven Eulerian currents (Fig. 3a). On the one hand, Stokes drift tends to increase Lagrangian surface speed, in agreement with the general assumptions that wind-generated surface waves predominantly propagate in the downwind direction (see Clarke and van Gorder, 2018) and that surface currents in the Ekman layer deviate by approximately 45° from the wind direction (see Bressan and Constantin, 2019). This increase is – as expected from the general seasonality of winds and surface wave activity (Barbariol et al., 2021) – weakest in summer and strongest in winter. On the other hand, wave-driven Eulerian currents tend to decrease Lagrangian surface speed, related to the effect of anti-Stokes forces and a reduction in atmospheric momentum transfer through increasing surface roughness (see Sect. 2.1). This decrease is – somewhat surprisingly – weakest in fall and, on average, slightly stronger in summer than in winter.

The contrasting seasonality in the contributions of Stokes drift and wave-driven Eulerian currents to Lagrangian surface drift speed can be largely explained by the related processes acting differently on the vertical velocity profile (Fig. 3c; see McWilliams and Restrepo, 1999). While the increase in Lagrangian speed due to Stokes drift generally occurs only in the upper few meters of the water column (< 15 m) and features a strong surface intensification, the decrease in Lagrangian speed due to wave-driven Eulerian currents reaches much larger depths (> 100 m) and is considerably less surface-intensified in winter than in summer due to stronger vertical mixing and deeper Ekman layers. If integrated over the entire depth, the wave-driven decrease in Lagrangian speed due to Eulerian currents is stronger in winter than in summer.

The total impact of waves on Lagrangian surface drift speed appears to be season-dependent as the contributions of Stokes drift and wave-driven Eulerian currents do not necessarily offset one another (Fig. 3a). In summer, surface drift speed decreases with wave coupling, dominated by wave-driven Eulerian currents, whereas in winter, surface drift speed increases with wave coupling, dominated by Stokes drift. As surface drift speed is generally weaker in summer and stronger in winter, this implies that the inclusion of waves increases the seasonal variation and, hence, the temporal variability in simulated Lagrangian surface speed for the Mediterranean Sea (Fig. 3b).

In addition to the seasonal differences, there are regional differences in the total impact of the representation of waves on Lagrangian surface speed (Fig. 4). Here, we compare regional averages of the annual, summer (June–August (JJA)), and winter (December–February (DJF)) changes in Lagrangian surface speed for 16 previously defined subregions of the Mediterranean Sea that approximately correspond to its major sub-basins (for a more general description of the dynamics and an evaluation of the model performance in these regions, see Clementi et al., 2021, and Moulin and Clementi, 2024b). Most regions show the previously described pattern of decreased speed in summer, increased speed in winter, and a small total impact on the annual mean (here, these areas are referred to as neutral-type regions). However, there are four regions that show increased speed over the entire year, including summer (region nos. 1, 3, 5, and 12; here referred to as winter-type regions), and two regions that show decreased speed over the entire year, including winter (region nos. 4 and 14; here referred to as summer-type regions) (Fig. S1 in the Supplement). These regional differences are mainly related to differences in the Eulerian current contribution. In contrast to neutral-type regions, almost all winter- and summer-type regions have stronger Eulerian current contributions in winter than in summer, with winter values being very negative for summer-type regions and summer values being only slightly negative or even slightly positive for winter-type regions.

Based on this initial analysis of the Lagrangian surface drift speed alone, one might assume that Lagrangian surface dispersal simulations would benefit from using the basic approximation (i.e., adding Stokes drift only) for most regions in winter and for winter-type regions in general, while the old standard may be the preferred choice for most regions in summer and for summer-type regions in general. In the following section, we test this hypothesis by evaluating Lagrangian surface dispersal simulations with and without (approximated) representations of waves for selected neutral-, winter-, and summer-type regions. Figure 5 shows the selected regions together with exemplary simulated trajectories: (1) a neutral-type region, located east of Sicily in the Ionian Sea; (2) the Gulf of Lion, situated in the northwestern Mediterranean Sea, representing a winter-type region; and (3) the Gulf of Antalya, located in the central-northern Levantine Sea, representing a summer-type region.

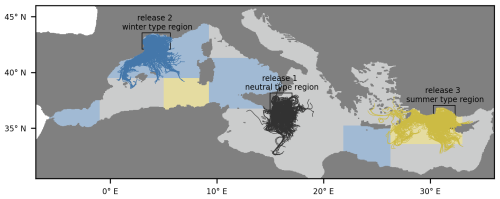
Figure 5 Exemplary trajectories from the best-guess surface particle dispersal simulations. Trajectories were calculated for particles released in three areas (indicated by the black frames): the Ionian Sea, east of Sicily (release 1, dark gray lines); the Gulf of Lion, located in the northwestern Mediterranean Sea (release 2, blue lines); and the Gulf of Antalya, situated in the central-northern Levantine Sea (release 3, yellow lines). The background color shading indicates the classifications of all the previously defined subregions (see Fig. 4), categorized as neutral (light gray), winter (light blue), or summer (light yellow) types.

4.2 Impact of waves on Lagrangian surface dispersal statistics

We assess Lagrangian dispersal statistics in terms of the along-track distance traveled by a particle, the magnitude and direction of the net particle displacement, and spatial patterns of binned particle distributions corresponding to the end of the 30 d integration period. The along-track distance is defined as the length of an individual particle trajectory. The magnitude and direction of the net displacement are obtained from the vectorial difference between the initial and final positions of a particle. Changes in the spatial patterns of binned particle distributions are characterized via changes in the retention rate (the percentage of particles that remain within or have returned to the region's release area by the end of the integration period), the overall dispersal area (the number of bins occupied by particles), and the area with the highest particle concentrations (the bins with the highest number of particle counts that cumulatively encompass 10 % of all particles).

To estimate the total impact of waves on surface dispersal statistics and the individual contributions of Stokes drift and wave-driven Eulerian currents, we compare the four Lagrangian simulation types introduced in Sect. 3.2 (see Table 2): the total wave impact is obtained from the comparison of the best guess versus the old standard, the Eulerian current impact from the comparison of the sensitivity simulation versus the old standard, the Stokes drift impact from the comparison of the best guess versus the sensitivity simulation, and the impact of the basic approximation from the comparison of the basic approximation versus the old standard.

It is important to note that the impact of the basic approximation, which results from adding Stokes drift to the Eulerian current fields from the uncoupled model, is distinct from the Stokes drift impact in the best-guess simulation. This is due to the fact that for the two different simulation types, Stokes drift is combined with different Eulerian velocity fields, meaning particles take different trajectories with different along-track values of Stokes drift. To estimate the potential errors that arise from using the basic approximation versus the old standard, we analyze the respective deviations from our best-guess experiment.

As in Sect. 4.1, we investigate potential seasonal differences. To do so, summer (JJA) and winter (DJF) trajectories are selected based on their release times. Due to the 30 d integration period for the trajectory calculation, particle positions are partly sampled in September and March for releases in summer and winter, respectively.

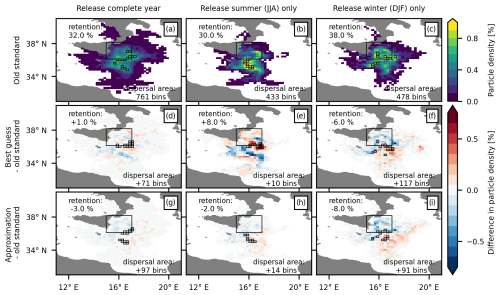
Figure 6 Impact of surface waves on the simulated dispersal pattern of particles released in the Ionian Sea (release 1, neutral-type region) 30 d after their release. (a–c) Particle density per 0.2°×0.2° bin at the end of the 30 d integration period (color shading) for the old-standard simulation; the bins with the highest particle densities, encompassing a total of 10 % of the particles, are marked with black borders. Changes in the particle density of (d–f) the best guess and (g–i) the approximation as compared to the old-standard simulation. The highest-particle-density bins for the best guess and approximation are marked with black borders. Values for the (change in) retention rate (i.e., the percentage of particles that remain within or have returned to the region's release area, indicated by the large black frame, by the end of the integration period) and the overall dispersal area (i.e., the total number of bins occupied by particles) are printed.

4.2.1 Ionian Sea, east of Sicily (release 1, neutral-type region)

In the old-standard simulation (Fig. 6a–c and the gray bars in Fig. 7; Table 3), particles released east of Sicily predominantly travel southeastward to southwestward, reaching an average net displacement of 147 km after 30 d while covering an average along-track distance of 291 km, which translates to an average along-track speed of 0.11 m s⁻¹. While individual pathways vary depending on the exact release location and time, leading to relatively large standard deviations for distance and displacement of 96 and 80 km, respectively, the distance and displacement distributions clearly show a singular maximum that remains relatively robust throughout the entire year. In winter, there is a slight shift toward shorter distances and smaller but more broadly spatially distributed net displacements compared to in summer, and the area with the highest particle concentrations is slightly less confined.

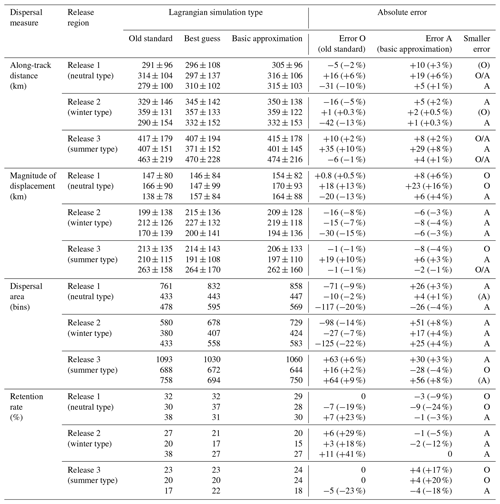
In the best-guess simulation (Fig. S2d–f and the black bars in Fig. 7), the average along-track distance and net displacement are reduced in summer (−6 % and −13 %, respectively) and enhanced in winter (+10 % and +13 %, respectively) compared to the old-standard simulation (Table 3). The total changes (red lines in Fig. 7) in the distance and displacement distributions are almost completely explained by changes in Eulerian currents (yellow lines in Fig. 7) in summer and by changes due to Stokes drift (blue lines in Fig. 7) in winter; the same holds for changes in the particle density distributions (Figs. 6d–f and S3a–i). Notably, the changes due to Eulerian currents in summer are of a similar magnitude to the changes due to Stokes drift in winter. When considering the distance and displacement distributions for the entire year, changes due to Stokes drift and Eulerian currents show opposing tendencies of the same magnitude, resulting in near-zero net changes. These patterns almost perfectly reflect our findings in Sect. 4.1 for neutral-type regions. Moreover, in agreement with decreased Lagrangian speed in summer and increased Lagrangian speed in winter, the relative percentage change in the retention rate shows an increase in summer (+19 %) and a decrease in winter (−23 %). While the dispersal area remains relatively unchanged in summer (+2 %), it is substantially larger in winter (+20 %).

Whether the basic approximation (Fig. S2g–i and the cyan lines in Fig. 7) can improve the simulated wave-driven changes in surface particle dispersal compared to the old standard is season-dependent. When considering only particles released in winter, all calculated dispersion measures show smaller absolute errors when they are inferred from the basic approximation instead of the old standard. However, when considering all particles or only those released in summer, almost all dispersion measures – except for the dispersal area – show better results when the old standard is applied (Table 3). Likewise, the total impact of waves on the particle density pattern is well captured by the approximation in winter but not at all in summer (Fig. 6g–i). The absolute error for the basic approximation is, however, in several cases, only slightly larger than that for the old standard.

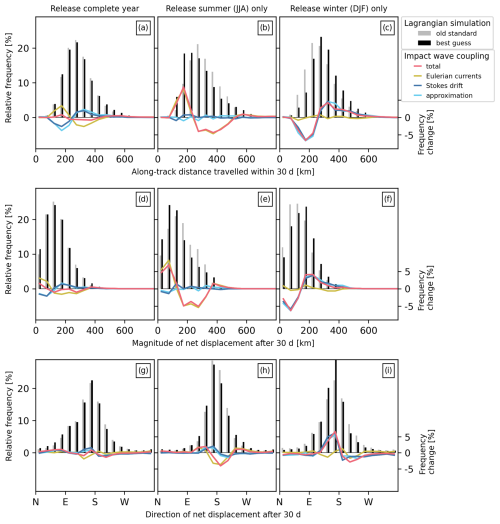
Figure 7 Impact of surface waves on the statistics of the simulated dispersal of particles released in the Ionian Sea (release 1, neutral-type region) at the end of the 30 d integration period. Shown are distributions for (a–c) the traveled along-track distance, as well as (d–f) the magnitude and (g–i) the direction of the net displacement for the old-standard simulation (gray bars) and the best-guess simulation (black bars). The total change due to wave coupling (red lines), changes resulting from either wave-driven Eulerian currents (yellow lines) or Stokes drift (blue lines) individually, and changes resulting from the basic approximation (cyan lines) are overlaid.

Altogether, the results for this region highlight that both Stokes drift and wave-driven Eulerian currents can have a non-negligible impact on surface particle dispersal and that their relative importance may be season-dependent. Hence, surface dispersal simulations should, ideally, be performed using output from coupled ocean–wave models. The hypothesis formulated in Sect. 4.1 is – with few exceptions – valid for this neutral-type region: if coupled ocean–wave model output is not available, the basic approximation should be preferred for winter dispersal simulations, while the old standard remains the slightly better choice for summer dispersal simulations.

Table 3 Impact of the representation of surface waves on basic surface particle dispersal measures. The considered measures include the final along-track distance and the magnitude of net displacement (mean ± standard deviation), as well as the overall retention rate and dispersal area (see Sect. 4.2 for their exact definitions). Values are listed for three particle release regions (see Fig. 5) and three Lagrangian simulation types (see Table 2), as well as for the absolute errors in simulations performed with the old standard (O) and the basic approximation (A), calculated as deviations from the best guess (with changes in percentage shown in parentheses). The last column indicates whether the magnitude of the absolute error is smaller for O or A (with differences of 1 % or less shown in parentheses). Each cell contains statistics computed over all released particles (first cell entry), as well as those calculated for subsets of particles released in summer (JJA; second cell entry) and winter (DJF; third cell entry).

4.2.2 Gulf of Lion, northwestern Mediterranean Sea (release 2, winter-type region)

In the old-standard simulation (Fig. 8a–c and the gray bars in Fig. 9; Table 3), particles released in the Gulf of Lion predominantly travel southeastward to southwestward, reaching an average net displacement of 199 km while covering an average along-track distance of 329 km within the 30 d integration period, which translates to an average along-track speed of 0.13 m s⁻¹. However, as in the Ionian Sea region previously discussed, individual particle pathways vary significantly depending on the exact release location and time, resulting in a relatively wide distribution of along-track distances and net displacements (standard deviations of 146 and 138 km, respectively). The final dispersal area extends far beyond the Gulf of Lion into the Algerian–Balearic basin, with well-established pathways connecting the Gulf of Lion to the Balearic Islands. However, there are profound seasonal differences. In summer, southwestward pathways along the French coast dominate the final particle distributions, with the largest number of particles found west of Mallorca. In winter, there are more trajectories with shorter along-track distances and net displacements, resulting in smaller mean along-track distance and magnitude of net displacement, as well as fewer particles reaching the area west of Mallorca and more particles remaining in the release area. At the same time, the largest individual displacements are greater, yielding connecting pathways to the area southwest of the Balearic Islands that are not present in summer. Accordingly, the retention rate and dispersal area are both larger in winter than in summer.

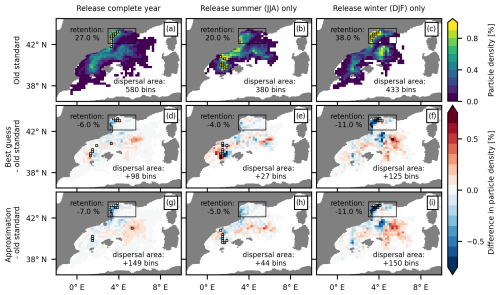
Figure 8 Impact of surface waves on the simulated dispersal pattern of particles released in the Gulf of Lion (release 2, winter-type region) 30 d after their release. (a–c) Particle density per 0.2°×0.2° bin at the end of the 30 d integration period (color shading) for the old-standard simulation; the bins with the highest particle densities, encompassing a total of 10 % of the particles, are marked with black borders. Changes in the particle density of (d–f) the best guess and (g–i) the approximation as compared to the old-standard simulation; the highest-particle-density bins for the best guess and approximation are marked with black borders. Values for the (change in) retention rate (i.e., the percentage of particles that remain within or have returned to the region's release area, indicated by the large black frame, by the end of the integration period) and the overall dispersal area (i.e., the total number of bins occupied by particles) are printed.

In the best-guess simulation (Fig. S4d–f and the black bars in Fig. 9; Table 3), the average along-track distance and magnitude of net displacement are increased to 345 and 215 km, respectively. The retention rate is reduced, and the dispersal area is increased compared to the old-standard simulation. Notably, this holds for the entire year, though the effect is more pronounced in winter than in summer (with a 41 % vs. 18 % relative decrease in the retention rate and a 22 % vs. 7 % increase in the dispersal area). This agrees with the findings in Sect. 4.1 that show that in the Gulf of Lion – a winter-type region – the inclusion of wave effects increases the Lagrangian surface drift speed over the entire year due to the dominant impact of Stokes drift and that this impact is intensified in winter.

The absolute errors in the retention rate and dispersal area (Table 3) are smaller for the basic approximation than for the old standard. The total impact of waves on the particle density pattern is generally well captured by the approximation (compare Fig. 8g–i with Fig. 8d–f). This benefit is also evident in the greatly improved estimates for the mean along-track distance (with the absolute error reduced from −13 % to +0.3 %) and the magnitude of net displacement (with the absolute error reduced from −15 % to −3 %) in winter. Hence, for this winter-type region and the selected dispersion measures, applying the basic approximation yields an improvement compared to the old-standard simulation, in which wave effects are not accounted for. However, while the old standard overestimates the retention rate and tends to underestimate the dispersal area, the basic approximation still tends to underestimate the retention rate and overestimates the dispersal area as the partially compensatory effects of wave-driven Eulerian currents are not accounted for (Table 3). Depending on the application of interest, the sign of the error may be crucial, such that the old standard might be preferred over the basic approximation, notwithstanding the larger absolute error. Moreover, individual distinct features of the dispersal pattern and statistics in the best-guess simulation cannot be reproduced by applying the basic approximation. While the total change (red lines in Fig. 9) in the winter distributions of distance and displacement can be primarily attributed to changes due to Stokes drift (blue lines in Fig. 9), changes in the summer distributions are largely impacted or even dominated by changes in the Eulerian currents (yellow lines in Fig. 9). Wave-driven Eulerian currents appear to impact important details of the particle density pattern for summer (Fig. S5b and h). The estimated connectivity to the Balearic Islands is similarly sensitive to the inclusion of wave-driven Eulerian currents: for summer, the inclusion of the impact of Stokes drift and wave-driven Eulerian currents together interrupts the connection between the Gulf of Lion and Mallorca, while connecting pathways still exist if only Stokes drift is added (Fig. S4e and h).

In summary, the results for this region support the hypothesis that applying the basic approximation in a winter-type region generally leads to an improvement in the dispersal simulations. However, the analyses also reveal that applying the basic approximation is not sufficient for capturing the total impact of waves on surface particle dispersal.

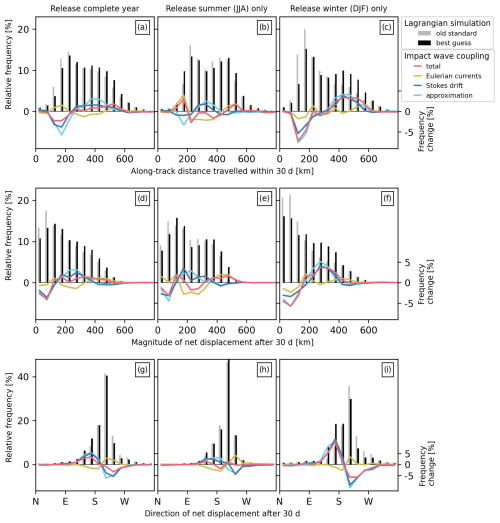
Figure 9 Impact of surface waves on the statistics of the simulated dispersal of particles released in the Gulf of Lion (release 2, winter-type region) at the end of the 30 d integration period. Shown are distributions for (a–c) the traveled along-track distance, as well as (d–f) the magnitude and (g–i) the direction of the net displacement for the old-standard simulation (gray bars) and the best-guess simulation (black bars). The total change due to wave coupling (red lines), changes resulting from either wave-driven Eulerian currents (yellow lines) or Stokes drift (blue lines) individually, and changes resulting from the basic approximation (cyan lines) are overlaid.

4.2.3 Gulf of Antalya, central-northern Levantine Sea (release 3, summer-type region)

In the old-standard simulation (Fig. 10a–c and the gray bars in Fig. 11; Table 3), particles released in the Gulf of Antalya typically travel westward or southeastward, reaching an average net displacement of 213 km after 30 d while covering an average along-track distance of 417 km, which translates to an average along-track speed of 0.16 m s⁻¹. As with the previously discussed regions, individual particle pathways vary significantly depending on the exact release location and time. Most notably, there are large differences between the summer and winter dispersal patterns. In summer, the southeastward paths dominate, and the distance and displacement distributions show clear maxima around 400 and 200 km, respectively, resulting in a well-defined area with the highest particle density just south of the release region. In winter, the westward pathways dominate, and distance and displacement are, on average, greater and show much broader distributions, resulting in a smaller retention rate, a larger dispersal area, and less concentrated final particle distributions.

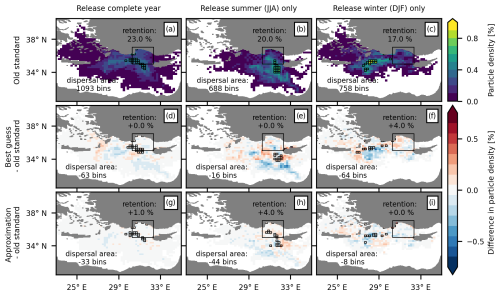
Figure 10 Impact of surface waves on the simulated dispersal pattern of particles released in the Gulf of Antalya (release 3, summer-type region) 30 d after their release. (a–c) Particle density per 0.2°×0.2° bin at the end of the 30 d integration period (color shading) for the old-standard simulation; the bins with the highest particle densities, encompassing a total of 10 % of the particles, are marked with black borders. Changes in the particle density of (d–f) the best guess and (g–i) the approximation as compared to the old-standard simulation; the highest-particle-density bins for the best guess and approximation are marked with black borders. Values for the (change in) retention rate (i.e., the percentage of particles that remain within or have returned to the region's release area, indicated by the large black frame, by the end of the integration period) and the overall dispersal area (i.e., the total number of bins occupied by particles) are printed.

In the best-guess simulation (Fig. S6d–f and the black bars in Fig. 11; Table 3), the average along-track distance and displacements are reduced in summer (−10 % for both measures) but marginally increased in winter (+1 % for both measures) compared to the old-standard simulation. This implies that the average along-track velocities are also decreased in summer but slightly increased in winter, though the Eulerian averages for Lagrangian speed in the summer-type region (Fig. 4) indicate a decrease for both seasons. This emphasizes the fact that Lagrangian averages can deviate from Eulerian averages since they depend on the exact trajectories of the particles – that is, on the part of the flow field they sample, when they sample it, and for how long. One would generally assume that Lagrangian means are smaller than Eulerian means as particles spend more time in regions with slow background flow; however – as in the present case – Lagrangian averaging can also result in higher speeds if particles are more confined to stronger currents. The dispersal area is decreased over the entire year (from −2 % to −9 %), whereas the retention remains largely unchanged in summer but increases in winter (with a relative percentage change of +23 %). Hence, for this region, there is no direct link between particle speed and the dispersal area or retention rate, further emphasizing the importance of the exact pathways taken by the particles.

As expected for a summer-type region, all net changes (Fig. 10d–f and the red lines in Fig. 11) between the best-guess and old-standard simulations are dominated by changes in Eulerian currents (Fig. S7a–c and the yellow lines in Fig. 11), and Stokes drift (Fig. S7d–f and the blue lines in Fig. 11) has a small net effect. Nevertheless, using the basic approximation (Fig. S6g–i and the cyan lines in Fig. 11) yields a small improvement over employing the old standard for several of the calculated dispersion measures (Table 3). This can be partly attributed to the fact that – in contrast to what has been discussed before – for these measures and in the considered region, the basic approximation introduces net changes that act approximately in the same direction as the wave-driven Eulerian currents (which, however, partially differ from changes due to Stokes drift in the best-guess simulation).

To conclude, our results do not support the hypothesis that applying the old standard instead of the basic approximation generally leads to an improvement in the dispersal simulations for the chosen summer-type region; for some dispersal measures, it does, while for others, it does not.

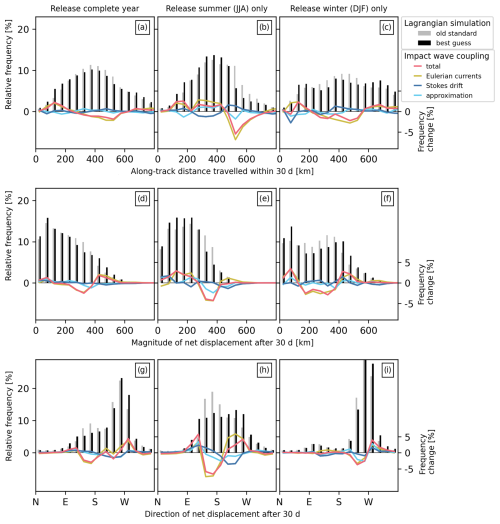
Figure 11 Impact of surface waves on the statistics of the simulated dispersal of particles released in the Gulf of Antalya (release 3, summer-type region) at the end of the 30 d integration period. Shown are distributions for (a–c) the traveled along-track distance, as well as (d–f) the magnitude and (g–i) the direction of the net displacement for the old-standard simulation (gray bars) and the best-guess simulation (black bars). The total change due to wave coupling (red lines), changes resulting from either wave-driven Eulerian currents (yellow lines) or Stokes drift (blue lines) individually, and changes resulting from the basic approximation (cyan lines) are overlaid.

5 Summary and discussion

We used the output of a newly developed coupled ocean–wave model configuration and that of a complementary stand-alone ocean model configuration for the Mediterranean Sea to quantify how Stokes drift and wave-driven Eulerian currents impact simulated idealized surface particle dispersal. Moreover, we assessed how well this combined wave impact is represented in surface particle dispersal simulations that make use of the basic approximation, i.e., those that employ a superposition of non-wave-driven Eulerian currents and Stokes drift obtained from independently run ocean and wave models for particle tracking.

We find that both Stokes drift and wave-driven Eulerian currents can have a non-negligible impact on surface particle dispersal. While both tend to act in opposing directions, they do not necessarily offset one another at the surface due to differences in temporal and spatial variability. Our analyses suggest a seasonal and regional dependence of the wave impact. For most of the Mediterranean Sea, ocean–wave coupling increases the simulated mean Lagrangian surface speed in winter due to a dominant impact from Stokes drift and decreases it in summer due to a dominant impact from wave-driven Eulerian currents. Yet some regions also exhibit a dominant impact from either Stokes drift or wave-driven Eulerian currents throughout the entire year. Consequently, applying the commonly used basic approximation is not always beneficial for surface particle simulations. In summer, in regions where the impact of wave-driven Eulerian currents dominates throughout the entire year, as well as during time periods when wave-driven Eulerian currents and Stokes drift effects tend to offset one another, it may be better to utilize the old-standard approach for particle dispersal simulations – that is, it may be better to ignore any wave effect. In addition, we highlight that the advantages and disadvantages of applying the basic approximation versus the old standard further depend on the Lagrangian measure of interest (see Table 3). One measure may be adequately represented by the basic approximation, another by the old standard, and a third by neither of the two simulation types that exclude wave-driven Eulerian currents. However, due to the complex interplay of wave-driven Eulerian currents, Stokes drift, and regional non-wave-driven circulation, these dependencies cannot be known a priori. Hence, we argue that – whenever possible – coupled ocean–wave models should be employed for surface particle dispersal simulations. This is especially true for studies that heavily rely on the accuracy of individual or low-probability particle tracks, such as those involving the estimation of connectivity patterns.

We acknowledge, however, that our results are based on idealized particle dispersal simulations for a short period, utilizing one specific regional one-way coupled ocean–wave model configuration. More studies with outputs from other fully coupled ocean–wave models, spanning larger regions and longer periods, are needed to further investigate the spatial and temporal variability in the impact of Stokes drift and wave-driven Eulerian currents on not only idealized but also realistic particle dispersal simulations. Open questions to be addressed by these follow-up studies include the following: how robust is the seasonality of the impact of Stokes drift and wave-driven Eulerian currents, and what are its major drivers? What is the relative importance of the impact of Stokes drift and wave-driven Eulerian currents on much shorter (i.e., hourly) or longer (i.e., decadal) timescales? What role do extreme events play? Stokes drift has been shown to have a significantly increased impact on surface particle dispersion during, for example, hurricanes (Curcic et al., 2016), but it is still unclear whether the impact of surface wave-driven Eulerian currents is increased proportionally.

Case-specific simulations for real applications with non-idealized particles can yield additional insights into how important wave impacts are compared to other particle-type-specific factors, such as windage or vertical motion. These analyses will indicate which findings from past studies relying on dispersal simulations without coupled ocean–wave models should be revisited. They can also be used to further improve the accuracy of Lagrangian dispersal simulations for which coupled ocean–wave model outputs remain unavailable. Specifically, we recommend comparisons between the findings of simulations based on coupled ocean–wave model output and those of simulations using the advanced approximation by Higgins et al. (2020) to identify which wave-driven processes are the most important to ensure the faithful simulation of particle dispersal.

5.1 Comparison with previous studies

Our results complement the findings of, e.g., Röhrs et al. (2012) and Cunningham et al. (2022), which show that – while Stokes drift often represents the dominant impact of waves on surface particle dispersal – wave-driven Eulerian currents can significantly alter dispersal patterns and need to be considered to accurately represent the impact of waves on surface particle dispersal simulations.

Why do other studies lead to conflicting results and suggest that only Stokes drift needs to be included (e.g., Tamtare et al., 2022) or that wave impact does not need to be considered at all (e.g., Wagner et al., 2023)? This controversy can partially be related to methodological issues. We highlighted that Eulerian and Lagrangian averages may be significantly different depending on which regions of the flow are sampled by the Lagrangian trajectories, when they are sampled, and for how long. Moreover, differences in spatiotemporal variability in non-coupled and coupled ocean–wave models may cancel each other out in an Eulerian mean sense but can accumulate along a Lagrangian trajectory; this effect can become even more pronounced with longer trajectory integration times. We argue that analyzing Lagrangian velocities in an Eulerian framework is insufficient for estimating the impact of certain flow components, such as Stokes drift and wave-driven Eulerian currents, on large-scale particle dispersal patterns. Study-specific Lagrangian simulations are required to capture the full impact. Following this argument, the analysis of Wagner et al. (2023) remains partially inconclusive, and there is no evidence that surface velocities from ocean models without the inclusion of any surface wave impact indeed represent actual particle drift velocities. Differences in spatial model resolution may also be a potential reason for the differences between our work and that of Wagner et al. (2023) as their scaling analysis and numerical simulations were explicitly performed for ocean mesoscales (and larger scales).

Furthermore, the validation of simulated surface particle drift trajectories remains challenging. Available comparisons between simulated and observed drifter trajectories do not allow for a clear separation between the impact of Stokes drift and that of other types of wind- and wave-induced particle drift. As surface drifters are subject to direct wind drag, they not only are advected by ocean surface velocities but also experience additional drift in the wind direction. In particle simulations, this is often accounted for by an additional leeway term (αu_A), also referred to as the wind correction term:

$$\begin{array}{}\text{(10)}& {\mathit{u}}_{\mathrm{L}}={\mathit{u}}_{\mathrm{E}}+{\mathit{u}}_{\mathrm{S}}+\mathit{\alpha }{\mathit{u}}_{\mathrm{A}},\end{array}$$

where u_A represents the near-surface atmospheric wind speed and α represents a dimensionless parameter that is empirically determined to minimize differences between observed and simulated trajectories (e.g., Tamtare et al., 2022; Röhrs et al., 2012). Since Stokes drift approximately aligns with the wind direction, and a substantial part of the wave-driven Eulerian currents tends to act in the opposing direction of Stokes drift, tuning α can, to some degree, also compensate for an under- or overestimation of Stokes drift and the neglect of wave-driven Eulerian currents in u_E. Likewise, we argue – in contrast to Tamtare et al. (2022) – that improved agreement between observed and simulated drifter trajectories, when including only Eulerian currents and Stokes drift from independently run ocean and wave models and omitting the wind correction term, does not necessarily imply that windage and other remaining drivers, such as wave-driven currents, are negligible. These additional factors could also offset one another or – if velocity products including data assimilation are employed – part of their impact may even be included in the Eulerian current fields. However, whether certain drift components partly or completely oppose each other depends on the intricate interplay between regional ocean current dynamics, prevailing wind and wave patterns, and drifter design. It is thus a natural consequence that some specific Lagrangian drift models with the inclusion of Stokes drift benefit from a wind correction term (Callies et al., 2017; Tamtare et al., 2022), while others do not (e.g., De Dominicis et al., 2013; Lebreton et al., 2018).

5.2 Potential implications for 3D particle dispersal simulations

While our analysis focused on 2D simulations of horizontal surface particle dispersal, our results have implications for 3D particle dispersal simulations. We highlighted that Stokes drift and horizontal wave-driven Eulerian currents are both strongest at the sea surface but show differences in their vertical profiles and temporal variability. The vertical Stokes drift profile can be directly inferred from surface wave characteristics, as defined, for example, in Eq. (2), and the overall magnitude of Stokes drift exhibits relatively clear seasonality, with maximum values in winter. In contrast, the vertical profile of horizontal wave-driven Eulerian currents is influenced by a range of processes that act on larger depth scales than Stokes drift and result in more complex temporal variability. In general, horizontal wave-driven Eulerian currents tend to be less surface-intensified during periods of strong vertical mixing, such as in fall and winter. Moreover, we find initial indications of different subsurface regimes of the surface wave impact on Lagrangian velocities, roughly corresponding to the Stokes layer, the Ekman layer, and the deep ocean (see Fig. 2 – not shown in detail). While impacts in the deep ocean most likely predominantly arise from a reduced strength of the surface wind stress forcing (which reduces the overall oceanic current strength), changes in the Stokes layer are dominated by Stokes drift and anti-Stokes forces, and changes in the Ekman layer consist of effects arising from reduced surface wind stress, anti-Stokes forces, and stratification changes due to wave-induced mixing. Consequently, to properly resolve the impact of waves on 3D particle dispersal simulations, the different vertical profiles of Stokes drift and horizontal wave-driven Eulerian currents need to be considered. Ideally, this also includes advanced formulations for the vertical Stokes drift profile that better account for swell, as described, for example, in Breivik and Christensen (2020). Moreover, the impact of surface waves on vertical particle velocities should be included in 3D Lagrangian dispersal simulations. This concerns changes in vertical velocities arising from the horizontal divergence of the resolved flow, as described in Eq. (7), as well as turbulent vertical motions responsible for wave-induced increases in mixing, such as Langmuir turbulence (see van Sebille et al., 2020, and references therein).

Further, it is important to note that throughout the paper, we use the term “surface” to refer to a circulation representative of the average over the upper meter of the water column (which corresponds to the thickness of the uppermost depth level in our model configuration). This is common for dispersal simulations that rely on ocean models covering scales larger than typical coastal and regional scales. However, Lagrangian velocities observed in the upper few centimeters of the water column may be significantly stronger compared to those averaged over the upper meter; this is due to the strong vertical shear of the Eulerian currents and Stokes drift, arising, for example, from microscale wave breaking and skin friction (Laxague et al., 2018). This implies that, strictly speaking, our results are not directly applicable to particles bound to the upper few centimeters of the ocean, such as those of non-emulsified and emulsifying oils, as well as macro- and mesoplastics. They are more representative of slightly submerged particles, such as microplastics, at 1 m depth.

5.3 Role of open-ocean Stokes drift in beaching

Finally, we would like to emphasize that – in contrast to what has been reported in various previous studies (Bosi et al., 2021; Delandmeter and van Sebille, 2019) – no significant beaching of particles occurred in our simulations, regardless of whether Stokes drift was added. This can be attributed to the fact that all the employed velocity fields (Eulerian currents and Stokes drift) are provided on the same grid, with zero velocities from ocean to land, and the particle-tracking scheme respecting this boundary condition. While a detailed analysis of this matter is beyond the scope of this paper, it calls for a reassessment of how realistic simulated Lagrangian particle-beaching statistics are if they include – or even fully rely on – beaching introduced by open-ocean Stokes drift provided on a non-matching grid with nonzero velocities from ocean to land. We suggest that adding open-ocean Stokes drift to the Eulerian current velocities of a large-scale ocean model should not result in particles leaving the ocean domain but should instead only change the probability of particles reaching and staying in the last ocean grid cells next to the coast. The beaching or grounding itself – if relevant for the type of particle under consideration – can then be obtained from a Lagrangian parameterization that accounts for all known unresolved processes occurring at the subgrid scale that are ultimately responsible for pushing particles ashore (Pawlowicz, 2021). There is an increasing number of, for example, marine plastic dispersal studies with basic implementations of this approach (Kaandorp et al., 2023; Liubartseva et al., 2018; van der Mheen et al., 2020; Onink et al., 2019; Vogt-Vincent et al., 2023; Ypma et al., 2022). Yet the existing grounding parameterizations still need further refinement and validation based on data from dedicated grounding experiments with customized surface drifters (Pawlowicz, 2021).

6 Conclusions

Returning to the two main research questions of our study, based on our idealized Lagrangian analyses using a newly developed high-resolution ($\mathrm{1}/\mathrm{24}$°) coupled ocean–wave model configuration for the Mediterranean Sea, we draw the following conclusions:

1. Stokes drift and wave-driven Eulerian currents can have a non-negligible impact on surface particle dispersal. They tend to act in opposing directions but do not necessarily offset one another due to differences in temporal variability and spatial variations.

2. If coupled ocean–wave model output is not available, applying the basic approximation of the wave impact via adding Stokes drift from a separately run wave model may not always be beneficial compared to not including any wave impact. However, the error in including only Stokes drift versus not including any wave impact varies both temporally and spatially and depends on the Lagrangian dispersal measure of interest. The benefit or disadvantage of applying the basic approximation is difficult to determine a priori.

More coupled ocean–wave model output – especially on longer and global scales – is needed to further quantify the time- and space-dependent relative impact of wave-driven Eulerian currents versus that of Stokes drift and to improve the accuracy of surface particle dispersal simulations.

Appendix A: Calculation of the contributions of Eulerian currents and Stokes drift to horizontal Lagrangian speed

For the coupled ocean–wave model, the contributions of Stokes drift and Eulerian currents to the horizontal Lagrangian speed ($∥{\mathit{u}}_{\mathrm{L}}^{\mathrm{c}}∥$) are obtained via scalar projections of the Stokes drift velocity (${\mathit{u}}_{\mathrm{S}}^{\mathrm{c}}$) and the horizontal Eulerian current velocity (${\mathit{u}}_{\mathrm{E}}^{\mathrm{c}}$) onto the total horizontal Lagrangian velocity vector (${\mathit{u}}_{\mathrm{L}}^{\mathrm{c}}$). These projections, denoted as ${\mathrm{comp}}_{{\mathit{u}}_{\mathrm{L}}^{\mathrm{c}}}{\mathit{u}}_{\mathrm{S}}^{\mathrm{c}}$ and ${\mathrm{comp}}_{{\mathit{u}}_{\mathrm{L}}^{\mathrm{c}}}{\mathit{u}}_{\mathrm{E}}^{\mathrm{c}}$, respectively (Fig. A1), are given by

$$\begin{array}{}\text{(A1)}& {\displaystyle }{\mathrm{comp}}_{{\mathit{u}}_{\mathrm{L}}^{\mathrm{c}}}{\mathit{u}}_{\mathrm{S}}^{\mathrm{c}}=∥{\mathit{u}}_{\mathrm{S}}^{\mathrm{c}}∥\cos \mathit{\alpha }={\displaystyle \frac{{\mathit{u}}_{\mathrm{L}}^{\mathrm{c}}\cdot {\mathit{u}}_{\mathrm{S}}^{\mathrm{c}}}{∥{\mathit{u}}_{\mathrm{L}}^{\mathrm{c}}∥}},\text{(A2)}& {\displaystyle }{\mathrm{comp}}_{{\mathit{u}}_{\mathrm{L}}^{\mathrm{c}}}{\mathit{u}}_{\mathrm{E}}^{\mathrm{c}}=∥{\mathit{u}}_{\mathrm{E}}^{\mathrm{c}}∥\cos \mathit{\beta }={\displaystyle \frac{{\mathit{u}}_{\mathrm{L}}^{\mathrm{c}}\cdot {\mathit{u}}_{\mathrm{E}}^{\mathrm{c}}}{∥{\mathit{u}}_{\mathrm{L}}^{\mathrm{c}}∥}},\end{array}$$

where α is the angle between ${\mathit{u}}_{\mathrm{S}}^{\mathrm{c}}$ and ${\mathit{u}}_{\mathrm{L}}^{\mathrm{c}}$ and β is the angle between ${\mathit{u}}_{\mathrm{E}}^{\mathrm{c}}$ and ${\mathit{u}}_{\mathrm{L}}^{\mathrm{c}}$. The scalar projection is positive if the angle is smaller than 90° and negative if the angle is larger than 90° and smaller than 180°, corresponding to increasing and decreasing contributions to $∥{\mathit{u}}_{\mathrm{L}}^{\mathrm{c}}∥$, respectively.

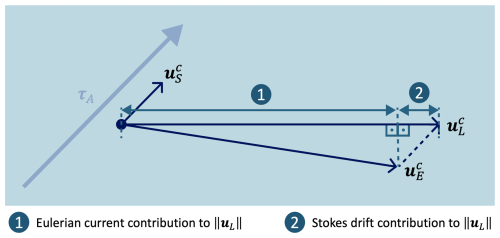
Figure A1 Derivation of the contributions of Eulerian currents and Stokes drift to the total horizontal Lagrangian speed (∥u_L∥) in the coupled ocean–wave model. The contributions of Stokes drift and Eulerian currents to the horizontal Lagrangian speed ($∥{\mathit{u}}_{\mathrm{L}}^{\mathrm{c}}∥$) are obtained via scalar projections of the Stokes drift velocity (${\mathit{u}}_{\mathrm{S}}^{\mathrm{c}}$) and the horizontal Eulerian current velocity (${\mathit{u}}_{\mathrm{E}}^{\mathrm{c}}$) onto the total horizontal Lagrangian velocity vector (${\mathit{u}}_{\mathrm{L}}^{\mathrm{c}}$). Stokes drift (${\mathit{u}}_{\mathrm{S}}^{\mathrm{c}}$) is approximately aligned with the atmospheric wind stress (τ_A), whereas ${\mathit{u}}_{\mathrm{L}}^{\mathrm{c}}$ and ${\mathit{u}}_{\mathrm{E}}^{\mathrm{c}}$ are deflected to the right of the wind (in the Northern Hemisphere).