What can seabirds tell us about the tide?

Small global positioning system (GPS) trackers are now routinely used to study the movement and behaviour of birds at sea. If the birds rest on the water they become “drifters of opportunity” and can be used to give information about surface currents. In this paper, we use a small data set from satellite-tracked razorbills (Alca torda) in the Irish Sea to test the potential of this idea for measuring tidal currents. Razorbills regularly rest on the sea overnight and their tracks at this time are consistent with their drifting with the tidal flows and changing direction as the flood turns to ebb and vice versa. Data from 4 years (2011–2014) have been binned in a geographical grid and analysed to give the variation of current over a mean tidal cycle in each grid element. A map of maximum current speed is consistent with a numerical model of the tidal currents in the region. The root mean square difference between observed maximum speed and that predicted by the model is 0.15 m s⁻¹, about 15 % of typical current speeds in the area. The divergence between bird-track speed and model prediction increases in regions of the fastest tidal currents. The method clearly has its limitations, but the results of this study show that tagged birds resting on the sea have potential to provide relatively inexpensive quantitative information about surface tidal currents over an extended geographical area.

1 Introduction

Passive surface drifters, tracked by shore radio or satellite, have been used to measure currents in the open sea for decades (Booth and Ritchie, 1983; Beardsley et al., 2004; Ohshima et al., 2002; Poulain, 2013). Tracked drifters are particularly useful for following a continuous current over a long distance. For example, drifters attached to a subsurface drogue have been used very successively to measure the geostrophic jet associated with tidal mixing fronts in shelf seas (Brown et al., 1999). Drifters also provide information on tidal currents, but this information is not always used as much as it could be: it is often seen as incidental to the main purpose of the drifter deployment. There is, however, renewed interest in measuring tidal currents – particularly fast tidal currents – to find the best sites to deploy tidal turbines (Lewis et al., 2015). In places where tidal currents are very fast, it is difficult and expensive to deploy traditional instrumented moorings. Additionally, a mooring can only provide data at one location, and tidal currents, especially in coastal waters, often vary greatly over short distances. A tracked drifter – or, better, a number of drifters – moving through an area of interest has the potential to provide valuable information about the spatial and temporal distribution of tidal currents in the region.

In recent decades, there have been great advances in using small electronic devices to monitor the behaviour and movement of seabirds (Burger and Shaffer, 2008). In the UK, the Royal Society for the Protection of Birds (RSPB) regularly uses global positioning system (GPS) tags attached to pelagic seabirds to study bird movement and feeding behaviour (Wakefield et al., 2017). The chosen bird is fitted with a GPS recorder small enough for the bird to carry on life much as usual. At the end of the experiment, the recorder is recovered and data, including time and position, are downloaded. During one of these studies (Kuepfer, 2012), it was noticed that, interspersed with the bird's flying routes, there were periods of several hours when the birds were moving in a regular pattern which was apparently related to the tide. The movement was in a straight line or slight curve at a speed which was too slow for flying. Crucially, the direction of movement changed at times when the currents in the area were expected to change from ebb to flood (or vice versa). The implication was that the birds were sitting on the sea surface (usually at night when they stop feeding) and drifting with the tide. There is clearly potential here to use these birds as novel “drifters of opportunity” to measure the speed and direction of tidal currents when they are sitting on the water.

Our aim in this study is to investigate this potential. We examine data from a colony of razorbills (Alca torda), a member of a family of birds called pursuit diving alcids, nesting on a small island off the coast of North Wales. Methods are developed for processing these data to give estimates of tidal current velocities. These are analysed to give the amplitude and phase of the currents, and these are compared to expected tidal currents generated by a numerical model.

2 Methods

2.1 The study site

This study uses data from razorbills tagged on Puffin Island, North Wales, during the breeding seasons (May to July) in the years 2011–2014. Puffin Island (latitude 53.32^∘ N, 4.03^∘ W) lies at the south-east corner of the larger island of Anglesey (Fig. 1). The water depth shoals from about 60 m in the west of the area to about 30 m in the east. The tidal currents in this region are fast: more than 1 m s⁻¹ on an average tide. The fastest currents are observed along the north coast of Anglesey, particularly in the north-west corner near the small island called the Skerries, an area which is currently of interest as a source of tidal current energy (Lewis et al., 2015).

The fast tidal currents create the large tidal range observed on the eastern shores of the Irish Sea, including those at Liverpool 70 km to the east of Puffin Island, where the tidal range can reach 9 m on a large spring tide. The tide in this northern part of the Irish Sea behaves, on the whole, as a standing wave. The currents flood towards Liverpool during the 6 lunar hours before high water and ebb away from Liverpool during the next 6 lunar hours. The currents turn throughout the region at about the times of high and low tide at Liverpool, although there are departures from this rule in places where tidal friction is great (Bowers, 2009).

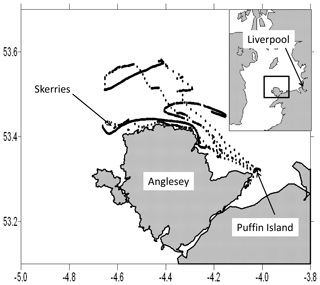
Figure 1 The study site and the track of one of the tagged birds over the period 17 to 21 May 2012. When the bird is flying from its base on Puffin Island the points are relatively widely spaced. When it is sitting on the water, they are closely spaced and the movement is consistent with that of travelling with the tide. Labels on axes show latitude in degrees north and longitude in degrees east. The inset map shows the position of the study area within the Irish Sea and relative to Liverpool, which lies 70 km east of Puffin Island.

2.2 Bird tracking

Razorbills breed in colonies and come ashore only during the breeding season. This study was concerned with a colony of birds on Puffin Island. Nesting occurs on rocky ledges and crevices, with parents taking turns brooding a single chick while the other parent is away foraging. Studies of other alcids have shown that the birds often stay out on the sea resting overnight (Harris et al., 2012; Wanless et al., 1990). It is thought to be part of a feeding regime in which the bird feeds to satisfy its own needs in the evening before resting and then foraging and returning to the nest with food in the early morning (Linnebjerg et al., 2015).

The data used in this study were collected by attaching packaged “igotU” GPS logger devices manufactured by Mobile Action Technology Inc. (Thailand) to the back feathers of captured birds using tesa tape. The loggers weigh approximately 16 g, including attachment material (approximately 3 % of the body weight of a typical razorbill) and, because they are minimally invasive, are not thought to affect the behaviour of the birds (Phillips et al., 2003). Data loggers were set to record position as latitude and longitude every 100 s with a positional precision of approximately 1000 mm. The loggers were retrieved after a period of 2–5 days, with a recovery rate of approximately 50 %. The sample data set used in this study consisted of records from 49 birds.

An example of the track of one of the birds, tagged from 17 to 20 May in 2012, is shown in Fig. 1. The track takes two forms. There are periods when the bird is moving to and from its nesting site on Puffin Island when the positions are spaced relatively far apart. At these times the speed of the bird is greater than the speed of any water current in the area and it must be flying. The birds fly fast. The maximum speed attained by the bird whose record is shown in Fig. 1 is about 20 m s⁻¹ or 40 knots. There is a second type of track shown in Fig. 1 in which the bird positions are much closer together and form straight or curved tracks. The speed at these times is less than 3 m s⁻¹, which is well below the minimum flight speed of 10 m s⁻¹ recorded for these birds (Pennycuick, 1997). It is notable that the motion along these tracks reverses at times which coincide approximately with the times of high and low tide at Liverpool. This behaviour is consistent with the bird sitting on the water and being carried by the tidal currents. The Irish Sea is close to resonance with the semi-diurnal tide, and diurnal tides are very small in comparison. The ratio of S₂ to M₂ is about 1∕3, so spring tidal currents (when M₂ and S₂ are added together) are about twice as great as neap currents.

The birds will not be perfect, passive drifters. They can paddle with their feet while sitting on the sea and they may “scoot” across the water by flapping their wings. Additionally, a significant portion of the bird's body will be above the water surface and the bird may be pushed along by the wind and the Stokes' drift motion of waves. Nevertheless, the regular nature of the tracks and the changes in direction at high and low tides suggest that further investigation is warranted to see if the motion is consistent with the tides in the area.

2.3 Data processing

The data recorded on the logger consist of a bird identification number, date and time, and latitude and longitude at an interval of approximately 100 s. Two consecutive positions can be used to calculate the velocity components u and v in the east–west and north–south directions by dividing the distance travelled by the time interval. Speeds greater than 5 m s⁻¹ (faster than any current in the area) were removed from the data set, as were observations close to the nesting site on Puffin Island when the bird could be on land. Of a total of 78 817 records, 5000 (6 % of the total) were discarded because the speed was too fast for a current and a further 26 148 (33 % of the total) because the bird was less than 1 nautical mile from its nesting site.

The data were averaged into 10 min intervals by taking the mean of six consecutive records. At this stage, individual readings which lay more than 1 standard deviation from the 10 min average were omitted from the averaging process. This was done in an attempt to cut out times when the bird might be scudding across the water. The processed data then consisted of 10 min values of u and v velocity components.

To fix the times of the currents relative to the tide at Liverpool, the data were time-stamped with the time of high water at Liverpool on the day of the observation. To allow for changes in current speed over the spring–neap cycle, the tidal range at Liverpool on the day of the observation was added to the data set. Speeds were multiplied by a factor f, equal to the mean tidal range at Liverpool for the whole data set (6.42 m) divided by the tidal range on the day. This scales the speeds to the value they would have when the tidal range at Liverpool has its mean value. The speeds can be considered to be equivalent to those of the principal lunar semi-diurnal tidal constituent, M₂.

The processed data consist of just under 7500 observations of the two velocity components u and v on a mean tide. The speed of the flow at any time and position can be calculated as the vector sum of the instantaneous u and v components. The direction of the current is given by taking the arc tangent of v∕u. Directions are given in degrees relative to east, so, for example, +45^∘ is a flow to the north-east and −45^∘ a flow to the south-east.

The observations are concentrated on the east and north coasts of Anglesey as Fig. 1 suggests. Occasionally, however, the birds will travel up to 40 nautical miles from their nesting site. To allow for the spatial variations of tidal currents in the area, the data were averaged into a grid of rectangular boxes. There is a trade-off when doing this. Smaller boxes give a higher spatial resolution but have fewer observations to analyse the bird movement to extract tidal information. We compromised on using boxes 0.1^∘ of latitude by 0.2^∘ of longitude (approximately 10 nautical miles or 18 km on a side). The minimum number of observations in these boxes was 27 (for the box located at the extreme north-east of the area, 53.7 to 53.8^∘ N and 3.6 to 3.8^∘ W). The maximum number of observations was 1365 in the box located at 53.4 to 53.5^∘ N, 4.0 to 4.2^∘ W.

The observations of the orthogonal velocity components on a mean tide, u and v, in each box were processed by fitting a sine curve with a period of 12.42 h, which is equal to that of the main lunar semi-diurnal constituent M₂, by least squares fitting. This procedure gives the amplitude and phase of the velocity components on a mean tide. The maximum speed of the current in each box can be calculated as the vector sum of the amplitudes of the u and v components.

A convenient way to express the phase of the currents is to note the time of the nearest slack water to high water at Liverpool. It is common in the Irish Sea for the current to turn at about the time of high and low tide at Liverpool. In the case of currents in an open seaway, however, there may not be a time when the current goes completely slack. The currents are not rectilinear but take the form of an ellipse. We therefore define the time of “slack water” as follows: the time of maximum current before Liverpool high water is determined by adding the u and v components of current velocity from the fitted curve at 1 min intervals over a tidal cycle. The time of slack water is then taken as one-quarter of a tidal cycle (3 h and 6 min) after the time of maximum current.

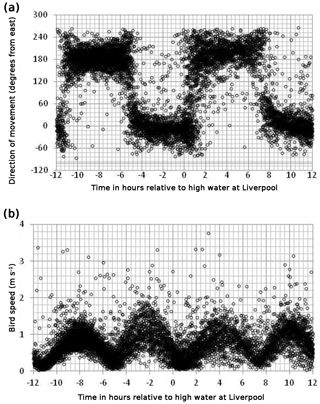
Figure 2 Direction (a) and speed (b) of bird movement relative to the time of high water at Liverpool. Directions are in degrees anticlockwise from east such that 0^∘ is due east and 180^∘ due west. Speeds have been normalised by the tidal range on the day so that the speed shown is that on an average tide – equivalent to M₂ speeds.

2.4 Comparison with a numerical model

To test the methods described above, the current speeds were compared to a numerical model of the depth mean tidal currents in the area. The output from the “fine” 1∕240th degree resolution grid (∼270 m spatial resolution) of the Regional Ocean Modelling System (ROMS) described in Lewis et al. (2015) was used for this purpose. The tidal constants determined from analysis of the ROMS-simulated velocities were used to simulate tidal currents in the same grid used for the bird data, and the amplitude of the principal lunar semi-diurnal tidal constituent (M₂) was noted in each grid element.

The model has been validated for both elevation (>10 tide gauges) and currents (>130 tidal current observations), including sites of fast tidal currents that are potential tidal energy sites (Lewis et al., 2017; Togneri et al., 2017). The computational domain of the Irish Sea ROMS model is based on Digimap bathymetry (interpolated to 1∕240^∘ spatial resolution) with 10 sigma depth layers and forced with FES2012 tidal data to simulate a 30-day period. The tidal constituents that produce the fortnightly spring–neap cycle (M₂ and S₂) were calculated using harmonic analysis of the ROMS-simulated tidal dynamics of this 30-day period (January 2014) with the t-tide MATLAB toolbox (Pawlowicz et al., 2002).

Figure 3 An example of curve fitting to bird velocity observations. The points show the east–west component of bird velocity in a box 53.5 to 53.6^∘ N, 4.4 to 4.6^∘ W (a different symbol is used for each bird). The continuous curve is a sine curve of period 12.42 h fitted to the data.

3 Results

3.1 Current speed and direction from all data

Taking the data set as a whole, the observations, filtered to remove times when the birds are flying (and scudding along the surface), are consistent with the movement of a bird sitting on the water and moving with the tide. Figure 2a shows the direction of movement plotted against the time of the observation relative to high tide at Liverpool on the day of the observation. Although there is a great deal of scatter, there are predominantly two directions of motion: one at about 0^∘ (due east), which lasts from about 5 h before high water at Liverpool to about 1 h after high water at Liverpool, and another at 180^∘ (due west), which is observed for the remainder of the tidal cycle. Figure 2b shows the speed of movement – the vector sum of the velocity components. Again there is a regular pattern apparent amongst the scattered points. Slack water occurs shortly after the time of high (and low) tide at Liverpool. There is a suggestion in this plot that the speeds in the 6 h before high water are greater than those in the 6 h after high water. We think that this difference is due to residual bird movement. The prevailing winds in the area are from the south-west and these will tend to speed up the bird during the flood tide and slow it down during the ebb. This effect can be removed when we carry out the analysis of the velocities: it will appear as a residual in that analysis.

Figure 4 Amplitude of the current speed (cm s⁻¹) in the study area on a mean tide. The amplitude shown is the vector sum of the east–west and north–south amplitudes. The crosses show the centres of the boxes used for drawing the contours.

3.2 Fitting curves to velocity components in boxed areas

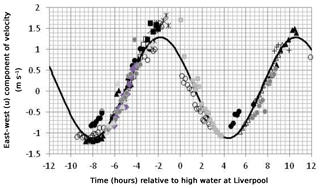
Figure 3 shows an example of how the east–west component (u, which is generally greater than the north–south component v in this area) of bird velocity changes with time, in this case in a rectangular box with limits 53.5 to 53.6^∘ N, 4.4 to 4.6^∘ W. The east–west velocity component of the different birds that visited this box is represented by different symbols and plotted against the time of the observation relative to high tide at Liverpool on the day of the visit. Each estimate of velocity has been scaled by the tidal range factor f to bring it in line with the velocity expected on a mean tide. The continuous curve is a sine curve with a period of 12.42 h that has the best fit (in a least squares sense) to the data. The amplitude of the u component of velocity for this box is 1.3 m s⁻¹ and R² for the fit is 0.92. The data from individual birds are mostly consistent although there is one bird (coded by the solid black circles) that appears to have a timing error of 1 h. This may be due to an incorrect setting of the logger clock. We have not tried to correct for such timing errors in this paper. In the case of Fig. 3, the discrepancy has little effect on the fitted curve.

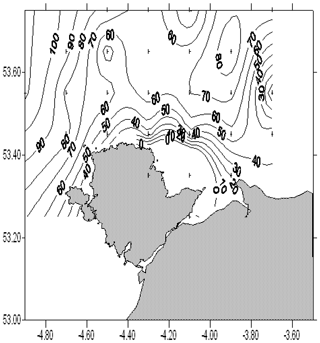
Figure 5 Current phase expressed as the time in minutes of the turn of the tide after high water at Liverpool. For a definition of the turn of the tide, see text.

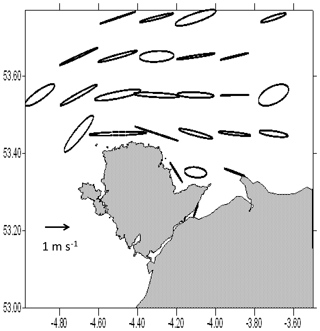
Figure 6 Tidal current ellipses derived from bird tracks. Each ellipse shows the path traced out by the current vector at mean tide about a point at the centre of each of the boxes used in the analysis. The scale is shown by the arrow. In most cases the current turns within the ellipse in a clockwise sense.

3.3 Maps of speed and phase

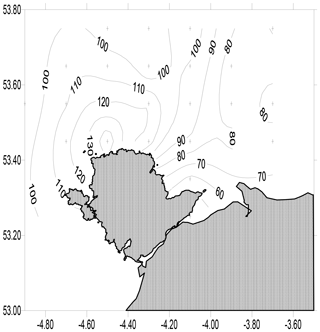
Figure 4 shows the speed of the currents in the area. The maximum speed in each rectangular box measuring 0.1^∘ of latitude by 0.2^∘ longitude is calculated as the vector sum of the amplitudes of the east–west and north–south components of velocity. This figure shows that the fastest currents in the area are found near the north-west corner of Anglesey; here speeds on a mean tide reach nearly 1.5 m s⁻¹.

Figure 5 shows the phasing of the currents expressed as the time of slack water (as defined above) relative to high water at Liverpool. Generally these phases have positive values: the current is still flooding at the time of high water at Liverpool and continues to flood for 1 h or so after that time. This behaviour is consistent with the effect of tidal friction and an incomplete reflection of the tidal wave at the coast. In the case of no friction and a perfect reflection, the tide in the area will be a standing wave and slack water will occur at the same time as high water everywhere. Friction reduces the amplitude of the reflected wave and the resulting tide has some progressive wave characteristics; in particular, the tide is still flooding weakly at the time of high water.

Figure 6 shows the current ellipses drawn from the u and v velocity components derived from the bird tracks in each box. These show the path traced out by the tip of the current vector over a tidal cycle. Most of the ellipses are almost rectilinear; the current flows back and forth along the same line, but in some areas a fatter ellipse is traced out by the current. In all cases but one, the vector moves around the ellipse in a clockwise sense. The exception is the most south-westerly ellipse located at 53.45^∘ N, 4.7^∘ W, in which the vector moves anticlockwise.

3.4 Comparison with numerical model

The estimates of current speed obtained from the bird tracks can be compared with those computed with a numerical model. The model produces depth-averaged currents and to compare these to the surface currents followed by the birds, the current amplitudes from the bird data were multiplied by a factor of 0.85 (Pugh, 1987). This figure is based on a power-law description of the current profile above the logarithmic layer, in which velocity increases as height above bed raised to the power 1∕m. For experimentally determined values of m in the range 5 to 7 the ratio of depth mean current to surface current is in the range 0.83 to 0.88,

Figure 7 shows a comparison between the bird-estimated current amplitudes and the output of the model. The agreement is generally good although the observations are lower than the model-predicted amplitudes in the areas of the fastest currents. We return to this point in the Discussion section. The root mean square (RMS) difference between observed and model speed is 0.15 m s⁻¹. In an area where currents are typically 1 m s⁻¹, this error is about 15 % of the observed current. There is one point, marked with an arrow on Fig. 7, which is particularly anomalous. This is from a grid element centred on 4.7^∘ W, 53.45^∘ N in which the data coverage is poor. There are just 35 observations of bird speed in this box and the observations are bunched in time, rather than evenly spread over a tidal cycle. This makes it difficult to fit a curve accurately to these data (and lowers the statistical significance of the fit). If this point is omitted, the RMS difference between observations and model is reduced to 0.12 m s⁻¹.

4 Discussion

As far as we are aware, this paper is the first to describe the use of tagged seabirds for measuring currents of any kind. It is an example of using data opportunistically. The reason for tagging the birds is to study their behaviour, but as an unexpected by-product, we obtain information about surface currents when the birds rest at sea.

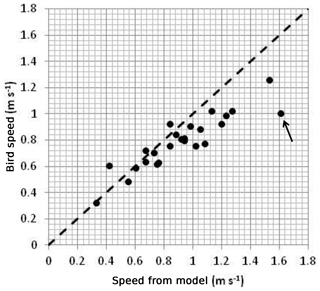
Figure 7 Plot of maximum bird speed in grid elements against maximum speed from the model of Lewis et al. (2015), both at mean tidal range. The dashed line represents a perfect fit. The point marked with an arrow is discussed in the text. The bird speeds have been adjusted to an average over the water depth by multiplying by a factor of 0.85 in order to match the model.

The method certainly has weaknesses. The birds and loggers used in this study provide information only about surface currents. We have no control over where the birds go, so the data will be sparse in some areas and at some times. The birds will be subject to wind drift while sitting on the water and they may also paddle, so they are not truly following the water flow. Some of these problems can be addressed as the data set grows. The gaps in the data will be filled as more information is gathered (bearing in mind that studies involving wild birds are licenced procedures and will also always need to be rigorously justified on welfare grounds).

Anomalous behaviour can be identified and eliminated, especially in the case of tidal currents which follow a repeating pattern. Moreover, the method has definite strengths. It is relatively inexpensive and there are very few methods for gathering data about surface tidal currents over a wide geographical area (HF radar and ship surveys will provide this information, but at a much greater cost).

We made the point in the Introduction that seabirds might be particularly useful for providing information about tides in places where tidal currents are fastest and there is potential for using the currents to generate electricity. There is, however, a possible conflict of interest here. Birds may be visiting areas with fast currents because they are important feeding grounds for them (Benjamins et al., 2015). Many of these birds come from protected colonies on land and this protection extends to their activity at sea. It is also possible, however, that better understanding the birds' interaction with tides may mean we can anticipate their use of the tidal cycle better and mitigate any potential negative impacts. For example, some wind farms are switched off during peak times in the day when migrating birds pass through an area.

The comparison between the speed amplitudes from bird tracks and model output (Fig. 7) is best in areas where the currents are less than about 1 m s⁻¹ (Fig. 7). At higher speeds, the bird data consistently underestimate the current predicted by the model. It is possible that the model is wrong at these higher speeds, although this seems unlikely as it has been tested against observations from current meters. The other possibility is that there is a fault in estimating the amplitude of the current from the bird track which manifests itself in areas of very fast currents. In Fig. 3, for example, the fitted curve does not capture the very highest speeds at about 2 h before high tide. We tested to see if adding a diurnal tidal constituent to the curve fitted to the observations of bird speed would improve matters, but the diurnal currents here are small (of the order of a few cm s⁻¹) and there was no noticeable improvement in the fit.

Another possibility is that the factor for converting surface currents to depth mean currents becomes higher at higher current speeds. As the current speed increases, the velocity profile will change as the higher turbulence becomes more effective at transferring the effect of bottom friction upwards. We have multiplied the surface currents from the bird data by a constant conversion factor of 0.85 to convert them to a depth mean current. The correct conversion factor may be higher than this in the regions of fastest currents. However, it is hard to imagine that it would be much higher. The absolute maximum is 1.0 and realistically it is unlikely to be greater than 0.9 (Davies, 1990). Variability in the conversion factor does not seem to be enough to bring the observations in line with the model at the higher speeds in Fig. 7. The difference between the bird data and the model at the higher speeds remains something for future research.

The work in this paper can be regarded as a pilot study aimed at testing the potential of a novel method. There are obvious improvements that could be made. Using a single semi-diurnal harmonic (adjusted for the spring–neap cycle) is a first step in the analysis. As the data set grows more exact methods of analysis using several tidal constituents can be developed. Data quality can be improved by referring to wind speed records and excluding bird-track data during periods of high wind speed.

In summary, the results of this pilot study have shown that tagged seabirds have the potential to provide relatively inexpensive quantitative information about surface tidal currents over limited geographical areas.